交错轴双滚子包络环面蜗杆传动啮合分析
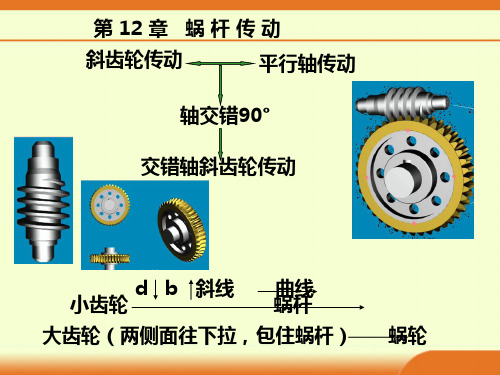
《机械设计》第12章 蜗杆传动
阿基米德蜗杆：αx=20°
标准值
法向直廓蜗杆、渐开线蜗杆：αn=20°
s
pz=zpx1 px1
2.蜗杆导程角γ和分度圆直径d1 螺纹
蜗杆
ψ πd1
tanψ =
s πd1
=
np πd1
∴ d1
=
Z1 tanγ
m
=
qm
γ πd1
tanγ
=
pZ πd1
=
πmZ πd1
1
=
mZ 1 d1
q
=
Z1 tanγ
具有良好的减摩性、耐磨性、跑合性和抗胶合能力
特点：软硬搭配
蜗杆硬：优质碳素钢、合金结构钢 经表面硬化及调制处理
蜗轮软：铸锡青铜、无锡青铜、灰铸铁
1、蜗杆材料
蜗杆一般采用碳素钢或合金钢制造。 对于高速重载的传动，蜗杆常用低碳合金钢， 如20Cr，20CrMnTi等，经渗碳淬火，表面硬度 HRC56～62，并应磨削。
MPa
= 12.86MPa < [σ F ]
齿根的弯曲疲劳强度校核合格。
（5）验算传动效率h
蜗杆分度圆速度为
v1
=
π d1n1
60×1000
=
3.14×112×1450 60×1000
m/
s
=
8.54m /
s
vs
= v1
cosλ
8.54
=
m / s = 8.59m / s
cos6.412°
查表4.9得
ρ v = 1°09′(1.15°)
h
(0.95
~
0.97)
tan tan( v)
H
480 d2
对滚柱包络环面蜗杆传动机构的一点思考
间隙 ， 为两节 蜗杆 问的相 互 转 动 ， 整异 常方 便快 捷 等 Ｊ 而 调 等 。本文 主要 介 绍一 种新 兴 的蜗 杆 传动 结 构—— 滚 柱包
络环 面蜗 杆传 动 机构 。该机 构最 早南 日本 三共 株 式会社 研 制 ，日前 已在 日本 ＭＡ Ａ Ｚ Ｋ公 司的 Ｉ Ｔ Ｒ Ｅ ｌ 系 Ｎ Ｅ ＧＲ Ｘ Ｉ ｌ
的 ～步 难 广 用 提 口 应 ７费 一 ｜ ｜ －毒誊 ｜｜ ｜ － ０｜ ≯ｌ｜ 掌 ；
关 臻０ 宫络 面掰 ｔ荸岔７ 笙 进蘑 囊 瘸厦 持 ｜ ｜ｊ｜ ｜ ｜ 一 祭 ０｜ ｜ ｌ ｜ 中图分类号： Ｈ１２４ 。－ ÷ Ｔ ３ ．４ － ０文献标识码 ． Ａ 文章编号： ０ ２ ２ ３ （ ０ ｏ １＿ １６ ０ １０ 謦 ３ ３ ２ １ Ｏ Ｏ ３ ￣ ２ １
滚 柱包 络 环 面 蜗 杆 传 动 机 构是 以 网柱 滚 子为 蜗 轮 轮
齿 ，通 过 柱 面 包络 生 成 环 而
｜一 爱 ＿＼
赢 １ ５ ０
２ 传动 结构 、 理 原
醴１ ∞
∞
墅 ！
～
’
・
．
．
测 试 ） ／ｇ Ｊｋ
蜗 杆 的一 种 新 型 减速 传 动 机 构 。该 结 构 传 动平 稳 、精 度 高 ，且 由于 蜗 轮 轮齿 为柱 而 滚 动轴 承 ，其 与蜗 杆 齿 而间
尽管此机构具备 以上优点 ， 由于其结构的特殊性 ， 但
更趋明显 ，但在间隔等分的使用场合却无法与蜗轮蜗杆
另 受 使其无法实现对大传动比结构所需要的紧凑体积 ，因此 式 转 台相 比。 外此 类机 构在 推广 应 用 方而 ， 其高 价格
蜗轮蜗杆参数_蜗轮蜗杆传动特点
蜗轮蜗杆基本参数模数m、压力角、蜗杆直径系数q、导程角、蜗杆头数、蜗轮齿数、齿顶高系数（取1）及顶隙系数（取0.2）。
其中，模数m和压力角是指蜗杆轴面的模数和压力角，亦即涡轮端面的模数和压力角，且均为标准值；蜗杆直径系数q 为蜗杆分度圆直径与其模数m的比值。
蜗杆传动的三大种类及特点一、圆柱蜗杆1、普通圆柱蜗杆（1）阿基米德蜗杆：这种蜗杆，在垂直于蜗杆轴线的平面（即端面）上，齿廓为阿基米德螺旋线，在包含轴线的平面上的齿廓（即轴向齿廓）为直线，其齿形角α0=20°。
它可在车床上用直线刀刃的单刀（当导程角γ≤3°时）或双刀（当γ》3°时）车削加工。
安装刀具时，切削刃的顶面必须通过蜗杆的轴线。
这种蜗杆磨削困难，当导程角较大时加工不便。
（2）渐开线蜗杆：渐开线蜗杆（ZI蜗杆）蜗杆齿面为渐开螺旋面，端面齿廓为渐开线。
加工时，车刀刀刃平面与基圆相切。
可以磨削，易保证加工精度。
一般用于蜗杆头数较多，转速较高和较精密的传动。
（3）法向直廓蜗杆：这种蜗杆的端面齿廓为延伸渐开线，法面（N-N）齿廓为直线。
ZN蜗杆也是用直线刀刃的单刀或双刀在车床上车削加工。
车削时车刀刀刃平面置于螺旋线的法面上，加工简单，可用砂轮磨削，常用于多头精密蜗杆传动。
（4）锥面包络蜗杆：这是一种非线性螺旋曲面蜗杆。
它不能在车床上加工，只能在铣床上铣制并在磨床上磨削。
加工时，盘状铣刀或砂轮放置在蜗杆齿槽的法向面内，除工件作螺旋运动外，刀具同时绕其自身的轴线作回转运动。
这时，铣刀（或砂轮）回转曲面的包络面即为蜗杆的螺旋齿面，在I-I及N-N截面上的齿廓均为曲线。
这种蜗杆便于磨削，蜗杆的精度较高，应用日渐广泛。
2、圆弧圆柱蜗杆圆弧圆柱蜗杆传动和普通圆柱蜗杆传动相似，只是齿廓形状有所区别。
这种蜗杆的螺旋面是用刃边为凸圆弧形的刀具切制的，而蜗轮是用范成法制造的。
在中间平面（即蜗杆轴线和蜗杆副连心线所在的平面）上，蜗杆的齿廓为凹弧，而与之相配的蜗轮的齿廓则为凸弧形。
大锥面二次包络环面蜗杆副传动的啮合特征及其应用
也可偏置安装（未画出）。a为蜗杆副中心为蜗轮分度圆 直径， T为蜗轮分度圆压力分别为蜗杆喉部齿根圆直径和 分度圆齿槽宽， r为砂轮半径，为砂轮安
装倾角。砂轮安装位置：在工作台上的其它两个坐标的 安装位置根据需要可取一较小值（即偏置安装）以使加 工的蜗杆副具有更好的啮合状态，但在一般情况下
总取为零。砂轮齿形角式中T砂轮齿顶宽为：ΔS为蜗杆单 侧磨削时所留倒隙。2. 3活动标架的建立以及相对速度、 角速度在活动标架上的投影活动标架法
e ]为与蜗杆固连的标架1， e ]为与第一作者：万方美，男， 34岁，工程师（博士研究生） ，重庆大学机械传动国家 重点实验室（ 40004
4）工作台固连的标架2.h和h分别为工作台与蜗杆的转角， 在h与e重合。2. 2砂轮齿廓形状和加工安装位置通过蜗杆 喉部齿槽对称位置时砂轮在加工
坐标系中的各位置参数。O和O分别为蜗杆轴线和产形轮 （工作台）回转轴线的公垂线的垂足， O为砂轮轴回转 中心， O在O中的位置系如图b，根据需要
便，只需进给磨头至能磨出整个蜗杆齿深即可，不必增 加任何附助调整装置。5结论大锥面二次包络环面蜗杆副 具有与平面二包相似的啮合性能，即同时双线多
齿接触，根据计算结果得知其接触区域尤其是一次包络 较平面二包要小。但随着工具砂轮半径增大，其接触区 域有所增加，在r时很接近于平面二次包络的接触
区域。大锥面二包的相对卷吸速度，接触线与相对速度 的夹角较平面一包的该平均值稍大，其加工性能要比平 面二包好，蜗杆磨削效率比平面包络蜗杆磨削效率
方程根据文献[1 ]的啮合理论，蜗杆齿面加工的啮合方程 为将式（ 6）与式（ 2）联立并将其转换到蜗杆齿面坐标 e中即得蜗杆齿面方程表达式（ 2
）2. 5第一次包络各啮合性能参数的计算根据文献[1， 2]， 且考虑到h令k二界曲线的表达一界曲线的表达为接触线 法线方向的诱导法曲率为相对速
环面蜗杆珩齿啮合分析及实现
当它 固溶于奥 氏体 中时 ． 高钢的淬透 性作 用很强 。 提
但是 对于化合钛 ， 由于其 细微 颗粒形成 新相 的晶核 ． 从 而促 进奥 氏体 分解 ， 因此降 低了钢 的淬透性 。 另外 ． 然 我国 在一 般 工程 用硬 齿 面减 速机 中 虽 很 少使用 含镍渗碳 钢 ， 们 也着 重分 析一 下 镍元 素 我
中图号 ：Ｔ ６ Ｇ１ 在传统 的齿 轮珩齿 加工工 艺 中， 蜗杆 式 珩齿 具 文献 标识 码 ：Ｂ
１ 环 面蜗杆珩齿 原理
如图 １ 所示 ． 原理 为 ： 其 把一 个与被加 工齿 轮 完
有生 产率高 、 产成本 低及 修正误差 能力 强等优点 ， 生 因此在生 产 中被广 泛采 用 。 但随着工 业 的发 展 ， 硬 对
与钢 中杂质硫 形 成 熔 点 较 高 的 Ｍ Ｓ 可 防 止 因 Ｆ ｓ ｎ． ｅ 而导致 的热脆现 象 。 元 素还 可 以 降低 钢 的下 临界 锰
点． 增加 奥 氏体冷 却时 的过 冷度 ， 细化 珠 光体组织 以 改善机 械性能 ， 高钢 的淬透 性 ， 提 但锰 元 素有增加晶
粒 粗化和 回化脆性 的不 利倾 向。 因此 ， 锰渗 碳锕在 含 锻前 下料时 不易采 用 气割 下 料 ， 以防 止材 料 的过 热 或过 烧现象 出现。 在有 些 渗碳 钢 中还含有 铝 元 素或 钛 元素 ， 钼元
８ ）为解 决 这 一 问题 ， 们提 出了环 面 蜗 杆珩 齿 加 ８。 我
工 工艺 。
等 。 类 材 料经 表 面 处 理 后 强 度 很 高 ， 面 耐磨 性 这 表 好 。 渗碳 钢 中最 好的钢 种 ， 用于 制造承受重 载和 是 常
环面蜗杆传动啮合理论研究进展-论文
环面蜗杆传动的设计和应用,肇端于文艺复兴时 期意大利著名学者列奥纳多达芬奇(1452 ~ 1519 年) 的工作。 在他设计的一种闹钟的执行机构中,采用了 如图 1 所示的环面蜗杆传动装置[2] 。
从达·芬奇的天才设想开始, 历经了几个世纪
0摇 引摇 言
分度曲面是圆环面的蜗杆被称为环面蜗杆,环面 蜗杆和与之相配合的蜗轮( 特殊条件下,可用圆柱齿 轮代替)形成环面蜗杆副[1] 。
长期的科学研究和生产实践表明,环面蜗杆传动 不但承载能力大、传动效率高,而且使用寿命长,工作 平稳,噪声小,是公认的优秀重载蜗杆传动之一,被广 泛应用于众多重载机械,例如冶金机械,建筑机械,以 及起重机械和运输机械等。
1951 年,日本学者佐藤发明了斜平面蜗轮副,如 图 5 所示。 其应用范围可以从大传动比向中、小传动 比扩展。 斜平面蜗轮的齿面,与上述平面蜗轮相同, 仍为平面,但齿线相对于蜗轮轴线倾斜一定角度。 这 种传动虽然制造简便,蜗杆蜗轮都能磨削展成,但就 承载能力和润滑性能而言,并没有直廓环面蜗杆传动 优越。
和标准传动中的蜗轮相类似,修形传动中的蜗 轮,也由与修形蜗杆一致的环面滚刀范成,所以修形 传动仍旧是线接触传动,且能在一定程度上,实现多 齿双线接触。
可以实现多齿双线接触,是环面蜗杆传动的固有 优点,但是,这也导致了齿间多余约束的产生,使得环 面蜗杆副对各种变形和误差较为敏感。 这也是环面 蜗杆副的一个主要不足之处。
分度曲面是圆环面的蜗杆被称为环面蜗杆环面蜗杆和与之相配合的蜗轮特殊条件下可用圆柱齿轮代替形成环面蜗杆副长期的科学研究和生产实践表明环面蜗杆传动不但承载能力大传动效率高而且使用寿命长工作平稳噪声小是公认的优秀重载蜗杆传动之一被广泛应用于众多重载机械例如冶金机械建筑机械以及起重机械和运输机械等
《机械设计基础》第12章 蜗杆传动
3、摩擦磨损问题突出，磨损是主要 的失效形式。为了减摩耐磨，蜗轮齿圈常需用青铜制造，成本较高；
4、传动效率低，具有自锁性时，效率低于50%。
由于上述特点，蜗杆传动主要用于传递运动，而在动力传输中的应用受到限制。
其齿面一般是在车床上用直线刀刃的 车刀切制而成，车刀安装位置不同， 加工出的蜗杆齿面的齿廓形状不同。
γ
β
γ＝β （蜗轮、蜗杆同旋向）
一、蜗杆传动的主要参数及其选择
1、模数m和压力角α
§12-2 蜗杆传动的参数分析及几何计算
ma1= mt2= m αa1=αt2 =α=20°
在蜗杆蜗轮传动中，规定中间平面上的模数和压力角为标准值，即：
模数m按表12-1选取，压力角取α=20° （ZA型αa＝20º；ZI型αn＝20º） 。
阿基米德蜗杆（ZA蜗杆） 渐开线蜗杆（ZI蜗杆）
圆柱蜗杆传动
环面蜗杆传动
锥蜗杆传动
其蜗杆体在轴向的外形是以凹弧面为母线所形成的旋转曲面，这种蜗杆同时啮合齿数多，传动平稳；齿面利于润滑油膜形成，传动效率较高。
同时啮合齿数多，重合度大；传动比范围大(10~360)；承载能力和效率较高。
三、分类
在轴剖面上齿廓为直线，在垂直于蜗 杆轴线的截面上为阿基米德螺旋线。
§12-5 圆柱蜗杆传动的强度计算
一、蜗轮齿面接触疲劳强度的计算
1、校核公式:
2、设计公式:
式中：a—中心距，mm；T2 —作用在蜗轮上的转矩，T2 = T1 iη； zE—材料综合弹性系数，钢与铸锡青铜配对时，取zE=150；钢与铝青铜或灰铸铁配对时， 取zE=160。 zρ—接触系数，由d1/a查图12-11，一般d1/a=0.3~0.5。取小值时，导程角大，故效率高，但蜗杆刚性较小。 kA —使用系数，kA =1.1~1.4。有冲击载荷、环境温度高(t>35oC)、速度较高时，取大值。
滚子包络环面蜗杆传动副接触特性分析
滚子包络环面蜗杆传动副接触特性分析
王文韬;陈燕
【期刊名称】《科技创新与应用》
【年(卷),期】2024(14)3
【摘要】建立滚子包络环面蜗杆传动副的数学模型和三维精确实体模型,在传动比和中心距确定的情况下,分析不同蜗杆喉部最小直径、滚子直径对传动副的齿面接触特性,探讨中心距误差、蜗杆轴向误差、蜗轮轴向误差和轴交角误差4类装配误差对传动副齿面啮合侧隙的影响规律。
结果表明,蜗杆喉部最小直径、滚子直径的变化会影响齿面等效应力,最大等效应力随蜗杆喉部最小直径的变化呈“V”字形;中心距误差、蜗杆轴向误差会导致传动副齿面法向出现啮合间隙或过盈情况。
蜗轮轴向误差、轴交角误差对传动副的齿面啮合区影响不大,但会出现一侧过盈增加、一侧过盈减少的现象,因此应将装配误差控制在一定范围内。
【总页数】4页(P102-105)
【作者】王文韬;陈燕
【作者单位】深圳市蓝蓝科技有限公司;重庆商务职业学院人工智能学院;四川大学空天科学与工程学院
【正文语种】中文
【中图分类】TH122
【相关文献】
1.倾斜式双滚子包络环面蜗杆传动热弹流润滑分析
2.并列倾斜式双滚子包络环面蜗杆传动啮合理论分析
3.滚子包络环面蜗杆传动副装配误差分析
4.倾斜式双滚子包络环面蜗杆传动几何特性分析
5.修形滚子包络环面啮合蜗杆传动啮合理论分析
因版权原因，仅展示原文概要，查看原文内容请购买。
第9讲-蜗杆传动分析
2.蜗杆导程角(是指蜗杆分度圆柱面)
蜗杆导程角
tg g
=
z1 px
pd1
=
z1p m pd1
= z1 m d1
在其他条件相同的情况下， g 越大则传动效率越
高，但考虑到 g 太大时，效率增量小而制造较困难， 因此在动力传动中，g 角的一般范围为：g =15～30 0
3.蜗杆的分度圆直径d1和直径系数q
应用 中小功率的动力传动或操纵机构中。一般：
P 50 kw v 15 m s i 5～80
二. 蜗杆传动的类型 蜗杆分类：根据蜗杆母体形状蜗杆可分为圆柱蜗杆，环 面蜗杆和锥蜗杆三类。
圆柱蜗杆最为常用，本章介绍圆柱蜗杆。 蜗杆还可以分为左旋右旋、单线和多线; 常用的是右旋蜗杆；蜗杆的线数就是蜗杆的齿数。
开式传动的主要失效形式为疲劳断齿和磨损，因 此应进行轮齿弯曲疲劳强度计算。
此外因蜗杆传动可分离性差，一般还应校核蜗杆 的刚度；蜗杆传动结构紧凑，效率较低，发热严重， 一般还应进行热平衡计算。
一. 接触疲劳强度和弯曲疲劳强度计算
计算原理与齿轮传动相同，影响强度的因素也大 致一样。接触强度和弯曲强度的计算公式分别为：
§3 蜗杆传动的失效形式、材料和结构
材料 蜗杆副材料要求：减摩、耐磨、抗胶合。
蜗杆是细长件，一般采用中碳钢、中碳合金钢调 质处理或低碳合金钢渗碳淬火。硬表面蜗杆能充分发 挥材料的潜能，值得提倡，但是必须要有专用的磨削 设备。
蜗轮常用铸造青铜。滑动速度大应采用含锡量大 的锡磷、锡锌铅青铜（价格相应也贵）；滑动速度较 小时可采用不含锡的铝铁青铜或黄铜；低速重载情况 下，也可采用铸铁。
4.齿数和传动比
蜗杆齿数z1少，传动比大，但效率低；齿 数多，效率高，但太多会导致加工困难，故蜗
包络环面蜗杆传动的实体建模和几何分析
包络环面蜗杆传动的实体建模和几何分析包络环面蜗杆传动是一种常用于输送、提升、开合装置等机械传动的机构。
该机构由环面蜗杆和包络面蜗轮组成，通过蜗杆的旋转驱动蜗轮的运动，从而实现传动功能。
在实体建模和几何分析方面，可以采用计算机辅助设计（CAD）软件进行建模和分析。
实体建模是指将机构的各个零件通过计算机软件建立几何模型的过程。
在包络环面蜗杆传动中，需要建立环面蜗杆和包络面蜗轮的几何模型。
首先，需要准确测量和获得蜗杆和蜗轮的尺寸数据。
然后，可以使用CAD软件中的绘图工具，根据尺寸数据进行绘图，建立几何模型。
在建模过程中，可以使用各种工具和技术，如绘制线段、圆弧、建立实体、填充颜色等，将蜗杆和蜗轮的几何形状表达出来。
建模的核心目标是准确地表达出蜗杆和蜗轮的形状，以便后续的几何分析和仿真。
几何分析是指对机构几何形状进行分析和计算的过程。
在包络环面蜗杆传动中，需要进行的几何分析主要包括齿轮传动参数的计算和齿面接触的分析。
齿轮传动参数包括模数、齿数、齿宽、分度圆直径等，可以根据需要进行计算和调整，以满足设计要求。
齿面接触分析主要是通过计算齿轮的接触应力、接触应力集中系数、接触疲劳寿命等参数，评估齿轮的强度和寿命。
几何分析的目标是确定齿轮传动参数的合理范围，以及验证齿轮的强度和寿命是否满足设计要求。
在进行包络环面蜗杆传动实体建模和几何分析时，需要注意以下几点。
首先，需要准确获取蜗杆和蜗轮的尺寸数据，以确保建模和分析的准确性。
其次，需要熟练掌握CAD软件的绘图和建模工具，以便能够高效地建立几何模型。
同时，还需要具备一定的机械传动知识和分析方法，以便能够进行准确的几何分析和评估。
最后，需要对建模和分析结果进行验证和修正，确保设计的准确性和可靠性。
总之，包络环面蜗杆传动的实体建模和几何分析是一项重要的工作，对于传动机构的设计和优化起到了关键作用。
通过建立几何模型和进行几何分析，可以评估和改进传动机构的性能和寿命，提高其可靠性和效率。
新型球面包络环面蜗杆副的啮合效率分析
新型球面包络环面蜗杆副的啮合效率分析
陈厚军;蔡雄;刘健
【期刊名称】《机械传动》
【年(卷),期】2012(36)12
【摘要】新型球面包络环面蜗杆副是一种以蜗杆、钢珠和蜗轮为主的活齿传动技术。
根据传动原理和齿形特征,在考虑摩擦力和摩擦力矩的情况下,以钢珠为分离体进行速度分析和受力分析;在此基础上,推导新型环面蜗杆副的啮合效率计算公式,分析设计参数对效率的影响规律,并通过原型机的效率测试来验证啮合效率公式的可靠性。
【总页数】6页(P75-79)
【关键词】环面蜗杆副;球面啮合件;啮合效率
【作者】陈厚军;蔡雄;刘健
【作者单位】南通大学机械工程学院;大连理工大学机械工程学院
【正文语种】中文
【中图分类】TH132.44
【相关文献】
1.无侧隙平面一次包络端面啮合环面蜗杆副弹流润滑分析 [J], 杨捷;王进戈;陈守安;邓星桥;李金宽
2.新型滚动式球面包络点啮合环面蜗杆传动啮合方程与效率 [J], 王其超;肖正扬
3.球面二次包络环面蜗杆传动的啮合原理与啮合性能 [J], 郜庆路;王小林;王森;李
志卫
4.双圆环面二次包络环面蜗杆传动的啮合界线与蜗杆螺旋面的结构 [J], 赵亚平
5.滚动圆锥面包络环面蜗杆副传动的啮合效率 [J], 龚国贤;朱雅兰
因版权原因，仅展示原文概要，查看原文内容请购买。
环面蜗杆传动设计与修形
环面蜗杆传动设计与修形环面蜗杆传动是一种常用的传动形式，它由蜗轮和蜗杆组成。
蜗轮是一个圆柱面，其外侧表面的齿轮形状称为蜗牙；而蜗杆则是一个螺旋型的圆柱体，其表面也有相应的齿轮形状。
环面蜗杆传动通过蜗杆的螺旋运动使蜗轮旋转，从而实现传动功能。
环面蜗杆传动具有一些优点，例如传动比大、承载能力强、传动效率高，并且不易反转。
因此，在一些需要大传动比和稳定传动的场合，环面蜗杆传动被广泛使用。
例如在工程机械、船舶、电动机等领域。
在设计环面蜗杆传动时，需要考虑以下几个方面：1.传动比的选择：传动比是指蜗杆传动输出转速与输入转速之间的比值。
一般来说，传动比越大，扭矩越大，但转速越低。
在选择传动比时，需要根据实际需求来确定。
2.蜗杆和蜗轮的材料选择：蜗杆通常采用硬度较高的材料，如合金钢或铸铁，并进行热处理以提高硬度和耐磨性。
蜗轮则可以选择材料硬度较低的铸铁或铜。
材料的选择要考虑到传动的工作环境和要求，以确保传动的可靠性和寿命。
3.齿轮参数的计算：设计中需要计算蜗杆和蜗轮的齿轮参数，包括模数、压力角、齿数等。
这些参数的选择要根据传动设计的要求和性能指标来确定。
同时，还要考虑到齿轮的强度和齿面接触疲劳寿命的要求。
4.修形及润滑：在实际应用中，为了提高蜗杆传动的效率和寿命，需要对蜗杆和蜗轮进行修形。
修形是通过改变蜗轮外侧齿轮的形状，使其能够更好地适应蜗杆的螺旋形状，减小齿轮与蜗杆之间的接触应力和表面磨损。
同时，对传动进行适当的润滑，可以减少摩擦和磨损，提高传动效能。
总之，设计和修形环面蜗杆传动需要综合考虑传动比、材料选择、齿轮参数计算、修形和润滑等因素。
只有在合理的设计和施工过程中，才能确保环面蜗杆传动的可靠性、高效性和耐用性。
滚锥包络端面啮合蜗杆传动啮合性能分析
Journal of Mechanical Strength2023,45(4):931-938DOI :10.16579/j.issn.1001.9669.2023.04.024∗20211213收到初稿,20220323收到修改稿㊂教育部春晖计划项目(Z2015105),西华大学自然科学基金项目(Z1420208)资助㊂∗∗文渝杰,男,1999年生,四川达州人,汉族,西华大学硕士研究生,主要研究方向为机械设计与传动㊂∗∗∗柳在鑫(通信作者),男,1978年生,湖北黄梅人,汉族,西华大学副教授,博士,硕士研究生导师,主要研究方向为机械设计与传动㊂滚锥包络端面啮合蜗杆传动啮合性能分析∗MESHING PERFORMANCE ANALYSIS OF TAPERED ROLLERENVELOPING END FACE MESHING WORM DRIVE文渝杰∗∗㊀廖鸿辉㊀柳在鑫㊀李玲玉(西华大学机械工程学院,成都610039)WEN YuJie ㊀LIAO HongHui ㊀LIU ZaiXin ㊀LI LingYu(School of Mechanical Engineering ,Xihua University ,Chengdu 610039,China )摘要㊀滚锥包络端面啮合蜗杆传动,该传动副的优点为同时啮合的齿对数多和可消除间隙等㊂根据齿轮啮合原理和微分几何原理建立该传动副的啮合数学模型,从而得到该传动副的啮合函数和蜗杆齿面方程,再推出啮合性能的计算公式,运用Matlab 软件分别分析滚锥小端半径㊁喉径系数及滚锥半锥角对该传动副啮合性能评定参数 诱导法曲率㊁润滑角㊁相对卷吸速度和自转角的影响㊂分析结果表明,该传动副具有较好的啮合性能㊂关键词㊀滚锥包络㊀端面啮合㊀啮合性能中图分类号㊀TH132.44Abstract ㊀The end face meshing worm drive with tapered roller envelope has many simultaneous meshing tooth pairs andcan eliminate clearance.According to the gear meshing principle and differential geometry principle,the meshing mathematical model of the transmission pair is established,the worm tooth surface equation and meshing function are deduced,and the meshing performance calculation formula is obtained.Matlab software is used to analyze the effects of small end radius,throat diameter coefficient and half cone angle of cone on the meshing performance evaluation parameters of the transmission pair induced normal curvature,lubrication angle,relative entrainment speed and self rotation angle.The analysis results show that thetransmission pair has good meshing performance.Key words㊀Cone rolling envelope ;End face engagement ;Meshing performance Corresponding author :LIU ZaiXin ,E-mail :313075259@ ,Fax :+86-28-87720507The project supported by the Chunhui Program of the Ministry of Education (No.Z2015105),and the Natural Science Foundation of Xihua University(No.Z1420208).Manuscript received 20211213,in revised form 20220323.0㊀引言㊀㊀蜗杆传递运动的方式通常是利用共轭齿面间的相互摩擦,具有传动平稳㊁传动比较大㊁冲击载荷相对较小和结构紧凑等优点[1],常应用于航空航天㊁医疗设施㊁建筑㊁海洋装备和机器人等行业范围㊂但是,与其他齿轮传动相比而言,传动效率较低,承载能力不大等缺点则非常明显,造成这些缺点的主要原因就是由于啮合齿面间始终存在着不可避免的相对滑动㊂当相对滑动速度很大且工作条件较差时,两啮合面间严重的摩擦磨损还会导致发热,从而引起蜗杆传动润滑情况恶化的情况[2]㊂近年来,随着啮合齿面间的润滑状态得到改善,在一些工作状况下蜗杆传动效率低的情况已经有了很大的改善,但据统计,在实际生产应用中的大部分蜗杆传动都处于部分弹流润滑状态下[3]㊂因此,生产应用中,粗糙峰的直接接触在两啮合齿面中是非常常见的㊂只要两啮合齿面间存在着金属的直接接触,两啮合齿面间的相对滑动就一直存在㊂为了解决这一问题,众多学者提出了不同的解决方法和新型的蜗杆传动形式㊂西华大学王进戈等[4-8]提出了滚锥包络环面蜗杆传动,一个个能绕自身轴线转动的圆锥滚子就是该传动副的蜗轮轮齿,把锥面当作原始母面包络而形成的环面蜗杆就是此传动副的蜗杆㊂为了减小啮合齿面间的相对滑动,可以把滚针轴承安装在滚锥和轴颈之间,把轴向滚动轴承安装在滚锥大端部,这样基本上就能转换为相对滚动㊂邓星桥等[9]提出了无侧隙平面包㊀932㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀络端面啮合蜗杆传动,蜗杆分为两段并且属于端面啮合是该蜗杆传动的优点,该传动装置的连接通过一个连接轴来实现㊂从动滚柱端面蜗轮副由西华大学李金宽等[10]提出,该传动副的蜗轮轮齿是活动齿,它可以绕自身轴线旋转,从动活动齿由滚柱通过滚动轴承与蜗轮本体相连㊂王凯等[11-14]提出了滚子包络端面内啮合蜗杆传动的新型传动装置,蜗轮轮齿是圆柱体,该传动副具有无侧隙双滚子包络环面蜗杆[15-19]和无侧隙平面包络端面啮合蜗杆传动[20]的优点,该传动副左端和右端都有端面蜗杆且与蜗轮为内啮合的方式㊂本文提出一种活动齿蜗杆传动副,即滚锥包络端面啮合蜗杆传动㊂其蜗杆是端面,蜗轮轮齿是滚锥㊂主要内容包括建立滚锥包络端面啮合蜗杆传动坐标系,并进行坐标与底矢的转换,推算了蜗轮蜗杆传动的相关方程;建立了传动啮合性能评定参数的计算公式;进行了啮合性能的分析㊂1㊀蜗杆传动的数学模型1.1㊀坐标系的设置㊀㊀根据微分几何原理和齿轮啮合原理[21]126-243,建立如图1所示的滚锥包络端面啮合蜗杆传动副的蜗杆静坐标系σ1i 1,j 1,k 1()㊁蜗轮静坐标系σ2i 2,j 2,k 2()㊁蜗杆的动坐标系σ1ᶄi 1ᶄ,j 1ᶄ,k 1ᶄ()㊁蜗轮的动坐标系σ2ᶄi 2ᶄ,j 2ᶄ,k 2ᶄ()㊂其中,k 1=k 1ᶄ为蜗杆的回转轴,k 2=k 2ᶄ为蜗轮的回转轴,ω1为蜗杆的角速度矢量,ω2为蜗轮的角速度矢量,A 为中心距㊂坐标系σ0i 0,j 0,k 0()建立在滚锥顶的中心,蜗轮的径向方向为滚锥的回转轴线㊂φ1㊁φ2分别为某一瞬时传动的旋转位移量,在蜗杆传动结构中满足φ1/φ2=ω1/ω2=Z 2/Z 1=i 12=1/i 21的关系,其中传动比用i 12表示,蜗杆头数用Z 1表示,蜗轮的齿数用Z 2表示㊂动㊁静坐标系重合时,规定φ1=φ2=0㊂设O 0在σ2中的坐标为(a 2,b 2,c 2),在接触点O p 处设置活动标架[22]σp e 1,e 2,n (),如图2所示㊂图1㊀坐标系的设置Fig.1㊀Setting of coordinatesystem图2㊀滚锥活动标架Fig.2㊀Tapered roller movable frame1.2㊀坐标转换㊀㊀滚锥包络端面啮合蜗杆在包络的过程中部分标架之间的坐标转换如下:σ1ᶄңσ2ᶄ的坐标变换关系为B 2ᶄ=i 2ᶄj 2ᶄk 2ᶄ[]TB 1ᶄ=i 1ᶄj 1ᶄk 1ᶄ[]T A 2ᶄ1ᶄ=a 11a 12a 13a 21a 22a 23a 31a 32a 33éëêêêêùûúúúúB 2ᶄ=A 2ᶄ1ᶄB 1ᶄìîíïïïïïïïïïï(1)式中,a 11=-cos φ1cos φ2;a 12=-sin φ1cos φ2;a 13=sin φ2;a 21=cos φ1sin φ2;a 22=sin φ1sin φ2;a 23=cos φ2;a 31=-sin φ1;a 32=cos φ1;a 33=0㊂σ0ңσp 的坐标变换关系为B p =e 1e 2n []TB 0=i 0j 0k 0[]T A p0=-sin θcos θ0sin βcos θsin βsin θcos βcos βcos θcos βsin θ-sin βéëêêêùûúúúB p =A p0B 0ìîíïïïïïïïï(2)1.3㊀相对速度㊀㊀为进行啮合方程㊁齿面方程等公式的推导,分别用r 0㊁r 1ᶄ㊁r 2ᶄ表示O p 在坐标系σ0㊁蜗杆动坐标系σ1ᶄ㊁蜗轮动坐标系σ2ᶄ中的矢径,用ξ表示中心距A 在蜗轮静坐标系σ2中的矢径,建立的矢量关系如图3所示㊂则滚锥面在坐标系σ0i 0,j 0,k 0()中的向量方程可表示为r 0=x 0i 0+y 0j 0+z 0k 0x 0=(R +u tan β)cos θy 0=(R +u tan β)sin θz 0=u ìîíïïïïïï(3)式中,R 为滚锥小端半径;β为滚锥半锥角;θ㊁u 均为㊀第45卷第4期文渝杰等:滚锥包络端面啮合蜗杆传动啮合性能分析933㊀㊀图3㊀接触点的矢量关系Fig.3㊀Vector relationship of contact points滚锥面上的轴向参数㊂矢径ξ在σ2ᶄ中可表示为ξ=Ai 2ᶄcos φ2-Aj 2ᶄsin φ2(4)㊀㊀根据齿轮啮合原理[21]126-243,滚锥包络端面啮合蜗杆传动的相对速度矢量为v (1ᶄ2ᶄ)=d ξd t +ω(1ᶄ2ᶄ)ˑr 1ᶄ-ω2ᶄˑξ(5)㊀㊀在该传动副中,d ξd t=0,则v (1ᶄ2ᶄ)在σp 下可表示为v(1ᶄ2ᶄ)=v 1(1ᶄ2ᶄ)e 1+v 2(1ᶄ2ᶄ)e 2+v n (1ᶄ2ᶄ)n v 1(1ᶄ2ᶄ)=-B 2sin θ-B 3cos θv 2(1ᶄ2ᶄ)=B 2sin βcos θ-B 1cos β-B 3sin βsin θv n (1ᶄ2ᶄ)=B 1sin β+B 2cos βcos θ-B 3cos βsin θìîíïïïï(6)1.4㊀啮合方程与齿面方程㊀㊀在齿轮传动的过程中,两齿面必须满足沿着接触点的公法矢方向无相对运动这一条件,即n ㊃v (1ᶄ2ᶄ)=0㊂因此可以得到滚锥包络端面啮合蜗杆传动的啮合函数为Φ=v (1ᶄ2ᶄ)n=M 1cos φ2+M 2sin φ2+M 3M 1=a 2cos βsin θ-R sin βsin θ-2u cos β/sin θM 2=0M 3=Ri 21sin β/cos θ-A cos βsin θ-㊀㊀i 21a 2cos βcos θ+2i 21u cos βcos θìîíïïïïïïïï(7)则啮合方程为Φ=v (1ᶄ2ᶄ)n=M 1cos φ2+M 2sin φ2+M 3=0(8)㊀㊀由齿轮啮合理论[21]126-243可知,蜗杆齿面就是蜗轮与滚锥母面同时运动时所构成的一条单参数曲面簇的包络面㊂滚锥包络端面啮合蜗杆的齿面方程为r 1ᶄ=x 1i 1ᶄ+y 1j 1ᶄ+z 1k 1ᶄx 1=cos φ1cos φ2(z 0-a 2)+cos φ1sin φ2x 0+㊀㊀y 0sin φ1+A cos φ1y 1=sin φ1cos φ2(z 0-a 2)+sin φ1sin φ2x 0-㊀㊀y 0cos φ1+A sin φ1z 1=sin φ2(a 2-z 0)+cos φ2xr 0=x 0i 0+y 0j 0+z 0k 0u =ƒ(θ,φ2)=P 3/P 4φ2=i 21φ1㊀-πɤφ1ɤπìîíïïïïïïïïïï(9)㊀㊀选取某组传动副几何数据,由式(9)可得如图4所示的蜗杆齿面图,图中为齿槽图,齿槽两侧为齿面,剖面图处形成的齿槽截面为锥形㊂图4㊀蜗杆齿面图Fig.4㊀Worm tooth surface diagram2㊀啮合性能分析㊀㊀通过Matlab 软件来分析滚锥包络端面啮合蜗杆传动的啮合性能,从数据和图象来判断该传动副的啮合性能的好坏㊂由蜗杆传动强度设计研究[23]可以得到该传动副某一啮合齿对在任一时刻的齿面接触应力σH 为σH =F n k 1ᶄ2ᶄσπLEᶄ(10)式中,F n 为接触点上的法向载荷;k 1ᶄ2ᶄσ为接触点处的诱导法曲率;L 为接触线的长度;Eᶄ为综合弹性模量㊂弹性流体动力润滑[24]中弹流润滑最小油膜厚度h min 公式为h min =2.65α0.54(η0v jx )0.7(Eᶄ)-0.13(k 1ᶄ2ᶄσ)-0.43w -0.18(11)式中,α为黏压系数;η0为润滑油黏度;v jx 为卷吸速度;Eᶄ为综合弹性模量;w 为单位长度上的载荷㊂由此可得齿面接触应力σH 与k 1ᶄ2ᶄσ成正比,弹流润滑最小油膜厚度h min 与(v jx 0.7成正比,与(k 1ᶄ2ᶄσ)0.43成反比㊂因此较小的诱导法曲率k 1ᶄ2ᶄσ可以使齿面接触应力σH 较小且最小油膜厚度h min 变大,从而提高该传动副的润滑性能;较大的卷吸速度v jx 也可以得到较大的最小油膜厚度h min 以提高该传动副的工作性能㊂而且润滑角μ和自转角μz0越接近90ʎ,传动副的润滑性能越好,就越容易形成动压油膜,传动副工作性能越好㊂2.1㊀啮合分析主要公式2.1.1㊀诱导法曲率㊀㊀由齿轮啮合原理[21]126-243可知,诱导法曲率为啮合接触点处两曲面在任意方向上的法曲率的差值,故滚锥包络端面啮合蜗杆传动副在接触线法线方向的诱导法曲率为㊀934㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀k (1ᶄ2ᶄ)δ=-k (2ᶄ1ᶄ)δ=-ω(1ᶄ2ᶄ)2+v (1ᶄ2ᶄ)1cos βR +u tan β()2+(ω(1ᶄ2ᶄ)1)2éëêêùûúúΨ(12)2.1.2㊀润滑角㊀㊀依据齿轮啮合原理[21]126-243,润滑角为接触线与相对速度方向之间的夹角,润滑角的最优极限值为90ʎ,最劣极限值为0ʎ㊂该传动副的润滑角计算公式为u =v (1ᶄ2ᶄ)1v (1ᶄ2ᶄ)1cos βR +u tan β-ω(1ᶄ2ᶄ)2()+v (1ᶄ2ᶄ)2ω(1ᶄ2ᶄ)1m =v (1ᶄ2ᶄ)1cos βR +u tan β-ω(1ᶄ2ᶄ)2()2+(ω(1ᶄ2ᶄ)1)2n =(v (1ᶄ2ᶄ)1)2+(v (1ᶄ2ᶄ)2)2μ=arcsin u mn ìîíïïïïïïïïïï(13)2.1.3㊀自转角㊀㊀自转角μz0定义为相对速度矢量v 12与滚锥轴线k 0之间的夹角㊂当自转角为90ʎ时,滚锥轴承的工作状态为最佳状态㊂该传动副的自转角为μz 0=arccosk 0㊃v 12|v 12|=arccos|v 122|(v 121)2+(v 122)2(14)2.1.4㊀相对卷吸速度㊀㊀传动副两共轭曲面上某啮合点的速度之和沿该点接触线法向分量的一半为相对卷吸速度,相对卷吸速度越大越易形成动压油膜㊂齿面接触点的相对卷吸速度计算公式为v jx =(v 1ᶄσ+v 2ᶄσ)2(15)式中v 1ᶄσ=v 1ᶄ1v 1ᶄ2ᶄ1cos βR +u tan β-ω1ᶄ2ᶄ2()+v 1ᶄ2ω1ᶄ2ᶄ1v 1ᶄ2ᶄ1cos βR +u tan β-ω1ᶄ2ᶄ2()2+(ω1ᶄ2ᶄ1)2v 2ᶄσ=v 2ᶄ1v 1ᶄ2ᶄ1cos βR +u tan β-ω1ᶄ2ᶄ2()+v 2ᶄ2ω1ᶄ2ᶄ1v 1ᶄ2ᶄ1cos βR +u tan β-ω1ᶄ2ᶄ2()2+(ω1ᶄ2ᶄ1)2ìîíïïïïïïïïïïïï(16)2.2㊀滚锥小端半径对啮合性能的影响㊀㊀取中心距A =140mm㊁Z 1=1㊁Z 2=25㊁k =0.3㊁β=4ʎ,通过控制变量法取R 的范围为4.5~6.5mm 来探讨滚锥小端半径R 对滚锥包络端面啮合蜗杆传动中诱导法曲率㊁润滑角㊁相对卷吸速度和自转角的影响㊂图5所示为滚锥小端半径对诱导法曲率的影响㊂由图5可知,诱导法曲率随蜗轮滚锥小端半径的增大而减小㊂图6所示为滚锥小端半径对润滑角的影响㊂啮合过程中,从啮入端到啮出端润滑角逐渐减小,啮出端比啮入端的变化幅度大,且随着滚锥小端半径的增大,润滑角变小且变化幅度变大㊂图7所示为滚锥小端半径对卷吸速度的影响,从啮入端到啮出端卷吸速度呈下降趋势,随着滚锥小段半径的增大,卷吸速度在左齿面增大,在右齿面减小㊂图8所示为滚锥小端半径对自转角的影响㊂啮合过程中,从啮入端到啮出端自转角逐渐变小且变化幅度变大㊂随着滚锥小端半径的增大,自转角逐渐减小㊂当滚锥小端半径较小时,啮入端和啮出端自转角的差值较小㊂图5㊀滚锥小端半径对诱导法曲率的影响Fig.5㊀Effect of small end radius of cone on induced normal curvature图6㊀滚锥小端半径对润滑角的影响Fig.6㊀Effect of small end radius of taper roller on lubrication angle㊀第45卷第4期文渝杰等:滚锥包络端面啮合蜗杆传动啮合性能分析935㊀㊀图7㊀滚锥小端半径对卷吸速度的影响Fig.7㊀Effect of small end radius of cone on coilingspeed图8㊀滚锥小端半径对自转角的影响Fig.8㊀Effect of small end radius of cone on rotation angle2.3㊀喉径系数对啮合性能的影响㊀㊀喉径系数用来衡量蜗轮蜗杆中心距的改变所引起的蜗杆喉部分度圆直径的相对变化,即d 1=kA (d 1为蜗杆喉部分度圆直径)㊂取中心距A =140mm㊁Z 1=1㊁Z 2=25㊁R =5.5㊁β=4ʎ,通过控制变量法取k 的范围为0.2~0.4来研究喉径系数k 对滚锥包络端面啮合蜗杆传动中诱导法曲率㊁润滑角㊁相对卷吸速度和自转角的影响㊂图9所示为喉径系数对诱导法曲率的影响㊂左侧齿面啮合过程中,从啮入端到啮出端诱导法曲率逐渐变大,且前半部分诱导法曲率随着喉径系数的增大而变大,后半部分相反㊂右侧齿面啮合时,从啮入端到啮出端诱导法曲率逐渐变小,随着喉径系数的增大,诱导法曲率变大㊂图9㊀喉径系数对诱导法曲率的影响Fig.9㊀Effect of throat diameter coefficient on induced normal curvature图10所示为喉径系数对润滑角的影响㊂啮合过程中,从啮入端到啮出端润滑角逐渐减小,啮出端比啮入端的变化幅度大,当喉径系数较小时,润滑角变化较大㊂图11所示为喉径系数对卷吸速度的影响,啮合过程中,从啮入端到啮出端的卷吸速度均呈减小趋势,啮入端到啮入中部卷吸速度随喉径系数的增大而减小,从啮入中部到啮出端时卷吸速度随喉径系数的增大而增大㊂图12所示为喉径系数对自转角的影响㊂啮合过程中,从啮入端到啮出端自转角逐渐变小,啮入端到啮入中段时,随着喉径系数的增大,自转角略微减小;啮入中段到啮出端时,自转角随喉径系数的增大而增大㊂图10㊀喉径系数对润滑角的影响Fig.10㊀Effect of throat diameter coefficient on lubrication angle㊀936㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀图11㊀喉径系数对卷吸速度的影响Fig.11㊀Effect of throat diameter coefficient on entrainmentspeed图12㊀喉径系数对自转角的影响Fig.12㊀Effect of throat diameter coefficient on rotation angle 2.4㊀滚锥半锥角对啮合性能的影响㊀㊀取中心距A=140mm㊁Z1=1㊁Z2=25㊁R=5.5㊁k=0.3,通过控制变量法取β的范围为2ʎ~6ʎ来论证滚锥半锥角β对滚锥包络端面啮合蜗杆传动中诱导法曲率㊁润滑角㊁相对卷吸速度和自转角的影响㊂图13所示为滚锥半锥角对诱导法曲率的影响,诱导法曲率随滚锥半锥角的增大而减小㊂图14所示为滚锥半锥角对润滑角的影响,由图14可以看出润滑角随滚锥半锥角的增大而减小,且变化幅度变大㊂图15所示为滚锥半锥角对卷吸速度的影响㊂齿面啮合过程中,从啮入端到啮出端的卷吸速度逐渐减小㊂但在左侧齿面啮合时,滚锥半锥角越大,卷吸速度图13㊀滚锥半锥角对诱导法曲率的影响Fig.13㊀Effect of half cone angle of cone rolling oninduced normal curvature就越大,而右侧齿面啮合时,滚锥半锥角越大,卷吸速度反而越小㊂图16所示为滚锥半锥角对自转角的影响㊂由图16可知,自转角从啮入端到啮出端逐渐减小,自转角随滚锥半锥角的增大而减小㊂图14㊀滚锥半锥角对润滑角的影响Fig.14㊀Effect of half cone angle on lubrication angle3㊀结论㊀㊀本文对滚锥包络端面啮合蜗杆传动进行分析,建立对应的数学模型,对啮合性能进行了分析,结论如下:1)以理想状态为前提,运用齿轮啮合原理和活动标架法,建立了该传动副的几何数学模型㊂推算了蜗㊀第45卷第4期文渝杰等:滚锥包络端面啮合蜗杆传动啮合性能分析937㊀㊀图15㊀滚锥半锥角对卷吸速度的影响Fig.15㊀Effect of half cone angle of cone rolling on coilingspeed图16㊀滚锥半锥角对自转角的影响Fig.16㊀Effect of half cone angle of conerolling on self rotation angle杆蜗轮传动相关的方程,即啮合方程㊁齿面方程等㊂2)以齿轮啮合原理为基础,建立了诱导法曲率㊁润滑角㊁自转角和相对卷吸速度等用来评价滚锥包络端面啮合蜗杆传动啮合性能评定参数的计算公式㊂3)分析了滚锥小端半径㊁喉径系数和滚锥半锥角对该传动副的啮合性能的影响,分析结果表明,滚锥端面啮合蜗杆左侧齿面和右侧齿面对比而言,左侧齿面啮合时的承载能力和润滑性更好㊂该传动副的诱导法曲率较小,润滑角㊁自转角和相对卷吸速度都比较大,说明它的承载能力优秀,润滑性能良好㊂分析结果可以作为对滚锥包络端面啮合蜗杆传动更深入的研究的对照㊂参考文献(References)[1]㊀段路茜.TI蜗杆传动啮合理论研究及优化设计[D].天津:天津大学,2004:1-9.DUAN LuQian.Meshing theory research and optimization design ofTI worm drive[D].Tianjin:Tianjin University,2004:1-9(InChinese).[2]㊀刘㊀淼,白国振.蜗轮蜗杆试验台测控系统设计[J].机械与电子,2014(10):28-30.LIU Miao,BAI GuoZhen.Design of measurement and control systemfor worm gear and worm test bench[J].Machinery&Electronics,2014(10):28-30(In Chinese).[3]㊀MERWIN J E,JOHNSON K L.An analysis of plastic deformation inrolling contact[J].Proc.Instn.Mech.Engrs,2006,177(25):676-690.[4]㊀王进戈.滚锥包络环面蜗杆传动[M].成都:四川科学技术出版社,2000:16-26.WANG JinGe.Rolling cone enveloping ring surface worm drive[M].Chengdu:Sichuan Science and Technology Press,2000:16-26(InChinese).[5]㊀王进戈,向中凡,戴跃洪.滚锥包络环面蜗杆传动载荷分布与分配研究[J].四川工业学院学报,1996(4):16-21.WANG JinGe,XIANG ZhongFan,DAI YueHong.Research on loaddistribution and distribution of cone enveloping ring surface wormdrive[J].Journal of Sichuan Institute of Technology,1996(4):16-21(In Chinese).[6]㊀王进戈,张均富,王㊀强.滚锥包络环面蜗杆传动的润滑状态分析[J].哈尔滨工业大学学报,2005(7):940-942.WANG JinGe,ZHANG JunFu,WANG Qiang.Lubrication stateanalysis of cone enveloping ring surface worm drive[J].Journal ofHarbin Institute of Technology,2005(7):940-942(In Chinese).[7]㊀王进戈,向中凡,戴跃洪,等.滚锥包络环面蜗杆副材料的摩擦磨损实验[J].机械传动,1996(S1):40-41.WANG JinGe,XIANG ZhongFan,DAI YueHong,et al.Frictionand wear experiments on materials of rolling cone enveloping ringsurface worm pair[J].Journal of Mechanical Transmission,1996(S1):40-41(In Chinese).[8]㊀王进戈,何㊀粒.误差作用下的啮合分析及其载荷分配与载荷分布[J].四川工业学院学报,1998(3):28-33.WANG JinGe,HE Li.Meshing analysis and load distribution undererror[J].Journal of Sichuan Institute of Technology,1998(3):28-33(In Chinese).[9]㊀邓星桥,王进戈,郑有春.两段式包络环面端面啮合蜗杆传动装置:CN203488637U[P].2013-12-04.DENG XingQiao,WANG JinGe,ZHENG YouChun.Two-stageenveloping ring face meshing worm transmission device:CN203488637U[P].2013-12-04(In Chinese).[10]㊀李金宽,蒲宇捷,全建军,等.一种从动滚柱端面蜗轮副:CN205036784U[P].2016-01-17.LI JinKuan,PU YuJie,QUAN JianJun,et al.A driven roller faceworm gear pair:CN205036784U[P].2016-01-17(In Chinese).[11]㊀王㊀凯,王进戈,邓星桥,等.滚子包络端面啮合蜗杆传动啮合理论分析[J].机械设计与研究,2018,34(5):88-91.㊀938㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀WANG Kai,WANG JinGe,DENG XingQiao,et al.Meshing theoryanalysis of roller enveloping end meshing worm drive[J].MachineDesign and Research,2018,34(5):88-91(In Chinese). [12]㊀王㊀凯,付㊀敏,王珏翎.滚子包络端面啮合蜗杆传动的啮合性能分析[J].西安交通大学学报,2019,53(3):135-142.WANG Kai,FU Min,WANG JueLing.Meshing performanceanalysis of roller enveloping end meshing worm drive[J].Journal ofXiᶄan Jiaotong University,2019,53(3):135-142(In Chinese).[13]㊀王㊀凯,王珏翎,王丽玮.滚子包络端面啮合蜗杆传动接触有限元分析[J].机械传动,2018,42(10):117-123.WANG Kai,WANG JueLing,WANG LiWei.Contact finite elementanalysis of roller enveloping end meshing worm drive[J].Journal ofMechanical Transmission,2018,42(10):117-123(In Chinese).[14]㊀王㊀凯,姚㊀进,邓星桥,等.无侧隙端面啮合蜗杆副瞬态动力学分析[J].工程科学与技术,2017,49(1):86-94.WANG Kai,YAO Jin,DENG XingQiao,et al.Transient dynamicsanalysis of non-backlash end meshing worm pair[J].EngineeringScience and Technology,2017,49(1):86-94(In Chinese). [15]㊀王进戈,张均富,洪㊀雷.无侧隙双滚子包络环面蜗杆传动机构:CN101290042[P].2008-10-22.WANG JinGe,ZHANG JunFu,HONG Lei.Non-backlash doubleroller enveloping ring surface worm transmission mechanism:CN101290042[P].2008-10-22(In Chinese).[16]㊀王㊀凯,王进戈,邓星桥.无侧隙双滚子包络环面蜗杆传动的啮合性能分析[J].机械传动,2009,33(6):12-15.WANG Kai,WANG JinGe,DENG XingQiao.Meshing performanceanalysis of no-backlash double-roller enveloping ring surface wormdrive[J].Journal of Mechanical Transmission,2009,33(6):12-15(In Chinese).[17]㊀邓星桥,王进戈,张均富,等.基于遗传算法的无侧隙双滚子包络环面蜗杆传动的参数优化设计[J].四川大学学报(工程科学版),2010,42(2):250-254.DENG XingQiao,WANG JinGe,ZHANG JunFu,et al.Parameteroptimization design of no-backlash double-roller enveloping ringsurface worm transmission based on genetic algorithm[J].Journal ofSichuan University(Engineering Science Edition),2010,42(2):250-254(In Chinese).[18]㊀王进戈,邓星桥,张均富,等.误差对无侧隙双滚子包络环面蜗杆传动啮合性能的影响研究[J].西华大学学报(自然科学版),2010,29(2):1-6.WANG JinGe,DENG XingQiao,ZHANG JunFu,et al.Influence oferror on meshing performance of no-backlash double-roller envelopingring surface worm drive[J].Journal of Xihua University(NaturalScience Edition),2010,29(2):1-6(In Chinese). [19]㊀邓星桥,向中凡,王进戈.加工和安装误差对无侧隙蜗杆传动接触线及齿廓的影响[J].西安交通大学学报,2011,45(2):111-116.DENG XingQiao,XIANG ZhongFan,WANG JinGe.Influence ofmachining and installation errors on contact line and tooth profile ofnon-backlash worm drive[J].Journal of Xiᶄan Jiaotong University,2011,45(2):111-116(In Chinese).[20]㊀杨㊀捷,王进戈,陈守安,等.无侧隙平面一次包络端面啮合环面蜗杆副弹流润滑分析[J].西安交通大学学报,2017,51(3):87-91.YANG Jie,WANG JinGe,CHEN ShouAn,et al.Elastohydrodynamiclubrication analysis of no-backlash plane primary enveloping end faceengagement ring surface worm pair[J].Journal of Xiᶄan JiaotongUniversity,2017,51(3):87-91(In Chinese).[21]㊀吴序堂.齿轮啮合原理[M].西安:西安交通大学出版社,2009:126-243.WU XuTang.Principle of gear meshing[M].Xiᶄan:Xiᶄan JiaotongUniversity Press,2009:126-243(In Chinese).[22]㊀张光辉,王朝晋.活动标架的应用及对Baxter诱导法曲率公式的改进[J].重庆大学学报(自然科学版),1983(2):1-12.ZHANG GuangHui,WANG ChaoJin.Application of movable frameand improvement of Baxter induced normal curvature formula[J].Journal of Chongqing University(Natural Science Edition),1983(2):1-12(In Chinese).[23]㊀侯㊀力,黄成祥,殷国富.蜗杆传强度设计研究[J].四川大学学报,2001,33(4):98-101.HOU Li,HUANG ChengXiang,YIN GuoFu.Research on transmissionstrength design of worm[J].Journal of Sichuan University,2001,33(4):98-101(In Chinese).[24]㊀温诗铸,杨沛然.弹性流体动力润滑[M].北京:清华大学出版社,1992.WEN ShiZhu,YANG PeiRan.Elastohydrodynamic lubrication[M].Beijing:Tsinghua University Press,1992(In Chinese).。
双圆环面二次包络环面蜗杆传动的啮合界线与蜗杆螺旋面的结构
界 线 的特性 ， 释蜗 杆螺 旋 面 的结 构 ， 出增加 蜗 诠 提
杆 蜗轮 瞬 时接 触线 总 长 度 的方 法 ， 以利 于提 高 传
动副 的承 载能 力 。
圈 １ 以 中 的砂 轮 轴 截 面
收 稿 日期 ：０ ７０ — １ ２０ —８３
边 齿顶 是 否变 尖 。算例 研究 表 明 ， ＴＴ环 面蜗 杆 Ｄ
式 中： 和 为砂轮 产 形 面 参 数 ； Ｐ和 ｑ是 砂 轮 轴
截 面 内圆弧 工 作 廓 线 圆心 坐 标 ； Ｐ是 砂 轮 轴 截 面 内圆弧 工作 廓线半 径 。 由于双 圆环 面砂 轮可 以 同时磨 削蜗 杆齿 槽 的
作者 简 介 ： 亚平 （９ ５）男 ， 汉 科 技 大 学 副 教 授 ， 士 ．Ｅ ｍａｌｚ ａｙ ｐｎ １ ７ ＠ １ ６ ｃｒ 赵 １ ７一 ， 武 博 — ｉ ｈ ｏ ａ ｉｇ ９ ５ ２ ．ｏ ： ｎ
维普资讯
二 次 包络 副 的 二 次 包络 啮 合 界 线 与 一 次 包络 啮 合 界 线 共 轭 线 重 合 ， 二 次 包络 新 接 触 线 族 的 包 络 线 ， 二 次 是 与
包络 原 接 触 线 族 相 交 ， 蜗 杆 螺 线 面 划 分 为 单 线 接 触 区与 双 线接 触 区 ， 而诠 释 了双 圆 环 面 包络 环 面 蜗 杆 螺 将 从 旋 面 的 结 构 。 同时 指 明 ， 以 通 过 合 理 搭 配 参数 ， 整 二 次 包络 啮 合 界 线 沿蜗 杆 轴 向 的 位 置 ， 加 瞬 时接 触 线 可 调 增
工 效率 高 ， 于保 证 精 度 ， 用 磨 头结 构 简 单 ； 易 所 而 且 齿 面硬度 高 、 粗糙 度低 『 。 １ ］ 文献 ［ ］ 究 了 标 准 型 Ｄ ２研 ＴＴ 蜗 杆 传 动 齿 面
机械设计基础之机械设计-第5章：蜗杆传动
第五章☞概述☞蜗杆传动的主要参数☞蜗杆传动的受力分析☞蜗杆蜗轮的失效形式☞蜗杆传动的材料选择☞蜗杆传动的设计计算☞蜗杆传动的结构设计第一节☞概述☞蜗杆传动的主要参数☞蜗杆传动的受力分析☞蜗杆传动的失效形式☞蜗杆蜗轮的材料选择☞蜗杆传动的设计计算☞蜗杆传动的结构设计机械传动分类及特点机械传动分类直接接触传动有中间机件的传动摩擦传动摩擦轮传动带传动绳传动摩擦无级变速器摩擦无级变速器啮合传动齿轮传动链传动蜗杆传动同步带传动螺旋传动凸轮机构等机械传动的特点主要体现在传动效率、单级传动比、传动功率、中心距、传动准确性、无级调速、过载保护、寿命、噪声、价格等等齿轮传动的分类齿轮传动平面齿轮传动空间齿轮传动直齿圆柱齿轮传动斜齿圆柱齿轮传动传递相交运动传递交错运动内啮合外啮合齿轮齿条直齿斜齿曲线齿交错轴斜齿轮蜗杆蜗轮准双曲面齿轮人字齿齿轮运动蜗杆传动的功能及特点传递空间交错轴间的运动或动力功能优点缺点⏹传动比大i = 7~80⏹结构紧凑⏹传动平稳(逐渐进入和退出啮合)⏹噪声小⏹有自锁性(蜗杆升角<当量摩擦角)⏹摩擦发热大⏹传动效率低η＝0.7~0.8⏹需要消耗有色金属⏹制造工艺复杂，成本高⏹不适于大功率长期工作∑通常二轴交角∑＝90°；蜗杆主动，蜗轮从动蜗杆传动主要用于传动比较大，结构要求紧凑的场合；或用于需要传动具有自锁性能的场合。
蜗杆整体形状●圆柱蜗杆传动●环面蜗杆传动●锥蜗杆传动阿基米德蜗杆（ZA型）蜗杆齿面为阿基米德螺旋面，端面齿廓为阿基米德曲线；中间平面上的啮合相当于齿条齿轮啮合。
通常在无需磨削加工的情况下广泛采用，需要时要采用特制截面形状的砂轮。
渐开线蜗杆（ZI型）端面齿廓为渐开线，与蜗杆基圆柱相切的截面上齿廓是直线，所以使用专用机床可以用平面砂轮磨削，容易得到高精度。
法向直廓蜗杆（ZN型）螺线的导程角很大。
加工时刀具的切削平面在垂至于齿槽（或齿厚）中点螺旋线的法平面内。
可以磨削出极接近于延伸渐开线蜗杆的轮廓，可与蜗轮得到正确啮合。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
交错轴双滚子包络环面蜗杆传动啮合分析柳在鑫1,2，王进戈2,1, 张均富2，向中凡2（1.四川大学制造科学与工程学院，四川成都610035；2. 西华大学机械工程与自动化学院，四川成都610039）摘要：为了消除环面蜗杆传动的齿侧间隙，提高其传动的精度和效率，分析了传统消隙蜗轮副的不足，在无侧隙双滚子包络环面蜗杆传动研究基础上提出一种交错轴双滚子包络环面蜗杆传动，采取双排滚子错位布置，且滚子轴线与蜗轮径向偏转一定角度。
阐述了交错轴双滚子包络环面蜗杆传动的工作原理，依据空间齿轮啮合理论和微分几何理论，采用运动学法建立了蜗杆副的动静坐标系及接触点处的活动坐标系，推导了该新型环面蜗杆齿面方程和蜗轮齿面接触线方程，并导出了该传动的一界函数、诱导法曲率、润滑角及自转角等齿面啮合参数计算公式。
最后运用matlab软件进行了数值仿真，并分析了滚柱偏置距离c2、滚柱半径R、交错角γ等参数对该蜗杆传动啮合性能的影响。
仿真实例表明：要使该传动保持良好的接触性能和润滑性能，c2不宜超过10cm，R在8cm～15cm之间，γ在28o～50o之间。
Meshing Analysis of Non-parallel Double-roller EnvelopingHourglass Worm GearingAbstract:To eliminate the backlash of enveloping worm and improve the precision and efficiency, by analyzing the shortcomings in the existing non-backlash worm gear sets, non-parallel double-roller enveloping hourglass worm gearing was proposed based on the research of non-backlash double-roller enveloping hourglass worm gearing. Two rows of rollers were assigned to misplace and there was a certain defection angle between the roller axis and the radial. The working principle was introduced. According to the theories of differential geometry and space engagement theory, the dynamic and static coordinate system based on worm gear pair and the moving coordinate system based on the contacting point were established. The tooth surface equations of worm and contacting line equations of worm gear were deduced. The formulas of meshing limit function, induced normal curvature, lubrication angle and rotation angle of the non-parallel double-roller enveloping hourglass worm gearing were derived by means of the theory of differential geometry. The simulation was conducted using MATLAB software, c2、R and γwhich impacted the engagement performance of this transmission, were analyzed. The numerical example showed that c2 should not be more than 10 cm, R should be controlled within 8 to 15cm, γshould be controlled within 28o to 50o, for effectively improving the meshing performance of the non-parallel double-roller enveloping hourglass worm gearing.Key words:non-parallel ; double-roller; hourglass worm gearing; meshing performance收稿日期:2011-10-20基金项目:国家自然科学基金资助项目(50775190)作者简介：柳在鑫(1978—)，男，副教授，博士研究生，研究方向：机械传动. E_mail: zhanxinliu@.随着现代传动技术的发展，对蜗杆传动的啮合侧隙提出越来越高的要求。
国内外无侧隙或齿侧间隙可补偿的蜗杆传动主要有双导程圆柱蜗杆传动[1]、正平面一次包络环面蜗杆传动[2]、侧隙可调式变齿厚平面蜗轮传动[3]、无侧隙双滚子包络环面蜗杆传动[4-6]和双蜗杆传动[7]。
其中双导程圆柱蜗杆加工麻烦，通用性差；正平面一次包络环面蜗杆传动效率低，齿侧间隙调整不方便；变齿厚平面蜗轮传动仅调整传动副磨损后的侧隙，无法完全消除齿侧间隙；双蜗杆传动体积大、结构复杂，很难适用于结构紧凑的传动装置；无侧隙双滚子包络环面蜗杆传动润滑角和自转角均不理想，直接影响整体传动性能，还有滚子承载能力也有限。
本文在无侧隙双滚子包络环面蜗杆传动研究基础上提出一种交错轴双滚子包络环面蜗杆传动，滚子轴线与蜗轮径向偏转一定角度。
蜗轮齿可采用滚动轴承代替，制造方便，成本低，而且安装方便，安装误差均不会影响蜗杆的齿面形状，蜗杆齿厚相对未交错时更符合等强度原则，接触性能和润滑性能也得到明显的提高。
该传动能够用于高精度数控机床上的精密分度、精密传动和精密动力传动，还可以用于汽车、仪器、冶金机械及其他机器设备，具有十分广阔的应用前景和推广价值。
1、传动的工作原理图1 蜗轮结构图Fig.1 Construction sketch of worm gears如图1，蜗轮由周向均布有滚子的两半个蜗轮构成，每排滚子与蜗轮中间平面偏离一定位置，滚子轴线与蜗轮径向偏转一定角度，滚子可绕自身轴线转动。
蜗杆左、右齿面分别与两半个蜗轮的滚子相啮合。
单排滚子与蜗杆齿面之间存在一定齿侧间隙，保证了传动的正常工作和良好的润滑，但对整体而言，通过自动消隙装置调节两半个蜗轮轮体的错位角度[8]，使滚子与蜗杆齿面始终保持接触，消除传动的回程误差。
2、传动副的啮合分析2.1 坐标系的设置及坐标变换图2 坐标系的设置Fig.2 Location of coordinate systems 如图2所示，),('1'1111k,j,i'''OS、),(11111k,j,iOS分别为蜗杆静、动坐标系；),('2'22'2'2'k,j,iOS、),(22222k,j,iOS分别为蜗轮静、动坐标系；)(200k,j,i,OS为蜗轮滚柱柱顶与蜗轮固联的坐标系，O0点在2S中坐标为),,(222cba。
2c为滚柱偏距；α为蜗轮齿周角；γ为滚柱轴线与蜗轮径向交错角；A为中心距；1'k、2'k分别为蜗杆、蜗轮回转轴；1ϕ、2ϕ分别为蜗杆、蜗轮转角。
其中坐标系1SS→的变换关系如下：TT)1,()1,(111,z,yx,z,yx10M=（1）式中：⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=1044104310421041103410331032103110241023102210211014101310121011MMMMMMMMMMMMMMMM10M⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧====-=+======--=-=--=---=--=-=-=-+-=+=-=-=21621521421321104410431042104110312210342221103321221032115310245231102351321022110211461014426110136241101211011D D D D ra r a D r a r a D ΜM M M Mb a M D D M D D M Ac b D a D M D D D D M D D D D M M c b D a D A M D D D D M D D D D M M ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕcos cos sin sin sin cos cos sin sin cos cos sin cos cos sin sin 10cos sin cos sin cos sin sin cos cos sin cos sin 22222222 （2）2.2 相对速度 如图3，在接触点P 处设置活动坐标系),(p n ,e ,e 21O S P 。
滚柱面在坐标系0S 中的向量方程为⎪⎪⎩⎪⎪⎨⎧===++=uz θR y θR x z y x 000000sin cos 0000k j i r （3） 式中，u 和θ为柱面参数，R 为滚柱半径。
图3 活动坐标系的设置Fig.3 Location of the dynamitic coordinate system由空间啮合理论[9]，接触点 P 处的相对速度矢量)12(ν在P S 中的表达式为 ⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧=+=-=-+-+=+-+=+-+=++=-=-+=++=002000200020220220222102202202221sin )(cos )()(sin )(cos )()(cos sin sin sin cos cos x z D z y D y D z D y x Ay b x a B x a i z c B z c y b i B θB θD B θD B νDB D B νθB θD B θD B νννν2112223222131221(12)n 1122(12)231221(12)1(12)n (12)2(12)1ϕϕϕϕn e e v 21(12) （4） 式中：)12(1ν、)12(2ν、)12(nν即为相对速度矢量(12)ν在坐标系P S 中的投影。