04二元关系
八年级数学专题 二元一次方程组重难点(参数问题、实际应用问题)(北师大版)
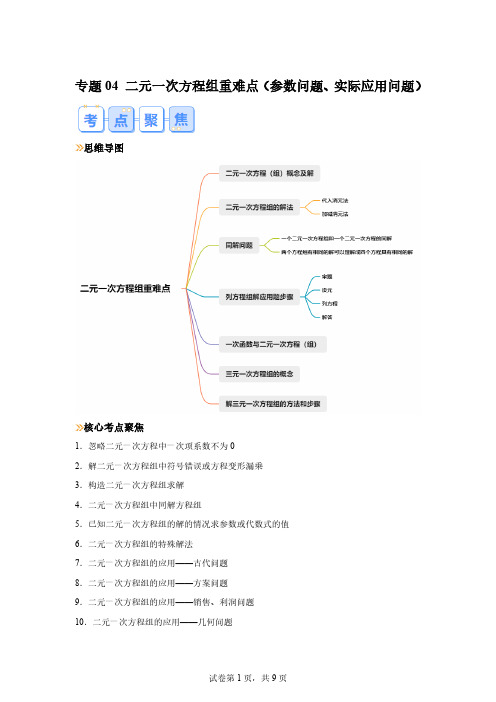
ì3x - 2 y = -1
ìx =1 ìm + 5 =1
ìm = -4
íî3x + 2 y = 7
,解得
í î
y
=
2
,即
íîn
+
3
=
2
,解得
íîn
=
-1
.
(1)学以致用,模仿乐乐同学的“整体换元”的方法,解方程组
ì ïï í ï ïî
x x
+ 3 + 3
y y
+ -
x x
5 5
y y
= =
4 .
-2
试卷第 2 页,共 9 页
义,否则,若把 y=ax+b 代入变形的原方程,必然得到一个恒等式; ③用代入法求出一个未知数的值后,再求另一个未知数时,一般代入变形后得到的方
程比较简单.
2.加减消元法
把方程组的两个方程(或先作适当变形)相加或相减,消去其中一个未知数,从而把
解二元一次方程组转化为解一元一次方程.这种解方程组的方法叫做加减消元法,简
联立成方程组,求出未知数的值,然后代入含有参数的方程即可求出参数的值.
四、列方程组解应用题步骤
1.列方程组解应用题是把“未知”转化为“已知”的重要方法,它的关键是把已知量和未 知量联系起来,找出题目中的相等关系.一般来说,有几个未知量就必须列出几个方
程,所列方程必须满足:
①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数值要相等.
y
=
与 41
íî2
x
+
3
y
=
-7
有相同的解,求
a,b
的值.
二元函数连续、偏导数与可微的关系

二元函数连续、偏导数与可微的关系二元函数是数学中常见的一种函数形式,它由两个变量组成,通常表示为f(x, y)。
在研究二元函数时,我们常常关注它的连续性、偏导数和可微性。
我们来了解一下二元函数的连续性。
一个二元函数在某一点(x0, y0)处连续,意味着当自变量的值在无限接近(x0, y0)时,函数值也会无限接近于f(x0, y0)。
换句话说,如果(x, y)接近于(x0, y0),那么f(x, y)就会接近于f(x0, y0)。
这种连续性的定义可以推广到整个定义域上,即函数在定义域内的每个点都连续。
我们来看二元函数的偏导数。
对于一个二元函数f(x, y),它的偏导数表示了函数在某一点(x0, y0)处对于其中一个变量的变化率。
具体来说,偏导数可以分为对x的偏导数和对y的偏导数。
对x的偏导数表示了当y固定时,函数在x方向上的变化率;对y的偏导数表示了当x固定时,函数在y方向上的变化率。
我们来讨论二元函数的可微性。
一个二元函数在某一点(x0, y0)处可微,意味着在该点附近可以用一个线性函数来近似表示原函数的变化。
具体来说,如果一个函数在某一点(x0, y0)处可微,那么它在该点的偏导数存在且连续,并且满足以下条件:f(x, y)≈f(x0, y0)+∂f/∂x(x0, y0)(x-x0)+∂f/∂y(x0, y0)(y-y0)。
二元函数的连续性、偏导数和可微性是密切相关的。
连续性是函数的基本性质,偏导数则描述了函数在不同方向上的变化率,可微性则表示了函数在某一点附近的近似性质。
这些概念在数学和物理学等领域中有着广泛的应用,对于理解和解决实际问题非常重要。
总结一下,二元函数的连续性、偏导数和可微性是相互关联的。
连续性描述了函数在定义域内的整体行为,偏导数表示了函数在某一点的变化率,而可微性则表示了函数在某一点附近的近似性质。
通过研究这些概念,我们可以更好地理解二元函数的性质和行为,为实际问题的解决提供有力的工具。
专题04 二元一次方程组(解析版)-2020-2021学年七年级数学期末复习特训

专题04 二元一次方程组一.选择题(共10小题,满分30分,每小题3分)1.(3分)下列方程中,为二元一次方程的是()A.2a+1=0B.3x+y=2z C.xy=9D.3x﹣2y=5【解答】解:A.是一元一次方程,不是二元一次方程,故本选项不符合题意;B.是三元一次方程,不是二元一次方程,故本选项不符合题意;C.是二元二次方程,不是二元一次方程,故本选项不符合题意;D.是二元一次方程,故本选项符合题意;故选:D.2.(3分)如果3x3m﹣2n﹣4y n﹣m+12=0是关于x、y的二元一次方程,那么m、n的值分别为()A.m=2,n=3B.m=2,n=1C.m=﹣1,n=2D.m=3,n=4【解答】解:∵3x3m﹣2n﹣4y n﹣m+12=0是关于x、y的二元一次方程,∴,解得:,故选:D.3.(3分)若是二元一次方程mx﹣y=3的解,则m为()A.7B.6C.D.0【解答】解:把代入方程得:m﹣3=3,解得:m=6,故选:B.4.(3分)下列方程组中,不是二元一次方程组的是()A.B.C.D.【解答】解:由二元一次方程组的定义可知,方程组中不是二元一次方程组的是,因为方程xy=0中未知数的次数是2次,故选:B.5.(3分)如果方程组的解为,那么“□”和“△”所表示的数分别是()A.14,4B.11,1C.9,﹣1D.6,﹣4【解答】解:设“□”为a,“△”为b,则方程组为的解是,代入②得:5﹣2b=3,解得:b=1,方程组的解是,代入①得:10+1=a,解得:a=11,即“□”为11,“△”为1,故选:B.6.(3分)已知x,y满足方程组,则无论m取何值,x,y恒有关系式是()A.x+y=1B.x+y=﹣1C.x+y=9D.x+y=﹣9【解答】解:由方程组,有y﹣5=m∴将上式代入x+m=4,得到x+(y﹣5)=4,∴x+y=9.故选:C.7.(3分)关于x,y的方程组的解是整数,则整数a的个数为()A.4个B.3个C.2个D.1个【解答】解:①×2﹣②得:(﹣2a﹣1)y=5,y=﹣,把y=﹣代入②得:4x﹣=7,解得:x=,∵方程组的解为整数,∴x、y都是整数,∴要使y为整数,a为整数,必须1+2a=﹣1或1+2a=5或1+2a=1或1+2a=﹣5,解得:a=﹣1或2或0或﹣3,当a=﹣1时,x==,不是整数,舍去;当a=2时,x==2,是整数,符合;当a=0时,x==3,是整数,符合;当a=﹣3时,x==,不是整数,舍去;故选:C.8.(3分)若﹣3xy2m与5x2n﹣3y8的和是单项式,则m、n的值分别是()A.m=2,n=2B.m=4,n=1C.m=4,n=2D.m=2,n=3【解答】解:由题意,得,解得.故选:C.9.(3分)天虹商场现销售某品牌运动套装,上衣和裤子一套售价500元.若将上衣价格下调5%,将裤子价格上调8%,则这样一套运动套装的售价提高0.2%.设上衣和裤子在调价前单价分别为x元和y元,则可列方程组为()A.B.C.D.【解答】解:根据题意可列方程组为,故选:C.10.(3分)方程组消去字母c后,得到的方程一定不是()A.a+b=1B.a﹣b=1C.4a+b=10D.7a+b=19【解答】解:,②﹣①得:3a+3b=3,即a+b=1,③﹣①得:24a+6b=60,即4a+b=10,③﹣②得:21a+3b=57,即7a+b=19,故选:B.二.填空题(共6小题,满分18分,每小题3分)11.(3分)对于方程3x+y=5,用含x的式子表示y=﹣3x+5.【解答】解:方程3x+y=5,解得:y=﹣3x+5.故答案为:﹣3x+5.12.(3分)一种运算:x*y=ax+by(a,b为常数),若3*4=2,5*(﹣1)=11,则2*6=﹣2.【解答】解:∵3*4=2,5*(﹣1)=11,,解得:a=2,b=﹣1,∴2*6=2×2+6×(﹣1)=﹣2,故答案为:﹣2.13.(3分)已知a﹣3b+c=8,7a+b﹣c=12,则5a﹣4b+c=18.【解答】解:由题意:a﹣3b+c=8①,7a+b﹣c=12②,②+①,得8a﹣2b=20.所以4a﹣b=10③.所以①+③,得5a﹣4b+c=18.故答案为:18.14.(3分)若满足方程组的x与y互为相反数,则m的值为11.【解答】解:,①+②得:5x=3m+2,解得:x=,把x=代入①得:y=,由x与y互为相反数,得到+=0,去分母得:3m+2+9﹣4m=0,解得:m=11,故答案为:1115.(3分)把一根长7m的钢管截成2m长和1m长两种规格的钢管,截成不造成浪费的截法有3种.【解答】解;截下来的符合条件的钢管长度之和刚好等于总长7米时,不造成浪费,设截成2米长的钢管x根,1米长的y根,由题意得,2x+y=7,因为x,y都是正整数,所以符合条件的解为:,,,则有3种不同的截法.故答案为:3.16.(3分)如图,由四个形状相同,大小相等的小矩形,拼成一个大矩形,大矩形的周长为12cm.设小矩形的长为xcm,宽为ycm,依题意,可列方程组得.【解答】解:设小矩形的长为xcm,宽为ycm,由题意得:,故答案为.三.解答题(共9小题,满分72分)17.(4分)解方程(组)(1);(2).【解答】解:(1)去分母得:4(2x+5)﹣3(3x﹣2)=24,去括号得:8x+20﹣9x+6=24,移项合并得:﹣x=﹣2,解得:x=2;(2),①﹣②得:3n=15,解得:n=5,将n=5代入②得:3m﹣5=1,解得:m=2,∴原方程组的解为:.18.(4分)已知关于x、y的方程组的x、y的值之和等于2,求m的值.【解答】解:关于x、y的方程组为:,由①﹣②得:x+2y=2,∵x、y的值之和等于2,∴,解这个方程组得,把代入②得:m=4.答:m的值是4.19.(6分)有大小两种货车,3辆大货车与2辆小货车一次可以运货17吨,5辆大货车与6辆小货车一次可以运货35吨,那么3辆大货车与6辆小货车一次可以运货多少吨?【解答】解:设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,依题意,得:,解得:,∴3x+6y=3×4+6×=27.答:3辆大货车与6辆小货车一次可以运货27吨.20.(8分)在等式y=ax2+bx+c中,当x=0时,y=﹣5;当x=2时,y=3;当x=﹣2时,y=11.(1)求a,b,c的值;(2)小苏发现:当x=﹣1或x=时,y的值相等.请分析“小苏发现”是否正确?【解答】解:(1)根据题意,得,②﹣③,得4b=﹣8,解得b=﹣2;把b=﹣2,c=﹣5代入②得4a﹣4﹣5=3,解得a=3,因此;(2)“小苏发现”是正确的,由(1)可知等式为y=3x2﹣2x﹣5,把x=﹣1时,y=3+2﹣5=0;把x=时,y=﹣﹣5=0,所以当x=﹣1或x=时,y的值相等.21.(8分)如图,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之和均相等.(1)求x,y的值;(2)在备用图中完成此方阵图.【解答】解:(1)根据题意得:,解得:.(2)∵x=﹣1,y=2,∴3+4+x=6,2y﹣x=5.∵每行的3个数、每列的3个数、斜对角的3个数之和均相等,∴6﹣(﹣2)﹣y=6;6﹣4﹣y=0;6﹣3﹣y=1.完成方阵图,如图所示.22.(10分)一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付给两组费用共3480元,问:(1)甲、乙两组单独工作一天,商店应各付多少元?(2)已知甲组单独完成需要12天,乙组单独完成需要24天,单独请哪组,商店所付费用较少?【解答】解:(1)设甲单独工作一天需要x元,乙单独工作一天商店需付y元,由题意得,,解得:.答:甲单独工作一天需要300元,乙单独工作一天商店需付140元;(2)甲单独完成需付:300×12=3600(元),乙单独完成需付:140×24=3360(元).答:选择乙组商店所付费用较少.23.(10分)甲、乙二人解关于x、y的方程组,甲正确地解出,而乙因把c抄错了,结果解得,求出a、b、c的值,并求乙将c抄成了何值?【解答】解:把代入方程组,可得:,解得:c=﹣2,把代入ax+by=2中,可得:﹣2a+2b=2,可得新的方程组:,解得:,把代入cx﹣7y=8中,可得:c=﹣11.答:乙把c抄成了﹣11,a的值是4,b的值是5,c的值是﹣2.24.(10分)已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?(2)请你帮该物流公司设计租车方案;(3)若A型车每辆需租金200元/次,B型车每辆需租金240元/次,请选出最省钱的租车方案,并求出最少租车费.【解答】解:(1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,依题意列方程组得:,解方程组,得:,答:1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.(2)结合题意和(1)得:3a+4b=35,∴a=∵a、b都是正整数∴或或答:有3种租车方案:方案一:A型车9辆,B型车2辆;方案二:A型车5辆,B型车5辆;方案三:A型车1辆,B型车8辆.(3)∵A型车每辆需租金200元/次,B型车每辆需租金240元/次,∴方案一需租金:9×200+2×240=2280(元)方案二需租金:5×200+5×240=2200(元)方案三需租金:1×200+8×240=2120(元)∵2280>2200>2120∴最省钱的租车方案是方案三:A型车1辆,B型车8辆,最少租车费为2120元.25.(12分)面对资源紧缺与环境保护问题,发展电动汽车成为汽车工业发展的主流趋势.我国某著名汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)如果工厂招聘m(0<m<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发8000元的工资,给每名新工人每月发4800元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?【解答】解:(1)设每名熟练工和新工人每月分别可以安装x、y辆电动汽车.根据题意,得:,解得:.答:每名熟练工和新工人每月分别可以安装4、2辆电动汽车.(2)设工厂有a名熟练工.根据题意,得12(4a+2m)=240,2a+m=10,m=10﹣2a,又a,m都是正整数,0<m<10,所以m=8,6,4,2.即工厂有4种新工人的招聘方案.①m=8,a=1,即新工人8人,熟练工1人;②m=6,a=2,即新工人6人,熟练工2人;③m=4,a=3,即新工人4人,熟练工3人;④m=2,a=4,即新工人2人,熟练工4人.(3)结合(2)知:要使新工人的数量多于熟练工,则m=8,a=1;或m=6,a=2;或m=4,a=3;根据题意,得W=8000a+4800m=8000a+4800(10﹣2a)=48000﹣1600a.要使工厂每月支出的工资总额W(元)尽可能地少,则a应最大.显然当m=4,a=3时,工厂每月支出的工资总额W(元)尽可能地少.。
核心知识理一横元素价类二维转化关系图合价2MgMg04- M

核心知识理一横元素价类二维转化关系
图合价2MgMg04- M
MgMgO4是一种重要的化学物质,它是一种二元离子化合物,由镁和氧组成。
它的分子式是MgMgO4,它的分子量是58.32 g/mol。
MgMgO4的结构是一个二维的八边形,它的每个角上都有一个氧原子,而每个边上都有一个镁原子。
MgMgO4的合价是2MgMgO4-,它是一种二维的八边形,它的每个角上都有一个氧原子,而每个边上都有两个镁原子。
它的分子式是2MgMgO4-,它的分子量是116.64 g/mol。
MgMgO4和2MgMgO4-之间的转化关系可以用一个二维的元素价类图来表示。
在这个图中,MgMgO4是一个八边形,它的每个角上都有一个氧原子,而每个边上都有一个镁原子。
而
2MgMgO4-则是一个八边形,它的每个角上都有一个氧原子,而每个边上都有两个镁原子。
因此,MgMgO4和2MgMgO4-之间的转化关系可以用一个二维的元素价类图来表示,它们之间的转化可以通过添加或删除镁原子来实现。
这种转化关系可以帮助我们更好地理解MgMgO4和2MgMgO4-之间的关系,从而更好地利用它们。
正比例函数的条件

正比例函数的条件
1.定义域为实数集:正比例函数是定义在实数集上的函数,即对于任意实数,函数都有定义。
这是因为正比例函数的关系可以在实数范围内无限延伸。
2. 二元关系:正比例函数是一种二元关系, 即函数的变量有两个。
一般来说, 正比例函数的输入变量被称为自变量, 而输出变量被称为因变量。
因此, 正比例函数可以表示为 y = kx, 其中 k 是常量。
3.变量间的线性关系:正比例函数的特点是变量之间存在线性关系。
换句话说,如果一个变量的取值增加了一倍,那么另一个变量的取值也会相应地增加一倍。
这种线性关系可以用比例关系符号(∝)表示,例如x∝y。
4.恒定的比例因子:正比例函数中的比例因子k是一个常量,它在整个函数定义域上都保持不变。
这意味着无论自变量的取值如何变化,因变量与自变量之间的比例关系都会保持稳定。
5.零因变量:正比例函数中,当自变量取值为零时,因变量也为零。
这是因为正比例函数的定义中包含了原点(0,0)。
换句话说,如果输入变量为零,那么输出变量也必须为零。
正比例函数在许多实际情况中都有应用。
例如,当物体的质量与其体积成正比时,就可以使用正比例函数来描述它们之间的关系。
同样,当速度与时间成正比时,也可以使用正比例函数来描述它们之间的关系。
正比例函数可以帮助我们理解和预测许多自然现象和实际问题。
04_序偶及笛卡尔积(精)

序偶),记为<a,b>,称a为第一元素,b
为第二元素;若它们无次序区别,称为二 元无序组(无序偶),记为(a,b)。
当ab时,有: <a,b> <b,a>
(a,b) = (b,a)
可用序偶表示两个元素之间的关系:
<老王,小王> 老王是小王的父亲
(小李,小张) 小李和小张是同学
定义: 给定两个有序偶<a,b>和<u,v>, 当且仅当a=u且b=v时,有序偶
记< x1 , x2 , x3 > 记< x1 , x2 , x3 , x4 >
注意: < < x1, x2 >, x3 > 是有序 3 元组 < x1, < x2, x3 > > 不是有序 3 元组 < x1 , x2 , x3 > 表示 < < x1, x2 >, x3 >
二、笛卡尔积
定义:给定集合A和B, AB = {<x,y>|xA∧yB}, 称 AB 为A和B的笛卡尔积。
(A∪B)C = (AC)∪(BC)
求证:A(B∩C) = (AB)∩(AC) 分析: 要证明 左式 和 右式 有相同的元素: <x,y>A(B∩C) <x,y>(AB)∩(AC)
证明:
∵ <x,y>A(B∩C)
xA ∧ yB∩C
xA∧(yB∧yC) (xA∧xA)∧(yB∧yC) (xA∧yB)∧(xA∧yC) <x,y>AB ∧ <x,y>AC <x,y>(AB)∩(AC) ∴ A(B∩C)=(AB)∩(AC)
04 双液系的气-液平衡相图的绘制

实验四 双液系的气-液平衡相图的绘制一、目的要求1.用沸点仪测定大气压下乙醇—环己烷或异丙醇-环己烷双液系气-液平衡时气相与液相组成及平衡温度,绘制温度—组成图,确定恒沸混合物的组成及恒沸点的温度。
2.了解物化实验中光学方法的基本原理,学会阿贝折光仪的使用。
3.进一步理解分馏原理。
二、预习要求1.理解分馏原理,了解影响双液系气-液平衡的因素。
2.熟悉阿贝折光仪的使用方法,了解折射率与物系组成的关系。
3.掌握如何由实验数据绘制t x -相图的方法。
三、实验原理两种在常温时为液态的物质混合起来而组成的二组分体系称为双液系。
两种液体若能按任意比例互相溶解,称为完全互溶的双液系;若只能在一定比例范围内互相溶解,则称部分互双液系。
双液系的气液平衡相图t x -图可分为三类。
如图4.1。
图 4.1 二元系统t x -图这些图的纵轴是温度(沸点),横轴是代表液体B 的摩尔分数B x 。
在t x -图中有两条曲线:上面的曲线是气相线,表示在不同溶液的沸点时与溶液成平衡时的气相组成,下面的曲线表示液相线,代表平衡时液相的组成。
例如图4.1(a)中对应于温度t 1的气相点为y 1,液相点为1l ,这时的气相组成y 1点的横轴读数是g B x ,液相组成点1l 点的横轴读数为lB x 。
y 1l 1t 1g B x l B x A B t/℃(a )气液t/℃A B B x →(b )t/ ℃气液A B B x →(c )如果在恒压下将溶液蒸馏,当气液两相达平衡时,记下此时的沸点,并分别测定气相图。
(馏出物)与液相(蒸馏液)的组成,就能绘出此t x图4.1(b)上有个最低点,图4.1(c)上有个最高点,这些点称为恒沸点,其相应的溶液称为恒沸混合物,在此点蒸馏所得气相与液相组成相同。
四、仪器和药品1.仪器玻璃沸点仪一套;阿贝折光仪一台;WLS系列可调式恒流电源一台;SWJ型精密数字温度计一台;SYC超级恒温槽一台。
2.药品无水乙醇(AR)或异丙醇(AR);环己烷(AR)。
二元关系传递闭包的求法及与图的可达矩阵的关系

2 eDp. o fm tnTco g,eigM ngm n ol eo otsadl Bin 004C ia . et, fno ai ehl yB rn aae et lg f l c n w,eig102 ,h ) I r o o C e Pi i a j n
Absr t h h rce siso ouin b u h r n iv ls r o iay rlto r n lzd. B sn h lto ewe n i a d tac :T ec aa tr t fslt sa o tte ta st e coue frbn r eain ae a aye i c o i y uig te r ain b t e t n e ra h bly mar fga h,W asalagrtm sa pe oc mp t gteta h blt t x cc a it tx o rp i i rh lo h i do t t o ui h e c a ii mar ,whc i ie h o uigpo e s l i d n y i ih smpliste cmp tn rc s. f
时我们可以只使用逻辑加和逻辑乘即可利用并将中主对角线元素全部变为传递闭包与图的可达性矩阵关系由可达性矩阵的定义以及上述两种求取方法可知有向图的可达性矩阵与二元关系的传递闭包具有密切关系两者都是寻找从某一元素的可达路径唯一区别即在于在可达性矩阵中由于其主对象线元素永远为而在二元关系传递闭包的关系图中可能不存在这种关系即不一定每个元素都有自环所以这里也可以采用求传递闭包的方法求取有向图的可达性矩阵
Ke r s i a y r l t n;ta st e co u e;r a h b lt ti y wo d :b n r a i e o rn iv lsr i e c a ii ma rx;W a s ala g r h y r h l o t m l i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013-7-10 离散数学 3
一、二元关系的概念(续)
例1:设A = { a, b },B = { 0, 1, 2 },求A B,B A。
解:由笛卡尔积的定义知
A B = { < a, 0 >, < a, 1 >, < a, 2 >, < b, 0 >, < b, 1>, < b, 2> } B A = { < 0, a >, < 0, b >, < 1, a >, < 1, b >, < 2, a >, < 2, b> } 一般地,若|A| = m, |B| = n, 则|A B| = |B A| = mn
如果< x, y > R ,记作
2013-7-10 离散数学
xRy
8
一、二元关系的概念(续)
从A到B的二元关系:设A、B为集合, A B的任何 子集所定义的二元关系叫做从A到B的二元关系。 设A={a,b,c}代表三个人的构成的集合
B={1,2,3,4}代表四项工作构成的集合
若a从事工作1,b从事工作2,c从事工作3,则人从事工
若|A| = n,则|A A| =
2
, A A的所有子集有 2 因此, A上有 2 n个不同的二元关系。 n2
2013-7-10 离散数学
2 n个,
10
一、二元关系的概念(续)
A的3种特殊关系:空关系,全域关系EA,恒等关系IA
空关系即空集
全域关系EA = { < x, y >| xA yA }= A A 恒等关系IA = { < x, x >| xA} 例3:设A = {a, b},写出P(A)上的包含关系R 。 解:P(A) = { , {a}, {b}, {a, b} } R = { <, >, <, {a}>, <, {b}>, <, {a, b}>,
A ( B C),即笛卡尔积不满足结合律。
2013-7-10
离散数学
5
一、二元关系的概念(续)
(4)笛卡尔积运算对∪或∩运算满足分配律, 即A (B∪C) = (A B)∪(A C) (B∪C) A = (B A)∪(C A) A (B∩C) = (A B)∩(A C) (B∩C) A = (B A)∩(C A) 证明:< x, y > (B∪C) A xB∪C yA ( xB xC ) yA ( xB yA ) ( xC yA ) ( < x, y > B A ) ( < x, y > C A ) < x, y >(B A)∪(C A)
第四章
二元关系和函数
§4.1 集合的笛卡尔积与二元关系 §4.2 关系的运算 §4.3 关系的性质 §4.4 关系的闭包 §4.5 等价关系和偏序关系
§4.6 函数的定义和性质
§4.7 函数的复合和反函数
2013-7-10 离散数学 1
§4.1 集合的笛卡尔积与二元关系
一、二元关系的概念
有序对(序偶):由两个元素x 和y 按一定顺序排成
x1
2013-7-10 离散数学
x2
x3
13
二、二元关系的表示方法(续)
例4:设A = {1, 2, 3, 4}, R = { <1, 2>, <1, 3>, <2, 2>,
<2, 4>, <3, 4>, <4, 2> }是A上的关系,试写出R的
关系矩阵并画出关系图。
解: 关系矩阵 关系图
0 0 0 0
的二元组。记作:< x, y >。其中x是它的第 一元素,y是它的第二元素。 如平面直角坐标系点的坐标。 特点:(1)当x y 时,< x, y > < y, x >
(2) < x, y > = < u, v > 当且仅当x = u, y = v
(1)(2)说明有序对区别于集合。
2013-7-10 离散数学 2
例: 设R={<1,2>,<1,3>,<2,2>,<2,4>,<3,2>}
R ↾{1}= {<1,2>,<1,3>}
R ↾ {2,3}= {<2,2>,<2,4> ,<3,2>} R[{1}]= {2,3} R[{3}]= {2}
2013-7-10
离散数学
18
二、关系的常用运算(续)
例6:设F, G是N上的关系,其定义为
<{a}, {a}> <{a}, {a, b}>, <{b}, {b}>,
<{b}, {a, b}>, <{a, b}, {a, b}> }
2013-7-10 离散数学 11
二、二元关系的表示方法
1、关系矩阵
设A = { x1, x2, …, xn },R是A上的关系, 令 1 若xi R xj
rij =
F = { < x, y > | x, yN y = x2 }
G = { < x, y > | x, yN y = x + 1 }
求G –1, F G, G F, F | {1, 2}, F [{1, 2}]。 解:G –1 = { < y, x > | x, yN y = x + 1 } 列出G –1中的元素即为 G –1 = {<1, 0>, <2, 1>, <3, 2>, … , < x + 1, x >, … }
作之间的关系可以表示为:
R={<a,1>,<b,2>,<c,4>}
为A到B的二元关系之一
2013-7-10
离散数学
9
特别地,若A = B,叫作A上的二元关系。
例如: 家庭成员集合A={a,b,c,d}上的成员分别代表父、母、兄、
弟,则该集合上的各种关系为: 父子关系:{ <a,c>,<a,d> }. 母子关系: { <b,c>,<b,d> }. 兄弟关系: 。。。夫妻关系。。。 都是A上的二元关系
(i, j = 1, 2, … , n)
0 若xi R xj
r12 r22 ... rn 2 ... r1n ... r2 n 是R的关系矩阵 ... ... ... rnn
离散数学 12
r11 则( rij )n×n = r21 ... r n1
2013-7-10
2013-7-10 离散数学 4
一、二元关系的概念(续)
笛卡尔积运算的性质:
(1) 如果A, B中有一个空集,则笛卡儿积是空集,
即: B = A =
(2) 当A B,且A, B都不是空集时,有A B B A, 即笛卡尔积不满足交换律。 (3) 当A, B, C都不是空集时,有(A B) C
2013-7-10
1 1 0 1
1 0 0 0
0 1 1 0
离散数学
1•
•2 •3
4•
思考:写出例3的关系矩阵和关系图
14
§4.2 关系的运算
一、关系的定义域与值域
关系R的定义域(domain) : dom R = { x | y(< x, y >R) } ,
即R中所有有序对的第一元素构成的集合。
2013-7-10 离散数学 20
二、关系的常用运算(续)
例6:设F, G是N上的关系,其定义为
F = { < x, y > | x, yN y = x2 }
G = { < x, y > | x, yN y = x + 1 }
求G –1, F G, G F, F | {1, 2}, F [{1, 2}]。 解:为了求G F可以先直观表示如下: 对任何xN x F x2 = z G z + 1 = y 即 y = x2 + 1 因此G F = {< x, y > | x, yN y = x2 + 1}
一、二元关系的概念(续)
n 元有序对:第一元素是一个n –1元有序对的有序对。
记作:< x1, x2, … , xn >。
即< x1, x2, … , xn > = << x1, … , xn-1 >, xn > 笛卡尔积:设A、B为两集合,以A中元素为第一元
素,B中元素为第二元素构成的二元有
序对的全体叫做A和B的笛卡儿积。
集合A在F 下的象,记作:F [A] 4、象: F [A] = ran (F ↾ A)
2013-7-10
离散数学
17
例: 设F={<3,3>,<6,2>}, G={<2,3>,<3,6>},
则F-1 ={<3,3>,<2,6>},
ቤተ መጻሕፍቲ ባይዱ
FG= {<2,3>, <3,2>} , GF= {<6,3>,<3,6>}
2013-7-10 离散数学 16
二、关系的常用运算
