第三节5节微分PPT课件
合集下载
【精品PPT】微分学课件

u v,
(u+v+…+ω)′=
u vω .
(2)积的导数:(uv)′= uv uv,
特例:(cu)′= cu (c为常数).
(3)商的导数: u =
uv - uv v2 (v≠0).
v
例1 设 y x4,则 y '
例2 求 y x3 2x2 sin x 的导数 .
f (x0 )
f(x0 )
lim
x0
y x
lim x0
f (x0 x) x
f (x0 )
注意 函数在一点可导的充分必要条件为:
f' (x0 ) f' (x0 )
导函数
(1)如果函数 y f (x)在开区间(a,b)内的每一点都可导,
就称函数 f (x)在开区间(a,b) 内可导.
y
y f (x)
T
M
o
x0
x
在(x0, f (x0 ))处的
切线方程为 y y0 f ( x0 )( x x0 ). 每年都考、重点掌握!
法线方程为
y y0
f
1 ( x0
)
(
x
x0
)
(f (x0 ) 0).
例1、曲线 y 2x2在点(1,2)处的切线方程为:.
A. y x 1 B. y x C. y x 1 D. y x
例. 曲线 y 3 x 在点 (0,0) 处的切线方程为(
)
A、 x 0
B、 y 0
C、 x y
例. 设 y (1 x2 ) arctan x, 求 y/
D、不存在
微积分课件第3节空间曲线及其在坐标面上的投影

方程组
所表示的曲线方程称为
空间曲线的一般方程. 特殊地,空间直线方程
三、空间曲线及其在坐标面上的投影
例1
方程组
x2
+
y2
+ z2
=
25,
表示什么曲线?
z= 3;
解 因为 x2 + y2 + z2 = 25是球心在原点, 半径为
5 的球面.
z
z = 3 是平行于 x y
坐标面的平面,
z=3
因而它们的交线是
柱面的概念
准线
母线
平行于定直线并沿定曲线 C 移动的直线L 所形成的曲面称为柱面.
复习
几种常用的柱面方程及图形
(1)圆柱面
(2)椭圆柱面
(3)双曲柱面
(4)抛物柱面
统 称 为 二 次 柱 面 圆柱面
椭圆柱面
抛物柱面
三、 旋转曲面
一平面曲线 C 绕同一平面上的一条定直线 L 旋转一周
所形成的曲面称为 旋转曲面. 曲线C 称为旋转曲面的
定直线 L 称为旋转曲面的 旋转轴.
z
1.圆锥面方程
2. 旋转抛物面
O
y
x
第三节 空间曲线及其在 坐标面上的投影
第四节 二次曲面
第三节 空间曲线及其在坐标 面上的投影
一、空间曲线的一般方程 二、空间曲线在坐标面上的投影 三、小结 思考题
第三节 空间曲线及其在坐标面上的投影
一、空间曲线的概念
1、空间曲线 把空间曲线C看作是两曲面的交线.
二、空间曲线在坐标面上的投影
补充: 空间立体或曲面在坐标面上的投影.
空间立体
曲面
二、空间曲线在坐标面上的投影
高等数学(微积分)ppt课件

,且f'(x0)=0,则可通过二阶导数 f''(x0)的符号来判断f(x)在x0处取得极大值还是极小值。
曲线的凹凸性与拐点
凹凸性
若函数f(x)在区间I上二阶可导,且 f''(x)>0(或<0),则称曲线y=f(x)在 I上是凹的(或凸的)。
拐点
拐点的判定
若函数f(x)在点x0处二阶可导,且 f''(x0)=0,则可通过三阶导数f'''(x0) 的符号来判断点(x0,f(x0))是否为曲线 的拐点。
THANKS
感谢观看
非线性微分方程
通过变量替换、积分等方法求解,或 利用数值方法近似求解
级数的概念与性质
级数的定义 无穷序列的部分和序列
级数的性质 加法、减法、乘法、除法、重排等性
质
级数的收敛与发散 部分和序列有极限则级数收敛,否则 发散
常见级数及其敛散性 等差级数、等比级数、调和级数、交 错级数等,通过比较法、比值法、根 值法等方法判断其敛散性
VS
极限的性质
唯一性、局部有界性、保号性、保不等式 性、迫敛性等。
极限的运算法则
极限的四则运算法则
若两个函数的极限存在,则它们的和、差、积、商(分母不为零)的极限也存在,且等于这两 个函数极限的和、差、积、商。
复合函数的极限运算法则
设函数$y=f[g(x)]$是由函数$u=g(x)$与函数$y=f(u)$复合而成,若$lim_{x
无穷小量的定义
如果函数$f(x)$当$x to x_0$(或$x to infty$)时的极限为零,那么称函数$f(x)$为当$x to x_0$(或$x to infty$)时 的无穷小量。
曲线的凹凸性与拐点
凹凸性
若函数f(x)在区间I上二阶可导,且 f''(x)>0(或<0),则称曲线y=f(x)在 I上是凹的(或凸的)。
拐点
拐点的判定
若函数f(x)在点x0处二阶可导,且 f''(x0)=0,则可通过三阶导数f'''(x0) 的符号来判断点(x0,f(x0))是否为曲线 的拐点。
THANKS
感谢观看
非线性微分方程
通过变量替换、积分等方法求解,或 利用数值方法近似求解
级数的概念与性质
级数的定义 无穷序列的部分和序列
级数的性质 加法、减法、乘法、除法、重排等性
质
级数的收敛与发散 部分和序列有极限则级数收敛,否则 发散
常见级数及其敛散性 等差级数、等比级数、调和级数、交 错级数等,通过比较法、比值法、根 值法等方法判断其敛散性
VS
极限的性质
唯一性、局部有界性、保号性、保不等式 性、迫敛性等。
极限的运算法则
极限的四则运算法则
若两个函数的极限存在,则它们的和、差、积、商(分母不为零)的极限也存在,且等于这两 个函数极限的和、差、积、商。
复合函数的极限运算法则
设函数$y=f[g(x)]$是由函数$u=g(x)$与函数$y=f(u)$复合而成,若$lim_{x
无穷小量的定义
如果函数$f(x)$当$x to x_0$(或$x to infty$)时的极限为零,那么称函数$f(x)$为当$x to x_0$(或$x to infty$)时 的无穷小量。
《高等数学》教学课件:第三节 微分方程在生物医学中的应用实例

数学与生物信息学教研室 Mathematics & Bioinformatics
6
把M(t)=V·C(t)代入上式,得一阶线性微分方程
dC(t) dt
kAC(t) V
kA V
c0
初始条件是 C(t) |t0 C(0) ,解该线性微分方程,得特解
kAt
C(t) c0(c0 C(0))e V
从特解可以看出,当初始时刻细胞的浓度C(0)高于细胞
细胞c0内的浓度是随时间变化的,记为C(t),又假
设细胞体积不变,记为V,细胞膜面积为A,那 么细胞内的浓度C(t)与质量M(t)的关系是 M(t)=V·C(t).细胞内的质量随时间的变化率与细
胞膜的面积和细胞膜内外的浓度差的乘积成正
比,比例系数为k,得微分方程
dM (t) dt
kA(c0
C(t))
(1)静脉注射给药
在快速静脉注射给药时,血药浓度C(t)下降率 与浓度成正比,比例系数k为消除速率常数, C(t)满足下面一阶微分方程和初始条件
数学与生物信息学教研室 Mathematics & Bioinformatics
11
dC (t )
kC(t)
dt
C(0) C0
它是一阶可分离变量的微分方程,求特解得:
数学与生物信息学教研室 Mathematics & Bioinformatics
14
注:使用微分方程描述生理过程时,有两种提法,一是解
正问题,另一是解反问题.解正问题指:用微分方程和初始 值求出问题的解,研究解随时间的变化,预言生理指标在 不同时刻的值.在解正问题时,必须要知道微分方程中各种 参数,可是,有时某些参数是不能事先知道的,而是要靠 实验数据决定的.因此,求解正问题有时是受到限制的,不 能实现.解反问题指:用实验数据决定微分方程中的参数, 所用的方法是拟合方法(关于拟合方法参见 ).拟合出微分 方程中的参数,就回到了解正问题.因为,微分方程是驱动 过程的本质,如果从专业知识知道了生理过程所满足的微 分方程,那么,根据微分方程的解的形式,选择拟合函数 就容易了. 总之,这里介绍的是最简单的一阶常微分方程在生理学和 医学中的部分应用,描述更复杂的问题时,还要用到诸如 常微分方程组(如肾透析问题)和高阶常微分方程,甚至用 到偏微分方程.请参考有关书籍.
导数与微分5-27页PPT精品文档

y
T
M
yf(x)
N
P
o(x)
dy y
x
记作 d x
)
o
x0 x0x
x
则有 dyf(x)dx
从而 dy f (x) dx
导数也叫作微商
Friday, September 20, 2019
7
例如, y x3,
d y x 2 3x2 dx x 2 0.24
dx 0.02
即 dyf(x0) x
Friday, September 20, 2019
5
说明: y f( x 0 ) x o ( x ) dyf(x0) x
当 f(x0)0时 , lim y lim y x 0 d y x0 f(x0)x 1 limy 1 f(x0)x0x
14
例4. 求
的近似值 .
解: 设 f(x)sixn,
取
则 dx π 180
sin29 sin 29 π sin π cos π ( π )
180
6
6 180
1 3 (0.017)5 22
Friday, September 20, 2019
15
例5. 计算 的近似值 .
得增量x 时, 面积的增量为
x x0x (x)2
关于△x 的 x0时为
线性主部 高阶无穷小
x 0 A x02
故
Friday, September 20, 2019
称为函数在 x 0 的微分
x0x
2
定义: 若函数
在点 x 0 的增量可表示为
A xo ( x)
( A 为不依赖于△x 的常数)
高等数学上册第七章课件.ppt
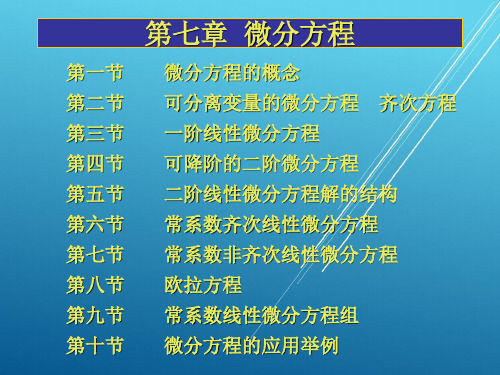
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
微分ppt课件

微分PPT课件
目录
微分的定义与性质导数的概念与性质导数在研究函数中的应用微分中值定理微分的应用
01
CHAPTER
微分的定义与性质
总结词
微分是一种数学运算,表示函数在某一点的局部变化率。
详细描述
微分是微积分的基本概念之一,它表示函数在某一点的切线的斜率。具体来说,如果函数在某一点的导数存在,那么这个导数就是函数在该点的微分。微分可以看作是函数值的增量与自变量增量的比的极限。
极值点是函数的重要特征点,利用导数研究函数的极值有助于找到这些关键点。
1
2
3
4
通过求二阶导数,可以找到函数的拐点。
二阶导数为0的点可能是拐点,需要进一步判断三阶导数的符号来确定是向上凸还是向下凸。
对于函数$f(x) = x^4$,其二阶导数$f''(x) = 12x^2$,令其为0得到拐点$x=0$,进一步求三阶导数$f'''(x) = 24x$,在$x=0$处为非正值,因此$x=0$为向下凸的拐点。
举例
单调性是函数的一个重要性质,利用导数研究函数的单调性有助于理解函数的述
举例
应用
通过求导数,可以找到函数的极值点。
一阶导数为0的点可能是极值点,需要进一步判断二阶导数的符号来确定是极大值还是极小值。
对于函数$f(x) = x^3$,其一阶导数$f'(x) = 3x^2$,令其为0得到极值点$x=0$,进一步求二阶导数$f''(x) = 6x$,在$x=0$处为非负值,因此$x=0$为极小值点。
罗尔定理是数学分析中的一个基本定理,由法国数学家罗尔发现。该定理在微分学、积分学等领域有着广泛的应用。它提供了一个判断函数是否存在导数为零的点的方法,对于研究函数的极值和拐点等问题具有重要的意义。
目录
微分的定义与性质导数的概念与性质导数在研究函数中的应用微分中值定理微分的应用
01
CHAPTER
微分的定义与性质
总结词
微分是一种数学运算,表示函数在某一点的局部变化率。
详细描述
微分是微积分的基本概念之一,它表示函数在某一点的切线的斜率。具体来说,如果函数在某一点的导数存在,那么这个导数就是函数在该点的微分。微分可以看作是函数值的增量与自变量增量的比的极限。
极值点是函数的重要特征点,利用导数研究函数的极值有助于找到这些关键点。
1
2
3
4
通过求二阶导数,可以找到函数的拐点。
二阶导数为0的点可能是拐点,需要进一步判断三阶导数的符号来确定是向上凸还是向下凸。
对于函数$f(x) = x^4$,其二阶导数$f''(x) = 12x^2$,令其为0得到拐点$x=0$,进一步求三阶导数$f'''(x) = 24x$,在$x=0$处为非正值,因此$x=0$为向下凸的拐点。
举例
单调性是函数的一个重要性质,利用导数研究函数的单调性有助于理解函数的述
举例
应用
通过求导数,可以找到函数的极值点。
一阶导数为0的点可能是极值点,需要进一步判断二阶导数的符号来确定是极大值还是极小值。
对于函数$f(x) = x^3$,其一阶导数$f'(x) = 3x^2$,令其为0得到极值点$x=0$,进一步求二阶导数$f''(x) = 6x$,在$x=0$处为非负值,因此$x=0$为极小值点。
罗尔定理是数学分析中的一个基本定理,由法国数学家罗尔发现。该定理在微分学、积分学等领域有着广泛的应用。它提供了一个判断函数是否存在导数为零的点的方法,对于研究函数的极值和拐点等问题具有重要的意义。
《微积分》(上下册) 教学课件 02.第2章 导数与微分 高等数学第一章第3-5节

1
记作
f
(
x),
y,
d2y dx2
或
d
2 f (x) dx2
.
二阶导数的导数称为三阶导数,记作
f ( x),
y,
d3y dx3 .
三阶导数的导数称为四阶导数, 记作
f (4)(x),
y(4) ,
d4y dx4 .
一般地, 函数f ( x)的n 1阶导数的导数称为
函数f ( x)的n阶导数, 记作
f (n)(x),
10
一、微分的概念
实例 半径为 x的0 金属圆板受热后面积的改变量.
设半径由x0变到x0 x,
圆板的面积 A x02,
A (x0 x)2 x02
2x0 x (x)2.
(1)
(2)
(1) x的线性函数,且为A的主要部分;
(2) x的高阶无穷小,当x 很小时可忽略.
11
再例如
设函数 y x3在点 x0处的改变量为x时, 求函数的 改变量 y.
§2.3 高阶导数
问题 变速直线运动的加速度.
设 s s(t), 则瞬时速度为v(t) s(t);
因为加速度a是速度v对时间t的变化率,所以
a(t) v(t) s(t).
定义 如果f (x)的导函数f (x)在点x处可导,即
( f (x)) lim f (x x) f (x)
x0
x
存在,则称( f (x))为f (x)在点x处的二阶导数.
dt dx
3a sin2 t cost 3a cos2 t(sint
)
tan t,
dt
d2y dx2
d (dy) dx dx
d ( tan t ) dx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究微分法与导数理论及其应用的科学,做微分学.
★ 导数与微分的联系: 可导 可微.
f ( x) df ( x) , dx
df ( x) f ( x)dx .
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
第五节 函数的微分
一、问题的提出 二、微分的定义 三、可微的条件 四、微分的几何意义 五、微分的求法 六、*微分在近似计算中的应用 七、小结
一、问题的提出——近似计算问题
设一边长为 x 的正方形 , 它的面积 s x2是 x
的函数, 若边长由 x0 增加 x ,
相应的正方形的面积的增量
x0
x (x)2
证 (1)必要性:由f (x)在点x0可微知, y A x x,
则 lim y A lim x =A
x0 x
x0 x
(2)充分性:由函数f
(x)在点x0可导知,
lim
x0
y x
A
则 y A ,其中 0(x 0),
x
则 y A x x
可导 可微 ; 且 A f ( x0 ),
即 df (x) |xx0 f (x0 ) x f (x0 ) dx,
x0x
x
S (x0 x)2 x02
2x0 x (x)2.
(1)
(2)
A x02
x0x x0
(1) : x 的线性函数 , 且为 S 的主要部分 ;
(2) : x 的高阶无穷小 , 当 x 很小时可忽略 .
S 2x0x
二、微分定义:
设y f (x)在x0的某领域有定义,x0及 x0 x在这区间 内,如果y f (x0 x) f (x0)可以表示成
四、微分的几何意义
y
T
C: y=fBiblioteka x) 在 M(x0, f(x0)) 的切线
T:y- f(x0)= f(x0)(x- x0) = f(x0)x = dy
N
P
o(x)
M
dy y
y f (x)
x
)
o
x0 x0 x
x
dy |x x0 f ( x0 )x 是 C : y f ( x) 在 M( x0 , f ( x0 )) 点的 切线纵坐标的增量 。
ω
ω
(2) d(sin x2 ) d( x )
2x cos x2dx 1 dx
4x
x cos x2 ,
2x
d(sin x2 ) (4x x cos x2 )d( x ).
*六、微分在近似计算中的应用
1. 求 函数增量的近似值 :
y |x x0 f ( x0 x) f ( x0 ) dy |x x0 f ( x0 ) x.
360
32
f ( π ) 3 .
3
2
有 cos 60o30 cos( ) cos sin
3 360
3 3 360
1 2
3 2
360
0.4924.
3. 估计误差(略)。
七、小结
★ 微分学所要解决的两类问题:
函数的变化率问题
导数的概念
函数的近计算似问题
微分的概念
求导数与微分的方法,叫做微分法.
例3 在下列等式左端的括号中填入适当的函数, 使 等式成立.
(1) d( ) cosωtdt; (2) d(sin x2 ) ( )d( x ).
解 (1)d(sinωt) ωcosωtdt,
cosωtdt 1 d(sinωt) d( 1 sin ωt);
d(
1
sin
ωt
ω
C)
cos
ωtdt .
五. 微分的求法
例1 设 y ln( x ex2 ) , 求 dy .
解
y
1
x
2
xe x 2 ex2
,
dy
1
x
2
xe x 2 ex2
dx.
例2 设 y e13x cos x , 求 dy .
解 因为 y e13x (3cos x sin x) 那么 dy= e13x (3cos x sin x)dx
y A x x
的形式,(其中A是常数) ,则称函数 y f (x)在点 x0可微, 并 且称A x为函数y f (x)在点 x0的微分,记为:
dy xx0 A x ,或 df (x0 ) A x 也可以简记为:dy=A x
三、可微的条件
定理 f ( x) 在 x0 可微 f ( x) 在 x0 可导 ( 且 A f ( x0 ) ) .
f
( x0 )
df
( x) |xx0 dx
df ( x) dx
|x x0
,即
y' dy , dx
导数又叫做“微商”。
例1 用导数与微分的关系求下列微分
求 :(1)y x3 的微分 ;
(2) y x3 x 2, x 0.02 的微分 .
解 (1) dy ( x3 )x 3x2x ;
(2) dy | x2 3x2 |x2 x |x0.02 0.24 . x0.02
( f ( x0 ) 0且 x 很小时)
例7 半径10厘米的金属圆片加热后 ,半径伸长了0.05 厘米,问面积增大了多 少? 解 记金属圆片的半径为 r,面积为A,则A πr 2 ,
当r 10厘米、r 0.05厘米时,
A dA 2πr r 2 10 0.05 (厘米2 ).
答:面积增大了约π 平方厘米。
You Know, The More Powerful You Will Be
结束语
感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
讲师:XXXXXX XX年XX月XX日
2. 求 f ( x) 在点 x x0 附近的近似值 :
f ( x0 x) f ( x0 ) f ( x0 ) x. ( x 很小时)
例8 计算 cos 60o30 的近似值 .
解 记 f ( x) cos x , 则 f ( x) sin x , ( x为弧度)
取
x0
π 3
,
x π , 由 f ( π ) 1 ,
