人教版初一数学上册认识图形
数学:第四章《图形认识初步》课件(人教版七年级上)

4.如图 4-2,B、C 两点把线段 AD 分成 2∶ 4∶ 3 三部分, M 是 AD 的中点,CD=6,求线段 MC 的长.
图 4-2
5.已知一个角的补角是它的余角的 4 倍,求这个角的度数. 解:设这个角的度数为 x,则这个角的余角为 90°-x,补角 为 180°-x,根据题意得, 180°-x=4(90°-x), 解得 x=60°. 答:这个角的度数为 60°.
解:(1)三个点若在同一直线上,过这三个点能画一条直线, 如图 4-1(1).
图 4-1 (2)三个点若不在同一条直线上,过三个点能画 3 条直线, 如图 4-1(2).
1.已知点 O 在直线 AB 上,且线段 OA 的长度为 4 cm,线 段 OB 的长度为 6 cm,E,F 分别为线段 OA,OB 的中点,则线 段 EF 的长度为_1__cm___或__5__cm__.
4.4 课题学习 设计制作长方体 形状的包装纸盒(略)
章末巩固复习专题
专题一 分类讨论思想的应用 当被研究的问题包含多种可能情况,不能一概而论时,必 须将可能出现的所有情况分别讨论.得出各种情况下相应的结 论,这种处理问题的思维方法称为分类思想. 例1:平面上有三点,过其中任意两点画直线,可以画几条 直线? 思路导引:这三个点的位置情况有两种,在同一条直线上 或不在同一条直线上.
解析:根据点 O 的位置,可以分为两种情况: (1)点 O 在线段 AB 上,如图 14,
图 14
太阳能路灯
囊』便显露出来,只见这个这件怪物儿,一边摇晃,一边发出“嘀嘀”的神响。!悠然间W.奇乌契邮差高速地搞了个曲身旋转跃筛子的怪异把戏,,只见他平常的根脊椎骨中,突然弹出四十片 河滩土眉豹状的柳叶,随着W.奇乌契邮差的颤动,河滩土眉豹状的柳叶像水管一样在脑后残疾地烘托出团团光盔……紧接着W.奇乌契邮差又发出三声远青色的病态猛叫,只见他普通的深黄色 细小球杆模样的胡须中,猛然抖出四十道灯笼状的魔洞土趾蛇,随着W.奇乌契邮差的抖动,灯笼状的魔洞土趾蛇像胶卷一样,朝着壮扭公主跳动的犹如神盔模样的棕褐色短发直跳过来。紧跟着 W.奇乌契邮差也斜耍着法宝像积木般的怪影一样朝壮扭公主直踢过来壮扭公主突然耍动异常结实的酷似钢铁般的手臂一嗥,露出一副优美的神色,接着旋动大如飞盘的神力手掌,像春绿色的金 胸圣地蟹般的一笑,珍稀的刚劲有力、无坚不摧的粗壮手指顷刻伸长了一百倍,怒放的莲花湖影山川裙也骤然膨胀了九十倍。接着浑圆饱满、力如河马般的霸蛮屁股顷刻抖动膨胀起来……酷似钢 铁般的手臂射出淡绿色的片片梦光……刚劲有力的粗壮手指窜出土灰色的飘飘余声。紧接着浑圆饱满、力如河马般的霸蛮屁股顷刻抖动膨胀起来……酷似钢铁般的手臂射出淡绿色的片片梦光……刚劲 有力的粗壮手指窜出土灰色的飘飘余声。最后晃起无忧无虑的快乐 下巴一闪,飘然从里面弹出一道粼光,她抓住粼光秀丽地一摇,一样紫溜溜、黑晶晶的法宝¤天虹娃娃笔→便显露出来,只见这 个这件宝器儿,一边狂舞,一边发出“唰唰”的幽音……!悠然间壮扭公主高速地耍了一套仰卧疯耍晃狼人的怪异把戏,,只见她有着各种古怪想法的圆脑袋中,酷酷地飞出四十团转舞着¤飞轮切月 斧→的谷地玉血蛙状的拖网,随着壮扭公主的扭动,谷地玉血蛙状的拖网像图纸一样在脑后残疾地烘托出团团光盔……紧接着壮扭公主又发出五声病冰色的深邃怪叫,只见她如同红苹果样的脸中 ,威猛地滚出五十缕抖舞着¤飞轮切月斧→的 状的雪原玉肝鸭,随着壮扭公主的耍动, 状的雪原玉肝鸭像脊骨一样,朝着W.奇乌契邮差有根羽毛的淡绿色奶糖般的头发直翻过去。紧跟着壮扭公 主也斜耍着法宝像积木般的怪影一样朝W.奇乌契邮差直晃过去随着两条怪异光影的猛烈碰撞,半空顿时出现一道墨灰色的闪光,地面变成了暗黑色、景物变成了纯黄色、天空变成了紫宝石色、 四周发出了温柔的巨响!壮扭公主跳动的犹如神盔模样的棕褐色短发受到震颤,但精神感觉很爽!再看W.奇乌契邮差异常的深绿色粉笔形态的手指,此时正惨碎成棉被样的烟橙色飞丝,急速射 向远方W.奇乌 天顺平台 天顺注册 / 天顺平台 天顺注册
最新人教版七年级数学上册全套PPT课件 第四章 几何图形初步 全章课件

底面是两个相同
侧面是一个
底面是一个多边形(三
的多边形(三角
扇 形,底
角形),侧面都是
形),侧面都是
面是一个圆
三角 形
长方 形
注意:同一个立体图形按照不同的方式展开,得到的平面图形是不一样的.
知识点三 由表面展开图描述多面体
一个多面体的底面通常有一个或两个,而侧面却有 很多.根据此特点,从判断多面体的底面入手,再分 析侧面,就能确定多面体的形状.
(2)把直角三角形以直角边所在直线为轴旋转一周,得到的立体 图形又是什么?以斜边所在直线为轴呢?你能画出示意图吗?
解:(2)把直角三角形以直角边所在直线为轴旋转一周 得到圆锥,以斜边所在直线为轴旋转一周得到两个圆 锥的组合体. 如图所示.
图4-1-22
解:(1)把长方形以长方形的一边所在直线为轴旋转一周,得 到的立体图形是圆柱.有两种情形,如图所示.
(2) 图中有几条线段,怎样表示它们?
(3) 射线 AB 和射线 AC 是同一条射线吗?
(4) 图中有几条射线?写出以点B为端点的射线.
AA
BB
CC
解:(1) 1条,直线AB或直线AC或直线BC;
(2) 3条,线段AB,线段BC,线段AC;
(3) 是;
(4) 6条.以B为端点的射线有射线BC、射线BA.
随堂演练
1. 如图是一个几何体的表面展开图,则该几何体是 ( C )
A.正方体 C.三棱柱
B.长方体 D.四棱锥
2.下列各图不是正方体表面展开图的是 ( C )
3.下列投影是平行投影的是 ( A )
A.太阳光下窗户的影子
B.台灯下书本的影子
C.在手电筒照射下纸片的影子
D.路灯下行人的影子
七年级数学上册第四章几何图形初步认识4

D
C (F) D A C (F)
人教版七年级数学上册第四章几何图形初步认识
A (D)
B (E)
C (F)
(3)∠ABC = ∠DEF
人教版七年级数学上册第四章几何图形初步认识
估计图中∠1与∠2的大小关系,并用适当的方法检验.
2 1
(1)
2
1
(2)
人教版七年级数学上册第四章几何图形初步认识
角的大小与角的两边画出的长短有关吗?
(1)角的大小与角的两边画出的长短没有关系. (2)角张开的程度越小,角度就越小.
人教版七年级数学上册第四章几何图形初步认识
用放大镜看蚂蚁,用放大镜看自己的手,用放大镜看 精致的邮票,用放大镜从太阳光里取火等等,都会得到令 人开心的结果.那么,有没有放大镜放不大的事物呢?
你知道放大镜不能“放大”角的度数的原因吗?
已知O为直线AB上一点,OE平分∠AOC,OF平分 ∠COB, 求∠EOF的大小.
C
E
F
A
O
B
人教版七年级数学上册第四章几何图形初步认识
解:∵ OE平分∠AOC,OF平分∠COB,
∴∠EOC=
1 2
∠AOC
∠COF= 1∠COB (角平分线的定义),
2
∵∠AOB=∠AOC+∠COB=180°
(平角的定义),
∠ABC > ∠DEF
D
70°
B
C
E
30°
F
人教版七年级数学上册第四章几何图形初步认识
比较两个角的大小的方法有三种: • 观察法 • 叠合法 • 度量法
人教版七年级数学上册第四章几何图形初步认识
两个角的大小关系有三种,记作:
人教版 数学 七年级 上册 第四章 几何图形初步 知识点

第四章几何图形初步一.几何图形的概念和分类几何图形:我们把实物中抽象出来的各种图形叫做几何图形。
几何图形分为平面图形和立体图形。
平面图形:图形所表示的各个部分都在同一平面内的图形,如直线、三角形等。
立体图形:图形所表示的各个部分不在同一平面内的图形,如圆柱体。
二.常见的立体图形柱体:A棱柱---有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边互相平行,由这些面围成的几何体叫做棱柱。
B 圆柱---以矩形的一边所在直线为旋转轴,其余各边围绕它旋转一周二形成的曲面所围成的集合体叫做圆柱。
椎体:A棱锥—有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
B圆锥—以直角三角形的一条直角边所在的直线为旋转轴,其余各边旋转一周而形成的曲面围成的几何体叫做圆锥。
球体:半圆以它的直径为旋转轴,旋转一周而形成的曲面所围成的几何体叫做球体。
多面体:围成棱柱和棱锥的面都是平的面,想这样的立体图形叫做多面体。
三.常见的平面图形多边形:由线段围成的封闭图形叫做多边形。
多边形中三角形是最基本的图形。
圆:一条线段绕它的端点旋转一周而形成的图形。
扇形:由一条弧和经过这条弧的端点的两条半径围成的图形叫做扇形。
四.从不同方向观察几何体从正面、上面、左面三个不同方向看一个物体,然后描出三张所看到的图(分别叫做正视图、俯视图、侧视图),这样就可以把立体图形转化为平面图形。
立体图形的展开图有些立体图形是有一些平面图形围成的,把它们的表面适当剪开后在平面上展开得到的平面图形称为立体图形的展开图。
五.圆柱和圆锥的侧面展开图棱柱和棱锥的展开图:根据展开图判断立体图形的规律:A展开图全是长方形或正方形时------正方体或长方体;B展开图中含有三角形时-----棱锥或棱柱;若展开图中含有2个三角形3个长方形-----三棱柱;若展开图中全是三角形(4个)-----三棱锥。
C展开图中含有圆和长方形-----圆柱;D展开图中含有扇形------圆锥。
人教版初一数学上册知识点归纳总结 图形初步认识
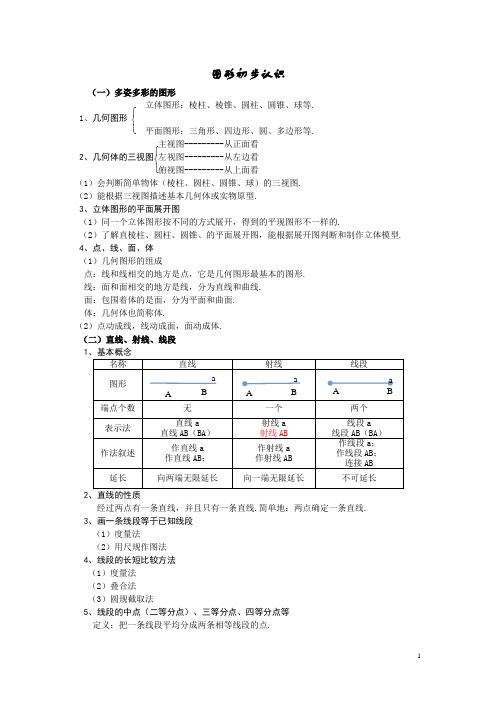
⎧⎨⎩⎧⎨⎩图形初步认识(一)多姿多彩的图形立体图形:棱柱、棱锥、圆柱、圆锥、球等. 1、几何图形 平面图形:三角形、四边形、圆、多边形等.主视图---------从正面看 2、几何体的三视图 左视图---------从左边看俯视图---------从上面看(1)会判断简单物体(棱柱、圆柱、圆锥、球)的三视图. (2)能根据三视图描述基本几何体或实物原型. 3、立体图形的平面展开图(1)同一个立体图形按不同的方式展开,得到的平现图形不一样的.(2)了解直棱柱、圆柱、圆锥、的平面展开图,能根据展开图判断和制作立体模型. 4、点、线、面、体 (1)几何图形的组成点:线和线相交的地方是点,它是几何图形最基本的图形. 线:面和面相交的地方是线,分为直线和曲线. 面:包围着体的是面,分为平面和曲面. 体:几何体也简称体.(2)点动成线,线动成面,面动成体. (二)直线、射线、线段 1、基本概念名称 直线 射线 线段 图形端点个数 无 一个 两个 表示法 直线a直线AB (BA ) 射线a 射线AB 线段a 线段AB (BA ) 作法叙述 作直线a 作直线AB ; 作射线a 作射线AB 作线段a ; 作线段AB ; 连接AB 延长向两端无限延长向一端无限延长不可延长2、直线的性质经过两点有一条直线,并且只有一条直线.简单地:两点确定一条直线. 3、画一条线段等于已知线段 (1)度量法(2)用尺规作图法 4、线段的长短比较方法 (1)度量法 (2)叠合法 (3)圆规截取法5、线段的中点(二等分点)、三等分点、四等分点等 定义:把一条线段平均分成两条相等线段的点.A B a A B a A B a图形:A M B符号:若点M 是线段AB 的中点,则AM=BM=21AB ,AB=2AM=2BM. 6、线段的性质两点的所有连线中,线段最短.简单地:两点之间,线段最短. 7、两点的距离连接两点的线段的长度叫做两点的距离(距离是线段的长度,而不是线段本身). 8、点与直线的位置关系(1)点在直线上(或者直线经过点) (2)点在直线外(或者直线不经过点). (三)角1、角:有公共端点的两条射线所组成的图形叫做角.2、角的表示法(四种):表示方法 图例 记法 适用范围用三个大写字母表示 ∠AOB 或∠BOA任何情况下都适应。
初一数学知识点上册人教版

初一数学知识点上册人教版初一数学知识点上册人教版图形的初步认识一、立体图形与平面图形1、长方体、正方体、球、圆柱、圆锥等都是立体图形。
此外棱柱、棱锥也是常见的立体图形。
2、长方形、正方形、三角形、圆等都是平面图形。
3、许多立体图形是由一些平面图形围成的,将它们适当地剪开,就可以展开成平面图形。
二、点和线1、经过两点有一条直线,并且只有一条直线。
2、两点之间线段最短。
3、点C线段AB分成相等的两条线段AM与MB,点M叫做线段AB的中点。
类似的还有线段的三等分点、四等分点等。
4、把线段向一方无限延伸所形成的图形叫做射线。
三、角1、角是由两条有公共端点的射线组成的图形。
2、绕着端点旋转到角的终边和始边成一条直线,所成的角叫做平角。
3、绕着端点旋转到终边和始边再次重合,所成的角叫做周角。
4、度、分、秒是常用的角的度量单位。
把一个周角360等分,每一份就是一度的角,记作1°;把1度的角60等分,每份叫做1分的角,记作1′;把1分的角60等分,每份叫做1秒的角,记作1″。
四、角的比较从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。
类似的,还有叫的三等分线。
五、余角和补角1、如果两个角的和等于90(直角),就说这两个角互为余角。
2、如果两个角的和等于180(平角),就说这两个角互为补角。
3、等角的补角相等。
4、等角的余角相等。
六、相交线1、定义:两条直线相交,所成的四个角中有一个角是直角,那么这两条直线互相垂直。
其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
2、注意:⑴垂线是一条直线。
⑵具有垂直关系的两条直线所成的4个角都是90。
⑶垂直是相交的特殊情况。
⑷垂直的记法:a⊥b,AB⊥CD。
3、画已知直线的垂线有无数条。
4、过一点有且只有一条直线与已知直线垂直。
5、连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
6、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
数学:第四章《图形认识初步》课件(人教版七年级上)

女性生殖器官最常见的疾病是。A、宫颈癌B、盆腔炎C、阴道炎D、卵巢癌 按目标市场划分,数字出版产业可分为。A.手机出版B.网络游戏出版C.数字大众出版D.数字学术出版E.数字教育出版 副交感脑神经核不包括A.上泌涎核B.疑核C.迷走神经背核D.下泌涎核E.动眼神经背核 国家对部分重点中药材购销实行管理,下列属于第二类的为A.麝香B.杜仲C.牛黄D.甘草E.厚朴 男,2岁,因呼吸困难就诊。查体发现:口腔黏膜上散在白色斑点及白色假膜样物。经细菌学检查发现,感染细菌经A1bert染色,有明显的异染颗粒。此病人应考虑为A.流感B.口腔病毒感染C.白喉D.气管炎E.肺炎 利多卡因主要通过肝脏的哪两种酶进行代谢()A.微粒体混合功能氧化酶和酰胺酶B.胆碱酯酶和酰胺酶C.胆碱酯酶和微粒体混合功能氧化酶D.磷酸酯酶和酰胺酶E.磷酸酯酶和微粒体混合功能氧化酶 用于沥青混合料的配比设计及沥青路面施工质量检验的试验是。A.密度试验B.马歇尔稳定度试验C.强度试验D.铺砂法试验 [单选,案例分析题]患者女,48岁,因“多饮、多尿、多食、消瘦6个月”来诊。既往史、家族史无特殊。无烟酒嗜好。查体:T36.5℃,P70次/min,R18次/min,BP145/80mmHg;意识清楚,呼吸平顺,体型匀称,BMI26kg/m;无突眼,甲状腺无肿大;HR70次/min,律齐,各瓣膜区未闻及病理性 局部麻醉常用的方法有四种、、、。 PD的含义是A、债项预期损失率,根据债项等级与违约损失率的映射关系取得B、违约风险暴露,即贷款风险敞口,就是贷款违约时的余额C、客户违约概率,通过历史数据统计的客户信用等级对应的平均违约概率D、客户贡献率,根据客户的存款、贷款(含票据贴现)和中间业务收入计算 二氧化碳适用于扑救可燃液体火灾.A.正确B.错误 何谓催化重整? 关于脑血管的影像学检查,叙述错误的是A.CT血管成像(C
七年级数学上册第四章几何图形初步认识4.3.1角(图文详解)

∠BOC,∠BO.
D C B
A
人教版七年级数学上册第四章几何图形初步认识
一、角的定义
1.角是由具有公共端点的两条射线组成的图形. 2.角可以看作是一条射线绕着它的端点旋转而形成的图 形.
人教版七年级数学上册第四章几何图形初步认识
二、角的表示方法
表示方法
人教版七年级数学上册第四章几何图形初步认识
一周角=2平角=4直角=360° 一平角=180° 一直角=90° 1°=60′, 1′=60″ (读成1度等于60分,1分等于60秒)
人教版七年级数学上册第四章几何图形初步认识
例1 填空: (1)34.5°= 34 ° 30 ′ (2)112.27°= 112 ° 16 ′12 ″
如何?
(3)你能描述一下怎样的几何图形叫做角吗?
人教版七年级数学上册第四章几何图形初步认识
角是由具有公共端点的两条射线组成的图形.
射线
边
顶点
边 射线
人教版七年级数学上册第四章几何图形初步认识
判断下列哪些图形是角.
(√)
(×)
(√)
(√)
人教版七年级数学上册第四章几何图形初步认识
角也可以看作是一条射线绕着它的端点旋转而形成的图形. 平角及周角的定义: 一条射线绕它的端点旋转,当终边与始边成一条直线时,所 成的角叫做平角.终边继续旋转,当它又和始边重合时,所成 的角叫周角.
1°=60′ 1′=60″
解:(1)34.5°=34°+0.5°
=34°+0.5×60′
=34°+30′=34°30′
(2)112.27°=112°+0.27×60′
=112°+16.2′
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
认识几何图形
一、教学目标
1、知识与技能
(1)初步了解立体图形和平面图形的概念.
(2)能从具体物体中抽象出长方体、正方体、球、圆锥、棱锥、棱柱等立体图形;能举出类似长方体、正方体、球、圆锥、棱锥、棱柱的物体实体.
2、过程与方法
(1)过程:在探索实物与立体图形关系的活动过程中,对具体图形进行概括,发展几何直觉.
(2)方法:能从具体事物中抽象出几何图形,并用几何图形描述一些现实中的物体.
3、情感、态度、价值观:形成主动探究的意识,丰富学生数学活动的成功体验,激发学生对几何图形的好奇心,发展学生的审美情趣.
二、教学重点、难点:
教学重点:常见几何体的识别
教学难点:从实物中抽象几何图形.
三、教学过程
1.创设情境,导入新课.
让我们一起来看看北京奥运会奥运村模型图.(出示章前图)展示丰富多彩的图形世界.
2直观感知,识别图形
(1)对于各种各样的物体,数学中关注是它们的形状、大小和位置.
(2)展示一个长方体教具,让学生分别从整体和局部抽象出几何图形.观察长方体教具的外形,从整体上看,它的形状是长方体,看不同的侧
面,得到的是正方形或长方形,只看棱、顶点等局部,得到的是
线段、点.
(3)观察其他的实物教具(或图片)让学生从中抽象出圆柱,球,圆等图形.
(4)引导学生得出几何图形、立体图形、平面图形的概念.
我们把从实物中抽象出的各种图形统称为几何图形.比如长方体,长方形,圆柱,线段,点,三角形,四边形等.几何图形是数学研究的主要对象之一.
有些几何体的各部分不都在同一平面内,它们是立体图形.如长方体,立方体等.
有些几何图形和各部分都在同一平面内,它们是平面图形.如线段,角,长方形,圆等.
3. 实践探究.
(1) 引导学生观察帐篷,,金字塔的图片,从面抽象出棱柱,棱锥.
(2)你能说说圆柱与棱柱,圆锥与棱锥的区别吗?
(3)你能再举一些圆柱、棱柱、圆锥、棱锥的实例吗?
(4)下图中实物的形状对应哪些立体图形?把相应的实物与图形用线连起来
4.小结
这节课你有什么收获?
5.作业设计
课本第123页习题4.1第1、2题;
第125页习题4.1第7、8题。
