提分细目表
小学数学试题双向细目表

小学数学试题双向细目表小学数学试题双向细目表是一种用于指导小学数学教育评估的工具,它可以帮助教师根据学生的不同学习水平和能力,设计出更加精准、有效的数学试题。
本文将详细介绍小学数学试题双向细目表,并探讨其在小学数学教育评估中的应用。
一、小学数学试题双向细目表概述小学数学试题双向细目表是一种以表格形式呈现的评估工具,它根据数学课程的目标和内容,列出了不同层次和能力的学生在完成数学试题时应该掌握的知识点和技能。
通常,双向细目表包括三个维度:认知目标、知识点和难度等级。
认知目标维度指出了学生应该达到的认知水平,如理解、应用、分析等;知识点维度列出了试题中涉及到的数学知识点;难度等级维度则指出了试题的难易程度,以便教师根据学生的实际情况进行评估。
二、小学数学试题双向细目表的应用1、确定评估目标在进行数学评估时,教师需要明确评估的目标,即学生应该掌握的数学知识和技能。
双向细目表可以帮助教师确定评估目标,使其更加明确和具体。
在细目表中,教师可以根据知识点维度,列出学生需要掌握的数学概念、方法和技能,进而设计出相应的试题。
2、制定评估计划评估计划是教师进行数学评估的基础,它可以指导教师设计出更加全面、系统的数学试题。
在制定评估计划时,教师可以根据双向细目表,将知识点和难度等级进行分类和排序,然后根据学生的实际情况,制定出适合不同层次和能力学生的评估计划。
3、设计数学试题在设计数学试题时,教师需要根据双向细目表中的知识点和难度等级,结合学生的实际情况,设计出更加精准、有效的试题。
例如,教师可以根据知识点维度,设计出涵盖不同数学概念的试题;可以根据难度等级维度,设计出适合不同能力学生的试题。
4、进行评估和反馈在进行数学评估时,教师需要根据双向细目表对学生的表现进行评估,并根据评估结果进行反馈和指导。
通过双向细目表的指导,教师可以更加准确地了解学生的学习情况和问题,进而提出更加精准的建议和指导。
三、总结小学数学试题双向细目表是一种非常实用的评估工具,它可以帮助教师根据学生的实际情况,设计出更加精准、有效的数学试题。
双向细目表介绍

双向细目表介绍一、认识双向细目表双向细目表是由考试考查及目标检测命题过程中,为了保证命题题目在内容上全面、准确,在能力目标分配上得当,而根据考查内容、时间及能力权重要求制定的一个测量认识目标达成度的命题蓝图设计;同时也分析测量结果的一个重要工具。
1、测量目标分类我们认识双向细目表是八十年代目标教学实验时,用于测量达成度的工具之一。
测试就要知道在认知行为上要达到的水平,通常采用识记、理解、应用、分析、综合、评价六个等级。
这就是美国教育家布鲁姆(B.Bloom)目标分类划分的,是从最简单的、基本的到复杂的、高级的认知能力。
每前一目标都是后面目标的基础。
即没有识记,就不能有理解,没有识记与理解,就难以应用。
(1)识记:是对知识的回忆。
其中包括对具体事物、普遍原理、方法、过程、模式、结构等方面的回忆。
(2)理解:是最低层次的理解。
它与完全理解并不是同意词,与完全掌握信息也不是一回事。
领会是指对交流内容中所含的文字信息的理解。
(3)运用:是在特定的情况下,对抽象概念的使用。
这些抽象概念可能是一般的观念、程序的规则、概括化的方法,也可能是专门性的原理、观念和理论。
(4 )分析:是将交流的内容分解成几个要素或组成部分,以便分清一个事物中各要素或各部分的层次关系。
(5)综合:是将所分解的各个要素或组成部分组合成一个整体。
是对各个要素或各个组成部分进行加工的过程和进行排列组合以构成一个比较清楚的模式或结构的过程。
(6)评价:是为了特定的目的对材料和方法的价值所作出的判断。
也就是说,对材料和方法符合标准的程度所作出的定量或定性的判断。
认知领域教育目标的这六个层次是从学习过程的理解能力来划分的,它适应于任何一门学科,而且有很高的实用价值。
2、双向细目表双向细目表是一种测量目标(能力)和考查内容之间的关联表。
一般地,表的纵向列出的各项是要考查的内容即知识点,横向列出的各项是要考查的能力,或说是在认知行为上要达到的水平,在知识与能力共同确定的方格内是考题分数所占的比例。
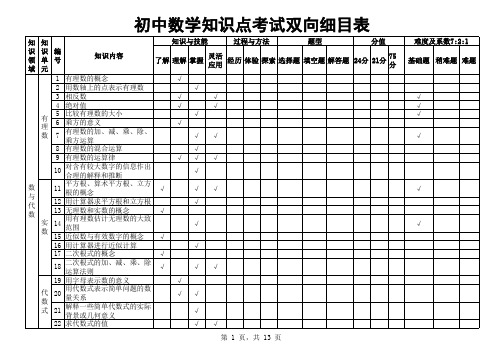
初中数学知识点考试双向细目表
√ √
初中数学知识点考试双向细目表
知 识 领 域 知识与技能 过程与方法 题型 分值 难度及系数7:2:1 知 识 编 知识内容 灵活 单 了解 理解 掌握 经历 体验 探索 选择题 填空题 解答题 24分 21分 75分 基础题 稍难题 难题 角 号 应用 元 86 补角、余角、对顶角 √ 等角的余角相等、等角的补 87 √ 角相等、对顶角相等 88 垂线、垂线段 √ 89 垂线段最短的性质 √ √ 90 点到直线距离的意义 √ 过一点有且仅有直线垂直于 91 √ √ 已知直线 相 用三角尺或量角器过一点画 交 92 √ 一条直线的垂线 线 93 线段垂直平分线及其性质 √ 与 94 两直线平行,同位角相等 √ √ √ 平 过直线外一点有且仅有一条 行 95 √ 直线平行于已知直线 线 用三角尺和直尺过已知直线 96 √ 外一点画这条直线的平行线 两条平行直线之间距离的意 97 √ √ 义 98 度量两条平行线之间的距离 √ 三角形有关概念(内角、外 99 √ 角、中线、高、角平分线) 画任意三角形的角平分线、 ## √ √ 中线和高 ## 三角形的稳定性 √ ## 三角形中位线的性质 √ √ ## 全等三角形的概念 √ 三 ## 两个三角形全等的判定 √ √ √ √ 角 ## 等腰三角形的有关概念 √ 形 ## 等腰三角形性质和判定 √ √ 第 5 页,共 13 页
45 不等式的基本性质 46 一元一次不等式的解法 在数轴上表示不等式(组) 47 的解集 48 解一元一次不等式组 根据具体问题中的数量关 系,列出一元一次不等式或 49 一元一次不等式组,解决简 单的问题 具体问题中的两个变量之间 50 的关系 从表格、图象中分析某些变 51 量之间的关系 用表格或关系式表示某些变 52 量之间的关系 53 常量、变量的意义 √ 54 函数的概念及其表示方法 √ 函 对简单实际问题中的函数关 数 55 系进行分析 56 确定函数的自变量取值范围 57 求函数值 用适当的函数表示法刻画某 58 些实际问题中变量之间的关 系 对变量的变化规律进行初步 59 预测 60 一次函数的意义 61 确定一次函数表达式 一 62 画一次函数的图象 函 次 数 函 数
整理初中语文中考双向细目表

初中语文中考双向细目表20 年月日A4打印/ 可编辑双向细目表简介双向细目表(two-way checklist)是一个测量的内容材料维度和行为技能所构成的表格,它能帮助成就测量工具的编制者决定应该选择哪些方面的题目以及各类型题目应占的比例。
双向细目表(Table of specifications)考试命题双向细目表是一种考查目标(能力)和考查内容之间的关联表。
双向细目表的制作应该同课程大纲及考试大纲的相关规定具有一致性。
考核知识内容的选择,要依照教学大纲(考试大纲)的要求,试题范围应覆盖课程的全部内容,既要注意覆盖面,又要选择重点内容,时间以中等学生120分钟能答完为限。
制作双向细目表时,试卷中拟对学生进行考核的“考核知识点”须按章次进行编排;双向细目表中考核知识点的个数须与试卷中涉及的知识点个数相一致。
双向细目表中的能力层次采用“识记”、“ 理解”、“ 应用”、“分析”、“ 综合”、“评价”等作目标分类,体现了对学生从最简单的、基本的到复杂的、高级的认知能力的考核。
每前一目标都是后续目标的基础,即没有识记,就不能有理解;没有识记与理解,就难以应用。
所以一个考核知识点在同一试卷中对应一种题型,原则上只能对应一种能力层次。
特点按照《考试规范》要求,识记、理解类试题须控制在60%以内,并应尽量避免单纯考核记忆水平的题目。
试题的题目类型应根据考试课程的特点和考试目标合理选择,例如填空题、选择题、判断题、名词解释、辨析题、简答题、证明题、计算题、案例分析等。
一份试卷中主观性试题和客观性试题的搭配应合理,且题型种类数应适中。
在双向细目表中不同“能力层次”和不同“题型”下面对应的各列中,应填写各考核知识点在试卷中所占的分值。
不能简单的划“∨”,也不能填写题号和题目个数如何编制双向细目表?一、什么是双向细目表?简单来说,双向细目表是测验编制的计划书、蓝图和命题的依据。
它是以能力层次和学习内容为两个轴,分别说明各项测评目标。
考试命题双向细目表
考试命题双向细目表(1)(2009-12-13 09:00:55)双向细目表(Table of specifications)考试命题双向细目表是一种考查目标(能力)和考查内容之间的关联表。
1.中等学生120分钟能答完2.“识记”、“理解”、“应用”、“综合”;识记、理解类试题须控制在60%以内3.“学时比例”既是教学时间、精力分配的比例,也是测验试题数量、考试时间、分数分配的依据。
考试命题双向细目表考试命题双向细目表是一种考查目标(能力)和考查内容之间的列联表。
制作考试命题双向细目表,是命题工作的一个重要环节。
双向细目表可以使命题工作避免盲目性而具有计划性;使命题者明确测验的目标,把握试题的比例与份量,提高命题的效率和质量。
同时,它对于审查试题的效度也有重要的指导意义。
双向细目表是包括两个维度(双向)的表格,细目表也可以是多维的,一般用双向细目表。
较常见的有四种:(1(2该表是上一个表的改进,增加了题型。
(3该表可以体现题型数量、难易度、测验内容的分配问题。
优点是试题取样代表性高,试题难易程度也可以作适当控制,表中数据容易分配。
局限性是未能反映测验目标。
(4)反映题型与难度、测验目标之间关系的双向细目表。
难易度:A.较易 B.中等 C.较难 D.难度较大认知度:Ⅰ识记Ⅱ理解Ⅲ简单应用Ⅳ综合运用下面主要说明反映测验内容与测验目标(学习水平)和题型分数的双向细目表。
即把要考查的知识内容与学习水平(能力)、试题的类型和分数呈现在一张表上,这样命题时,一目了然,便于操作。
该表是由一张概括程度比较高的知识内容和分类比较细的学习水平构成,在表中,纵、横两表头双向决定的每个点(交叉的格)为一个考察点,每个考察点要体现题型、题量、得分点三个参数。
这样对试卷结构、对考查的主要内容就具有了明确的指向性。
举例,假设每一个得分点的分数值定为2分,以100分为满分,则整个试卷可以有50个得分点。
再假定每个得分点考生平均能以一分钟时间答完题,并考虑考生复核、检查时间,那么这次测验时间可定为60分钟。
2023年初中数学中考考点归纳双向细目表

2023年初中数学中考考点一、代数1. 一元一次方程与一元一次不等式 1.1 解一元一次方程1.2 解一元一次不等式2. 整式2.1 整式的加减2.2 整式的乘除3. 因式分解3.1 提公因式法3.2 积因式分解4. 分式4.1 分式的加减4.2 分式的乘除二、几何1. 相似三角形1.1 判定相似三角形 1.2 相似三角形的性质2. 平行线与三角形2.1 平行线的性质2.2 三角形内角和3. 圆3.1 圆的性质3.2 圆内接四边形4. 三角形4.1 三角形的外角性质 4.2 三角形的面积计算三、函数与图像1. 一次函数1.1 一次函数的性质 1.2 一次函数图像2. 二次函数2.1 二次函数的性质2.2 二次函数图像3. 绝对值函数3.1 绝对值函数的性质 3.2 绝对值函数图像四、统计与概率1. 统计1.1 统计量的计算1.2 统计图的绘制2. 概率2.1 基本概率事件2.2 条件概率的计算五、解析几何1. 直线与圆1.1 直线与圆的位置关系 1.2 直线与圆的性质2. 空间图形2.1 空间图形的投影2.2 空间图形的体积计算六、实际问题1. 实际问题的解决方法1.1 将实际问题转化为数学问题1.2 利用数学方法解决实际问题2. 实际问题的综合运用2.1 结合多种数学知识解决实际问题 2.2 实际问题综合运用的技巧七、综合练习1. 综合练习题1.1 完形填空题1.2 阅读理解题2. 综合练习题解析2.1 完形填空题解析2.2 阅读理解题解析以上便是2023年初中数学中考的考点归纳双向细目表,同学们在备考中可根据此表进行有针对性的复习和练习,以取得更好的考试成绩。
2023年初中数学中考考点归纳双向细目表随着2023年初中数学中考的逐渐临近,同学们将面临着对数学知识的系统复习和全面梳理。
为了帮助同学们更好地备战数学中考,以下将就上文所述的考点进行更加详细的探讨和扩充。
一、代数代数是数学中的重要分支,它涵盖了一元一次方程与一元一次不等式、整式、因式分解和分式等内容。
五年级数学评价双向细目表

体 经历 验 3 1
1 1
探索 8
2 6 2
确定行、列合计吻合,
五年级数学期末评价双向细目表一
结果目标 88 试卷题型 分数合计 填空题 28 过程目标 12
了 解
14 10
理解 25 11
掌 握
49 5
经 历
3 1
体 验
1 1
探 索
8
难 中易
判断题
选择题 计算题
12
14 18
4
6
2 6
2
10 6 2 6
评价(命题)双向细目表
曙光小学 鲁冬霞
一、什么是评价(命题)双向细目表
命题:编制考试题.
什么是双向:纵向为测试内 容,横向为测试目标水平. 什么是细目表:详细的目标 量表.
课标和教材是双向对应的关系。
正向
课 标 教材
反向
课标与教材双向关联表是为了解 读课标和梳理教材,是学期教学的 前期准备。 教学双向细目表是为了课堂教学 服务的,是解决课堂教学将教学什 么内容,达到什么水平的。 评价(命题)双向细目表是为了 检测结果的,是对课标要求,教材 体现,教学的内容及水平的命题考 核。
3、试卷题型要根据学科的特点、惯例、考试说明 确定。 4、确定大题,大题是重点题、综合性题的出处。 5、确定小题,便于题的安排和分值分配。
五年级数学期末评价双向细目表二
结果目标 教材章节内容 观察物体 因数与倍数 课时量 折合 分数 了解 理解 掌握 经历 过程目标 体验 探索
横向 维度目标及水平 纵 向 教 材 章 节 内 容
选择题
计算题 应用题
14
18 28
细化学习水平,进一步分配分值。
确定行、列合计吻合, 与难易度吻合。
试卷分析双向细目表

试卷分析双向细目表试卷分析双向细目表篇一:自编小学数学期末测试题(内含期末试卷、双向细目表、试卷分析表、参考答案和评分意见)附一:人教版小学五年级数学(下册)期末测试双向细目表姓名:谢xx 专业:xxxx学号:xxxx附二:2011年度上学期五年级数学期末试卷参考答案及评分意见一、填空题1、1 42 45 3132、551893、9994、40 8 13680 9125、÷24 0.75 1216576、347、10 12 14 (注意,此题答案位置不可颠倒,题干中已经说明)8、50.24 9、>10、78二、选择题1、 D2、C3、A4、B5、C三、判断题1、×2、×3、×4、√5、×四、计算题1、102、335315(注意:本题只需写出最后结果)45981263725 (注意:本体需有一些解题过程)42095713此题需按照方程的标准求解步骤求解)207105 (注意:五、作图题1、注:该题比较开放,答案并不唯一教师视情况,可酌情给分。
2、注意:该题需要步骤,学生不能直接做出最后图形,须有过程。
六、应用题11、2 2、4153、55(分钟)4、480元5、150.72平方米6、本班学生的体重,整体情况趁较集中的趋势分布,最大值和最小值差距不是特别大,整体水平稳定。
附三:2011年上学期五年级数学期末试卷试卷分析表试卷分析双向细目表篇二:四年级数学上册试卷双向细目表四年级数学期末供题考试命题双向细目表编制:毛其存2012年1月试卷分析双向细目表篇三:考试命题双向细目表考试命题双向细目表考试是检查培养教学目标实现情况的重要手段。
当前,由于考试命题缺少一套规范化程序,命题的主观顺意性较大。
为式试卷更好的体现教学目标,应该加强编拟时间的计划性、科学性。
1987年,中央教课所组织九省市专家、教授和教研人员为小学语文教材实验班编拟毕业试卷,命题前分析教学大纲具体教学要求,设计了一份考试命题双向细目表。
