数字图像处理_第九章_形态学图像处理
数字图像处理第9章-数学形态学原理(1)..

集合代表图像中物体的形状,例如:在二进 制图像中所有黑色像素点的集合就是对这幅图像 的完整描述。在二进制图像中,当前集合指二维 整形空间的成员,集合中的每个元素都是一个二
9.2 数学形态学的基本概念和运算
在数学意义上,我们用形态学来处理一些图像, 用以描述某些区域的形状如边界曲线、骨架结构和 凸形外壳等。另外,我们也用形态学技术来进行预 测和快速处理如形态过滤,形态细化,形态修饰等。 而这些处理都是基于一些基本运算实现的。
用于描述数学形态学的语言是集合论。数 学形态学最初是建立在集合论基础上的代数系 统。它提出了一套独特的变换和概念用于描述 图像的基本特征。这些数学工具是建立在积分 几何和随机集论的基础之上。这决定了它可以 得到几何常数的测量和反映图像的体视性质。
1)提出所要描述的物体几何结构模式,即 提取物体的几何结构特征;
2)根据该模式选择相应的结构元素,结构 元素应该简单而对模式具有最强的表现力;
3)用选定的结构元对图像进行击中与否(HMT)变换, 便可得到比原始图像显著突出物体特征信息的图像。 如果赋予相应的变量,则可得到该结构模式的定量 描述;
4)经过形态变换后的ຫໍສະໝຸດ 像突出了我们需要的信息, 此时,就可以方便地提取信息;
1964年,法国学者J.Serra对铁矿石的岩相 进行了定量分析,以预测铁矿石的可轧性。几乎 在同时,G.Matheron研究了多孔介质的几何结构、 渗透性及两者的关系,他们的研究成果直接导致 “数学形态学”雏形的形成。
随后,J.Serra和 G.Matheron在法国共同建立了枫 丹白露(Fontainebleau)数学形态学研究中心。在 以后的几年的研究中,他们逐步建立并进一步完善 了“数学形态学”的理论体系,此后,又研究了基 于数学形态学的图像处理系统。
数字图像处理中的形态学图像处理技术

数字图像处理中的形态学图像处理技术数字图像处理是一种高级技术,它可以让人们对图片进行高效处理。
其中一项关键技术是形态学图像处理技术。
本文将重点介绍形态学图像处理技术的实现原理、应用场景以及优点。
一、如何实现形态学图像处理技术在数字图像处理中,形态学图像处理技术以数学形态学为理论基础。
数学形态学是一种数学分支,其研究对象不仅包括数字图像,还包括几何图形、拓扑图形等。
形态学图像处理技术是基于形态学思想而发展出来的,可以对数字图像进行缩小、填充、提取轮廓等处理。
形态学图像处理技术的主要实现原理包括腐蚀和膨胀两种操作。
腐蚀是利用结构元素对图像进行的一种缩小操作,它可以使得图像中的细小灰度部分逐渐消失;膨胀则是利用图像进行一种膨胀操作,它可以使图像中的细小灰度部分逐渐增大并扩展到附近像素。
二、形态学图像处理技术的应用场景形态学图像处理技术在许多领域都有广泛应用,例如医学图像分析、汽车驾驶辅助、人脸识别等。
以下将重点介绍几个典型的应用场景。
1、医学图像分析医学图像分析是医学领域重要的研究领域之一,它包括CT、MRI和X光等多种形式。
形态学图像处理技术可以有效的提取出CT图像中的主干血管、肿瘤等重要区域,对于诊断疾病有重要帮助。
2、汽车驾驶辅助在汽车驾驶辅助中,形态学图像处理技术可以有效地提取出车辆周围的区域,这对于车辆原地停车、跟车行车等操作有着重要的作用。
3、人脸识别在人脸识别中,形态学图像处理技术可以提取出人脸的特征数据,这些数据可以用来做人脸比对、活体检测等。
在安防、金融等领域有广泛应用。
三、形态学图像处理技术的优点形态学图像处理技术具有如下优点:1、提高了图像处理效率:形态学图像处理技术可以快速的将图像处理成为我们所需要的形态,提高了图像处理效率。
2、增加了图像处理的准确度:形态学图像处理技术可以将图像中的多余部分进行过滤,使得我们所关注的部分更加突出,增加了图像处理的准确度。
3、可扩展性强:形态学图像处理技术可以应用于不同领域的图像处理中,具有很强的可扩展性。
数字图像处理第九章

(1)A是A B的子集。
(2)如果C是D的子集,
则C B是D B的子集。
(3)(A B) B=A B
则C B是D B的子集。
(3)(A B) B=A B
多次开操作或 闭操作没有影 响,只能用一次
二值形态学中的运算对象是集合。设A为图像集合,B为 结构元/结构元素,数学形态学运算是用B对A进行操作。 需要指出,实际上结构元素本身也是一个图像集合。对每 个结构元素可以指定一个原点,它是结构元素参与形态学 运算的参考点。 应注意,原点可以包含在结构元素中,也可以不包含在结 构元素中,但运算的结果常不相同。 二值形态学中两个最基本的运算是腐蚀与膨涨 开操作:先用B对A腐蚀,然后再用B对结果进行膨胀 闭操作:先用B对A膨胀,然后再用B对结果进行腐蚀
使用3x3的结构元素:提取的边界宽度为1个像素 使用5x5的结构元素:提取的边界宽度为2~3个像素
• 使用迭代法进行区域填充/孔洞填充:
X k X k 1 B Ac
区域填充
k = 1,2,3,... Xk=Xk-1,则算法在迭代的第k步结束
初 始 点 条件膨胀:如果对上述公式的左部不加限制,则 膨胀将填充整个区域。利用与Ac的交集将 结果限制在感兴趣区域内,实现条件膨胀
多个目标孔洞的填充
第一个点填充的结果
难点:如何判断黑点是球体内部的点还是背景点? ——智能填充
连通分量的提取
令Y表示一个包含于集合A中的连通分量,并假设Y 中的一个点p是已知的。用下列迭代式生成Y的所有 元素: Xk Xk1 B A
k 1,2,3,...
x0=p,如果Xk=Xk-1,算法收敛,令Y=Xk 区域填充:寻找背景点 连通分量的提取:寻找前景 点
数字图像处理与分析形态学图像处理
第53页/共59页
7.6.4 灰度级形态学的一些应用
• 形态学图像平滑处理
先开操作,再闭操作:消除/减弱人为的亮 和暗的细节
第54页/共59页
• 形态学图像梯度
定义: 图示:
g f b f ??b
第55页/共59页
• Top-hat变换—可增强阴影细节
的亮元素和亮指纹部分的暗元素。 由闭操作后紧跟着开操作形成的形态学滤波器可以消除噪声。 图9.11(b)显示了所使用的结构元素。 图9.11(c)显示了使用结构元素对A腐蚀的结果。
背景噪声在开操作的腐蚀过程中消除了。而包含于指纹中的噪声元素的尺寸却增加了。 图9.11(d)显示包含于指纹噪声分量的尺寸被减小。然而,指纹纹路间产生了新的间断。 我们在开操作的基础上进行膨胀,如图9.11(e)所示。间断被恢复,但纹路变粗了,可以
变暗
消除/减 弱亮的 细节
第50页/共59页
变亮
消除/减 弱暗的 细节
7.6.3 开操作和闭操作
• 开操作: • 闭操作:
• 开操作和闭操作的对偶性: f b f ??b b f • b f b??b f • bc f c bˆ
第51页/共59页
• 图示: 第52页/共59页
例题:7.10 灰度级的开操作和闭操作的说明 图9.31(a)显示了使用与图9.29(a)中相同的结构元素对图像9.29(a)进行
(2)如果C是D的子集,则C B是D B的子集。
(3)(A B) B=A B
•
•
•
•• •
第17页/共59页
例题:7.3 对形态学上的开操作和闭操作的简单说明 图9.10进一步对开操作和闭操作进行了说明。 图9.10(a)显示了集合A, 图9.10(b)显示了在腐蚀过程中的一块原盘形结构元素的各种位置。 图9.10(c)显示了腐蚀的结果。 图9.10(d)显示了对腐蚀后的集合进行膨胀的操作。 图9.10(e)显示了开操作最后的结果。
最新《图像处理教学课件》第9章数字形态学及其应用ppt课件

43
第9章 数字形态学 §9.2 二值形态学 §9.2.3 二值开运算
形态学开操作
44
第9章 数字形态学 §9.2 二值形态学 §9.2.4 二值闭运算
闭运算是开运算的对偶运算,定义为先作膨胀后作腐蚀。
或
开、闭运算也互为对偶运算 开运算具有磨光图像外边界的作用 闭运算具有磨光图像内边界的作用
25
第9章 数字形态学 §9.2 二值形态学 §9.2.2 二值膨胀
26
第9章 数字形态学 §9.2 二值形态学 §9.2.2 二值膨胀
B
B1
B2
A
27
第9章 数字形态学 §9.2 二值形态学 §9.2.2 二值膨胀
A
B1
28
第9章 数字形态学 §9.2 二值形态学 §9.2.2 二值膨胀
B2 A
4
第9章 数字形态学 §9.1 概述 §9.1.1 数字形态学的发展简史及基本思想
数学形态学是研究空间结构的形状、框架的学科 ➢ 以积分几何、集合代数及拓扑论为理论基础,此外还涉
及随机集论、近世代数和图论等一系列数学分支。 ➢ 数学形态学的理论虽然很复杂,被称为“惊人的数学”,
但它的基本思想却是简单而完美的。 ➢ 数学形态学的基于集合的观点是极其重要的。
形态学方法优于低通滤波方法的一个直接优点是这种方 法在一幅二值图像中直接得到结果。
34
第9章 数字形态学 §9.2 二值形态学 §9.2.2 二值膨胀
利用膨胀将间断的字符连接起来
35
第9章 数字形态学 §9.2 二值形态学 §9.2.2 二值膨胀
结构元素
Pablo Picasso, Pass with the Cape, 1960
数字图像处理- 形态学处理

Pavlidis细化算法
Rosenfeld细化算法
三种细化算法,在程序中直接运算,并根据运算结 果来判定是否可以删除具体的像素,它们之间的差 别在于不同算法的判定条件是不同的。
数字图像处理
20
数字图像处理
21
1)内部点不能删除;
2)孤立点不能删除; பைடு நூலகம்)直线端点不能删除;
1)将条形区域变成一条薄线; 2)薄线应该位于原条形区域的中心; 3)薄线应该保持原图像的拓扑特性。
数字图像处理
18
根据是否使用迭代运算,可以将细化算法分成
两类,一是迭代算法,二是非迭代算法。
迭代算法,就是重复删除图像边缘中满足一定条件 的像素,以最终得到单像素宽的骨架。
对于迭代算法,又可以根据其检查像素的方式分成串行 算法和并行算法。 所谓串行算法,即为是否删除像素在每次迭代的执行 中是固定顺序的,它不仅取决于前次迭代的结果,而 且也取决于本次迭代中已处理过像素点分布的情况。 对于并行算法,像素点删除与否与像素值在图像中的 顺序无关,仅取决于前次迭代的结果。
相关。
常用的距离尺度有棋盘距离、曼哈顿距离、欧拉距 离。
数字图像处理
28
棋盘距离
曼哈顿距离
欧拉距离
数字图像处理
29
数字图像处理
30
对于距离变换可以进行如下的理解,
就是首先将二值图像的前景像素区域想象为是由某些均 匀缓慢易燃物质组成, 然后考虑对前景像素区域中的所有边界像素进行同时燃 烧, 并且将火一直燃烧至前景像素区域最内部。
如果对区域内部的所有像素进行标记,所标记的内 容为从火开始燃烧直到当前像素被烧到的时间,那 么就得到了二值图像距离变换的有效计算。 一种直观但是效率极其低下的方式就是使用一个合 适的结构元素对图像进行多次连续的腐蚀操作,直 至图像中所有的前景像素被腐蚀掉。
数字图象处理:九 形态学图像处理

(9.3.4)
子集,则 C B 是 D B 的子集;
(3) ( A B) B A B
●
闭操作的性质: (1) A是 A B的子集;
(2) 如果C是D的子集,则 C B 是 D B 的子集; (3) ( A B) B A B
(a)
(b)
(c)
(d)
边界提取实例
(a)
(b)
9.5.2 区域填充
●
如图(d)所示,在区域中选取一点p, 从p点开始,按照下式填充:
X k ( X k 1 B) Ac
k 1,2,3, (9.5.2)
(a) (b) (c)
当 X k X k 1 时,迭代结束。 则 X k 和A的并集包含了被填充的区域 和其边界。
闭操作
形态学操作及其性质的总结 (续)
边界提取 区域填充
提取连通分量
提取骨架
灰度图像的形态学处理
●
说明:形态学处理最主要是用于二值图像。 灰度图像的膨胀和腐蚀的定义和二值形态学不同(max, min); 开、闭的定义是一样的。
●
对灰度图像的形态学处理不要求。
本章小结:
主要介绍了形态学图像处理的基本概念和方法, 包括了膨胀、腐蚀、开操作、闭操作、形态学滤波、 区域填充、提取骨架等内容。 本章主要介绍的是二值形态学的内容。 形态学处理是图像处理的一大类方法,有其自 身的特点和用途。
k 0 K
(9.5.15)
这里, Sk ( A) kB 表示对 Sk (A)的k次连续膨胀
用具体图例来说明形态学的骨架提取过程
(1) (2) (3) (4) (5) (6)
形态学骨架提取的实例
(3×3结构元素)
数字图像处理 第9章 形态学图像处理(1,2)

HYH
第9章 –形态学图像处理
作业1
教材P454 9.2 (a) (b)第2张子图,9.6 (a) (提示:注意结构元素原点的位置 ),9.7 (a) (d) 。
实验五:任务1,2,3,4,6。
HYH
第9章 –形态学图像处理
集合A的边界表示为β (A):
( A) A ( A B)
其中B是一个适当的结构元素。
(9.5-1)
HYH
第9g
假定一个集合的子集的元素是一个8-连通的区域边界,所有非边界的 点为0,如果已知一个p起始点在边界内,下列过程将区域填充为1:
闭操作满足下列性质: (i) A 是A • B的子集。
(ii) 如果C是D的子集,则C • B是D • B的子集。
(iii) (A • B) • B = A • B (幂等)
HYH
第9章 –形态学图像处理
开操作和闭操作示例
HYH
第9章 –形态学图像处理
形态学滤波– 先开后闭
形态学滤波器“开-闭”能够用于去除椒盐噪声。 假定所有噪声分量物理大小小于结构元素B,则背景噪声 在腐蚀阶段被消除。腐蚀将增加物体自身噪声的大小, 这种情况将通过闭操作消除。
9.5.3 连通分量提取
设Y表示为集合A中的一个连通分量(教材P52),并且假定Y上的1 个点p已知,下面的过程可以生成Y的所有元素:
X k ( X k 1 B) A
k 1, 2, 3, ...
(9.5-3)
X0 = p,当Xk = Xk-1算法结束 且 Y = Xk
HYH
第9章 –形态学图像处理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC {w | w A} A的补:
A B {w | w , A B} A BC
ˆ {w | w b, b B} 集合B的反对 B
集合A平移到点 z ( z1 , z 2 )
,表示为(A)z
(A)z {c | c a z, a A}
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 设集合A的凸壳C(A) 令 Bi (i 1,2,3,4)表示图9.19(a)的4个结构元素
i Xk ( X k 1 Bi ) A
(i=1,2,3,4
k 1, 2,3, 4...... )
见图9.17,Y表示一个包含于集合A中的连通分量, 并假设Y中的一个点p已知,通过下式可生成Y的所有元素 X k ( X k 1 B) A k=1,2,3......
x0 p ,B为结 构元素,如果 X k X k 1 ,算法收敛,令 Y Xk
数字图像处理
Chapter 9 Morphological Image Processing
数字图像处理
Chapter 9 Morphological Image Processing
9.3 开操作与闭操作 开操作可写成:
A B U{(B)z | ( B) z A}
即 A B 由许许多多个 ( B) z 并集组成 图9.9为闭操作图示
数字图像处理
Chapter 9 Morphological Image Processing
9.2 膨胀与腐蚀 9.2.1 膨胀 A、B是z2中的集合,A被B膨胀定义:
ˆ ) z A } A B {z | ( B
是所有位移z的集合,还可写成:
ˆ ) z A] A} A B {z | [(B
集合B叫结构元素 上述表达式并不是唯一的。
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 例9.7为一实际例子
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 9.5.4 凸壳 如果连接集合A 内任意两点的直线段 都在A内部,就称A是 凸形的。任意集合S 的凸壳H是包含S的最 小凸集合,集合差HS称为S的凸缺。
9.5 一些基本的形态学算法
9.5 一些基本的形态学算法
本节主要使用二值图像,规定1为阴影,0为 白色。
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 9.5.1 边界提取 (A) 集合A的边界表示为 ( A) A ( AB)
数字图像处理
Chapter 9 Morphological Image Processing 第9章 形 态 学 图 像 处 理
形态学:原来是生物学的一个分支,研究动物和植物 形态和结构,数学形态学 这里借用数学形态学,从图像中的取表达和描述区域 表态的图像分量,如边界、凸壳骨架。 数学形态学的语言是集合论。如:在图像中所有黑色 像素的集合就是一个例子。 如:二值图像中,刚提到的集合是二维整数空间(z2 )坐标(x,y) 灰度图像可表示为空间分量集合。(x,y)+灰度
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法
9.5.5 细化
A B=A-(A*B)=A (A*B)C {B}={B1 ,B2 ,B3 ...Bn }
Bi是Bi-1旋转后的形式 更有用的形式: A {B}=((...((A B1 ) B2 )...) Bn
(击中击不中)
i X0 A
i i i Xk 令 D i X conv ,“conv”表示在X k 时收敛,则A的凸壳 1 为: 4 C ( A) U Di
i 1
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 这过程可以说4大步骤: ( 1) A A反复击中击不中变换,直到不变化,执行与 B1 的并集 B2 ( 2) B3 ( 3) ( 4) B4 最后4个D求并即可,这个过程有明显的缺点,凸壳可能 超出确保凸性所需的最小尺寸,减少这种影响的简单方法, 是限制生长,以便凸壳不会超出初始点集合,在水平方向和 垂直方向上的尺寸大小。
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 9.5.7 骨架(中轴变换、梦烧草地) 参见图9.23
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 集合A的骨架符号为S(A) k S (A) U S k ( A) A的骨架可用腐蚀和开操和表达 k 0 Sk ( A) (AkB)-(AkB) B B:结构元素 AkB 为对A,k次腐蚀 (AkB)=(...(AkB)B)...)B 第K次是A被腐蚀为空集前最后一次迭代 K=max={k|(AkB) } 还可以重构 k A U (S k ( A) kB)
A X ( AB1 ) ( AcB2 )
B1在A内找到匹配 B2在AC中找到匹配 根据腐蚀与膨胀间的对偶关系
A B ( AB1 ) ( Ac B2 )
以上3个公式叫形态学上的击中或击不中变换。
数字图像处理
Chapter 9 Morphological Image Processing
数字图像处理
Chapter 9 Morphological Image Processing
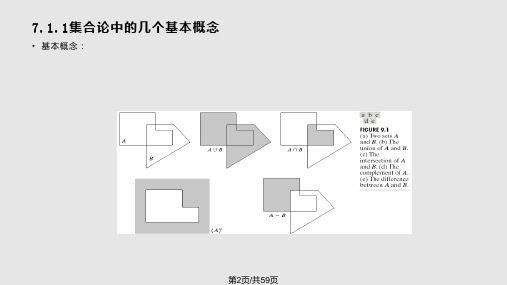
9.1 序言 图9.1为集合论基本概念图示
数字图像处理
Chapter 9 Morphological Image Processing
9.1 序言 图9.2为平移、反射图示
数字图像处理
Chapter 9 Morphological Image Processing
9.1 序言 9.1.2 二值图 像的逻辑运算 与或非, 图9.3为逻 辑运算图示
数字图像处理
Chapter 9 Morphological Image Processing
9.2 膨胀与腐蚀
9.2 膨胀与腐蚀
这两种运算是形态学的基础。
数字图像处理
Chapter 9 Morphological Image Processing
9.2 膨胀与腐蚀 图9.4为 膨胀的简单 说明
数字图像处理
Chapter 9 Morphological Image Processing
9.2 膨胀与腐蚀 图9.5为利用膨胀将裂缝桥接起来的例子。
数字图像处理
Chapter 9 Morphological Image Processing
9.2 膨胀与腐蚀 9.2.2 腐蚀 对z中集合A 、B,B对A腐蚀
数字图像处理
Chapter 9 Morphological Image Processing
9.3 开操作与闭操作
9.3 开操作与闭操作
使用结构元素B对集合A进行开操作:
A B ( AB) B
作用:使用对象轮廓平滑,断开狭窄的间断、消除细的 凸出物,去除小亮点(相对于结构元素)----“减” 使用结构元素B对集合A进行开操作:
Xk
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 例9.6形态学区域填充
Xk
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法
9.5.3 连接分量的提取
整个过程反复进行,直到没有变化为止
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 细化实例参见图9.21
数字图像处理
Chapter 9 Morphological Image Processing
9.5 一些基本的形态学算法 9.5.6 粗化 A· B=AU(A*B) B为结构元素 A· B=((…((A· B1)· B2)…)· Bn) 粗化处理结构元素和细化处理有关的结构元素具有相同 的形式,但所有0,1互换,但粗化算法实际中很少用,代之 的是经常先对背景细化,而后求补,
9.3 开操作与闭操作 例9.3为 开、闭操作简 单的说明
数字图像处理
Chapter 9 Morphological Image Processing
9.3 开操作与闭操作 性质: A是 B ( i) A的子集合 C B (ii)如果C是D子集,则 是 ( A B) B A B (iii) 同样: A的子集 B (i)A是 (ii)如果C是D的子集,则 (iii) ( A B) B A B
A B {z | (B)z A}
图9.2说明了腐 蚀的图解情况
数字图像处理
Chapter 9 Morphological Image Processing
9.2 膨胀与腐蚀
ˆ ( A B) c Ac B
证明如下:
(A - B)C z | (B) z A
C
如果 ( B) z A ,则 ( B) z AC
A B ( A B)B
作用:使轮廓平滑,融联狭窄间断和长细的深 沟,消除小孔洞,填补轮廓线的断裂----“加” 总之:开操作体现“分开” 闭操作体现“联接”
