第一讲 有理数的概念
第一讲《有理数》《数轴》

第一讲《有理数》《数轴》引言有理数是我们常见的一类数,包括整数和分数。
它们在数学中具有重要的地位,因为它们可以覆盖我们日常生活中的绝大部分数量关系。
在本讲中,我们将介绍有理数的定义、性质和表示方法,以及数轴的概念和使用方法。
一、有理数的定义和性质1.1 定义有理数是可以表示为两个整数的比值的数,其中分母不为零。
整数是有理数的特殊情况,可以看作分母为1的有理数。
有理数可以是正数、负数或零。
1.2 性质有理数有以下性质:•有理数的加法、减法和乘法运算仍然得到有理数。
•有理数的除法运算结果可能是有理数,也可能是无理数(不能表示为两个整数的比值)。
二、有理数的表示方法有理数可以用分数、整数或小数形式表示。
2.1 分数表示法分数是有理数最常见的表示形式,它由一个分子和一个分母组成,分子表示被分割的份数,分母表示总共的份数。
分数可以是正数、负数或零。
2.2 整数表示法整数是没有小数部分的有理数。
它可以是正整数、负整数或零。
2.3 小数表示法小数是有理数的一种特殊表示形式。
它可以有有限的数字部分和无限的循环部分,也可以是有限的数字部分。
三、数轴的概念和使用方法3.1 数轴的定义数轴是由一条直线和一个固定原点组成的图形,用来表示数的大小和位置关系。
原点通常表示零,正方向表示正数,负方向表示负数。
3.2 数轴的使用方法数轴可以用来表示有理数的位置和大小关系。
我们可以通过在数轴上画点、画线段等方式来表示有理数的位置。
数轴上两个数之间的距离,即两个数的差的绝对值,表示它们之间的差别大小。
有理数是我们日常生活中非常重要的数,它包括整数和分数。
有理数可以用分数、整数或小数形式表示,可以在数轴上表示它们的位置和大小关系。
了解和掌握有理数的定义、性质和表示方法,以及数轴的概念和使用方法,对我们的数学学习和实际应用都非常有帮助。
参考文献:•《数学教学参考书》•《高中数学学科教学大纲》。
讲义_有理数的基本概念及分类

第一讲 有理数【1.1 正数与负数】常识点对应练习常识点1:正数.负数的概念像3.2.0.5.1.8%如许比0大的数叫 ,依据须要,有时在正数前面加上“+”,如+5, , , ,….正数前面的“+”,一般省略不写:而像-3.-2.-3.5%如许在正数前面加上“—”号的数叫 .如-6, ,….“-6”读作 . 【例1】 下列各数中,哪些是正数?哪些是负数? -10,1,-0.5,0,36,52-,15%,-60,531- 解:1.下列各数 -11 ,0.2,81-,74+,1, -1, -a, -30%中,( )必定是正数,( )必定是负数.常识点2:对“0”的懂得.0既不是 数,也不是 数,它是正数与负数的分水岭.它的意义很特别,它既可以暗示“没有”,也可以暗示特定的意义. 【例2】对于“0”的说法准确的有 ( )①0是正数与负数的分界; ②0℃是一个肯定的温度;③0是正数;④0是天然数;⑤不消失既不是正数也不是负数的数. 解:2下列说法准确的有( ). ①0是最小的天然数; ②0是整数也是偶数; ③0既非正数也非负数;④一个数不是正数就是负数; ⑤负数也叫非正数.⑥一个数,假如不是正数,肯定就是负数.常识点3;用正数和负数暗示具有相反意义的量.相反意义的量必须具有两个要素:一是它们的意义 ;二是它们都具稀有目,并且必定是 量. 【例3】下面问题中:(1) 将水位上升3m 时水位变更记作+3m;则水位降低3m 时水位变更记作-3m.(2) 在一个月内,小明的身高增长,记作+;体重降低3kg,记作-3kg (3) 或人存进银行1900元,记作+1900元;掏出500元,记作-500元.(4) 向东走500m 记作+500m;向西走120m,记作-120m. (5) 小张往前走10m,记作+10m,那么他往左走5m 记作-5m. 表述有错误的是( ). 3.用正数和负数暗示统一问题中具有相反意义的量.①某校七年级举办足球比赛,一班胜两局,记作+2;则三班输一局,记作 .②假如糟蹋8度电,记作-8度;那么勤俭15度电记作 .③假如高于海平面100m 记作+100m,那么低于海平面36m 记作 .④我校的入学检测中,以60分为尺度,若王飞得了85分记作+25分,那么,张生得了45分记作 .二.当堂检测1.假如零上28度记作280C,那么零下5度记作 . 2.若上升10m 记作10m,那么-3m 暗示 .3.比海平面低20m 的地方,它的高度记作海拔 .4.加工一根轴,图纸上注明的直径是¢mm 3003.002.0+-,则及格品的最大直径可认为_____最小直径可为_____0.010*******.0,0,整数聚集{有理数聚集{常识预备:在一条器械偏向的马路上,有一个黉舍,黉舍东50m 和西150m 处分离有一个书店和一个超市,黉舍西100m 和160m 处分离有一个邮局和病院,分离用A.B.C.D 暗示书店.超市.邮局.病院,你会绘图暗示这一情境吗?(绘图)新常识:对比大家画的图,为了使表达更清晰,我们把0•阁下双方的数分离用正数和负数来暗示,即用一向线上的点把正数.负数.0都暗示出来.也就是──数轴.常识点对应练习常识点1:画数轴与数轴概念 第一步:画直线定原点原点暗示0.取一个适中的地位.第二步:划定从原点向右(向上)的为正偏向那么从原点向左(向下)则为负偏向.比方说温度计就是向上为正,向下为负.第三步:选择恰当的长度为单位长度.依据题意而定.步挪用九个字代替为 原点 正偏向 单位长度 有了以上基本,我们可以来试着界说数轴:划定了 . 和 的直线叫数轴. 任何有理数都可以用数轴上___的___来暗示.思虑:(1)原点暗示什么数?(2)原点右方暗示什么数?原点左方暗示什么数?(3)原点向右0.5个单位长度的A 点暗示什么数?原点向左211个单位长度的B 点暗示什么数?归纳:一般地,设a 是一个正数,则数轴上暗示数a 的点在原点的右边,与原点距离是a 个单位,暗示数-a 的点在原点的左边,与原点的距离是a 个单位长度.1、 下列所画数轴对不合错误?假如不合错误,指出错在哪里.2.假如a 是一个正数,则数轴上暗示数a 的点在原点的什么地位上?•暗示-a 的点在原点的什么地位上呢?②-10231③-1-2021--3①45231④0⑤-101⑦-1-2021⑥-1-20-321常识点2:数轴上的点与到原点的距离【例7】(1)与原点的距离为个单位的点有个,它们分离暗示有理数 •和(2)一个蜗牛从原点开端,先向左爬了4个单位,再向右爬了7•单位到达终点,那么终点暗示的数是1、填空:___(2)数轴上在原点左边距原点85个单位长度的点暗示数___.(3) 数轴上距原点2个单位长度的点有__个,它们分离暗示数___.2.从数轴上不雅察,大于-3小于3的整数有___个,分离是___.3.下列说法中错误的是()二.当堂检测1.把数轴上暗示2的点移动5个单位后,所得的对应点暗示的数是()A.7 B.-3 C.7或-3 D.不克不及肯定2.在数轴上,原点及原点左边的点所暗示的数是()A.正数 B.负数 C.不是负数 D.不是正数3.数轴上暗示5和-5的点分开原点的距离都是 ,但它们分离4.在数轴上与-1相距3个单位长度的点有个,为或;长为3个单位长度的木条放在数轴上,最多能笼罩个整数点.5.画一条数轴,并把下列数暗示在数轴上:+2,-3,,0,,4,31 3例6。
第一讲 有理数的相关概念

第一讲有理数的相关概念【知识要点及巩固】一、有理数基本概念1、正数:像3、1、+0.33等的数,叫做正数。
在小学学过的数,除0外都是正数。
正数都大于0。
2、负数:像-1、-3.12、-2012等在正数前加上“-”(读作负)号的数,叫做负数。
负数都小于0。
0既不是正数,也不是负数。
如果正数表示某种意义,那么负数表示它的相反的意义。
注意:正数和负数是表示相反意义的量。
如:南为正方向,向南km3表示为km-。
31表示为km1+,那么向北km3、有理数:整数与分数统称为有理数。
4、无理数:无限不循环小数,如π。
5.有理数的分类:6.几个重要概念:注意:⑴正数和零统称为非负数;⑵负数和零统称为非正数;⑶正整数和零统称为非负整数;⑷负整数和零统称为非正整数。
例1:判断下列说法正确与否⑴一个有理数不是整数就是分数()⑵一个有理数不是正数就是负数()⑶一个整数不是正的,就是负的()⑷一个分数不是正的,就是负的()例2:1、(2016山东德州)把下列各数填入表示相应集合的大括号中:-7.2,43,-9, 1.4,0, 3.14,π,5412,-2.5, 121121112.0,36整数集合{ } 正数集合{ } 分数集合{ } 有理数集合{ } 非正数集合{ } 负分数集合{ } 想一想:a +一定是正数吗?a -一定是负数吗?例3:(2014七中嘉祥)将一串有理数按下列规律排列,回答下列问题: (1)在A 处的数是正数还是负数? (2)负数排在A 、B 、C 、D 中的什么位置?(3)第2014个数是正数还是负数?排在对应于A 、B 、C 、D 中的什么位置? 例4:(2014七中嘉祥)观察下面依次排列的一列数,它的排列有什么规律?请根据你探索的规律接着写出后面的3个数,并尝试写出第100个数、第301个数。
1、6151-4131-211、、、、、-,_____,_______,_________,...;第100个数是_________,第301个数是________。
有理数课件--有理数概念

例8.判断正误
(1)相反数等于本身的数只有0 (√ )
(2)绝对值等于本身的数都是正数 ( ×)
(3)绝对值等于它的相反数的数都是 负数 (× )
分析:根据相反数和绝对值的意义来解题
四、层次训练
1.填空: (1)如果节约了-20千瓦/时电,实际上 20 浪费 是_________了_________千瓦/时电; 失了 (2)负一场得-1分,实际上是_____1分。 分析: (1)节约-20千瓦/时电中的“-”号表示的 是相反意义,它表示与“节约”相反, 实际上就是浪费; (2)中“-1” 的“-”表示与“得分”相反, 因此是失分。
例3.把下列各数填入表示它所在的数 集的括号内: 22 -15, ,-1.3,28,0.314,0,-0.275, 7 π。
…
负分数集
…
非负整数集
…
有理数集
分析:①本题重点是有理数的分类,应注意除 π 外所学数均为有理数;②非负整数包括正整 数和零;③括号内应加“…”
解:
-1.3, … -0.275
第一讲 有理数的概念
一、知识综览
(1)正数负数的概念 1、正数和负数 (2)具有相反意义的量 (3)有理数的分类
(1)数轴的三要素(原点、 正方向和单位长度)
2、数轴
(2)有理数与数轴上的点 的关系
(3)利用数轴比较有理数 的大小
(1)相反数的意义 3、绝对值 与相反数
(2)绝对值的代数及几何 意义
解:(1)-(+3)=-3
(2)+[-(-2)]= +[+2]= 2 (3)-{-[+(-4)]} = -{-[-4]} = -{+4} = -4 (4)+|-6|=6
初中数学第一章有理数知识点归纳总结

初中数学第一章有理数知识点归纳总结初中数学第一章主要涉及有理数的概念、运算规则、绝对值和相反数等知识点。
下面将对这些知识点进行归纳总结。
1.有理数的概念:有理数是整数和分数的统称,包括正整数、负整数、零,以及正分数和负分数。
有理数可以用分数形式表示,也可以用小数形式表示。
2.整数的概念:整数包括正整数、负整数和零。
正整数表示数量时为正,负整数表示数量时为负,零表示没有数量。
3.分数的概念:分数由分子和分母组成,分子表示被分成的份数,分母表示总的份数。
分数可以表示一个数在单位等分之中的一部分。
4.有理数的比较:有理数可以通过大小进行比较。
对于两个有理数a和b,如果a-b>0,则a>b;如果a-b<0,则a<b;如果a-b=0,则a=b。
5.有理数的加法与减法:有理数的加法和减法满足以下性质:-相同符号的两个数相加或相减,绝对值较大的数保留符号,结果的符号与原来的符号相同。
-不同符号的两个数相加或相减,绝对值较大的数保留符号,结果的符号与绝对值较大的数的符号相同。
6.有理数的乘法与除法:有理数的乘法和除法满足以下性质:-两个正数相乘或相除的结果为正数。
-两个负数相乘或相除的结果为正数。
-一个正数与一个负数相乘或相除的结果为负数。
-任何数除以零的结果为零。
7.绝对值:一个数的绝对值表示这个数离零的距离。
如果一个数是正数,那么它的绝对值就等于它本身;如果一个数是负数,那么它的绝对值等于它的相反数。
8.相反数:一个数与它的相反数的和为零。
一个数的相反数可以通过改变符号获得,正数变为负数,负数变为正数。
9.有理数的绝对值与相反数的关系:一个有理数的绝对值等于它的相反数的绝对值。
10.混合运算:混合运算指在一个表达式中同时包含加减乘除等不同的运算符号。
在混合运算中,先进行括号内的计算,然后进行乘除法运算,最后进行加减法运算。
11.近似数与精确数:在实际计算中,有时候需要使用近似数来代替精确数。
1.2.1 有理数(教师版)
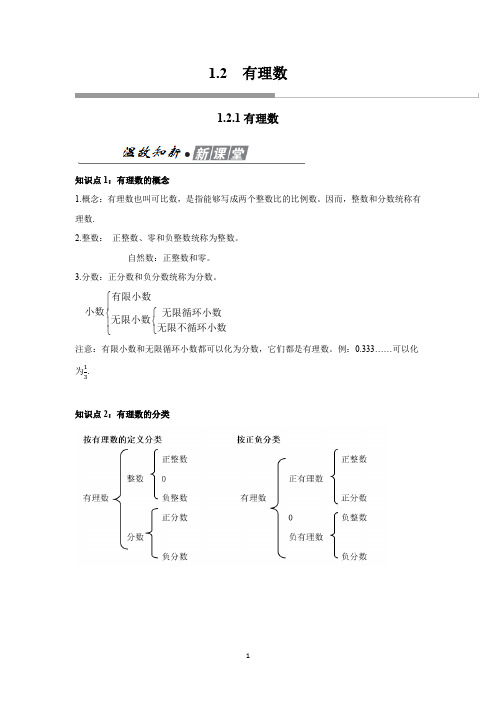
1.2 有理数1.2.1有理数知识点1:有理数的概念1.概念:有理数也叫可比数,是指能够写成两个整数比的比例数。
因而,整数和分数统称有理数.2.整数: 正整数、零和负整数统称为整数。
自然数:正整数和零。
3.分数:正分数和负分数统称为分数。
⎧⎪⎧⎨⎨⎪⎩⎩有限小数小数无限循环小数无限小数无限不循环小数 注意:有限小数和无限循环小数都可以化为分数,它们都是有理数。
例:0.333……可以化为.知识点2:有理数的分类知识点3:四非数①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数考点梳理·新认知考点1 有理数的辨别例1在-,π,0,-0.74四个数中,有理数的个数是()A.1B.2C.3D.4【解析】-,0,-0.74是有理数,而π是无限不循环小数,不是有理数,故选C.总结:1.整数和分数统称为有理数.凡是能写成(p,q为整数,且q≠0)形式的数,都是有理数.2.有限小数与无限循环小数都能表示成分数形式,无限不循环小数不是有理数,如π不是有理数.考点2 有理数的分类例2把下列各数填在相应的集合中:-7,3.5,-3.14,0,1713,0.03%,-314,10.自然数集合:{ …};整数集合:{ …};负数集合:{ …};正分数集合:{ …};正有理数集合:{ …}.【解析】解:在所给的所有数中,①自然数集合为{0,10…};②整数集合为{-7,0,10…};③负数集合为{-7,-3.14,-314…};④正分数集合为{3.5,1713,0.03%…};⑤正有理数集合为{0.03%,1713,3.5,10…}.总结:对有理数进行分类,首先要理解以下数的概念:1.正数:像3,1.8%,3.5这样大于0的数叫做正数.正数的前面可以加上正号(即加号)“+”来表示2.负数:在正数前加上“-”的数叫做负数;3.整数:像-2,-1,0,1,2这样的数叫做整数;4.分数:把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数.考点3 带非字的数例3﹣5,0,﹣3.14,,﹣12,0.1010010001…,+1.99,﹣(1)非负数集合:{ …}(2)非负整数数集合:{ …}(3)非正数集合:{ …}(4)非正整数数集合:{ …}【解析】解:在所给的所有数中,(1)非负数集合:{ 0,,0.1010010001…,+1.99,…}(2)非负整数数集合:{ 0 …}(3)非正数集合:{﹣5,﹣3.14,﹣12,﹣…}(4)非正整数数集合:{ ﹣5,﹣12,…}总结:1.有理数分为正数、0和负数三类,正数和0统称非负数;负数和0统称非正数.2.一个数不是0,则它可能是正数或负数;若一个数不是正数,则它可能是负数或者0;若一个数不是负数,则它可能是正数或者0.基础训练1.下列各数:-1,,4.112134,0,,3.14,其中有理数有( )A .6个B .5个C .4个D .3个 【解析】解:在-1,2π ,4.112134,0,227 ,3.14中不是有理数是2π:故选B .2. 在下列数, ,2.010010001…,25%,3.1415926,0, …中,属于分数的有( )A .2个B .3个C .4个D .5个【解析】解:属于分数的有25%,3.1415926,-0.222…, 故选B . 3. 下列表述中,正确的是( )A .有理数有最大的数,也有最小的数B .有理数有最大的数,但没有最小的数C .有理数有最小的数,但没有最大的数D .有理数既没有最大的数,也没有最小的数 【解析】解:有理数既没有最大的数,也没有最小的数. 故选D . 4. 下列说法正确的是( )A .一个有理数不是整数就是分数B .正整数和负整数统称为整数C .正整数、负整数、正分数、负分数统称为有理数D .0不是有理数【解析】解:A 、一个有理数不是整数就是分数,故本选项正确; B 、正整数和负整数和0统称为整数,故本选项错误; C 、正整数、负整数、正分数、负分数和0统称为有理数,故本选项错误; D 、0是有理数,故本选项错误;故选A .5.下列说法:①-2.5既是负数、分数,也是有理数;②-7既是负数也是整数,但不是自然数;③0既不是正数也不是负数;④0是非负数.其中正确的个数是( ) A .1 B .2 C .3 D .4【解析】解:①-2.5既是负数、分数,也是有理数,正确;②-7既是负数也是整数,但不是自然数,,正确;③0既不是正数也不是负数,正确;④0是非负数,正确, 则正确的个数是4,故选D .6. 把下列各数填在相应的大括号内:5,7-8,-10,0,2.4,+3,227,-3.01.正数集合{…};非负数集合{…};整数集合{…};负分数集合{…}.【解析】正数集合,.,,,…;非负数集合,,.,,,…; 整数集合{5,-10,0,+3,…};负分数集合-,-.,….能力晋升1.设三个互不相等的有理数,既可表示为1、a+b、a的形式,又可表示为0、ba、b的形式,则b的值为()A.0 B.-1 C.1 D.2【解析】解:由题意可知:a+b,a中有一个为0,且ba,b中有一个为1,当a=0时,则ba没有意义,不成立;∴b=1.故选C.2.下列判断正确的个数是()①一个有理数不是整数就是分数②一个有理数不是正数就是负数③一个整数不是正数就是负数④一个分数不是正数就是负数⑤一个偶数不是正偶数就是负偶数A.1 B.2 C.3 D.4【解析】解:①一个有理数不是整数就是分数,正确;②一个有理数不是正数就是负数,错误,也可能是0;③一个整数不是正数就是负数,错误,也可能是0;④一个分数不是正数就是负数,正确;⑤一个偶数不是正偶数就是负偶数,错误,也可能是0;故选B.3. 在有理数集合中,最小的正整数是,最大的负整数是.【解析】解:在有理数集合中,最小的正整数是1,最大的负整数是-1.故答案为1;-1.4. 在-2,1.5,+,0,27,100,-2.1,18,-,-30中,是非负整数的是.【解析】0,27,100,18.5. 在-2,5,-,0.63,0,7,-0.05,-6,9,,,1中,正分数有个,负分数有个,自然数有个,整数有个.【解析】正分数是0.63,,,有3个;负分数是-,-0.05,有2个;自然数是5,0,7,9,1,有5个;整数是-2,5,0,7,-6,9,1,有7个.6.把下列各数分别填入相应的集合内:-2,-3.14,0.3,0,,,-0.1212212221….(1)正数集合:{ };(2)负数集合:{ };(3)分数集合:{ };(4)有理数集合:{ }.【解析】解:(1)正数集合:{0.3,,};(2)负数集合:{ -2,-3.14,-0.1212212221…};(3)分数集合:{ -3.14,0.3,};(4)有理数集合:{ -2,-3.14,0.3,0,}.同步检测·新导向1.(2019•武汉模拟)下列各数中,属于正有理数的是()A.π B.0 C.-1 D.2【解析】解:由题意得:π是无理数,故选项A错误;0是有理数,但不是正数,故选项B错误;-1是负有理数,故选项C错误;2是正有理数,故选项D正确;故选D.2.(2019•沙坪坝区校级模拟)下列四个数中,是正整数的是()A.-2 B.-1 C.1 D.1 2【解析】解:A、-2是负整数,故选项错误;B、-1是负整数,故选项错误;C、1是正整数,故选项正确;D、12是非正整数,故选项错误.故选C.3.(2019•渝中区校级模拟)下列各数中是负整数的是()A.-2 B.5 C.12D.2-5【解析】解:A、-2为负整数,故选项正确;B、5为正整数,故选项错误;C、12为正分数,故选项错误;D、2-5为负分数,故选项错误.故选A.4.(2018秋•沈河区期末)在-4,227,0,2,3.14159,1.3,0.1010010001…有理数的个数有( )A .2个B .3个C .4个D .5个【解析】解:2,0.1010010001…不是有理数,故选D .5.(2018秋•卢龙县期末)下列说法正确的是( ) A .0是最小的有理数 B .一个有理数不是正数就是负数 C .分数不是有理数 D .没有最大的负数【解析】解:A 、没有最小的有理数,故本选项错误;B 、一个有理数不是正数就是负数或0,故本选项错误;C 、分数是有理数,故本选项错误;D 、没有最大的负数,故本选项正确; 故选D .6.(2018秋•门头沟区期末)在有理数-0.2,-3,0,132,-5,1中,非负整数有 . 【解析】解:非负整数有0,1, 故答案为:0,1.7.(2018秋•仪征市期中)有三个有理数,分别是-1、a 、a +b ,或者写成0、-b a、b ,那么数b 的值是 .【解析】解:由题意可知:a +b ,a 中有一个为0,且-b a ,b 中有一个为-1,当a =0时,则-b a没有意义,不成立;∴b =-1. 故答案为:-1. 8. (2018秋•武邑县校级月考)在数1-13,20%,227,0.3,0,-1.7,21,-2,1.0101001…,+6,π中,分数有 个. 【解析】解:分数有1-13,20%,227,0.3,-1.7, 故答案为:5。
第1讲 有理数的概念(数轴、相反数)

有理数的概念(数轴、相反数)要点一、正数与负数大于0的数,叫做正数; 像-3、-1.5、12-、-584等在正数前面加“-”号的数,叫做负数. 要点二、有理数的分类1.有理数:整数与分数统称为有理数. 2.有理数的分类:(1)有理数按性质分类: (2)有理数按符号分类⎧⎧⎫⎪⎪⎬⎨⎪⎭⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数自然数整数零有理数负整数正分数分数负分数⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎪⎨⎪⎪⎩⎩正整数正有理数正分数有理数零(既不是正数,也不是负数)负整数负有理数负分数 【注】注意以下几个概念的区分:非负数:正数和零;非正数:负数和零;非负整数:正整数和零;非正整数:负整数和零;非负有理数:正有理数和零;非正有理数:负有理数和零.要点三、数轴:规定了原点、正方向和单位长度的直线叫做数轴.要点四、相反数:只有符号不同的两个数互为相反数;0的相反数是0.类型一、正数和负数(1)仔细思考以下各对量: ①胜二局与负三局; ②气温为3C -︒与气温升高30C ︒; ③盈利5万元与亏损5万元; ④增加10%与减少20%. 其中具有相反意义的量有( ) A .1对 B .2对 C .3对 D .4对(2)①我国现采用国际通用的公历纪年法,如果我们把公元2017年记作+2017年,那么,处于公元前500年的春秋战国时期可表示为___________.②如果80m 表示向东走80m ,那么60m -表示________________.③A ,B 两地海拔高度分别是120米,10-米,则B 地比A 地低________米.(3)某饮料公司生产的一种瓶装饮料外包装上印有“60030(ml)±”字样,请问“60030(ml)±”是什么含义?质检局对该产品抽查5瓶,容量分别为603ml ,611ml ,589ml ,573ml ,627ml ,问抽查产品的容量是否合格?知识导航典题精练例题1举一反三:【变式1】一种大米的质量标识为“(50±0.5)千克”,则下列各袋大米中质量不合格的是( ) A .50.0千克 B .50.3千克 C .49.7千克 D .49.1千克【变式2】(1)如果节约16吨水记作+16吨,则浪费6吨水记作__________.(2)在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作___________.类型二、有理数的概念及分类(1)下列说法错误的是( ) A .0既不是正数也不是负数B .正整数和负整数统称整数C .整数和分数统称有理数D .正有理数包括正整数和正分数(2)把下列各数分别填在所属分类里:5-,0, 3.14-,32, 2.4-,227,327,π, 5.5-,2.4,311-,3.14159,34-,2003①正数:{ }; ②负数:{ }; ③非负整数:{ }; ④分数:{ }; ⑤非正有理数:{ };举一反三:【变式1】判断题:(1)0是自然数,也是偶数.( ) (2)0既可以看作是正数,也可以看成是负数.( ) (3)整数又叫自然数.( ) (4)非负数就是正数,非正数就是负数.( )例题2【变式2】下列四种说法,正确的是( ).(A)所有的正数都是整数(B)不是正数的数一定是负数(C)正有理数包括整数和分数 (D)0不是最小的有理数【变式3】下列说法正确的是()A.在有理数中,零的意义仅仅表示没有B.正有理数和负有理数组成全体有理数C.0.5既不是整数,也不是分数,因而它不是有理数D.零既不是正数,也不是负数【变式4】把下列各数填入表示它所在的大括号:.-24,3,2.008,10-3,114,0,()--2,3.14,||--4.正有理数:{ } 非负整数:{ } 负分数:{ }类型三、数轴(1)下面图形是数轴的是()A.B.C.D.(2)如图所示,数轴的一部分被墨水污染了,被污染的部分内含有的整数为_______.(3)已知:点A在数轴上的位置如图所示,点B也在数轴上,且A、B两点之间的距离是2,则点B表示的数是______.(4)在数轴上标出下列各数:0, 4.2,132,2,+7,113,并用“<”连接.举一反三:【变式】(1)如图,表示数轴正确的是()A.B.C.D.(2)已知点A,点B在数轴上,点A表示数为-2,A、B两点的距离为5,则点B表示的数是________.(3)在数轴上标出下列各数,并用“<”比较它们的大小:-3,+1,122,.-15,5.例题3(4)已知,a b 为有理数,在数轴上的位置如图所示,则a 1,b1,0,1的大小关系为_______________.(1)一个点沿着数轴的正方向从原点起移动2个单位长度后,又向反方向移动6个单位长度,则这个点表示的数是__________.(2)一个小虫在数轴上先向右爬2个单位,再向左爬6个单位,所在位置正好距离数轴原点2个单位,则小虫的起始位置所表示的数是________.(3)数轴上的点A 对应的数是1-,一只蚂蚁从A 点出发沿着数轴向右以每秒3个单位长度的速度爬行至B 点后,用2秒的时间吃光了B 点处的蜜糖,又沿原路以原速度返回A 点,共用去6秒,则蚂蚁爬行的路程是几个单位长度?B 点与A 点的距离是多少个单位长度?B 点对应的数是多少?举一反三:【变式】(1)点A 在数轴上距原点为3个单位,且位于原点左侧,若将A 向右移动4个单位,再向左移动2个单位,这时A 点表示的数是________.(2)一只小虫在数轴上先向右爬3个单位,再向左爬7个单位,正好停在-2的位置,则小虫的起始位置所表示的数是( ) A .-4 B .4 C .2 D .0类型、相反数(1)2017-的相反数是________,2017与________互为相反数.(2)已知有理数a 、b 在数轴上表示如图,则a 、b 、a -、b -的大小,正确的是( ) A .a b a b -<-<< B .a b b a <-<<-C .b a a b -<<-< D .a b b a <<-<-(3)下列说法正确的是( ) A .一个数的相反数一定是负数 B .π和.-314互为相反数 C .所有的有理数都有相反数 D .13和31互为相反数例题4例题5举一反三:【变式1】我们可以用字母表示数,比如a 、b 都能代表一个数,在一个数的前面添上“-”号,就得到这个数的相反数.(1)5的相反数是_______;13的相反数是_______,0的相反数是_______,数a 的相反数是________;(2)5-的相反数是_______,12-的相反数是________,4-的相反数是________;数a -的相反数是________;(3)(2)--的相反数是________;(5)+-的相反数是________,数()a -+的相反数是________,数()a --的相反数是_______;()a b ---与________互为相反数.【变式2】下列说法中正确的有( )①-3和+3互为相反数;②符号不同的两个数互为相反数;③互为相反数的两个数必定一个是正数,一个是负数;④π的相反数是-3.14;⑤一个数和它的相反数不可能相等. A. 0个 B.1个 C.2个 D.3个或更多化简下列各数中的符号.(1)123⎛⎫-- ⎪⎝⎭ (2)-(+5) (3)-(-0.25) (4)12⎛⎫+- ⎪⎝⎭(5)-[-(+1)] (6)-(-a)举一反三:【变式1】如果a <0,化简下列各数的符号,并说出是正数还是负数 ①()a -+; ②()a --; ③[()]a -+-; ④[()]a ---; ⑤{[()]}a -+--; ⑥{{{{{[()]}}}}}a -----+--【变式2】(1)37与________互为相反数;a 1-2是________的相反数.(2)()--2的相反数是________;b +4是________的相反数.(3){[()]}--+-4=________;{[()]}----5与________互为相反数.例题6一、选择题1.如图所示,在数轴上点A 表示的数可能是( )A .1.5 B.-1.5 C.-2.6 D.2.62.从原点开始向右移动3个单位,再向左移动1个单位后到达A 点,则A 点表示的数是( ). A.3 B.4 C.2 D.-23.关于数“0”,以下各种说法中,错误的是 ( ) A .0是整数 B .0是偶数C .0是正整数D .0既不是正数也不是负数 4.下列说法中:(1)0是最小的自然数;(2)0是最小的正数;(3)0是最大的负整数;(4)0属于整数集合;(5)0既非正数也非负数.正确的是( ) A .(1)(2)(4) B .(4)(5) C .(1)(4)(5) D .(1)(2)(5) 5.一个数的相反数是非负数,则这个数一定是( ) A.正数 B.负数 C.非正数 D.非负数 6.在①+(+1)与-(-1);②-(+1)与+(-1);③+(+1)与-(+1);④+(-1)与-(-1)中,互为相反数的是( )A. ①②B. ②③C. ③④D. ②④ 7.-(-2)=( ) A.-2B. 2C.±2D.4二、填空题1.不大于4的正整数的个数为 .2.已知数轴上有A ,B 两点,A ,B 之间的距离为1,点A 与原点O 的距离为3,那么点B 对应的数是 .3. 既不是正数,也不是负数的有理数是 .4.如图所示,矩形ABCD 的顶点A ,B 在数轴上,CD =6,点A 对应的数为-1,则点B 所对应的数为 .5.数轴上离原点的距离小于3.5的整数点的个数为m , 距离原点等于3.5的点的个数为n , 则3____m n -=.6.已知x 与y 互为相反数,y 与z 互为相反数,又2z =,则z x y -+= .7. 已知-1<a <0<1<b ,请按从小到大的顺序排列-1,-a ,0,1,-b 为 .8.一种零件的长度在图纸上是(03.002.010+-)毫米,表示这种零件的标准尺寸是 毫米,加工要求最大不超过 毫米,最小不小于 毫米.课堂巩固三、解答题9.小敏的家、学校、邮局、图书馆坐落在一条东西走向的大街上,依次记为A 、B 、C 、D ,学校位于小敏家西150米,邮局位于小敏家东100米,图书馆位于小敏家西400米. (1)用数轴表示A 、B 、C 、D 的位置(建议以小敏家为原点).(2)一天小敏从家里先去邮局寄信后.以每分钟50米的速度往图书馆方向走了约8分钟.试问这时小敏约在什么位置?距图书馆和学校各约多少米?10.把下列各数填在相应的大括号内: 1.2-,3,1,41,0,-14.3,101-,6.20,25-,1056,-7.正分数集合:{ …}; 非负数集合:{ …};正整数集合:{ …}; 负整数集合:{ …}.11.化简下列各数,再用“<”连接.(1)-(-54) (2)-(+3.6) (3)53⎛⎫-+ ⎪⎝⎭ (4)245⎛⎫-- ⎪⎝⎭12.若a 与b 互为相反数,c 与d 互为倒数,m 是最大的负整数.求代数式的值.13.在数轴上有三个点A ,B ,C 如图所示,请回答:(1)将B 点向左移动3个单位长度后,三个点表示的数谁最小? (2)与A 点相距3个单位长度的点所表示的数是什么?(3)将C 点左移6个单位长度后,这时B 点表示的数比C 点表示的数大多少?。
七年级数学第一单元有理数知识点

七年级数学第一单元有理数知识点有理数是七年级数学的重要基础内容,它为后续的数学学习打下了坚实的基础。
下面我们来详细了解一下有理数的相关知识点。
一、有理数的定义有理数是整数(正整数、0、负整数)和分数的统称。
有理数的小数部分是有限或为无限循环的数。
例如,5 是整数,属于有理数;025 是有限小数,属于有理数;1/3 是无限循环小数,也属于有理数。
与之相对的是无理数,无理数是无限不循环小数,如圆周率π。
二、有理数的分类1、按定义分类有理数可以分为整数和分数。
整数包括正整数、0、负整数。
例如 3、0、-5 等。
分数包括正分数和负分数。
比如 1/2、-3/4 等。
2、按性质分类有理数可以分为正有理数、0、负有理数。
正有理数包括正整数和正分数,比如 2、3/5 。
负有理数包括负整数和负分数,例如-1、-2/7 。
三、数轴数轴是规定了原点、正方向和单位长度的直线。
数轴的作用非常大,它可以帮助我们直观地理解有理数的大小关系。
在数轴上,右边的数总比左边的数大。
例如,在数轴上表示 2 的点在表示 1 的点的右边,所以 2 大于 1 。
任何一个有理数都可以用数轴上的一个点来表示。
四、相反数只有符号不同的两个数叫做互为相反数。
例如,5 和-5 互为相反数,0 的相反数是 0 。
互为相反数的两个数的和为 0 。
五、绝对值绝对值的定义:数轴上表示数 a 的点与原点的距离叫做数 a 的绝对值。
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是 0 。
例如,|5| = 5 ,|-3| = 3 ,|0| = 0 。
绝对值的性质:(1)绝对值具有非负性,即绝对值总是大于或等于 0 。
(2)互为相反数的两个数的绝对值相等。
六、有理数的大小比较1、正数都大于 0 ,负数都小于 0 ,正数大于一切负数。
2、两个负数比较大小,绝对值大的反而小。
例如,比较-2 和-5 的大小。
因为|-2| = 2 ,|-5| = 5 ,2 < 5 ,所以-2 >-5 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲 有理数的概念一、正数和负数在数学发展历史上,从发现自然数开始,随着人类文明进步,我们又逐渐定义了分数和小数等.在生活和学习中,我们会需要记录一些具有相反意义的量,比如:零下4︒C 和零上6︒C ,收入20元和支出30元,向东30米和向西100米等等.这些数据不仅意义相反,而且表示一定的量,为了表示它们,我们定义了正负数:1.用正负数表示相反意义的量: 我们把一种意义的量规定为正的,把另一种与它具有相反意义的量规定为负的,分别用正数和负数表示,给数字前面加上正号表示正数,加上负号表示负数.【例】以上几个例子分别记为:4-︒C 和6+︒C ,20+元和20-元,30+米和100-米.2.正数:像30、+6、12、π这样的数叫做正数,正数都大于零;3.负数:在正数前面加上“-”号的数叫做负数,比如:20-、3.14-、0.001-、172-.【注】①表示正数时,“+”号可以省略,但表示负数时,“-”号一定不能省略;②数0既不是正数也不是负数.二、有理数的概念及分类1.有理数:整数与分数统称为有理数. 2.有理数的分类:(1)有理数按性质分类:⎧⎧⎫⎪⎪⎬⎨⎪⎭⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数自然数整数零有理数负整数正分数分数负分数 (2)有理数按符号分类 ⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎪⎨⎪⎪⎩⎩正整数正有理数正分数有理数零(既不是正数,也不是负数)负整数负有理数负分数(3)小数的分类【注】注意以下几个概念的区分:非负数:正数和零;非正数:负数和零;非负整数:正整数和零;非正整数:负整数和零;非负有理数:正有理数和零;非正有理数:负有理数和零.⎧⎪⎧⎨⎨⎪⎩⎩有限小数小数无限循环小数无限小数无限不循环小数——不可化成分数,是无理数——可化成分数,是有理数三、数轴1.数轴:数轴是一条规定了原点、正方向和单位长度的直线. 【注】原点、正方向和单位长度称为数轴的三要素;①原点:表示数0的点;②正方向:数字从小到大排列的方向,一般规定向右为正方向; ③单位长度:人为规定的代表“1”的线段的长度.2.数轴的画法(1)画一条水平直线;(2)在这条直线上取一点作为原点; (3)一般用箭头表示正方向;(4)选取适当的长度为单位长度,用细短线画出刻度,并将数字对应标在数轴下方.【例】一个标准的数轴: 【注】画数轴的常见错误:①三要素缺失:没有原点、正方向箭头或者单位长度刻度; ②单位长度不统一:相邻两个刻度之间间距不一样;③方向不统一:数字增大的方向不是正方向,或者数字排列混乱.3.数轴与有理数的关系①任何一个有理数均可用数轴上的一个点来表示; 但数轴上的点不一定代表有理数,比如π. ②数轴上两个点表示的数,右边的总比左边的大;③数轴直观地说明了,正数大于零,负数小于零,正数大于负数. 4.数轴与数学思想①数形结合思想:数轴形象地反映了数和点之间的对应关系;②分类讨论思想:数轴表现了有理数的一种分类方法,即分成正数、负数和零. 四、相反数&倒数1.相反数:如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数.特别地,0的相反数是0.【例】5+与5-互为相反数;5-是5+的相反数;【注】相反数必须成对出现,单独一个数不能说是相反数.“5-是相反数”是错误的. 2.相反数的性质:(1)代数性质:若a 与b 互为相反数,则0a b +=;反之,若0a b +=,则a 与b 互为相反数.(2)几何性质:一对相反数在数轴上对应的点分别位于原点两侧,并且到原点的距离相等,即这两点是关于原点对称的.3.倒数:乘积为1的两个有理数互为倒数.【例】2与12,3-与13-,38-与83-.4.负倒数:乘积为1-的两个有理数互为负倒数.【例】2与12-,3-与13,38-与83.【注】①0没有倒数,也没有负倒数;②倒数是它的本身的数1或-1. 五、绝对值1.绝对值:数轴上表示数a 的点与原点的距离叫做数a 的绝对值,记作a . 2.绝对值运算:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩3.绝对值的性质: (1)非负性:||0a ≥;(2)双解性:若||||a b =,则a b =或a b =-.【注】如果若干个非负数的和为0,那么这若干个非负数都必为0.例如,若||||||a b c ++=0,则a =0,b =0,c =0.(1)仔细思考以下各对量: ①胜二局与负三局;②气温为3C -︒与气温升高30C ︒; ③盈利5万元与亏损5万元;④增加10%与减少20%.其中具有相反意义的量有( ) A .1对 B .2对C .3对D .4对(2)①我国现采用国际通用的公历纪年法,如果我们把公元2017年记作+2017年,那么,处于公元前500年的春秋战国时期可表示为___________.②如果80m 表示向东走80m ,那么60m -表示________________.③A ,B 两地海拔高度分别是120米,10-米,则B 地比A 地低________米.(3)学而思饮料公司生产的一种瓶装饮料外包装上印有“60030(ml)±”字样,请问“60030(ml)±”是什么含义?质检局对该产品抽查5瓶,容量分别为603ml ,611ml ,589ml ,573ml ,627ml ,问抽查产品的容量是否合格?模块一 正数和负数例题1(1)下列说法错误的是( ) A .0既不是正数也不是负数 B .正整数和负整数统称整数C .整数和分数统称有理数D .正有理数包括正整数和正分数(2)把下列各数分别填在所属分类里:5-,0, 3.14-,32, 2.4-,227,327,π, 5.5-,.24,311-,3.14159,34-,2003①正数:{ }; ②负数:{ }; ③非负整数:{ }; ④分数:{ }; ⑤非正有理数:{ };(3)在下表适当的空格里打上“√”号.整数 分数 正数 负整数 正分数非负数 非负整数无理数 0.-15-3.+062 14.031π98-模块二有理数的概念及分类例题2a b 0(1)下面图形是数轴的是( )A .B .C .D .(2)如图所示,数轴的一部分被墨水污染了,被污染的部分内含有的整数为_______.(3)已知:点A 在数轴上的位置如图所示,点B 也在数轴上,且A 、B 两点之间的距离是2,则点B 表示的数是______.(4)在数轴上标出下列各数:0, 4.2,132,2,+7,113,并用“<”连接.(1)一个点沿着数轴的正方向从原点起移动2个单位长度后,又向反方向移动6个单位长度,则这个点表示的数是__________.(2)一个小虫在数轴上先向右爬2个单位,再向左爬6个单位,所在位置正好距离数轴原点2个单位,则小虫的起始位置所表示的数是________. (3)数轴上的点A 对应的数是1-,一只蚂蚁从A 点出发沿着数轴向右以每秒3个单位长度的速度爬行至B 点后,用2秒的时间吃光了B 点处的蜜糖,又沿原路以原速度返回A 点,共用去6秒,则蚂蚁爬行的路程是几个单位长度?B 点与A 点的距离是多少个单位长度?B 点对应的数是多少?(1)2017-的相反数是________,2017与________互为相反数.(2)已知有理数a 、b 在数轴上表示如图,则a 、b 、a -、b -的大小,正确的是( ) A .a b a b -<-<< B .a b b a <-<<-C .b a a b -<<-<D .a b b a <<-<-(3)下列说法正确的是( ) A .一个数的相反数一定是负数 B .π和.-314互为相反数 C .所有的有理数都有相反数 D .13和31互为相反数模块三数轴例题3例题4模块四 相反数&倒数例题554BA13-1123-2-01-3 122-1-0 1232-1-012 1.3- 2.6 A 3-O 7-6-5-4-3-2-1-01234567我们可以用字母表示数,比如a 、b 都能代表一个数,在一个数的前面添上“-”号,就得到这个数的相反数.(1)5的相反数是_______;13的相反数是_______,0的相反数是_______,数a 的相反数是________;(2)5-的相反数是_______,12-的相反数是________,4-的相反数是________;数a -的相反数是________;(3)(2)--的相反数是________;(5)+-的相反数是________,数()a -+的相反数是________,数()a --的相反数是_______;()a b ---与________互为相反数.如果a <0,化简下列各数的符号,并说出是正数还是负数 ①()a -+; ②()a --; ③[()]a -+-; ④[()]a ---; ⑤{[()]}a -+--; ⑥{{{{{[()]}}}}}a -----+--(1)2017-的倒数是________,2017与________互为负倒数.(2)一个数的倒数等于它本身,这个数是_________;一个数的倒数等于它的相反数,则这个数________.(3)已知a 、b 为有理数,在数轴上如图所示,则( )A .a b 11<1<B .a b 11<<1C .b a 11<<1D .b a 111<<(1)2017-的绝对值是_________,|2017|--的相反数是________,|2017|-与________互为倒数.(2)①绝对值不大于3的整数有________;②绝对值大于2而小于5的负整数是________.(3)①若m 、n 满足||||=m n -2+-30,则mn 的值等于________;②||||x y =--7,则xy =________.(4)已知|5|a =,||2b =,则||a b -的值是__________.例题6例题7例题8模块五 绝对值例题91-a 01b(1)下列说法正确的个数( ) ①()a --表示正数;②||a 一定是正数,||a -一定是负数;③绝对值等于本身的数只有两个,是0和1;④如果||||a b >,则a b >.A .0个B .1个C .2个D .3个 (2)若x 表示有理数,则||x --一定是( ) A .正数 B .负数C .非正数D .非负数(3)下列说法正确的是( )A .若a 表示有理数,则a -表示非正数B .和为零的两数互为相反数C .一个数的绝对值必是正数D .若||||a b >,则a b <<0(1)如果节约16吨水记作+16吨,则浪费6吨水记作__________.(2)在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作___________. (3)把下列各数填入表示它所在的大括号:.-24,3,2.008,10-3,114,0,()--2,3.14,||--4.正有理数:{ } 非负整数:{ } 负分数:{ }(1)下列说法正确的是( )A .在有理数中,零的意义仅仅表示没有B .正有理数和负有理数组成全体有理数C .0.5既不是整数,也不是分数,因而它不是有理数D .零既不是正数,也不是负数 (2)下列说法不正确的是( ) A .绝对值等于本身的数是非负数 B .倒数等于本身的数有2个 C .有理数可分为整数和分数D .两个负数比较大小,绝对值越大的数越大例题10复习巩固演练1演练2(1)如图,表示数轴正确的是( )A .B .C .D .(2)已知点A ,点B 在数轴上,点A 表示数为-2,A 、B 两点的距离为5,则点B 表示的数是________.(3)在数轴上标出下列各数,并用“<”比较它们的大小:-3,+1,122,.-15,5.(4)已知,a b 为有理数,在数轴上的位置如图所示,则a 1,b1,0,1的大小关系为_______________.(1)点A 在数轴上距原点为3个单位,且位于原点左侧,若将A 向右移动4个单位,再向左移动2个单位,这时A 点表示的数是________.(2)一只小虫在数轴上先向右爬3个单位,再向左爬7个单位,正好停在-2的位置,则小虫的起始位置所表示的数是( ) A .-4 B .4 C .2 D .0(1)37与________互为相反数;a 1-2是________的相反数.(2)()--2的相反数是________;b +4是________的相反数.(3){[()]}--+-4=________;{[()]}----5与________互为相反数.(1)||||x y 2-2+7-3=0,求xy =________.(2)4-27的倒数是________,3.75的负倒数是___________.(3)给出下面说法:①互为相反数的两数的绝对值相等;②一个数的绝对值等于本身,这个数不是负数;③若||m m >,则0m <;④若||||a b >,则a b >,其中正确的有______.021-1-23-2-1120-2-112023-2-110演练3演练4演练5 演练610ba。
