小学六年级数学复习找规律练习题
六年级数学找规律题型

一、等差型数列规律1.有一组数:7,12,17,22,27,…请观察这组数的构成规律,用你发现的规律确定 第8个数为 , 第n 个数为 . 二、等比型数列规律2. 有一组数:1,4,16,64,……,请观察这组数的构成规律,用你发现的规律确定三、含n 2型数列规律3.有一组数:2,6,12,20,30,…请观察这组数的构成规律,用你发现的规律 确定第8个数为 , 第n 个数为 .四、其它数列规律列举4.观察下列一组数:32,54,76,98,1110,…… ,它们是按一定规律排列的,那么这一组数的 第k 个数是五、循环型数列.5. 已知221=,422=,32=8,42=16,25=32,……观察上面规律,试猜想20082 的末位数是 .6. 若1113a =-,2111a a =-,3211a a =-,… ;则2014a 的值为 . 六、算式型规律7. 已知22223322333388+=⨯+=⨯,,244441515+=⨯,……,若288a a b b+=⨯(a 、b 为正整数)则a b += .8. 研究下列算式,你会发现什么规律?1×3+1=22; 2×4+1=32; 3×5+1=42; 4×6+1=52 …………,(1) 请用含n 的式子表示你发现的规律:___________________.(2) 请你用发现的规律解决下面问题计算11111(1)(1)(1)(1)(1)132********+++++⨯⨯⨯⨯⨯的值七、数列阵型9.观察下列三行数: (课本P43页例4变式题)第一行:-1,2,-3,4,-5……第二行:1,4,9,16,25,……第三行:0,3,8,15,24,……(1)第一行数按什么规律排列?(2)第二行、第三行分别与第一行数有什么关系?(3)取每行的第10个数,计算这三个数的和.。
小学六年级数学复习找规律练习题

第 100 个图形的周长是(
)厘米。
)厘米 ,
12.
6
.
第 2页(共 29页)
二、选择题(共 4 小题)
1. 按 式摆放,有(
的方式摆放在桌面上. 8 个 )个面露在外面.
A.20 B.23 C.26 D.29
2.将一些小圆球如图摆放,第六幅图有(
)个小圆球.
按这种方
A.30 B.36 C.42 3.按下列规律印刷笑脸图案,第 8 幅图案有(
A.8 B.32 C.36 【分析】 第一幅图有 1 个笑脸,第二幅图有 3 个笑脸,第三幅图有 6 个笑脸 …; 1=1, 3=1+2, 6=1+2+3, 第 n 幅图中笑脸的数量就是 1+2+3+…+n. 【解答】 解: 1+2+3+4+5+6+7+8, =(1+8) +( 2+7)+( 3+6)+(4+5), =9×4, =36; 答:第 8 副图案有 36 个笑脸. 故选: C. 【点评】 解决本题关键是找出笑脸的个数变化的规律,再由此规律求解.
.
5.用小棒摆三角形 摆 n 个三角形需
,照这样摆下去, 摆 10 个三角形需 根小棒.
根小棒,
6.如图,用同样的小棒摆正方形.摆 10 个同样的正方形需要小棒
根;
现在有 46 根小棒可以摆
个正方形.
7.如图
,小明用小棒搭房子,他搭 3 间房子用 13 根小棒.照这样,
搭 10 间房子要用
根小棒;搭 n 间房子要用
,其中完整的圆共有 13 个,如果铺成一个 4×4 的正方形图案(如图④) ,
(小升初真题)六年级数学找规律题(易错题、难题)名师详解连载一

(小升初真题)六年级数学找规律题(易错题、难题)名师详解连载一第一关:我会找规律1.如下图,根据图形与数的规律,第10个数是()。
2.九张卡片上分别写着1~9九个数字。
甲、乙、丙、丁四人玩数字游戏,每人拿两张。
如果结果是:甲的两张数字之和是9,乙的两张数字之差是6,丙的两张数字之积是12,丁的两张数字之商是3。
那么剩下的这张数字是()。
3.六年级1、2、3、4四个班举行拔河比赛,甲、乙、丙三个同学猜测四个班比赛的前三名名次。
甲说:1班第三,3班第一;乙说:3班第二,2班第三;丙说:4班第二,1班第一。
比赛结果,三个人都猜对了一半。
那么,1班第()名,4班第()名。
4.按如右规律摆放三角形则第⑥个图三角形的个数为()。
A.15 B.17 C.20 D.245.下面的图形中,()是正方体的表面展开图。
1.根据规律填空:61,21,( ),29,227,( )。
2.海边灯塔上的一盏照明灯以固定的规律发出亮光。
下图表示前14秒灯光明暗变化的情况,第1秒亮( ),第2秒暗( ),第3秒暗( )……观察下图的变化规律,请你判断第39秒照明灯是( )的。
(填写“亮”或“暗”。
)3. 如下图所示,用白色和灰色小正方形按下图的规律摆大正方形。
照这样接着摆下去,第6幅图一共有( )个白色小正方形。
4.将同样大小的正方形按下列规律摆放,重叠部分涂上阴影,则下面图案中,第1个图案有3个正方形,第2个图案有7个正方形,那么:第1个 第2个 第3个(1)第六个图案中有( )个正方形;(2)若第n 个图案中有7999个正方形,则n=( )。
第二关:我会找规7. 31,91,271……按这组数的规律,第五个数应该是( );如果这样一直写下去,那么这个数会越来越接近( )。
8. 学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图所示) ,请你结合这个规律算一算, 6张桌子拼成一行能坐( )人, n 张桌子拼成一行能坐( )人。
六年级数学《找规律训练题》
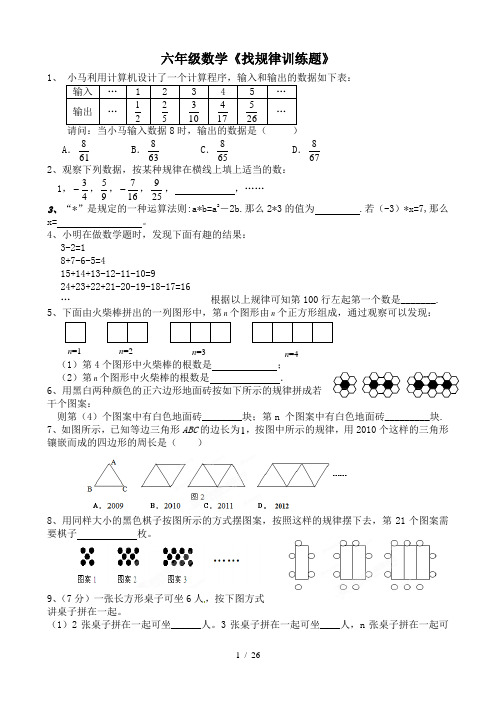
六年级数学《找规律训练题》1、 小马利用计算机设计了一个计算程序,输入和输出的数据如下表: 输入 … 1 2 3 4 5 … 输出 … 21 52 103 174 265 … 请问:当小马输入数据8时,输出的数据是( )A .618B .638C .658 D .678 2、观察下列数据,按某种规律在横线上填上适当的数:1,43-,95,167-,259, ,…… 3、“*”是规定的一种运算法则:a*b=a 2-2b.那么2*3的值为 .若(-3)*x=7,那么x= 。
4、小明在做数学题时,发现下面有趣的结果:3-2=18+7-6-5=415+14+13-12-11-10=924+23+22+21-20-19-18-17=16… 根据以上规律可知第100行左起第一个数是_______.5、下面由火柴棒拼出的一列图形中,第n 个图形由n 个正方形组成,通过观察可以发现:(1)第4个图形中火柴棒的根数是 ;(2)第n 个图形中火柴棒的根数是 .6、用黑白两种颜色的正六边形地面砖按如下所示的规律拼成若干个图案:则第(4)个图案中有白色地面砖________块;第n 个图案中有白色地面砖_________块.7、如图所示,已知等边三角形ABC 的边长为1,按图中所示的规律,用2010个这样的三角形镶嵌而成的四边形的周长是( )8、用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第21个图案需要棋子 枚。
9、(7分)一张长方形桌子可坐6人,按下图方式讲桌子拼在一起。
(1)2张桌子拼在一起可坐______人。
3张桌子拼在一起可坐____人,n 张桌子拼在一起可n =1 n =2 n =3 n =4坐______人。
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐______人。
10、如图所示,将多边形分割成三角形.图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n 边形可以分割出_________个三角形。
六年级的数学找规律练习题.doc

六年级数学找规律练习题班级 姓名等级例 1 假设 a#b=( a+b ) +(a —b );求 13#5 和 13#(5#4) 练习一1、将新运算定义为 a *b=(a+b )×(a —b );求 27*92、设 a *b=a 2 +2b ;求 10* 6 和 5*( 2*8)3、设 a *b=3a —b ×1;求 (15* 24)*( 10 *12)2例 2 设 p 、q 是两个数;规定: p # q=4×q —( p +q )÷2;求 3 #( 4# 6) 练习二1、设 p 、q 是两个数;规定: p # q=4×q —( p +q )÷2;求 5#( 6# 4)2、设 p 、q 是两个数;规定: p # q=p 2 +(p —q ) ×2;求 30#(5# 3)、设 M 、 N 是两个数;规定:MN ;求 10#20—13M # N=+4N M例 3 如果 1&5=1+11+111+1111+11111;2&4=2+22+222+2222;3&3=3+33+333 ;4&2=4+44 ; 那么 7&4= ;210&2= 。
练习三1、如果 1&5=1+11+111+1111+11111; 2&2=2+22 ;3&3=3+33+333 ⋯⋯ 那么 4&4= 。
2、规定 a&b=a+aa+aaa+aaaa+a ⋯⋯ a ( b 个 a );那么 8&5= 。
、如果1 ;3&2= 1 ; 4&3=1;那么( 6&3 )÷(2&6 )= 。
33 4442例 4 设 a@b=4a —2b+ 1ab ;求 x@(4@1) =34 中的未知数 x2练习四1、设 a@b=3a —2b ;已知 x@(4@1)=7;求 x、对两个整数 a 和 b 定义新运算“ & ”;a&b= 2a b ;求 6&4+9&82ba ba4xyx 和 y 定义新运算“ #”: x#y= (其中 m 是一个确定的整数) 。
小学六年级毕业卷数学小升初复习专项练习--找规律图形题
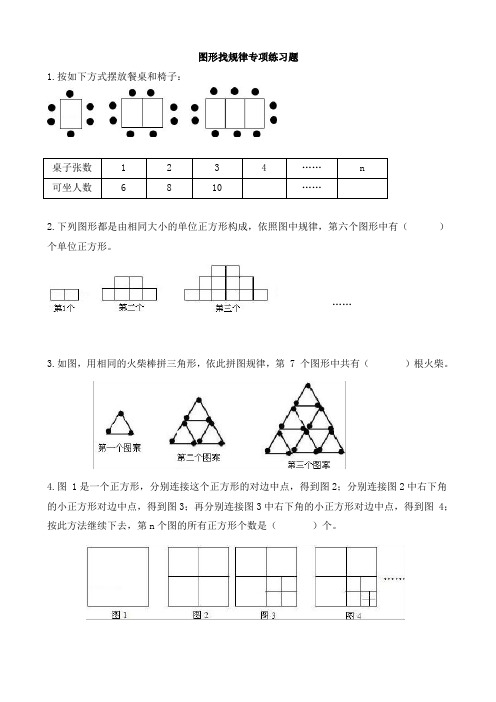
图形找规律专项练习题1.按如下方式摆放餐桌和椅子:桌子张数1234……n可坐人数6810……2.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有()个单位正方形。
……3.如图,用相同的火柴棒拼三角形,依此拼图规律,第7个图形中共有()根火柴。
4.图1是一个正方形,分别连接这个正方形的对边中点,得到图2;分别连接图2中右下角的小正方形对边中点,得到图3;再分别连接图3中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n个图的所有正方形个数是()个。
5.观察下列图案∶它们是按照一定规律排列的,依照此规律,第6个图案中共有()个三角形.6.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形;再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是();第六个正方形的面积是()。
7.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现∶第1个图形有1个小正方形,第2个图形有3个小正方形,第3个图形有6个小正方形,第4个图形有10个小正方形…,按照这样的规律,则第10个图形有____个小正方形.8.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为9.为庆祝"六一"儿童节,幼儿园举行用火柴棒摆"金鱼"比赛,如图所示,则摆n条"金鱼"需用火柴棒的根数为_____10.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有_____个交点,二十条直线相交最多有___个交点11.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表∶图形编号(1)(2)(3)……(n)火柴根数12.图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第2个图形(它的中间为一个白色,的正三角开);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形,如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是()。
六年级数学找规律练习

1、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+仁25, •- 根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+ • • +99+100+99+…+3+2+1 = 2、已知下列等式:3 .2=1 ;3 3 2+ 2 = 3 ;2 + 2 +3 =6 ;2+ 2 + 3 + 4 = 10 ;由此规律知,第⑤个等式是3、如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,4、如图是五角星灯连续旋转闪烁所成的三个图形。
照此规律闪烁,下一个呈现出来的图形是班级姓名等级摆出的正方形所用的火柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).①②③④当边长为n根火柴棍时,若☆ ☆ ☆6、如图,在图1中,互不重叠的三角形共有 4个,在图2中,互不重叠的三角形共有 7个,在图3中,互不重叠的三角形共有 10个, ,则在第n 个图形中,互不重叠的三角形共有 个(用含n 的代数式表示)。
8、在计算机程序中,二杈树是一种表示数据结构的方法。
如图,一层二杈树的结点总数是 二层二杈树的结点总数是 3,三层二杈树的结点总数是 7,四层二杈树的结点总数是15……照此规律七层二杈树的结点总数是▲ A一层二杈树二层二杈树三层二杈树☆ ☆ ☆7、小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第 n 个图案需要用白色棋子----------------- (oooc ooooooo 0*0 oooo ooooooon 的代数式表示)ooooo^ r1 ・rr J1,”需要火柴根。
12、如图,将第一个图(图①)所示的正三角形连结各边中点进行分割, 得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图 ③);再将第三个图中最中间的小正三角形按同样的方式进行分割,……,则得到的第五个图中, 共有 个正三角形。
小学数学找规律练习题

小学数学找规律练习题1. 以下数列中,每一项都是前一项的两倍,求第六项:2,4,8,16,32,...答案:第六项为64。
2. 以下数列中,第一项为1,从第二项开始每一项都是前一项加上一个偶数,求第七项:1,4,8,12,16,20,...答案:第七项为28。
3. 以下数列中,第一项为1,从第二项开始每一项都是前一项加上本项的下标,求第七项:1,3,6,10,15,21,...答案:第七项为28。
4. 以下数列中,第一项为0,从第二项开始每一项都是前一项加上9,求第六项:0,9,18,27,36,...答案:第六项为45。
5. 以下数列中,第一项为1,从第二项开始每一项都是前一项乘2再减去1,求第六项:1,1,1,1,1,...答案:第六项为1。
6. 以下数列中,第一项为10,从第二项开始每一项都是前一项减去3,求第七项:10,7,4,1,-2,-5,...答案:第七项为-8。
7. 以下数列中,第一项为1,从第二项开始每一项都是前一项加上它的倒数,求第六项:(结果保留两位小数)1,2,(5/3),(19/10),(87/49),...答案:第六项为(407/245)≈1.66。
8. 以下数列中,第一项为1,从第二项开始每一项都是前一项加上它的平方,求第五项:1,2,5,26,677,...答案:第五项为677。
9. 以下数列中,第一项为1,从第二项开始每一项都是前一项的平方根再加上1,求第六项:(结果保留两位小数)1,(1+√2),(1+√2+√(1+√2)),(1+√2+√(1+√2)+√(1+√2+√(1+√2))),...答案:第六项为(1.96+√(2.96+√(3.96+√(4.96))))≈4.57。
10. 以下数列中,第一项为1,从第二项开始每一项都是前一项的2倍再加上1,求第六项:1,3,7,15,31,...答案:第六项为63。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律习题一、填空题1.摆一个需要4根小棒,摆需要7根小棒,摆需要10根小棒…,像这样摆n个正方形需要根小棒,当n=20时,需要根小棒.2.如图方式摆放桌子和椅子,一张桌子能坐6人,3张桌子能坐人.3.…用相同的小棒按左图方法拼组,如果拼成的图形中含有10个小正方形,需要根小棒,154根小棒拼成的图形中含有个小正方体.4.如图,每个方框中数的排列是有规律的,则F=.5.用小棒摆三角形,照这样摆下去,摆10个三角形需根小棒,摆n个三角形需根小棒.6.如图,用同样的小棒摆正方形.摆10个同样的正方形需要小棒根;现在有46根小棒可以摆个正方形.7.如图,小明用小棒搭房子,他搭3间房子用13根小棒.照这样,搭10间房子要用根小棒;搭n间房子要用根小棒(用含有n的式子表示).8.下面一组图形中的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来。
9.按照下面的规律摆下去,图8应有()个三角形。
10.用3根小棒可以摆一个三角形,按下面的方式摆下趣,摆100个三角形需要()根小棒。
11.按照下面的方法拼下去(单位:厘米),第9个图的周长是()厘米,第100个图形的周长是()厘米。
12.6二、选择题(共4小题)1.按的方式摆放在桌面上.8个按这种方式摆放,有()个面露在外面.A.20 B.23 C.26 D.292.将一些小圆球如图摆放,第六幅图有()个小圆球.A.30 B.36 C.423.按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8 B.32 C.364.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+3112.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为3,6,9,12.按这个规律.由100个小等边三角形拼成的图形,周长为.13.对于一个多边形,定义一种“生长”操作(如图),将其中一边AB变成折线ACDEB,其中C和E是AB的三等分点,C、D、E三点可构成等边三角形,那么,一个边长是9的等边三角形,经过四次“生长”操作得到的图形的周长是.14.如图,它是由火柴棒拼成的图案,如果在这个图案中用了51根火柴棒,可拼成个三角形.15.如图,一张方桌可以坐4人,两张方桌拼起来可以坐6人,三张方桌拼起来可以坐8人…像这样n张方桌拼起来可以坐人,坐68人需要张方桌.16.用小棒摆正方形,如图摆6个正方形用小棒根,摆n个正方形用小棒根.17.把边长为1厘米的正方形纸片,按如图的规律拼成长方形;(1)用6个正方形拼成的长方形周长是厘米;(2)用n个正方形拼成的长方形周长是厘米.18.摆1个正方形需要4根小棒,摆2个需要7根小棒,摆3个需要10根小棒,摆n 个正方形需要 根小棒.三、解答题(共12小题) 19.探索规律. 正方体个数1 2 3 4 5 6 … N …正方形个数 6 10 14 18 … 62 …20.怎样巧妙的计算连续偶数的和呢?通过下面的探索,你就会有新的发现.(1)摆两层一共有:1+2=3个 摆三层一共有1+2+3=6个 摆四层一共有 个. 摆五层一共有 个. 摆六层一共有 个. …(2)用n 表示摆的层数,你能总结出一个计算公式吗? .28.观察下图中由棱长是1厘米的小正方体摆成的立体图形,寻找规律并完成下表.摆成立体图形的序号 ① ② ③ ④ ⑤ 小正方体的总个数18 27 看不见小正方体的个数 01看得见小正方体的个数182629.探寻规律.如图 是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个2×2的正方形图案(如图‚),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图 ),其中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个10×10的正方形图案,则其中完整的圆共有个.30.准备(1)每个都是棱长为1厘米的正方体.(2)一个挨着一个排成一排你要研究的问题是:正方体个数与拼成的长方体表面积之间的关系.探索过程:根据你的发现填空.当正方体个数为10时,所拼成的长方体表面积是平方厘米.当正方体个数为a时,所拼成的长方体表面积是平方厘米.当拼成的长方体表面积是202平方厘米时,正方体个数是.苏教版五年级(上)小升初题单元试卷:五找规律(01)参考答案与试题解析一、选择题(共4小题)1.按的方式摆放在桌面上.8个按这种方式摆放,有()个面露在外面.A.20 B.23 C.26 D.29【分析】1个小正体有5个面露在外面,再增加一个正方体,2个小正方体有8个面露在外面;3个小正方体有11个面露在外面.每增加1个正方体漏在外面的面就增加3个即:n个正方体有5+(n﹣1)×3;由此求解.【解答】解:根据题干分析可得,n个正方体有5+(n﹣1)×3=3n+2;所以8个小正方体时,露在外部的面有:3n+2=3×8+2=26(个)故选:C.【点评】解答此题应根据题意,进行推导,得出规律:即1个小正方体露出5个面,每增加1个小正方体增加3个面;进行解答即可.2.将一些小圆球如图摆放,第六幅图有()个小圆球.A.30 B.36 C.42【分析】从第一个图形开始分析小圆圈的个数:第一个图形中有1×2=2个小圆球,第二个图形中有2×3=6个小圆球,第三个图形中有3×4=12个小圆球,第四个图形中有4×5=20个小圆球,…第n个图形有n(n+1)个小圆球,利用规律解决问题.【解答】解:观察图形可知:第一个图形中有1×2=2个小圆球,第二个图形中有2×3=6个小圆球,第三个图形中有3×4=12个小圆球,第四个图形中有4×5=20个小圆球,…所以第六幅图有6×7=42个小圆球.故选:C.【点评】此题主要考查了图形的规律,通过归纳与总结结合图形得出图形个数之间的规律是解决问题的关键.3.按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8 B.32 C.36【分析】第一幅图有1个笑脸,第二幅图有3个笑脸,第三幅图有6个笑脸…;1=1,3=1+2,6=1+2+3,第n幅图中笑脸的数量就是1+2+3+…+n.【解答】解:1+2+3+4+5+6+7+8,=(1+8)+(2+7)+(3+6)+(4+5),=9×4,=36;答:第8副图案有36个笑脸.故选:C.【点评】解决本题关键是找出笑脸的个数变化的规律,再由此规律求解.4.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+31【分析】题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果.【解答】解:这些三角形数的规律是1,3,6,10,15,21,28,36,45,…,且正方形数是这串数中相邻两数之和,很容易看到:恰有36=15+21.故选:C.【点评】本题考查探究、归纳的数学思想方法.本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.二、填空题(共14小题)5.摆一个需要4根小棒,摆需要7根小棒,摆需要10根小棒…,像这样摆n个正方形需要3n+1根小棒,当n=20时,需要61根小棒.【分析】通过题意和观察图形可知,第一个正方形由四根火柴摆成,以后加三根就可加一个正方形,摆第两个要3×2+1=7根,摆第三个要3×3+1=10根,摆第四个要3×4+1=13根,以此类推,得出规律连着摆n个这样的正方形需3n+1根火柴,进一步代入n=20求得答案即可.【解答】解:第一个正方形由四根火柴摆成,以后加三根就可加一个正方形,摆n个正方形需要3n+1根小棒,当n=20时,需要3×20+1=61根小棒.故答案为:3n+1,61.【点评】本题是一道找规律的题目,首先应找出哪些部分发生了变化,是按照什么规律变化的,从而找出规律,然后利用规律解题.6.如图方式摆放桌子和椅子,一张桌子能坐6人,3张桌子能坐14人.【分析】第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.据此即可得解.【解答】解:有1张桌子时有6把椅子,有2张桌子时有10把椅子,10=6+4×1,有3张桌子时有14把椅子,14=6+4×2,答:3张桌子可以坐14人.故答案为:14.【点评】本题考查了图形的变化类问题,注意结合图形进行观察,即可得到规律.7.…用相同的小棒按左图方法拼组,如果拼成的图形中含有10个小正方形,需要31根小棒,154根小棒拼成的图形中含有51个小正方体.【分析】根据题干中的已知图形,推理得出这组图形的一般规律特点,即可解答.【解答】解:搭一个小正方形,需要1+1×3根小棒;搭2个小正方形,需要1+2×3根小棒;搭3个小正方形,需要1+3×3根小棒…;所以搭5个小正方形,需要小棒:1+5×3=1+15=16(根);则搭n个小正方形,需要小棒:1+3n根.当n=10时,需要1+3×10=31(根)当1+3n=154时,n=51答:如果拼成的图形中含有10个小正方形,需要31根小棒,154根小棒拼成的图形中含有51个小正方体.故答案为:31;51.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.8.如图,每个方框中数的排列是有规律的,则F=120.【分析】观察题干可知,左上方的数字=(左下方的数字+右上方的数字)×右下方的数字,且下方的数字排列依次为:3、4、5、6、7、8…,则最后一个正方形下方的数字分别是9、10,那么左上方的数字就是(9+3)×10=120,据此即可解答问题.【解答】解:根据题干分析可得,左上方的数字=(左下方的数字+右上方的数字)×右下方的数字,且下方的数字排列依次为:3、4、5、6、7、8…,则最后一个正方形下方的数字分别是9、10,则F=(9+3)×10=120答:F=120.故答案为:120.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.9.用小棒摆三角形,照这样摆下去,摆10个三角形需21根小棒,摆n个三角形需2n+1根小棒.【分析】摆一个三角形需3根小棒;摆二个三角形需5根小棒;摆三个三角形时需要7根小棒;摆四个三角形时需要9根小棒;…第一个三角形需要3根小棒,以后每增加1个三角形就需要增加2根小棒;当有n个三角形时小棒的数量就是3+2(n﹣1),然后化简,找出小棒的根数与与三角形个数直接的关系,进而求出摆10个三角形需多少根小棒.【解答】解:当有n个三角形时小棒的数量就是:3+2(n﹣1)=3+2n﹣2=2n+1摆10个三角形需:2n+1=2×10+1=20+1=21(根)故答案为:21,2n+1.【点评】解决本题关键是找出小棒的数量随三角形的数量变化的规律,写出通项公式,进而求解.10.如图,用同样的小棒摆正方形.摆10个同样的正方形需要小棒31根;现在有46根小棒可以摆15个正方形.【分析】根据小棒的摆设规律可知,多摆一个正方形就需要加三根小棒.【解答】解:第一个正方体需要4根火柴棒;第二个正方体需要4+3×1=7根火柴棒;第三个正方体需要4+3×2=10根火柴棒;…摆n个正方形需4+3×(n﹣1)=3n+1根火柴棒.当n=10时,3n+1=3×10+1=31,当3n+1=46时,3n=45,n=15,答:摆10个同样的正方形需要小棒31根;现在有46根小棒可以摆15个正方形.故答案为:31;15.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.11.如图,小明用小棒搭房子,他搭3间房子用13根小棒.照这样,搭10间房子要用41根小棒;搭n间房子要用1+4n根小棒(用含有n的式子表示).【分析】据图分析可得:每多搭一间房子就多4根小棒;搭3间房子用13根小棒,即1+3×4;搭4间用17根小棒,即1+4×4根;搭5间要用21根小棒,即1+5×4根,由此得出搭n间房子要用1+4n根小棒;据此解答即可.【解答】解:(1)每多搭一间房子就多4根小棒;搭3间房子用13根小棒,即1+3×4;搭4间用17根小棒,即1+4×4根;依此类推得:搭10间房子用:1+10×4=41(根)(2)搭n间房子用:1+4n(根)答:搭10间房子用41根小棒.照上面那样搭n个房子用1+4n根火柴棍.故答案为:41;1+4n.【点评】主要考查了通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.12.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为3,6,9,12.按这个规律.由100个小等边三角形拼成的图形,周长为30.【分析】编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为3,6,9,12,得出规律为:小等边三角形的个数为编号的平方,周长是编号的3倍,据此解答即可.【解答】解:因为:100=102所以由100个小等边三角形拼成的图形编号为(10),所以周长为:3×10=30.故答案为:30.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.13.对于一个多边形,定义一种“生长”操作(如图),将其中一边AB变成折线ACDEB,其中C和E是AB的三等分点,C、D、E三点可构成等边三角形,那么,一个边长是9的等边三角形,经过四次“生长”操作得到的图形的周长是85.【分析】根据“一边AB变成折线ACDEB,其中C和E是AB的三等分点,C、D、E三点可构成等边三角形”得到CD=DE=CE=AC=EB=AB,则AC+CD+DE+EB=AB×4,按照次规律,每次“生长”,都变成原来的,即为一个以为等比的等比数列.【解答】解:边长是9的等边三角形的周长是9×3=27第一次“生长”,得到的图形的周长是:27×=36第二次“生长”,得到的图形的周长是:36×=48第三次“生长”,得到的图形的周长是:48×=64第四次“生长”,得到的图形的周长是:64×==85答:经过四次“生长”操作得到的图形的周长是85.故答案为:85.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.14.如图,它是由火柴棒拼成的图案,如果在这个图案中用了51根火柴棒,可拼成25个三角形.【分析】第一个三角形有1+2=3根火柴棒组成,以后每多一个三角形就多用2根火柴棒,由此可以推理出一般规律.【解答】解:第一个三角形有1+2=3根火柴棒组成,以后每多一个三角形就多用2根火柴棒,所以组成n个三角形就需要1+2n根火柴棒;当1+2n=51时2n=50n=25答:可拼成25个三角形.故答案为:25.【点评】根据题干,从图中特殊的例子推理得出一般的规律是解决此类问题的关键.15.如图,一张方桌可以坐4人,两张方桌拼起来可以坐6人,三张方桌拼起来可以坐8人…像这样n张方桌拼起来可以坐2n+2人,坐68人需要33张方桌.【分析】观察摆放的桌子,不难发现:在1张桌子坐4人的基础上,多1张桌子,多2人.则有n张桌子时,有4+2(n﹣1)=2n+2人;由此即可计算当2n+2=68人时,求得桌子张数n的值.【解答】解:第一张桌子可以坐4人;拼2张桌子可以坐4+2×1=6人;拼3张桌子可以坐4+2×2=8人;故n张桌子拼在一起可以坐4+2(n﹣1)=2n+2.当2n+2=68时,n=33,答:像这样n张方桌拼起来可以坐2n+2人,坐68人需要33张方桌.故答案为:2n+2,33.【点评】此题考查了平面图形的规律变化,要求学生观察图形,分析、归纳并发现其中的规律,并应用规律解决问题.16.用小棒摆正方形,如图摆6个正方形用小棒19根,摆n个正方形用小棒3n+1根.【分析】根据小棒的摆设规律可知,多摆一个正方形就需要加三根火柴棒,由此推理出一般规律即可解答问题.【解答】解:第一个正方体需要4根小棒;第二个正方体需要4+3×1=7根小棒;第三个正方体需要4+3×2=10根小棒;摆n个正方形需4+3×(n﹣1)=3n+1根小棒.当n=6时,需要小棒:3×6+1,=18+1,=19(根);答:摆6个同样的正方形需要小棒18根,摆n个正方形需要小棒3n+1根.故答案为:19;3n+1.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.17.把边长为1厘米的正方形纸片,按如图的规律拼成长方形;(1)用6个正方形拼成的长方形周长是14厘米;(2)用n个正方形拼成的长方形周长是2n+2厘米.【分析】由图示得出规律:四个图形周长分别为4厘米、6厘米、8厘米,10厘米所以每增加一个正方形,周长增加2厘米,那么n个正方形拼成的长方形的周长是:4+(n﹣1)×2=2n+2(厘米),据此解答即可.【解答】解:根据题干分析可得:n个正方形拼成的长方形的周长是:4+(n﹣1)×2=2n+2(厘米),当n=6时,2n+2=2×6+2=14(厘米)答:用6个正方形拼成的长方形周长是14厘米;用n个正方形拼成的长方形周长是2n+2厘米.故答案为:14;2n+2.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.18.摆1个正方形需要4根小棒,摆2个需要7根小棒,摆3个需要10根小棒,摆n个正方形需要1+3n根小棒.【分析】观察图形可知:1个小正方形需要1+1×3根小棒,2个小正方形需要1+2×3根小棒,3个小正方形需要1+3×3根小棒…,由此找出规律解答即可.【解答】解:1个小正方形需要1+1×3根小棒,2个小正方形需要1+2×3根小棒,3个小正方形需要1+3×3根小棒…,所以n个小正方形需要1+3n根小棒,故答案为:1+3n.【点评】根据题干中特殊的例子,推理得出这组图形的一般规律,是解决此类问题的关键.三、解答题(共12小题)19.探索规律.123456…N …正方体个数61014 18…62…正方形个数【分析】通过分析可知:每增加一个正方体,正方形的个数增加4个,10=6+4,14=6+2×4,18=6+3×4,所以N个正方体的正方形的个数是6+(N﹣1)×4,据此解答即可.【解答】解:根据分析:第五个正方体:6+(5﹣1)×4=22第六个正方体:6+(6﹣1)×4=26有62个正方形时:6+(N﹣1)×4=624N=62﹣2N=15第N个正方体:6+(N﹣1)×4如图:探索规律.正方体个数123456…15N …正方形个数61014 182226…626+(N﹣1)×4…【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.20.怎样巧妙的计算连续偶数的和呢?通过下面的探索,你就会有新的发现.(1)计算:口算下列各题.2+4=62+4+6=122+4+6+8=202+4+6+8+10=(2)探索:观察上面的算式和如图,你一定会发现其中的规律.请你根据你发现的规律把下面的算式补充完整.2+4+6+8+10+12=6×72+4+6+8+10+12+14=7×82+4+6+8+…+98+100=50×51.【分析】(1)因为2+4=6=2×3,2+4+6=12=3×4,所以连续偶数的和等于加数的个数乘比它多1的数,这个乘积就是该算式的和;(3)连续偶数的和等于这些偶数的个数乘比它多1的数.【解答】解:(1)因为2+4=6=2×3,2+4+6=12=3×4所以:2+4+6+8=4×5=202+4+6+8+10=5×6=30;(2)2+4+6+8+10+12=6×72+4+6+8+10+12+14=7×82+4+6+8+…+98+100=50×51.故答案为:20,30;6,7;7,8;50,51.【点评】此题考查数于形结合的规律,找出数字的运算规律是解决问题的关键.21.摆放易拉罐,(如图)看图回答问题.(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有1+2+3+4=10个.摆五层一共有1+2+3+4+5=15个.摆六层一共有1+2+3+4+5+6=21个.…(2)用n表示摆的层数,你能总结出一个计算公式吗?n(n+1).【分析】观察所给出的图形知道,从第二个数起,每一个数分别是它前面的数加2、3、4、5、6…等自然数所得,由此得出答案.【解答】解:(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有1+2+3+4=10个.摆五层一共有1+2+3+4+5=15个.摆六层一共有1+2+3+4+5+6=21个(2)用n表示摆的层数:n(n+1)故答案为:1+2+3+4=10;1+2+3+4+5=15;1+2+3+4+5+6=21;n(n+1).【点评】根据题干得出图形或数字的排列规律是解决此类问题的关键.22.如图是边长为1cm的正方形ABCD,沿水平方向翻滚4次后的位置图形,此时A翻滚后所在的位置与A点开始位置之间的距离为4厘米.请你根据图形,完成下表:(此题只加分不扣分)翻滚次数415164n﹣14n与A点开始位置之间(厘米)4【分析】由题意得:每滚动3次就回到原处,这段距离是3个边长的长度之和,翻滚多少次就是多少厘米,据此计算即可.【解答】解:翻滚次数4 15 16 4n ﹣1 4n 与A 点开始位置之间(厘米)415164n ﹣14n【点评】解决本题的关键是根据操作得出规律,再解答.23.平面内6个点最多可以连成多少条线段?8个点呢?学着下面的图画一画,数一数,你一定能发现其中的规律.6个点最多可以连成 15 条线段,8个点最多可以连成 28 条线段. 点数增加条数﹣﹣ 2 3 4 总13610【分析】2个点连成线段的条数:1(条), 3个点连成线段的条数:1+2=3(条), 4个点连成线段的条数:1+2+3=6(条), 5个点连成线段的条数:1+2+3+4=10(条), …;由此得出规律:n 个点的线段数是:1+2+3+4…+n ﹣1条线段;据此规律解答即可. 【解答】解:1+2+3+4+5=15(条); 1+2+3+4+5+6+7=28(条)答:6个点,一共可以连15条线段;8个点,一共可以连28条线段. 故答案为:15,28.【点评】此题属于探索规律的题目,先在草纸上找几个点进行连线,然后得出规律,然后根据规律进行解答.24.观察图形找规律:(1)按照图形变化规律填表:正方形个数12345…048…直角三角形个数(2)如果画8个正方形能得到28个直角三角形,画n个正方形能得到4n ﹣4个直角三角形.【分析】1个正方形有0个直角三角形,可以写成(1﹣1)×4个;2个正方形有4个直角三角形,可以写成(2﹣1)×4个;3个正方形有8个直角三角形,可以写成(3﹣1)×4个;4个正方形有12个直角三角形,可以写成(4﹣1)×4个;每增加一个正方形就增加4个直角三角形;由此填表,并得出通项公式,进行求解.【解答】解:(1)根据已知图形可将上表补充完整如下所示:正方形个数12345…04812 16…直角三角形个数(2)(3)根据上表中的数据可得:1个正方形有0个直角三角形,可以写成(1﹣1)×4个;2个正方形有4个直角三角形,可以写成(2﹣1)×4个;3个正方形有8个直角三角形,可以写成(3﹣1)×4个;4个正方形有12个直角三角形,可以写成(4﹣1)×4个;所以当正方形的个数为n时,三角形的个数可以写成:(n﹣1)×4=4n﹣4个;所以当n=8时,直角三角形个数是:4×8﹣4=28;答:如果画8个正方形,能得到28个直角三角形;如果画n个正方形,能得到4n﹣4个直角三角形.故答案为:28;4n﹣4.【点评】对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.25.仔细观察下面的点子图,根据每个图中点子的排列规律,想一想,可以怎样计算每个图中点子的总个数?请你把下表填写完整.序号1 2 34… 表示点子数的算式 1 1+4… 点子的总个数1…观察表中数据,如果用A 表示第n 个图形中点子的个数,A 和n 之间的关系可以表示成: A= 4n ﹣3 .【分析】通过观察可知:第一个图的点子数是1个,第二个图的点子数是1+4=5个,第三个图的点子数是1+2×4=9个,第4个图的点子数是1+3×4=13个,由此可知:A 表示第n 个图形中点子的个数,A 和n 之间的关系可以表示成A=4n ﹣3,据此解答即可.【解答】解:由分析可得:A=1+4(n ﹣1)=4n ﹣3 如图:序号1 2 3 4 … 表示点子数的算式 1 1+4 1+2×4 1+3×4 … 点子的总个数 15913…故答案为:4n ﹣3.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.26.分析推理找规律点数增加条数 ﹣﹣ 2 3 4 总条数13610根据上表的规律,20个点能连成190条线段,n个点能连成条线段.【分析】观察图形我们会发现,每增加一个点,该点与之前每个点之间都会增加一条线段,所以n个点连成的总线段条数是1~n﹣1这n﹣1个自然数之和,所以n个点能连成1+2+3+…+(n﹣1)=条线段;当n=20时,能连成==190条线段!【解答】解:2个点连成1条线段,3个点连成1+2=3条线段,4个点连成1+2+3=6条线段,5个点连成1+2+3+4=10条线段,…n个点连成1+2+3+4+…+(n﹣1)=条线段,当n=20时,能连成==190条线段;故答案为:190,.【点评】认真观察图形,发现每增加一个点,该点与之前每个点之间都会增加一条线段,即增加n﹣1条线段是解决此题的关键.27.仔细研究图1表示数的方法.(1)根据图1表示数的方法,把图2答案写在括号里.(2)在格子图3里画点表示50.。
