2011广州市九年级数学中考 (2)
广州市中考数学历年考点分析.doc
广州市中考数学历年考点分析
1、试卷满分都是150分,考试时间120分钟;
2、题型的分布都是总共25道题,英中选择题10道(30分),填空题6道(18分),解答题9 道(102分);
3、试卷难度不大,基础题占有122分(82%),有难度拔高题占有28分(18%);
4、代数部分考查分数大概是90〜100分,儿何部分考査分数50〜60分(37%);
5、知识点的考查比较有规律,常规题型的变化不大
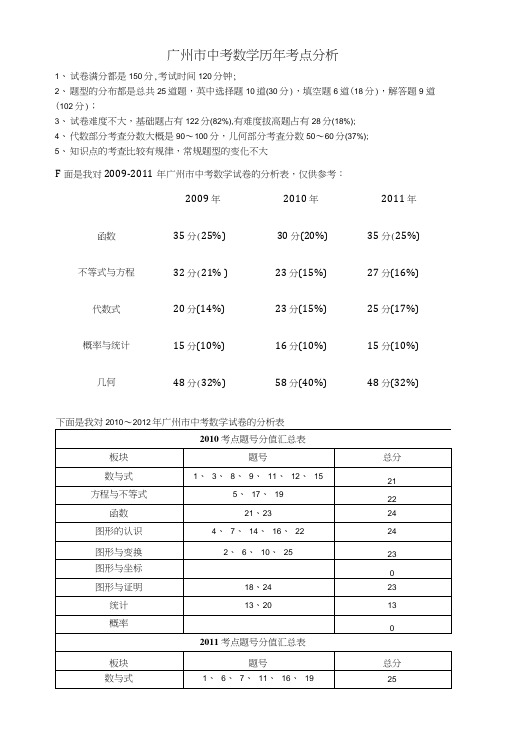
F面是我对2009-2011年广州市中考数学试卷的分析表,仅供参考:
2009 年2010 年2011 年函数35 分(25%)30 分(20%)35 分(25%)不等式与方程32 分(21% )23 分(15%)27 分(16%)代数式20 分(14%)23 分(15%)25 分(17%)
概率与统计15 分(10%)16 分(10%)15 分(10%)几何48 分(32%)58 分(40%)48 分(32%)
下面是我対2010〜2012年广州市中考数学试卷的分析表
各模块近三年考查分析。
广东省广州市白云区中考数学试题分类汇编考点25 等腰三角形2

等腰三角形一、选择题36,AB的中垂线MD交AC于点D、交AB 1.(2011某某某某,13,3分)如图,已知AB=AC,∠A=于点M。
下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③△ABC∽△BCD;④△AMD≌△BCD,正确的有( )个A.4 B.3 C.2 D.1(第13题)【答案】B2. (2011某某某某,12,3分)如图4, △ABC与△DEF均为等边三角形, O为BC、EF的中点,则AD:BE 的值为( )A. 3:1B.2:1C. 5:3D. 不确定【答案】A3. (2011某某呼和浩特市,7,3分)如果等腰三角形两边长是6cm和3cm ,那么它的周长是()A. 9cmB. 12cmC. 15cm或12cmD. 15cm【答案】D4. (2011某某某某,7,4分)等腰三角形的两条边长分别为3、6,那么它的周长为()A.15B.12 C【答案】A5. (2011某某某某,20,3分)如图在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B 与AC 上的点E 重合,展开后,折痕AD 交BO 于点E ,连结DE 、EF.下列结论:①tan ∠ADB=2 ②图中有4对全等三角形 ③将△DEF 沿E 折叠,则点D 不一定落在AC 上 ④BD=BF ⑤AOF DFOE S S ∆=四边形,上述结论中正确的个数是( )A 、1个B 、2个C 、3个D 、4个【答案】C6. (2011某某某某,8,3分)如图,直线1l ∥2l ,点A 在直线1l 上,以点A 为圆心,适当长为半径画弧,分别交直线1l 、2l 于B 、C 两点,连结AC 、BC .若54ABC ∠=,则1∠的大小为(A )36.(B )54.(C )72.(D )73.【答案】(C )7. (2011年某某地区,7,4分)下列关于等腰三角形的性质叙述错误的是( )B.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合D.等腰三角形是轴对称图形. 【答案】C8. (2011某某某某,8,3分)如图,在△ABC 中,AB =20㎝,AC =12㎝,点P 从点B 出发以每秒3㎝的速度向点A 运动,点Q 从点A 同时出发以每秒2㎝的速度向点C 运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ 是等腰三角形时,运动的时间是 ( ) A . 2.5B .3秒C .3.5秒D .4秒QCBPA【答案】D9. (2011某某某某,8,3分)如图,直线1l ∥2l ,点A 在直线1l 上,以点A 为圆心,适当长为半径画弧,分别交直线1l 、2l 于B 、C 两点,连结AC 、BC .若54ABC ∠=,则1∠的大小为(A )36. (B )54.(C )72.(D )73.【答案】(C )11. (2010乌鲁木齐,10,4分)如图,等边三角形ABC 的边长为3,点P 为BC 边上一点,且1BP =,点D 为AC 边上一点若60APD ∠=︒,则CD 的长为A.12 B.23 C.34【答案】B12.13. (2011某某某某,10,3分)如图6,在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADB +∠EDC =120°,BD =3,CE =2,则△ABC 的边长为A .9B .12C .16D .18【答案】A二、填空题1.(2011某某某某,12,4分)如图,在△ABC中,AB=AC,∠B=40°,则∠A=.【答案】100°;2. (2011某某,8,3分)如图,在△ABC中,AB=AC,CD平分∠ACB,∠A =36°,则∠BDC的度数为.【答案】723. (2011某某某某,15,3分)如图4,等腰直角三角形ABC的直角边AB的长为6cm,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中阴影部分面积等于_________cm2.AB′C′图4【答案】34. (2011某某莱芜,15,4分)如图,已知在△ABC 中,AB=B C,∠B=0120,AB 的垂直平分线交AC 于点D.若AC=6cm ,则AD=___________cm.(第15题图)DCBA【答案】25. (2011某某,14,3分)如图,在△A BC 中,A B =AC ,∠A =80°,E ,F ,P 分别是A B ,A C ,BC 边上一点,且BE =BP ,CP =CF ,则∠EPF =度.【答案】506. (2011某某某某,12,3分)如图,在△ABC 中,∠B=30°,ED 垂直平分BC ,ED=3,则CE 的长为_________.【答案】67. (2011某某某某,19,3分)如图4,△ABD 与△AEC 都是等边三角形,AB ≠AC ,下列结论中:①BE=DC ;②∠BOD=60°;③△BOD ∽△COE.正确结论的序号是.图4BA CEO【答案】①8. (2011某某某某,12,3分)如图,在△ABC 中,∠B=30°,ED 垂直平分BC ,ED=3,则CE 的长为_________.【答案】69. (2011某某,15,3分)如图,△ABC 中,AB=AC ,点D 为BC 的中点,∠BAD=20°,则∠C=.【答案】70° 10. 11. 12. 13. 14. 15. 16. 三、解答题1. (2011某某某某,21,本题满分9分)如图9,已知线段AB 的长为2a ,点P 是AB 上的动点(P 不与A ,B 重合),分别以AP 、PB 为边向线段AB 的同一侧作正△APC 和正△PBD .(1)当△APC 与△PBD 的面积之和取最小值时,AP=___________;(直接写结果)(2)连结AD 、BC ,相交于点Q ,设∠AQC=α,那么α的大小是否会随点P 的移动而变化?请说明理由;ACDB(3)如图10,若点P 固定,将△PBD 绕点P 按顺时针方向旋转(旋转角小于180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)【答案】(1)223a ;(2)α的大小不会随点P 的移动而变化, 理由:∵△APC 是等边三角形,∴PA=PC, ∠APC=600,∵△BDP 是等边三角形,∴PB=PD, ∠BPD=600, ∴∠APC=∠BPD, ∴∠APD=∠CPB, ∴△APD ≌△CPB, ∴∠PAD=∠PCB,∵∠QAP+∠QAC+∠ACP=1200,∴∠QCP+∠QAC+∠ACP=1200, ∴∠AQC=1800-1200=600; (3) 此时α的大小不会发生改变,始终等于600.2. (2011某某随州,18,7分)如图,在等腰三角形ABC 中,∠ABC=90°,D 为AC 边上中点,过D 点作DE ⊥DF ,交AB 于E ,交BC 于F ,若AE=4,FC=3,求EF 长.【答案】连结BD ,证△BED ≌△CFD 和△AED ≌△BFD ,求得EF=5 3. (2011某某襄阳,21,6分)如图6,点D ,E 在△ABC 的边BC 上,连接AD ,AE . ①AB =AC ;②AD =AE ;③BD =CE .以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②⇒③;①③⇒②;②③⇒①.(1)以上三个命题是真命题的为(直接作答);第18题图BAEDF C(2)请选择一个真命题进行证明(先写出所选命题,然后证明).【答案】(1)①②⇒③;①③⇒②;②③⇒①. ·········· 3分 (2)(略) 6分4. (2011某某达州,20,6分)如图,△ABC 的边BC 在直线m 上,AC⊥BC,且AC=BC ,△DEF 的边FE 也在直线m 上,边DF 与边AC 重合,且DF=EF .(1)在图(1)中,请你通过观察、思考,猜想并写出AB 与AE 所满足的数量关系和位置关系;(不要求证明)(2)将△DEF 沿直线m 向左平移到图(2)的位置时,DE 交AC 于点G ,连结AE ,BG .猜想△BCG 与△ACE 能否通过旋转重合?请证明你的猜想.【答案】解:(6分)(1)AB=AE, AB ⊥AE(2) 将△BCG 绕点C 顺时针旋转90°后能与△ACE 重合(或将△ACE 绕点C 逆时针旋转90°后能与△BCG 重合),理由如下:∵AC ⊥BC ,DF ⊥EF ,B 、F 、C 、E 共线,∴∠ACB=∠ACE=∠DFE=90° 又∵AC=BC ,DF=EF ,∴∠DFE=∠D=45°,在△CEG 中,∵∠ACE=90°,∴∠CGE=∠DEF=90°, ∴CG=CE , 在△BCG 和△ACE 中E DCB A图6∵⎪⎩⎪⎨⎧=∠=∠=CE CG ACE ACB AC BC ∴△BCG ≌△ACE (SAS )∴将△BCG 绕点C 顺时针旋转90°后能与△ACE 重合(或将△ACE 绕点C 逆时针旋转90°后能与△BCG 重合)5. (2011某某省随州市,18,8分)如图,在等腰直角三角形ABC 中,∠ABC =90°,D 为AC 边的中点,过D 点作DE ⊥DF ,交AB 于E ,交BC 于F 。
2011年中考数学试题及答案

2011年九年级教学质量检测数 学 试 题注意事项:本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题,36分;第Ⅱ卷为非选择题,84分;共120分.考试时间为120分钟.第Ⅰ卷 选择题 (共36分)一、选择题 (本题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来填入题后的括号内,每小题选对得3分.) 1.下列根式中与18是同类二次根式的是( ). A .321 B .27 C .6 D .32.抛物线y =2x 2+4x -3的顶点坐标是( ).A .(1,-5)B .(-1,-5)C .(-1,-4)D .(-2,-7) 3.国家游泳中心——“水立方”是2008年北京奥运会标志性建筑之一,其工程占地面积为62828平方米,将62828用科学记数法表示是(保留三个有效数字)( ). A .62.8×103 B .6.28×104 C .6.2828×104 D .0.62828×105 4.数据0,-1,6,1,x 的众数为-1,则这组数据的方差是( ). A .2B .534C .2D .5265.如图,⊙O 的直径为10,弦AB 的长为6,M 是弦AB 上的一动点,则线段OM 的长的取值范围是( ). A .3≤OM ≤5 B .4≤OM ≤5 C .3<OM <5 D .4<OM <56.小明随机地在如图所示的正三角形及其内部区域投针,则针扎 到其内切圆(阴影)区域的概率为( ). A .21 B .π63C .π93 D .π33第6题图第11题图7.如图,□ABCD 中,对角线AC 和BD 相交于点O , 如果AC =12,BD =10,AB =m ,那么m 的取值范围是( ).A .1<m <11B .2<m <22C .10<m <12D .5<m <68.如图,P 1、P 2、P 3是双曲线上的三点.过这三点分别 作y 轴的垂线,得到三个三角形P 1A 1O 、P 2A 2O 、P 3A 3O , 设它们的面积分别是S 1、S 2、S 3,则( ). A .S 1<S 2<S 3 B .S 2<S 1<S 3 C .S 1<S 3<S 2 D .S 1=S 2=S 39.直线1l :1y k x b =+与直线2l :2y k x =在同一平面直角坐标系中的图象如图所示,则关于x 的不等式12k x b k x +>的解为( ).A .1x >-B .1x <-C .2x <-D .无法确定10.如图,将A B C △沿D E 折叠,使点A 与B C边的中点F 重合,下列结论中①EF AB ∥且12E F A B =;②BAF C AF ∠=∠;③DE AF 21S ADFE∙=四边形;④2B D F F E C B A C ∠+∠=∠, 一定正确的个数是( ). A .1B .2C .3D .411.若关于x 的一元二次方程ax 2+2x -5=0的两根中有且仅有一根在0和1 之间(不含0和1),则a 的取值范围是( ). A .a <3 B .a >3 C .a <-3 D .a >-312.如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F ,已知∠A = 100°,∠C = 30°,则∠DFE 的度数是 ( ).A .55°B .60°C .65°D .70°DABCO第7题图xb +x第9题图第8题图第12题图第16题图第Ⅱ卷 非选择题(共84分)二、填空题(本题共5小题,共15分.只要求填写最后结果,每小题填对得3分.) 13.当m = 时,关于x 的分式方程213x m x +=--无解.14.已知关于x 的不等式组⎩⎨⎧--≥-0125a >x x 无解,则a 的取值范围是 .15.已知关于的一元二次方程012)1(2=-++x x k 有两个不相同的实数根,则k 的取值范围是 .16.如图,梯形ABCD 中,BC AD //,1===AD CD AB ,︒=∠60B直线MN 为梯形ABCD 的对称轴,P 为MN 上一点,那么PD PC +的最小值是 .17.在实数的原有运算法则中我们补充定义新运算“⊕”如下:当a ≥b 时,a ⊕b =b 2;当a <b 时,a ⊕b =a .则当x =2时,(1⊕x )-(3⊕x )的值为 . 三、解答题(本题共7小题,共69分.解答应写出文字说明、证明过程或推演步骤.)18.(本题满分8分)据《生活报》报道,有关部门要求各中小学要把“每天锻炼一小时”写入课表.为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题: (1)该校对多少名学生进行了抽样调查?(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?图2图1最喜欢的体育活 动项目的人数/人育活动项目19.(本题满分9分)某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w (千克)随销售单价x (元/千克)的变化而变化,具体关系式为:w =-2x +240.设这种绿茶在这段时间内的销售利润为y (元),解答下列问题: (1)求y 与x 的关系式; (2)当x 取何值时,y 的值最大?(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?20.(本题满分9分)经过江汉平原的沪蓉(上海—成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A 处测得对岸岸边的一根标杆B 在它的正北方向,测量员从A 点开始沿岸边向正东方向前进100米到达点C 处,测得∠ACB=68°.(1)求所测之处江的宽度(.48.268tan ,37.068cos ,93.068sin ≈≈≈ ); (2)除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.21.(本题满分10分)如图,B D 为圆O 的直径,A B A C =,A D 交B C 于E ,2A E =,4E D =.(1)求证:A B E A D B △∽△,并求A B 的长;(2)延长D B 到F ,使B F B O =,连接F A ,那么直线F A 与⊙O 相切吗?为什么?22.(本题满分10分)荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.C23.(本题满分11分)如图,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,过D点作DE∥AC 交BC的延长线于E点.(1)求证:四边形ACED是平行四边形;(2)若AD=3,BC=7,求梯形ABCD的面积.24.(本题满分12分)如图所示,在平面直角坐标系中,⊙M 经过原点O ,且与x 轴、y轴分别相交于A (-6,0),B (0,-8)两点.(1)请求出直线AB 的函数表达式;(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在⊙M 上,开口向下,且经过点B ,求此抛物线的函数表达式;(3)设(2)中的抛物线交x 轴于D ,E 两点,在抛物线上是否存在点P ,使得115PDE ABCS S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由.数学参考答案一、选择题1.A2.B3.B4.B5.B6.C7.A8.D9.B10.B11.B12.C 二、填空题13.-6 14.a ≥3 15.k >-2,且k ≠-1 16.3 17.-318.解:(1)由图1知:4810181050++++=(名)………2分 答:该校对50名学生进行了抽样调查.(2)本次调查中,最喜欢篮球活动的有18人.………………3分x181003650⨯=%%………………………………………….4分∴最喜欢篮球活动的人数占被调查人数的36%. (3)1(302624)20-++=%%%% 20020100÷=% (人)…6分8100100016050⨯⨯=% (人)答:估计全校学生中最喜欢跳绳活动的人数约为160人.………8分 19.解:⑴ y =(x -50)∙ w =(x -50) ∙ (-2x +240)=-2x 2+340x -12000,∴y 与x 的关系式为:y =-2x 2+340x -12000........3分 ⑵ y =-2x 2+340x -12000=-2 (x -85) 2+2450,∴当x =85时,y 的值最大. ……………………………6分 ⑶ 当y =2250时,可得方程 -2 (x -85 )2+2450=2250. 解这个方程,得 x 1=75,x 2=95. 根据题意,x 2=95不合题意应舍去.∴当销售单价为75元时,可获得销售利润2250元.…………9分20.解:(1)在BAC Rt ∆中, 68=∠ACB ,∴24848.210068tan =⨯≈⋅= AC AB (米)答:所测之处江的宽度约为248米…………………………………3分 (2)从所画出的图形中可以看出是利用三角形全等、三角形相似、解直角三角形的知识来解决问题的,只要正确即可得分……………9分21.(1)证明:A B A C = ,ABC C ∴=∠∠,C D = ∠∠,ABC D ∴=∠∠.又BAE D AB = ∠∠,ABE AD B ∴△∽△.A B A E A D A B∴=. AB 2=AD ·AE=(AE+ED )·AE=(2+4)×2=12.AB ∴=. ……………………………………………………5分(2)直线F A 与⊙O 相切.理由如下: 连接O A .BD 为⊙O 的直径,∴∠.BD ∴====1122B F B O B D ∴===⨯=AB = ,BF BO AB ∴==.90OAF ∴= ∠.∴直线F A 与⊙O 相切. ……………………………………10分22.解:(1)设租用一辆甲型汽车的费用是元,租用一辆乙型汽车的费用是元.由题意得解得答:租用一辆甲型汽车的费用是800元,租用一辆乙型汽车的费用是850元.……………………………………………………………3分 (2)设租用甲型汽车辆,则租用乙型汽车辆.由题意得解得……………………………………………………6分由题意知,为整数,或或共有3种方案,分别是:方案一:租用甲型汽车2辆,租用乙型汽车4辆; 方案二:租用甲型汽车3辆,租用乙型汽车3辆; 方案三:租用甲型汽车4辆,租用乙型汽车2辆. 方案一的费用是(元); 方案二的费用是(元);方案三的费用是(元),所以最低运费是4900元.……………9分答:共有3种方案,分别是:方案一:租用甲型汽车2辆,租用乙型汽车4辆; 方案二:租用甲型汽车3辆,租用乙型汽车3辆; 方案三:租用甲型汽车4辆,租用乙型汽车2辆.最低运费是4900元.……………………………………………10分 23.证: ⑴∵AD ∥BC ∴AD ∥CE 又∵DE ∥AC∴四边形ACED 是平行四边形……………… 3分 ⑵过D 点作DF ⊥BE 于F 点 ……………………4分∵DE ∥AC ,AC ⊥BD ∴DE ⊥BD ,即∠BDE=90° 由⑴知DE=AC ,CE=AD=3∵四边形ABCD 是等腰梯形∴AC=DB ………………………………………7分 ∴DE=DB ……………………………………8分∴△DBE 是等腰直角三角形,∴△DFB 也是等腰直角三角形 ∴DF=BF=21(7-3)+3=5……………………9分(也可运用:直角三角形斜边上的中线等于斜边的一半)()2553721DF BC)(AD 21S ABCD=⨯+=∙+=梯形……11分注:⑴过对角线交点O 作OF ⊥BC 于F ,延长FO 交AD 于H ,于是OH ⊥AD由△ABC ≌△DCB ,得到△OBC 是等腰直角三角形,OF=21BC=27同理OH=21AD=23,高HF=52327=+⑵过A 作AF ⊥BC 于F ,过D 作DH ⊥BC 于H ,由△AFC ≌△DHB得高AF=FC=21(AD+BC)=5⑶DOA COD BOC AOB ABCD S S S S S ∆∆∆∆+++=梯形(进行计算)24. 解:(1)设直线AB 的函数表达式为(y kx b k =+∵直线AB经过(60)(08)A B --,,,,∴由此可得60,8.k b b -+=⎧⎨=-⎩解得4,38.k b ⎧=-⎪⎨⎪=-⎩∴直线AB的函数表达式为483y x =--. (4)分(2)在R t AO B △中,由勾股定理,得10AB ===,x∵圆M 经过O A B ,,三点,且90AO B ∠=°,AB∴为圆M 的直径,∴半径5M A =,设抛物线的对称轴交x 轴于点N ,M N x ⊥∵,∴由垂径定理,得132A N O N O A ===.在R t A M N △中,4M N ===,541C N M C M N ∴=-=-=,∴顶点C 的坐标为(31)-,, 设抛物线的表达式为2(3)1y a x =++, 它经过(08)B -,,∴把0x =,8y =-代入上式,得28(03)1a -=++,解得1a =-,∴抛物线的表达式为22(3)168y x x x =-++=---.…………8分(3)如图,连结A C ,B C ,35213521ON MC 21AN MC 21S S S BMC AMC ABC ⨯⨯+⨯⨯=∙+∙=+=∆∆∆ =15在抛物线268y x x =---中,设0y =, 则2680x x ---=, 解得12x =-,24x =-.D E ∴,的坐标分别是(40)-,,(20)-,, 2D E ∴=;设在抛物线上存在点()P x y ,,使得111511515P D E A B C S S =⨯=△△=,则1y 221y DE 21S PDE =⨯⨯=∙=∆,1y ∴=±,当1y =时,2681x x ---=,解得123x x ==-,1(31)P ∴-,;当1y =-时,2681x x ---=-,解得13x =-+,23x =--2(3)P ∴-+-1,3(3)P ---1.综上所述,这样的P 点存在,且有三个,1(31)P -,,2(3)P -+-1,3(31)P ---.…………………….12分。
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
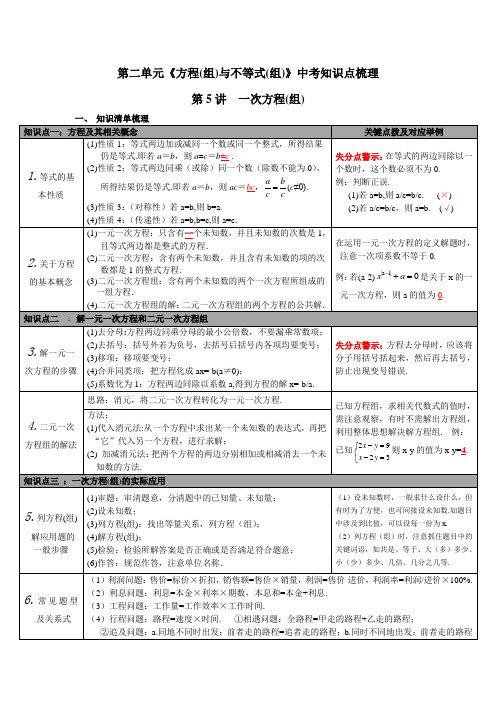
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
中考数学试题分项版解析汇编(第02期)专题11 圆(含解析)-人教版初中九年级全册数学试题

专题11:圆一、选择题1.(2017某某第8题)如图,AB 是O 的直径,,C D 是O 上位于AB 异侧的两点.下列四个角中,一定与ACD ∠互余的角是( )A .ADC ∠B .ABD ∠C . BAC ∠D .BAD ∠【答案】D【解析】∵AB 是直径,∴∠ADB=90°,∴∠BAD+∠B=90°,∵∠ACD=∠B ,∴∠BAD+∠ACD=90°,故选D.2. (2017某某第10题)如图,将半径为2,圆心角为120︒的扇形OAB 绕点A 逆时针旋转60︒,点O ,B 的对应点分别为'O ,'B ,连接'BB ,则图中阴影部分的面积是( )A .23πB .233π C.2233π D .2433π 【答案】C.【解析】试题分析:连接O 'O 、'O B ,根据旋转的性质及已知条件易证四边形AOB 'O 为菱形,且∠'O OB=∠O 'O B=60°,又因∠A 'O 'B =∠A 'O B=120°,所以∠B 'O 'B =120°,因∠O 'O B+∠B 'O 'B =120°+60°=180°,即可得O 、'O 、'B 三点共线,又因'O 'B ='O B ,可得∠'O 'B B=∠'O B 'B ,再由∠O 'O B=∠'O 'B B+∠'O B 'B =60°,可得∠'O 'B B=∠'O B 'B =30°,所以△OB 'B 为Rt 三角形,由锐角三角函数即可求得B 'B =3所以2''16022=S 2232323603OBB BOO S S ππ⨯-=⨯⨯=阴影扇形,故选C.考点:扇形的面积计算.3. (2017某某某某第9题)如图5,在O 中,在O 中,AB 是直径,CD 是弦,AB CD ⊥,垂足为E ,连接0,,20CO AD BAD ∠=,则下列说法中正确的是( )A .2AD OB = B .CE EO = C. 040OCE ∠= D .2BOC BAD ∠=∠【答案】D考点: 垂径定理的应用4.(2017某某某某第6题)如图3,O 是ABC ∆的内切圆,则点O 是ABC ∆的( )图3A . 三条边的垂直平分线的交点B .三角形平分线的交点C. 三条中线的交点 D .三条高的交点【答案】B【解析】试题分析:内心到三角形三边距离相等,到角的两边距离相等的点在这个角的角平分线上,故选B 。
九年级数学中考专题(空间与图形)-第十讲《四边形(二)》课件(北师大版)

B
E
参考答案
一、填空题: 1、180;2、20cm;3、3;4、;5、200 提示:4题过点P作矩形任一边的垂线,利用勾股定理求 解; 5题连结AC,证△ABE≌△ACF得AE=AF,从而△AEF 是等边三角形. 6、 2 1 ;7、2 1 ;8、②
参考答案
二、DDBBA 三、解答题: 14、可证△DEA≌△ABF 15、略证:AE平分∠BAC,且EG⊥AB, EC⊥AC,故EG=EC,易得∠AEC=∠CEF, ∵CF=EC,EG=CF,又因EG⊥AB,CD⊥AB, 故EG∥CF.四边形GECF是平行四边形,又因EG =FG,故GECF是菱形.
A
D G B E F C
能力训练
16、如图,以△ABC的三边为边在BC的同一侧分别作 三个等边三角形,即△ABD、△BCE、△ACF.请回答下 列问题(不要求证明): (1)四边形ADEF是什么四边形? (2)当△ABC满足什么条件时,四边形ADEF是矩形? (3)当△ABC满足什么条件时,以A、D、E、F为顶点 的四边形不存在? E F D
第十讲 四边形(二)
复习目标
1.复习矩形、菱形、正方形的判定与性质. 2.复习运用矩形、菱形、正方形的判定和性质 解决相关的证明和计算问题.
知识要点
1.矩形的四个角都是直角,对角线相等;菱形 的四条边相等,对角线互相垂直平分. 2. 三个角是直角的四边形,或对角线相等的平行 四边形是矩形;四边相等的四边形,或对角线互 相垂直的平行四边形是菱形. 3. 是矩形又是菱形的四边形是正方形.正方形既 具有矩形的性质又具有菱形的性质.
典型例题
例1 如图,已知矩形ABCD中,对角线AC、BD 相交于点O,AE⊥BD,垂足为E, ∠DAE∶∠BAE=3∶1,求∠EAC的度数. 分析:本题充分利用矩形对角线把矩形分成四个 等腰三角形的基本图形进行求解. 答案:45° A D
2011年中考数学试题精选汇编《实数》

【答案】B
7.(2011山东济宁,1,3分)计算―1―2的结果是
A.-1 B.1 C.-3 D.3
【答案】C
8.(2011四川广安,2,3分)下列运算正确的是()
A. B.
C. D. [来源:学科网]
【答案】C
9.(2011重庆江津,1,4分)2-3的值等于( )
A.1 B.-5 C.5 D.-1·
2011年中考数学试题精选汇编
《实数》
一、选择题
1.(2011福建泉州,1,3分)如在实数0,- , ,|-2|中,最小的是().
A. B.- C.0D.|-2|
【答案】B
2.(2011广东广州市,1,3分)四个数-5,-0.1, , 中为无理数的是().
A.-5B.-0.1C. D.
【答案】D
3.(2011山东滨州,1, 3分)在实数π、 、 、sin30°,无理数的个数为( )
16.(2011广东汕头,11,6分)计算:
【解】原式=1+ -4
=0
17.(2011浙江省嘉兴,17,8分)(1)计算: .
【答案】原式=4+1-3=2
18.(2011浙江丽水,17,6分)计算:|-1|- -(5-π)0+4cos45°.
【解】原式=1- ×2 -1+4× =1- -1+2 = .
A.3B.30C.1D.0
【答案】C
26.(2011湖南湘潭市,1,3分)下列等式成立是
A. B. C. ÷ D.
【答案】A
27.(2011台湾全区,2)计算 之值为何?
A.9 B.27 C.279 D.407
【答案】C
28.(2011台湾全区,12)12.判断312是96的几倍?
2025年广东省九年级中考数学第一部分+中考考点梳理课件+第二章 方程(组)与不等式(组)

5.会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等.
6.了解一元二次方程的根与系数的关系(例67)(2022版课标去掉“*”).
7.能解可化为一元一次方程的分式方程.
返回
目录
新课标示例:
例67
-元二次方程的根与系数的关系
知道一元二次方程的根与系数的关系,能通过系数表示方程的根,能
用方程的根表示系数.
设问角度
核心素养
一元一次不等式组
选择,T8/3分
- > ,
的解集为
<
运算能力
解答,T16/8分 解不等式组 - > ,
+<
返回
目录
考什么
年份
考点
2021
怎么考
题型/分值
设问角度
为什么考
核心素养
- > (-),
解答,T18/6分 解不等式组
-
>
解一元一
- ≥ -,
为什么考
素材情境 核心素养
=时间差,
甲
v甲=1.2v乙
追及问题
- =
.
求一元一次不等式的
最小解
打折问题
5×0.1x-4≥4×10%
模型观念
运算能力
应用意识
返回
目录
考什么
年份
考点
怎么考
题型/分值
一元一次方
程或二元一
设问角度
为什么考
素材情境 核心素养
数学文化:每人钱数8×学生
程解的意义
,经历估计方程解的过程.
2.能根据具体问题的实际意义,检验方程解的合理性.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年广州市初中毕业生学业考试一、选择题(每小题3分,共30分)1.四个数-5,-0.1,21,3中为无理数的是()A. -5B. -0.1C.21D. 32.已知□ABCD的周长为32,AB=4,则BC=()A. 4B. 121C. 24D. 283.某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数是( )A. 4B. 5C. 6D. 104.将点A(2,1)向左平移2个单位长度得到点A',则点A'的坐标是()A. (0,1)B. (2,-1)C. (4,1)D. (2,3)5.下列函数中,当x>0时,y值随x值增大而减小的是()A.2xy= B. 1-=xy C. xy43= D.xy1=6.若a<c<0<b,则abc与0的大小关系是()A. abc<0B. abc=0C. abc>0D. 无法确定7.下面的计算正确的是()A. 2221243xxx=⋅ B. 1553xxx=⋅ C. 34xxx=÷ D. 725)(xx=8.如图所示,将矩形纸片先沿虚线AB按箭头方向向右..对折,接着对折后的纸片沿虚线CD向下..对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是()9.当实数x的取值使得2-x有意义时,函数y=4x+1中y的取值范围是()A.y≥-7B. y≥9C. y>9D. y≤910.如图,AB切⊙O于点B,OA=23,AB=3,弦BC//OA,则劣弧BC的弧长为()A.π33B. π23C. πD. π23二、填空题:(每小题3分,共18分)11.9的相反数是______12.已知α∠=260,则α∠的补角是______度。
13.方程231+=xx的解是______14.如图,以点O为位似中心,将五边形ABCDE放大后得到五边[来源:学科网ZXXK]形EDCBA''''',已知OA=10cm,AO'=20cm,则五边形ABCDE的周长与五边形EDCBA'''''的周长的比值是______15.已知三条不同的直线a、b、c在同一平面内,下列四条命题:(①如果a //b ,a ⊥b ,那么b ⊥c ; ②如果b //a ,c //a ,那么b//c ; ③如果b ⊥a ,c ⊥a ,那么b ⊥c ;④如果b ⊥a ,c ⊥a ,那么b//c. 其中真命题的是_________。
(填写所有真命题的序号) 16.定义新运算“⊗”,b a b a 431-=⊗,则)1(12-⊗=________。
三、解答题(本大题共9大题,满分102分) 17.(9分)解不等式组⎩⎨⎧>+<-01231x x18. (9分)如图,AC 是菱形ABCD 的对角线,点E 、F 分别在边AB 、AD 上,且AE=AF 。
求证:△AC E ≌△ACF19. (10分)分解因式:8(x 2-2y 2)-x(7x+y)+xy20. (10分)5个棱长为1的正方体组成如图的几何体。
(1)该几何体的体积是_________(立方单位) 表面积是_________(平方单位) (2)画出该几何体的主视图和左视图。
21.(12分)某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠。
已知小敏5月1日前不是该商店的会员。
(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元? (2)请帮小敏算一算,所购买商品的价格在什么范围时,采用方案一更合算?A DF E BC正面22.(12分)某中学九年级(3)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: (1)求a 的值;(2)用列举法求以下事件的概率:从上网时间在6~10小时的5名学生中随机选取2人,其中至少..有1人的上网时间在8~10小时。
23.(12分)已知R t △ABC 的斜边AB 在平面直角坐标系的x 轴上,点C(1,3)在反比例函数y=xk的图象上,且sin ∠BAC=53。
(1)求k 的值和边AC 的长;(2)求点B 的坐标。
24.(14分)已知关于x 的二次函数y=a x 2+bx+c(a>0)的图象经过点C(0,1),且与x 轴交于不同的两点A 、B ,点A 的坐标是(1,0) (1)求c 的值;(2)求a 的取值范围;(3)该二次函数的图象与直线y=1交于C 、D 两点,设A 、B 、C 、D 四点构成的四边形的对角线相交于点P ,记△PCD 的面积为S 1,△PAB 的面积为S 2,当0<a<1时,求证:S 1- S 2为常数,并求出该常数。
25.(14分)如图7,⊙O中AB是直径,C是⊙O上一点,∠ABC=450,等腰直角三角形DCE 中∠DCE是直角,点D在线段AC上。
(1)证明:B、C、E三点共线;(2)若M是线段BE的中点,N是线段AD的中点,证明:MN=2OM;(3)将△DCE绕点C逆时针旋转α(00<α<900)后,记为△D1CE1(图8),若M1是线段BE1的中点,N1是线段AD1的中点,M1N1=2OM1是否成立?若是,请证明:若不是,说明理由。
2011广州中考数学试题参考答案一、选择题:1-5:DBBAD 6-10:CCDBA 二、填空题: 11-16:2111549=-x ①②④ 8三、解答题: 17、解:⎭⎬⎫⎩⎨⎧<<-⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧-><⇒-><421214124x x x x x x 所以不等式组的解集为18、解:在棱形ABCD 中,AF AE DACBAC =⎩⎨⎧∠=∠=又ACAC()SAS ACF ACE ∆≅∆∴19、 解:()()()()y x y x yx xy xy x y x xyy x x y x 441671687282222222-+=-=+---=++--20、解:()2251 ()221、 解:()()()112095.08.0168,211495.01201≥≤+=⨯x x x x 解不等式得则依题意有:假设商品价格是元22、 解:()()()21423256501=+++-=a2132110~88~6b b a a a 、小时的人记为:、、小时的人记为:12132a b b a a122131a b b a a 32121a b b a a12321b b a a a 21321b b a a a总共有:20种,至少有一人上网时间在8~10小时的有14种 所以至少有一人上网时间在8~10小时的概率是7.02014= 23、 解:()5445,5334AB CD BC AC 3CD D AB AB CD C 4AB 5AB ,3BC 53sin 331,C 122==∴=⨯=⋅⋅=⋅∴==-=====∠=⨯==∴=x AC x x x x xBC AC x x AB BC BAC xy k xk y 解得,即,则于点交垂直于做过点则假设在函数点()),)或(,点的坐标为(041304549CD BC BD 4153BC 222-∴=-===B x24、解:()()(){}()()()11211212112121212121)11()11(1)11()11(PBA ~PCD BPACPD ,//1101)1,(D 10C 111110)0,1(01A 01,AB CD P 3100,10401A 2100110C 121212121212121212212122为常数,值为解得联立又、,得点代入二次函数将、,,可解得点令则、的距离分别为、到假设证明:且又解不等式得轴交于不同的两点,与函数过点坐标,图像经过点S S aa a a a a h AB h CD S S a h a h h a h a h h h a h a BA CD h h PAB PDC PBA PCD CD AB aa b CD a b abbx ax y y aAB a aB y h h h h a a a a a a b b a x c c b a -∴=-⋅-⋅-+⋅+⋅=⋅⋅-⋅⋅=-∴⎪⎩⎪⎨⎧-=+=⎪⎩⎪⎨⎧+=-=++=-∴=∴∆∆∴∠=∠∠=∠∠=∠∴+=-=∴<--=-++==-=∴<<==+≠>∴>≠⎩⎨⎧>-=∆=++∴=∴+⨯+⨯=∴25、解:()()OM2MN MN OMN ON OM AEBF 90DFE 90ACE ,081DFE ACE DCEF 180ONOM AE BD ACE RT BCD RT CECD DCE DCE CABC BCA RT 45ABC AE 21OM OM//AE BD,21ON ON//BD BE ,AD N OB OA FAE BD BD ON AE 2E C B 180ACE ACB 90DCE ACE DCE 90ACB O AB 100000=∴∆⊥∴⊥=∠∴=∠=∠+∠∴=∠+∠=∠+∠=∴∠=∠=∴∆≅∆∴=∴∠=∆∴=∠==∴=∴=∠+∠∴=∠=∠∴∠=∠∴形为斜边的等腰直角三角为以,即可以得到即又中,在四边形是直角中等腰直角三角形中,在且且的中点是的中点是,于交并延长、、连接三点共线、、是直角的直径是圆证明:CDF AEC CDF BDC AECBDC M()()111111111110111011011111111011111111111111011111111011111111111111OM 2N M N M N OM ON OM AE BF 90E F D 90CE D ,081E F D CE D F CE D 180ON OM AE BD SAS ACE BCD 90BCD ACE CE CD CE D CE D CA BC BCA RT 45ABC AE 21OM //AE OM ,BD 21ON //BD ON BE ,AD N OB OA F AE BD BD ON AE 3=∴∆⊥∴⊥=∠∴=∠=∠+∠∴=∠+∠=∠+∠=∴∠=∠=∴∆≅∆∴-=∠=∠=∴∠=∆∴=∠==∴=形为斜边的等腰直角三角为以,即可以得到即又中,在四边形又是直角中等腰直角三角形中,在且且的中点是的中点是,于交并延长、、连接F CD C AE F CD C BD CAE C BD M α。
