六方最密堆积中正八面体空隙和正四面体空隙

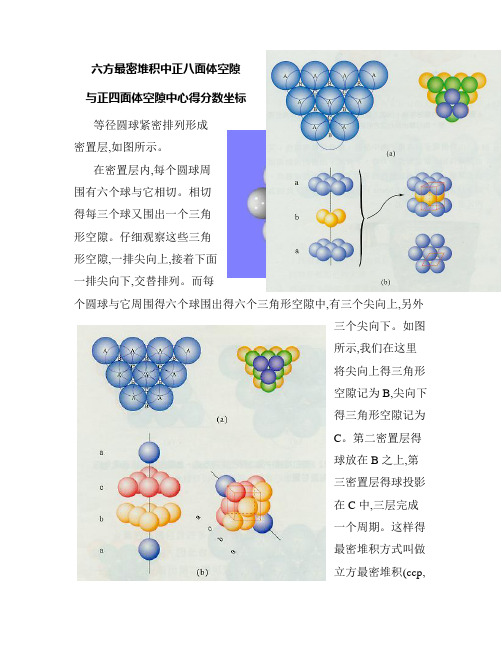
六方最密堆积中正八面体空隙与正四面体空隙中心得分数坐标等径圆球紧密排列形成密置层,如图所示。

在密置层内,每个圆球周围有六个球与它相切。

相切得每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙,一排尖向上,接着下面一排尖向下,交替排列。

而每个圆球与它周围得六个球围出得六个三角形空隙中,有三个尖向上,另外三个尖向下。

如图所示,我们在这里将尖向上得三角形空隙记为B,尖向下得三角形空隙记为C。

第二密置层得球放在B之上,第三密置层得球投影在C中,三层完成一个周期。

这样得最密堆积方式叫做立方最密堆积(ccp,记为A1型),形成面心立方晶胞。

若第三密置层得球投影与第一密置层得球重合,两层完成一个周期。

这样得最密堆积方式叫做六方最密堆积(hcp,记为A3型),形成六方晶胞,如图所示。

在这两种堆积方式中,任何四个相切得球围成一个正四面体空隙;另外,相切得三个球如果与另一密置层相切得三个球空隙对应,它们六个球将围成一个正八面体空隙。

也就就是说,围成正八面体空隙得这六个球可以分为相邻得两层,每层得正三角形中心得连线垂直于正三角形所在得密置层,参瞧下图,黑色代表得不就是球而就是正八面体得中心。

在这两种最密堆积方式中,每个球与同一密置层得六个球相切,同时与上一层得三个球与下一层得三个球相切,即每个球与周围十二个球相切(配位数为12)。

中心这个球与周围得球围出八个正四面体空隙,平均分摊到每个正四面体空隙得就是八分之一个球。

这样,每个正四面体空隙分摊到得球数就是四个八分之一,即半个。

中心这个球周围还围出六个八面体空隙,它平均分摊到每个正八面体空隙得就是六分之一个球。

这样,每个正八面体空隙分摊到得球数就是六个六分之一,即一个。

总之,这两种最密堆积中,球数: 正八面体空隙数: 正四面体空隙数= 1:1:2 。

面心立方最密堆积(ccp, A1型)中正八面体空隙与正四面体空隙得问题比较简单、直观。

下面我们集中讨论六方最密堆积(hcp,A3型)中正八面体空隙与正四面体空隙中心得分数坐标。

高三总复习正八面体空隙和正四面体空隙

，n= 。X–
堆积形成了正八面体和正四面体两种空隙，阳
离子占据的空隙类型为
，占有率为。
图(b)为X–堆积形成的正八面体，其边长为
______pm。
答案 A2BX4(1 分) 1(1 分) 正四面体(1 分) (2 分)
(2 分)
练习4、在某种含镁、镍、碳3种元素的超导材料晶体中，镁原子和镍原子一起以立方最密堆积方式形成有序结构。结构中的两种八面体空隙，一种完全由镍原子构成，另一种由镍原子和镁原子共同构成，碳原子只填充在由镍原子构成的八面体空隙中，晶胞如图所示。
氯化铯型
氯离子：简单立方堆积；铯离子：填充全部立方体空隙。
氯化钠型
氯离子：面心立方堆积，形成正八面体和正四面体
钠离子：填充
全部的正八面体空隙。
空隙，
正四面体空隙全部空着
硫化锌型
硫离子：
面心立方
堆积，形成正八面体和正四面体空隙。
锌离子：填充一半的正四面体
空隙。
八面体空隙全部空着
球数：正四面体空隙数：正八面体空隙 =6:12:6=1:2:1
六方最密堆积：球数∶四面体空隙数∶八面体空隙数＝2∶4∶2=1:2:1
小结：
二、填隙--离子晶体离子在晶体微观空间里有尽可能高的空间利用率，是离子晶体结构
重要制约因素之一。为了得到较高的空间利用率，构成离子晶体的“大” 离子，会在空间尽可能密堆积，然后“小”离子填充到堆积球之间的空隙中去，这种具有先后逻辑顺序的晶体结构分析思想被称为堆积-填隙模型。通常 “大”离子采取不同的堆积方式，构成正四面体或正八面体或立方体空隙 “小”离子再填充到全部或部分空隙中。
氟化钙型钙离子：采取面心立方堆积；氟离子：填充了全部正四面体空隙。

六方最密堆积中正八面体空隙和正四面体空隙

六方最密堆积中正八面体空隙和正四面体空隙This model paper was revised by the Standardization Office on December 10, 2020六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标等径圆球紧密排列形成密置层，如图所示。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙，一排尖向上，接着下面一排尖向下，交替排列。

而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下。

如图所示，我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C。

第二密置层的球放在B之上，第三密置层的球投影在C中，三层完成一个周期。

这样的最密堆积方式叫做立方最密堆积（ccp，记为 A1型），形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。

这样的最密堆积方式叫做六方最密堆积（hcp，记为A3型），形成六方晶胞，如图所示。

在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。

中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。

这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。

中心这个球周围还围出六个八面体空隙，它平均分摊到每个正八面体空隙的是六分之一个球。

这样，每个正八面体空隙分摊到的球数是六个六分之一，即一个。

总之，这两种最密堆积中，球数 : 正八面体空隙数 : 正四面体空隙数 = 1:1:2 。

【最新精选】六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标

密堆积中正八面体空隙和正四面体空隙晶体结构的密堆积原理密堆积结构是指在由无方向性的金属键,离子键和范德华力结合的晶体中,原子、分子或离子等微粒总是趋向于相互配位数高，能充分利用空间的堆积密度大的那些结构。

密堆积方式由于充分利用了空间，从而可使体系的势能尽可能降低。

结构稳定。

最常见的密堆积型式有：面心立方最密堆积（A1），六方最密堆积（A3）和体心立方密堆积（A2）。

我们主要介绍面心立方密堆积和六方密堆积。

等径圆球紧密排列形成密置层，如图所示。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙，一排尖向上，接着下面一排尖向下，交替排列。

而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下。

如图所示，我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C。

第二密置层的球放在B之上，第三密置层的球投影在C中，三层完成一个周期。

这样的最密堆积方式叫做立方最密堆积（ccp，记为 A1型），形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。

这样的最密堆积方式叫做六方最密堆积（hcp ，记为A3型），形成六方晶胞，如图所示。

在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。

中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。

这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。

六方最密堆积中正八面体空隙及正四面体空隙

六方最密聚集中正八面体缝隙和正四周体缝隙中心的分数坐标等径圆球亲近摆列形成密置层，以以下列图。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形缝隙。

认真察看这些三角形缝隙，一排尖向上，接着下边一排尖向下，交替排列。

而每个圆球与它四周的六个球围出的六个三角形缝隙中，有三个尖向上，其他三个尖向下。

如图所示，我们在这里将尖向上的三角形空隙记为 B，尖向下的三角形缝隙记为C。

第二密置层的球放在 B 之上，第三密置层的球投影在 C 中，三层达成一个周期。

这样的最密聚集方式叫做立方最密聚集（ccp，记为A1 型），形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层达成一个周期。

这样的最密聚集方式叫做六方最密聚集（ hcp，记为A3 型），形成六方晶胞，以以下列图。

在这两种聚集方式中，任何四个相切的球围成一个正四周体缝隙；其他，相切的三个球假如与另一密置层相切的三个球缝隙对应，它们六个球将围成一个正八面体缝隙。

也就是说，围成正八面体缝隙的这六个球能够分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看以下列图，黑色代表的不是球而是正八面体的中心。

在这两种最密聚集方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与四周十二个球相切（配位数为 12）。

中心这个球与四周的球围出八个正四周体缝隙，均匀分摊到每个正四周体缝隙的是八分之一个球。

这样，每个正四周体缝隙分摊到的球数是四个八分之一，即半个。

中心这个球四周还围出六个八面体缝隙，它均匀分摊到每个正八面体缝隙的是六分之一个球。

这样，每个正八面体缝隙分摊到的球数是六个六分之一，即一个。

总之，这两种最密聚集中，球数: 正八面体缝隙数: 正四周体缝隙数= 1:1:2 。

面心立方最密聚集（ccp， A1 型）中正八面体缝隙和正四周体空隙的问题比较简单、直观。

下边我们集中讨论六方最密聚集（hcp，A3型）中正八面体缝隙和正四周体缝隙中心的分数坐标。

六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标

密堆积中正八面体空隙和正四面体空隙晶体结构的密堆积原理密堆积结构是指在由无方向性的金属键,离子键和范德华力结合的晶体中,原子、分子或离子等微粒总是趋向于相互配位数高，能充分利用空间的堆积密度大的那些结构。

密堆积方式由于充分利用了空间，从而可使体系的势能尽可能降低。

结构稳定。

最常见的密堆积型式有：面心立方最密堆积（A1），六方最密堆积（A3）和体心立方密堆积（A2）。

我们主要介绍面心立方密堆积和六方密堆积。

等径圆球紧密排列形成密置层，如图所示。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙，一排尖向上，接着下面一排尖向下，交替排列。

而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下。

如图所示，我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C。

第二密置层的球放在B之上，第三密置层的球投影在C中，三层完成一个周期。

这样的最密堆积方式叫做立方最密堆积（ccp，记为A1型），形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。

这样的最密堆积方式叫做六方最密堆积（hcp ，记为A3型），形成六方晶胞，如图所示。

在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。

中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。

这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。

六方最密堆积中正八面体空隙和正四面体空隙

六方最密堆积中正八面体空隙和正四面体空隙编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（六方最密堆积中正八面体空隙和正四面体空隙）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为六方最密堆积中正八面体空隙和正四面体空隙的全部内容。

六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标等径圆球紧密排列形成密置层，如图所示.在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙,一排尖向上，接着下面一排尖向下，交替排列.而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下.如图所示,我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C.第二密置层的球放在B之上，第三密置层的球投影在C中，三层完成一个周期.这样的最密堆积方式叫做立方最密堆积（ccp，记为 A1型)，形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。

这样的最密堆积方式叫做六方最密堆积(hcp,记为A3型）,形成六方晶胞,如图所示。

在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。

晶胞的八面体和四面体填隙

一、立方与六方最密堆积中的正八面体与正四面体空隙从晶体中原子排列的刚球模型和对致密度（致密度指晶胞内原子球所占体积与晶胞体积之比值）分析可知，即使是最密堆积，金属晶体中依然存在空隙，这些空隙对金属的性能有重要影响。

晶体结构中最常见的空隙是八面体空隙（图1）和四面体空隙（图2）。

图1八面体空隙图2四面体空隙八面体空隙由6个原子围成，四面体空隙由4个原子围成，若设金属原子的半径为r A，空隙能容纳的最大外来原子半径为r B，利用几何关系可求出正八面体与正四面体空隙的r B/r A的比值分别为0.414、0.225。

图三八面体空隙计算图四四面体空隙计算小结面心立方最密堆积晶胞原子个数∶四面体空隙数∶八面体空隙数＝4∶8∶4巧记口诀1:2:1，原四八；八角六面当骨架四分之一填四面、棱心体心都填八二、体心立方晶胞的变形八面体与变形的四面体空隙体心立方堆积没有正多面体空隙，但有多种变形的多面体空隙，这里介绍变形的八面体空隙与变形的四面体空隙。

图5 变形的八面体空隙其中心位置位于晶胞每个面的中心与每条边的中心，是一个压扁的八面体，在垂直轴上从中心到顶点的距离为a/2（a为晶胞参数），比水平方向的距离√2a/2要短。

空隙最短处能容纳最大外来原子半径为rB 和堆积原子的半径rA的rB/rA比值为0.154。

图6 变形的四面体空隙每个面上都有4个四面体的中心，如图，这种空隙的rB /rA比值为0.291。

三、其它晶胞八面体与四面体空隙总结图7 体心立方晶胞的空隙体心立方堆积晶胞原子个数∶四面体空隙数∶八面体空隙数＝2∶12∶6各类堆积空隙小结图8 体心立方晶胞的空隙此总结系参考别人的，希望对各位老师有帮助！。

六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标

密堆积中正八面体空隙和正四面体空隙晶体结构的密堆积原理密堆积结构是指在由无方向性的金属键,离子键和范德华力结合的晶体中,原子、分子或离子等微粒总是趋向于相互配位数高，能充分利用空间的堆积密度大的那些结构。

密堆积方式由于充分利用了空间，从而可使体系的势能尽可能降低。

结构稳定。

最常见的密堆积型式有：面心立方最密堆积（A1），六方最密堆积（A3）和体心立方密堆积（A2）。

我们主要介绍面心立方密堆积和六方密堆积。

等径圆球紧密排列形成密置层，如图所示。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙，一排尖向上，接着下面一排尖向下，交替排列。

而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下。

如图所示，我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C。

第二密置层的球放在B之上，第三密置层的球投影在C中，三层完成一个周期。

这样的最密堆积方式叫做立方最密堆积（ccp，记为A1型），形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。

这样的最密堆积方式叫做六方最密堆积（hcp ，记为A3型），形成六方晶胞，如图所示。

在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。

中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。

这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。

【精选】六方最密堆积中正八面体空隙和正四面体空隙

六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标等径圆球紧密排列形成密置层，如图所示。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙，一排尖向上，接着下面一排尖向下，交替排列。

而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下。

如图所示，我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C。

第二密置层的球放在B 之上，第三密置层的球投影在C 中，三层完成一个周期。

这样的最密堆积方式叫做立方最密堆积（ccp，记为A1 型），形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。

这样的最密堆积方式叫做六方最密堆积（hcp，记为A3 型），形成六方晶胞，如图所示。

在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。

中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。

这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。

中心这个球周围还围出六个八面体空隙，它平均分摊到每个正八面体空隙的是六分之一个球。

这样，每个正八面体空隙分摊到的球数是六个六分之一，即一个。

总之，这两种最密堆积中，球数 : 正八面体空隙数 : 正四面体空隙数 = 1:1:2 。

面心立方最密堆积( ccp ， A1 型)中正八面体空隙和正四面体空隙的问题比较简单、直观。

下面我们集中讨论六方最密堆积( hcp ，A3 型)中正八面体空隙和正四面体空隙中心的分数坐标。

六方最密堆积中正八面体空隙和正四面体空隙中心的分数坐标

六⽅最密堆积中正⼋⾯体空隙和正四⾯体空隙中⼼的分数坐标密堆积中正⼋⾯体空隙和正四⾯体空隙晶体结构的密堆积原理密堆积结构是指在由⽆⽅向性的⾦属键,离⼦键和范德华⼒结合的晶体中,原⼦、分⼦或离⼦等微粒总是趋向于相互配位数⾼，能充分利⽤空间的堆积密度⼤的那些结构。

密堆积⽅式由于充分利⽤了空间，从⽽可使体系的势能尽可能降低。

结构稳定。

最常见的密堆积型式有：⾯⼼⽴⽅最密堆积（A1），六⽅最密堆积（A3）和体⼼⽴⽅密堆积（A2）。

我们主要介绍⾯⼼⽴⽅密堆积和六⽅密堆积。

等径圆球紧密排列形成密置层，如图所⽰。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球⼜围出⼀个三⾓形空隙。

仔细观察这些三⾓形空隙，⼀排尖向上，接着下⾯⼀排尖向下，交替排列。

⽽每个圆球与它周围的六个球围出的六个三⾓形空隙中，有三个尖向上，另外三个尖向下。

如图所⽰，我们在这⾥将尖向上的三⾓形空隙记为B，尖向下的三⾓形空隙记为C。

第⼆密置层的球放在B之上，第三密置层的球投影在C中，三层完成⼀个周期。

这样的最密堆积⽅式叫做⽴⽅最密堆积（ccp，记为A1型），形成⾯⼼⽴⽅晶胞。

若第三密置层的球投影与第⼀密置层的球重合，两层完成⼀个周期。

这样的最密堆积⽅式叫做六⽅最密堆积（hcp，记为A3型），形成六⽅晶胞，如图所⽰。

在这两种堆积⽅式中，任何四个相切的球围成⼀个正四⾯体空隙；另外，相切的三个球如果与另⼀密置层相切的三个球空隙对应，它们六个球将围成⼀个正⼋⾯体空隙。

也就是说，围成正⼋⾯体空隙的这六个球可以分为相邻的两层，每层的正三⾓形中⼼的连线垂直于正三⾓形所在的密置层，参看下图，⿊⾊代表的不是球⽽是正⼋⾯体的中⼼。

在这两种最密堆积⽅式中，每个球与同⼀密置层的六个球相切，同时与上⼀层的三个球和下⼀层的三个球相切，即每个球与周围⼗⼆个球相切（配位数为12）。

中⼼这个球与周围的球围出⼋个正四⾯体空隙，平均分摊到每个正四⾯体空隙的是⼋分之⼀个球。

这样，每个正四⾯体空隙分摊到的球数是四个⼋分之⼀，即半个。

六方最密堆积中正八面体空隙和正四面体空隙之欧阳美创编

六方最密堆积中正八面体空隙时间：2021.01.01 创作：欧阳美和正四面体空隙中心的分数坐标等径圆球紧密排列形成密置层，如图所示。

在密置层内，每个圆球周围有六个球与它相切。

相切的每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙，一排尖向上，接着下面一排尖向下，交替排列。

而每个圆球与它周围的六个球围出的六个三角形空隙中，有三个尖向上，另外三个尖向下。

如图所示，我们在这里将尖向上的三角形空隙记为B，尖向下的三角形空隙记为C。

第二密置层的球放在B之上，第三密置层的球投影在C中，三层完成一个周期。

这样的最密堆积方式叫做立方最密堆积（ccp，记为 A1型），形成面心立方晶胞。

若第三密置层的球投影与第一密置层的球重合，两层完成一个周期。

这样的最密堆积方式叫做六方最密堆积（hcp，记为A3型），形成六方晶胞，如图所示。

在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。

中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。

这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。

中心这个球周围还围出六个八面体空隙，它平均分摊到每个正八面体空隙的是六分之一个球。

这样，每个正八面体空隙分摊到的球数是六个六分之一，即一个。

总之，这两种最密堆积中，球数 : 正八面体空隙数 : 正四面体空隙数 = 1:1:2 。

面心立方最密堆积（ccp， A1型）中正八面体空隙和正四面体空隙的问题比较简单、直观。

六方最密堆积中正八面体空隙和正四面体空隙

六方最密【2 】聚积中正八面体闲暇和正四面体闲暇中间的分数坐标等径圆球慎密分列形成密置层,如图所示.在密置层内,每个圆球四周有六个球与它相切.相切的每三个球又围出一个三角形闲暇.细心不雅察这些三角形闲暇,一排尖向上,接着下面一排尖向下,瓜代分列.而每个圆球与它四周的六个球围出的六个三角形闲暇中,有三个尖向上,别的三个尖向下.如图所示,我们在这里将尖向上的三角形闲暇记为B,尖向下的三角形闲暇记为C.第二密置层的球放在B之上,第三密置层的球投影在C中,三层完成一个周期.如许的最密聚积方法叫做立方最密聚积（ccp,记为 A1型）,形成面心立方晶胞.若第三密置层的球投影与第一密置层的球重合,两层完成一个周期.如许的最密聚积方法叫做六方最密聚积（hcp,记为A3型）,形成六方晶胞,如图所示.在这两种聚积方法中,任何四个相切的球围成一个正四面体闲暇;别的,相切的三个球假如与另一密置层相切的三个球闲暇对应,它们六个球将围成一个正八面体闲暇.也就是说,围成正八面体闲暇的这六个球可以分为相邻的两层,每层的正三角形中间的连线垂直于正三角形地点的密置层,参看下图,黑色代表的不是球而是正八面体的中间.在这两种最密聚积方法中,每个球与统一密置层的六个球相切,同时与上一层的三个球和下一层的三个球相切,即每个球与四周十二个球相切（配位数为12）.中间这个球与四周的球围出八个正四面体闲暇,平均分摊到每个正四面体闲暇的是八分之一个球.如许,每个正四面体闲暇分摊到的球数是四个八分之一,即半个.中间这个球四周还围出六个八面体闲暇,它平均分摊到每个正八面体闲暇的是六分之一个球.如许,每个正八面体闲暇分摊到的球数是六个六分之一,即一个.总之,这两种最密聚积中,球数 : 正八面体闲暇数 : 正四面体闲暇数 = 1:1:2 .面心立方最密聚积（ccp, A1型）中正八面体闲暇和正四面体闲暇的问题比较简略.直不雅.下面我们分散评论辩论六方最密聚积（hcp,A3型）中正八面体闲暇和正四面体闲暇中间的分数坐标.在六方最密聚积中画出一个六方晶胞,如下面两幅图所示.平均每个六方晶胞中有两个正八面体闲暇,如下面两幅图所示.闲暇中间的分数坐标分离为：（2/3,1/3,1/4）,（2/3,1/3,3/4）.对于正四面体闲暇,消失如许一个问题,即正四面体的中间到它的底面的距离是它的高的若干倍？解法一（分体积法）：以正四面体的中间O 为极点,以正四面体的四个面为底面将正四面体平均分为四个等体积的小三棱锥,小三棱锥的高为OH,则有：4V 334S AH S OH AH OH==∴=即正四面体的中间到底面的距离是它的高的四分之一. 解法二（立方体法）：将正四面体的四个极点放在立方体相隔的四个极点.设立方体的边长为1,则正四面体的边长为2,正四面体的高为623233⨯=.因为立方体的体对角线为3,所以正四面体的中间（即立方体的中间）到它的底面的距离与它的高之比为：23323:1:4323⎛⎫-= ⎪ ⎪⎝⎭解法三（外接球法）：如图,设正四面体的边长为1,则22336,A 323362A 21364666341213BG G r G r r OG OG r =⨯=====∴=-=∴=解得即正四面体的中间到底面的距离是它的高的四分之一.解法四（正弦定理法）：如图,正四面体中间到两个极点之间的夹角为109.47°,等腰三角形的另两个角为35.27°.依据正弦定理即可求解.下面我们来找出六方最密聚积一个晶胞中的所有正四面体.六方晶胞内里间层的一个球与上面三个球和下面三个球各围成一个正四面体闲暇,闲暇中间的分数坐标分离是：（1/3,2/3,1/8）,（1/3,2/3,7/8）.别的在每个棱上,晶胞极点的八个球分离与中央层的球围成正四面体闲暇,这些闲暇平均只有四分之一在这个晶胞内,八个四分之一共为两个.闲暇中间的分数坐标分离是：（0,0,3/8）,（0,0,5/8）.四个坐标解释正四面体闲暇共有四个.用体积模子示意图来看各类闲暇也是很有意思的.请看左图.在六方硫化锌中,硫离子呈六方密聚积,锌离子填入闲暇.锌离子填入的是什么闲暇？（正四面体照样正八面体？）是否填满了所有的闲暇？将成果与立方硫化锌的情形作比较,看有哪些类似与不同.估量锌离子与硫离子的半径比.查阅锌离子与硫离子的半径数据,解释硫离子是不是最密聚积.。