运动学计算题及问题详解
高中物理强基习题专题一:运动学(Word版含详解)

高中物理强基习题专题一:运动学一.选择题1.如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动.设该人以匀速率v0 收绳,绳不伸长且湖水静止,小船的速率为v,则小船作( )(A) 匀加速运动,θcos 0v v = (B) 匀减速运动,θcos 0v v =(C) 变加速运动,θcos 0v v =( D) 变减速运动,θcos 0v v =(E) 匀速直线运动,0v v =答案:C2.如上题图1-5,此时小船加速度为( )A.0B.θθcos )tan (20l vC.lv 20)tan (θ D.θcos 0v 答案:B3.地面上垂直竖立一高20.0 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00 时,杆顶在地面上的影子的速度的大小为( )A.s m /1094.13-⨯B.s m /1094.14-⨯C.0D.s m /100.35-⨯答案:A解析:设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s =htg ωt,下午2∶00 时,杆顶在地面上影子的速度大小为132s m 1094.1cos d d --⋅⨯===tωωh t s v二.计算题4.质点沿直线运动,加速度a =4 -t2 ,式中a 的单位为m ·s-2 ,t 的单位为s.如果当t =3s时,x =9 m,v =2 m ·s-1 ,求质点的运动方程.解析: 由分析知,应有⎰⎰=t t a 0d d 0vv v 得 03314v v +-=t t (1)由 ⎰⎰=t xx t x 0d d 0v 得 00421212x t t t x ++-=v (2) 将t =3s时,x =9 m,v =2 m ·s-1代入(1) (2)得v0=-1 m ·s-1,x0=0.75 m .于是可得质点运动方程为75.0121242+-=t t x 5.一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a =A -Bv,式中A 、B 为正恒量,求石子下落的速度和运动方程.解析:本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式dv =a(v)dt 分离变量为t a d )(d =v v 后再两边积分. 解:选取石子下落方向为y 轴正向,下落起点为坐标原点.(1) 由题意知 v v B A ta -==d d (1) 用分离变量法把式(1)改写为 t B A d d =-vv (2) 将式(2)两边积分并考虑初始条件,有⎰⎰=-t t B A 0d d d 0v v v v v 得石子速度 )1(Bt e B A --=v 由此可知当,t →∞时,B A →v 为一常量,通常称为极限速度或收尾速度. (2) 再由)1(d d Bt e BA t y --==v 并考虑初始条件有 t eB A y tBt yd )1(d 00⎰⎰--= 得石子运动方程)1(2-+=-Bt e B A t B A y6.质点在Oxy 平面内运动,其运动方程为r =2.0ti +(19.0 -2.0t2 )j,式中r 的单位为m,t 的单位为s .求:(1)质点的轨迹方程;(2) 在t1=1.0s 到t2 =2.0s 时间内的平均速度;(3) t1 =1.0s时的速度及切向和法向加速度;(4) t =1.0s 时质点所在处轨道的曲率半径ρ.解析:根据运动方程可直接写出其分量式x =x(t)和y =y(t),从中消去参数t,即得质点的轨迹方程.平均速度是反映质点在一段时间内位置的变化率,即t ΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v .切向和法向加速度是指在自然坐标下的分矢量a t 和an ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a t 得到.在求得t1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ. 解 (1) 由参数方程x =2.0t, y =19.0-2.0t2消去t 得质点的轨迹方程:y =19.0 -0.50x2(2) 在t1 =1.00s 到t2 =2.0s时间内的平均速度j i r r 0.60.2ΔΔ1212-=--==t t t r v (3) 质点在任意时刻的速度和加速度分别为j i j i j i t ty t x t y x 0.40.2d d d d )(-=+=+=v v v j j i a 222220.4d d d d )(-⋅-=+=s m ty t x t 则t1 =1.00s时的速度v(t)|t =1s=2.0i -4.0j切向和法向加速度分别为t t y x t t t tt e e e a 222s 1s m 58.3)(d d d d -=⋅=+==v v v n n t n a a e e a 222s m 79.1-⋅=-=(4) t =1.0s质点的速度大小为122s m 47.4-⋅=+=y x v v v 则m 17.112==na ρv 8.已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求:(1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;*(4) 2 s 内质点所走过的路程s .分析 质点的轨迹方程为y =f(x),可由运动方程的两个分量式x(t)和y(t)中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,可根据其定义计算.其中对s 的求解用到积分方法,先在轨迹上任取一段微元ds,则22)d ()d (d y x s +=,最后用⎰=s s d 积分求s.解 (1) 由x(t)和y(t)中消去t 后得质点轨迹方程为 2412x y -= 这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置.(3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x 其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r 而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r *(4) 如图(B)所示,所求Δs 即为图中PQ 段长度,先在其间任意处取AB 微元ds,则22)d ()d (d y x s +=,由轨道方程可得x x y d 21d -=,代入ds,则2s内路程为 m 91.5d 4d 402=+==⎰⎰x x s s QP9.一质点P 沿半径R =3.0 m 的圆周作匀速率运动,运动一周所需时间为20.0s,设t =0 时,质点位于O 点.按(a)图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢;(2)5s时的速度和加速度.分析 该题属于运动学的第一类问题,即已知运动方程r =r(t)求质点运动的一切信息(如位置矢量、位移、速度、加速度).在确定运动方程时,若取以点(0,3)为原点的O ′x ′y ′坐标系,并采用参数方程x ′=x ′(t)和y ′=y ′(t)来表示圆周运动是比较方便的.然后,运用坐标变换x =x0 +x ′和y =y0 +y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢.采用对运动方程求导的方法可得速度和加速度.解 (1) 如图(B)所示,在O ′x ′y ′坐标系中,因t Tθπ2 ,则质点P 的参数方程为t T R x π2sin =', t T R y π2cos -=' 坐标变换后,在Oxy 坐标系中有 t T R x x π2sin='=, R t T R y y y +-=+'=π2cos 0 则质点P 的位矢方程为j i r ⎪⎭⎫ ⎝⎛+-+=R t T R t T R π2cos π2sin j i )]π1.0(cos 1[3)π1.0(sin 3t t -+=(2) 5s时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t v i j i r a )s m π03.0(π2cos )π2(π2sin )π2(d d 222222-⋅-=+-==t TT R t T T R t10.如图所示,半径为R 的半圆凸轮以等速v0沿水平面 向右运动,带动从动杆AB 沿竖直方向上升,O 为凸轮圆心,P 为其顶点.求:当∠AOP=α时,AB 杆的速度和加速度.根据解析:速度的合成,运用平行四边形定则,得:v 杆=v0tan α。
运动学计算题及答案
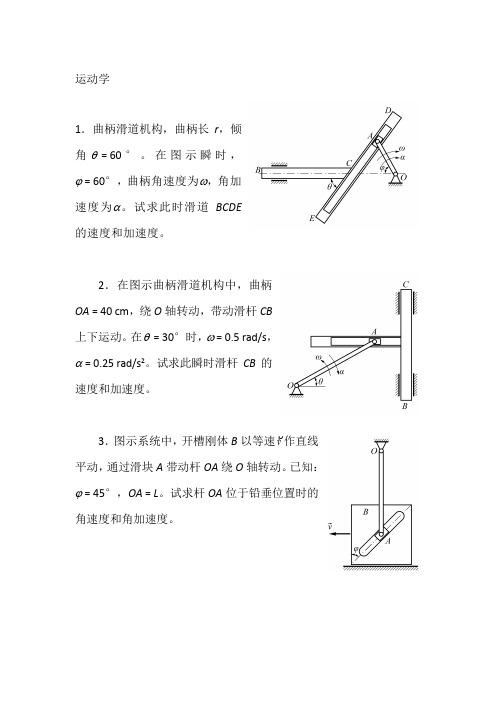
运动学 1.曲柄滑道机构,曲柄长r ,倾角θ = 60°。
在图示瞬时,ϕ = 60°,曲柄角速度为ω,角加速度为α。
试求此时滑道BCDE的速度和加速度。
2.在图示曲柄滑道机构中,曲柄OA = 40 cm ,绕O 轴转动,带动滑杆CB上下运动。
在θ = 30°时,ω = 0.5 rad/s ,α = 0.25 rad/s 2。
试求此瞬时滑杆CB 的速度和加速度。
3.图示系统中,开槽刚体B 以等速v作直线平动,通过滑块A 带动杆OA 绕O 轴转动。
已知:ϕ = 45°,OA = L 。
试求杆OA 位于铅垂位置时的角速度和角加速度。
4.图示曲柄滑道机构,OA = R,通过滑块A带动BC作往复运动。
当ϕ= 60°时,杆OA的角速度为ω,角加速度为α。
试求此瞬时滑块A相对滑槽BC的速度及滑槽BC的加速度。
5.在图示机构中,杆AB借助滑套B带动直角杆CDE运动。
已知:杆AB长为L,在图示β= 30°瞬时,角速度为ω,角加速度为α。
试求:该瞬时直角杆CDE的速度和加速度。
6.图示机构中,曲柄OA长为R,通过滑块A使导杆BC和DE在固定平行滑道内上下滑动,当ϕ=30°时,杆OA 的角速度为ω,角加速度为α。
试求该瞬时点B的速度与加速度。
7.图示系统当楔块以匀速v 向左运动时,迫使杆OA绕点O转动。
若杆OA长为L, ϕ =30°。
试求当杆OA与水平线成角β =30°时,杆OA的角速度与角加速度。
8.在图示机构中,曲柄长OA = 40 cm,绕O轴逆钟向转动,带动导杆BCD沿铅垂方向运动。
当OA与水平线夹角θ = 30°时,ω = 0.5 rad/s、α = 2 rad/s2。
试求此瞬时导杆BCD的速度和加速度。
= CD,9.在图示平面机构中,已知:OOOC = O1D = r, θ = 30°在图示位置ϕ= 60°时,杆OC的角速度为ω,角加速度为α。
高中物理运动学练习题及讲解

高中物理运动学练习题及讲解一、选择题1. 一个物体从静止开始做匀加速直线运动,其加速度为2m/s²。
若物体在第3秒内通过的位移为9m,求物体在第2秒末的速度是多少?A. 2m/sB. 3m/sC. 4m/sD. 5m/s2. 一辆汽车以10m/s的速度行驶,突然刹车,产生一个-5m/s²的加速度。
求汽车在刹车后5秒内的位移。
A. 25mB. 31.25mC. 40mD. 50m二、填空题3. 某物体做自由落体运动,下落时间为3秒,忽略空气阻力,求物体下落的高度。
公式为:\[ h = \frac{1}{2} g t^2 \],其中\( g \)为重力加速度,\( t \)为时间。
假设\( g = 9.8 m/s^2 \)。
三、计算题4. 一个物体从高度为10米的平台上自由落下,求物体落地时的速度。
四、解答题5. 一辆汽车从静止开始加速,加速度为4m/s²,行驶了10秒后,汽车的速度和位移分别是多少?五、实验题6. 实验中,我们用打点计时器记录了小车的运动。
已知打点计时器的周期为0.02秒,记录了小车在第1、3、5、7、9点的位置。
位置数据如下(单位:米):1点:0.00,3点:0.20,5点:0.56,7点:1.08,9点:1.76。
请根据这些数据计算小车的加速度,并判断小车的运动类型。
六、论述题7. 论述在斜面上的物体受到的力有哪些,以及这些力如何影响物体的运动。
参考答案:1. B2. B3. 14.7m4. 根据公式\( v = \sqrt{2gh} \),落地速度为\( \sqrt{2 \times 9.8 \times 10} \) m/s。
5. 速度为40m/s,位移为200m。
6. 根据两点间的平均速度公式,可以求出加速度为0.8m/s²,小车做匀加速直线运动。
7. 斜面上的物体受到重力、支持力和摩擦力的作用。
重力使物体有向下运动的趋势,支持力和摩擦力则与重力的垂直和水平分量相平衡,影响物体的加速度和运动状态。
运动学部分例题分析

上式两边求一阶及二阶导数,则得
A
vA vM
因此
aA a M
v A 0.4m / s
aA 0.4m / s 2
例7-3 在刮风期间,风车的角加速度 0.2 rad / s 2 ,其中转 s 角θ 以rad计。若初瞬时 0 0, w0 6rad /,其叶片半径为 0.75m 。 )时其顶端 4 rad 试求叶片转过两圈( P 点的速度。
将j =wt带入上式,得M点的运动方程:
x r sin wt
w
将上式对时间求一阶导数和二阶导数得:
O
j
x
dx v rw cos wt dt dv d 2 x a 2 rw 2 sin wt dt dt
例2 曲柄连杆机构是由曲柄、连杆及滑块组成的机构。当曲柄 OA绕O轴转动时,由于连杆AB带动,滑块沿直线作往复运动。 设曲柄OA长为r,以角速度w 绕O轴转动,即j=wt,连杆AB长 为l。试求滑块B的运动方程、速度和加速度。 解:取滑块B的直线轨迹为x轴, 曲柄的转动中心O为坐标原点。 w A l 在经过 t 秒后,此时B点的坐 B 标为: x j O x OB OC CB C x r cos j l cos 整理可得B的运动方程:
2 2
由此可得滑块B的速度和加速度:
dx v rw (sin wt sin 2wt ) dt 2 dv a rw 2 (cos wt cos 2w ) dt
例3 一人高 h2 ,在路灯下以匀速v1行走,灯距地面 的高为h1 ,求人影的顶端M沿地面移动的速度。
解: 取坐标系x如图所示,由几何关系得:
方向如图所示。
M点的全加速度及其偏角为
2 a a2 an (0.4) 2 (0.8) 2 0.894 m / s 2
八年级上册物理运动学计算练习

运动计算练习1.汽车在出厂前要进行测试,某次测试中,先让汽车在模拟山路上以10m/s 的速度行驶400s ,紧接着在模拟公路上以5m/s 的速度行驶500m 。
求:(1)该汽车在模拟山路上行驶的路程。
(2)汽车在这次整个测试过程中的平均速度。
2.某轿车在平直公路上行驶的 50s 内,其速度v 与时间t 图像如图所示,已知前10s 轿车运动的路程为100m 。
求:(1)前 10s 轿车运动的平均速度;(2)轿车在匀速直线运动阶段通过的路程;(3)轿车在整个过程的平均速度。
答案:1.(1)4000;(2)9m/s【详解】解:(1)由s v t= 可知,汽车在模拟山路上行驶的路程为 11110m/s 400s 4000m s v t ==⨯=(2)由题知,汽车在模拟公路上行驶的时间为222500m 100s 5m/ss t v === 汽车在这次整个测试中所用的时间为12400s 100s 500s t t t =+=+=整个测试所行驶的总路程为124000m 500m 4500m s s s =+=+=则汽车在这次整个测试过程中的平均速度为4500m 9m/s 500ss v t === 答:(1)该汽车在模拟山路上行驶的路程为4000m ;(2)汽车在模拟公路上的平均速度为9m/s 。
2.(1)10m/s ;(2)800m ;(3)18m/s【详解】解:(1)前10s 轿车运动的平均速度111100m 10m/s 10ss v t === (2)由图像可知,轿车在10s~50s 内,是匀速运动,故轿车在匀速直线运动阶段通过的路程222(20m/s 50s 10s)800m s v t ==⨯-=(3)轿车在整个过程行驶的总路程s =s 1+s 2=100m+800m=900m轿车在整个过程的平均速度900m 18m/s 50ss v t === 答:(1)前10s 轿车运动的平均速度为10m/s ;(2)轿车在匀速直线运动阶段通过的路程为800m ;(3)轿车在整个过程的平均速度为18m/s 。
专题3-运动学典型问题和解决方法

专题运动学典型问题及解决方法【例1】羚羊从静止开始奔跑,经过50m能加速到最大速度25m/s,并能维持一段较长的时间;猎豹从静止开始奔跑,经过60 m的距离能加速到最大速度30m/s,以后只能维持此速度4.0 s.设猎豹距离羚羊xm 时开时攻击,羚羊则在猎豹开始攻击后1.0 s才开始奔跑,假定羚羊和猎豹在加速阶段分别做匀加速运动,且均沿同一直线奔跑,求:猎豹要在从最大速度减速前追到羚羊,x值应在什么范围?【例2】高为h的电梯正以加速度a匀加速上升,忽然天花板上一颗螺钉脱落.螺钉落到电梯底板上所用的时间是多少?【例4】甲、乙两车相距S,同时同向运动,乙在前面做加速度为a1、初速度为零的匀加速运动,甲在后面做加速度为a2、初速度为v0的匀加速运动,试讨论两车在运动过程中相遇次数与加速度的关系。
【例5】在空中足够高的某处,以初速度v竖直上抛一小球,t s后在同一地点以初速度v/竖直下抛另一个小球,若使两个小球在运动中能够相遇,试就下述两种情况讨论t的取值范围:(l)0<v/<v,(2)v/>v一、选择题1、下列关于质点的说法,正确的是()A、只有小的物体才能看作质点B、大的物体也可以看作质点C、任何物体,在一定条件下都可以看作质点D、任何物体,在任何条件下都可以看作质点2、物体从静止开始作匀加速直线运动,第3 s时间内通过的位移为3m ,则()A、物体前3s内通过的位移是6mB、物体第3s末的速度为3.6m/sC、物体前3s内平均速度为2m/sD、物体第3s内的平均速度为3m/s3、一列火车匀减速进站,停靠一段时间后又匀加速(同方向)出站。
在如图所示的四个v-t图象中,正确描述了火车运动情况的是()4、关于自由落体运动,正确的说法是()A、自由落体运动是一种匀变速运动B、自由落体的快慢与物体质量的大小有关C、在地球表面上各处,物体自由落体运动的加速度大小相等D、在地球表面上经度较大处,物体自由落体运动的加速度较大5、某质点作直线运动,速度随时间的变化的关系式为v =(2t + 4)m/s ,则对这个质点运动描述,正确的是()A、初速度为4 m/sB、加速度为2 m/s2C、在3s末,瞬时速度为10 m/sD、前3s内,位移为30 m6、关于加速度的概念,以下说法中正确的是:A.物体运动加速度的方向与初速度方向相同,物体的运动速度将增大B.物体运动加速度的大小表示了速度变化的大小C.加速度的正负表示了物体运动的方向D.做匀变速直线运动的物体速度增大的过程中,它的加速废一定为正值7、如图展示的四个图象分别是反映物体在不同的运动过程中速度v、位移s、加速度a随时间t变化的图象,由此可以推断出物体受到的外力的合力为零的是:A.加速度越来越小B.加速度方向总跟运动方向相反C.位移随时间均匀减小D.速度随时间均匀减小9、甲、乙两辆汽车在同一水平公路上做直线运动,若在描述它们运动情况时规定甲的运动方向为正方向,得出它们运动的加速度分别为a甲= 0.4 m/s2,a乙= −0.4 m/s2。
运动学计算题解答

a a a ar a K
aA aC a a
n AC
a
n e
O
ar
B
A α
l
(4)用基点法求销钉A的加速度:
AC
a
e
22
??
0
√
0
ωOB =?
εOB =?
ar =?
Va
O Ve
A
(1)求摇杆的角速度
VC
C Vr R B
α
OB
l
点P为圆盘的速度瞬心,则 vC P C 2rad / s R 取销钉A为动点,动系固连在摇杆OB上。 由速度合成定理,有
向铅垂方向投影,得到:
ve va
vr 0
B
x'
va ve
ve v a AB OA 2 R
9
动点:圆盘中心O 动系:AB杆
计算题(2)解
A
va AB 2R
AB ?
va ve
(3) 速度分析:
AB
300
vr 0
n e
a
n e
AB
y'
(4) 加速度分析: a e
a
a a a a aK
va AB 2R
aa
n e
a
7
aa 3 va 2 AB ( ) 2R 3 2R
o
e
ar
B
“运动学”计算题(2) 解 已知图示瞬时圆盘中心O的速度v 和加速度a ,
a a
求此瞬时AB杆的角速度和角加速度。
A
AB
300
解: (1) 选动点、动系
OB
高一物理难题运动学知识点

高一物理难题运动学知识点运动学是物理学中的一个重要分支,研究物体的运动规律和运动状态,对于解决物理难题具有重要的作用。
本文将介绍几个高一物理常见的难题,并结合运动学知识点进行解析。
问题一:一辆汽车以15 m/s的速度匀速行驶了20 s,求汽车行驶的距离。
解析:根据题目中给出的速度和时间,我们可以使用运动学中的公式来计算汽车行驶的距离。
首先,我们知道匀速运动的速度保持不变,所以汽车的速度为15 m/s。
其次,题目给出的时间为20 s。
根据运动学公式:速度 = 距离 ÷时间,可得:距离 = 速度 ×时间。
代入已知的数值计算可得:距离 = 15 m/s × 20 s = 300 m。
所以,汽车行驶的距离为300米。
问题二:一个小球从地面上沿竖直上抛的轨迹飞起,求小球的最大高度和上升时间。
解析:对于这个问题,我们需要运用运动学中的竖直上抛运动的相关知识。
首先,我们假设小球从地面上抛的初速度为v0。
当小球达到最大高度时,它的速度为零。
根据上抛运动的运动学公式:v = v0 + at,其中v为最终速度,v0为初速度,a为加速度,t为时间。
由于最大高度时速度为零,代入相关数值可得:0 = v0 - 9.8t(重力加速度为9.8 m/s^2)。
解方程可得:t = v0 / 9.8。
所以,小球上升的时间为t = v0 / 9.8 s。
其次,利用竖直上抛运动的位移公式:h = v0t - (1/2)gt^2,其中h为位移(最大高度),将上升时间t代入可得:h = v0(v0 / 9.8) - (1/2)(9.8)(v0 / 9.8)^2。
化简后可得:h = (v0)^2 / (2 × 9.8)。
所以,小球的最大高度为h = (v0)^2 / (2 × 9.8)米。
问题三:一个自由下落的物体从100米高的位置下落,求物体落地的时间。
解析:对于自由下落的物体来说,我们可以利用重力加速度的概念来求解下落时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运动学 1.曲柄滑道机构,曲柄长r ,倾角 = 60°。
在图示瞬时,
= 60°,曲柄角速度为
,角加速度为。
试求此时滑道
BCDE 的速度和加速度。
2.在图示曲柄滑道机构中,曲柄
OA = 40 cm ,绕O 轴转动,带动滑
杆CB 上下运动。
在 = 30°时,
= 0.5 rad/s ,
= 0.25 rad/s 2。
试求此瞬时滑杆
CB 的速度和加速度。
3.图示系统中,开槽刚体B 以等速v
作直线平动,通过滑块A 带动杆OA 绕O 轴转动。
已知: = 45°,OA = L 。
试求杆OA 位于铅垂位置时的角速度和角加速度。
4.图示曲柄滑道机构,OA = R,通过滑块A带动BC作往复运动。
当= 60°时,杆OA的角速度为,角加速度为。
试求此瞬时滑块A相对滑槽BC的速度及滑槽BC的加速度。
5.在图示机构中,杆AB借助滑套B带动直角杆CDE运动。
已知:杆AB长为L,在图示= 30°瞬时,角速度为,角加速度为。
试求:该瞬时直角杆CDE的速度和加速度。
6.图示机构中,曲柄OA长为R,通过滑块A使导杆BC和DE在固定平行滑道内上下滑动,当°
时,杆OA的角速度为,角加速度为。
试求该瞬时点B的速度与加速度。
7.图示系统当楔块以匀速v 向左运
实用文档 动时,迫使杆OA 绕点O 转动。
若杆OA 长为L , °。
试求当杆OA 与水平线成角
°时,杆OA 的角速度与角加速度。
8.在图示机构中,曲柄长OA = 40 cm ,绕O 轴逆钟向转动,带动导杆BCD 沿铅垂方向运动。
当OA 与水平线夹角
°时,
、2。
试求此瞬时导杆BCD
的速度和加速度。
9.在图示平面机构中,已知:OO 1 = CD ,OC = O 1 D = r ,
°在图示位置
°时,杆OC 的角速度为,角加速度为。
试求此瞬时杆AB 的速度和加速度(杆AB 垂直于OO )。
实用文档。
