七年级数学上册5_3展开与折叠1学案无答案新版苏科版
七年级数学上册《5.3 展开与折叠(1)》教案(无答案) 苏科版

5.3 展开与折叠第一课时教学目标一、教学重难点重点:经历数学活动的过程,感受平面图形与立体图形的关系,发展空间想象力。
难点:想象简单几何体表面展开图形的形状,由简单几何体的表面展开图形,想象其折叠成立体图形的过程。
二、学情分析七年级的学生对自己身边的事充满好奇,他们非常乐意动手操作,有很强的好胜心和表现欲。
小学已学习过一些正方体、长方体、圆柱、圆锥、棱锥等基础知识。
因此完全可以在教师的引导下,展开合作与探究的学习活动,完成本课的学习任务。
本课针对青少年学生的身心发展的特点,以活动为主线,创设情境,让学生经历观察、操作、想象、交流与合作的过程,激发学生的学习兴趣和探究的欲望。
采用多媒体演示与学生实物操作相结合的方式,发展学生的空间观念。
三、教学准备学生准备:用卡纸做成的正方体模型(用六个面拼成,胶带粘接便于展开)及圆柱、圆锥、棱柱、棱锥(只有侧面供剪开用),画出剪裁线的卡纸(图见图5),小刀,剪刀、胶带。
教师准备:墨水瓶盒(剪去多余部分),学生用的模型一套。
课件视频展台。
五、教学教程(一)情境导入T.生活中有些东西是不可缺少的,如果让你来选,商品能够入选吗?S.能。
T.对于大多数商品来说,都离不开它的“外衣”——包装。
(放映几幅精美的包装盒的图片)。
你们想知道这些精美的包装盒是怎样制作出来的吗?S.想。
T.(实物展示),那就让我们先来探索最常见的墨水瓶盒的设计秘密吧!(二)教师活动,学生观察,感受课题T.(演示墨水瓶盒的展开成平面图形与折叠围成立体盒子的过程)一只墨水瓶盒可以展开成平面图形,反过来,这个平面图形也可以折叠围成立体盒子,本节课我们就来探索展开与折叠的奥秘。
(三)学生活动之一——几何体的侧面展开图。
T.放映问题:图(1)中纸筒纸盒沿红线或侧棱剪开,能展开成平面图形吗?会是什么形状呢?S.想象,猜测T.放映图(2),问题:把上面的立体图形与下面的平面图形用线连结起来。
S.口答T.生1的回答是否正确呢?请各小组拿出手中的模具按要求剪开并相互传看。
苏科版七年级数学上册:5.3展开与折叠导学案(无答案)

3、下列说法中正确的是()
A、正方体是四面体
B、棱锥的底面一定是四边形
C、长方体是四棱柱,四棱柱是长方体
D、圆柱的侧面展开图是长方形
4、如图3.3-2,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图上阴影部分),但是一不小心,少画了一个,请你给他补上一个,可以组合成正方体,你有几种画法,在图上用阴影注明。
7 6 8 5
10 9 12
11
(2)、把学生按四人一组分成许多小组,请学生从编号2的棱开始按任意编号顺序随意剪开一些棱展开成平面图形。
(3)、要求学生操作后相互讨论并思考:
①同一种正方体纸盒沿不同顺序先后剪开棱展开的平面图形是否相同?
②一个正方体纸盒展开成平面图形,要剪开几条棱?
三、展示交流
一位贴在黑板上指定的位置并写下自己剪棱的顺序。如图:
2 3 4 7 9 10 11
学生不断到讲台上展示成果直到没有完全相同的平面图。
思考:一个正方体有几种不同的展开图呢?
四、提炼总结
一个正方体有种不同的展开图,作图如下:
思维拓展:一个无盖正方体有种不同的展开图。
当堂达标
1、下列图形是四棱柱的侧面展开图的是()
(A)(B)(C)
2、下列图形中为三棱柱的展开图的是()
课题
5.3展开与折叠
自主空间
学习目标
认识多面体与它们展开图的关系、能正确判断展开图是哪个几何体的展开图;培养学生多动手,养成研究性学习的良好习惯。
学习重难点
能想象并画出几何体展开图,提升学生的空间想象能力
教学流程
预
习
导
航
1、演示一:
将长方体纸盒沿一些棱剪开展开成一个平面图形。
七年级数学上册5_3展开与折叠1学案无答案新版苏科版

5.3 展开与折叠
【学习目标】
1.通过展开、折叠,感受立体图形与平面图形的关系;体会有些平面图形能够折叠成立体图形;
2.能依照表面展开图判定、制作简单几何体.
【学习重点】将几何体展开成展开图,在几何体展开图中,能识别多个面在几何体中的对应位置.
【问题导学】
问题1.如图有五个完全一样的正方形用胶水将邻边粘在一路,折叠后能取得一个无盖的正方体纸盒吗?
可否移动右图中一个正方形的位置,使得折叠后能够取得一个无盖的正方体纸盒.画出移动后的图形,并用纸复制下来,然后折叠,验证你的方式.
上述问题,还有其他的移动方式吗,画出图形,整理一下你的方式,与同窗交流.
问题2.小马虎预备制作一个有盖的正方体纸盒,他先用5个大小一样的正方形制成如下图的拼接图形(实线部份),经折叠后发觉还少一个面,请你在图中拼接图形上再接一个正方形(用实线在图中画出来),使得接成的图形通过折叠后能成为一个封锁的正方体盒子,再用纸复制下来,然后折叠,验证你的方式.
【问题探讨】问题1.如图是一个正方体的展开图,依照正方体展开图上的编号,写出相对面的号码:3的相对面,
方式:先,再
.
【问题评判】
1.如下图是一个正方体纸盒的展开图,请把8,-3,-15别离填入余下的三个正方形中,
使得按虚线折成正方体后,相对面上的两个数互为相反数.
2.假设一个正方体的两个相对的面上都涂着相同的颜色,那么不可能是这一个正方体的展开图的是()
第1题图第2题图
3.假设一个长方形能折叠成一个所有棱长均相等的五棱柱的侧面,那么该长方形的宽与长之比是.
4.在以下正方体的展开中,确信点M、N的位置.。
苏科版数学七上5.3《展开与折叠》word学案2篇
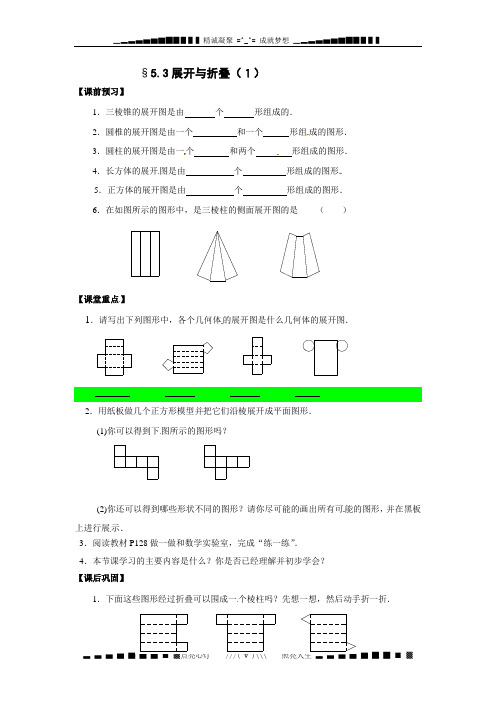
§5.3展开与折叠(1)【课前预习】1.三棱锥的展开图是由个形组成的.形组成的图形..圆柱的展开图是由一.长方体的展开图是由形组成的图形.【课堂重点】.请写出下列图形中,各个几何体的展开图是什么几何体的展开图.图所示的图形吗?(2)你还可以得到哪些形状不同的图形?请你尽可能的画出所有可能的图形,并在黑板上进行展示.3.阅读教材P128做一做和数学实验室,完成“练一练”.41.下面这些图形经过折叠可以围成一个棱柱吗?先想一想,然后动手折一折.2.下列图形是正方体的展开图形的是()A B C D3.一个无上盖的正方体纸盒,底面标有字母A,沿图中的粗线剪开,在右图中补上四个正方形,使其成为它的展开图.重合的点是哪几个?动手试一试.§5.3 展开与折叠(2)【课前预习】1 .下列图形中不可以折叠成正方体的是()A B C D2.一个同学画出了正方体的展开图的一个部分,还缺一个正方形(如下图所示),请在图中添上这个正方形.图1 图2 ,沿正三角形三边中点连线折起,可拼得一个【课堂重点】是一个正方体的展开图,根据正方体展开图上的编号,写出相对面的号码:互为相反数.3.用六个完全一样的正方形做成如图所示的拼接图形,它折叠后能得到一个密封的正方体纸盒吗?若不能,如何改?画出移动后的图形4.⑴如图所示的平面图形能折什么几何体?(2)折成的几何体共有多少条棱?哪些棱的长度相等? (3)这个几何体共有多少个面?它们分别是什么形状?哪些面的形状大小完全相同?5.阅读教材P129-130内容,完成“练一练”. 【课后巩固】1. 将下面4个图用纸复制下来,然后沿所画线折一下,把折成的立体图形名称写在图的下2中平面展开图按虚线折叠成正方体后,相对面上则3. 小强拿了一张正方形的纸如图(1),沿虚线对折一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪(第2题)去一个角,再打开后的形状应是()4.下列四个平面图形中,不能折叠成无盖的长方体盒子的是()(A)(B)(C)(D)5.如图的平面图形是有4个完全相同的等边三角形组成,能否沿某些边将它折叠成三棱锥?如果不能,请你改变其中一个三角形的位置,使其能沿某些边折叠成三棱锥,画出改变位置的平面图形.。
苏科版-数学-七年级上册-七年级数学上5.3展开与折叠 同步学案

课 题
学
习
内
容
订正栏
学习目标1.通过展开、折叠,感受立体图形与平面图形的关系;有些平面图形可以折叠成立体图形;
2.能根据表面展开图判断、制作简单几何体.
一、课前预习
1.图中不可以折叠成正方体的是( )
A B C D
2.一个正方体的平面展开图的如图所示,则正方形4的对面是正方形 。
二、合作探究
例1:下图是正方体的展开图,还原成正方体后,其中完全一样的是( )
1
234
5
6
1
2
3
456
12
3
45
6
1
23
4
5
6
(1) (2) (3) (4)
A .(1)和(2)
B .(1)和(3)
C .(2)和(3)
D .(3)和(4) 例2:下图是一正方体的展开图的一个部分,其中正方形A 、B 、C 、D 连成一排,还缺一个正方形F ,正方形F 应画在什么位置,在下面的两个图中画出所有可能的情况.
123
45
6
想一想,正方体的展开图中,若有四个正方形连成一排,它的另外两个正方形的位置有何特点? 三、达标检测
1. 下面这些图形经过折叠可以围成一个棱柱吗?先想一想,然后动手折一折.
(1) (2) (3)
2.在右图所示的正方体的平面展开图中,确定正方体上的点M 、N 的位置.
3.如图所示是一个正方体纸盒的展开图,请把8,-3,15分别填入余下的四个正方形中,使得按虚线折成正方体后,相对面上的两个数互为相反数.
3-8
15
D
C
B
A。
苏科版七年级上册 5.3 展开和折叠(1)导学案(无答案)

5.3展开与折叠(1)导学案班级姓名【学习目标】1、通过动手实验,发挥讨论等方法,认识多面体与它们展开图的关系.2、能正确判断展开图是哪个几何体的展开图.3、经历和体验图形的变化过程,发展空间概念,养成研究性学习的良好习惯.【学习重点】将几何体展开成平面图【学习难点】能识别展开图中多个面在几何体中的对应位置.一、情境导入对于大多数商品来说,都离不开它的“外衣”——包装。
你们知道这些精美的包装盒是怎样制作出来的吗?二、学生活动活动一:圆柱、圆锥的展开图。
1.圆柱的两个底面展开是两个大小_______的_______,侧面展开是一个_______.2.圆锥的底面是一个_______,侧面展开是一个_______.活动二:正方体的展开图。
各小组拿出正方体纸盒,你能通过剪开某些棱,把它展开成一个各面连在一起的平面图形吗?(注意:每两个面都由一条棱相连)思考:1.同一个正方体沿不同的棱剪开,展成的平面图形是否相同?,的相对面的相对面.123456例2. 小壁虎的难题:如图:一只无盖的圆桶下方有一只壁虎,上方有一只蚊子,壁虎要想尽快吃到蚊子,应该走哪条路径?四、课堂小结今天你有什么收获?五、课堂检测(必做题)1.下列第二行的哪种几何体的表面能展开成第一行的平面图形?请对应连线.2.如图,从方格纸中剪下6个相连的正方形,然后折成一个正方体盒子,图中带阴影的是其中的5个,那么最后一个可能是_____________(填序号).(选做题)3. 有一只虫子在正方体的顶点A,要爬到距它最远的另一个顶点B去,哪条路径最短?这样的路径共有几条?●蚊子壁虎●AB。
苏科版-数学-七年级上册-5.3 展开与折叠(1) 教案

初中-数学-打印版
图8
图9
图 10
5.试一试。 ①对于图 8 可以怎样移动两个底面? ②如图 11:a.把它折成立体图形后,是什么几 何体?b. 由此可得,该几何体还有两种或两种以上 的平面展开图吗?
初中-数学-打印版
初中-数学-打印版
图 11 三、小结。 1.通过本堂课的教学,你了解立体图形和平 面图形的关系了吗? 2.一个立体图形的平面展开图是否惟一? 三、【布置作业】 课本 P164 T1-2
初中-数学-打印版
课题
§5.3 展开与折叠
课时 2-1 授课时间
班级
课型 新授 授课人
教学目标
教学 重、难点
1.经历展开与折叠、模型制作等活动过程,发展空间观念,积累数学 学习的经验。
2.在操作活动中认识棱柱的某些特征;了解棱柱、圆柱、圆锥的侧面 展开图,能根据展开图判断和制作简单的立体模型。
3.培养合作学习的能力。 重点:利用实物模型,发现并认识棱柱的一些特征。 难点:对棱柱性质的理解和空间想像的验证。
段画出五边形。
③把纸片对折,画出一个五边形和半个长方
形,再剪开。
(4)新问题的出现:教师拿出上底面活动的 分小组讨论。指名学生
五棱柱模型,故意不小心把上底面掉在地上,捡回 回答。
后错放对应边的位置,请求学生帮忙如何把上底面
装回去,让学生分组讨论解决的方法。
(5)引导学生概括:只要对应边相连,都能
把上底面装回去。进一步引导学生考虑:图 1 的上
学生感受、讨论回答
旁注
图1 图2
初中-数学-打印版
初中-数学-打印版
(2)问题的出现:由于事先老师故意不告诉 学生怎样制作图 1 的纸板,使一些同学只能用“描 分小组讨论。 红”的方法,这样的棱柱过小,不易制作;也有些
苏科版-数学-七年级上册-5.3 展开与折叠 (1) 导学案

课题主备主核执教教师课型新授课使用日期学习目标1.经历展开与折叠、模型制作等活动过程,发展空间观念,积累数学学习的经验;2.在操作活动中认识棱柱的某些特征;了解棱柱、圆柱、圆锥的侧面展开图,能根据展开图判断和制作简单的立体模型;3.培养合作学习的能力.重点难点预测重点将几何体展开成展开图.难点几何体展开图中,能识别各个面在几何体中的对应位置.学生活动过程教师导学过程一、自主学习(独学)任务1:拿出圆柱形纸筒,沿圆柱形纸筒上所画虚线展开.圆柱形纸筒的侧面是一个图形.任务2:拿出圆锥形冰淇淋纸筒,沿虚线展开.圆锥形冰淇淋纸筒的侧面是图形.二、合作探究(对学、群学)1.对学:任务1:出示各个棱处标有编号的正方体, 从编号2的棱开始按任意编号顺序随意剪开一些棱展开成平面图形.任务2:画出展开后的成平面图形.2.群学:任务1:操作后相互讨论并思考总结:①同一种正方体纸盒沿不同顺序先后剪开后共有种不同的展开图.②一个正方体纸盒展开成平面图形,要剪开条棱.三、拓展提升任务1: 一个无盖正方体有种不同的展开图.【反馈练习】1.完成课本P130练习第1.2.2、下列图形中为三棱柱的展开图的是()(A)(B)(C)3、在下列图形中(每个小正方形都是相同的正方形),是正方体的表面展开图的是()(A)(B)(C)(D)4一个几何体的表面能展开成如图所示,那么这个几何体是。
5、如图3.3-2,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图上阴影部分),但是一不小心,少画了一个,请你给他补上一个,可以组合成正方体,你有几种画法,在图上用阴影注明。
6.如图所示图是长方体的表面展开图,折叠成一个长方体,那么与字母 J重合的点是 .四、当堂检测:《补充习题》第页的第题.五、小结与反思六、作业必做: 课本第132页第1、2、3.题,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.3 展开与折叠
【学习目标】
1.通过展开、折叠,感受立体图形与平面图形的关系;体会有些平面图形可以折叠成立体图形;2.能根据表面展开图判断、制作简单几何体.
【学习重点】将几何体展开成展开图,在几何体展开图中,能识别多个面在几何体中的对应位置.
【问题导学】
问题1.如图有五个完全一样的正方形用胶水将邻边粘在一起,折叠后能得到一个
无盖的正方体纸盒吗?
能否移动右图中一个正方形的位置,使得折叠后可以得到一个无盖的正方体纸
盒.画出移动后的图形,并用纸复制下来,然后折叠,验证你的想法.
上述问题,还有其他的移动方法吗,画出图形,整理一下你的想法,与同学交流.
问题2.小马虎准备制作一个有盖的正方体纸盒,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中拼接图形上再接一个正方形(用实线在图中画出来),使得接成的图形经过折叠后能成为一个封闭的正方体盒子,再用纸复制下来,然后折叠,验证你的想法.
问题1.如图是一个正方体的展开图,根据正方体展开图上的编号,写出相对面的号码:3的相对,的相对面的相对面.
方法:先,再
【问题评价】
1.如图所示是一个正方体纸盒的展开图,请把8,-3,-15分别填入余下的三个正方形中,
使得按虚线折成正方体后,相对面上的两个数互为相反数.
2.若一个正方体的两个相对的面上都涂着相同的颜色,那么不可能是这一个正方体的展开图的是()
第1题图第2题图
3.若一个长方形能折叠成一个所有棱长均相等的五棱柱的侧面,则该长方形的宽与长之比是.
4.在下列正方体的展开中,确定点M、N的位置.。
