《算法设计与分析实用教程》习题参考解答
算法设计与分析-习题参考答案
算法设计与分析基础习题1.15..证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn；显然，若d能整除n和r，也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集，其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)6.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.7.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息If a≠0D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”else //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答：a.将十进制整数转换为二进制整数的算法输入：一个正整数n输出：正整数n相应的二进制数第一步：用n除以2，余数赋给Ki(i=0,1,2...)，商赋给n第二步：如果n=0，则到第三步，否则重复第一步第三步：将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入：正整数n//输出：该正整数相应的二进制数，该数存放于数组Bin[1...n]中i=1while n!=0 do {Bin[i]=n%2;n=(int)n/2;i++;}while i!=0 do{print Bin[i];i--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表‖60,35,81,98,14,47‖排序b.该算法稳定吗?c.该算法在位吗?解:a. 该算法对列表‖60,35,81,98,14,47‖排序的过程如下所示:b.该算法不稳定.比如对列表‖2,2*‖排序c.该算法不在位.额外空间for S and Count[] 4.(古老的七桥问题)习题1.41.请分别描述一下应该如何实现下列对数组的操作,使得操作时间不依赖数组的长度. a.删除数组的第i 个元素(1<=i<=n)b.删除有序数组的第i 个元素(依然有序) hints:a. Replace the i th element with the last element and decrease the array size of 1b. Replace the ith element with a special symbol that cannot be a value of the array ’s element(e.g., 0 for an array of positive numbers ) to mark the i th position is empty. (―lazy deletion ‖)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。
算法设计与分析习题答案
算法设计与分析习题答案算法设计与分析是计算机科学中一个重要的领域，它涉及到算法的创建、优化以及评估。
以下是一些典型的算法设计与分析习题及其答案。
习题1：二分查找算法问题描述：给定一个已排序的整数数组，编写一个函数来查找一个目标值是否存在于数组中。
答案：二分查找算法的基本思想是将数组分成两半，比较中间元素与目标值的大小，如果目标值等于中间元素，则查找成功；如果目标值小于中间元素，则在左半部分继续查找；如果目标值大于中间元素，则在右半部分继续查找。
这个过程会不断重复，直到找到目标值或搜索范围为空。
```pythondef binary_search(arr, target):low, high = 0, len(arr) - 1while low <= high:mid = (low + high) // 2if arr[mid] == target:return Trueelif arr[mid] < target:low = mid + 1else:high = mid - 1return False```习题2：归并排序算法问题描述：给定一个无序数组，使用归并排序算法对其进行排序。
答案：归并排序是一种分治算法，它将数组分成两半，分别对这两半进行排序，然后将排序好的两半合并成一个有序数组。
```pythondef merge_sort(arr):if len(arr) > 1:mid = len(arr) // 2left_half = arr[:mid]right_half = arr[mid:]merge_sort(left_half)merge_sort(right_half)i = j = k = 0while i < len(left_half) and j < len(right_half): if left_half[i] < right_half[j]:arr[k] = left_half[i]i += 1else:arr[k] = right_half[j]j += 1k += 1while i < len(left_half):arr[k] = left_half[i]i += 1k += 1while j < len(right_half):arr[k] = right_half[j]j += 1k += 1arr = [38, 27, 43, 3, 9, 82, 10]merge_sort(arr)print("Sorted array is:", arr)```习题3：动态规划求解最长公共子序列问题问题描述：给定两个序列，找到它们的最长公共子序列。
算法分析与设计作业参考答案
算法分析与设计作业参考答案《算法分析与设计》作业参考答案作业⼀⼀、名词解释：1.递归算法：直接或间接地调⽤⾃⾝的算法称为递归算法。
2.程序：程序是算法⽤某种程序设计语⾔的具体实现。
⼆、简答题：1.算法需要满⾜哪些性质？简述之。
答：算法是若⼲指令的有穷序列，满⾜性质：（1）输⼊：有零个或多个外部量作为算法的输⼊。
（2）输出：算法产⽣⾄少⼀个量作为输出。
（3）确定性：组成算法的每条指令清晰、⽆歧义。
（4）有限性：算法中每条指令的执⾏次数有限，执⾏每条指令的时间也有限。
2.简要分析分治法能解决的问题具有的特征。
答：分析分治法能解决的问题主要具有如下特征：（1）该问题的规模缩⼩到⼀定的程度就可以容易地解决；（2）该问题可以分解为若⼲个规模较⼩的相同问题，即该问题具有最优⼦结构性质；（3）利⽤该问题分解出的⼦问题的解可以合并为该问题的解；（4）该问题所分解出的各个⼦问题是相互独⽴的，即⼦问题之间不包含公共的⼦问题。
3.简要分析在递归算法中消除递归调⽤，将递归算法转化为⾮递归算法的⽅法。
答：将递归算法转化为⾮递归算法的⽅法主要有：（1）采⽤⼀个⽤户定义的栈来模拟系统的递归调⽤⼯作栈。
该⽅法通⽤性强，但本质上还是递归，只不过⼈⼯做了本来由编译器做的事情，优化效果不明显。
（2）⽤递推来实现递归函数。
（3）通过Cooper 变换、反演变换能将⼀些递归转化为尾递归，从⽽迭代求出结果。
后两种⽅法在时空复杂度上均有较⼤改善，但其适⽤范围有限。
三、算法编写及算法应⽤分析题： 1.冒泡排序算法的基本运算如下： for i ←1 to n-1 dofor j ←1 to n-i do if a[j]交换a[j]、a[j+1]；分析该算法的时间复杂性。
答：排序算法的基本运算步为元素⽐较，冒泡排序算法的时间复杂性就是求⽐较次数与n 的关系。
（1）设⽐较⼀次花时间1；（2）内循环次数为：n-i 次,（i=1,…n ），花时间为：∑-=-=in j i n 1)(1（3）外循环次数为：n-1，花时间为：2.设计⼀个分治算法计算⼀棵⼆叉树的⾼度。
计算机算法设计和分析习题及答案解析
计算机算法设计与分析习题及答案一．选择题1、二分搜索算法是利用 A 实现的算法;A、分治策略B、动态规划法C、贪心法D、回溯法2、下列不是动态规划算法基本步骤的是 A ;A、找出最优解的性质B、构造最优解C、算出最优解D、定义最优解3、最大效益优先是A 的一搜索方式;A、分支界限法B、动态规划法C、贪心法D、回溯法4. 回溯法解旅行售货员问题时的解空间树是 A ;A、子集树B、排列树C、深度优先生成树D、广度优先生成树5．下列算法中通常以自底向上的方式求解最优解的是B ;A、备忘录法B、动态规划法C、贪心法D、回溯法6、衡量一个算法好坏的标准是 C ;A 运行速度快B 占用空间少C 时间复杂度低D 代码短7、以下不可以使用分治法求解的是 D ;A 棋盘覆盖问题B 选择问题C 归并排序D 0/1背包问题8. 实现循环赛日程表利用的算法是A ;A、分治策略B、动态规划法C、贪心法D、回溯法9．下面不是分支界限法搜索方式的是D ;A、广度优先B、最小耗费优先C、最大效益优先D、深度优先10．下列算法中通常以深度优先方式系统搜索问题解的是D ;A、备忘录法B、动态规划法C、贪心法D、回溯法11.备忘录方法是那种算法的变形; BA、分治法B、动态规划法C、贪心法D、回溯法12．哈夫曼编码的贪心算法所需的计算时间为B ;A、On2nB、OnlognC、O2nD、On13．分支限界法解最大团问题时,活结点表的组织形式是B ;A、最小堆B、最大堆C、栈D、数组14．最长公共子序列算法利用的算法是B;A、分支界限法B、动态规划法C、贪心法D、回溯法15．实现棋盘覆盖算法利用的算法是A ;A、分治法B、动态规划法C、贪心法D、回溯法16.下面是贪心算法的基本要素的是C ;A、重叠子问题B、构造最优解C、贪心选择性质D、定义最优解17.回溯法的效率不依赖于下列哪些因素 DA.满足显约束的值的个数B. 计算约束函数的时间C.计算限界函数的时间D. 确定解空间的时间18.下面哪种函数是回溯法中为避免无效搜索采取的策略BA．递归函数 B.剪枝函数 C;随机数函数 D.搜索函数19. D是贪心算法与动态规划算法的共同点;A、重叠子问题B、构造最优解C、贪心选择性质D、最优子结构性质20. 矩阵连乘问题的算法可由 B 设计实现;A、分支界限算法B、动态规划算法C、贪心算法D、回溯算法21. 分支限界法解旅行售货员问题时,活结点表的组织形式是 A ;A、最小堆B、最大堆C、栈D、数组22、Strassen矩阵乘法是利用A 实现的算法;A、分治策略B、动态规划法C、贪心法D、回溯法23、使用分治法求解不需要满足的条件是 A ;A 子问题必须是一样的B 子问题不能够重复C 子问题的解可以合并D 原问题和子问题使用相同的方法解24、下面问题 B 不能使用贪心法解决;A 单源最短路径问题B N皇后问题C 最小生成树问题D 背包问题25、下列算法中不能解决0/1背包问题的是 AA 贪心法B 动态规划C 回溯法D 分支限界法26、回溯法搜索状态空间树是按照 C 的顺序;A 中序遍历B 广度优先遍历C 深度优先遍历D 层次优先遍历27．实现合并排序利用的算法是A ;A、分治策略B、动态规划法C、贪心法D、回溯法28．下列是动态规划算法基本要素的是D ;A、定义最优解B、构造最优解C、算出最优解D、子问题重叠性质29．下列算法中通常以自底向下的方式求解最优解的是 B ;A、分治法B、动态规划法C、贪心法D、回溯法30．采用广度优先策略搜索的算法是A ;A、分支界限法B、动态规划法C、贪心法D、回溯法31、合并排序算法是利用 A 实现的算法;A、分治策略B、动态规划法C、贪心法D、回溯法32、背包问题的贪心算法所需的计算时间为 BA、On2nB、OnlognC、O2nD、On33．实现大整数的乘法是利用的算法C ;A、贪心法B、动态规划法C、分治策略D、回溯法34．0-1背包问题的回溯算法所需的计算时间为AA、On2nB、OnlognC、O2nD、On35．采用最大效益优先搜索方式的算法是A;A、分支界限法B、动态规划法C、贪心法D、回溯法36．贪心算法与动态规划算法的主要区别是B;A、最优子结构B、贪心选择性质C、构造最优解D、定义最优解37. 实现最大子段和利用的算法是B ;A、分治策略B、动态规划法C、贪心法D、回溯法38.优先队列式分支限界法选取扩展结点的原则是 C ;A、先进先出B、后进先出C、结点的优先级D、随机39.背包问题的贪心算法所需的计算时间为 B ;A、On2nB、OnlognC、O2nD、On40、广度优先是A 的一搜索方式;A、分支界限法B、动态规划法C、贪心法D、回溯法41. 一个问题可用动态规划算法或贪心算法求解的关键特征是问题的 B ;A、重叠子问题B、最优子结构性质C、贪心选择性质D、定义最优解42．采用贪心算法的最优装载问题的主要计算量在于将集装箱依其重量从小到大排序,故算法的时间复杂度为 B ;A 、On2nB 、OnlognC 、O2nD 、On43. 以深度优先方式系统搜索问题解的算法称为 D ;A 、分支界限算法B 、概率算法C 、贪心算法D 、回溯算法44. 实现最长公共子序列利用的算法是B ;A 、分治策略B 、动态规划法C 、贪心法D 、回溯法45. Hanoi 塔问题如下图所示;现要求将塔座A 上的的所有圆盘移到塔座B 上,并仍按同样顺序叠置;移动圆盘时遵守Hanoi 塔问题的移动规则;由此设计出解Hanoi 塔问题的递归算法正确的为：B46. 动态规划算法的基本要素为 CA. 最优子结构性质与贪心选择性质 B ．重叠子问题性质与贪心选择性质C ．最优子结构性质与重叠子问题性质 D. 预排序与递归调用 47. 能采用贪心算法求最优解的问题,一般具有的重要性质为： AA. 最优子结构性质与贪心选择性质 B ．重叠子问题性质与贪心选择性质C ．最优子结构性质与重叠子问题性质 D. 预排序与递归调用48. 回溯法在问题的解空间树中,按 D 策略,从根结点出发搜索解空间树;A.广度优先B. 活结点优先C.扩展结点优先D. 深度优先49. 分支限界法在问题的解空间树中,按 A 策略,从根结点出发搜索解空间树;A.广度优先B. 活结点优先C.扩展结点优先D. 深度优先50. 程序块 A 是回溯法中遍历排列树的算法框架程序;A.B. C. D. 51. 常见的两种分支限界法为DA. 广度优先分支限界法与深度优先分支限界法；B. 队列式FIFO 分支限界法与堆栈式分支限界法；C. 排列树法与子集树法；D. 队列式FIFO 分支限界法与优先队列式分支限界法；1.算法的复杂性有 时间 复杂性和 空间 ;2、程序是 算法用某种程序设计语言的具体实现;3、算法的“确定性”指的是组成算法的每条 指令 是清晰的,无歧义的;4. 矩阵连乘问题的算法可由 动态规划 设计实现;5、算法是指解决问题的 一种方法 或 一个过程 ;6、从分治法的一般设计模式可以看出,用它设计出的程序一般是 递归算法 ;7、问题的 最优子结构性质 是该问题可用动态规划算法或贪心算法求解的关键特征;8、以深度优先方式系统搜索问题解的算法称为 回溯法 ;9、计算一个算法时间复杂度通常可以计算 循环次数 、 基本操作的频率 或计算步; Hanoi 塔A. void hanoiint n, int A, int C, int B{ if n > 0{ hanoin-1,A,C, B;moven,a,b; hanoin-1, C, B, A; }} B. void hanoiint n, int A, int B, int C { if n > 0 { hanoin-1, A, C, B; moven,a,b; hanoin-1, C, B, A; } }C. void hanoiint n, int C, int B, int A { if n > 0 { hanoin-1, A, C, B; moven,a,b; hanoin-1, C, B, A; } }D. void hanoiint n, int C, int A, int B { if n > 0 { hanoin-1, A, C, B; moven,a,b; hanoin-1, C, B, A; } } void backtrack int t{ if t>n outputx; else for int i=t;i<=n;i++ { swapxt, xi; if legalt backtrackt+1; swapxt, xi; } } void backtrack int t { if t>n outputx;elsefor int i=0;i<=1;i++ { xt=i; if legalt backtrackt+1; } }void backtrack int t { if t>n outputx; else for int i=0;i<=1;i++ { xt=i; if legalt backtrackt-1; } }voidbacktrack int t{ if t>n outputx; else for int i=t;i<=n;i++ { swapxt, xi; if legalt backtrackt+1;}}10、解决0/1背包问题可以使用动态规划、回溯法和分支限界法,其中不需要排序的是动态规划 ,需要排序的是回溯法 ,分支限界法 ;11、使用回溯法进行状态空间树裁剪分支时一般有两个标准：约束条件和目标函数的界,N皇后问题和0/1背包问题正好是两种不同的类型,其中同时使用约束条件和目标函数的界进行裁剪的是 0/1背包问题 ,只使用约束条件进行裁剪的是 N皇后问题 ;12、贪心选择性质是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别;13、矩阵连乘问题的算法可由动态规划设计实现;14.贪心算法的基本要素是贪心选择性质和最优子结构性质 ;15. 动态规划算法的基本思想是将待求解问题分解成若干子问题 ,先求解子问题 ,然后从这些子问题的解得到原问题的解;16.算法是由若干条指令组成的有穷序列,且要满足输入、输出、确定性和有限性四条性质;17、大整数乘积算法是用分治法来设计的;18、以广度优先或以最小耗费方式搜索问题解的算法称为分支限界法 ;19、贪心选择性质是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别;20.快速排序算法是基于分治策略的一种排序算法;21.动态规划算法的两个基本要素是. 最优子结构性质和重叠子问题性质 ;22.回溯法是一种既带有系统性又带有跳跃性的搜索算法;23.分支限界法主要有队列式FIFO 分支限界法和优先队列式分支限界法;24.分支限界法是一种既带有系统性又带有跳跃性的搜索算法;25.回溯法搜索解空间树时,常用的两种剪枝函数为约束函数和限界函数 ;26.任何可用计算机求解的问题所需的时间都与其规模有关;27.快速排序算法的性能取决于划分的对称性 ;28.所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到 ;29.所谓最优子结构性质是指问题的最优解包含了其子问题的最优解 ;30.回溯法是指具有限界函数的深度优先生成法 ;31.用回溯法解题的一个显着特征是在搜索过程中动态产生问题的解空间;在任何时刻,算法只保存从根结点到当前扩展结点的路径;如果解空间树中从根结点到叶结点的最长路径的长度为hn,则回溯法所需的计算空间通常为 Ohn ;32.回溯法的算法框架按照问题的解空间一般分为子集树算法框架与排列树算法框架;33.用回溯法解0/1背包问题时,该问题的解空间结构为子集树结构;34.用回溯法解批处理作业调度问题时,该问题的解空间结构为排列树结构;35.旅行售货员问题的解空间树是排列树 ;三、算法填空1.背包问题的贪心算法void Knapsackint n,float M,float v,float w,float x{//重量为w1..n,价值为v1..n的 n个物品,装入容量为M的背包//用贪心算法求最优解向量x1..nint i; Sortn,v,w;for i=1;i<=n;i++ xi=0;float c=M;for i=1;i<=n;i++{if wi>c break;xi=1;c-=wi;}if i<=n xi=c/wi;}2.最大子段和: 动态规划算法int MaxSumint n, int a{int sum=0, b=0； //sum存储当前最大的bj, b存储bjfor int j=1； j<=n； j++{ if b>0 b+= aj ；else b=ai; ； //一旦某个区段和为负,则从下一个位置累和 ifb>sum sum=b;}return sum；}3.贪心算法求活动安排问题template<class Type>void GreedySelector int n, Type s, Type f, bool A{A1=true;int j=1;for int i=2;i<=n;i++if si>=fj{ Ai=true;j=i;}else Ai=false;}4.快速排序template<class Type>void QuickSort Type a, int p, int r{if p<r{int q=Partitiona,p,r;QuickSort a,p,q-1; //对左半段排序QuickSort a,q+1,r; //对右半段排序}}5. 回溯法解迷宫问题迷宫用二维数组存储,用'H'表示墙,'O'表示通道int x1,y1,success=0; //出口点void MazePathint x,int y{//递归求解:求迷宫maze从入口x,y到出口x1,y1的一条路径mazexy=''; //路径置为if x==x1&&y==y1 success=1; //到出口则成功else{if mazexy+1=='O' MazePathx,++y;//东邻方格是通路,向东尝试if success&&mazex+1y=='O' MazePath++x,y;//不成功且南邻方格是通路,向南尝试if success&&mazexy-1=='O' MazePathx,--y;//不成功且西邻方格是通路,向西尝试if success&&mazex-1y=='O' MazePath--x,y;//不成功且北邻方格是通路,向北尝试}if success mazexy=''; //死胡同置为}四、算法设计题1. 给定已按升序排好序的n个元素a0:n-1,现要在这n个元素中找出一特定元素x,返回其在数组中的位置,如果未找到返回-1;写出二分搜索的算法,并分析其时间复杂度;template<class Type>int BinarySearchType a, const Type& x, int n{//在a0:n中搜索x,找到x时返回其在数组中的位置,否则返回-1Int left=0; int right=n-1;While left<=right{int middle=left+right/2;if x==amiddle return middle;if x>amiddle left=middle+1;else right=middle-1;}Return -1;}时间复杂性为Ologn2. 利用分治算法写出合并排序的算法,并分析其时间复杂度void MergeSortType a, int left, int right{if left<right {//至少有2个元素int i=left+right/2; //取中点mergeSorta, left, i;mergeSorta, i+1, right;mergea, b, left, i, right; //合并到数组bcopya, b, left, right; //复制回数组a}}算法在最坏情况下的时间复杂度为Onlogn;3.N皇后回溯法bool Queen::Placeint k{ //检查xk位置是否合法for int j=1;j<k;j++if absk-j==absxj-xk||xj==xk return false;return true;}void Queen::Backtrackint t{if t>n sum++;else for int i=1;i<=n;i++{xt=i;if 约束函数 Backtrackt+1;}}4.最大团问题void Clique::Backtrackint i // 计算最大团{ if i > n { // 到达叶结点for int j = 1; j <= n; j++ bestxj = xj;bestn = cn; return;}// 检查顶点 i 与当前团的连接int OK = 1;for int j = 1; j < i; j++if xj && aij == 0 // i与j不相连{OK = 0; break;}if OK { // 进入左子树xi = 1; cn++;Backtracki+1;xi = 0; cn--; }if cn+n-i>bestn { // 进入右子树xi = 0;Backtracki+1; }}5. 顺序表存储表示如下：typedef struct{RedType rMAXSIZE+1; //顺序表int length; //顺序表长度}SqList;编写对顺序表L进行快速排序的算法;int PartitionSqList &L,int low,int high //算法10.6b{//交换顺序表L中子表L.rlow..high的记录,枢轴记录到位,并返回其所在位置, //此时在它之前后的记录均不大小于它.int pivotkey;L.r0=L.rlow; //用子表的第一个记录作枢轴记录pivotkey=L.rlow.key; //枢轴记录关键字while low<high //从表的两端交替地向中间扫描{while low<high&&L.rhigh.key>=pivotkey --high;L.rlow=L.rhigh; //将比枢轴记录小的记录移到低端while low<high&&L.rlow.key<=pivotkey ++low;L.rhigh=L.rlow; //将比枢轴记录大的记录移到高端}L.rlow=L.r0; //枢轴记录到位return low; //返回枢轴位置}void QSortSqList &L,int low,int high{//对顺序表L中的子序列L.rlow..high作快速排序int pivotloc;if low<high //长度>1{pivotloc=PartitionL,low,high; //将L.rlow..high一分为二QSortL,low,pivotloc-1; //对低子表递归排序,pivotloc是枢轴位置 QSortL,pivotloc+1,high; //对高子表递归排序}}void QuickSortSqList &L{//对顺序表L作快速排序QSortL,1,L.length; }。
算法设计与分析常见习题及详解
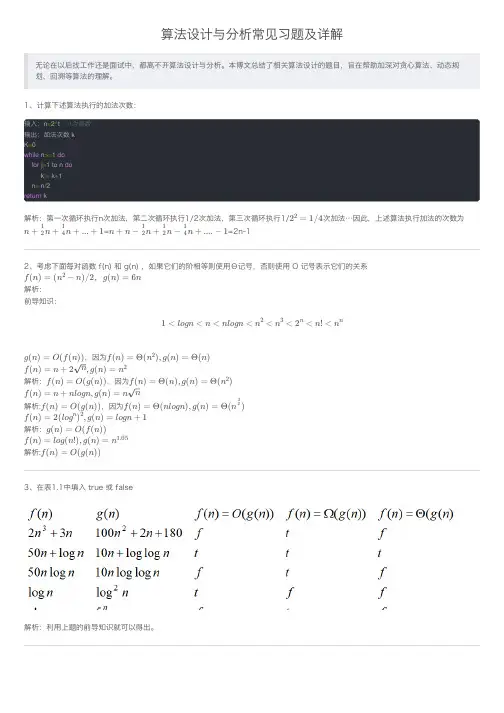
算法设计与分析常见习题及详解⽆论在以后找⼯作还是⾯试中，都离不开算法设计与分析。
本博⽂总结了相关算法设计的题⽬，旨在帮助加深对贪⼼算法、动态规划、回溯等算法的理解。
1、计算下述算法执⾏的加法次数：输⼊：n =2^t //t 为整数输出：加法次数 k K =0while n >=1 do for j =1 to n do k := k +1 n = n /2return k解析：第⼀次循环执⾏n次加法，第⼆次循环执⾏1/2次加法，第三次循环执⾏1/次加法…因此，上述算法执⾏加法的次数为==2n-12、考虑下⾯每对函数 f(n) 和 g(n) ，如果它们的阶相等则使⽤Θ记号，否则使⽤ O 记号表⽰它们的关系解析：前导知识：，因为解析：，因为解析:，因为解析：解析:3、在表1.1中填⼊ true 或 false解析：利⽤上题的前导知识就可以得出。
2=21/4n +n +21n +41...+1n +n −n +21n −21n +41....−1f (n )=(n −2n )/2，g (n )=6n1<logn <n <nlogn <n <2n <32<n n !<n ng (n )=O (f (n ))f (n )=Θ(n ),g (n )=2Θ(n )f (n )=n +2,g (n )=n n 2f (n )=O (g (n ))f (n )=Θ(n ),g (n )=Θ(n )2f (n )=n +nlogn ,g (n )=n nf (n )=O (g (n ))f (n )=Θ(nlogn ),g (n )=Θ(n )23f (n )=2(log ),g (n )=n 2logn +1g (n )=O (f (n ))f (n )=log (n !),g (n )=n 1.05f (n )=O (g (n ))4、对于下⾯每个函数 f(n),⽤f(n) =Θ(g(n))的形式，其中g(n)要尽可能简洁，然后按阶递增序排列它们（最后⼀列）解析：最后⼀个⽤到了调和公式：按阶递增的顺序排列：、、、、、、、、、(n −2)!=Θ((n −2)!)5log (n +100)=10Θ(logn )2=2n Θ(4)n 0.001n +43n +31=Θ(n )4(lnn )=2Θ(ln n )2+3n logn =Θ()3n 3=n Θ(3)n log (n !)=Θ(nlogn )log (n )=n +1Θ(nlogn )1++21....+=n1Θ(logn )=∑k =1nk 1logn +O (1)1++21....+n 15log (n +100)10(lnn )2+3n logn log (n !)log (n )n +10.001n +43n +313n 22n (n −2)!5、求解递推⽅程前导知识：主定理前导知识：递归树：例⼦：递归树是⼀棵节点带权的⼆叉树，初始递归树只有⼀个结点，标记为权重W(n)，然后不断进⾏迭代，最后直到树种不再含有权为函数的结点为⽌，然后将树根结点到树叶节点的全部权值加起来，即为算法的复杂度。
《算法设计与分析》复习题参考答案
《算法设计与分析》复习题参考答案一、概念题：请解释下列术语。
1．数据元素的集合。
2．队列是一个线性表，限制为只能在固定的一端进行插入，在固定的另一端进行删除。
3．对于算法a，如果存在一多项式p()，使得对a的每个大小为n的输入，a的计算时间为o(p(n))，则称a具有多项式复杂度4．二叉树的层数i与该层上的结点数n的关系为：n(i)=i2。
5．如果可满足性约化为一个问题L，则称该问题为NP-难度的。
6．算法就是一组有穷的规则，它规定了解决某一特定类型问题的一系列运算。
7．多数据单指令流8．若图的任意两个节点间均存在路径可达，则称该图为连通图。
9. 是指一个数学模型以及定义在该模型上的一组操作。
10．算法的复杂度只能用指数函数对其限界。
11．函数或过程直接或间接调用它自己。
12．和高度相同的满二叉树的每个对应的顶点编号相同的树13．由所有可行状态所构成的树。
14．如果L时NP难度的且L∈NP，则称问题L是NP-完全的。
15．算法是一个步骤的序列，满足：有穷性、可行性、确定性、输入、输出；过程不需要满足由穷性。
16．有向图的每条边有起点与终点之分，且用箭头指向边的终点。
无向图的边无起点和终点之分，边无箭头。
17．树(tree)是一个或多个结点的有限集合，，它使得：①有一个特别指定的称作根(root)的结点；②剩下的结点被分成m≥0个不相交的集合tl，…，tm，这些集合的每一个都是一棵树，并称t1，…，tm为这根的子树(subtree)。
18．P是所有可在多项式时间内用确定算法求解的判定问题的集合。
19．运算结果是唯一确定的算法20. nP是所有可在多项式时间内用不确定算法求解的判定问题的集合二、填空题1.n2.O ( n )3.最优化问题4.宽度优先搜索5.结点的最大级数6.互异7.内结点和外结点8.方形9.内部路径长度、外部路径长度10.一次11.归并分类算法12.贪心选择性质13.最优子结构14.二元归并15.最小成本生成树16.最优性17.最优决策18.可容许最大成本c19.最小成本三、程序填空题。
算法设计与分析-课后习题集答案
（2）当 时， ，所以，可选 ， 。对于 ， ，所以， 。
（3）由（1）、（2）可知，取 ， ， ，当 时，有 ，所以 。
11. (1)当 时， ，所以 ， 。可选 ， 。对于 ， ，即 。
（2）当 时， ，所以 ， 。可选 ， 。对于 ， ，即 。
（3）因为 ， 。当 时， ， 。所以，可选 ， ，对于 ， ，即 。
第二章
2-17.证明：设 ，则 。
当 时， 。所以， 。
第五章
5-4.SolutionType DandC1(int left,int right)
{while(!Small(left,right)&&left<right)
{int m=Divide(left,right);
所以n-1<=m<=n (n-1)/2;
O(n)<=m<=O(n2);
克鲁斯卡尔对边数较少的带权图有较高的效率，而 ，此图边数较多，接近完全图，故选用普里姆算法。
10.
T仍是新图的最小代价生成树。
证明：假设T不是新图的最小代价生成树，T’是新图的最小代价生成树，那么cost(T’)<cost(T)。有cost(T’)-c(n-1)<cost(t)-c(n-1)，即在原图中存在一颗生成树，其代价小于T的代价，这与题设中T是原图的最小代价生成树矛盾。所以假设不成立。证毕。
13.template <class T>
select (T&x,int k)
{
if(m>n) swap(m,n);
if(m+n<k||k<=0) {cout<<"Out Of Bounds"; return false;}
黄宇《算法设计与分析》课后习题解析(二)精选全文
黄宇《算法设计与分析》课后习题解析（⼆）第2章：从算法的视⾓重新审视数学的概念2.1：(向下取整)题⽬：请计算满⾜下⾯两个条件的实数的区间解析：根据向下取整的含义，令，讨论a的取值范围即可解答：令，则可得：即：故的取值区间为：2.2: (取整函数)题⽬：证明：对于任意整数,（提⽰：将n划分为）。
解析：根据提⽰将n进⾏划分，根据取整函数的定义⽤k表⽰取整函数，即可证明；证明如下：因为对于任意整数,可划分为，则:① ；② ；综上：对于任意整数,, 得证；2.3: (斐波拉契数列)对于斐波拉契数列，请证明：1）题⽬：是偶数当且仅当n能被3整除解析：由斐波拉契数列的递归定义式，容易联想到数学归纳法；证明如下：（采⽤数学归纳法）i)当n = 1,2,3时，依次为1，1，2，符合命题；ii)假设当（k>=1）时命题均成⽴，则：① 当n = 3k+1时，是奇数，成⽴；② 当n = 3k+2时，是奇数，成⽴；③ 当 n = 3(k+1)时，是偶数，成⽴；综上：归纳可得为偶数当且仅当，得证;2）题⽬：x x =1+a (0<a <1)x =1+a (0<a <1)⌊x ⌋=1⇒⌊x ⌋=21⌊x ⌋=2⌊1+a +22a ⌋=1a +22a <1⇒0<a <−21⇒1<a +1<⇒21<x <2x (1，)2n ≥1⌈log (n +1)⌉=⌊logn ⌋+12≤k n ≤2−k +11n ≥12≤k n ≤2−k +11k +1=⌈log (2+k 1)⌉≤⌈log (n +1)⌉≤⌈log (2)⌉=k +1k +1=>⌈log (n +1)⌉=k +1k =⌊log (2)⌋≤k ⌊logn ⌋≤⌊log (2−k +11)⌋=k =>⌊logn ⌋=k n ≥1⌈log (n +1)⌉=k +1=⌊logn ⌋+1F n F n n ≤3k F =n F +n −1F =n −2F +3k F =3k −1>F 3k +1F =n F +3k +1F =3k >F 3k +2F =n F +3k +2F =3k +1>F 3k +3F n 3∣n F −n 2F F =n +1n −1(−1)n +1解析：同1）理，容易联想到数学归纳法证明如下：（采⽤数学归纳法）i)当n = 2时，, 易知成⽴；ii)假设当 n = k 时命题成⽴，① 若k = 2m, 则,当n = k+1 = 2m+1时，要证命题成⽴，即证： => ,代⼊递推式, 得：, 易知是恒等式，故命题成⽴；②当 k=2m+1时，同①理可证命题成⽴；综上：归纳可得，得证；2.4：(完美⼆叉树)给定⼀棵完美⼆叉树，记其节点数为，⾼度为，叶节点数为，内部节点数为1）题⽬：给定上述4个量中的任意⼀个，请推导出其他3个量解析：根据完美⼆叉树的结构特点易得解答：（仅以已知⾼度h推导其他三个量为例，其余同理）已知⾼度为h，可得：节点数：叶节点数：内部节点数：2）题⽬：请计算完美⼆叉树任意⼀层的节点个数：① 如果任意指定深度为的⼀层节点，请计算该层节点个数；② 如果任意指定⾼度为的⼀层节点，请计算该层节点个数；解析：根据完美⼆叉树的结构特点易得（注意节点深度和节点⾼度是互补的，相加为树⾼）解答：① ; ② ;2.5: (⼆叉树的性质)对于⼀棵⾮空的⼆叉树T，记其中叶节点的个数为，有1个⼦节点的节点个数为，有两个⼦节点的节点个数为1）题⽬：如果T是⼀棵2-tree，请证明。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《算法设计与分析实用教程》参考解答1-1 加减得1的数学游戏西西很喜欢数字游戏，今天他看到两个数，就想能否通过简单的加减，使最终答案等于1。
而他又比较厌烦计算，所以他还想知道最少经过多少次才能得到1。
例如，给出16,9：16-9+16-9+16-9-9-9+16-9-9=1，需要做10次加减法计算。
设计算法，输入两个不同的正整数，输出得到1的最少计算次数。
（如果无法得到1，则输出-1）。
（1）若输入两个不同的正整数a,b均为偶数，显然不可能得到1。
设x*a与y*b之差为“1”或“-1”,则对于正整数a,b经n=x+y-1次加减可得到1。
为了求n的最小值，令n从1开始递增，x在1——n中取值，y=n+1-x：检测d=x*a+y*b，若d=1或-1，则n=x+y-1为所求的最少次数。
（2）算法描述// 两数若干次加减结果为1的数学游戏#include <stdio.h>void main(){long a,b,d,n,x,y;printf(" 请输入整数a,b: ");scanf("%ld,%ld",&a,&b);if(a%2==0 && b%2==0){ printf(" -1\n");return;}n=0;while(1){ n++;for(x=1;x<=n;x++){ y=n+1-x;d=x*a-y*b;if(d==1 || d==-1) // 满足加减结果为1{ printf(" n=%ld\n",n);return;}}}}请输入整数a,b: 2012,19961请输入整数a,b: 101,20136061-2 埃及分数式算法描述分母为整数分子为“1”的分数称埃及分数，试把真分数a/b 分解为若干个分母不为b 的埃及分数之和。
（1） 寻找并输出小于a/b 的最大埃及分数1/c ； （2） 若c>900000000，则退出；（3） 若c ≤900000000，把差a/b-1/c 整理为分数a/b ，若a/b 为埃及分数，则输出后结束。
（4） 若a/b 不为埃及分数，则继续（1）、（2）、（3）。
试描述以上算法。
解：设)(int ab d = (这里int(x)表示取正数x 的整数)，注意到1+<<d ab d ，有)1()1(11+-+++=d b bd a d ba算法描述：令c=d+1，则 input (a,b) while(1){c=int(b/a)+1;if(c>900000000) return; else{ print(1/c+); a=a*c-b;b=b*c; // a,b 迭代，为选择下一个分母作准备 if(a==1){ print(1/b);return;} } }1-3 求解时间复杂度求出以下程序段所代表算法的时间复杂度。
（1）m=0;for(k=1;k<=n;k++) for(j=k;j>=1;j--) m=m+j;解：因s=1+2+…+n=n(n+1)/2时间复杂度为O(n 2)。
（2）m=0; for(k=1;k<=n;k++) for(j=1;j<=k/2;j++)m=m+j;解：设n=2u+1，语句m=m+1的执行频数为 s=1+1+2+2+3+3+…+u+u=u(u+1)=(n −1)(n+1)/4 设n=2u ，语句m=m+1的执行频数为s=1+1+2+2+3+3+…+u=u 2=n 2/4时间复杂度为O(n 2)。
（3）t=1;m=0;for(k=1;k<=n;k++) {t=t *k;for(j=1;j<=k *t;j++)m=m+j; }解：因s=1+2×2!+ 3×3!+…+ n ×n!=(n+1)!−1 时间复杂度为O((n+1)!). （4）for(a=1;a<=n;a++) {s=0;for(b=a *100−1;b>=a *100−99;b −=2) {for(x=0,k=1;k<=sqrt(b);k+=2) if(b%k==0){x=1;break;} s=s+x; } if(s==50)printf("%ld \n",a);break;} }解：因a 循环n 次；对每一个a,b 循环50次；对每一个b,k2次。
因而k 循环体的执行次数s 满足250(1250250s L L ＜＜＜算法的时间复杂度为O(n n )。
1-4 时间复杂度的一个性质若p(n)是n 的多项式，证明：O(log(p(n)))=O(logn)。
证：设m 为正整数，p(n)=a1×n m +a2×n m-1+…+am ×n ， 取常数c>ma1+(m-1)a2+…+am, 则log(p(n))=ma1×logn+(m-1)a2×logn+…=(ma1+(m-1)a2+…)×logn <clogn因而有O(log(p(n)))=O(logn)。
1-5 统计n!中数字“0”的个数修改1.3.2计算n!的算法，统计并输出n!中数字“0”的个数及其尾部连续“0”的个数（n<10000）。
解：计算n!完成后，在j（1——m）循环过if(a[j]==0) p++;统计n!中数字“0”的个数p。
应用q=1; while(a[q]==0) q++;统计尾部连续“0”的个数q-1。
// 统计n!中0的个数及尾部连续0的个数（n<10000）#include<stdio.h>#include<math.h>void main(){ int g,j,k,m,n,p,q,t,a[40000];double s;printf(" 请输入正整数n(n<10000): ");scanf("%d",&n); // 输入ns=0;for(k=2;k<=n;k++)s+=log10(k); // 对数累加确定n!的位数mm=(int)s+1;for(k=1;k<=m;k++)a[k]=0; // 数组清零a[1]=1;g=0;for(k=2;k<=n;k++)for(j=1;j<=m;j++){ t=a[j]*k+g; // 数组累乘并进位a[j]=t%10;g=t/10;}p=0;for(j=m;j>=1;j--)if(a[j]==0) p++; // p统计n!中0的个数q=1;while(a[q]==0) q++; // q尾部连续0的个数printf(" p=%d,q=%d\n",p,q-1); // 输出结果}数据测试：请输入正整数n(n<10000): 1000p=472,q=249请输入正整数n(n<10000): 2013p=1032,q=5011-6 构建斜折对称方阵图1-4是一个7阶斜折对称方阵，试观察斜折对称方阵的构造特点，总结归纳其构造规律，设计并输出n（奇数）阶斜折对称方阵。
图1-4 7阶斜折对称方阵（1）构造规律与赋值要点对n阶方阵中的每一个元素都必须赋值，但不可能逐行逐列地一个个赋值，有必要分析方阵的构造特点，分块或分片实施。
斜折对称方阵的构造特点：两对角线上均为“0”，依两对角线把方阵分为4个区域，每一区域表现为同数字依附两对角线折叠对称，至上下左右正中元素为n/2。
同样设置2维a[n][n]数组存储方阵中元素，行号为i，列号为j，a[i][j]为第i行第j 列元素。
令m=(n+1)/2, 按m把方阵分成的4个小矩形区如图1-5所示。
图1-5 按m分成的4个小矩形注意到方阵的主对角线（从左上至右下）上元素为：i=j，则左上区与右下区依主对角线赋值：a[i][j]=abs(i-j);注意到方阵的次对角线（从右上至左下）上元素为：i+j＝n+1，则右上区与左下区依次对角线赋值：a[i][j]=abs(i+j-n-1);(2) 程序设计// 斜折对称方阵#include <math.h>#include <stdio.h>void main(){int i,j,m,n,a[30][30];printf(" 请确定方阵阶数(奇数)n: "); scanf("%d",&n);if(n%2==0){ printf(" 请输入奇数！");return;}m=(n+1)/2;for(i=1;i<=n;i++)for(j=1;j<=n;j++){ if(i<=m && j<=m || i>m && j>m)a[i][j]=abs(i-j); // 方阵左上部与右下部元素赋值if(i<=m && j>m || i>m && j<=m)a[i][j]=abs(i+j-n-1); // 方阵右上部与左下部元素赋值}printf(" %d阶对称方阵为:\n",n);for(i=1;i<=n;i++){ for(j=1;j<=n;j++) // 输出对称方阵printf("%3d",a[i][j]);printf("\n");}}1-7 构建横竖折对称方阵试观察图1-6所示的横竖折对称方阵的构造特点，总结归纳其构造规律，设计并输出n （奇数）阶横竖折对称方阵。
图1-6 7阶横竖折对称方阵（1）构造规律与赋值要点观察横竖折对称方阵的构造特点，方阵横向与纵向正中有一对称轴。
两对称轴所分4个小矩形区域表现为同数字横竖折递减，至4顶角元素为1。
设阶数n（奇数）从键盘输入，对称轴为m=(n+1)/2。
设置2维a数组存储方阵中元素，行号为i，列号为j，a[i][j]为第i行第j列元素。
可知主对角线（从左上至右下）有：i=j；次对角线（从右上至左下）有：i+j=n+1。
按两条对角线把方阵分成上部、左部、右部与下部4个区,如图1-7所示。
图1-7 对角线分成的4个区对角线上元素可归纳到上、下部，即上、下部区域带等号即可。
上、下部按列号j的函数m-abs(m-j)赋值：if(i+j<=n+1 && i<=j || i+j>=n+1 && i>=j)a[i][j]=m-abs(m-j);左、右部按行号i的函数m-abs(m-i)赋值：if(i+j<n+1 && i>j || i+j>n+1 && i<j)a[i][j]=m-abs(m-i);（2）算法描述// 横竖折对称方阵#include <stdio.h> // 调用2个头文件#include <math.h>void main(){int i,j,m,n,a[30][30]; // 定义数据结构printf(" 请确定方阵阶数(奇数)n: "); scanf("%d",&n);if(n%2==0){printf(" 请输入奇数！");return;}m=(n+1)/2;for(i=1;i<=n;i++)for(j=1;j<=n;j++){if(i+j<=n+1 && i<=j || i+j>=n+1 && i>=j)a[i][j]=m-abs(m-j); // 方阵上、下部元素赋值if(i+j<n+1 && i>j || i+j>n+1 && i<j)a[i][j]=m-abs(m-i); // 方阵左、右部元素赋值}printf(" %d阶对称方阵为:\n",n);for(i=1;i<=n;i++){ for(j=1;j<=n;j++) // 输出对称方阵printf("%3d",a[i][j]);printf("\n");}}1-8 应用定义求最大公约与最小公倍数应用定义求n个正整数的最大公约数与最小公倍数, 给出算法设计。