1-5的数学组合计算练习题
2021-2022学年北师大版七年级数学下册《1-5平方差公式》同步练习题(附答案)

2021-2022学年北师大版七年级数学下册《1-5平方差公式》同步练习题(附答案)1.下列运算结果正确的是()A.3a﹣a=2B.a2•a4=a8C.(a+2)(a﹣2)=a2﹣4D.(﹣a)2=﹣a22.从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加6米,相邻的另一边减少6米,变成矩形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会()A.没有变化B.变大了C.变小了D.无法确定3.如果一个数等于两个连续奇数的平方差,那么我们称这个数为“幸福数”.下列数中为“幸福数”的是()A.205B.250C.502D.5204.下列整式的乘法中,不能用平方差公式进行计算的是()A.(x+y)(x﹣y)B.(﹣x﹣y)(﹣x+y)C.(﹣x﹣y)(x+y)D.(﹣x+y)(x+y)5.下列运算正确的是()A.a2+a2=2a4B.a6÷a2=a3C.(a+3)(a﹣3)=a2﹣6a+9D.(﹣3a3)2=9a66.下列计算正确的是()A.a+a2=a3B.a6÷a3=a2C.(﹣a2b)3=a6b3D.(a﹣2)(a+2)=a2﹣47.如图1,将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式()A.x2﹣2x+1=(x﹣1)2B.x2﹣1=(x+1)(x﹣1)C.x2+2x+1=(x+1)2D.x2﹣x=x(x﹣1)8.下列多项式乘以多项式能用平方差公式计算的是()A.(a+b)(﹣b﹣a)B.(﹣a+b)(﹣b﹣a)C.(a+b)(b+a)D.(﹣a+b)(b﹣a)9.若a+b=6,a2﹣b2=30,则a﹣b=()A.5B.6C.10D.1510.若(2m+5)(2m﹣5)=15,则m2=.11.1002﹣992+982﹣972+962﹣952+…+22﹣12=.12.已知a+b=2,a﹣b=3.则a2﹣b2的值为.13.已知a2+a﹣1=0,则代数式(a+2)(a﹣2)+a(a+2)值为.14.已知x2﹣y2=21,x﹣y=3,则x+y=.15.已知x+2y=13,x2﹣4y2=39,则多项式x﹣2y的值是.16.观察下列各式:(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,…根据规律可得:(x﹣1)(x2021+x2020+…+x+1)=.17.请阅读以下材料:[材料]若x=12349×12346,y=12348×12347,试比较x,y的大小.解:设12348=a,那么x=(a+1)(a﹣2)=a2﹣a﹣2,y=a(a﹣1)=a2﹣a.因为x﹣y=(a2﹣a﹣2)﹣(a2﹣a)=﹣2<0,所以x<y.我们把这种方法叫做换元法.请仿照例题比较下列两数大小:x=997657×997655,y=997653×997659.18.计算:x(x+2)+(1+x)(1﹣x).19.课堂上,老师让同学们计算(3a﹣b)(3a+b)﹣a(4a﹣1).(3a﹣b)(3a+b)﹣a(4a﹣1)=3a2﹣b2﹣4a2﹣a=﹣a2﹣b2﹣a左边是小朱的解题过程.请你判断其是否正确?如果有错误,请写出正确的解题过程.20.用乘法公式计算:100×99.21.计算:(x﹣2)(x+2)﹣6x(x﹣3)+5x2.22.利用乘法公式有时能进行简便计算.例:102×98=(100+2)(100﹣2)=1002﹣22=10000﹣4=9996.请参考给出的例题,通过简便方法计算:(1)31×29;(2)195×205.23.计算:(﹣x2y﹣x2y2)•(﹣xy)2﹣(﹣2x2y2﹣3)•(﹣3+2x2y2).24.如图1,是边长分别为a和b的两种正方形纸片.(1)若用这两种纸片各1张按照如图2方式放置,其未叠合部分(阴影部分)面积为S1,则S1=;(用含a,b的代数式表示)(2)在(1)中图2的基础上,再在大正方形的右下角摆放一张边长为b的小正方形纸片(图3),两个小正方形叠合部分(阴影部分)面积为S2,试求S2.(用含a,b的代数式表示)25.某同学化简a(a+2b)﹣(a+b)(a﹣b)出现了错误,解答过程如下:原式=a2+2ab﹣(a2﹣b2)(第一步)=a2+2ab﹣a2﹣b2(第二步)=2ab﹣b2(第三步)(1)该同学解答过程从第几步开始出错,错误原因是什么;(2)写出此题正确的解答过程.26.如图,边长为a的大正方形中有一个边长为b的小正方形,图2由图1中的阴影部分拼成的一个长方形.(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请用含a,b的代数式表示:S1=,S2=(只需表示,不必化简);(2)以上结果可以验证哪个乘法公式?请写出这个乘法公式;(3)运用(2)中得到的公式,计算:20222﹣2023×2021.27.计算:(3x+2)(3x﹣2)(9x2+4).28.计算:(1)2(﹣3xy+x2)﹣[2x2﹣3(5xy﹣2x2)﹣xy];(2)(a﹣2)(a+2)(2a+1).29.若xy=﹣1,且x﹣y=3.(1)求(x﹣2)(y+2)的值;(2)求x2﹣xy+y2的值.30.如图1所示,边长为a的正方形中有一个边长为b的小正方形,图2是由图1中阴影部分拼成的一个长方形,设图1中阴影部分面积为S1,图2中阴影部分面积为S2.(1)请直接用含a和b的代数式表示S1=,S2=;写出利用图形的面积关系所得到的公式:(用式子表达).(2)应用公式计算:.(3)应用公式计算:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1.参考答案1.解:3a和a属于同类项,所以3a﹣a=2a,故A项不符合题意,根据同底数幂的乘法运算法则可得a2•a4=a6,故B项不符合题意,根据平方差公式(a+2)(a﹣2)=a2﹣4,故C项符合题意,(﹣a)2=a2,故D项不符合题意,故选:C.2.解:矩形的面积为(a+6)(a﹣6)=a2﹣36,∴矩形的面积比正方形的面积a2小了36平方米,故选:C.3.解:设较小的奇数为x,较大的为x+2,根据题意得:(x+2)2﹣x2=(x+2﹣x)(x+2+x)=4x+4,若4x+4=205,即x=,不为整数,不符合题意;若4x+4=250,即x=,不为整数,不符合题意;若4x+4=502,即x=,不为整数,不符合题意;若4x+4=520,即x=129,符合题意.故选:D.4.解:A、原式=x2﹣y2,不符合题意;B、原式=(﹣x)2﹣y2=x2﹣y2,不符合题意;C、原式=﹣(x+y)2=﹣x2﹣2xy﹣y2,符合题意;D、原式=y2﹣x2,不符合题意.故选:C.5.解:A、a2+a2=2a2,原计算错误,故此选项不符合题意;B、a6÷a2=a4,原计算错误,故此选项不符合题意;C、(a+3)(a﹣3)=a2﹣9,原计算错误,故此选项不符合题意;D、(﹣3a3)2=9a6,原计算正确,故此选项符合题意;故选:D.6.解:A、a与a2不是同类项,不能合并,原计算错误,故此选项不符合题意;B、a6÷a3=a3,原计算错误,故此选项不符合题意;C、(﹣a2b)3=﹣a6b3,原计算错误,故此选项不符合题意;D、(a﹣2)(a+2)=a2﹣4,原计算正确,故此选项符合题意,故选:D.7.解:由图可知,图1的面积为:x2﹣12,图2的面积为:(x+1)(x﹣1),所以x2﹣1=(x+1)(x﹣1).故选:B.8.解:能用平方差公式计算的是(﹣a+b)(﹣b﹣a),其它的不能用平方差公式计算.故选:B.9.解:∵a+b=6,a2﹣b2=30,∴(a+b)(a﹣b)=30,∴a﹣b=30÷6=5,故选:A.10.解:由(2m+5)(2m﹣5)=15,得4m2﹣25=15.解得m2=10.故答案是:10.11.解:原式=(1002﹣992)+(982﹣972)+(962﹣952)+…+(22﹣12)=(100+99)×(100﹣99)+(98+97)×(98﹣97)+...+(2+1)×(2﹣1)=100+99+98+97+...+4+3+2+1=(100+1)+(99+2)+...+(51+52)=50×101=5050.故答案为:5050.12.解:当a+b=2,a﹣b=3时,a2﹣b2=(a+b)(a﹣b)=2×3=6.故选:6.13.解:(a+2)(a﹣2)+a(a+2)=a2﹣4+a2+2a=2a2+2a﹣4=2(a2+2a)﹣4.∵a2+a﹣1=0,∴a2+a=1.∴原式=2×1﹣4=﹣2.故答案为:﹣2.14.解:因为x2﹣y2=(x﹣y)(x+y)=21,x﹣y=3,所以x+y==7.故答案为:7.15.解:∵x+2y=13,x2﹣4y2=39,∴x2﹣4y2=(x+2y)(x﹣2y)=39,∴x﹣2y=3.故答案为:3.16.解:观察每一个等式左边的代数式与右边的代数式,得(x﹣1)(x2021+x2020+…+x+1)=x2022﹣1.故答案为:x2022﹣1.17.解:令a=997653,b=997655,则x=(a+4)b=ab+4b,y=a(b+4)=ab+4a,∵x﹣y=(ab+4b)﹣(ab+4a)=4(b﹣a)=4×2=8>0,∴x>y.18.解:原式=x2+2x+1﹣x2=2x+1.19.解:不正确,原式=9a2﹣b2﹣4a2+a=5a2﹣b2+a,即正确答案为:5a2﹣b2+a.20.解:100×99=(100+)(100﹣)=10000﹣=9999.21.解:(x﹣2)(x+2)﹣6x(x﹣3)+5x2=x2﹣4﹣6x2+18x+5x2=18x﹣4.22.解:(1)31×29=(30+1)×(30﹣1)=302﹣12=900﹣1=899;(2)195×205=(200﹣5)×(200+5)=2002﹣52=40000﹣25=39975;23.解:原式=(﹣x2y﹣x2y2)•x2y2﹣[(﹣3)2﹣(2x2y2)2]=﹣x4y3﹣x4y4﹣9+4x4y4=﹣x4y3+x4y4﹣9.24.解:(1)由题意可得,S1是图1中两个正方形面积的差,又∵图1中大正方形的面积为a²,小正方形的面积为b²,∴S1=a²﹣b²,故答案为:a²﹣b²;(2)由题意可得,S2是两个小正方形在长为a,宽为b的矩形内的重叠部分,∴S2=b²+b²﹣ab=2b²﹣ab.25.解:(1)该同学解题过程从第二步开始出错,错误的原因是去括号时第二项没有变号;(2)正确解答为:原式=a2+2ab﹣(a2﹣b2)=a2+2ab﹣a2+b2=2ab+b2.26.解:(1)图1阴影部分的面积为边长为a的大正方形的面积减去边长为b的小正方形的面积,即S1=a2﹣b2,图2中阴影部分的面积是长为(a+b),宽为(a﹣b)的长方形的面积,即S2=(a+b)(a ﹣b),故答案为:a2﹣b2,(a+b)(a﹣b);(2)由(1)中S1=S2可得,a2﹣b2=(a+b)(a﹣b),因此可以验证平方差公式,即:(a+b)(a﹣b)=a2﹣b2;(3)原式=20222﹣(2022+1)(2022﹣1)=20222﹣(20222﹣1)=1.27.解:(3x+2)(3x﹣2)(9x2+4)=(9x2﹣4)(9x2+4)=81x4﹣16.28.解:(1)原式=﹣6xy+2x2﹣(2x2﹣15xy+6x2﹣xy)=﹣6xy+2x2﹣2x2+15xy﹣6x2+xy=10xy﹣6x2;(2)原式=(a2﹣4)(2a+1)=2a3+a2﹣8a﹣4.29.解:(1)∵xy=﹣1,x﹣y=3,∴(x﹣2)(y+2)=xy+2(x﹣y)﹣4=﹣1+6﹣4=1;(2)∵xy=﹣1,x﹣y=3,∴x2﹣xy+y2=(x﹣y)2+xy=9+(﹣1)=8.30.解:(1)图1中阴影部分的面积为大正方形与小正方形的面积差,即a2﹣b2,图2中阴影部分是长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),由图1和图2中阴影部分的面积相等可得,a2﹣b2=(a+b)(a﹣b),故答案为:a2﹣b2,(a+b)(a﹣b),a2﹣b2=(a+b)(a﹣b);(2)原式====;(3)原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)+1=(22﹣1)(22+1)(24+1)(28+1)(216+1)(232+1)+1=(24﹣1)(24+1)(28+1)(216+1)(232+1)+1=(28﹣1)(28+1)(216+1)(232+1)+1=(216﹣1)(216+1)(232+1)+1=(232﹣1)(232+1)+1=264﹣1+1=264.。
人教版小学五年级上册数学单元练习题(1-5单元全)

亲爱的同学,如果把这份试卷⽐作⼀份湛蓝的海,那么,我们现在启航,展开你⾃信和智慧的双翼,乘风踏浪,你定能收获⽆限风光!⼩编整理了⼈教版⼩学五年级上册数学单元练习题(1-5单元全),希望对你有帮助!第⼀单元 ⼀、填空。
1.表⽰4个1.2是多少的乘法算式是(),表⽰4的1.2倍是多少的算式是()。
2.因为8×0.5是求8的()是多少,所以它的积⽐8()。
3.⽤“四舍五⼊”把8.954保留两位⼩数约是(),精确到⼗分位约是()。
4.在乘法中,如果两个因数都不为0,⼀个因数不变,另⼀个因数扩⼤10倍,积就(),⼀个因数扩⼤100倍,另⼀个因数扩⼤10倍,积就()。
5.不⽤计算,写出 (1)1.8×0.27的积有()位⼩数。
(2)9.12÷0.24的商的位是在()位上。
6.0.7除以0.3,商求到⼗分位,商是(),余数是()。
7.在○⾥填上“>”、“1.46×0.99○1.46 54÷0.18○54 0.57×1○0.57 7.6×1.01○7.6 4.8÷1.5○4.8 35÷0.1○35×10 8.由48×32=1536,可知480×0.32=(),0.48×3.2=() 9.由21.45÷15=1.43,可知2.145÷15=(),214.5÷0.15=()。
10.在3.82,5.6,0.35,0.002,2.75,3.2727……中,,是有限⼩数的是(),是循环⼩数的数()。
⼆、判断题。
(正确的在题后的括号内打“√”,错误的打“×”。
) 1. 整数乘以⼩数,积⼀定⼩于被乘数。
() 2. 纯⼩数乘以纯⼩数,积⼀定⼩于其中⼀个因数。
() 3. 2.7×0.4×2.5=2.7×(0.4×2.5)这种运算过程没有依次运算是错误的。
人教版小学五年级上册数学单元练习题(1-5单元全)

人教版小学五年级上册数学单元练习题(1-5单元全)1.表示4个1.2是多少的乘法算式是(),表示4的1.2倍是多少的算式是()。
2.因为8×0.5是求8的()是多少,所以它的积比8()。
3.用“四舍五入”把8.954保留两位小数约是(),精确到十分位约是()。
4.在乘法中,如果两个因数都不为0,一个因数不变,另一个因数扩大10倍,积就(),一个因数扩大100倍,另一个因数扩大10倍,积就()。
5.不用计算,写出(1)1.8×0.27的积有()位小数。
(2)9.12÷0.24的商的位是在()位上。
6.0.7除以0.3,商求到十分位,商是(),余数是()。
7.在○里填上“>”、“1.46×0.99○1.46 54÷0.18○54 0.57×1○0.57 7.6×1.01○7.6 4.8÷1.5○4.8 35÷0.1○35×108.由48×32=1536,可知480×0.32=(),0.48×3.2=()9.由21.45÷15=1.43,可知2.145÷15=(),214.5÷0.15=()。
10.在3.82,5.6,0.35,0.002,2.75,3.2727……中,,是有限小数的是(),是循环小数的数()。
二、判断题。
(正确的在题后的括号内打“√”,错误的打“×”。
)1. 整数乘以小数,积一定小于被乘数。
()2. 纯小数乘以纯小数,积一定小于其中一个因数。
()3. 2.7×0.4×2.5=2.7×(0.4×2.5)这种运算过程没有依次运算是错误的。
()4. 2.5÷4的商是0.6,余数是1。
()5. 20÷9的商是无限循环小数。
()6. 3.0与3不一定相等。
()7. 0.666……保留两位小数写作0.666……=0.67。
小学四年级数字的组合练习题

小学四年级数字的组合练习题题一:数字的顺序和大小比较1. 请将以下数字按从小到大的顺序排列:26、19、33、8、45。
()2. 小红和小亮都在数数,小红说:“365比137要大。
”小亮说:“137比365要小。
”他们谁说得对?()3. 用适当的符号(>, < 或 =)将下列数字连起来,并注明结果:25 40 25 ()4. 找出下列数字中的最小值:58,29,36,48。
()5. 请输入一个能够使下列等式成立的数字: 54 + 36 = ________题二:数字的组合与拆分1. 小明家里有16个苹果,他想要吧这些苹果分给自己和弟弟。
如果小明拿走8个苹果,弟弟能拿走多少个苹果?()2. 请将下面的数字组合成一个最大的两位数:3、5、8、7。
()3. 请分别用两个数的和和差表示下列的数字:25 ()4. 请拆分下面的数,使其和为30:23 ()5. 小华有12根火柴,她想要用这些火柴拼成一个数字。
请你告诉他可以拼出哪几个数字。
()题三:数字的进位与退位1. 请计算下面两个数的和:52 + 47 = _____()2. 小明正在测试自己的计算能力,他计算得到了以下结果:841 + 244 = 1165。
请问小明是否出错了?()3. 小亮在解决一个数学问题,他计算得到:279 + 74 = 334。
请问小亮盘算正确吗?()4. 请将下面的两个数相加并写出结果:315+ 487_____5. 请输入下面两个数的差:258 - 103 = _____题四:数字的倍数和因数1. 请问18是否是9的倍数?()2. 如果一个数被2整除,那它能被什么数整除?()3. 请计算下面两个数的最小公倍数:8和6。
()4. 请计算下面两个数的最小公约数:16和24。
()5. 请将下面的数字分别写成因数的形式:36 = __ x __48 = __ x __题五:数字的应用1. 小明的奶奶今年60岁,小明今年10岁。
2022-2023学年北师大版九年级数学下册《1-5三角函数的应用》题型分类练习题(附答案)

2022-2023学年北师大版九年级数学下册《1.5三角函数的应用》题型分类练习题(附答案)一.测量计算物体高度问题1.如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC,CD与AB始终在同一平面上.(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.(2)将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:≈1.41,≈1.73)2.两栋居民楼之间的距离CD=30米,楼AC和BD均为10层,每层楼高3米.(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部?3.如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).(1)求灯杆CD的高度;(2)求AB的长度(结果精确到0.1米).(参考数据:=1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)4.某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)5.一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为△ABC,点B、C、D在同一条直线上,测得∠ACB=90°,∠ABC=60°,AB=32cm,∠BDE=75°,其中一段支撑杆CD=84cm,另一段支撑杆DE=70cm.求支撑杆上的点E到水平地面的距离EF是多少?(用四舍五入法对结果取整数,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.732)6.“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)7.第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行,我国冬奥选手取得了9块金牌、4块银牌、2块铜牌,为祖国赢得了荣誉,激起了国人对冰雪运动的热情.某地模仿北京首钢大跳台建了一个滑雪大跳台(如图1),它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成.图2是其示意图,已知:助滑坡道AF=50米,弧形跳台的跨度FG=7米,顶端E到BD的距离为40米,HG∥BC,∠AFH=40°,∠EFG=25°,∠ECB=36°.求此大跳台最高点A距地面BD的距离是多少米(结果保留整数).(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)8.如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)9.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号).10.图1是太阳能热水器装置的示意图.利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:如图2,AB⊥BC,垂足为点B,EA⊥AB,垂足为点A,CD∥AB,CD=10cm,DE=120cm,FG⊥DE,垂足为点G.(1)若∠θ=37°50′,则AB的长约为cm;(参考数据:sin37°50′≈0.61,cos37°50′≈0.79,tan37°50′≈0.78)(2)若FG=30cm,∠θ=60°,求CF的长.11.汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A至B共有30级阶梯,平均每级阶梯高30cm,斜坡AB的坡度i=1:1;加固后,坝顶宽度增加2米,斜坡EF的坡度i=1:,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号)12.如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.(1)求坝高;(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈,cos37°≈,tan37°≈)二.实际问题数学抽象13.如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2(+1)m.请计算说明,工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门?14.日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.如图②,山坡EF朝北,EF长为15m,坡度为i=1:0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.(1)求山坡EF的水平宽度FH;(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C 处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?15.图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.(1)求点M到地面的距离;(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:≈1.73,结果精确到0.01米)16.如图是把一个装有货物的长方体形状的木箱沿着坡面装进汽车货厢的示意图.已知汽车货厢高度BG=2米,货厢底面距地面的高度BH=0.6米,坡面与地面的夹角∠BAH=α,木箱的长(FC)为2米,高(EF)和宽都是1.6米.通过计算判断:当sinα=,木箱底部顶点C与坡面底部点A重合时,木箱上部顶点E会不会触碰到汽车货厢顶部.三.三角函数的应用17.如图1是某中学教学楼的推拉门,已知门的宽度AD=2米,且两扇门的大小相同(即AB=CD),将左边的门ABB1A1绕门轴AA1向里面旋转35°,将右边的门CDD1C1绕门轴DD1向外面旋转45°,其示意图如图2,求此时B与C之间的距离(结果保留一位小数).(参考数据:sin35°≈0.6,cos35°≈0.8,≈1.4)18.2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB、BC为机械臂,OA=1m,AB=5m,BC=2m,∠ABC=143°.机械臂端点C到工作台的距离CD=6m.(1)求A、C两点之间的距离;(2)求OD长.(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈2.24)19.随着我国科学技术的不断发展,科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一.图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据,BC=8,CD=2,∠D=135°,∠C=60°,且AB∥CD,求出垂尾模型ABCD的面积.(结果保留整数,参考数据:≈1.414,≈1.732)20.如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m.(1)若移动滑块使AE=EF,求∠AFE的度数和棚宽BC的长.(2)当∠AFE由60°变为74°时,问棚宽BC是增加还是减少?增加或减少了多少?(结果精确到0.1m,参考数据:≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)21.小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2,已知AD=BE=10cm,CD=CE=5cm,AD⊥CD,BE⊥CE,∠DCE=40°.(1)连结DE,求线段DE的长.(2)求点A,B之间的距离.(结果精确到0.1cm.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)参考答案一.测量计算物体高度问题1.解:(1)如图2中,作BO⊥DE于O.∵∠OEA=∠BOE=∠BAE=90°,∴四边形ABOE是矩形,∴∠OBA=90°,∴∠DBO=150°﹣90°=60°,∴OD=BD•sin60°=20(cm),∴DE=OD+OE=OD+AB=20+5≈39.6(cm).(2)作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,∵∠CBH=60°,∠CHB=90°,∴∠BCH=30°,∵∠BCD=165°,∴∠DCP=45°,∴CH=BC sin60°=10(cm),DP=CD sin45°=10(cm),∴DF=DP+PG+GF=DP+CH+AB=(10+10+5)(cm),∴下降高度:DE﹣DF=20+5﹣10﹣10﹣5=10﹣10≈3.2(cm).2.解:(1)延长BG,交AC于点F,过F作FH⊥BD于H,由图可知,FH=CD=30m,∵∠BFH=∠α=30°,在Rt△BFH中,BH=,FC=30﹣17.32=12.68,再用12.68÷3≈4.23,所以在四层的上面,即第五层,答:此刻B楼的影子落在A楼的第5层;(2)连接BC,∵BD=3×10=30=CD,∴∠BCD=45°,答:当太阳光线与水平面的夹角为45度时,B楼的影子刚好落在A楼的底部.3.解:(1)延长DC交AN于H.∵∠DBH=60°,∠DHB=90°,∴∠BDH=30°,∵∠CBH=30°,∴∠CBD=∠BDC=30°,∴BC=CD=10(米).(2)在Rt△BCH中,CH=BC=5米,BH=5≈8.65(米),∴DH=15(米),在Rt△ADH中,AH=≈=20(米),∴AB=AH﹣BH=20﹣8.65≈11.4(米).答:AB的长度约为11.4米.4.解:如图作CM∥AB交AD于M,MN⊥AB于N.由题意=,即=,CM=(米),在Rt△AMN中,∵∠ANM=90°,MN=BC=4,∠AMN=72°,∴tan72°=,∴AN≈12.32(米),∵MN∥BC,AB∥CM,∴四边形MNBC是平行四边形,∴BN=CM=(米),∴AB=AN+BN=12.32+1.5≈13.8(米).5.解:方法一:如图1,过点D作DM⊥EF于M,过点D作DN⊥BA交BA延长线于N,在Rt△ABC中,∠ABC=60°,AB=32(cm),∴BC=AB•cos60°=32×=16(cm),∵DC=84(cm),∴BD=DC+BC=84+16=100(cm),∵∠F=90°,∠DMF=90°,∴DM∥FN,∴∠MDB=∠ABC=60°,在Rt△BDN中,sin∠DBN=sin60°=,∴DN=×100=50(cm),∵∠F=90°,∠N=90°,∠DMF=90°,∴四边形MFND是矩形,∴DN=MF=50,∵∠BDE=75°,∠MDB=60°,∴∠EDM=∠BDE﹣∠MDB=75°﹣60°=15°,∵DE=70(cm),∴ME=DE•sin∠EDM=70×sin15°≈18.2(cm),∴EF=ME+MF=50+18.2≈104.8≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.方法二:如图2,过点D作DH⊥BA交BA延长线于H,过点E作EG⊥HD延长线于G,在Rt△ABC中,∠ABC=60°,AB=32(cm),∴BC=AB•cos60°=32×=16(cm),∵DC=84(cm),∴BD=DC+BC=84+16=100(cm),同方法一得,DH=BD•sin60°=50(cm),∵在Rt△BDH中,∠DBH=60°,∴∠BDH=30°,∵∠BDE=75°,∴∠EDG=180°﹣∠BDH﹣∠BDE=180°﹣75°﹣30°=75°,∴∠DEG=90°﹣75°=15°,∴DG=DE•sin15°≈18.2(cm),∴GH=DG+DH=18.2+50≈104.8≈105(cm),∵∠F=90°,∠H=90°,∠G=90°,∴EF=GH≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.6.解:∵BN∥ED,∴∠NBD=∠BDE=37°,∵AE⊥DE,∴∠E=90°,∴BE=DE•tan∠BDE≈18.75(cm),如图,过C作AE的垂线,垂足为F,∵∠FCA=∠CAM=45°,∴AF=FC=25cm,∵CD∥AE,∴四边形CDEF为矩形,∴CD=EF,∵AE=AB+EB=35.75(cm),∴CD=EF=AE﹣AF≈10.8(cm),答:线段BE的长约等于18.8cm,线段CD的长约等于10.8cm.7.解:如图,过点E作EN⊥BC于点N,交HG于点M,则AB=AH﹣EM+EN.根据题意可知,∠AHF=∠EMF=∠EMG=90°,EN=40(米),∵HG∥BC,∴∠EGM=∠ECB=36°,在Rt△AHF中,∠AFH=40°,AF=50,∴AH=AF•sin∠AFH≈50×0.64=32(米),在Rt△FEM和Rt△EMG中,设MG=m米,则FM=(7﹣m)米,∴EM=MG•tan∠EGM=MG•tan36°≈0.73m,EM=FM•tan∠EFM=FM•tan25°≈0.47(7﹣m),∴0.73m=0.47(7﹣m),解得m≈2.7(米),∴EM≈0.47(7﹣m)=2.021(米),∴AB=AH﹣EM+EN≈32﹣2.021+40≈70(米).∴此大跳台最高点A距地面BD的距离约是70米.8.解:如图作MF⊥PQ于F,QE⊥MN于E,则四边形EMFQ是矩形.在Rt△QEN中,设EN=x米,则EQ=2x米,∵QN2=EN2+QE2,∴20=5x2,∵x>0,∴x=2,∴EN=2(米),EQ=MF=4(米),∵MN=3米,∴FQ=EM=1(米),在Rt△PFM中,PF=FM•tan60°=4(米),∴PQ=PF+FQ=(4+1)米.9.解:过A作AG⊥CD于G,则∠CAG=30°,在Rt△ACG中,CG=AC sin30°=50×=25(cm),∵GD=50﹣30=20(cm),∴CD=CG+GD=25+20=45(cm),连接FD并延长与BA的延长线交于H,则∠H=30°,在Rt△CDH中,CH==2CD=90(cm),∴EH=EC+CH=AB﹣BE﹣AC+CH=300﹣50﹣50+90=290(cm),在Rt△EFH中,EF=EH•tan30°=290×=(cm),答:支撑角钢CD和EF的长度各是45cm,cm.10.解:(1)如图,作EP⊥BC于点P,作DQ⊥EP于点Q,则CD=PQ=10,∠2+∠3=90°,∵∠1+∠θ=90°,且∠1=∠2,∴∠3=∠θ=37°50′,则EQ=DE sin∠3=120×sin37°50′,∴AB=EP=EQ+PQ=120sin37°50′+10=83.2(cm),故答案为:83.2;(2)如图,延长ED、BC交于点K,由(1)知∠θ=∠3=∠K=60°,在Rt△CDK中,CK==(cm),在Rt△KGF中,KF===(cm),则CF=KF﹣KC=﹣==(cm).11.解:过A作AH⊥BC于H,过E作EG⊥BC于G,则四边形EGHA是矩形,∴EG=AH=30×30=900,GH=AE=2,∵斜坡AB的坡度i=1:1,∴AH=BH=9米,∴AB=9,∴BG=BH﹣HG=7米,∵斜坡EF的坡度i=1:,∴FG=9米,∴BF=FG﹣BG=9﹣7,∴S梯形ABFE=(2+9﹣7)×9=,∴共需土石为×200=100(81﹣45)立方米.12.解:(1)作DM⊥AB于M,CN⊥AN于N.由题意:tan∠DAB==2,设AM=x,则DM=2x,∵四边形DMNC是矩形,∴DM=CN=2x,在Rt△NBC中,tan37°===,∴BN=x,∵x+3+x=14,∴x=3,∴DM=6,答:坝高为6m.(2)作FH⊥AB于H.设DF=y,则AE=2y,EH=3+2y﹣y=3+y,BH=14+2y﹣(3+y)=11+y,由△EFH∽△FBH,可得=,即=,解得y=﹣7+2或﹣7﹣2(舍弃),∴DF=2﹣7,答:DF的长为(2﹣7)m.二.实际问题数学抽象13.解:工人师傅搬运此钢架能通过一个直径为2.1m的圆形门,理由是:过B作BD⊥AC于D,∵AB>BD,BC>BD,AC>AB,∴求出DB长和2.1m比较即可,设BD=xm,∵∠A=30°,∠C=45°,∴DC=BD=xm,AD=BD=xm,∵AC=2(+1)m,∴x+x=2(+1),∴x=2,即BD=2m<2.1m,∴工人师傅搬运此钢架能通过一个直径为2.1m的圆形门.14.解:(1)在Rt△EFH中,∵∠H=90°,∴tan∠EFH=i=1:0.75==,设EH=4xm,则FH=3xm,∴EF==5xm,∵EF=15m,∴5x=15m,x=3,∴FH=3x=9m.即山坡EF的水平宽度FH为9m;(2)∵L=CF+FH+EA=CF+9+4=CF+13,H=AB+EH=22.5+12=34.5,H1=0.9,∴日照间距系数=L:(H﹣H1)==,∵该楼的日照间距系数不低于1.25,∴≥1.25,∴CF≥29.答:要使该楼的日照间距系数不低于1.25,底部C距F处29m远.15.解:(1)如图,过M作MN⊥AB于N,交BA的延长线于N,Rt△OMN中,∠NOM=60°,OM=1.2,∴∠M=30°,∴ON=OM=0.6,∴NB=ON+OB=3.3+0.6=3.9;即点M到地面的距离是3.9米;(2)取CE=0.65,EH=2.55,∴HB=3.9﹣2.55﹣0.65=0.7,过H作GH⊥BC,交OM于G,过O作OP⊥GH于P,∵∠GOP=30°,∴tan30°==,∴GP=OP=≈0.404,∴GH=3.3+0.404=3.704≈3.70>3.5,∴货车能安全通过.16.解:∵BH=0.6米,sinα=,∴AB==1米,∴AH=0.8米,∵AF=FC=2米,∴BF=1米,作FJ⊥BG于点J,作EK⊥FJ于点K,∠EKF=∠FJB=∠AHB=90°,∠EFK=∠FBJ=∠ABH,BF=AB,∴△EFK∽△FBJ∽△ABH,△FBJ≌△ABH,∴,BJ=BH=0.6米,即,解得,EK=1.28,∴BJ+EK=0.6+1.28=1.88<2,∴木箱上部顶点E不会触碰到汽车货厢顶部.三.三角函数的应用17.解:作BE⊥AD于点E,作CF⊥AD于点F,延长FC到点M,使得BE=CM,∵AB=CD,AB+CD=AD=2,∴AB=CD=1,在Rt△ABE中,∠A=35°,AB=1,∴BE=AB•sin A=1×sin35°≈0.6,∴AE=AB•cos A=1×cos35°≈0.8,在Rt△CDF中,∠D=45°,CD=1,∴CF=CD•sin D=1×sin45°≈0.7,∴DF=CD•cos D=1×cos45°≈0.7,∵BE⊥AD,CF⊥AD,∴BE∥CM,又∵BE=CM,∴四边形BEMC是平行四边形,∴BC=EM,在Rt△MEF中,FM=CF+CM=1.3,EF=AD﹣AE﹣FD=0.5,∴EM==≈1.4,答:B与C之间的距离约为1.4米.18.解:(1)如图,过点A作AE⊥CB,垂足为E,在Rt△ABE中,AB=5m,∠ABE=37°,∵sin∠ABE=,cos∠ABE=,∴=0.60,=0.80,∴AE=3m,BE=4m,∴CE=6m,在Rt△ACE中,由勾股定理AC==3≈6.7m.(2)过点A作AF⊥CD,垂足为F,∴FD=AO=1m,∴CF=5m,在Rt△ACF中,由勾股定理AF==2m.∴OD=2≈4.5m.19.解:如图,过点A作CD的垂线,交CD的延长线于F,过点C作AB的垂线,交AB 的延长线于E,∵AB∥CD,∴四边形AECF是矩形,∵∠BCD=60°,∴∠BCE=90°﹣60°=30°,在Rt△BCE中,∠BCE=30°,BC=8,∴BE=BC=4,CE=BC=4,∵∠ADC=135°,∴∠ADF=180°﹣135°=45°,∴△ADF是等腰直角三角形,∴DF=AF=CE=4,由于FC=AE,即4+2=AB+4,∴AB=4﹣2,∴S梯形ABCD=(2+4﹣2)×4=24,答:垂尾模型ABCD的面积为24.20.解:(1)∵AE=EF=AF=1m,∴△AEF是等边三角形,∴∠AFE=60°,连接MF并延长交AE于K,则FM=2FK,∵△AEF是等边三角形,∴AK=(m),∴FK==(m),∴FM=2FK=(m),∴BC=4FM=4≈6.92≈6.9(m),答:∠AFE的度数为60°,棚宽BC的长约为6.9m;(2)∵∠AFE=74°,∴∠AFK=37°,∴KF=AF•cos37°≈0.80(m),∴FM=2FK=1.60(m),∴BC=4FM=6.40(m)<6.92(m),6.92﹣6.40=0.52≈0.5(m),答:当∠AFE由60°变为74°时,棚宽BC是减少了,减少了0.5m.21.解:(1)如图,过点C作CF⊥DE于点F,∵CD=CE=5cm,∠DCE=40°.∴∠DCF=20°,∴DF=CD•sin20°≈5×0.34≈1.7(cm),∴DE=2DF≈3.4cm,∴线段DE的长约为3.4cm;(2)∵横截面是一个轴对称图形,∴延长CF交AD、BE延长线于点G,连接AB,∴DE∥AB,∴∠A=∠GDE,∵AD⊥CD,BE⊥CE,∴∠GDF+∠FDC=90°,∵∠DCF+∠FDC=90°,∴∠GDF=∠DCF=20°,∴∠A=20°,∴DG=≈≈1.8(cm),∴AG=AD+DG=10+1.8=11.8(cm),∴AB=2AG•cos20°≈2×11.8×0.94≈22.2(cm).∴点A,B之间的距离22.2cm.。
小学数学10道口算练习题

小学数学10道口算练习题1. 123 + 456 = ?2. 789 - 123 = ?3. 234 × 5 = ?4. 630 ÷ 9 = ?5. 876 + 543 = ?6. 982 - 345 = ?7. 456 × 7 = ?8. 972 ÷ 6 = ?9. 789 + 654 = ?10. 876 - 432 = ?在这篇文章中,我将给你提供十个小学数学的口算练习题。
这些题目旨在帮助小学生们练习他们的口算能力,并提高他们的数学思维能力。
1. 123 + 456 = ?计算:123加456等于多少?2. 789 - 123 = ?计算:789减去123等于多少?3. 234 × 5 = ?计算:234乘以5等于多少?4. 630 ÷ 9 = ?计算:630除以9等于多少?5. 876 + 543 = ?计算:876加543等于多少?6. 982 - 345 = ?计算:982减去345等于多少?7. 456 × 7 = ?计算:456乘以7等于多少?8. 972 ÷ 6 = ?计算:972除以6等于多少?9. 789 + 654 = ?计算:789加654等于多少?10. 876 - 432 = ?计算:876减去432等于多少?通过这十道口算练习题,孩子们可以提高他们加减乘除的能力,并增加对数字的理解。
这些练习题旨在培养他们的逻辑思维和注意力,为更复杂的数学问题打下坚实的基础。
希望你通过这些练习题能够巩固自己的数学技能,提高你的口算能力,并且享受到解题的乐趣。
加油!。
一年级数学分类专项练习题

一年级数学分类专项练习题第一部分:简单加法1. 2 + 3 =2. 5 + 1 =3. 4 + 2 =4. 3 + 4 =5. 1 + 1 =第二部分:简单减法1. 4 - 2 =2. 6 - 3 =3. 5 - 1 =4. 3 - 1 =5. 2 - 2 =第三部分:简单乘法1. 2 × 2 =2. 1 × 3 =3. 3 × 1 =4. 5 × 0 =5. 4 × 4 =第四部分:简单除法1. 4 ÷ 2 =2. 6 ÷ 3 =3. 9 ÷ 3 =4. 7 ÷ 2 =5. 10 ÷ 5 =第五部分:组合运算1. 2 + 3 × 4 =2. (5 + 1) ÷ 2 =3. 6 - 3 × 2 =4. (4 + 2) ÷ 2 =5. 3 + 4 - 1 =第六部分:大小比较1. 3 > 2,对或错?2. 5 < 2,对或错?3. 4 > 8,对或错?4. 6 < 9,对或错?5. 10 > 10,对或错?第七部分:找规律1. 2, 4, 6, 8, __2. 5, 10, 15, 20, __3. 3, 6, 9, 12, __4. 1, 4, 7, 10, __5. 8, 6, 4, 2, __第八部分:填空题1. 3 + __ = 52. __ + 4 = 93. 6 - __ = 24. __ - 3 = 75. 2 × __ = 10第九部分:数字排序请将以下数字按照从小到大的顺序进行排列:6, 3, 8, 1, 5第十部分:解决问题小明有5个苹果,他送给小红2个苹果,小红原本已经有3个苹果。
请问现在小明和小红手上分别还有几个苹果?以上是一年级数学分类专项练习题,请按照题目要求完成每个题目的计算或填空。
祝您顺利完成!。
小学数学一年级上册5以内数的分解练习题(共10套)
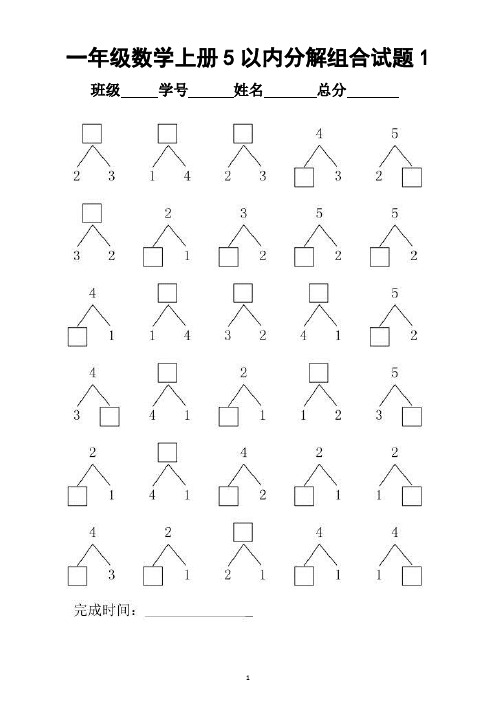
班级学号姓名总分
一年级数学上册5以内分解组合试题2
班级学号姓名总分
一年级数学上册5以内分解组合试题3
班级学号姓名总分
一年级数学上册5以内分解组合试题4
班级学号姓名总分
一年级数学上册5以内分解组合试题5
班级学号姓名总分
一年级数学上册合试题7
班级学号姓名总分
一年级数学上册5以内分解组合试题8
班级学号姓名总分
一年级数学上册5以内分解组合试题9
班级学号姓名总分
一年级数学上册5以内分解组合试题10
班级学号姓名总分
