国民经济结构的投入产出分析实验报告
我国产业结构基本分析--基于投入产出表的分析

感应度系数
影响力系数
2002
2005
2007
2002
2005
2007
农业
1.0918
1.0673
1.0144
0.7819
0.7236
0.721
采掘业
1.3707
1.5879
1.5607
0.8225
0.9065
0.9209
食品制造业
0.6639
0.652
0.7581
我国产业机构基本分析
——基于投入产出表的实证研究
摘要:产业结构的合理化是经济发展的客观要求,本文利用2002年、2005年、2007年的17部门投入产出表,分别计算不同年份的中间需求率和中间投入率、感应度系数和影响力系数、最终需求项目诱发依存度,并进行比较分析,为制定产业结构调整政策、发展战略、提升产业竞争力提供依据。
0.772
0.8708
0.8319
0.7694
房产与租赁和商务服务业
0.8901
0.6762
0.5921
0.8267
0.8227
0.7422
金融保险业
0.7673
0.6131
0.6711
0.7231
0.7056
0.5955
其他服务业
0.6221
0.6325
0.7119
0.8789
0.8958
0.8515
0.8126
0.8734
0.9002
1.1197
1.1006
1.1332
化学工业
1.6038
1.6543
1.7368
1.1687
4.4投入产出分析

m m m 可见 A → 0 Λ → 0 λi → 0 λ i < 1
1
(2)如果 A 不与对角阵相似,则必与 Jordan 形相似,类似可证。
引理 3 有 ∑A
投入产出分析
在一个国家或区域的经济系统中,各部门(或企业)既有 消耗又有生产,或说既有投入又有产出,生产的产品供给系统 内部各部门和系统以外的需求,同时也消耗系统内各部门所提 供的产品。消耗的目的是为了生产,生产的结果又必然要创造 新价值,以支付工资和获取利润。对每一部门,物质消耗和新 创造的价值等于它生产的总产值,这就是投入和产出之间的平 衡关系。 美国经济学家哈佛大学教授 W.Leontief 于 20 世纪 30 年代 首先提出并成功建立了国民经济的投入产出数学模型,并数次 制定主持美国的国民经济投入产出表,这一方法即投入产出法 以其重要的应用价值迅速为世界各国经济学界和决策部门所采 纳,因此他获得 1973 年的 Nobel 经济学奖。这里仅列出投入产 出模型中一个部分。
k =0 ∞ k
方阵级数 I + A + A2 + L + Ak + L收敛 A k → 0(k → ∞) ,且
= ( I A) 1 。
证:必要性显然。下证充分性: 由引理 2,对 λ , λ < 1, 故 I A ≠ 0 , 因此 ( I A) 1 存在。
( I + A + A2 + L + Ak )( I A) = I Ak +1
j =1
n
设 max x j
j
gdp核算实验的实验报告

gdp核算实验的实验报告GDP核算实验的实验报告一、引言GDP(国内生产总值)是衡量一个国家经济发展水平的重要指标。
通过对GDP 的核算,可以了解一个国家或地区的经济总量、增长速度以及产业结构等方面的情况。
本次实验旨在通过对一国GDP的核算,探讨GDP的计算方法以及其对经济发展的意义。
二、实验方法本次实验选择了某国的一年数据进行GDP核算。
首先,我们使用了两种常见的GDP计算方法,即生产法和支出法。
生产法是通过统计各产业的产出值来计算GDP,而支出法则是通过统计各个部门的支出来计算GDP。
我们将对比这两种方法的结果,以了解它们的异同。
三、实验结果使用生产法计算GDP的结果是X元,而使用支出法计算的结果是Y元。
通过对比两种方法的结果,我们可以发现它们在数值上存在一定的差异。
这是因为生产法和支出法计算GDP的角度不同,统计的内容也不同,因此会导致结果的差异。
四、讨论与分析通过对实验结果的分析,我们可以看出GDP的计算方法对于经济发展的评估具有重要意义。
生产法主要关注各个产业的产出,能够反映出一个国家或地区的产业结构和产出能力。
而支出法则更加关注各个部门的支出,能够反映出一个国家或地区的消费水平和投资水平。
因此,通过对GDP的计算,我们可以了解一个国家或地区的经济发展状况以及产业结构的变化。
此外,GDP的核算还可以帮助政府制定经济政策和发展战略。
通过对GDP的核算,政府可以了解到经济的总量和增长速度,从而判断经济是否处于增长阶段或衰退阶段,进而采取相应的措施。
同时,GDP的核算还可以帮助政府了解各个产业的发展情况,从而制定产业政策和促进产业升级。
因此,GDP核算对于国家的经济发展具有重要的指导意义。
然而,GDP核算也存在一些局限性。
首先,GDP只是一个总量指标,不能完全反映一个国家或地区的经济状况。
例如,GDP无法反映出收入分配的不平等问题,也无法反映出环境污染和资源消耗等问题。
其次,GDP核算还存在统计数据的不准确性和滞后性等问题,可能导致对经济状况的误判。
投入产出分析报告基础

入产出方法的普及应归功于改革开放初期由关肇直先生等许多著名学者 向国家提出的建议。
第一节 投入产出分析基本知识
投入产出分析中的投入,是指经济活动过程中的各种消耗(包括中间投 入和最初投入)及其来源。例如,国民经济各部门在产品生产和服务过 程中的中间投入(又称中间消耗)包括各种原材料、燃料、动力及各种 服务。最初投入是指增加值各要素的投入,包括固定资产折旧、劳动者 报酬、生产税净额和营业盈余。显然,中间投入是指生产性消耗,包括 各种直接消耗和全部间接消耗。例如,生产钢要直接消耗电和生铁,而 生产生铁又要直接消耗电,这是生产钢通过消耗生铁对电的间接消耗。 广义而言,投入还包括经济活动过程中对固定资产、流动资产、自然资 源和劳动力的占用。 投入产出中的产出,是指经济活动的成果(如得到一定数量的某种产品 和劳务)及其使用去向(包括中间使用和最终使用)。中间使用是指经 济系统各部分,如国民经济各部门所生产的产品被用于中间消耗的部分 产品;最终使用是指被用于最终消费、资本形成和净出口的产品。 投入产出法主要由两部分构成:投入产出表和投入产出数学模型。
第一节 投入产出分析基本知识
4.消耗系数相对稳定性假定 这是一个动态上的假定。即假定在一定时期(1~2年)里,各种消耗系 数是相对稳定的。在投入产出分析中,各种消耗系数都是关键性数据, 它们表示各部门之间的经济技术联系的密切程度。在投入结构、工艺技 术和管理水平相对稳定的条件下,假定消耗系数在一定时期内是稳定的, 这是利用投入产出模型进行经济分析和预测的前提。 除了以上基本假定之外,还有一些其他假定。例如,假定在所研究的 时期内不存在生产的时间因素,即在静态模型中,本期所需要的产品在 本期的任何时候都能立即得到。在实际经济生活中,每种产品的生产时 间总是有先后且都有一定的生产周期,生产时间上的差异很可能使各部 门相互不能及时交货而影响生产,这一问题比较复杂。为了使问题简化, 投入产出分析假定在所研究的时期内(如一年)不存在这样的生产时间 因素。 投入产出的基本假定使部门间复杂的技术经济联系得到简化,可用线 性投入产出模型模拟国民经济的运行,进行经济分析、政策模拟和计划 计算。
实验三投入产出分析

实验三投入产出分析一、实验目的1.复习线性代数中矩阵、矩阵运算、逆矩阵及其求法等概念和理论。
2.理解投入产出分析中的基本概念和模型。
3.掌握Matlab软件中矩阵输入、矩阵运算、求逆矩阵等的命令和方法。
4.从数学和投入产出理论的角度,理解矩阵相乘、逆矩阵等的含义。
二、背景知识投入产出分析(Input-output Analysis):分析特定经济系统内投入与产出间数量依存关系的原理和方法。
亦称产业部门间分析。
也是进行经济预测和制定经济政策和措施所依据的经济数学模型。
这种模型最早是由美国经济学家、原哈佛大学教授瓦·列昂节夫(W. Leontief)于1936年提出,此后数十年间被愈来愈多的国家所采用并取得了良好的效果。
列昂节夫本人也因此获得了1973年的诺贝尔经济学奖。
投入产出表:以下面的表2-5-1的具体数据为例,表中第1行是农业,第3列表示建筑业,其交叉处的数字是229亿元。
从横行看,表示农业部门提供了229亿元的产品给建筑业作生产使用;从纵列看,表示农业部门生产中消耗了229亿元的建筑业产品。
第1行和第1列交叉处的数字464亿元,表示464亿元农业产品提供给农业部门生产使用,或者农业部门生产过程中消耗了464亿元本部门的产品。
第1行最后一个数字2918亿元表示农业部门的总产出,除了分配给6个中间部门作生产使用外,剩下的1284亿元用于消费、积累、出口等外部需求;第1列最后一个数字2918亿元表示对农业部门的总投入,农业部门生产过程中除了需要6个部门的投入外,还需要1663亿元的初始投入。
根据投入产出关系,每个中间部门的总投入等于总产出。
由于投入产出表的编制是受时间限制的,因此需要依靠一些相对稳定的因素来分析其中的内在规律:1.直接消耗系数,记作,它表示第部门生产单位产值消耗第部门的产品产值量。
第部门对第部门的直接消耗系数的计算公式为:(1) 即第部门在生产过程中消耗第部门的产品价值与第部门的总产品价值之比。
实验六 投入产出分析

0.0003 0.0006 0.1500 0.0018 0.0130 0.0345
0.0230 0.0239 0.6680 0.0190 0.1687 0.0960
0.0440 0.1010 0.1000 0.0650 0.0610 0.1000
(5)若在以后的三星期内,企业外部需求的增长速度是:煤每周增长15%,电力每周增长3%,铁路每周增长12%,则各企业的总产值将平均每周增长多少?
实验任务:
1.完成前面经济预测部分所要求的编制该经济系统(煤矿、电厂和铁路)在以后第三周的计划投入产出表;
2.下表是1992年我国的经济生产六部门之间产品消耗量、外部需求(消费与积累)和新创价值(劳动报酬与社会纯收入)的数据,其中每一行的数字是某一部门提供给各部门外部的产品价值.
(4)假如在1992年的基础上,下一年各部门的最终产品值的增长分别为农业5%、工业10%、建筑业16%、交通运输业和商业均为7%、其他各部门6%,试计算依照这样的方案执行后,各部门的总产值为多少?各部门新创价值又是多少?(假定下一年各部门之间的直接消耗不变)
(5)在第(4)小题的基础上编制下一年的投入产出简表,其中外部需求和新创价值可以不再细分。
E=eye(3);
X=inv(E-A)*Y;
B=[163801 0 0;
0 84484 0;
0 0 119919];
C=A*B
中间产品
最终产品
总产值
煤矿
电厂
铁路
小计
中间产品
煤矿
0
33793
53964
87757
76044
163801
投入产出分析报告论文设计
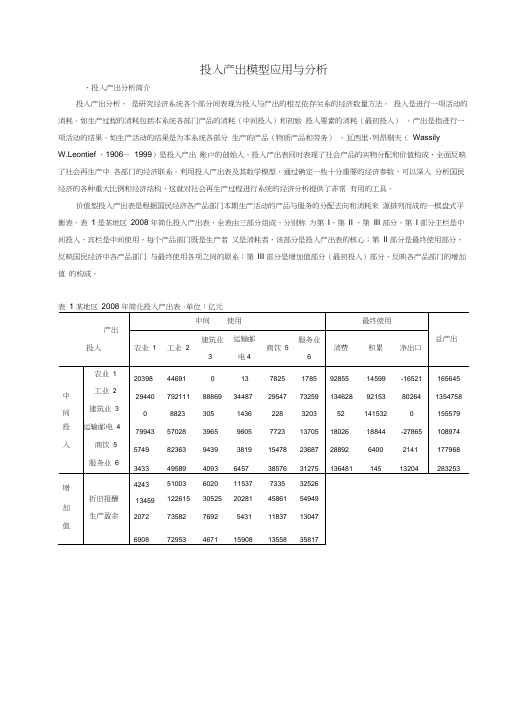
投入产出模型应用与分析、投入产出分析简介投入产出分析,是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。
投入是进行一项活动的消耗。
如生产过程的消耗包括本系统各部门产品的消耗(中间投入)和初始投入要素的消耗(最初投入)。
产出是指进行一项活动的结果。
如生产活动的结果是为本系统各部分生产的产品(物质产品和劳务)。
瓦西里·列昂剔夫(WassilyW.Leontief ,1906—1999)是投入产出账户的创始人。
投入产出表同时表现了社会产品的实物分配和价值构成,全面反映了社会再生产中各部门的经济联系。
利用投入产出表及其数学模型,通过确定一些十分重要的经济参数,可以深入分析国民经济的各种重大比例和经济结构,这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。
价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一棋盘式平衡表。
表1是某地区2008 年简化投入产出表,全表由三部分组成,分别称为第I、第II 、第III 部分。
第I 部分主栏是中间投入,宾栏是中间使用,每个产品部门既是生产者又是消耗者,该部分是投入产出表的核心;第II 部分是最终使用部分,反映国民经济中各产品部门与最终使用各项之间的联系;第III 部分是增加值部分(最初投入)部分,反映各产品部门的增加值的构成。
表1 某地区2008 年简化投入产出表i单位:亿元产出投入中间使用最终使用总产出农业 1 工业 2建筑业3运输邮电4商饮 5服务业6消费积累净出口农业 120398 44691 0 13 7825 1785 92855 14599 -16521 165645中工业 229440 792111 88869 34487 29547 73259 134628 92153 80264 1354758间建筑业 30 8823 305 1436 228 3203 52 141532 0 155579投运输邮电 479943 57028 3965 9605 7723 13705 18026 18844 -27865 108974入商饮 55749 82363 9439 3819 15478 23687 28892 6400 2141 177968服务业 63433 49589 4093 6457 38576 31275 136481 145 13204 283253增424313459 51003 6020 11537 7335 32526折旧报酬122615 30525 20281 45861 54949 加生产盈余2072 73582 7692 5431 11837 13047 值6908 72953 4671 15908 13558 35817二、投入产出模型(一)建立模型 1. 行模型(1)建立行模型:xijy iX i (i =1,2, ... ,n ) 引入直接消耗系数 a ij ,即: a ij =x ij / X j( 2)计算相关矩阵 A ,B=(I-A) -1-I , B =(I-A) -1 =B+I直接消耗系数矩阵:0.1231 0.0330 0.0000 0.0001 0.0440 0.0063 0.1777 0.5847 0.5712 0.3165 0.1660 0.2586 0.00000.00650.0020 0.0132 0.00130.0113 A=0.48260.0421 0.0255 0.0881 0.0434 0.0484 0.0347 0.0608 0.0607 0.0350 0.0870 0.0836 0.02070.03660.0263 0.0593 0.21680.11040.1976 0.1204 0.0775 0.0504 0.0955 0.05621.2551 1.8655 1.7485 1.1191 0.8764 1.0073 0.01970.02400.01780.02500.0133 0.0227B=0.70950.2174 0.1689 0.1908 0.1664 0.1508 0.1731 0.2227 0.2087 0.1385 0.1958 0.1885 0.16960.19020.16600.16110.3412 0.22351.1976 0.1204 0.0775 0.0504 0.0955 0.0562 1.25512.8655 1.7485 1.1191 0.8764 1.0073 0.01970.0240 1.0178 0.0250 0.0133 0.0227 B=0.7095 0.2174 0.1689 1.1908 0.16640.15080.1731 0.2227 0.20870.1385 1.1958 0.1885 0.16960.1902 0.16600.16110.3412 1.2235n可得: a ij X j y i X i 即用矩阵表示为 : AX+Y=X j1化简后可得价值型行数学模型: X=(I-A ) -1Y 或 X= B Y完全消耗系数矩阵:完全需要系数矩阵:3)价值型行数学模型X=(I-A)-1Y= B YX1 1.1976 0.1204 0.0775 0.0504 0.0955 0.0562 Y1X2 1.2551 2.8655 1.7485 1.1191 0.8764 1.0073 Y2X3 0.0197 0.0240 1.0178 0.0250 0.0133 0.0227 Y3X4 =0.7095 0.2174 0.1689 1.1908 0.1664 0.1508 Y4X5 0.1731 0.2227 0.2087 0.1385 1.1958 0.1885 Y5X6 0.1696 0.1902 0.1660 0.1611 0.3412 1.2235 Y62 列模型(1)建立列模型ni 1x ijd j v j t j s j X j (j =1,2,...,n)引入直接消耗系数a ij 可得:na ij X d j v j t j s j X j 即用矩阵表示为:AcX+N=Xi1ij j化简后可得价值型列数学模型:X=(I-Ac)-1N(2)计算相关矩阵A C,(I-Ac)-1物耗系数矩阵:0.8389 0 0 0 0 00 0.7637 0 0 0 00 0 0.6856 0 0 0Ac=0 0 0 0.5122 0 00 0 0 0 0.5584 00 0 0 0 0 0.5187增加值系数矩阵:6.2081 0 0 0 0 00 4.23159 0 0 0 0-1 0(I-Ac) -1= 0 3.1810 0 0 00 0 0 2.0500 0 00 0 0 0 2.2644 00 0 0 0 0 2.07753)价值型列数学模型X=(I-Ac) -1NX1 6.2081 0 0 0 0 0 N1 X2 0 4.23159 0 0 0 0 N2 X3 0 0 3.1810 0 0 0 N3 X 4=0 0 0 2.0500 0 0 N4 X5 0 0 0 0 2.2644 0 N5X6 0 0 0 0 0 2.0775 N6x ij:第i 部门(行部门)生产的产品或服务分配给第j 部门(列部门)用于生产消耗的产品产值;第j 部门(列部门)生产过程中直接消耗第i 部门的产品或服务的产品产值;y i:第i 部门在本期产品中提供的最终使用额,包括消费和积累;d j 、v j 、t j 、s j :分别为第j 部门的折旧,劳动报酬,生产税净额,和营业盈余;m j :为第j 部门的社会纯收入,等于t j + s j ;N j : 为第j 部门的增加值,等于d j + v j + t j + s j ;X i : 第i 部门总产出;X j: 第j 部门总投入;A:直接消耗系数矩阵(a ij )n nX=(X1 X 2 X N )T—总产出的列向量;Y=(y1 y2 ................ y N )T—最终使用的列向量;i, j =1,2,3,4,5,6 分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门;n=6。
6我国产业结构的投入产出分析

基于投入产出分析的我国产业结构研究王贤文 杨 名(大连理工大学21世纪发展研究中心,辽宁 大连 116023)摘 要:本文应用投入产出经济学的方法,通过对我国2000年投入产出调查资料中影响力系数和感应度系数的测算来对中国17个部门的产业进行关联分析,对我国的产业结构进行评价,以期有助于了解我国产业结构的特征,对将来产业结构的变化趋势和发展方向加以揭示。
关键词:影响力系数;感应度系数;产业分类;产业结构 中图分类号: F121.3 文献标识码: A产业结构调整是我国当前经济实现跨越性发展所面临的重要课题。
产业结构的投入产出关联分析, 可以深刻地揭示产业结构变动的内在机理。
我国的全国性投入产出调查开始于1987年,每5年(逢2、逢7的年份)调查一次,迄今已有四次即1987、1992、1997、2000年投入产出调查的资料。
本文主要是以最新的投入产出调查资料(2000年度)来对我国产业之间的关联状况进行定量分析,以期为我国产业结构调整提供可供参考的启示。
1.我国产业结构中两类系数的测算在进行区域经济主导产业研究时,主要是利用投入产出法中的影响力系数和感应度系数来衡量、分析和反映产业关联强度的。
(1)影响力系数F j影响力系数(F j )表示第J 产业增加一个单位的最终产品时,对国民经济各产业产量需求的波动程度[1]。
当影响力系数大于1时,表示该产业的生产对其它产业所产生的影响程度超过社会的平均水平;反之则表示该产业生产对其它产业的波及影响程度低于社会平均水平。
其计算公式如下:F j =∑∑∑===n 1j n1i ij n1i ijb n 1b(j=1,2,3,…,n ) (1)式中,ij b ——第j 部门对第i 部门的完全需要系数;∑=n1i ijb——完全需要系数矩阵B 中第j 列之和;∑∑==n 1j n1i ij b n 1——完全需要系数矩阵B 列和之均值。
(2)感应度系数E i与影响力系数类似,感应系数也是反映各产业关联程度的一个重要的指标[1]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告课程名称投入产出分析实验项目名称国民经济结构的投入产出分析班级与班级代码实验室名称(或课室)北校区实验楼601 专业统计学任课教师学号:姓名:李希实验日期:2012年10月28日广东商学院教务处制姓名施琪实验报告成绩评语:指导教师(签名)年月日说明:指导教师评分后,实验报告交院(系)办公室保存。
目录实验一经济结构的分析 (1)一.实验目的 (1)二.实验内容 (1)三.实验步骤及结果分析 (1)1、打开工作文件,合并投入产出表 (1)2.最终需求产品结构系数的计算 (3)3.最终需求分配结构系数 (4)4.最终需求结构对总产出影响分析 (5)实验二部门关联分类方法 (10)一.实验目的 (10)二.实验内容 (10)三.实验步骤及结果分析 (10)1、中间产品需求系数和中间产品投入系数 (10)2、产业结构分析 (11)实验一 经济结构的分析一、实验目的熟悉经济结构分析的各种系数,掌握经济结构分析的基本方法二、实验内容计算最终需求产品结构系数、最终需求分配结构系数、生产诱发额、生产诱发系数、生产依存度、增加值诱发额和增加值诱发系数。
三、实验步骤及结果分析1、打开工作文件,合并投入产出表 (1)开机进入excel 。
(2)打开广东省2007年42部门投入产出表,中间部门合并(见实验表1)。
实验表1 12部门中间部门合并表原42部门 代码 序号现12部门农林牧渔业 A01 1 农林牧渔业煤炭开采和洗选业 A02 2 采掘业 石油和天然气开采业 A03 金属矿采选业A04 非金属矿及其他矿采选业 A05 食品制造及烟草加工业 A06 3 商饮业 纺织业A07 4 纺织服装业 纺织服装鞋帽皮革羽绒及其制品业 A08 木材加工及家具制造业A09 5 木材加工造纸业造纸印刷及文教体育用品制造业 A10 石油加工、炼焦及核燃料加工业 A11 6 化工业化学工业 A12 非金属矿物制品业 A13 金属冶炼及压延加工业 A14 金属制品业A15 通用、专用设备制造业 A16 7 制造业交通运输设备制造业 A17 电气机械及器材制造业A18 通信设备、计算机用其他电子设备制造业 A19 仪器仪表及文化办公用机械制造业 A20 工艺品及其他制造业 A21 废品废料A22 电力、热力的生产和供应业 A23 8 电力、燃气及水的生产和供应业 燃气生产和供应业 A24 水的生产和供应业 A25 建筑业A26 9 建筑业 交通运输及仓储业 A27 10 运邮仓储业邮政业A28信息传输、计算机服务和软件业 A29 12 批发和零售业 A30 3住宿业和餐饮业 A31 金融 A32 11 金融房地产业房地产业 A33 租赁和商务服务业 A34 12 其他服务业研究与试验发展业 A35 综合技术服务业A36 水利、环境和公共设施管理业 A37 居民服务和其他服务业 A38 教育A39 卫生、社会保障和社会福利事业 A40 文化、体育和娱乐业 A41 公共管理和社会组织A42(3)最终产品合并要求。
居民消费,政府消费,总消费(居民消费和政府消费合计),固定资本形成,存货增加,总投资(固定资本形成和存货增加合计),调出,出口,输出(调出和出口合计),最终使用合计(总消费、总投资、输出合计),调进,进口,输入(调进和进口合计)。
(4)投入产出表的合并第一步,按行合并。
把中间部门根据中间部门合并要求按行合并。
原42部门中代码为A01的农林牧渔业仍为12部门中序号为1的农林牧渔业部门,那么,直接复制整合到新的区域,完成第一部门的合并。
12部门中序号为2的采掘业部门包括了原42部门中代码为A02、A03、A04和A05这四个部门,那么,先对这四个部门按列求和,把得到的求和行复制到新的区域,完成第二部门的合并。
其他部门的合并均按相同方法进行。
第二步,按列合并。
把中间部门和最终产品分别根据中间部门和最终产品的合并要求进行列的合并,合并方法同行的合并相同。
第三步,得到广东省2007年12部门投入产出表(见实验表2),存盘。
实验表2 广东省2007年12部门投入产出表2.最终需求产品结构系数的计算(1)根据广东省2007年12部门投入产出表,分析整理得到广东省2007年投入产出最终使用表(见实验表3),并进行相关投入产出分析的计算。
实验表3 广东省2007年投入产出最终使用表单位:万元下:最终需求的产品结构系数表示的是某种最终使用产品占最终使用总量的比例。
根据定义得到实验表4。
实验表4 广东省2007年最终使用产品结构系数表是其他服务业、商饮业、金融房地产业、制造业、农林牧渔业;用于资本形成的最主要是建筑业,其次是制造业、金融房地产业;用于输出的最主要是制造业、化工业和纺织服装业;对于输入产品而言,主要是制造业、化工业和采掘业。
3.最终需求分配结构系数分析最终需求的分配结构就是分析最终需求的项目构成,其系数定义如下:最终需求的分配结构系数表示的是某部门某项最终使用产品占该部门最终使用总量的比例。
根据定义计算得到实验表5。
实验表5 广东省2007年最终使用分配结构系数表及水的生产和供应业,商饮及其他服务业,金融房地产业其最终需求主要用于最终消费;建筑业其最终需求主要用于资本形成;采掘业,纺织服装业,木材加工造纸业,化工业,制造业,运输仓储业其最终需求主要用于输出。
4.最终需求结构对总产出影响分析最终需求是影响生产的主要因素,最终需求决定了总产出。
利用列昂惕夫逆矩阵对各产业的生产诱发额和生产诱发系数进行分析。
(1)生产诱发额的计算。
第一步,打开12部门投入产出表,计算第二步,根据计算各种生产诱发额。
得到广东省2007年生产诱发额表见实验表6.实验表6 广东省2007年最终使用生产诱发额表单位:万元(2)生产诱发系数。
生产诱发系数定义如下:根据定义计算得到广东省2007年生产诱发系数表见实验表7。
实验表7 广东省2007年生产诱发系数表(3)生产依存度。
生产依存度定义如下:根据定义计算得到广东省2007年最终使用生产依存度表见实验表8。
实验表8 广东省2007年最终使用生产依存度表存度分析:农林牧渔业,其他服务业,金融房地产业其最终消费的依存度较高,可将这些产业归属为“消费依赖型”产业;建筑业其资本形成的依存度较高,可将这些产业归属于“投资依赖型”产业;采掘业,商饮业,纺织服装业,木材加工造纸业,化工业,制造业,电力、燃气及水的生产和供应业,运邮仓储业其输出的依存度较高,即可将这些产业归属于“出口依赖型”产业。
(4)最终需求结构对增加值影响分析。
第一,计算增加值诱发额。
增加值诱发额定义如下:根据定义计算得到广东省2007年增加值诱发额表见实验表9。
实验表9 广东省2007年最终使用增加值诱发额表单位:万元增加值诱发系数定义如下:根据定义计算得到广东省2007年增加值诱发系数表见实验表10。
实验表10 广东省2007年最终使用增加值诱发系数表实验二部门关联分类方法一、实验目的掌握分析国民经济各部门之间联系的方法。
二、实验内容计算赫希曼系数和拉斯姆森系数,并分别据此将各部门作归类分析。
三、实验步骤及结果分析1、中间产品需求系数和中间产品投入系数(1)开机进入excel。
(2)打开工作文件,获取2007年和2002年12部门投入产出表及其各自的直接消耗系数和列昂惕夫逆系数。
(3)分别输入W i和U j的计算公式,计算W和U。
广东省2002年和2007年中间产品需求系数和中间产品投入系数如实验表11。
实验表11 广东省2002年和2007年中间产品需求系数和中间产品投入系数年的变化不大,其中变化较为明显的主要有农林牧渔业、运邮仓储业。
对于农林牧渔业,其在2002年的前向关联效应大而后向关联效应小,属于最终需求型基础产业,而在2007年,其前向关联效应明显大于后向关联效应,正逐渐转为中间投入型基础产业。
对于运邮仓储业,从2002年到2007年,其前后关联系数都有较明显变大,但前向关联效应增加的较为多,说明该产业正趋向于前关联效应大于关联效应大的方向发展,即该产业在经济发展中起推动作用,且作用越来越明显。
2、产业结构分析根据(I-A)-1计算r i和s j。
广东省2002年和2007年感应度系数和影响力系数见实验表12。
实验表12 广东省2002年和2007年感应度系数和影响力系数表14.实验表13中各系数与总投入系数0.6843比较大小;实验表14中各系数与平均值1比较大小。
实验表13 按中间产品需求系数和中间产品投入系数对部门分类的结果实验表14 按推动系数和带动系数对部门进行分类的结果对部门分类和按推动系数和带动系数(拉斯姆森系数)对部门分类是有所差异的。
出现这样的差异主要是因为拉斯姆森划分产业考虑了间接联系,其采用完全需求系数,考虑了波及效应;而赫希曼划分产业只考虑直接联系,其采用的是直接系数,不考虑波及效应。
赫希曼系数体现的是产业的特征,而拉斯姆森系数体现的是前后关联的特征,更加完善。
