人教版9.1不等式课件1
合集下载
人教版数学下册：9.1.1不等式及其解集 课件(共20张PPT)
D．18≤t≤27
2．无论x取什么数，下列不等式总成立的是（D ）
A．x+5＞0
B．x+5＜0
C．x2＜0 D．x2≥0
随堂检测
3．高钙牛奶的包装盒上注明“每100克内含钙≥150毫克”，它的含义是指（ B ）
A．每100克内含钙150毫克 B．每100克内含钙不低于150毫克 C．每100克内含钙高于150毫克 D．每100克内含钙不超过150毫克
本节目标
了解不等式概念，理解不等式的解集，能正确表示
1 不等式的解集 .
2 培养数感，渗透数形结合的思想. .
3 培养自主学习的能力，合作交流意识与探究精神 .
预习反馈
1．下面给出了5个式子：①3＞0，②4x+3y＞O，③x=3，④x﹣1，⑤x+2≤3，
其中不等式有（B ）
A．2个 B．3个 C．4个 D．5个
2．若m是非负数，则用不等式表示正确的是（ D ）
A．m＜0 B．m＞0 C．m≤0
D．m≥0
预习反馈
3．用不等号“＞、＜、≥、≤”填空：a2+1 > 0．
4.“a＜b”的反面是（ C ）
A．a≠b B．a＞b
C．a≥b
D．a=b
课堂探究
问题
一辆匀速行驶的汽车在11 :20距离A地50千米，要在12 :00之前驶过A地，车 速应满足什么条件？
一般地，一个含有未知数的不等式的 所有的解，组成这个不等式的 解集.求不等式的 解集 的过程叫做解不等式.
典例精析
4.不等式的解集的表示方法 第一种:用式子(如x>3),即用最简形式的不等式(如x>a或x<a)来表示.
第二种:利用数轴表示不等式的解集.
人教版七年级下册课件9.1.1 不等式及其解集(共18张PPT)
在这个式子中 你发现了什么？
1.当x=80时，23 x ＞ 5 0 ； 2.当x=78时，2 x ＞ 5 0 ；
3
3.当x=75时，2 x = 5 0 ；
3
4.当x=72时，2 x ＜ 5 0 .
3
也就是说当x取某些值（如80，78）时不 等 72式）时23 ，x ＞ 不5 0 等成式立，23 当x ＞ x5取0 不某成些立值. （如75，
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/8/122021/8/122021/8/122021/8/128/12/2021 14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年8月12日星期四2021/8/122021/8/122021/8/12 15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年8月2021/8/122021/8/122021/8/128/12/2021 16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/8/122021/8/12August 12, 2021 17、儿童是中心，教育的措施便围绕他们而组织起来。2021/8/122021/8/122021/8/122021/8/12
2 3
x＞
50
总成立；而当x＜75
x ＞ 5 0 不成立.
3
任任何 何一一个 个大小于于或75等的于数都75是的不数等都式不是23 x不＞ 等5 0 的式解2 x，＞ 5 0
的解.因此x＞75表示了能使不等式
2
x＞
50
3
成立
的x的取值范围.
1.当x=80时，23 x ＞ 5 0 ； 2.当x=78时，2 x ＞ 5 0 ；
3
3.当x=75时，2 x = 5 0 ；
3
4.当x=72时，2 x ＜ 5 0 .
3
也就是说当x取某些值（如80，78）时不 等 72式）时23 ，x ＞ 不5 0 等成式立，23 当x ＞ x5取0 不某成些立值. （如75，
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/8/122021/8/122021/8/122021/8/128/12/2021 14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年8月12日星期四2021/8/122021/8/122021/8/12 15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年8月2021/8/122021/8/122021/8/128/12/2021 16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/8/122021/8/12August 12, 2021 17、儿童是中心，教育的措施便围绕他们而组织起来。2021/8/122021/8/122021/8/122021/8/12
2 3
x＞
50
总成立；而当x＜75
x ＞ 5 0 不成立.
3
任任何 何一一个 个大小于于或75等的于数都75是的不数等都式不是23 x不＞ 等5 0 的式解2 x，＞ 5 0
的解.因此x＞75表示了能使不等式
2
x＞
50
3
成立
的x的取值范围.
人教版数学七年级下9.1.1不等式课件(22张PPT)
30＜55 ① 30+55＞75 ②
问题2．你能用数学式子表示下面数量之间的关系吗？
（1）一辆轿车在公路上正常行驶的速度是a km/h,已知 公路对轿车的限速（不超过）是100 km/h,那么你如何 表示a与100的大小关系？ a≤100 ③
（2）某种袋装牛奶中，每100g牛奶含xg蛋白质、yg脂
（1）a 是负数； （2）a 与5的和小于-7； （3）a 的一半大于3.
ห้องสมุดไป่ตู้
例2 按题意列不等式： (1)一个数m的绝对值不小于0；
(2)两数m、n积的2倍不大于这两数的平方和。
（1）如何表示下面气温之间的关系？某城市某天的 最低气温是-2℃,最高气温是6℃,该市这天某一时刻的 气温是t℃.
（2）建设中的三峡水电站的水库水位在145m-175m （包括145m，175m）时，发电机能正常工作，设 水库水位为x（m）．你能用关于x的一个式子刻画水 位需满足的高度要求吗？
3
从路程上看，汽车要在12：00之前驶过A地，
则以这个速度行驶 2 h 的路程要超过50 km．
3
① 30＜55 ② 30+55＞75 ③a≤100 ⑤y≥3.1
⑥100-x-y≥8.1 ⑦ 50 2 ⑧ 2 x 50
x3
3
像上面这样用符号“＜”、“≤”、“＞”、“≥” 表示大小关系的式子叫做不等式。
1、下列说法中，是不等关系的是（ ） A、老师的年龄是你的年龄的2倍 B、小军与小海一样高 C、小明岁数比爸爸岁数小26岁 D、x2是非负数
2、小林在水果摊上称了两斤苹果，摊主称了几 个苹果说：“你看秤，高高的。”如果设苹果 的实际质量为x斤，用不等式把这个“高高的” 的意思表示出来是（ ）
9.1不等式教学课件 (1)
a＋b＞c, b＋c＞a, c＋a＞b.
由式子a＋b＞c 移项可得 a＞c－b, b＞c－a . 类似地，由式子b+c＞a及c+a＞b移项可得 c＞a-b, b＞a-c 及 c＞b-a, a＞b-c
三角形中任意两边之差小于第三边
小结
本节课你的收获是什么？
※利用不等式的性质解不等式 ※不等式性质的运用
x ×4≥100．
0.8
解得： x≥20
答：导火索的长度应大于20 cm．
例1 某长方体形状的容器长5cm，宽3cm， 高10cm。容器内原有水的高度为3cm，
现准备向它继续注。用V(单位：cm3 ）
表示新注入水的体积，写出V的取值范围。 解：新注入水的体积V与原有水的体积的和不能 超过容器的容积，即
V+3×7×3≤3×5×10 解得 V≤105 又由于新注入水的体积不能是负数，因此， V的取值范围是 V≥10并且V≤105 在数轴上表示V的取值范围如图
0
105
从中你得到什么规律？
例2 三角形中任意两边之差
与第三边有怎样的大小关系？ a
b
解：如图，设a,b,c为任意一个三角
形的三条边的长，则
c
-5.
x 2.如果 y >0, 那么xy
&b
-1-b.
3 >1
45..-0.789＜x -01.3,两,两边边都都乘除以 (-870.3，),得得___x_________87_..
用炸药爆破时，如果导火索燃烧的 速度是0.8 cm/s，人跑开的速度是每秒4 m，为了使点导火索的战士在爆破时能 够跑到100 m以外的安全区域，这个导 火索的长度应大于多少厘米？ 解：设导火索的长度是x cm ．根据题意，得
人教版数学七年级下册 9.1.1不等式及其解集课件 (共15张PPT)
1.使不等式成立的未知数的值叫做不等式的解. 例3、 当x取下列数值时，哪些是不等式 x＋3＞6解，哪些不是？ －2.5 0 1 3
不等式的解
3.5 不是 4 不是 4.5 不是 7 不是
有多少个？
是
是
是
是
知识要点
2.一般地，一个含有未知数的不等式的所有的解，组成
这个不等式的解集.
3.不等式的解是不等式解集中的一个元素，而不等式的
-1，-2，-3 ； （2）写出不等式x≥-3的所有负整数解：______________
0，1，2，3 （3）写出不等式x≤3的所有非负整数解：______________； -1 （4）写出不等式x＞-2的最小整数解：_________________.
课堂小测验 5.将下列不等式的解集在数轴上表示出来： （1）a是正数；（2）b是非负数；（3）-1＜x≤4．
第九章 不等式与不等式组
9.1.1 不等式及其解集
新课导入
1、什么是等式？
2、现阶段我们学过哪些等式？ 3、从字面意思你怎么理解“ 不等式 ”？
知识要点
知识点1：不等式的概念.
用符号“＞”或“＜”号表示大小关系的式子，是不等式 常见的不等号：“＞”、“＜”、“≥”、“≤”、“≠”. 【例1】给出下列表达式：①a（b+c）=ab+ac；②-2＜0； ③x≠5；④2a＞b+1；⑤x2-2xy+y2；⑥2x-3＞6，其中不
知识类比 思考：1、什么是一元一次方程的解？ 那你能类比 使一元一次方程等号两边相等的未知数的值 得出不等式 1.感知生活中的不等式关系，了解不等式的意义，初步体会 如 X-2=1 的解为X=3 解的定义？ 不等式是研究量与量之间关系的重要模型之一。
人教版七年级数学下册全册9.1《不等式》PPT课件
三 利用不等式的性质解简单的不等式
例4 利用不等式的性质解下列不等式：
第二种:用数轴,一般标出数轴上某一区间,其中的 点对应的数值都是不等式的解. 用数轴表示不等式的解集的步骤: 第一步:画数轴; 第二步:定界点; 第三步:定方向.
画一画: 利用数轴来表示下列不等式的解集.
空心圆圈表 (1)x＞-1 ；
示不含此点
(2)
x＜
1 2
.
表示
1 2
的点
-1 0
表示-1的点
方向向右
观察由上述问题得到的关系式：x＞1 ， x＜100， x>50，s>60x，s<100x ，它们有什么共同的特点？
左右不相等
总结归纳 一般地，用不等号“>”，“<”连接而成的式
子叫做不等式.像a≠2这样的式子也叫做不等式.
练一练 判断下列式子是不是不等式： （1）-3>0; （2）4x+3y<0；
则都点点大表因不A于示此等右2的可式，边数以的而所都像解点有小图集A的于左那x点>2边样2表. 所表示有示的的数 先在数轴上标出表示2的点A
把表示2 的点Ａ
画成空心圆圈，表 示解集不包括2.
A -1 0 1 2 3 4 5 6
解集的表示方法： 第一种:用式子(如x>2),即用最简形式的不等式 (如x>a或x<a)来表示.
不等式性质1：不等式两边加（或减）同一个数（或 式子），不等号的方向不变.
如果a>b,那么a+c>b+c，a－c>b－c.
典例精析 例1 用“>”或“<”填空： （1）已知 a>b，则a+3 > b+3 解： 因为 a>b，两边都加上3，
人教版七年级下册数学第九章：9.1 不等式课件课件
4、在－3＞－4 的两边都乘以7可得
。
5、在－－281＜＞0－的2两8 边都除以8 可得 －1＜0 。
仿照下表，分组探讨
不等式的两边
不等式
都乘以（或除
以）同一个负
数
7 ＞ 4 乘以－5
结果
与原不等式 比较不等号 的方向是否 改变了
－35＜－20 改变了
－8＜4
…
除以－4
…
2 ＞－1
…
改变了
…
由上面的探讨我们可以继续得出： 不等式的基本性质 3：
解：∵ 5 ＞ 3
∴ 5a 3a
这种解法对吗？如果正确，说出它根据 的是不等式的哪一条基本性质；如果不正确， 请就明理由。
答：这种解法不正确，因为字母 的取值范
围我们并不知道。如果
，那么
；
如果
，那么
。
例 根据不等式的基本性质，把下列不等式
化成 x＜ 或 x＞ 的形式：
（1） x －2＜ 3
（2） 6 x ＜ 5 x －1
（3） 3 x 2 + 2 x
√ （4） x＜ 2 x +1
（5） x ＝2 x －5
√ （6） x 2+4 x ＜ 3 x +1 √ （7） a + b ≠ c
2（（（（、1357用 ） ） ） ）“4－ 77+＞×＞833＜＞－”＞6或4－4+ד33 3＜”（（（（填6248空））））：－7－7+×1(4－.＜(5－3＜)30＞)＜－44+4×(－(－3) 3)
4、9在＜不1等2 式
的两边都乘以－1可得
ab
如果 a b ，那么：
① a 3 ＞ b 3（不等式的性质 1 ） ② 2a ＞ 2b （不等式的性质 2 ）
人教版七年级数学下册第九章《 9.1不等式及其解集》优质课课件(共17张PPT)
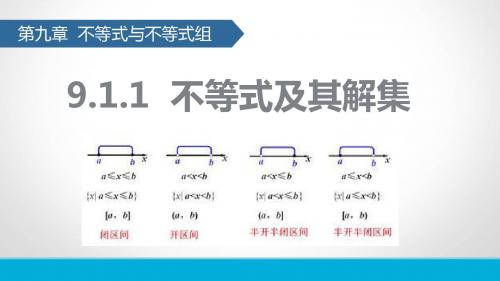
根据以下图形，写出不等式的解集：
(1)
( x≤4 )
(2)
( x>2 )
(3)
( x≥-2 )
育才初一数学备课组
⒈你能求出适合不等式－1≤x＜4的整数 解吗？其中的x的最大整数值是多少呢？
－2－1 0 1 2 3 4 5 6
答：整数解为－1、0、1、2、3， 其中x的最大整数值为3.
育才初一数学备课组
不等式解集的表示方法
第一种:用式子(如x>2),即用最简形式的不等式(如 x>a或x<a)来表示. 第二种:用数轴,标出数轴上某一区间,其中的点对 应的数值都是不等式的解.
例题：直接想出不等式的解集:
⑴ x+2>6 ⑵ 3x>9 ⑶ x－3>0
解: ⑴ x>4 ; ⑵ x>3 ; ⑶ x>3.
例题： 用数轴表示下列不等式的解集:
第九章 不等式与不等式组
9.1.1不等式及其解集
9.1.1不等式及其解集
问题：一辆匀速行驶的汽车在11：20距离 A地50千米，要在12：00之前驶过A地， 车速应满足什么条件？
A
汽车
分析：设车速是x千米/时
从时间上看，汽车要在12：00之前驶过A地，则以 这个速度行驶50千米所用的时间不到2/3小时，即
如：
76， 79，80，75.1，90 不等式 2 x 50 的解 。
这个不等式的解有无数个。
3
三.不等式的解集
一个含有未知数的不等式的所有解组成 这个不等式的解集. 注意:不等式的解和不等式的解集是一样的吗?
练习:下列说法正确的是( A ) A. x=3是2x>1的解 B. x=3是2x>1的唯一解 C. x=3不是2x>1的解 D. x=3是2x>1的解集 求不等式的解集的过程叫解不等式.
人教版七年级数学下册全册9.1《不等式》PPT课件
导入新课
情境引入 摩拜单车在2017年3月推出了红包车的运动.用
户扫码解锁后有效骑行红包车超过10分钟，锁车后 即可获得1个现金红包；骑行红包车次数及领取红包 次数不限.红包金额随机，高于1元，且低于100元. 你能用关系式表示可获红包金额的大小吗？
x＞1 且 x＜100
讲授新课
一 不等式的概念
合作与交流
如图所示，托盘天平的右盘放上一质量为bg的
立体木块，左盘放上一质量为ag的立体木块，天平
向左倾斜.
用不等号填一填：
ቤተ መጻሕፍቲ ባይዱ1.a
2.2a 3.2a
2
> b;
> 2b;
>
2b .
2
ag
bg
ag
你发现了什么？
bg
总结归纳
不等式基本性质2 不等式的两边都乘（或除 以）同一个正数，不等号的方向不变.
即，如果a
根据路程与速度、时 间之间的关系可得：
s>60x，且s<100x.
观察由上述问题得到的关系式：x＞1 ， x＜100， x>50，s>60x，s<100x ，它们有什么共同的特点？
左右不相等
总结归纳 一般地，用不等号“>”，“<”连接而成的式
子叫做不等式.像a≠2这样的式子也叫做不等式.
练一练 判断下列式子是不是不等式： （1）-3>0; （2）4x+3y<0；
实用的方法.
练一练 判断下列数中哪些是不等式 2 x > 50 的解：60，73，
3
74.9，75.1，76，79，80，90.你还能找出这个不等式
的其他解吗？这个不等式有多少个解？ 无数个
七年级数学下册《9.1.1_不等式及其解集》课件_新人教版(1)
不等式定义与表示方法
不等式定义
用不等号连接两个解析式而成的 数学式子，称为不等式。
不等式的表示方法
不等式可以用符号“<”、“>” 、“≤”、“≥”表示，分别代表 “小于”、“大于”、“小于等 于”、“大于等于”。
不等式基本性质
传递性
可加性
若a>b且b>c，则a>c； 若a<b且b<c，则a<c。
确定分子和分母
找出分式不等式中的分子和分 母。
交叉相乘
根据不等式的性质，将分式不 等式转化为整式不等式。
判断分母的正负
确定分母在给定区间内的正负 性。
求解整式不等式
利用整式不等式的解法，求解 得到解集。
分数与分式混合不等式解法
1 2
分别处理分数和分式部分
将混合不等式中的分数部分和分式部分分开处理 。
求解不等式。
解法步骤
首先确定参数的取值范围，然后根 据参数的取值分别求解不等式，最 后对解集进行合并和讨论。
示例解析
通过具体示例，展示含参数一元一 次不等式的解法步骤和思路。
含参数二元一次不等式组解法
解法概述
含参数的二元一次不等式组解法 同样需要对参数进行讨论和分类 ，通过消元或代入等方法求解不
等式组。
PART 04
分数与分式不等式解法
REPORTING
分数不等式转化为整式不等式方法
01
02
03
04
找出分母
确定分数不等式中分母的表达 式。
确定分母的正负
判断分母在给定区间内的正负 性。
交叉相乘
根据不等式的性质，将分数不 等式转化为整式不等式。
求解整式不等式
人教版七年级数学下册9.1.1不等式(1)ppt精品课件
9.1 ห้องสมุดไป่ตู้等式 （第1课时）
课件说明
学习目标： 了解不等式概念，理解不等式的解和解集.
学习重点： 不等式及解集概念的理解.
2．探索新知
问题1 一辆匀速行驶的汽 车在11：20距离A地50 km， 要在12：00之前驶过A地. 你能用式子表示出车速应 满足的条件吗？
2．探索新知
（1）汽车在12:00之前驶过A地的意思是什么？
9.1.1 不等式及其解集
不等式的解集的表示方法主要有两种：一是用式子(如 ＞2),即用最简形式的不等式(如x＞a或x＜a)来表示；另 一种是用数轴，标出数轴上某一区间，其中的点对应的 数值都是不等式的解。对于一元一次不等式的解集一般 来说有以下四种情况：
9.1.1 不等式及其解集
如图所示,x＞a
当x＝80时， 当x＝75时，
2 3
x
；50
2 3
x
； 5 0
当x＝78时， 当x＝80时，
2 3
x
； 50
2 3
x ．
50
2．探索新知
（4）不等式
2 x 还 有5其0 他解吗？如果有，
3
这些解应满足什么条件？
满足 x75
第一步: 画数轴 第二步: 定界点 第三步; 定方向
“＞” “＜”是空心； “≥” “≤”是实心 “＞” “≥”向右画； “＜” “≤” 向左画
1、下列式子中哪些是不等式？
① a+b=b+a
④x+3＞6 ⑦ 2 x 50
3
② -3＞-5 ③ x≠1 ⑤ 2m≤n ⑥ 2x-3 ⑧ y +3≥3
解：（2）、（3）、（4）、（5）、⑺、⑻是不等 式
课件说明
学习目标： 了解不等式概念，理解不等式的解和解集.
学习重点： 不等式及解集概念的理解.
2．探索新知
问题1 一辆匀速行驶的汽 车在11：20距离A地50 km， 要在12：00之前驶过A地. 你能用式子表示出车速应 满足的条件吗？
2．探索新知
（1）汽车在12:00之前驶过A地的意思是什么？
9.1.1 不等式及其解集
不等式的解集的表示方法主要有两种：一是用式子(如 ＞2),即用最简形式的不等式(如x＞a或x＜a)来表示；另 一种是用数轴，标出数轴上某一区间，其中的点对应的 数值都是不等式的解。对于一元一次不等式的解集一般 来说有以下四种情况：
9.1.1 不等式及其解集
如图所示,x＞a
当x＝80时， 当x＝75时，
2 3
x
；50
2 3
x
； 5 0
当x＝78时， 当x＝80时，
2 3
x
； 50
2 3
x ．
50
2．探索新知
（4）不等式
2 x 还 有5其0 他解吗？如果有，
3
这些解应满足什么条件？
满足 x75
第一步: 画数轴 第二步: 定界点 第三步; 定方向
“＞” “＜”是空心； “≥” “≤”是实心 “＞” “≥”向右画； “＜” “≤” 向左画
1、下列式子中哪些是不等式？
① a+b=b+a
④x+3＞6 ⑦ 2 x 50
3
② -3＞-5 ③ x≠1 ⑤ 2m≤n ⑥ 2x-3 ⑧ y +3≥3
解：（2）、（3）、（4）、（5）、⑺、⑻是不等 式
人教版数学七下《9.1 不等式》ppt(第1课时)课件
75 km/h呢？72 km/h呢？
出车速应的取值吗？
当x＝80时，32 x
50
；
2 当x＝78时，3
x
50
；
当x＝75时，23
x
50
；
当x＝80时，2 3
x
50．
2．探索新知 （2）类比方程的解，什么叫不等式的解？
使不等式成立的未知数的值.
2．探索新知
（3）不等式 2 x 50 还有其他解吗？如果有， 3
2
3．运用新知
例2 直接说出不等式的解集，并在数轴上表 示出来.
（1） x 3 6 ； （2） x 2 0 .
3．运用新知
（1） x 3 ；
0
3
（2） x 2 .
-2 0
4．归纳总结
（1）什么叫不等式？ （2）什么叫不等式的解？不等式的解和方程的 解的区别？ （3）什么叫不等式的解集？不等式的解和不等 式的解集的区别？
5．布置作业 教科书 习题9.1 第1、2 50
3
问题1 一辆匀速行 驶的汽车在11:20距 离A地50 km，要在 12：00之前驶过A地.
你能用式子表示出车 速应满足的条件吗？
2．探索新知
问题2 一辆匀速行驶
的汽车在11:20距离A
（1）对于不等式 而言，车速 地50 km，要在12：00
可以是80 km/h吗？78 km/h呢？ 之前驶过A地．你能求
9.1 不等式 （第1课时）
课件说明
本课由实际问题中的不等关系引出 不等式的概念；类比方程的解，明确不 等式解和解集的概念，以及不等式解集 的两种表示方法.
课件说明
学习目标： 了解不等式概念，理解不等式的解和解集.
9.1 不等式课件(3份打包)1
希家距学校有2千米，而他的步行速度为每小时10千米.那
么，小希上午几点从家里出发才能保证提前到学校？ （2）你会解这个不等式吗？请说说解的过程.
1 根据“不等式性质1”,在不等式的两边减去 , 5 4 1 1 1 得：x <8 ， 即 x＜7 . 5 5 5 5
二、探究新知
小希就读的学校上午第一节课上课时间是8时开始.小
同的倍数，天平会平衡吗？缩小相同的倍数呢？
二、探究新知
(一)探究不等式的性质
1.用“＞”或“＜”填空.
（1）5＞3，5+2 ＞ 3+2， 5-2 ＞ 3-2；
（2）-1＜3，-1+2 ＜ 3+2，-1-3 ＜ 3-3； ＞
（3 ） 6 ＞2 ，6 × 5
2×5，6×(-5)
＜ 2×(-5)；
（4）-2＜3，(-2)×6 ＜ 3×6，(-2)×(-6) ＞ 3×(-6)； ＞ (-6)÷2；
2.用不等式表示下列语句并写出解集，并在数轴上表
示解集：
1 （3）y与1的差不大于0； （4）y的 小于或等于-2. 4 1 （3）y-1≤0； y≤1 ； （4） y≤-2； y≤-8. 4
0 1 -8 0
四、小结与作业 小结：这节课你学会了什么？ 通过学习，我们学会了简单的不等式的解 法，还明白了生活中的许多实际问题都是可以 用不等式的知识去解决的.
二、探究新知
例题
解下列不等式，并在数轴上表示解集：
（1）x-7＞26；（2）3x＜2x+1；
2 （3） x>50 ； （4）-4x＞3. 3
二、探究新知 例题
解下列不等式，并在数轴上表示解集：
（1）x-7＞26；（2）3x＜2x+1； （1）x＞33