高考数学思维导图
合集下载
高中数学知识框架思维导图(整理版)

基本初等函数 指数函数、对数函数、幂函数、三角函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用 分段探究,整体考察 复合函数的单调性:同增异减 赋值法、典型的函数模型 零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换:������ = ������(������) → ������ = ������(������ ± ������),������ = ������(������) → ������ = ������(������) ± ������,������, ������ > 0 函数图象 及其变换 对称变换:������ = ������(������) → ������ = −������(������),������ = ������(������) → ������ = ������(−������),������ = ������(������) → ������ = −������(−������) 翻折变换:������ = ������(������) → ������ = |������(������)|,������ = ������(������) → ������ = ������(|������|) 伸缩变换:������ = ������(������) → ������ = ������������(������),������ = ������(������) → ������ = ������(������������)
������
第二部分
角的概念
三角函数与平面向量
弧长公式������ = ������������、扇形面积公式������ = ������������
2 1 π 2
三角函数-高考数学复习思维导图(人教版)
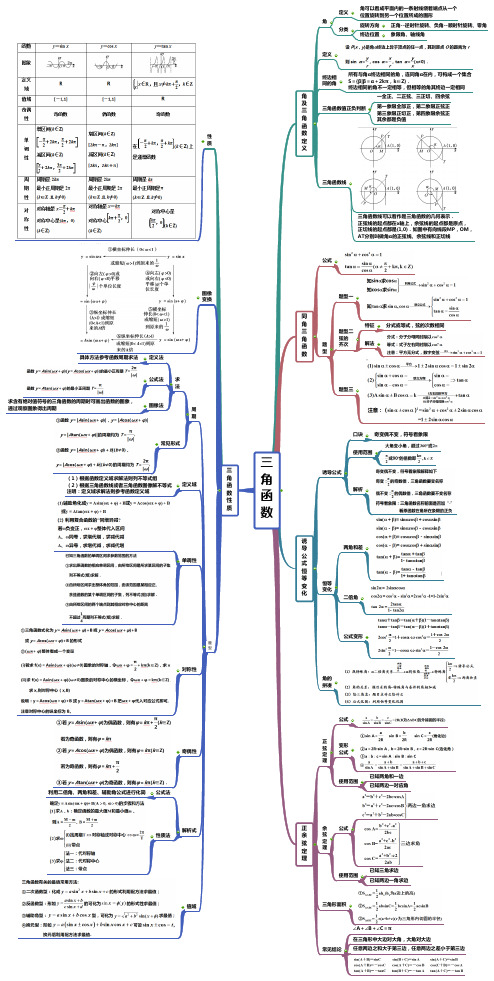
所有与角α终边相同的角,连同角α在内,可构成一个集合特征
解法
分式或等式,弦的次数相同
奇变偶不变,符号看象限
求含有绝对值符号的三角函数的周期时可画出函数的图象,通过观察图象得出周期
(1)根据函数定义域求解法则列不等式组
(2)根据三角函数线或者三角函数图像解不等式公式法
利用二倍角、两角和差、辅助角公式进行化简
已知两角和一边已知两边一对应角
已知三角求边已知两边一角求边
A +∠
B +∠
C =π
在三角形中大边对大角,大角对大边。
(1)集合与常用逻辑用语——高考数学一轮复习思维导图
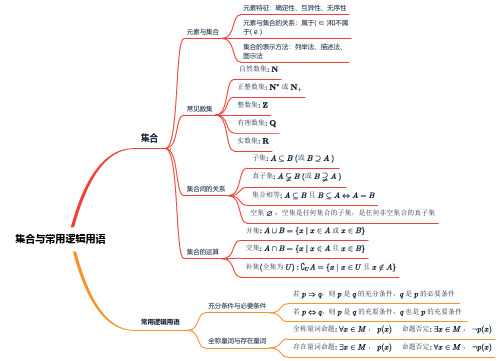
元素特征:确定性、互异性、无序性 元素与集合的关系:属于(∈)和不属 元素与集合 于(∈) 集合的表示方法:列举法、描述法、 图示法 自然数集:N 正整数集:N*或N+ 常见数集 整数集:Z 有 集合间的关系 集合相等:ACB且BCA台A=B 空集:空集是任何集合的子集,是任何非空集合的真子集 并集:A∪B={x|x∈A或x∈B} 集合与常用逻辑用语 集合的运算 交集:A∩B={x|x∈A且x∈B} 补集(全集为U):CUA={x|x∈U且x∈A} 若p→q,则p是q的充分条件,q是p的必要条件 充分条件与必要条件 若p台q,则p是q的充要条件,q也是p的充要条件 常用逻辑用语 全称量词命题:Vx∈M,p(x)命题否定:3x∈M,-p(x) 全称量词与存在量词 存在量词命题:3x∈M,p(x)命题否定:Vx∈M,-p(x)
高中数学思维导图知识图谱(全高清版)
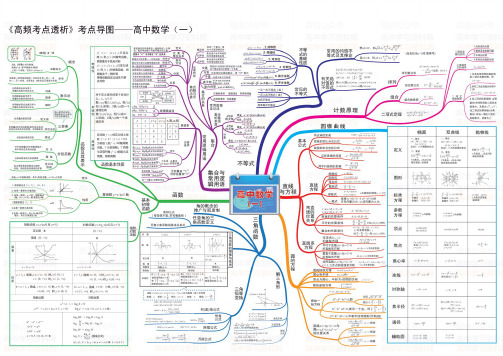
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
高中学科思维导图
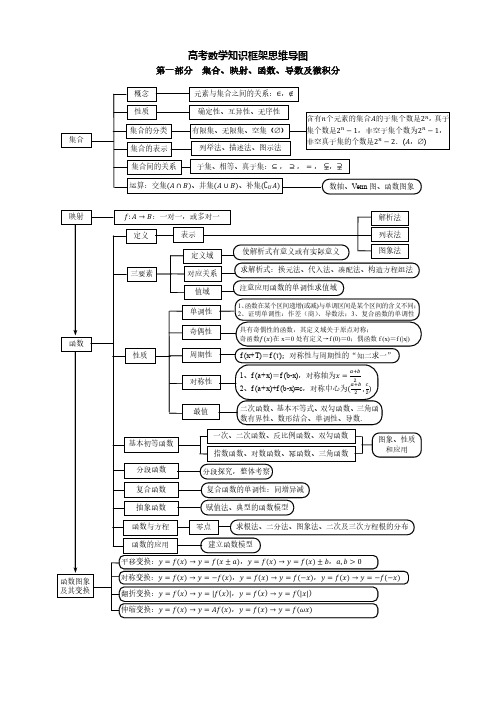
高中数学知识框架思维导图(整理版)
2 : 2 + 2 + 2 = 0.
点斜式:y-y0=k(x-x0)
注意:截距可正、
可负,也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式: + =1
a b
两直线的交点
距离
一般式:Ax+By+C=0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 .
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
与 的关系
1 ,
= 1,
= {
− −1 , ≥ 2.
构造等差数列
an+1 p an
= · +1 转为③
qn q qn-1
⑤an + 1=pan+qn
点斜式:y-y0=k(x-x0)
注意:截距可正、
可负,也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式: + =1
a b
两直线的交点
距离
一般式:Ax+By+C=0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 .
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
与 的关系
1 ,
= 1,
= {
− −1 , ≥ 2.
构造等差数列
an+1 p an
= · +1 转为③
qn q qn-1
⑤an + 1=pan+qn
2020年高考数学复习思维导图(人教版)02——函数
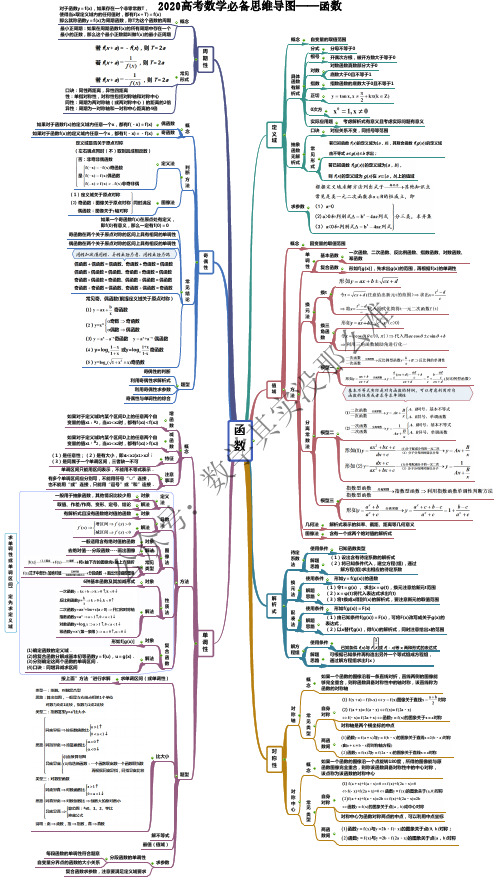
基本不等式实际是对勾函数的特例,可以考虑利用对勾实际应用题考虑解析式有意义且考虑实际问题有意义
解析式表示的斜率、截距、距离等几何意义一般适用含有绝对值的函数
6种基本函数及其加减形式
形如f[g(x)]
确定函数的定义域.
将复合函数分解成基本初等函数y =f(u),u =g(x).分别确定这两个函数的单调区间.如果一个函数的图像沿一个点旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,对称轴是两个横坐标的中点
对称中心为函数对称两点的中点,可以利用中点坐标
如果一个奇函数f(x)在原点处有定义,即f(0)有意义,那么一定有奇偶性的判断利用奇偶性求解析式公
众
么
难。
极坐标与参数专题 高考数学复习思维导图
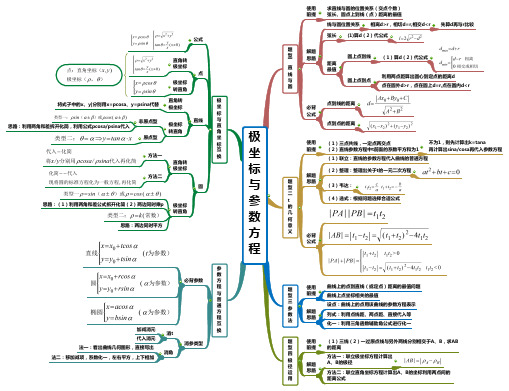
三
参 数 法
解题 思路
设点:曲线上的点用该曲线的参数方程表示 列式:利用点线距、两点距、直接代入等 化一:利用三角函数辅助角公式进行化一
题
使用 (1)三线(2)一过原点线与另外两线分别相交于A、B,求AB
型
前提 的距离
四 极 径
解题
方法一:联立极坐标方程计算出 A、B的极径
运
思路
方法二:联立直角坐标方程计算出A、B的坐标利用两点间的
不为1,则先计算出k=tana 再计算出sina/cosa再代入参数方程
(1)联立:直线的参数方程代入曲线的普通方程
解题
(2)整理:整理出关于t的一元二次方程
题
思路
型
(3)韦达:
二
t
(4)选式:根据问题选择合适公式
的
几
何
意
义 必背
公式
题
使用
曲线上的点到直线(或定点)距离的最值问题
型
前提
曲线上点坐标相关的最值
极坐标 转直角
思路:两边同时平方
参
数
必背参数
方
程
与
普
通
方
程
互
加减消元 消t
换
代入消元
消参类型
法一:看出曲线几何图形,直接写出
消角法二:移加减项,系Fra bibliotek化一,左右平方,上下相加
极 坐 标 与 参 数 方 程
使用 前提
求直线与圆的位置关系(交点个数) 弦长、圆点上到线(点)距离的最值 线与圆位置关系 相离d>r,相切d=r,相交d<r
弦长 (1)算d(2)代公式
先算d再与r比较
题
解题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等比数列
an≠0,q≠0
解析法:an=f (n) 图象法
数列是特殊的函数
列表法
等差数列与等比数列的类比
通项公式 求和公式
性质 判断
an=a1+(n-1)d an+am=ap+ar
前 n 项和 n(a1+an)
Sn= 2
an=a1qn-1 anam=apar
前 n 项积(an>0) Tn= (a1an)n
两点分布
X~B(1,p) E(X)=p,D(X)=p(1-p)
常用的分布及 随机变量
期望、方差
二项分布
X~B(n,p) E(X)=np,D(X)=np(1-p)
若 Y=aX+b,则
E(Y)=aE(X)+b D(Y)=a2D(X)
超几何分布
X~H(N,M,n)
M E(X)=n N
( ) nM M N-n
概率的基本性质
互斥事件
对立事件
P(A)=1-P(A)
古典概型
P(A+B)=P(A)+P(B)
几何概型 用随机模拟法求概率 条件概率 事件的独立性
P(A B) P(B | A)= P(A)
P(A B)=P(A)·P(B)
n 次独立重复试验恰好
发生 k 次的概率为
k
Pn(k)=Cn
pk(1-p)n-k
截距的 b 倍.
z= (x-a)2+(y-b)2:构造距离
基本不等式:
a+b ab≤ 2
最值问题 变形
和定值,积最大;积定值,和最小 应用时注意:一正二定三相等
2ab
a+b
a2+b2
≤ a+b
ab≤
2
≤
2
3
直线的方程
圆的方程 圆锥曲线 对称性问题
第四部分 解析几何
倾斜角和斜率
倾斜角的变化与斜率的变化
m
m
m-1
Cn+1=Cn+C n
二项式系数性质
首末两端“等距离”两项的二项式系数相等
C0n+C1n+…+Cnn=2n
C0n+C2n+C4n…=C1n+C3n+C5n…=2n-1
推理
合情推理
归纳 类比
猜想
演绎推理 三段论
大前提、小前提、结论
证明
直接证明 间接证明
综合法 分析法 反证法
由因导果 执果索因
k 称中心为( 2 ,0)(k∈Z).
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
②图象也可以用五点作图法;③用整体代换求单调区间(注意的符号);
2
(2k+1)-2
k-
④最小正周期
T= |
;⑤对称轴 |
x=
2
,对称中心为( ,b)(k∈Z).
平面向量 解三角形
概念 线性运算 基本定理 坐标表示 数量积
一次、二次函数、反比例函数
翻折变换 伸缩变换
幂函数 指数函数 对数函数
图象、性质 和应用
三角函数
复合函数
复合函数的单调性:同增异减
抽象函数
赋值法、典型的函数
函数与方程
零点
二分法、图象法、二次及三次方程根的分布
函数的应用
建立函数模型
导数
导数的概念
几何意义、物理意义
基本初等函数的导数
三次函数的性质、图象与应用
| a |·| b |
→a ∥→b →b =→a x1y2-x2y1=0
→a ⊥→b →b ·→a =0 x1x2+y1y2=0
11
a+b+c
S△=2ah=2absinC= p(p-a)(p-b)(p-c)(其中 p= 2 )
2
数列 不等式
第三部分 数列与不等式
概念
表示
通项公式 递推公式
等差数列
正切函数 y=tan x
y=Asin(x+)+b
弧长公式、扇形面积公式 三角函数线
公式的变形、逆用、“1”的替换
化简、求值、证明(恒等变形)
定义域 奇偶性 单调性 周期性 对称性
最值
值域
图象
对称轴(正切函数除外) 经过函数图象的最高(或 低)点且垂直 x 轴的直线, 对称中心是正余弦函数图 象的零点,正切函数的对
命题
数学归纳法 关系
原命题:若 p 则 q
互否
否命题:若p 则q
互逆 互为逆否 等价关系
互逆
逆命题:若 q 则 p
互否
逆命题:若q 则p
条件
复合命题
全称量词与 存在量词
或:p q 且:p q 非: p
充分非必要条件、必要非充分条件、充要条件 一真便真 一假则假
算法的特征
概括性、逻辑性、有穷性、不唯一性、普遍性 顺序结构
导数的运算法则 导数的应用
单调性 极值
导数的正负与单调性的关系
最值
生活中的优化问题
定积分与微积分
定积分与图形的计算
1
第二部分 三角函数与平面向量
三角函数
三角函数 的图象
角的概念
弧度制
任意角的三角函数的定义
同角三角函数的关系
诱导公式 和角、差角公式
二倍角公式
正弦函数 y=sin x =
余弦函数 y=cos x
1、函数在某个区间递增(或减)与单调区间是某个区间的含义不同; 2、证明单调性:作差(商)、导数法;3、复合函数的单调性
奇偶性
定义域关于原点对称,在 x=0 处有定义的奇函数→f (0)=0
周期性 对称性 最值
平移变换 对称变换
T
周期为 T 的奇函数→f (T)=f (2)=f (0)=0 二次函数、基本不等式、打钩(耐克)函 数、三角函数有界性、数形结合、导数.
用样本估计总体
样本频率分布 估计总体
样本数字特征 估计总体
变量间的相关关系 正态分布
两个变量的 线性相关
抽签法 随机数表法
共同特点:抽样 过程中每个个体 被抽到的可能性 (概率)相等
频率分布表和频率分布直方图 总体密度曲线
茎叶图 众数、中位数、平均数 方差、标准差
散点图
回归直线
列联表(2×2)独立性分析
程序框图
条件结构
基本算法语言
循环结构
算法案例
辗转相除法、更相减损术、秦九韶算法、进位制
概念
虚数、纯虚数、实部、虚部、实轴、虚轴、模、共轭复数
运算
加、减、乘、除、乘方
几何意义
复数与复平面内点(向量)的对应关系、复数模的几何意义
7
线与面 面与面
棱柱 正棱柱、长方体、正方体 圆柱 棱台 圆台 棱锥 三棱锥、四面体、正四面体 圆锥
三视图 直观图
长对正 高平齐 宽相等
侧面积、表面积
体积
点在直线上 点在直线外 点在面内 点在面外 共面直线 异面直线
直线在平面外 直线在平面内 平行 相交
相交 平行
平行 相交
只有一个公共点 没有公共点 没有公共点
共线与垂直
正弦定理 余弦定理
面积 实际应用
模 加、减、数乘 几何意义
|→a |= (x2-x1)2+(y2-y1)2
几何意义 投影 夹角公式 共线(平行)
垂直 解的个数的讨论
→→
→b 在→a 方向上的投影为|→b |cos=— a · →— b
|a|
→→
设→a 与→b 夹角,则 cos=— →a ·— →b
D(X)= N 1-N N-1
6
计算原理 二项式定理 推理与证明
简易逻辑 算法语言 复数
第七部分 其他部分内容
两个原理 排列与组合 通项公式
分类加法计算原理和分步乘法计算原理
排列数:Amn =(n-n!m)! 组合数:Cmn=m!(nn-! m)!
Tr+1=Cnran-rbr
性质
m n-m
Cn=C n
有公共点
平行关系的 相互转化
线线 平行
线面 平行
面面 平行
空间直角坐标系
垂直关系的 相互转化
线线 垂直
线面 垂直
面面 垂直
空间的角 空间的距离
异面直线所成的角 直线与平面所成的角 二面角
点到面的距离 直线与平面的距离 平行平面之间的距离
范围:(0,90] 范围:[0,90] 范围:[0,180]
相互之间的转化
常见求和方法
不等式的性质 一元二次不等式 简单的线性规划
公式法:应用等差、等比数列的前 n 项和公式
倒序相加法
分组求和法
裂项求和法
错位相加法
借助二次函数的图象
三个二次的关系
可行域 目标函数 应用题
一次函数:z=ax+by
y-b z= :构造斜率
x-a
几何意义: z 是直线 ax+by -z=0 在 x 轴截 距的 a 倍,y 轴上
轴对称
轨迹方程的求法:直接法、定义法、相关点法
定义及标准方程
性质 离心率
范围、对称性、顶点、焦点、长轴(实轴)、 短轴(虚轴)、渐近线(双曲线)、准线(只 要求抛物线)
点(x1,y1) ─关─于─点─(a─,b─)对─称→点(2a-x1,2b-y1)
曲线 f (x,y) ─关─于─点─(a─,b─)对─称→曲线 f (2a-x,2b-y)
na1,q=1 Sn=a1(11--qqn),q≠1
常见递推类型及方法
①an+1-an=f (n) ②an + 1 =f (n) an ③an+1=pan+q
逐差累加法 逐商累积法
q 构造等比数列{an+p-1}
④pan+1an=an-an+1
构造等差数列
⑤an + 1=pan+qn
化为aqn+n 1=qp·qan-n 1+1 转为③
