公务员考试考行测数字推理通用技巧盘点
公务员行测中的数字推理与解题技巧

公务员行测中的数字推理与解题技巧数字推理是公务员行测中的重要内容之一,它需要考生运用逻辑思维和数学知识进行推理和解题。
本文将介绍一些数字推理的基本方法和解题技巧,帮助考生更好地应对公务员行测中的数字推理题。
一、数字推理的基本方法在解决数字推理题时,考生首先需要明确题目给出的数字序列或者关系,并找到其中的规律。
下面介绍几种常见的数字推理方法。
1. 数列推理数列推理题是公务员行测中常见的题型,它要求考生根据已知的数字序列,推断出接下来的数字。
解决这类题目的关键在于找到数列中数字的变化规律。
常见的数列规律有等差数列和等比数列。
其中,等差数列的每个数字之间的差值相等,等比数列的每个数字之间的比值相等。
通过观察数列中数字间的关系,找出变化规律,即可准确推测出下一个数字。
2. 数字关系推理数字关系推理题要求考生从一组数字中找出相互之间的关系,进而推断出缺失的数字。
解决这类题目需要考生具备较强的逻辑思维能力。
常见的数字关系有加减乘除、平方立方等运算关系;还有数字的奇偶、大小关系等。
考生需要仔细观察数字间的变化规律,找出其中的逻辑关系,才能正确推断出缺失的数字。
3. 数字排列与组合推理数字排列与组合推理题要求考生从一组数字排列或者组合中找出符合一定条件的数字。
解决这类题目需要考生熟练掌握排列组合的知识。
在排列与组合的题目中,数字的顺序、重复与否等都可能是解题的关键。
考生需要根据题目给出的条件,灵活运用排列组合的规则,准确地确定符合条件的数字。
二、数字推理解题技巧除了掌握数字推理的基本方法,考生还可以借助一些解题技巧,提高解决数字推理题的效率。
1. 注意整体和局部在解决数字推理题时,考生既要关注数字序列的整体规律,又要注意其中的局部规律。
有时候,数字序列的整体规律并不明显,但是通过观察数字间的局部规律,也可以推断出接下来的数字。
2. 多角度观察考生要习惯从不同的角度观察数字推理题。
有时候,单一的数学运算规律并不能完全解释题目中的数字关系,此时考生可以从逻辑思维、几何形状等其他角度出发,寻找隐藏的规律。
行测数字推理题技巧

行测数字推理题技巧
1.规律分析:首先看给出的数字序列是否存在其中一种规律,例如递增、递减、交替等。
通过观察规律,可以将下一个数字或者数字序列进行
推理。
2.数字运算:在数字推理题中,经常出现的是数字的运算关系。
可以
通过加减乘除等简单的运算符号,对给出的数字进行运算,从而得出新的
数字或者数字序列。
3.数字特征:观察给出的数字是否有一些特殊的特征,例如是否为质数、完全平方数、斐波那契数列等,可以通过这些特征进行逻辑推理。
4.数字拆分:有些数字推理题给出的数字较大,可以将其拆分成小的
数字,然后再进行运算或者找规律。
5.条件限制:有些数字推理题在给出的数字序列中存在一些限制条件,例如数字的位数、数字之间差距等。
可以通过这些限制条件进行推理。
6.平均数:在有些数字推理题中,给出的数字序列的平均数可能有特
殊的含义,通过计算平均数,可以得到下一个数字或者数字序列。
7.数字替换:有些数字推理题中,给出的数字序列中存在一些数字可
以进行替换,通过替换数字,可以发现其中一种规律。
公考数字推理攻略汇总
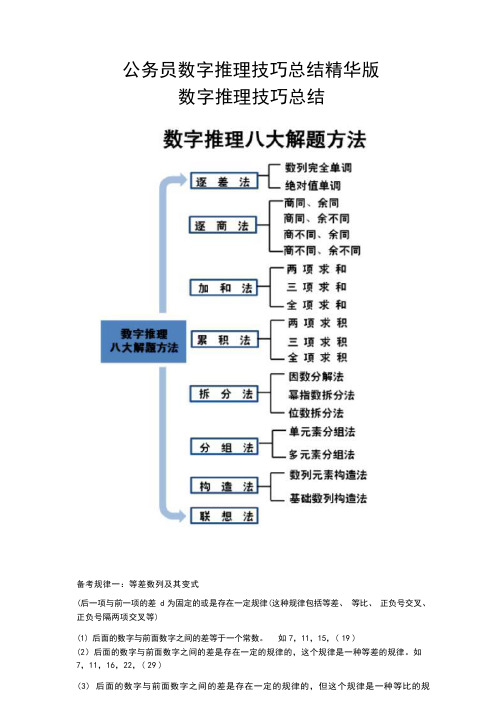
公务员数字推理技巧总结精华版数字推理技巧总结备考规律一:等差数列及其变式(后一项与前一项的差 d 为固定的或是存在一定规律(这种规律包括等差、等比、正负号交叉、正负号隔两项交叉等)(1) 后面的数字与前面数字之间的差等于一个常数。
如7,11,15,( 19 ) (2)后面的数字与前面数字之间的差是存在一定的规律的,这个规律是一种等差的规律。
如7,11,16,22,( 29 )(3)后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种等比的规律。
如7,11,13,14,( 14.5 )(4)后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号进行交叉变换的规律。
【例题】7,11,6,12,( 5 )(5) 后面的数字与前面数字之间的差是存在一定的规律的,但这个规律是一种正负号每“相隔两项”进行交叉变换的规律。
【例题】7,11,16,10,3,11,(20 )备考规律二:等比数列及其变式(后一项与除以前一项的倍数 q 为固定的或是存在一定规律(这种规律包括等差、等比、幂字方等)(1)“后面的数字”除以“前面数字”所得的值等于一个常数。
【例题】4,8,16,32,( 64 )(2)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数加1。
【例题】4,8,24,96,( 480 )(3)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数乘 2【例题】4,8,32,256,( 4096 )(4)后面的数字与前面数字之间的倍数是存在一定的规律的,倍数为 3 的n 次方。
【例题】2,6,54,1428,( 118098 )(5)后面的数字与前面数字之间的倍数是存在一定的规律的,“倍数”之间形成了一个新的等差数列。
【例题】2,-4,-12,48,(240 )备考规律三:“平方数”数列及其变式(an=n2+d,其中d为常数或存在一定规律)(1) “平方数”的数列【例题】1,4,9,16,25,36 ,49,64,81,100,121,144,169,196(2)每一个平方数减去或加上一个常数【例题】 0,3,8,15,24,(35 )【例题变形】2,5,10,17,26,(37 )(3) 每一个平方数加去一个数值,而这个数值本身就是有一定规律的。
行测数字推理秒杀口诀

行测数字推理秒杀口诀
题型一、和倍问题。
问题描述:已知两数之和及倍数关系,可快速得出这两数。
秒杀公式:大+小=和;大=倍×小,则:小=和÷(倍+1);大=倍×小=和-小。
题型二、差倍问题。
问题描述:已知两数之差及倍数关系,可快速得出这两数。
秒杀公式:大-小=差;大=倍×小,则:小=差÷(倍-1);大=倍×小=差+小。
题型三、和差问题。
问题描述:已知两数之和及两数之差,可快速得出这两数。
秒杀公式:大+小=和;大-小=差;则:大=(和+差)÷2;小=(和-差)÷2。
题型四、日期问题。
问题描述:若2017年7月10日星期三,则2018年8月10日星期几。
秒杀公式:平年:365=52×7+1 平过1;闰年:366=52×7+2 闰过2。
题型五、植树问题。
问题描述:在一个路段上植树,植树方式不同,棵数和段数的关系不同。
秒杀公式:①不封闭路段:两端植:棵数=段数+1;一端植:棵数=段数,②两端都不植:棵数=段数-1;③封闭路线:棵数=段数。
行测数字推理之解题技巧(精华版)

数字推理之解题技巧(精华版)(1)等差,等比这种最简单的不用多说,深一点就是在等差,等比上再加、减一个数列,如24,70,208,622,规律为a*3-2=b(注:a、b为前后数)(2)深一层次的,①各数之间的差有规律,如 1、2、5、10、17。
它们之间的差为1、3、5、7,成等差数列。
这些规律还有差之间成等比之类。
②各数之间的和有规律,如1、2、3、5、8、13,前两个数相加等于后一个数。
(注:前一就是高中数学常说的差后等差数列或等比数列)(3)看各数的大小组合规律,作出合理的分组。
如 7,9,40,74,1526,5436,可以划分为7和9,40和74,1526和5436三组,这三组各自是大致处于同一大小和位数级别,那规律就要从组方面考虑,即不把它们看作6个数,而应该看作3个小组。
而组和组之间的差距不是很大,用乘法就能从一个组过渡到另一个组。
所以7*7-9=40 , 9*9-7=74 ,40*40-74=1526 ,74*74-40=5436,这就是规律。
(4)如根据大小不能分组的,①,看首尾关系,如7,10,9,12,11,14,这组数 7+14=10+11=9+12。
首尾关系经常被忽略,但又是很简单的规律。
②,数的大小排列看似无序的,可以看它们之间的差与和有没有顺序关系。
(5)各数间相差较大,但又不相差大得离谱,就要考虑乘方,这里就要看各位对数字敏感程度如何了。
如6、24、60、 120、210,感觉它们之间的差越来越大,但这组数又看着比较舒服(个人感觉,嘿嘿),它们的规律就是2^3-2=6、3^3-3=24、4^3-4=60、5^3-5=120、6^3-6=210。
(注意,这组数比较巧的是都是6的倍数,大家容易导入歧途。
)6)看大小不能看出来的,就要看数的特征了。
如21、31、47、56、69、72,它们的十位数就是递增关系;如 25、58、811、1114 ,这些数相邻两个数首尾相接,且2、5、8、11、14的差为3;如论坛上fjjngs所解答的一道题:256,269,286,302,(),2+5+6=132+6+9=17 2+8+6=16 3+0+2=5,∵256+13=269 269+17=286 286+16=302 ∴下一个数为302+5=307。
公务员行政能力测试数字推理答题技巧(非常有用)

公务员行政能力测试数字推理答题技巧(非常有用)数字推理一、基本要求熟记熟悉常见数列,保持数字的敏感性,同时要注意倒序。
自然数平方数列:4,1,0,1,4,9,16,25,36,49,64,81,100,121,169,196,225,256,289,324,361,400……自然数立方数列:-8,-1,0,1,8,27,64,125,216,343,512,729,1000质数数列:2,3,5,7,11,13,17……(注意倒序,如17,13,11,7,5,3,2)合数数列:4,6,8,9,10,12,14…….(注意倒序)二、解题思路:1 基本思路:第一反应是两项间相减,相除,平方,立方。
所谓万变不离其综,数字推理考察最基本的形式是等差,等比,平方,立方,质数列,合数列。
相减,是否二级等差。
8,15,24,35,(48)相除,如商约有规律,则为隐藏等比。
4,7,15,29,59,(59*2-1)初看相领项的商约为2,再看4*2-1=7,7*2+1=15……2 特殊观察:项很多,分组。
三个一组,两个一组4,3,1,12,9,3,17,5,(12)三个一组19,4,18,3,16,1,17,(2)2,-1,4,0,5,4,7,9,11,(14)两项和为平方数列。
400,200,380,190,350,170,300,(130)两项差为等差数列隔项,是否有规律0,12,24,14,120,16(7^3-7)数字从小到大到小,与指数有关1,32,81,64,25,6,1,1/8每个数都两个数以上,考虑拆分相加(相乘)法。
87,57,36,19,(1*9+1)256,269,286,302,(302+3+0+2)数跳得大,与次方(不是特别大),乘法(跳得很大)有关1,2,6,42,(42^2+42)3,7,16,107,(16*107-5)每三项/二项相加,是否有规律。
1,2,5,20,39,(125-20-39)21,15,34,30,51,(10^2-51)C=A^2-B及变形(看到前面都是正数,突然一个负数,可以试试)3,5,4,21,(4^2-21),4465,6,19,17,344,(-55)-1,0,1,2,9,(9^3+1)C=A^2+B及变形(数字变化较大)1,6,7,43,(49+43)1,2,5,27,(5+27^2)2/3,1/3,2/9,1/6,(2/15)3/1,5/2,7/2,12/5,(18/7)分子分母相减为质数列1/2,5/4,11/7,19/12,28/19,(38/30)分母差为合数列,分子差为质数列。
行测考试数字推理快速秒杀三招

数字推理,是数学运算的一部分,虽然2011年的国考和省考都没有考数字推理,但是在湖南的选调生考试、村官考试、两院考试以及一些事业单位的招考中还是会经常考到,那么如何在事业单位招考中快速突破数字推理,专家将结合部分真题给广大的考生朋友,介绍一下数字推理快速秒杀的技巧。
第一招:看趋势。
拿到题目以后,用2秒钟迅速判断数列中各项的趋势,例如:是越来越大,还是越来越小,还是有大有小。
通过判断走向,找出该题的突破口。
有规律找规律,没有规律做差。
【例1】(2011年湖南两院)7,9,12,17,24,( )A.27B.30C.31D.35【答案】D【解析】本题属于多级数列。
先看趋势,越来越大,规律不明显,两两做差,得到质数数列2,3,5,7,(11),所以选择D选项。
【例2】(2007应届生)14 ,6 ,2 ,0 ,( )A.-2B.-1C. 0D.1【答案】B【解析】本题属于多级数列。
题目中的一先看趋势,越来越小,也就是趋势是递减的,是一致的。
对于这类递减的数列,我们通常的做法是从相邻两项的差或做商入手,很明显,这道题目不能从做商入手(因为14/6不是整数),那么,我们就作差,相邻两项的差为8,4,2成等比数列,因此,0减去所求项应等于1,故所求项等于-1,所以选择B选项。
利用数列的趋势,可以迅速判断出应该采取的方法,所以,趋势就是旗帜,趋势就是解题的命脉。
第二招,看特殊数字。
比如质数、平方数、立方数等。
一些数字推理题目中出现的数距离这些特殊的数字非常近,因此当出现某个整数的平方或者立方周围的数字时,我们可以从这些特殊数字入手,进而找出原数列的规律。
【例3】(2011湖南选调)61,59,53,47,43,( ),37A.42B.41C.39D.38【答案】B【解析】本题属于质数数列。
递减的质数数列,所以选择B选项。
【例4】(2011湖南选调)0,9,26,65,124,( )A.186B.199C.215D.217【答案】D【解析】本题属于幂次修正数列。
公务员考试数字推理题解题技巧大全

公务员考试数字推理题解题技巧大全公务员考试是一项重要的选拔机制,而数字推理题是其中的一项难点。
在数字推理题中,考生需要通过数字、图表等信息,寻找一定的规律和推理思路,从而解决问题。
为了帮助考生顺利应对数字推理题,本文将为大家介绍一些解题技巧和思路。
一、理解题目和数据在做数字推理题时,首先需要认真阅读题目和给出的数据,了解题目的背景和要求。
在阅读中要注意对数据进行分类和总结,分析数字间的关系和规律。
二、寻找常见数字规律数字推理题中存在着许多常见的数字规律,例如:相邻数的关系、乘法和除法关系、平方、倒数等规律。
若能找出这些规律,便能够轻松解决此类推理题。
三、寻找图形规律数字推理题中,常常会配有一些图形数据。
对于这些图形,我们可以通过寻找它们的共性和特点,来发现其中的规律。
例如,周期性图形的规律常常是循环或对称性;封闭型图形的规律常常是不变性或连通性。
通过这些规律,我们可以迅速地推断出答案。
四、确定类型和答案数字推理题大致可以分为数列和图形两类。
对于数列题,我们可以看其中的差值和倍数规律,以及数列的加和、中位数、众数等;对于图形题,我们可以寻找变化和相似性规律,以及图形的方向、角度、面积和比例等。
同时,我们也可以先推断出答案,然后再用已有的数据进行验证,验证结果。
五、注意隐形陷阱在数字推理题中,经常会隐藏着一些陷阱,这些陷阱可能会导致我们犯错。
例如,数据中可能存在重复数字、相同数字或相同图形,这就需要我们仔细分辨;同时也要注意看清题目要求,不要遗漏信息或多读信息。
总之,数字推理题是公务员考试中的难点之一,但是只要我们掌握题目信息,查找数字和图形规律,注意隐形陷阱,便能够较为轻松地应对此类题目。
希望以上简单的技巧和思路能够对大家在公务员考试中取得好成绩有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公务员考试考行测数字推理通用技巧盘点
专家在近几年浙江公务员行测考试中发现,与国家公务员考试和其他多省联考相比,浙江省公务员考试在题目设置方面具有其独特之处。
其中最为明显的是对数字推理的考查,不仅有经典的数列形式数字推理,还有在其他省市中极少出现的图形形式数字推理。
由于数字推理的考查核心包括数字敏感度与对数字运算关系的把握能力,属于最基础的分析能力,因此该部分试题的题量一直保持在10道左右,在浙江公务员考试中占有一定的比例,考生需要予以适当的关注。
针对数字推理入手难,推理规律繁杂的特点,中公教育专家特地在考前整理出一套具有普适性的通用技巧,帮助考生轻松应对数字推理。
一、数列形式数字推理
数列的变化趋势主要有三类,一是持续递增或递减,二是先增后减或先减后增,三是增减交替(注:增减交替特指数列后项减前项形成的差数列是一个正负数交替排列的数列)。
变化趋势往往预示了规律特征,例如:增幅很大的数列是多次方数列或递推数列的可能性较大,因为等差数列是一个线性递增的过程,不会有很夸张的增幅。
1.整体单调增减或增减交替的数列,都可能是等差数列变式,不要放弃作差尝试。
2.先增后减(先减后增)或增减无序的不是等差数列,因为作差后的数列先正后负不具有规律。
【例题1】32, 48, 40, 44, 42,()
A.43
B.45
C.47
D.49
3.递增(减)趋势明显,或出现先增后减的数列,可考虑等比数列。
【例题2】1, 2, 4, 4, 1,()
中公解析:此题答案为C。
数列先增后减,说明该数列不是作差得到规律。
先增后减说明有一个因子在减少数列数值,可以考虑作商寻求这个比例因子,发现是一个三级等比数列。
4.和数列或其变式往往在数列整体趋势上并非单调递增或递减,会出现增减很杂乱的情况。
【例题3】82, 98, 102, 118, 62, 138,()
A.68 B.76 C.78 D.82
中公解析:此题答案为D。
题干数字较大,且62与整体递增趋势不符,故可排除等差数列变式或等比数列变式的可能。
题干数字的个位数字2、8交替出现,二者之和为10,这提示考虑数列相邻两项之和。
5.两项积数列通常表现为1,A,A……,数列递增(减)趋势明显。
【例题4】2, 2, 3, 4, 9, 32,()
A.129
B.215
C.257
D.283
中公解析:此题答案为D。
选项数值较大,考虑递推规律。
9到32大概是4倍关系,4到9则只有2倍左右关系,因此前项并非乘以一个常数得到后项,判断是积数列变式。
前两项之积减自然数列得到第三项。
6.单调递增的多次方数列增幅明显,集中体现在选项数字极大,可从选项入手定位规律。
【例题5】2, 3, 13, 175,()
A.30625
B.30651
C.30759
D.30952
7.数位组合数列的题干数字以多位数为主,解题时需要将这些多位数分解成几个相对独立的部分。
【例题6】4938, 3526, 3124, 2621, 1714,()
A.1565 B.1433 C.1916 D.1413
中公解析:此题答案为D。
从数位特征的角度分析,将每个四位数的前两位数字和后两位数字分别看成一个两位数,这两个两位数的差依次是49-38=11、35-26=9、31-24=7、
26-21=5、17-14=3。
因此空缺项千位和百位组成的数减去十位与个位组成的数所得的差应是1,选项中符合这一规律的是D。
二、图形形式数字推理
与数列形式数字推理有所不同的是,在数列形式数字推理中,数字较多,有时考虑的角度就会很多。
而在图形形式数字推理中,由于数字较少,内容就没有那么复杂,主要规律是关于数字之间的运算关系。
归纳了以下几个考虑的角度,结合例题予以说明。
1.周围数字之和与中心数字的关系
如果四周数字之和小于中心数字,则四周数字的运算过程很有可能涉及乘法运算,否则,就应该优先考虑减法或除法运算。
这种分析虽然过程简单,但有利于确定大致的方向。
【例题1】
中公解析:此题答案为D。
观察前两个图形,中间数字是两位数,周围数字都是一位数。
四周数字之和均小于中间数字,说明周围四个数字运算得到中间数字的过程中,可能涉及到乘法运算。
在这个思路的基础上,考虑将数字分组,分别运算,然后相乘得到中心数字。
第一个图形中(9-5)×(4+5)=36;第二个图形中(8-3)×(5+6)=55;第三个图形中(7-1)×(6+7)=(78)。
2.考虑乘法运算
从各类考查运算关系的数字推理规律来看,出现频率最高的运算就是乘法。
有时是数字的倍数,有时是两个数字相乘。
在解决图形形式数字推理题时也要充分考虑乘法。
【例题2】
中公解析:此题答案为D。
前两个图形中的数字相差不大,分组后若考虑加法、减法不能得到规律,数字之间的倍数关系也不明显,不易使用除法,可考虑乘法。
第一个图形中,一条对角线上的数字5和7相乘等于35,由另一条对角线上的数字组合而成;第二个图形中,6×8=48,也符合这种规律,则在第三个图形中,8×9=72,应填入2。
3.分析图形中最大的数字
在数字推理中,几个数字运算得到另一个数字,通常都是几个较小的数运算得到较大的数。
如果几个较小的数字运算得到一个远大于它们的数字,则一定要通过乘法等使数字增大的运算。
因此可以以图形中最大的数字作为突破口,寻找运算关系。
【例题3】
中公解析:此题答案为D。
图形中最大的数字是218,若从每行来考虑,72和37都小于218,若想得到218可能需要涉及乘法运算。
72+37=109,109的2倍正好是218。
第三行[23+(-12)]×2=22,所以第一行中,(84+9)×2=(186)。
4.分析图形中的质数
质数由于其只能被1和它本身整除的特性,在运算过程中,质数通常涉及加法或减法的运算,这是分析图形中质数的原因。
【例题4】
中公解析:此题答案为A。
第一个图形中有质数7,中心数字是15,它不是7的倍数,则7在运算过程中极有可能涉及加法或减法;第二个图形中,中心数字23是质数,它可由3、5、8运算得到,运算过程中也有可能涉及加法或减法。
按此思路得到,第一个图形中,2×4+7=15;第二个图形中,3×5+8=23;第三个图形中,6×4+2=(26)。
