3 土力学(permeability)土的渗透性及渗流
合集下载
土力学3-土的渗透性及渗流
10
静水 A zB
0 基准面
zA
0
《土力学》 土力学》 第3章 土的渗透性及渗流
水往低处流
速度v 速度
位置: 位置:使水流从位置势能 高处流向位置势能低处
流速: 流速:水具有的动能
水往高处“ 水往高处“跑”
压力u 压力
压力: 压力:水所具有的压力势能 也可使水流发生流动
水流动的驱动力
11
《土力学》 土力学》 第3章 土的渗透性及渗流 板桩墙
基坑
透水层 不透水层
1. 渗流量? 渗流量? 2. 渗透破坏? 渗透破坏? 3. 渗水压力? 渗水压力?
板桩围护下的基坑渗流
工程实例
5
《土力学》 土力学》 第3章 土的渗透性及渗流
Q
天然水面
渗流问题: 渗流问题: 1. 渗流量 ? 渗流量Q?
透水层
2. 降水深度? 降水深度?
不透水层
水井渗流
6
《土力学》 土力学》 第3章 土的渗透性及渗流
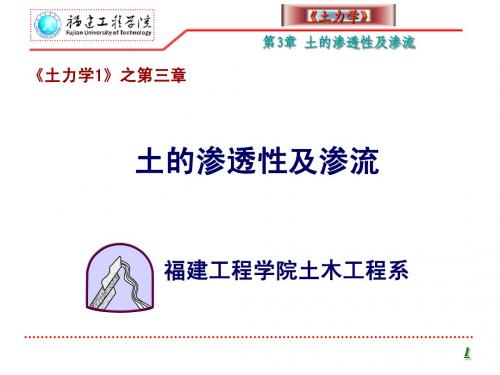
位置水头Z 水体的位置势能(任选基准面) 位置水头Z:水体的位置势能(任选基准面) 压力水头p/γw:水体的压力势能(u孔隙水压力) 压力水头 γ 水体的压力势能( 孔隙水压力) 孔隙水压力 流速水头V2/(2g):水体的动能(对渗流多处于层流 ) 流速水头 :水体的动能(对渗流多处于层流≈0)
渗流的总水头: 渗流的总水头: h = z +
o ib
i
18
《土力学》 土力学》 第3章 土的渗透性及渗流
3.2.3 渗透系数的测定方法
• 常水头试验法 室内试验方法 • 变水头试验法 • 井孔抽水试验 • 井孔注水试验
野外试验方法
19
《土力学》 土力学》 第3章 土的渗透性及渗流
静水 A zB
0 基准面
zA
0
《土力学》 土力学》 第3章 土的渗透性及渗流
水往低处流
速度v 速度
位置: 位置:使水流从位置势能 高处流向位置势能低处
流速: 流速:水具有的动能
水往高处“ 水往高处“跑”
压力u 压力
压力: 压力:水所具有的压力势能 也可使水流发生流动
水流动的驱动力
11
《土力学》 土力学》 第3章 土的渗透性及渗流 板桩墙
基坑
透水层 不透水层
1. 渗流量? 渗流量? 2. 渗透破坏? 渗透破坏? 3. 渗水压力? 渗水压力?
板桩围护下的基坑渗流
工程实例
5
《土力学》 土力学》 第3章 土的渗透性及渗流
Q
天然水面
渗流问题: 渗流问题: 1. 渗流量 ? 渗流量Q?
透水层
2. 降水深度? 降水深度?
不透水层
水井渗流
6
《土力学》 土力学》 第3章 土的渗透性及渗流
位置水头Z 水体的位置势能(任选基准面) 位置水头Z:水体的位置势能(任选基准面) 压力水头p/γw:水体的压力势能(u孔隙水压力) 压力水头 γ 水体的压力势能( 孔隙水压力) 孔隙水压力 流速水头V2/(2g):水体的动能(对渗流多处于层流 ) 流速水头 :水体的动能(对渗流多处于层流≈0)
渗流的总水头: 渗流的总水头: h = z +
o ib
i
18
《土力学》 土力学》 第3章 土的渗透性及渗流
3.2.3 渗透系数的测定方法
• 常水头试验法 室内试验方法 • 变水头试验法 • 井孔抽水试验 • 井孔注水试验
野外试验方法
19
《土力学》 土力学》 第3章 土的渗透性及渗流
土力学土的渗透性及渗流

8
2、渗流量的计算及渗透变形控制问题
基坑围护结构下的渗流
板桩墙
基坑
透水层
渗流问题:
1. 渗流量? 2. 渗透破坏? 3. 渗水压力?
不透水层
9
基坑开挖降水
井点降水
10
管井降水
11
工程实例 湖南浯溪水电站二期基坑出现管涌
12
2、渗流量的计算及渗透变形控制问题
水井渗流 Q
天然水面
含水层
渗流问题:
38
三、成层土的平均渗透系数
天然土层多呈层状
✓确立各层的k ✓考虑渗流方向
等效渗透系数
39
水平渗流 将土层简化为均质土,便于计算
总流量等于各土层流量之和 (各层的水力梯度相等)
条件:
im
i
h L
Q q j kxiH
q j v j H j k jiH j
等效渗透系数:
m
Q kxiH i k j H j j 1
P1 = γwhw
P2 = γwh2
R + P2 = W + P1
R + γwh2 = L(γ + γw) + γwhw
R = ? R = γ L
0
45
静水中的土体 R = γ L
渗流中的土体
ab
P1
W A=1
P2 R
W = Lγsat=L(γ + γw)
贮水器 hw L 土样
0
Δh
h1 h2
0 滤网
非线性流(紊流) 地下水的渗流速度与 水力梯度成非线性关系
线性稳定流
线性非稳定流
非线性稳定流 非线性非稳定流
我们现在需要掌握和理解的达西定律
2 土力学 第二章 土的渗透性及水的渗流
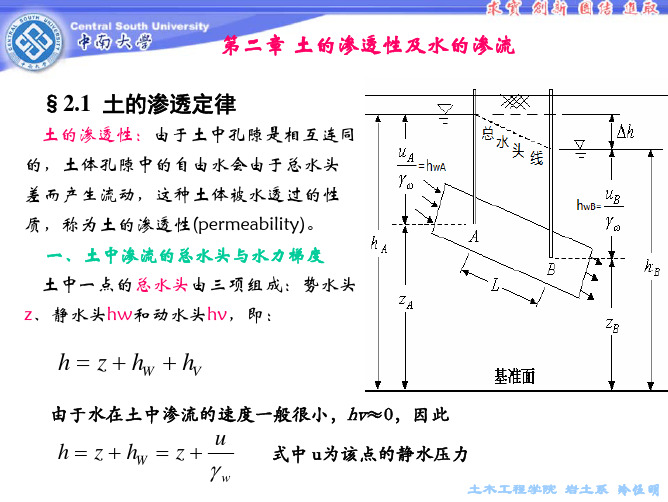
作用方向与渗流方向一致!
二、临界水力梯度及渗透破坏 当土中水向上渗流时,渗透力垂直向上而与土样重力方向相反,若渗透力 等于土样浮度,即
j = iγ w = γ , 得临界水力梯度: i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此,若土中水向上渗流: ⑴若i>icr,会发生流土破坏,即“管涌”; ⑵若i=icr,流土处于临界状态,即“悬浮”; ⑶若i<icr,不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小,hv≈0,因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为:
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差:
作业题:P54: 2-7,2-9 补题1:什么是渗透力、临界水力梯度?
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性:由于土中孔隙是相互连同 的,土体孔隙中的自由水会由于总水头 差而产生流动,这种土体被水透过的性 质,称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成:势水头 z、静水头hw和动水头hv,即:
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得,只能通过试验确定。 测定k值室内方法:定水头法、变水头法。 (1)定水头法 保持总水头差Δh不变,在t时间内,量得透过土样的水量为Q,求k: 根据达西定律
二、临界水力梯度及渗透破坏 当土中水向上渗流时,渗透力垂直向上而与土样重力方向相反,若渗透力 等于土样浮度,即
j = iγ w = γ , 得临界水力梯度: i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此,若土中水向上渗流: ⑴若i>icr,会发生流土破坏,即“管涌”; ⑵若i=icr,流土处于临界状态,即“悬浮”; ⑶若i<icr,不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小,hv≈0,因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
A、B两点的总水头可分别表示为:
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差:
作业题:P54: 2-7,2-9 补题1:什么是渗透力、临界水力梯度?
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性:由于土中孔隙是相互连同 的,土体孔隙中的自由水会由于总水头 差而产生流动,这种土体被水透过的性 质,称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成:势水头 z、静水头hw和动水头hv,即:
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得,只能通过试验确定。 测定k值室内方法:定水头法、变水头法。 (1)定水头法 保持总水头差Δh不变,在t时间内,量得透过土样的水量为Q,求k: 根据达西定律
03工程地质及土力学-土的渗透性及渗流

iix ix
又整个土层总的单位渗水量qn 为各土层单位渗水量之和
qx
n
q
i 1
n
ix
H
垂直成层土
由达西定律
h qiy kiyiiy A iiy i Hi
q1y
H1
k1y qiy
h
hi
q iy k iy A
H
Hi
kiy
qny
hi
Hi
qy k yi y A
h iy H
v z dz z
dz
dx
vx
流出单元体的流量:
v y v x dqo (v x )dydz (v y )dxdz x y v x (v z z )dxdy z
0
vy
dy
vy
v y y
y
dy
vx
v x dx x
vz
dqe dqo
v x v y v z 0 x y z
曲正方形流网
曲正方形流网的特性 通过正方形网格A、B的渗流量相等, 为:
q kiA k ( h h ' )(d1 1) k ( )(d 2 1) d1 d2
流线、等势线正交
得性质1
h h
即表示各方格网水头损失相等。
比较通过正方形网格A、C的渗流量
得
h )(d1 1) k h d1 h q k ( )(d 3 1) k h d3 q k(
水压力 压力水头 w
水平的地下水位为等势线
建筑物在水下的边界线为流线 (3)根据流网特征加绘流线和等势线,尽量采用曲正方形网格 。 上述过程不可能一次就合适,经反复修改调整,直到满足
土力学土的渗透性及渗流

j 1
三、 渗透力及临界水力梯度
1. 渗透力
h
hwb b-b
孔隙水 whwb Aw
土颗粒
hwa
渗
L
wLAw
LA
流
a-a
Jw J Jw Js
J s whAw
A
whwa Aw
R
? whwa Aw whwb Aw + wLAw +J w
J Jw J whAw A Aw 总渗透力 J whA
黏性土 e lg k
(3)土的结构和构造
黏性土:絮凝结构>分散结构
层状土:kx k y
(4)土的饱和度 不饱和土中气泡对渗透性的影响
(5)水的动力黏滞度 dynamic coefficient of viscosity
k20
kT
T 20
3. 成层土的平均渗透系数 将土层简化为均质土,便于计算
(1)连续方程的建立 流入微单元的水量(厚度为1)
qx vxdz 1 kxixdz qz kzizdx
流出微单元的水量
qz dqz kz (iz diz )dx
z
qx
dz
qz dqz qx dqx
qz
dx
x
qx dqx kx (ix dix )dz
对稳定流,流入量=流出量
对稳定流,流入量=流出量
qx qz qx dqx qz dqz
kxdixdz kzdizdx 0
水力梯度
ix
h x
iz
h z
水头
kx
2h x2
kz
2h z 2
0
对各项同性土 kx kz
Pierre Simon de Laplace 1749~1827
三、 渗透力及临界水力梯度
1. 渗透力
h
hwb b-b
孔隙水 whwb Aw
土颗粒
hwa
渗
L
wLAw
LA
流
a-a
Jw J Jw Js
J s whAw
A
whwa Aw
R
? whwa Aw whwb Aw + wLAw +J w
J Jw J whAw A Aw 总渗透力 J whA
黏性土 e lg k
(3)土的结构和构造
黏性土:絮凝结构>分散结构
层状土:kx k y
(4)土的饱和度 不饱和土中气泡对渗透性的影响
(5)水的动力黏滞度 dynamic coefficient of viscosity
k20
kT
T 20
3. 成层土的平均渗透系数 将土层简化为均质土,便于计算
(1)连续方程的建立 流入微单元的水量(厚度为1)
qx vxdz 1 kxixdz qz kzizdx
流出微单元的水量
qz dqz kz (iz diz )dx
z
qx
dz
qz dqz qx dqx
qz
dx
x
qx dqx kx (ix dix )dz
对稳定流,流入量=流出量
对稳定流,流入量=流出量
qx qz qx dqx qz dqz
kxdixdz kzdizdx 0
水力梯度
ix
h x
iz
h z
水头
kx
2h x2
kz
2h z 2
0
对各项同性土 kx kz
Pierre Simon de Laplace 1749~1827
土力学-第3章土的渗透性及渗流

第三章
土的渗透性及渗流
§3 土的渗透性及渗流
本章特点
• 有较严格的理论(水流的一般规律) • 有经验性规律(散粒体多孔介质特性)
学习要点
• 注重对物理概念和意义的深入理解 • 注意土是散粒体(多孔介质)这一特点
主要难点
• 水头及水力坡降 • 二维流网及其应用 • 渗透力及其分析方法
2
§3 土的渗透性及渗流
§3.2土的渗透性
➢ 同一过水断面,渗流模型的流量等于真实渗流的流量; ➢ 任一界面上,渗流模型的压力与真实渗流的压力相等; ➢ 相同体积内,渗流模型所受阻力与真实渗流相等。
图3-1 渗流模型
24
§3 土的渗透性及渗流
§3.2土的渗透性
渗流速度
断面面积为A,通过的渗透流流量为q,则平均流速为:
v=q/A
§3.2土的渗透性
水在土的孔隙中流动,其形式可以分为: 层流:水的流速很慢,认为相邻两个水分子运动轨迹相互平行而不混掺。 紊流:紊流与层流的意义相反。
渗流模型基本假定:
图3-1 渗流模型
➢ 不考虑渗流路径的迂回曲折,只分析它的主要流向;
➢ 认为孔隙和土粒所占的空间之总和均为渗流所充满。
23
§3 土的渗透性及渗流
土中通常含有水,土中含水量的变化及 土体中水的流动对土特性的影响非常大。有时 这种影响可能会带来灾难。
水对土特性影响的直观理解为:土的含水量 小时,土比较硬;土中适当含水可使散粒土颗 粒粘合在一起,使其具有一定的粘结强度,但 当土的含水量过大时则会变软。 当水在土中流动较快时,将引起坝基渗流、 基坑渗流、塌方、泥石流及流土、地下工程受 淹等灾害。
代表单位重量的液体从基准面算起
uB w
u0pa
土的渗透性及渗流
§3 土的渗透性及渗流
本章特点
• 有较严格的理论(水流的一般规律) • 有经验性规律(散粒体多孔介质特性)
学习要点
• 注重对物理概念和意义的深入理解 • 注意土是散粒体(多孔介质)这一特点
主要难点
• 水头及水力坡降 • 二维流网及其应用 • 渗透力及其分析方法
2
§3 土的渗透性及渗流
§3.2土的渗透性
➢ 同一过水断面,渗流模型的流量等于真实渗流的流量; ➢ 任一界面上,渗流模型的压力与真实渗流的压力相等; ➢ 相同体积内,渗流模型所受阻力与真实渗流相等。
图3-1 渗流模型
24
§3 土的渗透性及渗流
§3.2土的渗透性
渗流速度
断面面积为A,通过的渗透流流量为q,则平均流速为:
v=q/A
§3.2土的渗透性
水在土的孔隙中流动,其形式可以分为: 层流:水的流速很慢,认为相邻两个水分子运动轨迹相互平行而不混掺。 紊流:紊流与层流的意义相反。
渗流模型基本假定:
图3-1 渗流模型
➢ 不考虑渗流路径的迂回曲折,只分析它的主要流向;
➢ 认为孔隙和土粒所占的空间之总和均为渗流所充满。
23
§3 土的渗透性及渗流
土中通常含有水,土中含水量的变化及 土体中水的流动对土特性的影响非常大。有时 这种影响可能会带来灾难。
水对土特性影响的直观理解为:土的含水量 小时,土比较硬;土中适当含水可使散粒土颗 粒粘合在一起,使其具有一定的粘结强度,但 当土的含水量过大时则会变软。 当水在土中流动较快时,将引起坝基渗流、 基坑渗流、塌方、泥石流及流土、地下工程受 淹等灾害。
代表单位重量的液体从基准面算起
uB w
u0pa
土力学_第3章(土的渗透性和渗流问题)

土中的水沿着流线 方向每前进Δs的距 离,就要有- Δh的 水头损失。
h A hB h i L L
h
uB
总水头线
w
uA
hA zA
w
hB
L
zB
(2)Darcy定律
(法国工程师,1856年提出)
水头梯度
渗透速度
v k i
渗透流量
Q k i A
渗透系数,单位:cm/s
Q v A
1
(Gs 1) icr 1 e
h 2 a
临界坡降取决于土的物理性质
②管涌的临界坡降
通过经验和实验总结得出管涌的临界坡降:
icr
d k n3
其中,d-为被冲动的细颗粒粒径,一般小于d5-d3,单位 cm; n-为砂砾料的孔隙率; k-为砂砾料的渗透系数,单位 cm/s。
六、流网及工程中的渗流场计算
常水头试验示意图
h Q qt kiAt k At L
故,渗透系数为:
k
QL hAt
②变水头渗透试验
土样的截面积A,高度为L 储水管截面积为a 试验开始储水管水头为h0
经过时间t后降为h1
时间dt内水头降低dh,水量为:
dQ adh
另外: 变水头渗透试验示意图
Kx 1 (k1 H1 k 2 H 2 k3 H 3 ) H
A
•y方向的平均渗透系数Ky (电阻串联)
* 每层土的水头损失之和等于总的水头损失
qy q1 q2 q3
Ky H H1 H 2 H 3 k1 k2 k3
水平方向由最大的 一层渗透系数决定, 垂直方向由最小的 一层渗透系数决定。
h A hB h i L L
h
uB
总水头线
w
uA
hA zA
w
hB
L
zB
(2)Darcy定律
(法国工程师,1856年提出)
水头梯度
渗透速度
v k i
渗透流量
Q k i A
渗透系数,单位:cm/s
Q v A
1
(Gs 1) icr 1 e
h 2 a
临界坡降取决于土的物理性质
②管涌的临界坡降
通过经验和实验总结得出管涌的临界坡降:
icr
d k n3
其中,d-为被冲动的细颗粒粒径,一般小于d5-d3,单位 cm; n-为砂砾料的孔隙率; k-为砂砾料的渗透系数,单位 cm/s。
六、流网及工程中的渗流场计算
常水头试验示意图
h Q qt kiAt k At L
故,渗透系数为:
k
QL hAt
②变水头渗透试验
土样的截面积A,高度为L 储水管截面积为a 试验开始储水管水头为h0
经过时间t后降为h1
时间dt内水头降低dh,水量为:
dQ adh
另外: 变水头渗透试验示意图
Kx 1 (k1 H1 k 2 H 2 k3 H 3 ) H
A
•y方向的平均渗透系数Ky (电阻串联)
* 每层土的水头损失之和等于总的水头损失
qy q1 q2 q3
Ky H H1 H 2 H 3 k1 k2 k3
水平方向由最大的 一层渗透系数决定, 垂直方向由最小的 一层渗透系数决定。
土力学_卢廷浩_CH.3PermeabilityofSoil

h = 12 m h=9m h=6m h=3m
NF 5 qT k H k 15 15k Nd 5
2005 23
3.5.6 Pore-water pressure (孔隙水压力)
Estimate the number of equipotential drops from a known total head to the given point (A) from the flow net. Calculate the total head at the point A as:
Bodies of water, such as
reservoirs behind a dam, are equipotentials. e.g. AB in the figure on the
bottom right is an equipotential line.
2005
20
3.5.5 Flow rate (渗流量)
Water flows from A to B if hA > hB
uA/w A zA z2
z1
hA hB
uA zA w uB zB w
Datum
uB/w
B zB
Water flow
2005 6
3.2 Darcy’s Law (达西定律)
h q k A k i A L
vd Re 1
where is density of water (水的密度) v is velocity of water (流速) is viscosity of water (水的粘滞系数)
d is average diameter of soil grains(土粒子平均粒径)
NF 5 qT k H k 15 15k Nd 5
2005 23
3.5.6 Pore-water pressure (孔隙水压力)
Estimate the number of equipotential drops from a known total head to the given point (A) from the flow net. Calculate the total head at the point A as:
Bodies of water, such as
reservoirs behind a dam, are equipotentials. e.g. AB in the figure on the
bottom right is an equipotential line.
2005
20
3.5.5 Flow rate (渗流量)
Water flows from A to B if hA > hB
uA/w A zA z2
z1
hA hB
uA zA w uB zB w
Datum
uB/w
B zB
Water flow
2005 6
3.2 Darcy’s Law (达西定律)
h q k A k i A L
vd Re 1
where is density of water (水的密度) v is velocity of water (流速) is viscosity of water (水的粘滞系数)
d is average diameter of soil grains(土粒子平均粒径)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各类土的渗透系数
k反映了土渗透性的强弱
砾砂、粗砂 中砂 细砂、粉砂 粉土 粉质黏土 黏土
10-3~10-4 m/s
10-4~10-5 m/s
10-5~10-6 m/s
10-6~10-8 m/s
10-8~10-9 m/s
10-9~10-12 m/s
砂、砾的透水性强,可以起到排水作用; 粘性土的透水性弱,可以起到截水的作用。 砾砂、粗砂、中砂属强透水材料,粉、细砂属中透水性材料, 粉土属弱透水材料,粉质粘土属于基本不透水材料, 粘土属于不透水材料。
不透水层
成层地基竖向等效渗透系数
Equivalent permeability determination- ertical flow in stratified soil
kV eq H H1 H 2 H 3 Hn kV kV kV kV 1 2 3 n
土石坝坝基坝身渗流
防渗斜墙及铺盖
土石坝
浸润线
渗流量
透水层
不透水层
渗透变形
板桩围护下的基坑渗流
板桩墙
渗水压力
渗流量
基坑
透水层 不透水层
渗透变形
扬压力
水井渗流
Q
天然水面
透水层
渗流量
不透水层
渠道渗流
渗流量
渗流时地下水位
原地下水位
土的渗透性及渗透规律
渗流量
渗透力与渗透变形
渗透变形 渗流滑坡
挡水建筑物 集水建筑物 引水结构物 基坑等地下施工 多雨地区边坡
依据(b) 达西定律 v = ki Kozen-Carman公式表达式
P 1 e3 3 k Cs ( ) S S 2 1 e 0
k=渗透系数; S0 = 单位体积颗粒的比表面积 S = 饱和度;Cs = 形状系数; = 粘滞系数
§3.2 土的渗透性和渗流
静水 A zB
0 基准面
zA
0
水流动的驱动力
水往低处流
位置:使水流从位置势能 高处流向位置势能低处
速度v
流速:水具有的动能
水往高处“跑”
压力u
压力:水所具有的压力势能
也可使水流发生流动
位置势能: 压力势能:
u w
mgz
mg u w
动能:
1 mv 2 2
总能量:
质量 m 压力 u 流速 v 0 基准面
Figure 3-9 Pumping test from a well penetrating the full depth in a confined aquifer
4 影响因素
粒度成分 孔隙比、密实度 饱和度 土的结构 土的构造 孔隙水粘滞性
5 固有渗透系数 (Intrinsic permeability) K
积 分
Q ln
k
地下水位≈测压管水面 不透水层
r2 2 k (h 2 h 2 1) r1
Q ln( r2 / r1 ) 2 h2 h 2 1
优点:可获得现场较为可 靠的平均渗透系数 缺点:费用较高,耗时较长
§3 土的渗透性和渗流问题
r1 qlog10 r 2 k 2.727H h1 h2
伯努力Bernowlli方程
1 渗流问题的水头
总水头:单位重量水体所具有的能量
v2 h z w 2g u
位置水头Z:水体的位置势能(任选基准面)
压力水头u/w:水体的压力势能(u孔隙水压力)
流速水头v2/(2g):水体的动能(对渗流多处于层流≈0)
渗流的总水头: h z
由于渗透造成的构筑物破坏
基坑降水 示意图
井点降水 示意图
固体废弃物填埋场对地下水的污染示意图
堆石坝
堤坝中防止渗流破坏采取的工程措施
渗透性与工程紧密相关的有:
1. 渗流量问题:基坑开挖或施工 (P61 图31(a))。 2. 渗透破坏问题:堆石坝下游趾部管涌及上游填 土流土。 3. 渗流控制问题:基坑、大坝。 4. 水体污染问题:废弃物填埋场。
v ki m
( m 1)
对致密的粘性土,存在起始水力 坡降i0 ?? i>ib, v=k(i - ib) 砾土:水头梯度较大时,不适合 达西定律,p64
3. 渗透系数的测定方法
• 常水头试验法
室内试验方法 • 变水头试验法
野外试验方法
• 井孔抽水试验
• 井孔注水试验
经验估算法
室内试验法确定渗透系数 (常水头法)
3.1
动,这一现象称为渗流
概述
1.渗流:水在重力作用下,透过土体发生运
2.土的渗透性:土体被水透过的性质 3.岩土工程实践中的渗流问题
见下页
水在地圈中的循环示意图
Teton坝
11:50左右 洞口扩大加速,泥 水对坝基的冲蚀更 加剧烈。
5
大坝下游趾部 流土
大坝上游入渗处 管涌造成空洞
大坝上游入渗处 管涌
2.0 1.5
水 力 梯 度
1.0 0.5 达西定律 适用范围
0
0 0.5 1.0 1.5 2.0 2.5
流速 (m/h)
v d 10 Re h
Re<5时层流 Re >200时紊流 200> Re >5时为过渡区
两种特例
在纯砾以上的很粗的粗粒土如堆 石体中,在水力坡降较大时,达 西定律不再适用,此时:
土坡稳定分析
3.2 土的渗流性
一 位置、压力和测管水头
位置水头:到基准面的竖直距 离,代表单位重量的液体从基 准面算起所具有的位置势能
uB w
u 0 p a
B
uA w
压力水头:水压力所能引起的 自由水面的升高,表示单位重 量液体所具有的压力势能 测管水头:测管水面到基准面 的垂直距离,等于位置水头和 压力水头之和,表示单位重量 液体的总势能 在静止液体中各点的测管水头 相等
单位时间流入单元的水量:
dq e v x dz v z dx
z
单位时间内流出单元的水量:
dq o ( v x v x dx )dz x v ( v z z dz )dx z
vx
dz
v z v z dz z v x v x dx x
层状地基的等效渗透系数 水平渗流
条件:
h im i L
1 q1x q2x q3x 1 L Fig 3-13 (a) z
2 k1 k2 k3 2
Δh
x H1
q x q mx
H Hm
等效渗透系数:
H2
H3
H
qx=vxH=kxiH Σqmx=ΣkmimHm
1 k x k m Hm H
一 平面稳定渗流
平面问题:渗流剖面和产生 渗流的条件沿某一个方向不 发生变化,则在垂直该方向 的各个平面内,渗流状况完 全一致。 对平面问题,常取dy=1m单 位宽度的一片来进行分析 稳定渗流:流场不随时间发生变化的渗流 h=h(x,z), v=v(x,z) 与时间无关 Δh
渗流的连续性方程
h i L
h LA A B L
A点的总水头 hA=ZA+LA B点的总水头
LB
DL
hB=ZB+LB
两点总水头差 不透水层
hA-hB=(ZA-ZB)+(LA-LB)
=DL+ LA-LB=L-LB=h
三 渗透试验与渗透系数
1856 年达西(Darcy)在研究城 市供水问题时进行的渗流试验
h Q A L
或: Q
A
kAi
其中,A是试样的断面积
Q v k i A
1 达西定律
达西定律:在层流状态的渗流中,渗透速度v与水力坡降i 的一次方成正比,并与土的性质有关
v 渗透系数k: 反映土的透水性能的比例系数,其物理意义为 水力梯度(坡降)i=1时的渗流速度,单位: m/s (SI 单位)
第三章 土的渗透性及渗透稳定
§ 3.1 概述
§ 3.2 土的渗透性
§ 3.3 土中二维渗流及流网简介
§ 3.4 渗透破坏与控制
重要术语中英文对照
■ 渗透系数: Permeability, hydraulic conductivity (k) ■ 水力梯度: hydraulic gradient (i) ■ 达西定律:Darcy’s Law ■ 平均流速:Real average velocity, Darcy velocity (v, va) (假想平均流速) ■ 实际平均流速:seepage velocity (vr, vs) (孔隙水平均流速) ■ 渗透力: seepage force ■ 临界水力梯度:critical hydraulic gradient (icr)
各种类性土的e-logk关系图 (Lamb & Whittman 1969)
2 达西定律的适用范围
适用条件:层流(线性流动)
岩土工程中的绝大多数渗 流问题,包括砂土或一般 粘土,均属层流范围 在粗粒土孔隙中,水流形 态可能会随流速增大呈紊 流状态,渗流不再服从达 西定律。可用雷诺数进行 判断 :
E mgz mg
u 1 mv 2 w 2
z
0
单位重量水流的能量:
u v2 h z γ w 2g
称为总水头,是水流动 的驱动力
二 渗流中的水头与水力梯度
板桩墙
A
基坑
B L
透水层 不透水层
渗流为水体的流动,应满 足液体流动的三大基本方 程:连续性方程、能量方 程、动量方程
