截一个几何体专项练习30题
千题百炼- 立体几何空间距离与截面100题(原卷版)

专题18 立体几何空间距离与截面100题任务一:空间中的距离问题1-60题一、单选题1.《九章算术·商功》:“斜解立方,得两塹堵,斜解塹堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以基,其形露矣.”文中“阳马”是底面为长方形且有一条侧棱与底面垂直的四棱锥.在阳马P ABCD -中,侧棱PA ⊥底面ABCD ,且1PA =,2AB AD ==,则点A 到平面PBD 的距离为( )A .3 B C D2.已知直线l 过定点()2,3,1A ,且方向向量为0,1,1s,则点4,3,2P 到l 的距离为( )A B C D3.在ABC 中,5AB AC ==,8BC =,若PA ⊥平面ABC ,4PA =,则点P 到BC 的距离是( )A B .5 C .D .4.在四面体P ABC -中,P A ,PB ,PC 两两垂直,设PA PB PC a ===,则点P 到平面ABC 的距离为( )A B C .3a D5.已知直线l 的方向向量为()=1,0,1a ,点()1,2,1A -在l 上,则点()3,1,1P 到l 的距离为( )A .B .1C .3D .26.已知棱长为2的正方体1111ABCD A B C D -,E ,F 分别为1A B 和11B D 的中点,则点B 到EF 的距离为( )A B C .2 D7.若平面α的一个法向量为()1,2,2n →=,点()3,0,2A ,()5,1,3B ,A α,B α∈,A 到平面α的距离为( )A .1B .2C .3D .48.已知(2,1,0),(1,0,1),(3,2,3)A B C ,则点A 到直线BC 的距离为( )A B C D9.如图,在棱长为2的正方体ABCD A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为( )A BC D 10.如图所示的三棱锥P ABC -,PA ⊥平面ABC ,π2ABC ∠=,若PA a =,AB c =,10PB =,BC =ac 取最大值时,点A 到平面PBC 的距离为( )A B C .D .511.已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2,E 为A 1B 1的中点,下列说法中正确的是()A .ED 1与B 1C 所成的角大于60°B .点E 到平面ABC 1D 1的距离为1C .三棱锥E ﹣ABC 1D .直线CE 与平面ADB 1所成的角为4π12.如图,正方体1111ABCD A B C D -的棱长为2,M 为棱11D C 的中点,N 为棱1CC 上的点,且(02)CN a a =<<,现有下列结论: ①当23a =时,//AM 平面BDN ;②存在(0,2)a ∈,使得MN ⊥平面BDN ;③当1a =时,点C 到平面BDN ;④对任意(0,2)a ∈,直线AM 与BN 都是异面直线.其中所有正确结论的编号为( )A .①②B .①③C .②④D .③④13.重心是几何体的一个重要性质,我国的国宝级文物东汉铜奔马(又名:马踏飞燕)就是巧妙利用了重心位于支点正上方这一性质而闻名于世.已知正三棱锥的重心是其每个顶点与其所对的面的三角形重心连线的交点.若正三棱锥H ABC -的底面边长为2,侧棱长为G 到底面的距离为( )A B C D14.三棱锥S ABC -中,SA ⊥底面ABC ,4SA =,3AB =,D 为AB 的中点,90ABC ∠=︒,则点D 到面SBC 的距离等于( ) A .125 B .95 C .65 D .3515.在棱长为a 的正方体1111ABCD A B C D -中,E ,F ,G 分别是AD ,1AA ,11A B 的中点,则点B 到平面EFG 的距离为( ).A .12a B C .a D16.已知正方形ABCD 的边长为4,CG ⊥平面ABCD ,CG =2,E 、F 分别是AB 、AD 的中点,则点B 到平面GEF 的距离为( )A B C D17.如图,在长方体1111ABCD A B C D -中,4AB =,2BC =,12CC =,E 是CD 的中点,求D 到面1D EB 的距离为( )A BC D18.如图,在长方体1111ABCD A B C D -中,2AB BC ==,1AA E ,F 分别是平面1111D C B A 与平面11BCC B 的对角线交点,则点E 到直线AF 距离为( )A B C D 19.已知AB ⊥平面α,垂足为点B ,且AO 与α相交于点O ,60AOB ∠=︒,射线OC 在α内,且30BOC ∠=︒,6OA =,则点A 到直线OC 的距离是( )A .6BC D .20.定义:两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值.在棱长为1的正方体1111ABCD A B C D -中,直线AC 与1BC 之间的距离是( )A .2 B C .12 D .1321.如图,在正方体1111ABCD A B C D -中,M 、N 、P 、Q 分别是所在棱的中点,则下列结论不正确的是( )A .点1C 、1D 到平面PMN 的距离相等B .PN 与QM 为异面直线C .90PNM ∠=D .平面PMN 截该正方体的截面为正六边形22.正方体1111ABCD A B C D -的棱长为2,G 为1AA 的中点,则直线BD 与平面11GB D 的距离为( )A B C D23.如图,在棱长为1的正方体1111ABCD A B C D -中,P 为11A D 的中点,Q 为11A B 上任意一点,E ,F 为CD 上两个动点,且EF 的长为定值,则点Q 到平面PEF 的距离( )A B .和EF 的长度有关C D .和点Q 的位置有关24.如图所示,在棱长为2的正方体1111ABCD A B C D -中,M ,N 分别为11C D ,1C C 的中点,其中正确的结论是( )A .直线MN 与AC 所成的角为45°B .直线AM 与BN 是平行直线C .二面角N BD C --D .点C 与平面MAB25.在三棱锥P ABC -中,AB BC ⊥,AB BC ==PA =O 是AC 的中点,OP ⊥底面ABC ,则点O 到平面PAB 的距离为( )A B C D26.如图,已知在长方体1111ABCD A B C D -中,14,8AB BC AA ===,点H 在棱1AA 上,且12HA =,在侧面11BCC B 内作边长为2的正方形1,EFGC P 是侧面11BCC B 内一动点,且点P 到平面11CDD C 的距离等于线段PF 的长,则当点P 在侧面11BCC B 上运动时,2HP 的最小值是( )A .12B .24C .48D .6427.如图所示,ABCD —EFGH 为边长等于1的正方体,若P 点在正方体的内部且满足321432AP AB AD AE =++,则P 点到直线BC 的距离为( )A .34BC .45 D28.若正四棱柱1111ABCD A B C D -的底边长为2,13B AB π∠=,E 是1D D 的中点,则11A C 到平面EAC 的距离为( )A B .C D 29.已知正方体1111ABCD A B C D -的棱长为1,点P 为线段1AC 上一点,1PA =,则点P 到平面ABCD 的距离为( )A .BC .3D .430.已知△ABC 在平面β内,不重合的两点P ,Q 在平面β同侧,在点M 从P 运动到Q 的过程中,记四面体M -ABC 的体积为V ,点A 到平面MBC 的距离为d ,则可能的情况是( )A .V 保持不变,d 先变大后变小B .V 保持不变,d 先变小后变大C .V 先变大后变小,d 不断变大D .V 先变小后变大,d 不断变小二、多选题31.已知四面体ABCD 的每个顶点都在球O (O 为球心)的球面上,ABC 为等边三角形,M 为AC 的中点,2AB BD ==,AD AC BD ⊥,则( )A .BM ⊥平面ACDB .O ∉平面ABCC .O 到ACD .二面角A CD O --32.如图,在四棱柱1111ABCD A B C D -中,底面ABCD 是等腰梯形,//AB CD ,4AB =,12BC CD D C ===,1D C ⊥底面ABCD ,则( )A .BC ⊥平面1ACDB .直线1DD 与底面ABCD 所成的角为4πC .平面11ABCD 与平面ABCD 夹角的余弦值为7D .点C 到平面11ABC D 33.如图,在正方体1111ABCD A B C D -中,点O 在线段AC 上移动,点M 为棱1BB 的中点,则下列结论中正确的有( )A .1//D O 平面11A BCB .1D OM ∠的大小可以为90°C .异面直线1D O 与11A C D .存在实数[]0,1λ∈,使得()111312D M C B D C AB λλ---=成立34.在直三棱柱中,13AA AB BC ===,2AC =,D 是AC 的中点,下列判断正确的是()A .1BC ∥平面1A BD B .面1A BD ⊥面11AAC CC .直线1B C 到平面1A BDD .点1A 到直线BC35.关于棱长为()0a a >的正方体1111ABCD A B C D -,下列结论正确的是( )A .11AB AD ⊥ B .点C 到平面1A BDC .异面直线1BD 与1C D 所成的角是60︒D .二面角11A BD C --的余弦值为1336.如图,四棱柱1111ABCD A B C D -的底面ABCD 是正方形,O 为底面中心,1A O ⊥平面ABCD ,1AB AA = )A .1B 坐标是()1,1,1B .平面1OBB 的法向量()1,1,1n =-C .1A C ⊥平面1OBBD .点A 到平面1OBB 37.正方体1111ABCD A B C D -的棱长为2,E ,F ,G 分别为11,,BC CC BB 的中点,则( )A .直线1D D 与直线AF 垂直B .直线1A G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为92D .点C 到平面AEF 的距离为2338.如图所示,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,侧面P AD 是边长为面ABCD 为矩形,且CD =Q 是PD 的中点,则下列结论描述正确的是( )A .CQ ⊥平面P ADB .B ,Q 两点间的距离等于C .DC 与平面AQC 所成的角为60°D .三棱锥B AQC -的体积为1239.如图,在菱形ABCD 中,AB =60BAD ∠=︒,沿对角线BD 将ABD △折起,使点A ,C 之间的距离为P ,Q 分别为直线BD ,CA 上的动点,则下列说法正确的是( )A .当AQ QC =,4PD DB =时,点D 到直线PQB .线段PQC .平面ABD ⊥平面BCDD .当P ,Q 分别为线段BD ,CA 的中点时,PQ 与AD40.已知四面体ABCD 的所有棱长均为2,则下列结论正确的是( )A .异面直线AC 与BD 所成角为60︒B .点A 到平面BCDC .AB CD ⊥D .四面体ABCD第II 卷(非选择题)三、填空题41.已知正方体1111ABCD A B C D -的棱长为1,异面直线1BB 与AC 的距离为____________.42.已知直线l 过点(0,0,0)A ,点(1,1,0)B ,则点(0,1,1)C 到直线l 的距离是_________.43.如图,正三角形ABC 的边长为2,P 是三角形ABC 所在平面外一点,PA ⊥平面ABC ,且1PA =,则P 到BC 的距离为___________.44.平面α的法向量是()2,2,1n =--,点()1,3,0A -在平面α内,则点()2,1,4P -到平面α的距离为______.45.在直三棱柱111ABC A B C -中,1AC BC ==,AB =,12AA =,则点C 到平面1ABC 的距离为____________.46.如图,已知,,60,1AP BP AP PC ABP ACP BAC PA ⊥⊥∠=∠=∠=︒=,D 是BC 中点,则点B 到平面APD 的距离是___________.47.在正方体1111ABCD A B C D -中,4AB =,则异面直线AB 和1A C 的距离为___________.48.如图所示,正方形ABCD 和正方形ABEF 的边长都是1,且它们所在平面互相垂直,若点M 在线段BF 上运动,记BM a =,则当=a ___________时,点M 到直线AC 的距离有最小值.49.如图,已知111ABC A B C -是各条棱长均等于a 的正三棱柱,D 是侧棱1CC 的中点,点1C 到平面1AB D 的距离为_____________.50.已知正方体1111ABCD A B C D -的棱长为2,点E 为11A D 中点,点P 、M 在四边形ABCD 内(包括边界),点P 到平面11ABB A 的距离等于它到点D 的距离,直线1//MB 平面1EC D ,则PM 的最小值为___________.四、解答题51.如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=,30BAC ∠=,1A AC 是边长为2的等边三角形.(1)求二面角1A BC A --的大小的正切值;(2)求直线11B C 到平面1A BC 的距离.52.如图,在四棱锥E ABCD -中,底面为菱形,已知60DAB BAE ∠=∠=︒,2AD AE ==,DE =(1)求证:平面ABE ⊥平面ABCD ;(2)求点B 到平面AED 的距离.53.在长方体1111ABCD A B C D -中,12,1AB BB BC ===,E 是面对角线1CD 上一点,且145CE CD =.(1)求证:1AE CD ⊥;(2)设异面直线1AB 与1BD 所成角的大小为α,求cos α的值. (3)求点A 到平面1BCD 的距离.54.如图,在三棱锥D ABC -中,AB BD ⊥,BC CD ⊥,M 、N 分别是线段AD 、BD 的中点,1MC =,AB BD ==(1)证明:平面MNC ⊥平面BCD ;(2)若60CBD ∠=︒,求点B 到平面MNC 的距离.55.如图,三棱柱111ABC A B C -的所有棱长都是2,1AA ⊥平面ABC ,M 为AB 的中点,点N 为1CC 的中点.(1)求证:直线//MN 平面11A BC ;(2)求直线MN 到平面11A BC 的距离.56.如图,四边形ABCD 是边长为3的正方形,DE ⊥平面ABCD ,//AF DE ,3DE AF =,BE 与平面ABCD 所成角为60︒.(1)求证://BF 平面CDE ;(2)求点D 到平面BEF 的距离.57.如图所示的四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 为直角梯形,//AD BC ,90BAD ∠=︒,2PA AB BC AD ===,点E 为PB 的中点.(1)求证://AE 平面PCD ;(2)若四棱锥P ABCD -的体积为2,求点A 到平面PCD 的距离.58.如图所示,边长为2的正方形ABFC 和高为2的直角梯形ADEF 所在的平面互相垂直且DE =//ED AF 且90DAF ∠=︒.(1)求BD 和面BEF 所成的角的正弦; (2)求点C 到直线BD 的距离;(3)线段EF 上是否存在点P 使过P 、A 、C 三点的平面和直线DB 垂直,若存在,求EP 与PF 的比值:若不存在,说明理由.59.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 为菱形,2AP AD ==,60ABC ∠=︒.点E ,F 分别在棱P A ,PB ,且//EF AB .(1)求证://EF CD ;(2)若直线PD 与平面CEF (i )求点P 与到平面CEF 的距离;(ii )试确定点E 的位置.60.如图,已知在四棱锥P ABCD -中,PA ⊥平面ABCD ,点Q 在棱PA 上,且44PA PQ ==,底面为直角梯形,90CDA BAD ∠=∠=︒,2AB =,1CD =,AD =M ,N 分别是PD ,PB 的中点.(1)求证://MQ 平面PCB ;(2)求点A 到平面MCN 的距离.任务二:几何体截面问题1-40题一、单选题1.已知正方体1111ABCD A B C D -的棱长为1,P 是空间中任意一点,有下列结论:△若P 为棱1CC 中点,则异面直线AP 与CD ;△若P 在线段1A B 上运动,则1AP PD + △若P 在以CD 为直径的球面上运动,当三棱锥P ABC -体积最大时,三棱锥P ABC -外接球的表面积为2π;△若过点P 的平面α与正方体每条棱所成角相等,则α 其中正确结论的个数为( ) A .4 B .3 C .2 D .12.已知正方体1111ABCD A B C D -,平面π和线段1AA ,1BB ,1CC ,1DD 分别交于点E ,F ,G ,H ,则截面EFGH 的形状不可能是( ) A .梯形 B .正方形 C .长方形 D .菱形3.如图正方体1111ABCD A B C D -,棱长为1,P 为BC 中点,Q 为线段1CC 上的动点,过A 、P 、Q 的平面截该正方体所得的截面记为Ω.若1CQ CC λ→→=,则下列结论错误的是( )A .当102λ∈⎛⎫⎪⎝⎭,时,Ω为四边形B .当12λ=时,Ω为等腰梯形C .当3,14λ⎛⎫∈ ⎪⎝⎭时,Ω为六边形D .当1λ=时,Ω4.如图,在正方体1111ABCD A B C D -中,M 、N 、P 分别是棱11C D 、1AA 、BC 的中点,则经过M 、N 、P 的平面与正方体1111ABCD A B C D -相交形成的截面是一个( )A .三角形B .平面四边形C .平面五边形D .平面六边形5.如图,在正方体1111ABCD A B C D -中,E 是棱1CC 的中点,则过三点A 、D 1、E 的截面过( )A .AB 中点 B .BC 中点 C .CD 中点 D .BB 1中点6.正方体1111ABCD A B C D -的棱长为2,E 是棱1DD 的中点,则平面1AC E 截该正方体所得的截面面积为( )A .5B .C .D .7.正三棱柱ABC ﹣A 1B 1C 1中,所有棱长均为2,点E ,F 分别为棱BB 1,A 1C 1的中点,若过点A ,E ,F 作一截面,则截面的周长为( )A .B .C .D .8.在立体几何中,用一个平面去截一个几何体得到的平面图形叫截面.平面α以任意角度截正方体,所截得的截面图形不可能为( ) A .等腰梯形 B .非矩形的平行四边形 C .正五边形 D .正六边形9.如图,正方体111ABCD A B C D -的棱长为1△P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S . ①当102CQ时,S 为四边形; ②当34CQ 时,S 与11C D 的交点R 满足113C R ; ③当314CQ时,S 为六边形;④当1CQ =时,S 则下列选项正确的是( )A .①②③B .①②④C .①③④D .②③④10.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q 的平面截该正方体所得的截面记为S .则下列命题中正确命题的个数为( )①当102CQ时,S 为四边形; ②当12CQ 时,S 为等腰梯形; ③当34CQ 时,S 与11C D 的交点1R 满足1113C R =;④当314CQ时,S 为六边形;A .1B .2C .3D .411.正方体1111ABCD A B C D -的棱长为1,E 、F ,G 分别为BC ,1CC ,1BB 的中点,有下述四个结论,其中正确的结论是( )①直线1GA 与平面AEF 平行;②平面AEF 截正方体所得的截面面积为98;③直线1A G 与直线EF 所成的角的余弦值为; ④点C 与点B 到平面AEF 的距离相等. A .①④ B .①②C .①②④D .①②③④12.如图,正方体1111ABCD A B C D -中,点E ,F ,分别是AB ,BC 的中点,过点1D ,E ,F 的截面将正方体分割成两个部分,记这两个部分的体积分别为()1212,V V V V <,则12:V V =( )A .13B .35C .2547 D .7913.如图,在正方体1111ABCD A B C D -中,点P 为线段11A C 上的动点(点P 与1A ,1C 不重合),则下列说法不正确的是( )A .BD CP ⊥B .三棱锥C BPD -的体积为定值C .过P ,C ,1D 三点作正方体的截面,截面图形为三角形或梯形 D .DP 与平面1111D C B A 所成角的正弦值最大为1314.正方体1111ABCD A B C D -的棱长为4,12B P PC =,113D Q QC =,用经过B ,P ,Q 三点的平面截该正方体,则所截得的截面面积为( )A.B .C D .15.如图,ABCD A B C D ''''-为正方体,任作平面α与对角线AC '垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S ,周长为l ,则( )A .S 为定值,l 不为定值B .S 不为定值,l 为定值C .S 与l 均为定值D .S 与l 均不为定值16.如图,在正方体1111ABCD A B C D -中,AB =2,E 为棱BC 的中点,F 为棱11A D 上的一动点,过点A ,E ,F 作该正方体的截面,则该截面不可能是( )A .平行四边形B .等腰梯形C .五边形D .六边形17.如图,在棱长为2的正方休1111ABCD A B C D -中,E ,F ,G 分别为11A D ,11A B ,1BB ,的中点,过E ,F ,G 三点的平而截正方休1111ABCD A B C D -所得的截面面积为( )A .4B .CD .18.正方体1111ABCD A B C D -的棱长为2,,,E F G 分别为11,,BC CC BB 的中点.则下列说法错误的是( )A .直线A 1G 与平面AEF 平行B .直线DD 1与直线AF 垂直C .异面直线A 1G 与EFD .平面AEF 截正方体所得的截面面积为9219.如图所示,在正方体1111ABCD A B C D -中,4AB =,M 、N 分别为棱11A D 、11A B 的中点,令过点B 且平行于平面AMN 的平面α被正方体的截面图形为Ω,若在Ω内随机选择一点P ,则点P 在正方体1111ABCD A B C D -内切球内的概率为( )A .427π B .1681πC .827π D .3281π20.已知正方体1111ABCD A B C D -内切球的表面积为π,P 是空间中任意一点: △若点P 在线段1AD 上运动,则始终有11C P CB ⊥; △若M 是棱11C D 中点,则直线AM 与1CC 是相交直线; △若点P 在线段1AD 上运动,三棱锥1D BPC -体积为定值;△E 为AD 中点,过点1B ,且与平面1A BE 以上命题为真命题的个数为( ) A .2 B .3 C .4 D .5二、多选题21.已知正方体1111ABCD A B C D -的棱长为1,下列结论正确的有( ) A .异面直线1CA 与11B D 所成角的大小为π3B .若E 是直线AC 上的动点,则1DE ∥平面11A BCCD .若此正方体的每条棱所在直线与平面α所成的角都相等,则α22.如图,棱长为1的正方体111ABCD A BC D -中P 为线段1A B 上的动点(不含端点)则下列结论正确的是( )A .直线1D P 与AC 所成的角可能是6π B .平面11D A P ⊥平面1A AP C .三棱雉1D CDP -的体积为定值D .平面1APD 截正方体所得的截面可能是直角三角形23.如图,在正方体1111ABCD A B C D -中,点E ,F 分别为11A B ,BC 的中点,设过点E ,F ,1D 的平面为α,则下列说法正确的是( )A .1EFD △为等边三角形;B .平面α交正方体1111ABCD A BCD -的截面为五边形;C .在正方体1111ABCD A B C D -中,存在棱与平面α平行; D .在正方体1111ABCD A B C D -中,不存在棱与平面α垂直;24.(多选)已知正方体1111ABCD A B C D -,若1AC ⊥平面α,则关于平面α截此正方体所得截面的判断正确的是( )A .截面形状可能为正三角形B .截面形状可能为正方形C .截面形状可能为正六边形D .截面形状可能为五边形25.如图,在棱长为1的正方体1111ABCD A B C D -中,P ,M ,N 分别为棱1CC ,CB ,CD 上的动点(点P 不与点C ,1C 重合),若CP CM CN ==,则下列说法正确的是( )A .存在点P ,使得点1A 到平面PMN 的距离为43B .用过P ,M ,1D 三点的平面去截正方体,得到的截面一定是梯形C .1//BD 平面PMND .用平行于平面PMN 的平面α去截正方体,得到的截面为六边形时,该六边形周长一定为26.如图所示,在棱长为2的正方体1111ABCD A B C D -中,M ,N 分别为棱11C D ,1C C 的中点,则下列结论正确的是( )A .直线AM 与BN 是平行直线B .直线MN 与AC 所成的角为60°C .直线MN 与平面ABCD 所成的角为45°D .平面BMN 截正方体所得的截面面积为3227.如图,在正方体1111ABCD A B C D -中,点P 为线段11A C 上的动点(点P 与1A ,1C 不重合),则下列说法正确的是( )A .BD CP ⊥B .三棱锥C BPD -的体积为定值C .过P ,C ,1D 三点作正方体的截面,截面图形为三角形或梯形D .DP 与平面1111D C B A 所成角的正弦值最大为1328.如图所示,在棱长为1的正方体1111ABCD A B C D -中,M ,N 分别为棱11A D ,1DD 的中点,则以下四个结论正确的是( )A .1//BC MNB .若P 为直线1CC 上的动点,则111B P BC ⋅为定值C .点A 到平面1C MN 的距离为13D .过MN 作该正方体外接球的截面,所得截面的面积的最小值为38π29.如图,正方体1111ABCD A B C D -的棱长为2,E ,F 分别为AD ,1AA 的中点,则以下说法正确的是( )A .平面EFC 截正方体所得截面周长为B .1BB 上存在点P ,使得1C P ⊥平面EFCC .三棱锥B EFC -和1D FB C -体积相等D .1BB 上存在点P ,使得//AP 平面EFC30.如图,正方体1111ABCD A B C D -的棱长为1,E ,F ,G 分别为BC ,1CC ,1BB 的中点,则( )A .直线1A D 与直线AF 垂直B .直线1A G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为98D .点B 到平面AEF 的距离为13第II 卷(非选择题)三、填空题31.已知正四棱柱1111ABCD A B C D -中,1124BE BB ==,143AB AA =,则该四棱柱被过点1A ,C ,E 的平面截得的截面面积为______.32.正三棱锥P ABC -AB ==E 在棱PA 上,且3PE EA =,已知点P A B C 、、、都在球O 的表面上,过点E 作球O 的截面α,则α截球O 所得截面面积的最小值为___________.33.已知在棱长为6的正方体ABCD -A 1B 1C 1D 1中,点E ,F 分别是棱C 1D 1,B 1C 1的中点,过A ,E ,F 三点作该正方体的截面,则截面的周长为________.34.正方体1111ABCD A B C D -的棱长为1,,,E F G 分别为11,,BC CC BB 的中点,下列四个选项①直线1D D 与直线AF 垂直②直线1A G 与平面AEF 平行③平面AEF 截正方体所得的截面面积为98④点C 和点G 到平面AEF 的距离相等;其中正确的是____________35.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A ,P ,Q的平面截该正方体所得的截面记为S ,则下列命题正确的是______ (写出所有正确命题的编号).①当102CQ 时,S 为四边形; ②当12CQ时,S 为等腰梯形; ③当34CQ时,S 与11C D 的交点R 满足113C R ; ④当314CQ 时,S 为六边形 四、解答题36.如图,在正方体1111ABCD A B C D -中,E F ,分别为11A D 和1CC 的中点.(1)画出由A ,E ,F 确定的平面β截正方体所得的截面,(保留作图痕迹,使用铅笔作图);(2)求异面直线EF 和AC 所成角的大小.37.已知正三棱柱的所有棱长都是1(1)画经过ABC 三点的截面(2)过棱BC 作和底面成60二面角的截面,求此截面面积.38.如图,在正方体1111ABCD A B C D 中,S 是11B D 的中点,E ,F ,G 分别是BC ,DC ,SC 的中点.求证:(1)直线//EG 平面11BDD B ;(2)平面//EFG 平面11BDD B ;(3)若正方体棱长为1,过A ,E ,1C 三点作正方体的截面,画出截面与正方体的交线,并求出截面的面积.39.(1)如图,棱长为2的正方体1111ABCD A B C D -中,M ,N 是棱11A B ,11A D 的中点,在图中画出过底面ABCD 中的心O 且与平面AMN 平行的平面在正方体中的截面,并求出截面多边形的周长为:______;(2)作出平面PQR 与四棱锥ABCDE 的截面,截面多边形的边数为______.40.如图①,正方体1111ABCD A B C D -的棱长为2,P 为线段BC 的中点,Q 为线段1CC 上的动点,过点A 、P 、Q 的平面截该正方体所得的截面记为S .(1)若12CQ <<,请在图①中作出截面S (保留尺规作图痕迹);(2)若1CQ =(如图②),试求截面S 将正方体分割所成的上半部分的体积1V 与下半部分的体积2V 之比.。
2021最新精选《截一个几何体》同步提升训练

《截一个几何体》提升训练
1(教材P15习题T3变式)一个几何体的截面是三角形,则原几何体一定不是下列图形中的()
A圆柱和圆锥 B球体和圆锥 C球体和圆柱 D正方体和圆锥
2下列几何体:①圆柱;②正方体:③棱锥;④球;⑤圆锥;⑥长方体中,截面可能是圆的有()
个个个个
3下列几何体的截面分别是()
A圆、平行四边形、三角形、圆 B圆、长方形、三角形、圆
C圆、长方形、长方形、三角形 D圆、长方形、三角形、三角形
4(太原调研)用一个平面去截下列几何体,其截面可能是六边形的几何体是()A圆柱 B圆锥 C三棱柱 D四棱柱
5一个圆柱形蛋糕,三刀最多切成()
块块块块
6用一个平面分别截六棱柱、长方体、圆柱、圆锥,得到的截面不可能为四边形的几何体是_______
7用一个平面去截一个正方体,所得截面的边数最少是______,最多是______ 8用一个平面去截一个圆柱:
(1)所得截面可能是三角形吗
(2)如果能得到正方形的截面,那么圆柱的底面半径和高有什么关系
9过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其展
开图正确的为
10如图,有一个外观为圆柱形的物体,它的内部构造看不到,当分别用一组平面沿水平方向(自上而下)和竖直方向(自左而右)截这个物体时,得到了如图所示的(1)(2)两组形状不同的截面,请你试着说出这个物体的内部构造
参考答案
6圆锥
6
8解:(1)用一个平面去截一个圆柱,所得截面不可能是三角形(2)圆柱的底面半径r与圆柱的高h之间的关系为h≤2r
10解:这个圆柱的内部构造为:圆柱中间有一球状空洞,即空心球。
2023-2024学年北师大版七年级数学上册随堂练习(附解析)1
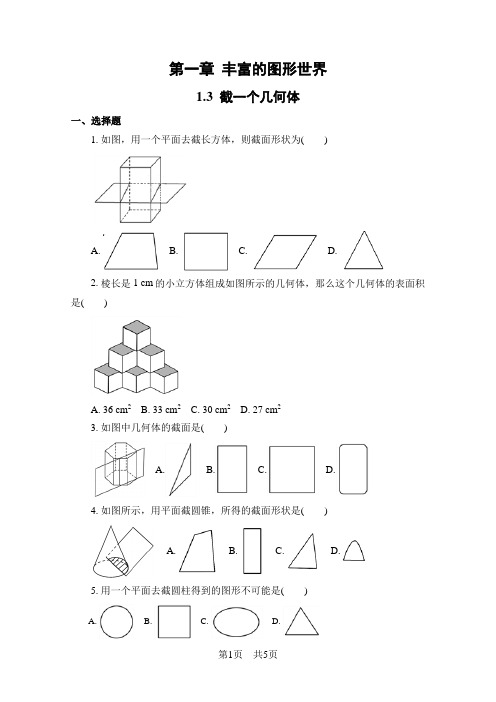
第一章丰富的图形世界1.3 截一个几何体一、选择题1. 如图,用一个平面去截长方体,则截面形状为()A. B. C. D.2. 棱长是1 cm的小立方体组成如图所示的几何体,那么这个几何体的表面积是()A. 36 cm2B. 33 cm2C. 30 cm2D. 27 cm23. 如图中几何体的截面是()A. B. C. D.4. 如图所示,用平面截圆锥,所得的截面形状是()A. B. C. D.5. 用一个平面去截圆柱得到的图形不可能是()A. B. C. D.第1页共5页二、填空题6. 在医学诊断上,有一种医学影像诊断技术叫CT,它的工作原理是______________.7. 用一个平面截一个正方体,所得截面是一个三角形,则留下的较大的一块几何体一定有________个面.8. 如图中几何体是一个圆锥被一平面截下的,由________个面围成,面与面的交线有________条,其中直线有____条.底面形状是________.9. 下面几何体的截面分别是什么?__________ ____________ __________ ________10. 如图给出一个圆锥,用一个平面去截这个圆锥,若要得到下列图形,应怎样去截?11. 把一个边长为2 cm的立方体截成八个边长为1 cm的小立方体,至少需要截___次.三、解答题12.如图,截一个正方体,可以得到三角形,但要得到一个最大的等边三角形,你会切吗?你能说出你的切法吗?13. 将图①的正方体切去一块,不同的切法可以得到图②~⑤的几何体,它们各有多少个面?多少条棱?多少个顶点?参考答案1. 【答案】B【解析】根据长方体的形状及截面与底面平行判断即可.横截长方体,截面平行于两底,那么截面应该是个长方形.故选B.点评:本题考查了长方体的截面.截面的形状既与被截的几何体有关,还与截面的角度和方向有关.2. 【答案】A【解析】正视图中正方形有6个;左视图中正方形有6个;俯视图中正方形有6个.则这个几何体中正方形的个数是:2×(6+6+6)=36个.则几何体的表面积为36cm2.故选A.考点:几何体的表面积.3. 【答案】B【解析】由图可知:截面是长方形.故选B.4. 【答案】D【解析】如果用平面取截圆锥,平面过圆锥顶点时得到的截面图形是一个三角形;如果不过顶点,且平面与底面平行,那么得到的截面就是一个圆;如果不与底面平行,平面与圆锥的侧面截得一条弧线,与底面截得一条直线,所以截面第3页共5页的形状应该是D.故选D.5. 【答案】D【解析】A.用平面截圆柱,横切就是圆,故可以得到,不符合题意;B. 竖切就是长方形,故可以得到,不符合题意;C. 如果倾斜着切圆柱,可以得到椭圆形,故可以得到,不符合题意;D. 唯独不可能是三角形,故此无法得到,符合题意;故选:D.6. 【答案】利用射线截几何体,图象重建原理【解析】CT实际上是用取得人体的一个平面,即把人体看做是几何体,把CT的面看作截面,因此工作原理与截“几何体”相似.故答案为:利用射线截几何体,图象重建原理.7. 【答案】7【解析】用一个平面截正方体,若所得的截面是一个三角形,此时剩下的较大的几何体一定比正方体多了一个面.故答案为:7.8.【答案】 (1). 3 (2). 4 (3). 3 (4). 有可能是半圆,有可能是弓形,但不可能是扇形【解析】如图几何体是一个圆锥被一平面截下的,由3个面围成,面与面的交线有4条,其中直线有3条.底面形状是有可能是半圆,有可能是弓形,但不可能是扇形.故答案为:(1).3 (2).4 (3)3 (4)有可能是半圆,有可能是弓形,但不可能是扇形.9. 【答案】 (1). 长方形 (2). 圆 (3). 长方形 (4). 圆10. 【答案】见解析.【解析】根据题意,用平面去截圆锥,平面过圆锥顶点且垂直于底面时,得到的截面图形是一个等腰三角形;当平面与底面平行截取时,得到的截面就是一个圆;如果不过顶点且倾斜于底面时,得到的截面图形是一个类似椭圆的形状,自己尝试着画出截取时对应的图形.解:如图所示.11. 【答案】3【解析】要截成八个边长为1cm的小立方体,应该横着从中间截一次,然后竖着从中间截两次,并且这两次截得方向垂直.由图片可知,共需截3次.12.【答案】见解析.【解析】沿对角线切即可.解:如图所示.沿着对角线切即可.13. 【答案】见解析.【解析】图②中,切去一部分后,观察发现,增加了一个面、两个顶点、三条棱,再结合正方体的特点,即可得出图形①中面、棱、顶点的个数.接下来,结合所给图形以及面、棱、顶点的定义算出几何体的面、棱和顶点.解:第5页共5页。
截一个几何体练习

3截一个几何体预习要点:1.用一个去截一个几何体,截出的面叫做截面。
2.用一个平面去截一个圆柱体,截面不可能的是()A.B.C.D.3.正方体的截面不可能是()A.四边形B.五边形C.六边形D.七边形4.用一个平面去截:①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆的图形是()A.①②④B.①②③C.②③④D.①③④5.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②圆柱;③圆锥;④正三棱柱(写出所有正确结果的序号).6.用一个平面去截一个几何体,若截面是长方形,则该几何体可能是(写三个).7.如图,截面依次是.同步小题12道一.选择题1.用一个平面去截一个正方体,截面不可能是()A.梯形B.五边形C.六边形D.圆2.用一个平面去截一个正方体,截面的形状不可能是()A.梯形B.五边形C.六边形D.七边形3.用一个平面去截圆柱体,则截面形状不可能是()A.梯形B.正方形C.长方形D.圆4.如图所示,用一个平面去截一个圆柱,则截得的形状应为()A.B.C.D.5.下列几何体的截面是()A.B.C.D.6.如图所示几何体的截面是()A.四边形B.五边形C.六边形D.五棱柱二.填空题7.用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是.8.一个平面去截球,截面的形状一定是.9.在如图所示的四个图形中,图形可以用平面截长方体得到;图形可以用平面截圆锥得到(填序号)10.如图是一个正方体,用一个平面去截这个正方体,截面形状不可能是选项中的(填序号)三.解答题11.如图是三个三棱柱,用一刀切下去.(1)把图①中的三棱柱分割成两个完全相同的三棱柱;(2)把图②中的三棱柱分割成一个四棱锥与一个三棱锥;(3)把图③中的三棱柱分割成一个四棱柱与一个三棱柱.12.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.如A(1、5、6);则B(______);C(______);D(______);E(______).答案:预习要点:1.平面2.解析:当截面与轴截面平行时,得到的形状为长方形;当截面与轴截面垂直时,得到的截面形状是圆;当截面与轴截面斜交时,得到的截面的形状是椭圆;所以截面的形状不可能是等腰梯形.故选B3.解析:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.故选D4.解析:圆锥,如果截面与底面平行,那么截面就是圆;圆柱,如果截面与上下面平行,那么截面是圆;球,截面一定是圆;五棱柱,无论怎么去截,截面都不可能有弧度.故选B5.解析:①正方体能截出三角形;②圆柱不能截出三角形;③圆锥沿着母线截几何体可以截出三角形;④正三棱柱能截出三角形.故截面可能是三角形的有3个.答案:①③④.6.解析:用一个平面去截一个几何体,如果截面的形状是长方形,原来的几何体可能是长方体、正方体、圆柱.答案:长方体、正方体、圆柱(答案不唯一).7.答案:长方形、三角形、圆形.同步小题12道1.解析:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此不可能是圆.故选D2.解析:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.故选D3.解析:本题中用平面截圆柱,横切就是圆,竖切就是长方形,如果这个圆柱特殊点,底面圆的直径等于高的话,那有可能是正方形,唯独不可能是梯形.故选A4.解析:平面平行圆柱底面截圆柱可以得到一个圆,而倾斜截得到椭圆,故选B5.解析:用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,由图象可知截面是三角形.故选A6.解析:此几何体是五棱柱,故其截面的形状是五边形.故选:B7.解析:长方体沿体面对角线截几何体可以截出三角形;五棱柱沿顶点截几何体可以截得三角形;圆柱不能截出三角形;圆锥沿顶点可以截出三角形.故不能截出三角形的几何体是圆柱.答案:圆柱.8.解析:根据球的几何特征,一平面截球面产生的截面形状是圆.答案:圆.9.解析:图形②③④可以用平面截长方体得到;图形①④可以用平面截圆锥得到,答案:②③④;①④.10.解析:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为圆.答案:4.11.解:(1)(2)(3)如图所示:12.解析:B三棱锥,截面有可能是三角形,正方形,梯形C正方体,截面有可能是三角形,四边形(矩形,正方形,梯形),五边形,六边形D球体,截面只可能是圆E圆柱体,截面有可能是椭圆,圆,矩形.答案:B(1、3、4);C(1、2、3、4);D(5);E(3、5、6)。
初中数学七年级上册《1.3截一个几何体》习题

初中数学七年级上册《1.3截一个几何体》习题一、基础过关1.如图,是一个正方体的平面展开图,在正方体中写有“心”字的那一面的对面的字是()A.祝B.您C.事D.成2.如图给定的是纸盒的外表面,下面能由它折叠而成的是()3.用平面去截一个正方体,截面的形状不可能是()A.四边形B.五边形C.六边形D.七边形4.如图所示的图形可以被折成一个长方体,则该长方体的表面积为cm2.5.如图,将正方体沿面AB′C剪下,则截下的几何体为.6.已知小立方块面A,B,C的对面上分别写有数字4,5,6,如图所示,小立方块沿平面上写有数字1→2→3→4→5→6→7→8的方向滚动,那么当小立方块滚动到8时,小立方块最上面的面写的是.二、综合训练7.如图是一个棱柱形状的食品包装盒的侧面展开图.(1)请写出这个包装盒的多面体形状的名称.(2)根据图中所标的尺寸,计算这个多面体的侧面积.8.如图是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:(1)如果A面在长方体的底部,那么哪一个面会在上面?(2)如果F面在前面,B面在左面,那么哪一个面会在上面?(字母朝外)(3)如果C面在右面,D面在后面,那么哪一个面会在上面?(字母朝外)三、拓展应用9.如图1,大正方体上截去一个小立方块后,可得到图2的几何体.(1)设原大正方体的表面积为S,图2中几何体的表面积为S′,那么S′与S的大小关系是()A.S′>SB.S′=SC.S′<SD.不确定(2)小明说:“设图1中大正方体各棱的长度之和为c,图2中几何体各棱的长度之和为c′,那么c′比c正好多出大正方体3条棱的长度.”若设大正方体的棱长为1,小立方块的棱长为x,请问x 为何值时,小明的说法才正确?(3)如果截去的小立方块的棱长为大正方体棱长的一半,那么图3是图2中几何体的展开图吗?如有错误,请在图3中修正.参考答案一、基础过关1.D.2.B.3. D.4. 885.三棱锥6. 6二、综合训练7. (1)共有3个长方形组成侧面,2个三角形组成底面,故是三棱柱.(2)因为AB=5,AD=3,BE=4,DF=6,所以侧面积为3×6+5×6+4×6=18+30+24=72.8.由图可知,“A”与“F”相对,“B”与“D”相对,则“C”与“E”相对.(1)因为面“A”与面“F”相对,所以A面是长方体的底部时,F面在上面.(2)由图可知,如果F面在前面,B面在左面,那么“E”面在下面,因为“C”与“E”相对,所以C面会在上面.(3)由图可知,如果C面在右面,D面在后面,那么“F”面在下面,因为“A”与“F”相对,所以A面会在上面.三、拓展应用(1)选B.因截去的是小立方块,且截掉的是小立方块的3个面,在大正方体中又“截出”的面是小立方块的另外3个面,而正方体的6个面相等,故表面积不变.(2)由题意得:6x=3,所以x=12,所以x为12时,小明的说法才正确.(3)不正确,如图:。
【奥数系列训练】(含答案)12——几何体的计算

【奥数系列训练】(含答案)12——几何体的计算请填入正确答案:【题目1】用棱长为1cm的18个正方体做长方体,要使他的表面积最小,问最小表面积应该多大?【题目2】有两个边长为8cm正方体盒子。
A盒子放入直径8cm,高8cm的圆柱体铁块一个,B盒子放入直径4cm、高8cm的圆柱体铁块4个。
现在A盒注满水,把A盒中水倒入B盒,使B盒注满水。
A盒剩下水是多少立方公分?【题目3】一个正方体木块,棱长是5,如果在他上面截去一个棱长为5×3×2的长方体,那么,他的表面积减少百分之几?【题目4】现有一张长40公分,宽20公分的长方形铁皮。
请你用它做一只深是5公分的正方体无盖铁片盒(焊接处及铁片厚度不计,容积越大越好)。
你做的铁皮盒的容积是多少立方公分?【题目5】把12件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体包装物。
如何包装使长方体的表面积最小,最小表面积是多少?【题目6】从一个长9公分、宽7公分、高5公分的长方体中截下一个最大的立方体,剩下部分的棱长总和最大是多少公分?【题目7】在底面是正方形,棱长都是整公尺数,棱长总和为96公尺的长方体中,居中打一个底面为正方形,面积为4平方公尺的上下直穿的长方体的洞。
前、后、左、右也分别居中打一个长14公尺,宽2公尺的长方体洞。
这个几何体的表面积是多少平方公尺?【题目8】一个长方体盒子,从里面量长40公分,宽12公分,高7公分。
在这个盒子里放一个长5公分,宽4公分,高3公分的方形木块。
问最多可以放多少块?【题目9】一个棱长为6公分的正方体,沿着△ADE所在的平面将正方体切掉一个角,问切掉的三棱锥EABD的体积是多少?【题目10】用一张长30公分,宽20公分的长方形铁皮,做一个深5公分的长方体无盖铁皮盒(焊接处与铁皮厚度不计)。
这个铁皮盒的容积最大是多少立方公分?【参考答案】1.【解答】要使着18个棱长为1cm的小正方体做成的长方体的表面积最小,就应该使做成的长方体接近于正六面体(正方体)。
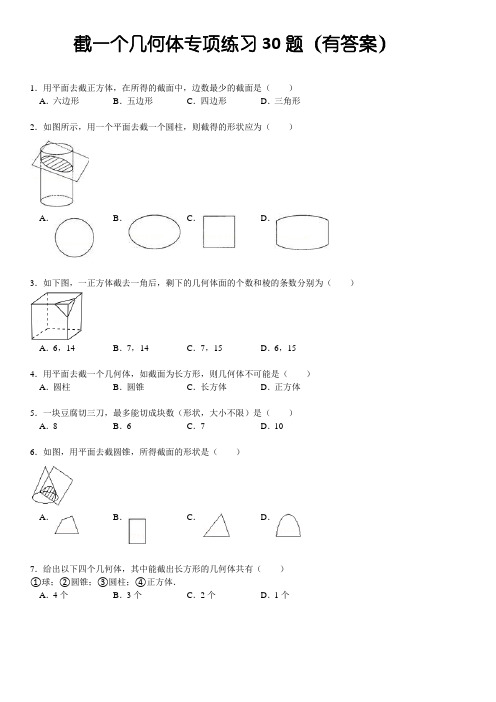
截一个几何体专项练习30题(有答案)ok
截一个几何体专项练习30题(有答案)1.用平面去截正方体,在所得的截面中,边数最少的截面是()A.六边形B.五边形C.四边形D.三角形2.如图所示,用一个平面去截一个圆柱,则截得的形状应为()A.B.C.D.3.如下图,一正方体截去一角后,剩下的几何体面的个数和棱的条数分别为()A.6,14 B.7,14 C.7,15 D.6,154.用平面去截一个几何体,如截面为长方形,则几何体不可能是()A.圆柱B.圆锥C.长方体D.正方体5.一块豆腐切三刀,最多能切成块数(形状,大小不限)是()A.8B.6C.7D.106.如图,用平面去截圆锥,所得截面的形状是()A.B.C.D.7.给出以下四个几何体,其中能截出长方形的几何体共有()①球;②圆锥;③圆柱;④正方体.A.4个B.3个C.2个D.1个8.请指出图中几何体截面的形状()A.B.C.D.9.如图是一个长方形截去两个角后的立体图形,如果照这样截去长方形的八个角,那么新的几何体的棱有()A.26条B.30条C.36条D.42条10.下列说法中,正确的是()A.用一个平面去截一个圆锥,可以是椭圆B.棱柱的所有侧棱长都相等C.用一个平面去截一个圆柱体,截面可以是梯形D.用一个平面去截一个长方体截面不能是正方形11.下列说法上正确的是()A.长方体的截面一定是长方形B.正方体的截面一定是正方形C.圆锥的截面一定是三角形D.球体的截面一定是圆12.下列说法中正确的是()A.圆柱的截面可能是三角形B.球的截面有可能不是圆C.圆锥的截面可能是圆D.长方体的截面不可能是六边形13.如图所示,几何体截面的形状是()A.B.C.D.14.用平面截一个正方体,可能截出的边数最多的多边形是()A.七边形B.六边形C.五边形D.四边形15.下面说法,不正确的是()A.将一块直角三角板绕着它的一条直角边旋转1周,能形成一个圆锥B.用一个平面截一个正方体,得到的截面可以是五边形C.一个平面截一个球,得到的截面一定是圆D.圆锥的截面不可能是三角形16.用不同的方法将长方体截去一个角,在剩下的各种几何体中,顶点最多的个数以及棱数最少的条数分别为()A.9个,12条B.9个,13条C.10个,12条D.10个,13条17.用平面去截下列几何体,能截得长方形、三角形、等腰梯形三种形状的截面,这个几何体是()A.B.C.D.18.一块方形蛋糕,一刀切成相等的两块,两刀最多切成4块,试问:五刀最多可切成_________块相等体积的蛋糕,十刀最多可切成_________块(要求:竖切,不移动蛋糕).19.仔细观察,用一个平面截一个正方体所得截面形状,试写出这些截面的名称:想一想:用一个平面截一个正方体,截面的形状可能是七边形吗?_________.20.一个物体的外形是长方体,其内部构造不详.用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是_________.21.用平面去截一个三棱锥,截面可能是_________形或_________形.22.如图是一个正方体劈去一个角后得到的多面体,有_________个面,_________个顶点,_________条棱,则其顶点数+面数﹣棱数=_________.23.把三棱锥截去一个角,所得的截面是_________形.24.一个正方体的8个顶点被截去后,得到一个新的几何体,这个新的几何体有_________个面,_________个顶点,_________条棱.25.用一个平面去截一个正方体,图中画有阴影的部分是截面,下面有关截面画法正确的序号有_________.26.一个五棱柱有_________个面,用一个平面去截五棱柱,则得到的截面的形状不可能是_________(填“七边形“或“八边形“)27.下列图形:①等腰三角形,②矩形,③正五边形,④正六边形.其中只有三个是可以通过切正方体而得到的切口平面图形,这三个图形的序号是_________.28.如图从边长为10的正方体的一顶点处挖去一个边长为1的小正方体,则剩下图形的表面积为_________.29.用一个平面去截一个五棱柱,可把这个五棱柱分成一个三棱柱和一个四棱柱,一个八棱柱用_________个平面去截可把这个八棱柱分成六个三棱柱.30.请问:平面图形①②③④⑤分别可由平面截几何体A、B、C、D中的哪些得到?截一个几何体专项练习30题参考答案:1.解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,∴边数最少的截面是三角形,故选D.2.解:平面平行圆柱底面截圆柱可以得到一个圆,而倾斜截得到椭圆,故选B3.解:原来正方体的面数为6,增加1变为7;原来正方体的棱数为12,增加3变为15,故选C.4.解:A、圆柱的轴截面为长方形,不符合题意,本选项错误;B、圆锥的轴截面为三角形,其它截面为圆、椭圆,不可能是长方形,符合题意,本选项正确;C、长方体的轴截面为长方形,不符合题意,本选项错误;D、正方体的轴截面可以是长方形,不符合题意,本选项错误.故选B5.解:如图切三刀,最多切成8块,故选A6.解:用平面取截圆锥,如图:平面与圆锥的侧面截得一条弧线,与底面截得一条直线,所以截面的形状应该是D.故选D7.解:当截面与圆柱的底面垂直时可以截得长方形,当截面截取正方形两条平行的面对角线组成的面时,可以截得长方形,球和圆锥都不能截出长方形,故选C8.解:根据图中所示,平面与圆锥侧面相截得到一条弧线,与底面相截得到一条直线,那么截面图形就应该是C.故选C9.解:∵一个长方体有4+4+4=12条棱,一个角上裁出3条棱,即8个角共3×8条棱,∴12+3×8=36,故选C.10.解:A、用一个平面去截一个圆锥,不可以是椭圆,故选项错误;B、根据棱柱的特征可知,棱柱的所有侧棱长都相等,故选项正确;C、用一个平面去截一个圆柱体,截面不可以是梯形,故选项错误;D、用一个平面去截一个长方体,截面可能是正方形,故选项错误.故选B11.解:A、长方体的截面还可能是三角形,故本选项错误;B、正方体的截面还可能是三角形,故本选项错误;C、圆锥的截面为与圆有关的或与三角形有关的形状,故本选项错误;D、球体的截面一定是圆,故本选项正确.故选D12.解:A、圆柱体中如果截面和底面平行是可以截出圆的,如果不平行截面有可能是椭圆,但不可能是三角形,故本选项错误;B、球体中截面是圆,故本选项错误;C、圆锥中如果截面和底面平行截出的是圆,故本选项正确;D、长方体的截面如果经过六个面,则截面是六边形,如右图,故本选项错误.故选C.13.解:几何体初中阶段有:圆柱、球体、圆锥,∴其截面的形状有圆、长方形、三角形、梯形等.故选B14.解:正方体有六个面,截面与其六个面相交最多得六边形,故选B.15.解:A、将一块直角三角板绕着它的一条直角边旋转1周,能形成一个圆锥,正确;B、用一个平面截一个正方体,得到的截面可以是三角形,四边形或五边形或六边形,正确;C、一个平面截一个球,得到的截面一定是圆,正确;D、圆锥的截面可能是圆或三角形,错误.故选D16.解:依题意,剩下的几何体可能有:7个顶点、12条棱、7个面;或8个顶点、13条棱、7个面;或9个顶点、14条棱、7个面;或10个顶点、15条棱、7个面.如图所示:因此顶点最多的个数是10,棱数最少的条数是12,故选C17.解:圆台的截面不能得到长方形;圆锥的截面不能得到长方形;圆柱的截面不能得到等腰梯形;当截面经过正方体的3个面时,得到三角形,当截面与正方体的一个面平行时得到长方形,当截面经过正方体的一个正方形的对角的顶点,经过4个面,又与对面斜交时,可得到等腰梯形,故选D18.解:当切1刀时,块数为1+1=2块;当切2刀时,块数为1+1+2=4块;当切3刀时,块数为1+1+2+3=7块;…当切n刀时,块数=1+(1+2+3…+n)=1+.则切5刀时,块数为1+=16块;切8刀时,块数为1+=56块.故答案为:16,5619.解:平行四边形、等腰三角形、等腰梯形,六边形、五边形、三角形,不可能是七边形.20.一个物体的外形是长方体,其内部构造不详.用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是圆锥状空洞.21.用平面去截一个三棱锥,截面可能是三角形或四边形.22.如图是一个正方体劈去一个角后得到的多面体,有7个面,10个顶点,15条棱,则其顶点数+面数﹣棱数=2.23.把三棱锥截去一个角,所得的截面是三角形.24.解:每截去一个顶点就会多出1个面,2个顶点和3条棱,那么得到的新的几何体就应该有6+8=14个面,8+8×2=24个顶点,12+8×3=36条棱.故填14、24、3625.解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,即阴影部分必须至少分布在三个平面,因此①是错误的,故②③④正确.故答案为:②③④26.解:一个五棱柱有5个侧面和2个底面构成,所以它有7个面.截面可以经过三个面,四个面,五个面,七个面那么得到的截面的形状可能是三角形,四边形,或五边形,七边形,所以截面不可能是八边形.故答案是:7;八边形27.解:可以通过切正方体而得到的切口平面图形应该是①②④28.解:由图可知,挖去小正方体后,其实剩下的图形的表面积与原正方体的面表积是相等的,因此,剩下图形的表面积=10×10×6=60029.解:如图所示:一个八棱柱用5个平面去截可把这个八棱柱分成六个三棱柱.故答案为:5.30.解:根据图形可得出:平面图形①可由平面截几何体A、B、D得到;平面图形②可由平面截几何体B得到;平面图形③可由平面截几何体B、C得到;平面图形④可由平面截几何体B、D得到;平面图形⑤可由平面截几何体A、C得到(注:文档可能无法思考全面,请浏览后下载,供参考。
知识点229 截一个几何体(解答题)

12.把一个正方体用刀切去一块,能否还得到正方体?长方体、三棱柱、三棱锥、四棱柱、五棱柱呢?考点:截一个几何体。
专题:应用题。
分析:当截面的角度和方向不同时,圆柱体的截面不相同.解答:解:不能得到正方体,当截面平行正方体一面截取正方形时可以截得长方体,把正方体按面对角线垂直截取正方体可以得到三棱柱,经过正方体三个相邻的顶点截取可以得到三棱锥,经过两个相对面棱上中点截取可以得到四棱柱,经过上下两面棱的中截取可以得到五棱柱.点评:截面的形状既与被截的几何体有关,还与截面的角度和方向有关.13.今有正方形蛋糕,切两刀把蛋糕分成形状相同的4块,请设计三种不同的方法.考点:截一个几何体。
专题:作图题。
分析:可沿正方形的两条对角线切;沿过正方形的对边中点的两条线切;由此推出只要经过正方形的对角线的交点且互相垂直的两条直线均可且成形状相同的4部分.解答:解:点评:用到的知识点为:经过正方形的中心且互相垂直的两条直线把正方形分成形状相同的4块.14.如图是一个三棱柱,把它一刀切去一部分,剩下的部分会是一个什么图形?先动手做做实验,然后得出结论.考点:截一个几何体。
专题:操作型。
分析:沿垂直于轴截面剪去,可得三棱柱;沿经过上底面的一个顶点及下底面相对的顶点的对边的面剪去,可得到三棱锥;沿平行于三棱柱的一个侧面面剪去,可得到的一个四棱柱.解答:解:可以切成三棱柱、三棱锥、四棱柱.点评:用到的知识点为:棱柱的侧面是四边形;棱锥的侧面是三角形;注意根据截面经过的不同位置得到相应的几何体的形状.15.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.如A(1、5、6);则B();C();D();E().考点:截一个几何体。
分析:分别分析其余四种图形的所有的截面情况,再写出答案.解答:解:B三棱锥,截面有可能是三角形,正方形,梯形C正方体,截面有可能是三角形,四边形(矩形,正方形,梯形),五边形,六边形D球体,截面只可能是圆E圆柱体,截面有可能是椭圆,圆,矩形,梯形因此应该写B(1、3、4);C(1、2、3、4);D(5);E(3、5、6).点评:截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.16.附加题:(1)解方程:.(2)按图示切割正方体就可以切割出正六边形(正六边形的各顶点恰是其棱的中点),请你任意画出此正方体的两种平面展开图,并在展开图上画出所有的切割线.考点:截一个几何体;解一元一次方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
截一个几何体专项练习30题(有答案)1.用平面去截正方体,在所得的截面中,边数最少的截面是()A.六边形B.五边形C.四边形D.三角形2.如图所示,用一个平面去截一个圆柱,则截得的形状应为()A.B.C.D.3.如下图,一正方体截去一角后,剩下的几何体面的个数和棱的条数分别为()A.6,14B.7,14C.7,15D.6,154.用平面去截一个几何体,如截面为长方形,则几何体不可能是()A.圆柱B.圆锥C.长方体D.正方体5.一块豆腐切三刀,最多能切成块数(形状,大小不限)是()A.8B.6C.7D.106.如图,用平面去截圆锥,所得截面的形状是()A.B.C.D.7.给出以下四个几何体,其中能截出长方形的几何体共有()①球;②圆锥;③圆柱;④正方体.A.4个B.3个C.2个D.1个8.请指出图中几何体截面的形状()A.B.C.D.9.如图是一个长方形截去两个角后的立体图形,如果照这样截去长方形的八个角,那么新的几何体的棱有()A.26条B.30条C.36条D.42条10.下列说法中,正确的是()A.用一个平面去截一个圆锥,可以是椭圆B.棱柱的所有侧棱长都相等C.用一个平面去截一个圆柱体,截面可以是梯形D.用一个平面去截一个长方体截面不能是正方形11.下列说法上正确的是()A.长方体的截面一定是长方形B.正方体的截面一定是正方形C.圆锥的截面一定是三角形D.球体的截面一定是圆12.下列说法中正确的是()A.圆柱的截面可能是三角形B.球的截面有可能不是圆C.圆锥的截面可能是圆D.长方体的截面不可能是六边形13.如图所示,几何体截面的形状是()A.B.C.D.14.用平面截一个正方体,可能截出的边数最多的多边形是()A.七边形B.六边形C.五边形D.四边形15.下面说法,不正确的是()A.将一块直角三角板绕着它的一条直角边旋转1周,能形成一个圆锥B.用一个平面截一个正方体,得到的截面可以是五边形C.一个平面截一个球,得到的截面一定是圆D.圆锥的截面不可能是三角形16.用不同的方法将长方体截去一个角,在剩下的各种几何体中,顶点最多的个数以及棱数最少的条数分别为()A.9个,12条B.9个,13条C.10个,12条D.10个,13条17.用平面去截下列几何体,能截得长方形、三角形、等腰梯形三种形状的截面,这个几何体是()A.B.C.D.18.一块方形蛋糕,一刀切成相等的两块,两刀最多切成4块,试问:五刀最多可切成_________ 块相等体积的蛋糕,十刀最多可切成_________ 块(要求:竖切,不移动蛋糕).19.仔细观察,用一个平面截一个正方体所得截面形状,试写出这些截面的名称:想一想:用一个平面截一个正方体,截面的形状可能是七边形吗?_________ .20.一个物体的外形是长方体,其内部构造不详.用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是_________ .21.用平面去截一个三棱锥,截面可能是_________ 形或_________ 形.22.如图是一个正方体劈去一个角后得到的多面体,有_________ 个面,_________ 个顶点,_________ 条棱,则其顶点数+面数﹣棱数= _________ .23.把三棱锥截去一个角,所得的截面是_________ 形.24.一个正方体的8个顶点被截去后,得到一个新的几何体,这个新的几何体有_________ 个面,_________ 个顶点,_________ 条棱.25.用一个平面去截一个正方体,图中画有阴影的部分是截面,下面有关截面画法正确的序号有_________ .26.一个五棱柱有_________ 个面,用一个平面去截五棱柱,则得到的截面的形状不可能是_________ (填“七边形“或“八边形“)27.下列图形:①等腰三角形,②矩形,③正五边形,④正六边形.其中只有三个是可以通过切正方体而得到的切口平面图形,这三个图形的序号是_________ .28.如图从边长为10的正方体的一顶点处挖去一个边长为1的小正方体,则剩下图形的表面积为_________ .29.用一个平面去截一个五棱柱,可把这个五棱柱分成一个三棱柱和一个四棱柱,一个八棱柱用_________ 个平面去截可把这个八棱柱分成六个三棱柱.30.请问:平面图形①②③④⑤分别可由平面截几何体A、B、C、D中的哪些得到?截一个几何体专项练习30题参考答案:1.解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,∴边数最少的截面是三角形,故选D.2.解:平面平行圆柱底面截圆柱可以得到一个圆,而倾斜截得到椭圆,故选B3.解:原来正方体的面数为6,增加1变为7;原来正方体的棱数为12,增加3变为15,故选C.4.解:A、圆柱的轴截面为长方形,不符合题意,本选项错误;B、圆锥的轴截面为三角形,其它截面为圆、椭圆,不可能是长方形,符合题意,本选项正确;C、长方体的轴截面为长方形,不符合题意,本选项错误;D、正方体的轴截面可以是长方形,不符合题意,本选项错误.故选B5.解:如图切三刀,最多切成8块,故选A6.解:用平面取截圆锥,如图:平面与圆锥的侧面截得一条弧线,与底面截得一条直线,所以截面的形状应该是D.故选D7.解:当截面与圆柱的底面垂直时可以截得长方形,当截面截取正方形两条平行的面对角线组成的面时,可以截得长方形,球和圆锥都不能截出长方形,故选C8.解:根据图中所示,平面与圆锥侧面相截得到一条弧线,与底面相截得到一条直线,那么截面图形就应该是C.故选C9.解:∵一个长方体有4+4+4=12条棱,一个角上裁出3条棱,即8个角共3×8条棱,∴12+3×8=36,故选C.10.解:A、用一个平面去截一个圆锥,不可以是椭圆,故选项错误;B、根据棱柱的特征可知,棱柱的所有侧棱长都相等,故选项正确;C、用一个平面去截一个圆柱体,截面不可以是梯形,故选项错误;D、用一个平面去截一个长方体,截面可能是正方形,故选项错误.故选B11.解:A、长方体的截面还可能是三角形,故本选项错误;B、正方体的截面还可能是三角形,故本选项错误;C、圆锥的截面为与圆有关的或与三角形有关的形状,故本选项错误;D、球体的截面一定是圆,故本选项正确.故选D12.解:A、圆柱体中如果截面和底面平行是可以截出圆的,如果不平行截面有可能是椭圆,但不可能是三角形,故本选项错误;B、球体中截面是圆,故本选项错误;C、圆锥中如果截面和底面平行截出的是圆,故本选项正确;D、长方体的截面如果经过六个面,则截面是六边形,如右图,故本选项错误.故选C.13.解:几何体初中阶段有:圆柱、球体、圆锥,∴其截面的形状有圆、长方形、三角形、梯形等.故选B14.解:正方体有六个面,截面与其六个面相交最多得六边形,故选B.15.解:A、将一块直角三角板绕着它的一条直角边旋转1周,能形成一个圆锥,正确;B、用一个平面截一个正方体,得到的截面可以是三角形,四边形或五边形或六边形,正确;C、一个平面截一个球,得到的截面一定是圆,正确;D、圆锥的截面可能是圆或三角形,错误.故选D16.解:依题意,剩下的几何体可能有:7个顶点、12条棱、7个面;或8个顶点、13条棱、7个面;或9个顶点、14条棱、7个面;或10个顶点、15条棱、7个面.如图所示:因此顶点最多的个数是10,棱数最少的条数是12,故选C17.解:圆台的截面不能得到长方形;圆锥的截面不能得到长方形;圆柱的截面不能得到等腰梯形;当截面经过正方体的3个面时,得到三角形,当截面与正方体的一个面平行时得到长方形,当截面经过正方体的一个正方形的对角的顶点,经过4个面,又与对面斜交时,可得到等腰梯形,故选D18.解:当切1刀时,块数为1+1=2块;当切2刀时,块数为1+1+2=4块;当切3刀时,块数为1+1+2+3=7块;…当切n刀时,块数=1+(1+2+3…+n)=1+.则切5刀时,块数为1+=16块;切8刀时,块数为1+=56块.故答案为:16,5619.解:平行四边形、等腰三角形、等腰梯形,六边形、五边形、三角形,不可能是七边形.20.一个物体的外形是长方体,其内部构造不详.用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是圆锥状空洞.21.用平面去截一个三棱锥,截面可能是三角形或四边形.22.如图是一个正方体劈去一个角后得到的多面体,有7 个面,10 个顶点,15 条棱,则其顶点数+面数﹣棱数= 2 .23.把三棱锥截去一个角,所得的截面是三角形.24.解:每截去一个顶点就会多出1个面,2个顶点和3条棱,那么得到的新的几何体就应该有6+8=14个面,8+8×2=24个顶点,12+8×3=36条棱.故填14、24、3625.解:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,即阴影部分必须至少分布在三个平面,因此①是错误的,故②③④正确.故答案为:②③④26.解:一个五棱柱有5个侧面和2个底面构成,所以它有7个面.截面可以经过三个面,四个面,五个面,七个面那么得到的截面的形状可能是三角形,四边形,或五边形,七边形,所以截面不可能是八边形.故答案是:7;八边形27.解:可以通过切正方体而得到的切口平面图形应该是①②④28.解:由图可知,挖去小正方体后,其实剩下的图形的表面积与原正方体的面表积是相等的,因此,剩下图形的表面积=10×10×6=60029.解:如图所示:一个八棱柱用5个平面去截可把这个八棱柱分成六个三棱柱.故答案为:5.30.解:根据图形可得出:平面图形①可由平面截几何体A、B、D得到;平面图形②可由平面截几何体B得到;平面图形③可由平面截几何体B、C得到;平面图形④可由平面截几何体B、D得到;平面图形⑤可由平面截几何体A、C得到。
