随机过程第4章离散部分复习题与参考答案
随机过程习题集-第四章马尔可夫过程

1第四章 马尔可夫过程内容提要1. 马尔可夫过程的概念 (1)马尔可夫过程给定随机过程{}(),X t t T ∈,如果对122,∀≥∀<<<∈n n t t t T ,有11221111{()|(),(),,()}{()|()}n n n n n n n n P X t x X t x X t x X t x P X t x X t x ----<====<=则称{}(),X t t T ∈为马尔可夫过程。
称(){}:,==∈E x X t x t T 为状态空间。
参数集和状态空间都是离散的马尔可夫过程称为离散参数马氏链. 参数连续、状态空间离散的马尔可夫过程称为连续参数马氏链. (2)k 步转移概率设{}(),0,1,2,=X n n 为离散参数马氏链,称()(),(,){|},0,1=+==≥≥i j p n k P X n k j X n i n k为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率,称(),(,)((,)),P =∈i j n k p n k i j E为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率矩阵. 特别地,当1k =时,在时刻n 的一步转移概率和一步转移概率矩阵分别简记为()ij p n 和()n P . (3)初始分布、绝对分布称((0)),,==∈i p P X i i E 为离散参数马氏链{}(),0,1,2,=X n n 的初始分布,记为0P ,称()(){},,==∈j p n P X n j j E 为马尔可夫链{}0n X n ≥的绝对分布,记为P n . (4)离散参数齐次马氏链设{}(),0,1,2,=X n n 是一离散参数马氏链,如果其一步转移概率()ij p n 恒与起始时刻n 无关,记为ij p ,则称{}(),0,1,2,=X n n 为离散参数齐次马氏链。
若{}(),0,1,2,=X n n2是离散参数齐次马氏链,则其k 步转移概率记为(),i j p k ,一步转移概率矩阵和k 转移概率矩阵分别记为P 和().P k(5) 离散参数齐次马氏链的遍历性离散参数齐次马氏链{X (n ) ,n=0,1,2… },若对一切状态i ,j ,存在与i 无关的极限()()lim 0,ij j n p n i j E →+∞=π>∈则称此马氏链具有遍历性.0,1j j j Ej E ππ∈>∈=∑若且则称{},j j E π∈为离散参数齐次马氏链{X (n ) ,n=0,1,2… }的极限分布,或称为最终分布,记为{},j j E ∏=∈π(6)离散参数齐次马氏链的平稳分布离散参数齐次马氏链{X (n ) ,n=0,1,2… },若存在{v j , j ∈E } 满足条件:1)0,2)13)j jj Ej i iji Ev j E vv v p ∈∈≥∈==∑∑则称此马氏链是平稳的,称 { v j , j ∈E } 为此马氏链的平稳分布。
随机过程第四章
pii
(n)
1
i
0
证:(1)如i为零常返则i
,由lim n
pii nd
d
i
0
而当n不能被周期d整除时n 0modd ,
必然有pii
(n)
0,故
lim
n
pii
n
0
反之,若lim n
pii
(n)
0,
而i是正常返,
则由lim n
pii (nd )
d
i
0矛盾.
(2) 如i为遍历,即d 1,由上面定理得
即 Tij minn:X m i, X mn j,n 1
而称:
fij (n) P Tij n
P{X mv j,1 v n 1,X mn j / X m i},n 1 为自状态i出发,经n步首次到达状态j的概率, 简称首达概率。
注:由齐次马氏链性质知,首达概率与出发时刻
p3
① q1 q2
p1
③ q3 ②
p2
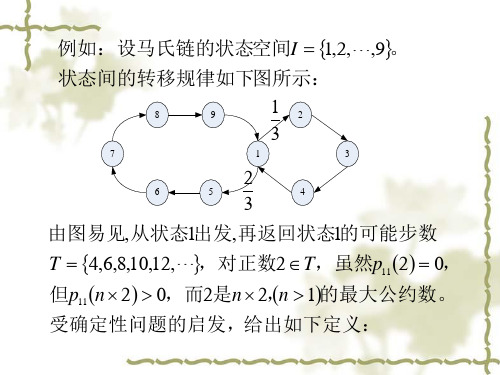
求从状态1出发经n步转移首次到达各个状态的概率。
f12
(n)qq11p3 p3源自q m1 1m p1,
q3
,
n 2m, n 2m 1,
m 1 m0
同理:
f13 (n)
p1q2 p1q2
p m1 1
m q1,
p2
,
n 2m, n 2m 1,
m 1 m0
互通关系的状态是同一类型.
定理:如果i j, 则
(1) i与j同为常返或非常返,如为常返,则它们
同为正常返或零常返;
(2) i与j有相同的周期。
1证:因为i j,故存在正整数k与m,使
pij (m) 0, p ji (k ) 0
《随机过程》第四章作业解答

20. 解:由例 4.8 中的结果可知甲最终赢的概率为:
(1)
P (甲最终赢)
=
(
1−p p
)a
−
1
(
1−p p
)a+b
−
1
=
(
2 3
)16
(
2 3
)36
− −
1 ;
1
(2)
P (甲最终赢)
=
(
1−p p
)a
−
1
(
1−p p
)a+b
−
1
=
(
2 3
)4
−
1
(
2 3
)24
−
1
21. 解:(1) 状态空间可以分为三个等价类:{1, 2}, {3, 4}, {5, 6}。其中 {1, 2} 与 {3, 4} 是常 返的,{5, 6} 是瞬时的,而且状态 {1, 2, 3, 4} 是非周期的。从而由推论 4.1 可知:
不妨记 p11 ≥ p12 ≥ · · · ≥ pn1 ≥ 0,若 p11 > p12 严格成立,从而有:
n
n
p11 = p1ipi1 < p11 p1i = p11
i=1
i=1
得到矛盾,从而有 p11 = p12。类似可证:对 ∀j ≤ n,p11 = p1j 均成立。从而类似可证:
对 ∀i, j ≤ n, p1j = pjj。
19.
解:结合概率转移矩阵画出有向图,可以得到: f1(1n) = a,
n=1 , 从而状态{1}是
0, n > 1
如有疏漏,欢迎指正
4
《随机过程》第四章作业解答
随机过程第4章Markov过程(PDF)

第四章 Markov 过程本章我们先讨论一类特殊的参数离散状态空间离散的随机过程,参数为0{0,1,2,}T N ==L ,状态空间为可列{1,2,}I =L 或有限{1,2,,}I n =L 的情况,即讨论的过程为Markov 链。
Markov 链最初由Markov 于1906年引入,至今它在自然科学、工程技术、生命科学及管理科学等诸多领域中都有广泛的应用。
之后我们将讨论另一类参数连续状态空间离散的随机过程,即纯不连续Markov 过程。
§4.1 Markov 链的定义与性质一、Markov 链的定义定义 4.1设随机序列{;0}n X n ≥的状态空间为I ,如果对0n N ∀∈,及0110011,,,,,{,,,}0n n n n i i i i I P X i X i X i +∈===>L L ,有:11001111{,,,}{}n n n n n n n n P X i X i X i X i P X i X i ++++=======L (4.1.0)则称{;0}n X n ≥为Markov 链。
注1:等式(4.1.0)刻画了Markov 链的特性,称此特性为Markov 性或无后效性,简称为马氏性。
Markov 链也称为马氏链。
定义4.2 设{;0}n X n ≥为马氏链,状态空间为I ,对于,i j I ∀∈,称1{}()ˆn n i j P X j X i p n +===为马氏链{;0}n X n ≥在n 时刻的一步转移概率。
注2:一步转移概率满足:()0,,()1,i j i jj Ip n i j Ipn i I ∈≥∈=∈∑若对于,i j I ∀∈,有1{}()ˆn n i j i j P X j X i p n p +===≡即上面式子的右边与时刻n 无关,则称此马氏链为齐次(或时齐的)马氏链。
设{}0()(0),p i P X i i I ==∈,如果对一切i I ∈都有00()0,()1i Ip i p i ∈≥=∑,称0()p i 为马氏链的初始分布。
随机过程课后题答案

第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtkk X k f t E eepq ∞===∑()k jtkk p q e∞==∑ =0()1jt kjtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰202201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则10()()p jtxp bxX b f t ex e dx p ∞--=Γ⎰ 1()0()p p jt b x b x e dx p ∞--=Γ⎰101()()()()(1)p u p p p p p b e u b u jt b x du jt p b jt b jt b∞----==Γ---⎰ 10(())x p p e x dx ∞--Γ=⎰ (2)'1()(0)X p E X f j b∴== 2''221(1)()(0)X p p E X f j b +== 222()()()PD XE X E X b∴===(4) 若(,)i i X p b Γ 1,2i = 则121212()()()()(1)P P X X X X jt f t f t f t b-++==-1212(,)Y X X P P b ∴=+Γ+同理可得:()()iiP X b f t b jt∑=∑-3、设X 是一随机变量,()F x 是其分布函数,且是严格单调的,求以下随机变量的特征函数。
(解答)《随机过程》第四章习题

第四章 二阶矩过程、平稳过程和随机分析 习题解答1、 设∑=-=Nk k k kn U n X 1)cos(2ασ,其中k σ和k α为正常数,)2,0(~πU U k ,且相互独立,N k ,,2,1 =,试计算},1,0,{ ±=n X n 的均值函数和相关函数,并说明其是否是平稳过程。
解:计算均值函数和相关函数如下0)}{cos(2)cos(2}{)(11=-=⎭⎬⎫⎩⎨⎧-==∑∑==Nk k k k N k k k k n X U n E U n E X E n ασασμ∑∑∑∑∑∑======-=--=--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-⋅⎥⎦⎤⎢⎣⎡-=Ni i i N i i i i i i Ni Nj j j i i j i N j j j j N i i i i X m n U m U n E U m U n E U m U n E m n R 12121111)](cos[)}cos(){cos(2)}cos(){cos(2)cos(2)cos(2),(ασαασαασσασασ因此可知,},1,0,{ ±=n X n 是平稳随机过程。
2、 设有随机过程))(cos()(t t A t X πηω+=,其中0>ω为常数,}0),({≥t t η是泊松过程,A 是与)(t η独立的随机变量,且2/1}1{}1{===-=A P A P 。
(1) 试画出此过程的样本函数,并问样本函数是否连续? (2) 试求此过程的相关函数,并问该过程是否均方连续? 解:(1)样本函数不连续。
(2)令:012≥>t t ,下面求相关函数:)(221)(212210)(1212211212121211212212122112221122121121212cos cos )]}(cos[)]({cos[21!)]([)]}(cos[)]({cos[)1(21))]}()(()(cos[))]()(()(2)({cos[21))]}()(()(cos[))]()(()({cos[21))}(cos())({cos(}{))}(cos())(cos({)}()({),(t t t t k t t k kX e t t e t t t t e k t t t t t t t t t t t t t t t E t t t t t t t t E t t t t E A E t t t t A E t X t X E t t R ----∞=--⋅=⋅-++=⋅-⋅-++-=-+-+-+++=-+-++++=++⋅=++==∑λλλωωωωλωωηηπωηηππηωηηπωηηπωπηωπηωπηωπηω因为:t t t R ωξ2cos ),(=因此该过程是均方连续的随机过程。
随机过程答案

随机过程第三章与第四章习题解答3.1 解:令()N t 表示(0,)t 时间内的体检人数,则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
4030(30)((1)40)!k k P N e k -=≤=∑。
3.2 解:法一:(1)乘坐1、2路汽车所到来的人数分别为参数为1λ、2λ的poisson 过程,令它们为1()N t 、2()N t 。
1N T 表示1()N t =1N 的发生时刻,2N T 表示2()N t =2N 的发生时刻。
1111111111()exp()(1)!N NN T f t t t N λλ-=-- 2221222222()exp()(1)!N NN T f t t t N λλ-=--1212121221112,12|12211122212(,)(|)()exp()exp()(1)!(1)!N N N N N NNN N T T T T T f t t f t t f t t t t t N N λλλλ--==---- 12212121112211122210012()exp()exp()(1)!(1)!NNt N N N N P T T dt t t t t dt N N λλλλ∞--<=----⎰⎰(2)当1N =2N 、1λ=2λ时,12121()()2N N N N P T T P T T <=>=法二:(1)乘车到来的人数可以看作参数为1λ+2λ的泊松过程。
令1Z 、2Z 分别表示乘坐公共汽车1、2的相邻两乘客间到来的时间间隔。
则1Z 、2Z 分别服从参数为1λ、2λ的指数分布,现在来求当一个乘客乘坐1路汽车后,下一位乘客还是乘坐1路汽车的概率。
212211122210()exp()exp()z p P Z Z dz z z dz λλλλ∞=<=--⎰⎰112λλλ=+。
故当一个乘客乘坐1路汽车后,下一位乘客乘坐2路汽车的概率为1-p 212λλλ=+上面的概率可以理解为:在乘客到来的人数为强度1λ+2λ的泊松过程时,乘客分别以112λλλ+概率乘坐公共汽车1,以212λλλ+的概率乘坐公共汽车2。
随机过程试题及答案

随机过程试题及答案一、选择题1. 关于随机过程的描述,错误的是:A. 随机过程是一种由随机变量组成的集合B. 随机过程是一种在时间上有序排列的随机变量序列C. 随机过程可以是离散的,也可以是连续的D. 随机过程是一种确定性的数学模型答案:D2. 以下哪种过程不是随机过程?A. 白噪声过程B. 马尔可夫过程C. 布朗运动D. 正态分布答案:D3. 随机过程的一阶矩描述的是:A. 均值B. 方差C. 偏度D. 峰度答案:A4. 当随机过程的各个时间点上的随机变量是独立同分布时,该随机过程为:A. 马尔可夫过程B. 马尔可夫链C. 平稳随机过程D. 白噪声过程答案:B5. 下列关于马尔可夫过程的说法中,正确的是:A. 当前状态只与上一状态有关,与历史状态无关B. 当前状态只与历史状态有关,与上一状态无关C. 当前状态只与上一状态和历史状态有关D. 当前状态与所有历史状态均无关答案:A二、填空题1. 随机过程中,时域函数常用的表示方法是__________。
答案:概率分布函数或概率密度函数2. 马尔可夫过程的状态转移概率只与__________相关。
答案:当前状态和下一状态3. 随机过程的时间参数称为__________。
答案:时刻或时间点4. 白噪声过程的自相关函数是一个__________函数。
答案:冲激函数5. 平稳随机过程的自相关函数只与__________相关。
答案:时间差三、解答题1. 请简要解释随机过程的概念。
随机过程是一种由随机变量组成的集合,表示一个在时间上有序排列的随机变量序列。
它可以是离散的,也可以是连续的。
随机过程的描述通常包括概率分布函数或概率密度函数,以及相关的统计特征,如均值、方差等。
随机过程可以用于对随机现象进行建模和分析。
2. 请简要说明马尔可夫过程的特点及应用。
马尔可夫过程是一种具有马尔可夫性质的随机过程,即当前状态只与上一状态有关,与历史状态无关。
其状态转移概率只与当前状态和下一状态相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学本科课程《随机过程》第4章习题及参考答案主讲教师:何松华 教授30.设X(n)为均值为0、方差为2的离散白噪声,通过一个单位脉冲响应为h(n)的线性时不变离散时间线性系统,Y(n)为其输出,试证:2[()()](0)E X n Y n h σ=,2220()Y n h n σσ∞==∑证:根据离散白噪声性质,220()[()()]()0X m R m E X n m X n m m σσδ⎧==+==⎨≠⎩ 0()()()()()m Y n X n h n X n m h m ∞==⊗=-∑220[()()]{()()()][()()]()()()()()(0)m m X m m E X n Y n E X n X n m h m E X n X n m h m R m h m m h m h σδσ∞∞==∞∞===-=-===∑∑∑∑12121222112202121221210000[()]{()()()()][()()]()()[()()]()Y m m m m m m E Y n E X n m h m X n m h m E X n m X n m h m h m m m h m h m σσδ∞∞==∞∞∞∞======--=--=-∑∑∑∑∑∑(对于求和区间的每个m 1,在m 2的区间存在唯一的m 2=m 1,使得21()0m m δ-≠)1222110()()()m n h m h m h n σσ∞∞====∑∑(求和变量置换) 31.均值为0、方差为2的离散白噪声X(n)通过单位脉冲响应分别为h 1(n)=a n u(n)以及h 2(n)=b n u(n)的级联系统(|a|<1,|b|<1),输出为W(n),求W2。
解:该级联系统的单位脉冲响应为121211100()()()()()()()1(/)()1/n mm m m mn n n nnn m m n nm m h n h n h n h n m h m au n m b u m b b a aba b a a u n a b a a b∞∞-=-∞=-∞+++-===⊗=-=---⎛⎫====⎪--⎝⎭∑∑∑∑参照题30的结果可以得到21122222211212000222222222()[()2()()]()2(1)[]()111(1)(1)(1)n n n n n W n n n a b h n a ab b a b a b a ab b ab a b a ab b a b ab σσσσσσ++∞∞∞+++===⎡⎤-===-+⎢⎥--⎣⎦+=-+=-------∑∑∑32.设离散系统的单位脉冲响应为()() (1)n h n na u n a -=>,输入为自相关函数为2()()X X R m m σδ=的白噪声,求系统输出Y(n)的自相关函数和功率谱密度。
解:根据离散时间随机过程通过离散时间线性系统理论,有1221121212002122100()()()()[()]Y Xm m m mXm m R m Rm m m h m h m m m m m a m a σδ∞∞==∞∞--===-+=-+∑∑∑∑注:对比因果连续系统的输出过程与输入过程相关函数的关系12120()()()()Y X R R h h ττττττ∞∞=-+⎰⎰不妨设0m ≥,则只有当m 1m 时,求和区间存在脉冲点21m m m =-,因此1111111()211222211()()[]m m m Y X m m m m m X m mm mR m m m m a a a m a m m a σσ∞---=∞∞--===-=-∑∑∑令:1111211()m m m mm mx m am q∞∞-====∑∑,则1112(1){}{}1(1)m m m m m m d d q mq m q x q q q dq dq q q +∞=--=⨯=⨯=--∑ 令:111122211()m m m mm my ma mq ∞∞-====∑∑,则11112221223(1){}{}(1)(221)(21)(1)m m m m m m m m d d mq m q y q m q q dq dq q m q m m q m m qq +∞=++--=⨯=⨯----+-+=-∑2212221232124222323(221)(21)(1)()[](1)(1)(1)(1)(1)(1)(1)(1)m m m m m mY X m m mmX X m q m m q m m q m q m m q R m a q q m qm qa m a m a a q a σσσ+++++----+-+--=---+--+--==--考虑到相关函数的偶函数特性,得到:422||23(||1)(||1)()(1)m Y X a m a m R m aa σ-+--=-下面求功率谱密度函数,采用频域法。
-100220()() ()1{}{}1(1)()j nn j nn j n n n n j j n j n j j j n H j h n ena enp e p a d d pe ae p p e p dp dp pe pe a e ωωωωωωωωωω∞∞∞----===--∞----======⨯=⨯==---∑∑∑∑222222222222()|()|()()(|cos()sin()|)[12cos()]j X Y X X j X a ae G H j G a e a j aa a ωωσωωωσωωσω--===--+=+-可以通过相关函数的傅立叶变换进行验证。
典型双边序列的离散时间傅立叶变换对:2||||21 (||1)12cos()m m m a aa a a a ω∞--=-∞-↔=>+-∑ 222||22212(1)cos()4||12cos()[12cos()]m d a a a a m aa da a a a a ωωω-⎛⎫-+-↔-⨯=⎪+-+-⎝⎭ 242242422||||||23232324224222223222322222()()(||1)(||1)()||(1)(1)(1)()()2(1)cos()41(1)[12cos()](1)12cos()[12cos()]m m m X X Y X X X X a a a a a m a m R m am a aa a a a a a a a a a a a a a a a a a a a σσσσσωωωσω----++--==+----++--↔+-+--+-=+-33.序列X(n)和Y(n)满足差分方程()()()Y n X n a X n a =+--其中a 为整常数,试用X(n)的相关函数表示Y(n)的相关函数。
解:1212112212121212(,)[()()]{[()()][()()]}(,)(,)(,)(,)Y X X X X R n n E Y n Y n E X n a X n a X n a X n a R n a n a R n a n a R n a n a R n a n a ==+--+--=++--+-+-+--当X(n)为平稳随机过程时,则Y(n)也为平稳的,且有()2()(2)(2)Y X X X R m R m R m a R m a =---+34.实值一阶自回归过程X(n)满足差分方程1()(1)()X n a X n V n +-=其中a 1为常数,V(n)为方差为2的白噪声,输入从n=0开始,(1)0X -=。
(1)证明:若V(n)均值非零,则X(n)非平稳;(2)证明:若V(n)均值为零、|a 1|<1,则当n 足够大时,2221[()]/(1)V E X n a σ=-;(3)若V(n)均值为零,|a 1|<1,求X(n)的自相关函数的平稳解。
证:(1) 采用Wold 分解方法211123111111100()()(1)()(1)(2)()(1)(2)(3)...()()()(1)()()nnmn m m m X n V n a X n V n a V n a X n V n a V n a V n a X n a V n m a X a V n m +===--=--+-=--+---==--+--=--∑∑1111001[1()][()][()()]()1n nnmmV V m m m a E X n E a V n m a m a +==--=--=-=+∑∑ 显然,若V(n)均值非零,则X(n)的均值函数不是一个常数,是非平稳的。
(2) 若V(n)均值为零,则X(n)的均值为常数0,则210[()][()][()()]nm m E X n Var X n Var a V n m ===--∑根据相互独立随机变量的和的方差等于方差之和的性质,得到2211022(1)2211201[()][()()]()[()][1]()1nnmm m m n nm V V m E X n Var a V n m a Var V n m aa aσσ==+==--=---==-∑∑∑显然,若输入从n=0开始,则即使在V(n)均值为零的情况下,方差也不为常数,X(n)是非平稳的,当|a 1|<1且n 足够大时,渐近平稳,2221[()]1V E X n aσ=-。
(3) 不妨假设时刻差m0,则根据Wold 分解得到121212121212111201112002111200(,)[()()]{[()()][()()]}()()[()()]()()()n mnm m X m m n mnm m m m n mnm m V m m R n m n E X n m X n E a V n m m a V n m a a E V n m m V n m a a m m m σδ+==+==+==+=+=-+---=--+--=---+∑∑∑∑∑∑根据求和区间的脉冲点21m m m =-的存在条件:1n m m m +≥≥,得到:11111()222111122(1)211121(,)()()()()[1]()1n mn mm m m m mX V V m mm mm n mV R n m n a a a aa a a a σσσ++--==+-+=--=--=--∑∑当n 足够大时,输出过程是渐近平稳的,自相关函数的平稳解为:2121()()1mV X a R m a σ-=-35.考察如下的二阶自回归过程X(n)12()(1)(2)()X n a X n a X n V n =----+(1)若已知随机过程的相关函数值(0)X R 、(1)X R 、(2)X R ,试写出用于计算系数a 1,a 2以及零均值白色噪声()V n 的方差2V σ的Yule-Walker 方程;(2)反过来,若已知a 1= -1,a 2=0.5, 20.5V σ=,求(0)X R 、(1)X R 、(2)X R 的值;(3)求相关函数的通解。
