初三《圆》课时基础练习题(含答案)
中考数学总复习《圆的综合题》练习题(附答案)
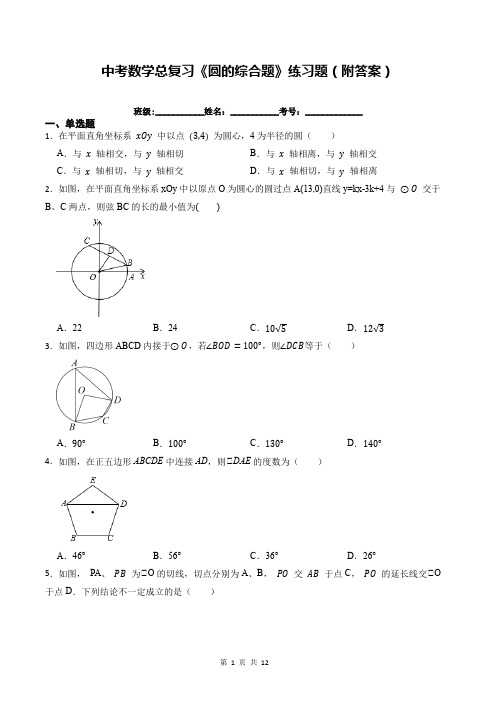
中考数学总复习《圆的综合题》练习题(附答案)班级:___________姓名:___________考号:_____________一、单选题1.在平面直角坐标系xOy中以点(3,4)为圆心,4为半径的圆()A.与x轴相交,与y轴相切B.与x轴相离,与y轴相交C.与x轴相切,与y轴相交D.与x轴相切,与y轴相离2.如图,在平面直角坐标系xOy中以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为()A.22B.24C.10√5D.12√33.如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DCB等于()A.90°B.100°C.130°D.140°4.如图,在正五边形ABCDE中连接AD,则∠DAE的度数为()A.46°B.56°C.36°D.26°5.如图,PA、PB为∠O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交∠O 于点D.下列结论不一定成立的是()A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A,B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线6.如图,四边形ABCD内接于半径为6的∠O中连接AC,若AB=CD,∠ACB=45°,∠ACD=12∠BAC,则BC的长度为()A.6 √3B.6 √2C.9 √3D.9 √27.如图,点A,B,D,C是∠O上的四个点,连结AB,CD并延长,相交于点E,若∠BOD=20°,∠AOC=90°,则∠E的度数为()A.30°B.35°C.45°D.55°8.∠ABC中∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则AE的长为()A.95B.125C.185D.3659.如图,AB为∠O的直径,点C在∠O上,若∠B=60°,则∠A等于()A.80°B.50°C.40°D.30°10.两个圆的半径分别是2cm和7cm,圆心距是5cm,则这两个圆的位置关系是() A.外离B.内切C.相交D.外切11.已知正三角形的边长为12,则这个正三角形外接圆的半径是()A.B.C.D.12.一个扇形的弧长为4π,半径长为4,则该扇形的面积为()A.4πB.6πC.8πD.12π二、填空题13.在Rt∠ABC中∠C=90°,AB=5,BC=4,求内切圆半径14.如图,∠C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则∠C的半径为.15.一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的侧面积为.16.一个半径为5cm的球形容器内装有水,若水面所在圆的直径为8cm,则容器内水的高度为cm.17.如图,在直角坐标系中以点P为圆心的圆弧与x轴交于A,B两点,已知P(4,2)和A(2,0),则点B的坐标是.18.下面是“作一个30°角”的尺规作图过程.已知:平面内一点A.求作:∠A,使得∠A=30°.作法:如图①作射线AB;②在射线AB取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;③以C为圆心,OC C为半径作弧,与⊙O交于点D,作射线AD.则∠DAB即为所求的角.请回答:该尺规作图的依据是.三、综合题19.如图,在△ABC中AC=BC=BD,点O在AC边上,OC为⊙O的半径,AB是⊙O 的切线,切点为点D,OC=2,OA=2√2.(1)求证:BC是⊙O的切线;(2)求阴影部分的面积.20.如图,△ABC内接于⊙O,CD是直径,∠CBG=∠BAC,CD与AB相交于点E,过点E作EF⊥BC,垂足为F,过点O作OH⊥AC,垂足为H,连接BD、OA.(1)求证:直线BG与⊙O相切;(2)若BEOD=54,求EFAC的值.21.如图,四边形ABCD 内接于∠O,BD是∠O的直径,过点A作∠O的切线AE交CD的延长线于点E,DA平分∠BDE.(1)求证:AE∠CD;(2)已知AE=4cm,CD=6cm,求∠O的半径.22.如图,∠O是∠ABC的外接圆,BC为∠O的直径,点E为∠ABC的内心,连接AE并延长交∠O 于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为∠O的切线.23.公元前5世纪,古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱,在狱中他对方铁窗和圆月亮产生了兴趣.他不断变换观察的位置,一会儿看见圆比正方形大,一会儿看见正方形比圆大,于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了:作一个正方形,使它的面积等于已知圆的面积(1)设有一个半径为√3的圆,则这个圆的周长为,面积为,作化圆为方得到的正方形的边长为(计算结果保留π)(2)由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图),包括化圆为方在内的几何三大问题都已被证明是不可能的.但若不受标尺的限制,化圆为方并非难事。
《圆的周长、面积》练习题丨精品(含答案)

《圆的周长、面积》练习题一.选择题(共10题,共20分)1.如下图所示的比赛场中(弯道部分为半圆R=150m、r=50m),左右轮子的距离为2.5米.如果把弯道半径都扩大2倍,若绕赛场一圈,两个轮子行走的距离之差()。
A.不变B.扩大2倍C.缩小2倍D.无法确定2.用两个不可能拼成下面的哪个图形?()A.长方形B.圆C.三角形3.一个钟表的时针长10cm,从中午12时到当天晚上9时,时针针尖走过了()cm。
A.31.4B.62.8C.314D.47.14.圆规两脚间的距离为2分米,那么画出的圆的半径为()。
A.1分米B.2分米C.4分米5.连接圆上任意两点的线段,它的长度一定()直径。
A.小于B.大于C.不大于6.要画一个直径是5厘米的圆,圆规两脚之间的距离是()。
A.5厘米B.2.5厘米C.10厘米7.赛车行进的过程中,右、左两个轮子行走的路程()。
A.相同B.不同C.走直道时相同D.走弯道时相同8.某点到一圆的圆心距离大于半径,该点在()。
A.圆内B.圆上C.圆外9.在一块长12m,宽8m的长方形铁皮上剪半径是1.5m的小圆,至多能剪()个。
A.8B.10C.11D.1310.在400米道上进行200米赛跑,弯道部分是半圆,半径为36米,每条跑道宽1.2米,第4道与第1道起跑线相差()米。
A.1.21πB.2.4πC.3.6πD.36π二.判断题(共10题,共20分)1.圆周率π是一个无限不循环小数。
()2.小圆半径是大圆半径的,那么小圆周长也是大圆周长的。
()3.周长相等的长方形、正方形、圆形,圆的面积最大。
()4.圆的周长与直径的比值是3.14。
()5.把一张圆形纸片对折,沿折痕剪开,得到两个半圆.每个半圆的周长等于原来圆周长的一半。
()6.圆只有一条对称轴。
()7.由一条弧和两条半径围成的图形叫做扇形。
()8.大圆的圆周率与小圆的圆周率相等。
()9.圆的一部分就是扇形。
()10.两端都在圆上的线段叫做直径。
人教版九年级数学上册第24章《圆》选择专项练习题(含答案)

人教版九年级数学上册第24章《圆》选择专项练习题 1.若⊙A 的半径为5,圆心A 与点P 的距离是25,则点P 与⊙A 的位置关系是( ) A .P 在⊙A 上 B .P 在⊙A 外 C .P 在⊙A 内 D .不确定 2.扇形的半径为20cm ,扇形的面积2100cm π,则该扇形的圆心角为( ) A .120︒ B .100︒ C .90︒ D .60︒ 3.在下列命题中,正确的是( )A .长度相等的弧是等弧B .直径所对的圆周角是直角C .三点确定一个圆D .三角形的外心到三角形各边的距离相等 4.如图,点A 、B 、C 是⊙O 上的三个点,若∠AOB =82°,则∠C 的度数为( )A .82°B .38°C .24°D .41° 5.如图,AB 是O 的直径,点E ,C 在O 上,点A 是EC 的中点,过点A 画O 的切线,交BC 的延长线于点D ,连接EC .若58.5ADB ∠=︒,则ACE ∠的度数为( )A .29.5︒B .31.5︒C . 58.5︒D .63︒ 6.如图,在⊙O 中,半径r =5,弦AB =8,P 是弦AB 上的动点(不含端点A ,B ),若线段OP 长为正整数,则点P 的个数有( )A .2个B .5个C .4个D .3个 7.已知⊙O 的直径为12,直线l 上有一点P ,OP =6,则直线l 与⊙O 的位置关系是( )A.相交B.相切C.相离D.相切或相交8.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为()A.103cm B.10cm C.102cm D.83cm9.一个圆锥体底面半径为3cm,高为4cm,则这个圆锥体的侧面积为()A.12πcm²B.28πcm²C.15πcm²D.20πcm²10.如图,A,B,C是⊙O上的三个点,若∠B=32°,则∠AOC=()A.64°B.58°C.68°D.55°11.如图,BD是⊙O的直径,点A、C在圆上,且CD=OB,则∠BAC=()A.120°B.90°C.60°D.30°12.下列命题:①平⾏四边形是中⾏对称图形,也是轴对称图形;②直径是最长的弦,半径是最短的弦;③过切点的直线是圆的切线;④三角形的外⾏是三条边垂直平分线的交点;⑤三角形的内⾏是三条内角平分线的交点;其中正确的有()A.1个B.2个C.3个D.4个13.如图,PA、PB切⊙O于点A、B,PA=10,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是()A.10 B.18 C.20 D.2214.下列关于圆的说法,正确的是()A.在同圆或等圆中,相等的弦所对的圆周角相等B.平分弦的直径垂直于弦C.圆的每一条直径所在的直线都是它的对称轴D.过三点可以作一个圆15.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,大正六边形在绕点O旋转过程中,下列说法正确的是()A.S变化,l不变B.S不变,l变化C.S变化,l变化D.S与l均不变16.下列四个命题:①直角三角形斜边上的中线等于斜边的一半;②对角线相等的平行四边形是菱形;③一组邻边相等的矩形是正方形;④三角形三条角平分线的交点是三角形的外心.其中真命题共有()A.1个B.2个C.3个D.4个17.下列说法正确的是()A.三角形三条中线的交点是三角形重心B.等弦所对的圆周角相等C.长度相等的两条弧是等弧D.三角形的外心到三边的距离相等18.如图,四边形ABCD内接于⊙O,若∠C=100°,则∠A的度数是()A .80°B .100°C .110°D .120°19.下列说法正确的是( )A .等弧所对的圆心角相等B .同弦所对的圆周角相等C .经过三点可以作一个圆D .相等的圆心角所对的弧相等20.如图,P 是O 外一点,PA 、PB 切O 于点A 、B ,点C 在优弧AB 上,若68P ∠=︒,则ACB ∠等于( )A .22︒B .34︒C .56︒D .68︒21.有四个命题:①直径相等的两个圆是等圆 ②长度相等的两条弧是等弧;③圆中最大的弦是过圆心的弦;④圆周角是圆心角的一半.其中真命题是( )A .①③B .①③④C .①④D .④22.⊙O 的直径是10,两平行弦的长度分别是6和8,那么这两弦的距离是( ) A .1 B .7 C .8 D .1或723.△ABC 的顶点都在⊙O 上,若∠BOC =120°,则∠BAC 等于( )A .60°B .90°C .120°D .60°或120° 24.如图,OA 为⊙O 的半径,弦BC ⊥OA 于点P .若BC =8,AP =2,则⊙O 的半径长为( )A .5B .6C .10D 1725.如图,两个同心圆的半径分别是3cm 和5cm ,大圆的一条弦AB 与小圆相切,则弦ABA .3cmB .4cmC .6cmD .8cm26.如图,已知O 的半径为2,AC 与O 相切,连接AO 并延长,交O 于点B ,过点C 作CD AB ⊥,交O 于点D ,连接BD ,若30A ∠=︒,则弦BD 的长为( )A .3B .5C .23D .3227.下列说法正确的是( )A .在同一平面内,三点确定一个圆B .等弧所对的圆心角相等C .旋转会改变图形的形状和大小D .平分弦的直径垂直于弦28.如图,⊙O 内切于ABC ,切点分别为D ,E ,F .已知50B ∠=︒,60C ∠=°,连接OE ,OF ,DE ,DF ,那么EDF ∠等于( )A .40︒B .55︒C .65︒D .70︒29.下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤圆内接四边形的对角互补;⑥在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等,不正确的有( )A .5个B .4个C .3个D .2个30.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应该假设这个三角A .有一个内角小于60°B .每一个内角都小于60°C .有一个内角大于60°D .每一个内角都大于60°31.AB =12cm ,过A 、B 两点画半径为6cm 的圆,能画的圆的个数为( ) A .0个 B .1个 C .2个 D .无数个 32.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为点E ,CE =1寸,AB =10寸,则直径CD 的长度是( )A .12寸B .24寸C .13寸D .26寸33.如图,将边长为a 的正六边形123456A A A A A A 在直线l 上由图1的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图2位置时,顶点1A 所经过的路径( )A 843a +B 423a +C 43a +D 423a + 34.已知⊙O 的半径为1,点P 在⊙O 外,则OP 的长( )A .大于1B .小于1C .大于2D .小于235.如图,在Rt △ABC 中,∠ACB =90°, AC =3,以点C 为圆心、CA 为半径的圆与AB 交于点D ,若点D 巧好为线段AB 的中点,则AB 的长度为( )A.32B.3 C.6 D.936.如图所示,在⊙O中,AB AC=,∠A=30°,则∠B=()A.150°B.75°C.60°D.15°37.如图,F为正方形ABCD的边CD上一动点,AB=2.连接BF,过A作AH⊥BF交BC于H,交BF于G,连接CG,当CG为最小值时,CH的长为()A.2B.225C.3﹣5D.3+538.如图,ABC内接与O,50A∠=,E是边BC的重点,连接OE并延长,交O于点D,连接BD,则DBC∠的大小为()A.55°B.6 C.25°D.75°39.已知圆心角为120°的扇形的面积为12π,则扇形的半径为( )A .4B .6C .43D .6240.如图O 的直径AB 垂直于弦CD ,垂足是E ,225A ∠=︒.,4OC =,CD 的长为( )A .22B .4C .42D .841.如图,AB 是⊙O 的直径,点C 在⊙O 上,∠ABC =30°,AC =1,则⊙O 的半径为( )A .1B .2C .3D .2342.如图,点A 、B 、C 是⊙O 上的三个点,若∠AOB =66°,则∠C 的度数为( )A .33°B .34°C .44°D .46°43.已知⊙O 的直径是10,圆心O 到直线l 的距离是5,则直线l 和⊙O 的位置关系是( ) A .相离 B .相交 C .相切 D .无法确定 44.下列说法中一定正确的是( )A .相等的圆心角所对的弧相等B .圆上任意两点间的部分叫做圆弧C .平分弦的直径垂直于弦D .圆周角等于圆心角的一半45.已知O 的半径为2,点P 为O 内一定点,且1PO =,过点P 作O 的弦,其中最短的弦的长度是()A.4 B.3C.23D.246.如图,AB是☉O的直径,∠CAB=40°,则∠D=()A.60°B.30°C.40°D.50°47.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是()A.1个B.2个C.3个D.4个48.将一个底面半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的圆心角是( )A.54︒B.126︒C.136︒D.144︒49.如图,⊙O的直径CD垂直弦AB于点E,且CE=4,OB=8,则AB的长为()A.3B.4 C.6 D.350.已知⊙O半径为6,圆心O在坐标原点上,点P的坐标为(3,4),则点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O上C.点P在⊙O外D.不能确定51.⊙O的半径为5,点P到圆心O的距离为5,点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O外C.点P在⊙O上D.无法确定52.如图.在⊙O中,直径AB⊥CD,下列说法不正确的是()A.AB是最长的弦B.∠ADB=90°C.PC=PD D.∠ABD=2∠ADC53.如图,在Rt ABC中,∠ACB=90°,∠A=54°,以BC为直径的⊙O交AB于点D.E是⊙O上一点,且CE=CD,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为()A.92°B.108°C.112°D.124°54.如图,Rt△ABC的直角顶点C在⊙O上滑动,且各边与⊙O分别交于点D,E,F,G,若EF,DG,DE的度数比为2:3:5,BE=BF,则∠A的度数为()A.30°B.32°C.34°D.36°55.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P 是直径MN上一动点,则PA+PB的最小值为()A.5B.3C.5D.356.如图,正方形ABCD的四个顶点分别在⊙O上,点P是弧CD上不同于点C的任意一点,则∠BPC=()A.45°B.60°C.75°D.90°57.如图,点A、B、P在⊙O上,且∠APB=50°.若点M是⊙O上的动点,要使△ABM为等腰三角形,则所有符合条件的点M有()A.1个B.2个C.3个D.4个58.O的半径为6cm,圆心O到直线l的距离为7cm,则直线l与O的位置关系是()A.相交B.相切C.相离D.不能确定59.如图,已知直线334y x=-与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最小值为()A.5.5 B.10.5 C.8 D.1260.如图,⊙O的半径为2,定点P在⊙O上,动点A,B也在⊙O上,且满足∠APB=30°,C为PB的中点,则点A,B在圆上运动的过程中,线段AC的最大值为()A.3B3C.3 2 D.3参考答案1.C2.C3.B4.D5.B6.D7.D8.B9.C10.A11.C12.B13.C14.C15.D16.B 17.A18.A19.A20.C21.A22.D23.D24.A25.D26.C27.B28.B29.A30.D 31.B32.D33.B34.A35.C36.B37.C38.C39.B40.C41.A42.A43.C44.B 45.C46.D47.C48.D49.D50.A51.C52.D53.B54.D55.B56.A57.D58.C 59.A60.A。
人教版九年级数学上册:24.1 圆(第一课时 )同步测试题及答案【新】

第二十四章圆24.1 圆(第一课时)知识点1、圆的定义:⑴形成性定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转形成的图形叫做圆,固定的端点叫,线段OA叫做。
⑵描述性定义:圆是到定点的距离等于的点的集合【特别注意】:1、在一个圆中,圆心决定圆的,半径决定圆的。
2、直径是圆中的弦,弦不一定是直径。
2、弦与弧:弦:连接圆上任意两点的叫做弦。
弧:圆上任意两点间的叫做弧,弧可分为、、三类。
3、圆的对称性:⑴轴对称性:圆是轴对称图形,有条对称轴,的直线都是它的对称轴。
⑵中心对称性:圆是中心对称图形,对称中心是。
一、选择题1.下列命题正确的有()①弦是圆上任意两点之间的部分②半径是弦③直径是最长的弦④弧是半圆,半圆是弧A.1个B.2个C.3个D.4个2.如图所示,MN为⊙O的弦,∠N=52°,则∠MON的度数为()A.38°B.52°C.76°D.104°3.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C 的度数是()A.25°B.40°C.30°D.50°4.一个点到圆上的最小距离是4cm,最大距离是9cm,则圆的半径是().A.2.5cm或6.5 cmB.2.5cmC.6.5cmD.5cm或13cm5.如图,已知在⊙O中,AB、CD为直径,则AD与BC的关系是().A.AD =BCB.AD ∥BCC.AD ∥BC 且AD =BCD.不能确定6.如图,已知AB 为⊙O 的直径,点C 在⊙O 上,∠C=15°,则∠BOC 的度数为( )A .15°B . 30°C . 45°D .60°二、填空题1.⊙O 的半径为2cm ,则它的弦长d cm 的取值范围是.2.⊙O 中若弦AB 等于⊙O 的半径,则△AOB 的形状是 .3.如图,已知AB 是⊙O 的直径,点C 在⊙O 上,点D 是BC 的中点,若AC =10cm ,则OD = cm.4.如图4,AB 是⊙O 的直径,CD 是⊙O 的弦,AB ,CD 的延长线交于E ,若AB=2DE , ∠E=18°,∠C=______,∠AOC=________;5. P 为⊙O 内一点,OP=3cm ,⊙O 半径为5cm ,则经过P 点的最长弦长为_______,最短弦长为________;三、解答题BDO CAABCOBCDO1.在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,D为AB的中点,E为AC的中点,以B为圆心,BC为半径作⊙B,A、C、D、E与⊙B的位置关系如何?A2、如图,M,N为线段AB上的两个三等分点,点A、B在⊙O上,求证:∠OMN=∠ONM。
人教版 九年级数学上册 第24章 圆 同步课时训练 (含答案)

人教版九年级数学第24章圆同步课时训练一、选择题1. 如图半径为1的⊙O与正五边形ABCDE相切于点A,C,则劣弧AC的长度为()图A.35π B.45π C.34π D.23π2. 如图所示,AB是⊙O的直径,C,D是⊙O上的两点,CD⊥AB.若∠DAB=65°,则∠BOC等于()A.25°B.50°C.130°D.155°3. 如图某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以点A为圆心,AB长为半径的扇形(忽略铁丝的粗细),则所得扇形ADB的面积为()A.6 B.7 C.8 D.94. 如图,已知⊙O1,⊙O2,⊙O3,⊙O4是四个半径为3的等圆,在这四个圆中,若某圆的圆心到直线l的距离为6,则这个圆可能是()A.⊙O1B.⊙O2C.⊙O3D.⊙O45.如图,AP为⊙O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PD C=60°,则∠OBC等于( )A. 55°B. 65°C. 70°D. 75°6. 如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为P,则OP的长为() A.3 B.2.5 C.4 D.3.57.如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠A OD的度数为( )A. 70°B. 35°C.20°D. 40°8. 一条排水管的截面如图所示,已知排水管的半径OA=1 m,水面宽AB=1.2 m,某天下雨后,排水管水面上升了0.2 m,则此时排水管水面宽为()A.1.4 m B.1.6 mC.1.8 m D.2 m二、填空题9. 如图所示,AB是☉O的直径,弦CD⊥AB于H,∠A=30°,CD=2,则☉O 的半径是.10. 如图是一个圆锥形冰激凌外壳(不计厚度),已知其母线长为12 cm,底面圆的半径为3 cm,则这个冰激凌外壳的侧面积等于________ cm2(结果精确到个位).11. 2018·孝感已知⊙O 的半径为10 cm ,AB ,CD 是⊙O 的两条弦,AB ∥CD ,AB =16 cm ,CD =12 cm ,则弦AB 和CD 之间的距离是________cm.12. 如图,点A ,B ,C 都在⊙O 上,OC ⊥OB ,点A 在BC ︵上,且OA =AB ,则∠ABC =________°.13. 已知一个圆心角为270°,半径为3 m 的扇形工件未搬动前如图示,A ,B 两点触地放置,搬动时,先将扇形以点B 为圆心,做如图示的无滑动翻转,再使它紧贴地面滚动,当A ,B 两点再次触地时停止,则圆心O 所经过的路线长为________m .(结果用含π的式子表示)14. 如图,在扇形ABC 中,CD ⊥AB ,垂足为D ,⊙E 是△ACD 的内切圆,连接AE ,BE ,则∠AEB 的度数为________.15. 如图,⊙O与正五边形ABCDE 的边AB ,DE 分别相切于点B ,D ,则BD ︵所对的圆心角∠BOD 的大小为________度.16. 如图中的小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”(阴影部分)图案的面积为________.三、解答题17. 已知:如图5,在⊙O 中,M ,N 分别为弦AB ,CD 的中点,AB =CD ,AB不平行于CD.求证:∠AMN =∠CNM.18. 如图,在正六边形ABCDEF中,点O是中心,AB=10,求这个正六边形的半径、边心距、周长、面积.19. 在平面直角坐标系中,圆心P的坐标为(-3,4),以r为半径在坐标平面内作圆:(1)当r为何值时,⊙P与坐标轴有1个公共点?(2)当r为何值时,⊙P与坐标轴有2个公共点?(3)当r为何值时,⊙P与坐标轴有3个公共点?(4)当r为何值时,⊙P与坐标轴有4个公共点?20.(2020·临沂)已知的半径为,的半径为.以为圆心,以的长为半径画弧,再以线段的中点为圆心,以的长为半径画弧,两弧交于点,连接,,交于点,过点作的平行线交于点.(1)求证:是的切线;(2)若,,,求阴影部分的面积.人教版九年级数学第24章圆同步课时训练-答案一、选择题1. 【答案】B[解析] 连接OA,OC,则∠OAE=∠OCD=90°.∵五边形ABCDE 为正五边形,∴∠E=∠D=108°,∴∠AOC=540°-∠OAE-∠OCD-∠E-∠D=144°,∴劣弧AC的长度为144180×π×1=45π.2. 【答案】C3. 【答案】D[解析] ∵正方形的边长为3,∴BD ︵的长度为6,∴S 扇形ADB =12lR =12×6×3=9.4. 【答案】B5.【答案】B【解析】连接OP ,如解图,则OP ⊥AP .∵∠D =60°,∴∠COP =120°,∵∠A =20°,∠APO =90°,∴∠AOP =70°,∴∠AOC =50°,∵OB =OC ,∴∠OBC =180°-50°2=65°.解图6. 【答案】C7.【答案】D【解析】∵AB 是⊙O 的直径,AC 切⊙O 于点A ,∴∠BAC =90°,∵∠C =70°,∴∠B =20°,∴∠AOD =∠B +∠BDO =2∠B =2×20°=40°.8. 【答案】B[解析] 如图,过点O 作OE ⊥AB 于点E ,交CD 于点F ,连接OC.∵AB=1.2 m,OE⊥AB,OA=1 m,∴AE=0.6 m,∴OE=0.8 m. ∵排水管水面上升了0.2 m,∴OF=0.8-0.2=0.6(m).由题意可知CD∥AB.∵OE⊥AB,∴OE⊥CD,∴CF=OC2-OF2=0.8 m,CD=2CF,∴CD=1.6 m.故选B.二、填空题9. 【答案】2[解析]连接OC,则OA=OC,∴∠A=∠ACO=30°,∴∠COH=60°.∵OB⊥CD,CD=2,∴CH=,∴OH=1,∴OC=2.10. 【答案】113[解析] 这个冰激凌外壳的侧面积=12×2π×3×12=36π≈113(cm2).故答案为113.11. 【答案】2或14[解析] ①当弦AB和CD在圆心同侧时,连接OA,OC,过点O作OE⊥CD于点F,交AB于点E,如图①,∵AB=16 cm,CD=12 cm,∴AE=8 cm,CF=6 cm.∵OA=OC=10 cm,∴EO=6 cm,OF=8 cm,∴EF=OF-OE=2 cm;②当弦AB和CD在圆心异侧时,连接OA,OC,过点O作OE⊥CD于点E并反向延长交AB于点F,如图②,∵AB=16 cm,CD=12 cm,∴AF=8 cm,CE=6 cm.∵OA=OC=10 cm,∴OF=6 cm,OE=8 cm,∴EF=OF+OE=14 cm.∴AB与CD之间的距离为2 cm或14 cm.12. 【答案】15[解析] ∵OC⊥OB,∴∠COB=90°.又∵OC=OB,∴△COB是等腰直角三角形,∴∠OBC=45°.∵OA=AB,OA=OB,∴OA=AB=OB,∴△AOB是等边三角形,∴∠OBA=60°,∴∠ABC=∠OBA-∠OBC=15°.13. 【答案】6π [解析] 由题意易知∠AOB =90°,OA =OB ,∴∠ABO =45°,圆心O 旋转的长度为2×45π×3180=3π2(m),圆心O 平移的距离为270π×3180=9π2(m),则圆心O 经过的路线长为3π2+9π2=6π(m).14. 【答案】135° [解析] 连接CE.∵∠ADC =90°,∴∠DAC +∠DCA =90°.∵⊙E 内切于△ADC ,∴∠EAC +∠ECA =45°,∴∠AEC =135°.由“边角边”可知△AEC ≌△AEB ,∴∠AEB =∠AEC =135°.15. 【答案】144 [解析] ∵⊙O 与正五边形ABCDE 的边AB ,DE 分别相切于点B ,D ,∴OB ⊥AB ,OD ⊥DE.∵正五边形每个内角均为108°,∴∠BOD =∠C +∠OBC +∠ODC =108°×3-90°×2=144°.16. 【答案】2π-4 [解析] 如图所示,由题意,得阴影部分的面积=2(S 扇形OAB-S △OAB)=2(90π×22360-12×2×2)=2π-4.故答案为2π-4.三、解答题17. 【答案】证明:连接OM ,ON ,OA ,OC ,如图所示.∵M ,N 分别为AB ,CD 的中点,∴OM ⊥AB ,ON ⊥CD ,AM =12AB ,CN =12CD.又∵AB =CD ,∴AM =CN.在Rt △AOM 和Rt △CON 中,⎩⎨⎧OA =OC ,AM =CN , ∴Rt △AOM ≌Rt △CON(HL),∴OM =ON ,∴∠OMN =∠ONM ,∴∠AMO +∠OMN =∠CNO +∠ONM ,即∠AMN =∠CNM.18. 【答案】解:连接OB ,OC ,过点O 作OH ⊥BC 于点H.∵正六边形的中心角为360°6=60°,OB =OC ,∴△OBC 是等边三角形,∴半径R =OB =BC =AB =10.∵OH ⊥BC ,∴∠BOH =30°,∴BH =12OB =5.在Rt △OBH 中,边心距r =OH =102-52=5 3,周长l =6AB =6×10=60.∵S △OBC =12BC·OH =12×10×5 3=25 3,∴正六边形的面积S=6S△OBC=6×25 3=150 3.19. 【答案】解:(1)根据题意,知⊙P和y轴相切,则r=3.(2)根据题意,知⊙P和y轴相交,和x轴相离,则3<r<4.(3)根据题意,知⊙P和x轴相切或经过坐标原点,则r=4或r=5.(4)根据题意,知⊙P和x轴相交且不经过坐标原点,则r>4且r≠5.20. 【答案】证明:(1)连接AP,过点作直线BC的垂线,垂足为点M,如下图:∵线段的中点是点,以的长为半径画弧∴∴∠PAO1=∠PO1A,∠PAO2=∠PO2A,∴∠O1A O2=∠PAO1+∠PAO2=90°∴△O1A O2是直角三角形∵∴∠O1A O2=∠ABC=90°又∵∠O2MB=90°∴四边形ABM O2是平行四边形∴O2M=AB= O1A-O1B=∴是的切线;M(2)∵,,,∴O1A =又∵∠O1A O2=90°∴cos∠A O1 O2=∴∠A O1 O2=60°在Rt△B O1 C中:设O1 O2与的交点为点N,则阴影部分的面积为:.NM【解析】(1)证切线常用的方法有“作垂线证半径”和“作半径证垂直” ,考虑到题目中的已知条件,用“作垂线证半径”更简便一些,为此我们可以过点作直线BC的垂线,垂足为点M;同时考虑到∠O1A O2可能是直角,可以连接AP用等腰三角形的等角对等边和三角形内角和定理进行证明;条件中还给出了平行线,因此可以证明∠ABC=90°,则四边形ABM O2是平行四边形,最后证明O2M=AB= O1A-O1B=,问题得以解决.(2)求阴影部分的面积,可以根据割补法来求.解决问题的关键是分别求出△BO1C和扇形BO1N的面积,根据已知条件,可以先求出O1A =,然后根据三角函数求出∠A O1 O2的度数,需要的数据再通过三角函数求出,问题得解.。
(word版)九年级圆基础测试题参考答案

九年级上册 圆的根底测试题 一、选择题:〔每题2分,共20分〕 1.有4个命题:①直径相等的两个圆是等圆;②长度相等的两条弧是等弧;③圆中最大的弧是过圆心的弧;④一条弦把圆分为两条弧,这两条弧不可能是等弧. 其中真命题是〔 〕〔A 〕①③ 〔B 〕①③④ 〔C 〕①④ 〔D 〕①2.如图,点 I 为△ABC 的内心,点 O 为△ABC 的外心,∠O =140°,那么∠I 为〔 〕〔A 〕140° 〔B 〕125° 〔C 〕130° 〔D 〕110°3.如果正多边形的一个外角等于60°,那么它的边数为〔〔A 〕4 〔B 〕5 〔C 〕6 〔D 〕74.如图,AB 是⊙O 的弦,点 C 是弦AB 上一点,且 BC ︰CA =2︰1,连结OC 并延长交⊙ O 于,又 =2厘米, =3厘米,那么圆心 O 到 的距离为〔〕D DC OCAB〔A 〕6厘米 〔B 〕7厘米 〔C 〕2厘米 〔D 〕3厘米5.等边三角形的周长为 18,那么它的内切圆半径是〔〕〔A 〕63 〔B 〕33〔C 〕3 〔D 〕 33OAE6.如图,⊙ 的弦 、 相交于点,=4厘米, =3厘米, =6厘米, 切⊙ 于点 , 与 的ABCD PPAPB PC EAO ACD 延长线交于点 E ,AE =2 5 厘米,那么PE 的长为〔 〕〔A 〕4厘米 〔B 〕3厘米〔C 〕5厘米 〔D 〕 2厘米 47.一个扇形的弧长为 20 厘米,面积是 240 厘米2,那么扇形的圆心角是〔 〕〔A 〕120° 〔B 〕150° 〔C 〕210° 〔D 〕240°8.两圆半径之比为2︰3,当两圆内切时,圆心距是 4厘米,当两圆外切时,圆心距为〔 〕〔A 〕5厘米〔B 〕11厘米〔C 〕14厘米 〔D 〕20厘米9.一个圆锥的侧面积是底面积的2倍,那么这个圆锥的侧面展开图的圆周角是〔〕1〔A〕60°〔B〕90°〔C〕120°〔D〕180°AB10.如图,等腰直角三角形AOB的面积为S,以点O为圆心,OA为半径的弧与以1为直径的半圆围成的图形的面积为S2,那么S1与S2的关系是〔〕〔A〕S>S〔B〕S<S〔C〕S=S〔D〕S≥S12121212二、填空题〔每题2分,共20分〕11.⊙O1和⊙O2的半径分别为2和3,两圆相交于点A、B,且AB=2,那么O1O2=______.12.四边形ABCD是⊙O的外切等腰梯形,其周长为20,那么梯形的中位线长为_____.13.如图,在△ABC中,AB=AC,∠C=72°,⊙O过A、B两点,且与BC切于点B,与AC交于D,连结BD,假设BC=5-1,那么AC=______.14.用铁皮制造一个圆柱形的油桶,上面有盖,它的高为80厘米,底面圆的直径为50厘米,那么这个油桶需要铁皮〔不计接缝〕厘米2〔不取近似值〕.15、两圆的半径分别为3和7,圆心距为5,那么这两个圆的公切线有_____条.16.如图,以为直径的⊙O与直线相切于点,且⊥,⊥,AB CD E ACCDBDCDAC=8cm,BD=2cm,那么四边形ACDB的面积为______.17.如图,、、分别切⊙O 于、、,⊙的半径长为6cm,=10cm,PA PB DE ABC O PO那么△PDE的周长是_____。
中考数学模拟题汇总《圆》专项练习(附答案)

中考数学模拟题汇总《圆》专项练习(附答案)一、选择题1.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )A.60°B.70°C.120°D.140°2.如图,⊙O直径为10,圆心O到弦AB的距离OM长为3,那么弦AB长是( )A.4B.6C.7D.83.如图,Rt△ABC中,∠C=90°,AC=4,BC=3.以点A为圆心,AC长为半径作圆.则下列结论正确的是( )A.点B在圆内B.点B在圆上C.点B在圆外D.点B和圆的位置关系不确定4.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )A.与x轴相切,与y轴相切B.与x轴相切,与y轴相交C.与x轴相交,与y轴相切D.与x轴相交,与y轴相交5.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )A.90°B.120°C.180°D.135°6.如图,将△ABC 绕点C 按顺时针旋转60°得到△A ′B ′C,已知AC=6,BC=4,则线段AB 扫过图形面积为( )A.πB.πC.6πD.π7.已知圆锥的底面半径为4cm ,母线长为6cm ,则它的侧面展开图的面积等于( )A.24cm 2B.48cm 2C.24πcm 2D.12πcm 28.“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD 为⊙O 的直径,弦AB ⊥CD 垂足为E ,CE =1寸,AB =10寸,求直径CD 的长”,依题意,CD 长为( )A.12寸B.13寸C.24寸D.26寸9.下列关于三角形的外心的说法中,正确的是( )A.三角形的外心在三角形外B.三角形的外心到三边的距离相等C.三角形的外心到三个顶点的距离相等D.等腰三角形的外心在三角形内10.如图,⊙C 过原点O ,且与两坐标轴分别交于点A 、B ,点A 的坐标为(0,4),点M 是第三象限内OB ︵ 上一点,∠BMO =120°,则⊙C 的半径为( )A.4B.5C.6D.2 311.如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°.设OP=x,则△PAB的面积y关于x的函数图象大致是( )12.如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是( )A. 5π3-2 3 B.5π3+2 3 C. 23-5π3D. 3+5π3二、填空题13.如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=______.14.如图,正方形网格中每个小正方形边长都是l,则△ABC的外接圆的圆心坐标为 .15.如图,四边形ABCD为⊙O的内接四边形,连接AC、BO,已知∠CAB=36°,∠ABO=30°,则∠D= .16.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步.”该问题的答案是________步.17.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于________.(结果保留根号)18.如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1∶r2= .三、解答题19.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,(1)如图1,尺规作图,找到桥弧所在圆的圆心O(保留作图痕迹);(2)如图2,求桥弧AB所在圆的半径R.20.如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°.(1)求证:直线AD是⊙O的切线;(2)若直径BC=4,求图中阴影部分的面积.21.如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.(1)若∠ADE=25°,求∠C的度数;(2)若AC=4,CE=2,求⊙O半径的长.22.如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.(1)求证:DF⊥AC;(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).23.如图,已知:AB是⊙O的弦,过点B作BC⊥AB交⊙O于点C,过点C作⊙O的切线交AB的延长线于点D,取AD的中点E,过点E作EF∥BC交DC的延长线于点F,连接AF并延长交BC 的延长线于点G.求证:(1)FC=FG;(2)AB2=BC·BG.24.如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是⊙O的切线;(2)若A为EH的中点,求EFFD的值;(3)若EA=EF=1,求⊙O的半径.参考答案1.D 2.D 3.C. 4.C. 5.C 6.D 7.C8.D. 9.C. 10.A. 11.D. 12.A13.答案为:48°.14.答案为:(172,2).15.答案为:96°.16.答案为:617.答案为:1+ 218.答案为:3∶2;19.解:(1)如图1所示;(2)连接OA.如图2.由(1)中的作图可知:△AOD为直角三角形,D是AB的中点,CD=10,∴AD=0.5AB=20.∵CD=10,∴OD=R﹣10.在Rt△AOD中,由勾股定理得,OA2=AD2+OD2,∴R2=202+(R﹣10)2.解得:R=25.即桥弧AB所在圆的半径R为25米.20.证明:(1)连接OA,则∠COA=2∠B,∵AD =AB ,∴∠B =∠D =30°,∴∠COA =60°,∴∠OAD =180°﹣60°﹣30°=90°,∴OA ⊥AD ,即CD 是⊙O 的切线;(2)∵BC =4,∴OA =OC =2,在Rt △OAD 中,OA =2,∠D =30°,∴OD =2OA =4,AD =23,所以S △OAD =12OA •AD =12×2×23=23,因为∠COA =60°,所以S 扇形COA =2π3,所以S 阴影=S △OAD ﹣S 扇形COA =23﹣2π3.21.解:(1)连接OA ,∵∠ADE =25°,∴由圆周角定理得:∠AOC =2∠ADE =50°,∵AC 切⊙O 于A ,∴∠OAC=90°,∴∠C=180°﹣∠AOC﹣∠OAC=180°﹣50°﹣90°=40°;(2)设OA=OE=r,在Rt△OAC中,由勾股定理得:OA2+AC2=OC2,即r2+42=(r+2)2,解得:r=3,答:⊙O半径的长是3.22.(1)证明:连接OD,如图所示.∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∴∠CFD=∠ODF=90°,∴DF⊥AC.(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴的长===π.23.证明:(1)如解图,∵EF∥BC,AB⊥BG,∴EF⊥AD.∵E是AD的中点,∴FA=FD,∴∠FAD=∠D.又∵GB⊥AB,∴∠GAB+∠G=∠D+∠1=90°,∴∠1=∠G,∵∠1=∠2,∴∠2=∠G,∴FC=FG;(2)如图,连接AC,∵AB⊥BG,∴AC是⊙O的直径,∵FD是⊙O的切线,切点为C,∴AC⊥DF,∴∠1+∠4=90°,∵∠3+∠4=90°,∴∠1=∠3,由(1)可知∠1=∠G,∴∠3=∠G,又∵∠ABC=∠GBA=90°,∴△ABC∽△GBA,∴ABGB=BCBA,∴AB2=BC·BG.24. (1)证明:如图,连接OD,∵AB=AC,∴∠1=∠2,∵OB=OD,∴∠1=∠3,∴∠2=∠3,∴OD∥AC,∵DH⊥AC,∴OD⊥DH,∵OD是⊙O的半径,∴DH是⊙O的切线;(2)解:由圆周角定理知,∠1=∠5,又∵∠1=∠2,∴∠2=∠5,∴△EDC是等腰三角形,∵DH⊥AC,∴H是EC的中点,∵A是EH的中点,∴EA=AH=12HC=13AC,由(1)知OD∥AC,∵O是AB的中点,∴OD=12 AC,∴EFFD=AEOD=2AEAC=23;(3)解:设OD=x,∵OD∥EC,EA=EF=1,∴OD=FD=x,∴ED=DC=x+1,又∵AC=2OD=2x,∴EC=2x+1,∵在△CDE与△CAB中,∠2=∠2,∠1=∠5,∴△CDE∽△CAB,∴CDCA=CECB,即CD·CB=CA·CE,得(x+1)(2x+2)=2x(2x+1),解得x1=5+12,x2=1-52(舍去),5+1 2.∴⊙O的半径为。
九年级圆知识点及习题(含答案)

圆圆的有关概念与性质1.圆上各点到圆心的距离都等于半径。
2.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;圆又是中心对称图形,圆心是它的对称中心。
3.垂直于弦的直径平分这条弦,并且平分弦所对的弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
4.在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量相等,那么它们所对应的其余各组量都分别相等。
5.同弧或等弧所对的圆周角相等,都等于它所对的圆心角的一半。
6.直径所对的圆周角是 90°,90°所对的弦是直径。
7.三角形的三个顶点确定 1 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫外心,是三角形三边垂直平分线的交点。
8.与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点的交点,叫做三角形的内心。
9.圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角与圆有关的位置关系1.点与圆的位置关系共有三种:①点在圆外,②点在圆上,③点在圆内;对应的点到圆心的距离d和半径r之间的数量关系分别为:①d > r,②d = r,③d < r.2.直线与圆的位置关系共有三种:①相交,②相切,③相离;对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为:①d < r,②d = r,③d > r.3.圆与圆的位置关系共有五种:①内含,②相内切,③相交,④相外切,⑤外离;两圆的圆心距d和两圆的半径R、r(R≥r)之间的数量关系分别为:①d < R-r,②d = R-r,③ R-r < d < R+ r,④d = R+r,⑤d > R+r.4.圆的切线垂直于过切点的半径;经过直径的一端,并且垂直于这条直径的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长 相等,这点与圆心之间的连线 平分 这两条切线的夹角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i n
b e
i n g
o o
B .3
C .4
J24-1-1 图J24-1-2 图J24-1-3
.如图J24-1-2,在半径为的⊙O 内有长为的弦AB ,则∠60° B .90° 150°二、填空题(每小题.过圆内的一点(非圆心________条弦,有条直径..如图J24-1-3,OE 图J24-1-4
a
n d
A
l l t h i n
g s
i n
t h
e i r
b e
i n g
a r
e 时间:10分钟 满分:25分
一、选择题(每小题3分,共6分)
1.如图J24-1-5,AB 是⊙O 的直径,=,∠BOD =60°,则∠AOC =( )A BD
A CD A .30°
B .45°
C .60°
D .以上都不正确
2.如图J24-1-6,AB ,CD 是⊙O 的直径,=,若∠AOE =32°,则A
AE A BD ∠COE 的度数是( )
A .32°
B .60°
C .68°
D .64°
图J24-1-5 图J24-1-6 图J24-1-7 图J24-1-8二、填空题(每小题4分,共8分)
3.如图J24-1-7,CD ⊥AB 于点E ,若∠B =60°,则∠A =________.4.如图J24-1-8,D ,E 分别是⊙O 的半径OA ,OB 上的点,
CD ⊥OA ,CE ⊥OB ,CD =CE ,则与的弧长的大小关系是A
AC A CB ______________.
三、解答题(共11分)
5.如图J24-1-9,已知AB =AC ,∠APC =60°.(1)求证:△ABC 是等边三角形;(2)求∠APB 的度数.
图J24-1-9
时间:10分钟 满分:25分
一、选择题(每小题3分,共9分)
1.已知圆的半径为3,一点到圆心的距离是5,则这点在( )A .圆内 B .圆上
C .圆外
D .都有可能答案
2.在△ABC 中,∠C =90°,AC =BC =4 cm ,点D 是AB 边的中点,以点C 为圆心,4 cm 长为半径作圆,则点A ,B ,C ,D 四点中在圆内的有( )
A .1个
B .2个
C .3个
D .4个
3.⊙O 的半径r =5 cm ,圆心到直线l 的距离OM =4 cm ,在直线l 上有一点P ,且PM =3 cm ,则点P ( )
A .在⊙O 内
B .在⊙O 上
C .在⊙O 外
D .可能在⊙O 上或在⊙O 内二、填空题(每小题4分,共8分)
4.锐角三角形的外心在________;直角三角形的外心在________;钝角三角形的外心在________.
5.在Rt △ABC 中,∠C =90°,AC =5 cm ,BC =12 cm ,则Rt △ABC 其外接圆半径为________cm.
三、解答题(共8分)
6.通过文明城市的评选,人们增强了卫生意识,大街随地乱扔生活垃圾的人少了,人们自觉地将生活垃圾倒入垃圾桶中,如图J24-2-1所示,A ,B ,C 为市内的三个住宅小区,环保公司要建一垃圾回收站,为方便起见, 要使得回收站建在三个小区都相等的某处,请问如果你是工程师,你将如何选址.
图J24-2-1
h
e i r
b e
i n g
a r
e g
时间:10分钟 满分:25分
图J24-2-2 图J24-2-3 图J24-2-4 J24-2-5
二、填空题(每小题4分,共12分3.已知⊙O 的直径为10 cm ,圆心到直线l 的距离分别是:①3 cm ;③7 cm.那么直线和⊙O 的位置关系是:________;②________;③________.
的延长线上,过点D 作⊙DCF =32°,求∠A 的度数.
图J24-2-6
i n
e
i 时间:10分钟 满分:25分
ABCDEF 内接于⊙图J24-3-1
D .22.5°分)
________.
,它的边心距等于的圆形纸片上裁出一个最大的正方形,则此正方形的图J24-3-2
g s
i n
b e
i n 时间:10分钟 满分:25分
图J24-4-1图J24-4-2
,在两个同心圆中,两圆半径分别为2,1,∠____________.
分)
,在正方形ABCD 边的长为1,点为半径作圆,分别交M ,N 两点,与图J24-4-3
i r
b e
i n g
a 时间:10分钟 满分:25分
B .180°
C .
图J24-4-4图J24-4-5 图二、填空题(每小题4分,共J24-4-5,小刚制作了一个高12 cm ,底面直径为10 cm 的圆锥,这个圆锥的侧面积是________cm J24-4-6,Rt △ABC 分别绕直角边AB ,BC 旋转一周,旋转后得到的两个圆锥的母线长分别为____________。
