初中数学余切函数公式知识点整理
余切函数的定义和性质
余切函数的定义和性质余切函数，又称作切割函数，是一种用于描述角度的数学函数。
它的定义域为全体实数，值域为全体实数。
在三角函数和解析几何中，余切函数的作用至关重要。
在这篇文章中，我们将讨论余切函数的定义和性质，帮助读者更好地理解和应用此函数。
一、余切函数的定义余切函数定义为正切函数的倒数，即：$$cotx=\frac{1}{tanx}$$其中，$x$ 为弧度制下的角度。
例如，当$x=\frac{\pi}{4}$ 时，$cotx$ 的值为 $1$。
二、余切函数的图像余切函数的图像可以通过正切函数的图像推导得到。
正切函数的周期为 $\pi$，在 $[0,\pi]$ 区间内是单调上升的。
正切函数在$x=0$ 处不存在定义，且在 $x=\frac{\pi}{2}$ 时不存在极限。
因此，在 $[0,\pi]$ 区间内，$cotx$ 的图像将存在一个垂直于 $x$ 轴的渐近线，且图像在 $0$ 和 $\pi$ 处存在一个奇点。
余切函数的图像如下所示：图像中黄色部分是余切函数的图像，蓝色的 $y=-\frac{\pi}{2}$ 和 $y=\frac{\pi}{2}$ 分别是余切函数的渐近线，绿点和紫点分别是余切函数的奇点。
三、余切函数的性质(1) 周期性余切函数的周期为 $\pi$，即 $cot(x+n\pi)=cotx$，其中 $n$ 为任意整数。
(2) 偶函数余切函数是偶函数，即 $cot(-x)=cotx$。
(3) 奇点余切函数在 $x=0$ 和 $x=\pi$ 处存在奇点。
当 $x$ 趋近于$0$ 或 $\pi$ 时，$cotx$ 的绝对值将趋近于无穷大。
(4) 符号变化余切函数的符号随角度的变化而变化。
当 $x$ 在$(0,\frac{\pi}{2})$ 范围内时，$cotx$ 为正数；当 $x$ 在$(\frac{\pi}{2},\pi)$ 范围内时，$cotx$ 为负数；当 $x$ 等于 $0$ 或$\pi$ 时，$cotx$ 不存在符号。
中考复习：初中数学三角函数公式
中考复习：初中数学三角函数公式中考复习：初中数学三角函数公式三角函数公式正弦（ sin）:角的对边比上斜边余弦（ cos） :角的邻边比上斜边正切（ tan）:角的对边比上邻边余切（ cot）:角的邻边比上对边正割（ sec） :角的斜边比上邻边余割（ csc） :角的斜边比上对边sin30=1/2sin45=根号 2/2sin60=根号 3/2cos30=根号 3/2cos45=根号 2/2cos60=1/2tan30=根号 3/3tan45=1tan60=根号 3两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinB ?cos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA) ? cot(A-B) = (cotAcotB+1)/(cotB-cotA) 2019 倍角公式Sin2A=2SinA?CosACos2A=Cos^A-Sin^A=1-2Sin^A=2Cos^A-1 tan2A=2tanA/1-tanA^22019 三倍角公式tan3a = tan a tan(/3+a) tan(/3-a)2019 半角公式2019 和差化积sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosB 2019 积化和差sin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)]cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)] 2019 引诱公式sin(-a) = -sin(a)cos(-a) = cos(a)sin(/2-a) = cos(a)cos(/2-a) = sin(a)sin(/2+a) = cos(a)cos(/2+a) = -sin(a)sin(-a) = sin(a)cos(-a) = -cos(a)sin(+a) = -sin(a)cos(+a) = -cos(a)tanA=tanA = sinA/cosA2019 全能公式2019 其余公式2019 其余非要点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)2019 双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tg h(a) = sin h(a)/cos h(a)公式一：设为随意角，终边同样的角的同一三角函数的值相等：sin（ 2k＋） = sincos（2k＋） = costan（ 2k＋） = tancot（ 2k＋） = cot公式二：设为随意角，的三角函数值与的三角函数值之间的关系：sin（＋） = -sincos（＋） = -costan（＋） = tancot（＋） = cot公式三：随意角与-的三角函数值之间的关系：sin（ -）= -sincos（-） = costan（ -） = -tancot（ -） = -cot公式四：利用公式二和公式三能够获得与的三角函数值之间的关系：sin（） = sincos（） = -costan（） = -tancot（） = -cot公式五：利用公式 -和公式三能够获得 2 与的三角函数值之间的关系：sin（ 2） = -sincos（2） = costan（ 2） = -tancot（ 2） = -cot公式六：/2 及 3/2 与的三角函数值之间的关系：sin（ /2+） = coscos（/2+ ）= -sintan（ /2+ ）= -cotcot（ /2+ ）= -tansin（ /2-） = coscos（/2-） = sintan（ /2-） = cotcot（ /2-） = tansin（ 3/2+） = -coscos（3/2+ ）= sintan（ 3/2+） = -cotcot（ 3/2+） = -tansin（ 3/2-） = -coscos（3/2-） = -sintan（ 3/2- ）= cotcot（ 3/2- ）= tan(以上 kZ)个物理常用公式我了半天的才来,希望大家有用Asin(t+)+ Bsin(t+) ={(A^2 +B^2 +2ABcos(-)} ? sin{ t + arcsin[ (A?sin+B?sin)/ {A^2 +B^2; +2ABcos(-)} }表示根号 ,包含 { ⋯⋯}中的内容函数名正弦余弦正切余切正割余割在平面直角坐系 xOy 中，从点 O 引出一条射 OP，旋角，OP=r ， P 点的坐（ x， y）有正弦函数sin=y/r余弦函数cos=x/r正切函数tan=y/x余切函数cot=x/y正割函数sec=r/x余割函数csc=r/y（斜 r，y， x。
直角三角形的正切与余切
直角三角形的正切与余切直角三角形是指其中一个角为90度的三角形。
在直角三角形中，正切和余切是两个重要的三角函数，它们可以帮助我们计算角度和边长之间的关系。
本文将详细介绍直角三角形的正切和余切，以及它们的性质和应用。
一、什么是正切和余切？在直角三角形中，正切（tan）是指直角三角形一直角边上的边长与另一直角边的比值。
正切的定义可以用以下公式表示：tan(θ) = 对边 / 临边其中，θ为直角三角形的一个非直角角度，对边指与该角相对的直角边，临边指与该角相邻的直角边。
余切（cot）则是指正切的倒数，即余切等于临边与对边的比值。
余切的定义可以用以下公式表示：cot(θ) = 临边 / 对边二、正切和余切的性质1. 范围：正切和余切的值没有上限和下限，可以是任何实数。
2. 周期性：正切和余切的图像在每个周期内都是重复的。
正切的周期为180度或π弧度，余切的周期为360度或2π弧度。
3. 对称性：正切和余切的图像关于坐标原点对称。
即tan(-θ) = -tan(θ)，cot(-θ) = -cot(θ)。
4. 奇偶性：正切和余切都是奇函数，即tan(-θ) = -t an(θ)，cot(-θ) = -cot(θ)。
5. 关系：正切和余切之间存在以下关系：tan(θ) = 1 / cot(θ)cot(θ) = 1 / tan(θ)6. 值域：正切和余切的值域均为实数集合R。
三、正切和余切的应用正切和余切在实际问题中有广泛的应用，尤其在测量和工程领域。
1. 角度测量：正切和余切可以帮助我们计算角度的大小。
通过已知两条边的长度，可以借助正切和余切函数求解对应的角度。
2. 斜率计算：在平面几何中，直线的斜率可以利用正切和余切来计算。
斜率等于直线与x轴的夹角的正切值，或者直线与y轴的夹角的余切值。
3. 距离测量：若已知直角三角形中一条直角边的长度和另一条角上的边长，则可以利用正切和余切来计算未知边的长度。
4. 三角恒等式：正切和余切与其他三角函数之间存在多种恒等式，这些恒等式在解决三角方程和化简复杂三角式等问题时起到重要作用。
math 函数库的余切函数
math 函数库的余切函数余切函数是数学中常见的三角函数之一，常用于解决各种实际问题以及在数学推导和证明中的应用。
在数学函数库中，余切函数常被表示为tan(x)或ctg(x)两种形式。
余切函数的定义如下：余切函数是正切函数的倒数。
在右边的直角三角形中，余切函数定义为直角边的长除以相邻直角边的长。
可以用如下公式表示：cot(x) = 1/tan(x)其中cot(x)表示x的余切值，tan(x)表示x的正切值。
在数学中，余切函数常被用于解决各种实际问题，包括物理、工程、计算机科学和经济等领域。
下面我们将介绍余切函数在这些领域中的应用。
在物理学中，余切函数常用于计算角度、速度和加速度等物理量之间的关系。
特别是在电工和电子工程中，余切函数被广泛应用于计算交流电路中的电流、电压和功率等参数。
余切函数的高级应用包括计算电路中的相位差、阻抗和反射系数等问题。
在工程中，余切函数被用于计算力、压力和扭矩等问题。
例如，在机械工程中，余切函数可以帮助工程师计算材料的强度和刚度，以便设计出更安全和可靠的机械结构。
在土木工程中，余切函数常被用于计算结构的稳定性和变形性能。
在计算机科学领域，余切函数被广泛应用于图形学和计算机视觉等方面。
例如，在计算机图形学中，余切函数可用于计算三维物体的旋转、平移和缩放变换。
在计算机视觉中，余切函数可以用于计算图像中的角度和位置信息。
在经济学中，余切函数被用于计算利率、回报率和贝叶斯估计等问题。
特别是在金融学中，余切函数可以帮助分析投资组合的回报率和风险。
此外，余切函数还可以用于计算供需关系、价格弹性和市场规模等经济指标。
除了上述领域之外，余切函数还在数学建模和数值计算等方面发挥着重要作用。
例如，在数学建模中，余切函数可以用于描述物体的周期性运动和振动。
在数值计算中，余切函数常被用于解决非线性方程和微分方程等数值问题。
总之，余切函数在数学中扮演着重要的角色，并在各个领域中得到广泛的应用。
无论是解决实际问题还是进行数学推导，了解和掌握余切函数的性质和应用都对我们的学习和研究具有重要意义。
初中数学tan sin cos公式
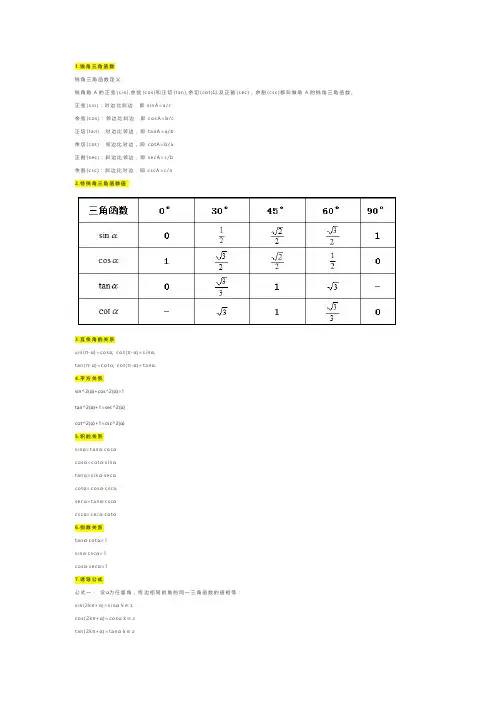
1.锐角三角函数锐角三角函数定义:锐角角A的正弦(s i n),余弦(c o s)和正切(t an),余切(c o t)以及正割(s e c)，余割(c s c)都叫做角A的锐角三角函数。
正弦(s i n)：对边比斜边，即s i n A=a/c余弦(c o s)：邻边比斜边，即c o s A=b/c正切(t a n)：对边比邻边，即t a n A=a/b余切(c o t)：邻边比对边，即c o t A=b/a正割(s e c)：斜边比邻边，即s e c A=c/b余割(c s c)：斜边比对边，即c s c A=c/a2.特殊角三角函数值3.互余角的关系s i n(π-α)=c o sα,c o s(π-α)=s i nα,t an(π-α)=c o tα,c o t(π-α)=t a nα.4.平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)5.积的关系s i nα=t a nα·c o sαc o sα=c o tα·s i nαt anα=s i nα·s e cαc o tα=c o sα·c s cαs e cα=t anα·c s cαc s cα=s e cα·c o tα6.倒数关系t anα·c o tα=1s i nα·c s cα=1c o sα·s e cα=17.诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：s i n(2kπ+α)=s i nαk∈zc o s(2kπ+α)=c o sαk∈zt an(2kπ+α)=t a nαk∈zc o t(2kπ+α)=c o tαk∈z公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：s i n(π+α)=-s i nαc o s(π+α)=-c o sαt an(π+α)=t anα8.两角和差公式(1)s i n(A+B)=s i n A c o s B+c o s A s i n B(2)s i n(A-B)=s i n A c o s B-s i n B c o s A(3)c o s(A+B)=c o s A c o s B-s i n A s i n B(4)c o s(A-B)=c o s A c o s B+s i n A s i n B(5)t a n(A+B)=(t a n A+t a n B)/(1-t an A t an B)(6)t a n(A-B)=(t a n A-t a n B)/(1+t a n A t an B)(7)c o t(A+B)=(c o t A c o t B-1)/(c o t B+c o t A)(8)c o t(A-B)=(c o t A c o t B+1)/(c o t B-c o t A)除了以上常考的三角函数公式外，掌握下面半角公式，积化和差和万能公式有利于快速解决选择题，达到事半功倍的效果哦！1.半角公式注：正负由α/2所在的象限决定。
【初中数学】三角函数的余切公式大全
【初中数学】三角函数的余切公式大全
【—余切公式定理】简单点理解余切的定义指的就是直角三角形任意一锐角的邻边和对边的比，叫做该锐角的余切。
余切
表示时用“cot+角度”，如：30°的余切表示为cot30°;角A的余切表示为cotA
旧用ctgA来表示余切，至今仍在使用，和cosA是一样的。
(注：现在已经不常用了)
任意角终边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边则与正x轴重合。
假设∠A的对边为a、邻边为b，那么:
cot A= b/a(即邻边比对边)
余切的性质
1.与正切互为倒数
2.单调递减
3.奇函数
4.值域R
编辑本段相关公式和的关系
1+cot^2α=csc^2α
积的关系
cotα=cosα×cscα
tanα ·cotα=1
商的关系
cosα/sinα=cotα=cscα/secα
由泰勒级数得出
cotx=1/tanx=[ie^(ix)+ie^(-ix)]/[e^(ix)-e^(-ix)]
和角公式
cot(α+β)=(cotαcotβ-1)/(cotα+cotβ)
cot(α-β)=(cotαcotβ+1)/(cotβ-cotα)
我们经常会说到的一句话就是余切是混沌的，可能同学们不太能理解，简单就是我们得到的数字完全可以看作是随机的，混沌的。
感谢您的阅读，祝您生活愉快。
余切函数知识点总结数学
余切函数知识点总结数学一、余切函数的定义余切函数通常用cot(x)表示，定义为正切函数的倒数，即cot(x) = 1/tan(x)。
在数学中，正切函数是指一个角的正切值，这个角是一个直角三角形中的角，其两条腿长度比值。
正切函数的定义域为除了所有余弦函数值为0的角外的所有角度。
也就是说，正切函数的定义域为（0, π）和（π, 2π）这两个区间之外的所有角度。
二、余切函数的性质1. 值域：余切函数的值域为所有实数，即cot(x)∈R。
2. 周期性：余切函数的周期是π，即cot(x+π) = cot(x)。
3. 奇偶性：余切函数是奇函数，即cot(-x) = -cot(x)，这也可以从定义cot(x) = 1/tan(x)出发，tan(-x) = -tan(x)得到。
4. 导数性质：余切函数的导数是负正切函数的平方，即cot'(x) = -1/(tan(x))^2。
5. 反函数性质：余切函数的反函数是反余切函数，即cot^(-1)(x) = arccot(x)。
三、余切函数的图像余切函数的图像可以通过正切函数的图像进行推导得到。
根据正切函数的定义tan(x) =sin(x)/cos(x)，可以得到cot(x) = 1/tan(x) = cos(x)/sin(x)。
因此，可以从正切函数的图像推导出余切函数的图像。
余切函数的图像在每个周期内有无穷多个渐近线，其周期是π，且在x=kπ与x=(k+1)π（k∈Z）处有垂直渐近线。
余切函数的图像是以(x,y) = (kπ, 0)为对称中心关于y轴对称的奇函数。
四、余切函数的导数求余切函数的导数需要将余切函数的定义cot(x) = 1/tan(x)代入正切函数的导数公式。
正切函数的导数是sec^2(x)，所以cot(x)的导数就是cot'(x) = -1/(tan(x))^2 = -1/(1+cot^2(x))。
这个导数公式可以用来求余切函数的导数。
余切函数推导公式大全
余切函数推导公式大全1. 余切函数的定义余切函数（cotangent function）是三角函数中的一种，表示为cot(x)或ctg(x)。
它的定义为正切函数（tan(x)）的倒数，即：cot(x) = 1 / tan(x)2. 基本性质余切函数满足以下基本性质：- 定义域：所有实数x，除了满足tan(x)=0的点（即x=kπ，其中k为整数）。
- 值域：所有实数。
- 周期性：cot(x)的周期为π。
- 对称性：cot(-x) = -cot(x)。
3. 余切函数的推导公式3.1. 余弦函数与正弦函数的关系余切函数与余弦函数和正弦函数有以下关系：cot(x) = cos(x) / sin(x)3.2. 余切函数的倒数余切函数的倒数可以通过互余函数（cosecant function）来表示：csc(x) = 1 / sin(x)cot(x) = 1 / csc(x)3.3. 余切函数的和差公式余切函数的和差公式如下：cot(x + y) = (cot(x) * cot(y) - 1) / (cot(x) + cot(y))cot(x - y) = (cot(x) * cot(y) + 1) / (cot(y) - cot(x))3.4. 余切函数的倍角公式余切函数的倍角公式如下：cot(2x) = (cot(x)^2 - 1) / (2 * cot(x))3.5. 余切函数的三角和差公式余切函数的三角和差公式如下：cot(x + y) = (cot(x) * cot(y) - 1) / (cot(x) + cot(y))cot(x - y) = (cot(x) * cot(y) + 1) / (cot(y) - cot(x))4. 总结以上是余切函数的一些推导公式，通过这些公式可以简化计算和证明一些三角函数的性质。
根据需要，可以利用这些公式进行相应的推导和计算。
请注意，余切函数的定义域有限制，需避开tan(x)=0的点。
余切函数知识点总结期末
余切函数知识点总结期末1. 余切函数的定义在一个直角三角形中，假设角A为直角，则余切函数定义如下：$$\cot A = \frac{{\text{邻边}}}{{\text{对边}}}, \text{其中对边不等于零。
}$$其中，邻边是指角A的对边，对边指角A的邻边。
在三角形中，余切函数的定义只能应用于直角角度。
2. 余切函数的周期性与正弦函数和余弦函数一样，余切函数也具有周期性。
它的周期是π，即$$\cot(x + \pi) = \cot x. $$3. 余切函数的图像余切函数的图像是一个周期性的曲线，其在每个周期内有无穷多个渐近线。
当自变量为整数倍的π时，函数值为零。
当自变量为奇数倍的π/2时，函数值为正无穷或负无穷。
在每个周期内，余切函数的图像都是一条有无穷多个渐近线的曲线。
4. 余切函数的性质余切函数有以下性质：- 余切函数是奇函数，即$$\cot(-x) = -\cot x.$$- 余切函数的定义域是一切余弦函数为零的点，即$$x \neq k\pi, k \in Z.$$- 余切函数的值域是一切实数。
5. 余切函数的应用余切函数可以用于解决和角度相关的问题，尤其是在直角三角形中。
通过余切函数，可以计算出三角形中的各个角度的余切值。
在物理学和工程学中，余切函数也常常用于解决角度相关的问题。
总结：- 余切函数是三角函数中的一种，表示在直角三角形中邻边与对边的比值。
- 余切函数具有周期性，其周期为π。
- 余切函数的图像是一条周期性曲线，其在每个周期内有无穷多个渐近线。
- 余切函数是奇函数，其定义域是一切余弦函数为零的点，值域是一切实数。
- 余切函数在解决和角度相关的问题中有广泛的应用。
综上所述，余切函数是三角函数中的重要概念，具有周期性和特定的性质。
了解余切函数的定义和特性有助于我们更好地理解三角函数，并能够应用余切函数解决实际问题。
同时，余切函数也具有广泛的应用领域，在物理学、工程学等领域中起着重要的作用。
余切知识点总结
余切知识点总结一、余切函数的定义余切函数的定义如下：在直角三角形ABC中，直角边为a，另一直角边为b，斜边为c，角A对应的余切值为cotA，定义为cotA = a/b。
其中a/b称为余切值，cotA表示角A的余切值。
二、余切函数的值域和定义域余切函数的定义域为R - {kπ|k为整数}，即除去所有π的整数倍的实数集合。
余切函数的值域为R。
三、余切函数的性质1. 余切函数是一个奇函数，即cot(-x)=-cotx，对任意实数x成立。
2. 余切函数是周期函数，其周期为π，即cot(x+π)=cotx。
3. 余切函数的性质与正切函数互补，即cotx=1/tanx。
4. 余切函数与正切函数的关系可以通过三角恒等式tanx=1/cotx推导得出。
5. 余切函数的图像与正切函数的图像互为镜像，即以原点为对称中心对称。
四、余切函数的应用1. 余切函数常用于计算直角三角形的边长和角度。
在已知直角三角形的两个边长或一个角度的情况下，可以利用余切函数来求解其余的边长和角度。
例如，已知直角三角形的一条直角边为3，斜边为5，可以利用余切函数求解另一直角边的长度。
2. 余切函数也常用于求解特定角度的正切值。
由于余切函数与正切函数互为倒数关系，因此可以通过余切函数来求得某一角度的正切值，从而进一步得到该角度的正弦值和余弦值。
3. 余切函数还可以用于解决与角度相关的物理问题和工程问题。
例如，利用余切函数可以计算地面上物体的倾斜角度、建筑物的倾角和斜率等。
五、余切函数与其他三角函数的关系1. 余切函数与正切函数是互为倒数关系的，即cotx=1/tanx。
2. 余切函数与正切函数的图像是互为镜像的，即以原点为对称中心对称。
3. 余切函数与正弦函数、余弦函数的关系通过三角恒等式tanx=1/cotx可以推导出。
通过以上几点知识点的总结，我们可以更全面地了解余切函数的定义、性质、应用以及与其他三角函数的关系。
余切函数作为三角函数的一种，在数学和实际生活中都具有一定的重要性，掌握余切函数的知识可以帮助我们更好地理解和解决与角度相关的问题。
余切计算公式
余切计算公式余切是三角函数中的一个重要概念，它在数学学习和实际应用中都有着不可或缺的地位。
咱先来说说余切的定义哈，余切就是正切的倒数。
如果一个角的正切值是 a，那么它的余切值就是 1/a 。
那余切的计算公式是啥呢？一般来说，如果角 A 的对边是 a，邻边是 b ，那么角 A 的余切值 cot A 就等于邻边 b 除以对边 a 。
我记得之前教过一个学生小明，他在学习余切的时候，那叫一个头疼啊！每次一看到余切的题目，就愁眉苦脸的。
有一次做练习题，题目是这样的：一个直角三角形，其中一个锐角的对边是3 ，邻边是4 ，求这个角的余切值。
小明一看，脑子就乱了，嘴里还嘟囔着：“这可咋办呀，余切咋算啊？”我走到他身边，耐心地跟他说：“小明，别着急，你先想想余切的定义，它是邻边除以对边，那这个角的余切值不就是4÷3 嘛。
”小明听了恍然大悟，一拍脑袋说：“哎呀，我怎么就没想到呢！”咱们继续说余切的计算公式。
在单位圆中，余切也可以通过坐标来计算。
假设角 A 的终边上一点的坐标是 (x,y) ，那么余切值 cot A 就等于 x/y 。
还有啊，余切函数也有一些性质。
比如说，它是一个周期函数，周期是π 。
而且，余切函数在定义域内是奇函数。
在实际解题中，运用余切计算公式的时候一定要仔细。
就像上次考试，有一道题是这样的：已知一个角的余切值是 2/3 ，且这个角在第二象限，求这个角的正弦值和余弦值。
很多同学一看到这道题就慌了，不知道从哪里下手。
其实呢，咱们先根据余切的定义求出这个角的正切值，然后再利用三角函数的基本关系式就能算出来啦。
余切的计算公式虽然看起来简单，但要真正熟练掌握并运用自如，还需要多做练习。
比如说，多做一些关于直角三角形中求余切值的题目，或者是利用单位圆中的坐标来计算余切值的题目。
总之啊，余切计算公式是数学中的一个重要工具，只要咱们认真学习，多思考多练习，就一定能掌握好它，让它为我们解决更多的数学问题！就像小明后来通过不断努力，在余切这部分的学习上取得了很大的进步，做题也越来越得心应手啦。
余切函数的性质及其应用
余切函数的性质及其应用余切函数是三角函数中的一种，也叫做切割函数。
它是正切函数的倒数，常记为cot(x)。
在数学和物理学中，余切函数有着广泛的应用，尤其在三角学领域。
一、余切函数的定义和性质余切函数可以通过正切函数的定义来得到：cot(x) = 1/tan(x)。
在单位圆上，余切函数在不同象限的值有以下性质：1. 第一象限：余切函数的值为正，且无上界。
当角度接近0时，它趋近于正无穷大；2. 第二象限：余切函数的值为负，且无下界。
同样地，在角度接近180度时，它趋近于负无穷大；3. 第三象限：余切函数的值为负，且无上界。
在角度接近180度时，它趋近于负无穷大；4. 第四象限：余切函数的值为正，且无下界。
当角度接近0度时，它趋近于正无穷大。
二、余切函数的应用余切函数在数学和物理学中有着广泛的应用，下面将介绍其中的一些应用。
1. 三角恒等式的证明：余切函数在证明三角恒等式中起到了重要的作用。
例如，借助余切函数可以很容易地证明正弦余弦的和差公式和倍角公式等。
2. 三角方程的解：在解三角方程时，余切函数经常扮演着关键的角色。
通过使用余切函数，可以求解各种复杂的三角方程，如cot(x)=a的解等。
3. 函数图像的分析：余切函数的图像具有特定的周期性和对称性。
利用余切函数的性质，可以分析函数图像的特点，包括最大值、最小值、增减性等。
4. 物理学中的应用：在物理学中，特别是在震动和波动的研究中，余切函数经常用于描述振幅的变化情况。
例如，可以利用余切函数来计算谐振子在稳定状态下的振幅和相位差。
5. 工程问题的求解：在工程领域，如电路分析、信号处理和通信系统等，余切函数也有着重要的应用。
例如，利用余切函数可以计算电路的阻抗和相位差，进而解决相关的实际问题。
综上所述，余切函数作为一种重要的三角函数，在数学和物理学中发挥着重要作用。
它具有特殊的性质，不仅可以用于证明三角恒等式和解三角方程，还可以应用于函数图像的分析、物理问题的求解以及工程领域的实际应用中。
余切函数的特性解析与变化规律
余切函数的特性解析与变化规律余切函数（cot）是三角函数的一种，它表示正切函数（tan）的倒数。
在数学中，余切函数的特性及其变化规律具有一定的重要性。
本文将对余切函数的特性进行解析，并讨论其变化规律。
一、余切函数的定义余切函数cot(x)表示正切函数tan(x)的倒数，即cot(x) = 1/tan(x)。
然而，由于在某些特定的角度值上正切函数为零，因此在这些角度处无定义。
这些特定角度被称为余切函数的奇点。
二、余切函数的周期性余切函数具有周期性，且其周期等于π。
这意味着当x增加π，或减去π的整数倍时，余切函数的值会重复。
例如，cot(x) = cot(x + π) = cot(x - π)。
三、余切函数的图像余切函数的图像具有一些显著特点。
当x接近奇点时，余切函数的值会趋向正无穷大或负无穷大。
当x不是奇点时，余切函数的值在正无穷到负无穷之间变化。
这可以通过绘制余切函数的图像来观察到。
四、余切函数的变化规律1. 正值和负值：在第一象限和第三象限，余切函数值为正；而在第二象限和第四象限，余切函数值为负。
因此，余切函数在不同象限上的值有着不同的符号。
2. 最大值和最小值：余切函数在奇点处无定义，因此不存在最大值或最小值。
然而，在非奇点处，余切函数的值在-1和+1之间变化。
当x接近奇点时，余切函数的值趋近于无穷大。
3. 渐进线：余切函数的图像在奇点处有两条渐近线，即x = (2n +1)π/2，其中n为整数。
这两条渐近线将图像划分成多个区域。
4. 奇偶性：余切函数具有奇偶性，即cot(-x) = -cot(x)。
这意味着余切函数关于原点是奇函数，即对于任意x，cot(x) = -cot(-x)。
五、余切函数的应用余切函数在数学和物理等领域有着广泛的应用。
例如，在电路分析中，余切函数可以用来表示电阻和电抗的比值。
在三角恒等式和复数运算中，余切函数也起到重要的作用。
综上所述，余切函数cot(x)是一种具有周期性和奇偶性的三角函数。
余切函数知识点总结
余切函数知识点总结余切函数的定义域是所有实数，但是在x等于nπ时（n为整数），余切函数是无定义的，因为此时正切函数等于零，余切函数为正切函数的倒数，所以在这些点上无定义。
余切函数的值域是所有的实数。
余切函数的图像是周期性的，其周期为π。
图像显示出余切函数是一条在零点和π点之间无界的曲线，其极值为正无穷和负无穷。
余切函数的图像在零点和π点都有角点，角点会导致图像在这些点不连续，并且在这些点上无定义。
余切函数的性质有许多，下面将分别阐述余切函数的奇偶性、周期性、单调性、渐近线、导数和积分等方面。
1. 余切函数的奇偶性余切函数是奇函数，即cot(-x)=-cot(x)。
这是因为余切函数是正切函数的倒数，而正切函数是奇函数，所以余切函数也是奇函数。
这意味着余切函数在原点对称，图像关于原点对称。
2. 余切函数的周期性余切函数是周期函数，其周期为π。
这意味着余切函数在每个周期内的图像是相似的，呈现出周期性的特点。
当x增加π时，余切函数的值会再次回到相同的位置。
3. 余切函数的单调性余切函数在每个周期内是单调递减的。
从图像上看，余切函数的曲线是向下趋势的，其值在π/2到3π/2之间是递减的。
4. 余切函数的渐近线余切函数的图像有两条渐近线，分别是x=0和x=π。
当x趋向于这两个渐近线时，余切函数的值会趋向正无穷和负无穷。
这意味着余切函数在这两个渐近线上有极值，且在这两个点上是不连续的。
5. 余切函数的导数余切函数的导数是-csc^2(x)，其中csc(x)是余割函数。
这意味着余切函数的导数是负的余割函数的平方。
这与余切函数与余割函数的关系相符，表明余切函数是正切函数的倒数。
6. 余切函数的积分余切函数的积分可以表示为-ln|sin(x)|+C，其中C为积分常数。
这个积分表达式是通过余切函数的导数而来，和余切函数与余割函数的关系有关。
通过这个积分表达式，可以求得余切函数在某一区间内的面积。
在数学的实际应用中，余切函数也有一些重要的应用。
余切和角公式
余切和角公式
在数学的世界里，余切（cosecant）是对边与邻边之比的倒数，它是三角函数的一种，通常用于直角三角形的研究中。
在平面直角坐标系中的角度α而言，其餘切公式可以表示为：
余切cot(α) = 邻边/ 对边
若以直角三角形ABC来形象地说明，其中∠A为所关心的角度，那么cot(∠A) = AB / AC。
进一步扩展到复数领域或者周期性函数的概念上，余切函数也遵循特定的周期性规律：cot(x + π) = -cot(x)，这体现了它在π上的周期特性。
请注意，在实际应用或解题过程中，理解并熟练运用余切与其他三角函数的关系（如正弦sin, 余弦cos以及正切tan之间的关系）至关重要，这些关系构成了几何学、物理学以及其他科学和技术领域中的重要工具。
数学余割函数公式定理知识点总结
f(x)=cscx=1/sinx
1、定义域：{x|x≠kπ，k∈Z}
2、值域：{y|y≤-1或y≥1}
3、奇偶性：奇函数
4、周期性：最小正周期为2π
5、图像：
图像渐近线为：x=kπ ，k∈Z
其实有一点需要注意，就是余割函数与正弦函数互为倒数。[数学余割函数公Fra bibliotek定理知识点总结]
对于任意一个实数x都对应着唯一的角弧度制中等于这个实数而这个角又对应着唯一确定的余割值cscx与它对应按照这个对应法则建立的函数称为余割函数
数学余割函数公式定理知识点总结
余割函数
对于任意一个实数x，都对应着唯一的角(弧度制中等于这个实数)，而这个角又对应着唯一确定的余割值cscx与它对应，按照这个对应法则建立的函数称为余割函数。
cot函数中考会考
cot函数中考会考
余切函数（cot函数）是三角函数的一种，表示正切函数的倒数，即cot(x) = 1/tan(x)。
在数学中，cot函数有着广泛的应用，特别是在三
角函数的关系和计算中。
下面将详细介绍cot函数的定义、性质和一些常
见的应用。
一、定义和性质：
（1）cot函数的定义：
（2）cot函数的图像：
cot函数的图像可以通过借助tan函数的图像转换得到。
tan函数的
图像是以原点为对称中心的周期函数，因此cot函数的图像也具有类似的
特点。
它在每个区间[x = nπ, x = (n+1)π]（其中n为整数）上都表现
出多个单调递减或递增的周期，并在每个周期的中点有一条倾斜的渐进线。
（3）cot函数的周期性：
（4）cot函数的奇偶性：
（5）cot函数的导数：
二、cot函数的应用：
（1）三角恒等式：
cot(x) = 1/tan(x) = cos(x)/sin(x) = 1/sin(x)/cos(x) =
csc(x)/sec(x)。
（2）角度的度量：
在三角函数的运算中，cot函数经常用来测量角度的度量。
例如，一
个角的正切值为√3，则可以通过cot函数计算得到这个角度的度量，即
cot^(-1)(√3)。
（3）解三角方程：
（4）傅里叶级数：
（5）电工学和物理学中的应用：
以上是cot函数的定义、性质和应用的一些基本介绍。
cot函数作为
三角函数家族中的一员，在数学和应用科学中具有重要的地位。
通过了解cot函数的性质和应用，可以帮助我们更好地理解和运用三角函数的知识。
初中正弦余弦正切公式
初中正弦余弦正切公式“初中数学必背三角函数公式、三角函数值”主要包括正弦、余弦、正切函数的定义式和关系式，特殊锐角的正弦、余弦、正切值。
一、正弦、余弦、正切的定义假设在直角三角形ABC中，∠C为直角，∠A、∠B、∠C的对边长度分别记为a、b、c，则有（注：初中数学里，三角函数的定义只适用于直角三角形。
）：1、锐角A的正弦值、余弦值、正切值的定义式分别如下：（1）∠A的正弦值=∠A的对边：斜边，记作sinA=a/c。
（2）∠A的余弦值=∠A的邻边：斜边，记作cosA=b/c。
（3）∠A的正切值=∠A的对边：∠A的邻边，记作tanA=a/b。
2、锐角B的正弦值、余弦值、正切值的定义式分别如下：（1）∠B的正弦值=∠B的对边：斜边，记作sinB=b/c。
（2）∠B的余弦值=∠B的邻边：斜边，记作cosB=a/c。
（3）∠B的正切值=∠B的对边：∠B的邻边，记作tanB=b/a。
【注】正弦=“对比斜”、余弦=“邻比斜”、正切=“对比邻”。
3、互余的两个角间的正弦、余弦、正切值关系假设在直角三角形ABC中，∠C为直角，则∠A与∠B互余。
通过∠A和∠B的正弦、余弦、正切值的定义式的对比，我们不难发现：∠A的正弦值与∠B的余弦值相等，∠A的余弦值与∠B的正弦值相等，∠A的正切值与∠B的正切值互为倒数。
所以，当∠A与∠B互余时我们有以下3个同时成立的等式关系：（1）sinA=cosB；（2）sinB=cosA；（3）tanA·tanB=1。
二、同角的正弦值、余弦值、正切值间的关系式1、商数关系：tanA=sinA/cosA；tanB=sinB/cosB.2、平方关系：同一个锐角的‘正弦的平方’与‘余弦的平方’的和为1，即(sinA)^2+(cosA)^2=1；(sinB)^2+(cosB)^2=1.3、倒数关系：tanA·cotA=1；tanB·cotB=1.【注】“cotA”称为为∠A的余切，它等于∠A的邻边比上∠A的对边。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中数学余切函数公式知识点整理
对于任意一个实数x，都对应着唯一的角(弧度制中等于这个实数)，而这个角又对应着唯一确定的余切值cotx与它对应，按照这个对应法则建立的函数称为余切函数。
形式是f(x)=cotx
余切函数的图像
在平面直角坐标系中，函数y=cotx的图像叫做余切曲线。
具体图像如附图示，它是由相互平行的x=kπ(k∈Z)直线隔开的无穷多支曲线所组成的。
通过把正切函数图像向左平移π/2，然后把该图像绕x=(2k+1)π/2旋转 180度就可以得到余切函数的图像，也就是说cotx=tan(-x+π/2)，性质和正切函数的性质基本一样。
利用三角比也可定义余切函数 y=cotx=x/y
温馨提示：继续为大家整合的是余切函数的定义介绍，相信每一位同学都已经熟记于心了吧。
①正方形的四边相等；
②正方形的四个角都是直角；
③正方形的两条对角线相等，且互相垂直平分，每一条对角线平分一组对角；
①有一个角是直角的菱形是正方形；
②有一组邻边相等的矩形是正方形。
希望上面对正方形定理公式知识的讲解学习，同学们都能很好的掌握，相信同学们会取得很好的成绩的哦。
①平行四边形的对边相等；
②平行四边形的对角相等；
③平行四边形的对角线互相平分；
①两组对角分别相等的四边形是平行四边形；
②两组对边分别相等的四边形是平行四边形；
③对角线互相平分的四边形是平行四边形；
④一组对边平行且相等的四边形是平行四边形。
上面对数学中平行四边形定理公式知识的讲解学习，同学们都能很好的掌握了吧，相信同学们会从中学习的更好的哦。
①直角三角形的两个锐角互为余角；
②直角三角形斜边上的中线等于斜边的一半；
③直角三角形的两直角边的平方和等于斜边的平方；
④直角三角形中30度
角所对的直角边等于斜边的一半；
①有两个角互余的三角形是直角三角形；
②如果三角形的三边长a、b 、c有下面关系a^2+b^2=c^2
，那么这个三角形是直角三角形。
以上对数学直角三角形定理公式的内容讲解学习，同学
们都能很好的掌握了吧，希望同学们都能考试成功。
①等腰三角形的两个底角相等；
②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
上面对等腰三角形的性质定理公式的内容讲解学习，同学们都能很好的掌握了吧，希望同学们在考试中取得很好的成绩。
三角形的三边关系定理及推论：三角形的两边之和大于第三边，两边之差小于第三边；
三角形的内角和定理：三角形的三个内角的和等于180度；
三角形的外角和定理：三角形的一个外角等于和它不相邻的两个的和；
三角形的外角和定理推理：三角形的一个外角大于任何一个和它不相邻的内角；
三角形的三条角平分线交于一点；
三角形的三边的垂直平分线交于一点；
三角形中位线定理：三角形两边中点的连线平行于第三边，并且等于第三边的一半；。