偏导数的几何意义
二元函数的偏导数

二元函数的偏导数偏导数是微积分中的重要概念之一,用于描述函数在某一点上对于其中一个变量的变化率。
在二元函数中,我们需要考虑两个自变量,并求解它们的偏导数。
本文将简要介绍二元函数的偏导数的概念、计算方法以及相关性质。
一、二元函数的偏导数概念在二元函数中,我们使用两个自变量来描述函数的变化情况。
设函数为f(x, y),其中x和y分别表示两个自变量。
在某一点(x0, y0),我们可以固定其中一个自变量,而考察另一个自变量对函数值的影响。
定义:1. 对于二元函数f(x, y),以x为自变量,y为常数,求得的导数称为对x的偏导数,记作∂f/∂x。
2. 对于二元函数f(x, y),以y为自变量,x为常数,求得的导数称为对y的偏导数,记作∂f/∂y。
二、二元函数的偏导数计算方法为了求解二元函数的偏导数,我们可以使用偏导数定义进行计算。
对于∂f/∂x,我们将y视为常数,将x作为自变量,利用求导法则进行计算。
对于∂f/∂y,我们将x视为常数,将y作为自变量,同样利用求导法则进行计算。
例如,对于函数f(x, y) = x^2 + y^3,我们可以依次计算∂f/∂x和∂f/∂y:1. ∂f/∂x = 2x2. ∂f/∂y = 3y^2计算结果表明,在任意一点(x, y)处,∂f/∂x的值等于2x,∂f/∂y的值等于3y^2。
三、偏导数的几何意义偏导数可以用来描述函数在某一点上的切线斜率,从而进一步研究函数的变化趋势和极值情况。
对于二元函数f(x, y),在点(x0, y0)处的偏导数:1. ∂f/∂x表示过点(x0, y0)处曲面在x方向上的切线斜率。
2. ∂f/∂y表示过点(x0, y0)处曲面在y方向上的切线斜率。
通过计算偏导数,我们可以得到在某一点的切线斜率,从而了解函数在该点附近的变化情况。
四、偏导数的相关性质1. 交换性:∂^2f/∂x∂y = ∂^2f/∂y∂x,即混合偏导数的求导顺序可以交换。
2. 连续性:如果函数f(x, y)在某一点处的偏导数连续,则该点的偏导数存在且连续。
偏导数的物理几何意义

偏导数的物理几何意义偏导数是多元函数微分学中的重要概念,它描述了函数在其中一点沿着一些坐标轴的变化率。
在物理学中,偏导数有着重要的几何和物理意义。
以下是偏导数的物理几何意义的详细解释:1.变化率:函数的一阶偏导数描述了函数在其中一点的变化率。
在物理学中,这可以理解为物理量在该点的变化率。
例如,在空间中考虑一个以时间t为参数的三维位置矢量函数r(t)=(x(t),y(t),z(t)),其中x、y和z分别是位置矢量在x、y和z轴的分量。
三个分量的一阶偏导数分别是x的速度、y的速度和z的速度,它们描述了位置矢量在每个轴上的变化率。
2.切线和切平面:二元函数的两个偏导数代表了函数图像上的切线和切平面。
在物理学中,这对于描述曲线和曲面的切线和切平面是非常重要的。
例如,在二维平面上考虑一个函数z=f(x,y),其中x和y是平面上的坐标变量。
函数的偏导数∂z/∂x和∂z/∂y分别表示函数图像上的沿着x轴和y轴方向的切线斜率。
这意味着我们可以借助偏导数来找到函数图像上的切线和切平面,从而描述函数在其中一点的局部行为。
3. 法向量:在多元函数的高阶偏导数中,Hessian矩阵的特征向量对应的特征值具有重要的物理和几何意义。
特别地,Hessian矩阵是一个对称矩阵,它描述了函数图像局部的二次曲率信息。
Hessian矩阵的特征向量对应的特征值是曲面在该点法向量的方向和曲率。
例如,在二维平面上考虑一个函数z = f(x, y),其中x和y是平面上的坐标变量。
Hessian矩阵的特征向量对应的特征值描述了曲面在该点的法向量方向和曲率大小,这对于描述曲面的形态和弯曲性质具有重要作用。
4.极值点:在多元函数中,偏导数可以帮助我们找到函数的极值点。
在物理学中,这对于优化和最优化问题的求解是非常重要的。
例如,考虑一个具有多个变量的能量函数E(x,y,z),其中x、y和z是能量函数的自变量。
函数的偏导数∂E/∂x,∂E/∂y和∂E/∂z可以帮助我们找到能量函数的极小值点,这在工程和科学应用中广泛用于优化问题和最优化算法。
偏导数的几何意义
— 1 —
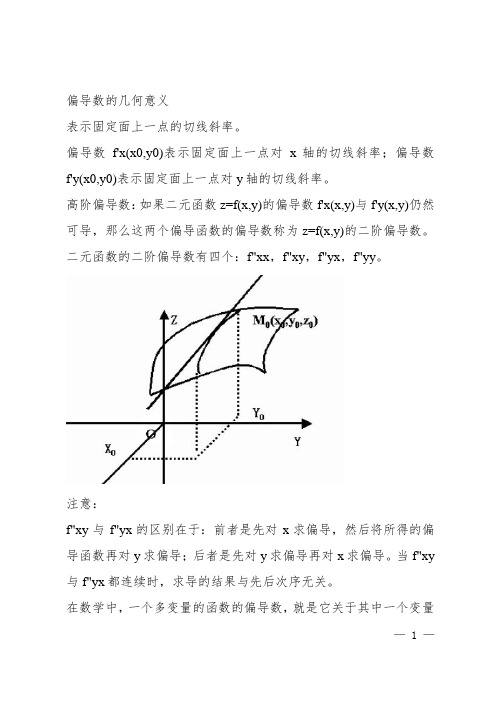
偏导数的几何意义
表示固定面上一点的切线斜率。
偏导数f'x(x0,y0)表示固定面上一点对x 轴的切线斜率;偏导数f'y(x0,y0)表示固定面上一点对y 轴的切线斜率。
高阶偏导数:如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导,那么这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。
二元函数的二阶偏导数有四个:f"xx ,f"xy ,f"yx ,f"yy 。
注意:
f"xy 与f"yx 的区别在于:前者是先对x 求偏导,然后将所得的偏导函数再对y 求偏导;后者是先对y 求偏导再对x 求偏导。
当f"xy 与f"yx 都连续时,求导的结果与先后次序无关。
在数学中,一个多变量的函数的偏导数,
就是它关于其中一个变量
的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
偏导数在向量分析和微分几何中是很有用的。
第二节 偏导数

V k , T V, T P P k
从而
P V
V T
T P
kT V2
k P
V k
kT PV
1
.
2019年12月24日星期二
徐州工程学院数理学院
上页 下页 返回 结束
警告各位!
偏导数 z 是一个整体记号, 不能拆分. x
不能像一元函数那样将 z , z 看成是
2019年12月24日星期二
徐州工程学院数理学院
上页 下页 返回 结束
1997年研究生考题, 选择, 3分
f
(
x,
y)
x2
xy
y2
( x, y) (0,0)在点(0,0)处( C
).
0 ( x, y) (0,0)
A. 连续,偏导数存在;
B. 连续,偏导数不存在; C. 不连续,偏导数存在; D. 不连续,偏导数不存在.
x y
z 与 x , y 的商.
2019年12月24日星期二
徐州工程学院数理学院
上页 下页 返回 结束
例7 求 u e x xy2z3 的偏导数 .
解:
u e xxy2z3 (1 y2 ) ;
x
u e xxy2z3 2x y ; y
u e xxy2z3 (3z2 ) . z
函数有相应的增量 (称为关于x的偏增量), 即
x z f ( x0 x, y0 ) f ( x0 , y0 )
如果极限
lim x z lim f ( x0 x, y0 ) f ( x0 , y0 )
x0 x x0
偏导数不存在的几何意义

偏导数不存在的几何意义偏导数是多元函数中的一个概念,用于研究函数在其中一点的方向导数。
然而,并不是所有的函数都在所有点都存在偏导数。
这种情况在几何上有着非常重要的意义。
从几何意义上来看,偏导数不存在意味着函数在该点的变化趋势不同。
具体来说,偏导数不存在的情况有以下几种情形:1.针对一个变量来说,函数在其中一点不可导。
这意味着函数在该点无法找到弧度为零的切线。
在几何上,这表示函数在该点出现了一个尖点、角点或奇点。
在这种情况下,函数的变化不连续,无法定义唯一的方向导数。
2.函数在其中一点不满足一阶连续性条件。
一个函数在其中一点不满足一阶连续性条件意味着函数在该点处存在跳跃、间断或者振荡。
在几何上,这种情况下函数的值和斜率会出现突变。
3.函数在其中一点附近存在垂直于坐标轴的间断。
这种情况下,函数的变化方向对坐标轴的变化不敏感。
可以将其理解为函数对坐标轴的变化不连续。
考虑函数f(x,y)=,x,+,y。
这个函数由,x,和,y,两个绝对值函数构成。
在点(0,0)处,函数的定义式为f(0,0)=0。
然而,在点(0,0)处,函数无法取得一阶偏导数。
为了确定偏导数是否存在,我们需要考察函数在x轴和y轴上的变化。
当x<0时,f(x,y)=-x+,y,在y轴上f(x,0)=,x。
在坐标平面上绘制这两个函数,可以看到x轴和y轴上的变化趋势不相同。
在y轴上,函数f(x,0)在点(0,0)处存在一个切线,而在x轴上却不存在。
这意味着f(x,y)=,x,+,y,在点(0,0)处的偏导数不存在。
也可以从几何上理解为,函数在点(0,0)处无法找到一个唯一的切线,因为这个点是函数的折返点。
这个例子说明了偏导数不存在的几何意义:函数在其中一点的变化趋势不统一、这是因为函数可能出现了尖点、角点、奇点,在这些位置上函数的变化是不连续的。
这种情况下,计算函数在该点的方向导数变得困难甚至不可能。
总结来说,偏导数不存在意味着函数在其中一点存在不连续、不光滑、出现尖点、角点或奇点等情况。
偏微分方程与偏导数的几何意义及其应用

偏微分方程与偏导数的几何意义及其应用偏微分方程(Partial Differential Equations, 简称PDEs)是数学中重要的一个分支,它描述了多元函数的各个方向的变化率,具有广泛的应用于自然科学和工程领域。
本文将探讨偏微分方程和偏导数的几何意义,以及在物理学、流体力学和电动力学等领域的常见应用。
一、偏微分方程的几何意义1. 偏导数的几何意义偏导数描述了函数在某个指定方向上的变化率。
在二元函数中,对于函数f(x, y),f对于x的偏导数(∂f/∂x) 表示函数沿x方向的变化率,而f对于y的偏导数(∂f/∂y) 表示函数沿y方向的变化率。
对于高维函数,类似地,偏导数可以描述函数在各个方向上的变化率。
2. 偏微分方程的几何意义偏微分方程描述了函数在空间中的变化和分布规律。
一些重要的偏微分方程,如热传导方程、抛物线方程、椭圆方程和双曲线方程等,通过描述函数在物理空间中的波动、扩散和稳定性等现象,使我们能够从几何角度更好地理解和分析系统的行为。
二、偏微分方程的应用1. 物理学中的应用偏微分方程在解释和解析物理现象中起到了重要的作用。
例如,波动方程可以描述机械波传播、声波和光波的传播;热传导方程可以用来解释热量在材料中的传递过程;薛定谔方程可以描述量子力学中的微观粒子行为。
通过将物理现象建模成偏微分方程,可以预测和模拟复杂系统的行为,促进科学研究的发展。
2. 流体力学中的应用偏微分方程在流体力学中广泛应用于描述流体的运动和行为。
例如,纳维尔-斯托克斯方程描述了流体的运动和粘度,可以用于解释液体和气体的流动行为;欧拉方程描述了不可压缩流体的流动,可以分析水流和风力等现象。
通过求解这些偏微分方程,我们可以优化设计水力系统、气象预测以及模拟天然和人工湍流等问题。
3. 电动力学中的应用偏微分方程也广泛应用于电动力学问题中。
例如,麦克斯韦方程组描述了电磁感应、电场和磁场之间的相互作用,可以解释电磁波的传播行为和光的传播;泊松方程和拉普拉斯方程描述了电势分布,可以用于解决电场的引力和磁场的保持。
偏导数知识点公式总结

偏导数知识点公式总结一、偏导数的概念1.1 偏导数的定义偏导数是多元函数对其中一个自变量的导数。
对于一个函数 $f(x_1, x_2, ..., x_n)$,它的偏导数 $\frac{\partial f}{\partial x_i}$ 表示在$x_i$方向上的变化率。
偏导数的定义可以表示为:$$\frac{\partial f}{\partial x_i} = \lim_{\Delta x_i \to 0} \frac{f(x_1, x_2, ..., x_i + \Delta x_i, ..., x_n) - f(x_1, x_2, ..., x_i, ..., x_n)}{\Delta x_i}$$1.2 偏导数的图示解释偏导数可以通过函数曲面的切线来解释。
对于函数 $z = f(x, y)$,在点$(x_0, y_0, z_0)$处的偏导数 $\frac{\partial f}{\partial x}$可以理解为曲面在$x$方向的斜率,即曲面在$x$方向上的变化率。
同样地,$\frac{\partial f}{\partial y}$表示曲面在$y$方向上的变化率。
这样的解释有助于我们更直观地理解偏导数的含义。
二、偏导数的性质2.1 对称性对于二元函数 $f(x, y)$,它的偏导数满足对称性,即$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$。
这一性质表明,在计算混合偏导数时,可以不必考虑自变量的顺序。
2.2 连续性在函数的定义域内,若偏导数存在且连续,则函数规定可微。
这一性质是偏导数与函数连续性的关系,对于函数的导数性质有着重要的影响。
2.3 性质总结:和与积对于函数 $u = u(x, y)$ 和 $v = v(x, y)$,它们的偏导数具有和与积的运算法则。
3.1-2 偏导数与高阶偏导

f yx ( x 2x, y 1y) f xy ( x 3x, y 4y)
由 于f xy , f yx连 续, 令x 0, y 0得 : f xy ( x , y ) f yx ( x , y )
( x0 , y0 ) 处的函数值。偏导函数简称偏导数。
偏导数的概念还可以推广到二元以上的多元函数。例如三元
函数 u f ( x, y, z ) 在点 ( x, y, z ) 处对 x 的偏导数定义为
函数 u f ( x, y, z ) 在点 ( x , y, z ) 处对 x 的偏导数定义为 f ( x x , y , z) f( x , y , z) f x ( x , y , z ) lim 。 x 0 x 5
第三节
偏导数与全微分
第五章
多元函数微分学及其应用
3.1 偏导数概念与几何意义
1.函数 z f ( x , y ) 在点 M 0 ( x0 , y0 ) 处的偏导数的定义
定义 3.1 设 z f ( x, y) 在点 M0 ( x0 , y0 ) 的某一邻域 N ( M0 )
上有定义,当 y 固定在 y0 而 x 在 x0 处有增量 x 时 ,相应地 函数有增量 f ( x0 x, y0 ) f ( x0 , y0 ) ,
f xy (0,0) f yx (0,0)
例1 中 2 y 2 y 2 y 2 y , 而例 2 中 , xy yx xy yx
问:混合偏导数相等需要什么条件?
18
第五章
多元函数微分学及其应用
定理 3.1:如果 f xy ( x, y) , f yx ( x, y) 在点 ( x, y) 的某邻域 内连续,则有 f xy ( x, y) f yx ( x, y) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏导数的几何意义
实验目的:通过实验加深学生对偏导数定义的理解掌握偏导数的几何意义并从直观上理解二阶混合偏导数相等的条件
背景知识:
一偏导数的定义
在研究一元函数时.我们从研究函数的变化率引入了导数概念.对于多元函数同样需要讨论它的变化率.但多元函数的变化量不只一个,因变量与自变量的关系要比一元函数复杂的多.
所以我们首先考虑多元函数关于其中一个自变量的变化率,以二元函数= 为例,
如果只有自变量变化,而自变量y固定(即看作常量),这时它就是的一元函数,这函数对x 的导数,就称为二元函数z对于的偏导数,即有如下定义
定义设函数z= 在点的某一邻域内有定义,当y固定在,而在
处有增量时,相应的函数有增量
- ,
如果 (1)
存在,则称此极限为函数= 在点处对的偏导数,记做
, , ,或
例如,极限(1)可以表为
=
类似的,函数z= 在点处对的偏导数定义为
记做, , 或
如果函数= 在区域D内每一点( )处对的偏导数都存在,那么这个偏导数就是的函数,它就称为函数= 对自变量的偏导函数,记做
, , ,或
类似的,可以定义函数= 对自变量的偏导函数,记做
, , ,或
由偏导数的概念可知, 在点处对的偏导数显然就是偏导
函数在点处的函数值,就像一元函数的导函数一样,以后在不至于混淆的地方也把偏导函数简称为偏导数.
至于求= 的偏导数,并不需要用新的方法,因为这里只有一个自变量在变动,另外一个自变量看作是固定的,所以仍旧是一元函数的微分法问题,求时,只要把暂时看作常量而对求导;求时,则只要把暂时看作是常量,而对求导数.
偏导数的概念还可以推广导二元以上的函数,例如三元函数在点( )处对的偏导数定义为
=
其中( )是函数的定义域的内点,它们的求法也仍旧是一元函数的微分法问题
例求的偏导数
解= ,
=
二偏导数的几何意义
二元函数= 在点的偏导数的几何意义
设为曲面= 上的一点,过点作平面,截此曲面得一曲线,此曲线在平面上的方程为= ,则导数,即偏导数,就是这曲线在点处的切线对轴的斜率.同样,偏导数的几何意义是曲面被平面所截得的曲线在点处的切线对的斜率
三偏导数的几何意义
我们知道,如果一元函数在某点具有导数,则它在该点必定连续,但对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续.这是因为各偏导数存在只能保证点P沿着
平行于坐标轴的方向趋于P 时,函数值趋于,但不能保证点P按任何方式趋于P 时,函数值都趋于.例如,函数
= ={
在点(0,0)对的偏导数为
同样有
但是我们在前面的学习中知道这函数在点(0,0)并不连续
四二阶混合偏导数
设函数= 在区域D内具有偏导数
= , =
那么在D内, 都是的函数.如果这里两个函数的偏导数也存在,则它们是函数= 的二阶偏导数,按照对变量求导次序的不同有下列四个二阶偏导数:
,
,
其中第二,第三个偏导数称为混合偏导数
例2 设,求, , ,
,
从例子中,我们看到两个二阶混合偏导数相等,即, =
我们再看用maple作求的图形
第一个图形为
第二个图形为
从图中我们看到两个连续的偏导函数,它们是相等的
这不是偶然的,事实上我们有下述定理
定理如果函数= 的两个二阶混合偏导数及在区域D里连续,那么在该区域内这两个二阶混合偏导数必定相等
换句话说,二阶混合偏导数在连续的条件下与求导的次序无关。
