有理数的运算复习课初一数学
初一数学上册 有理数及其运算

有理数及其运算(复习)一、正负数有理数的分类:_____________统称整数,试举例说明。
_____________统称分数,试举例说明。
____________统称有理数。
正确理解非负数和非正数。
练习:1、把下列各数填在相应额大括号内:1,-0.1,-789,25,0,-20,-3.14,-590,6/7正整数集{ …};正有理数集{ …};负有理数集{ …} 负整数集{ …};自然数集{ …};正分数集{ …} 负分数集{ …}2、某种食用油的价格随着市场经济的变化涨落,规定上涨记为正,则-5.8元的意义是 ;如果这种油的原价是76元,那么现在的卖价是 。
二、数轴规定了 、 、 的直线,叫数轴练习:1、如图所示的图形为四位同学画的数轴,其中正确的是( )2、在数轴上画出表示下列各数的点,并按从大到小的顺序排列,用“>”号连接起来。
4,-|-2|, -4.5, 1, 03、下列语句中正确的是( )A数轴上的点只能表示整数B数轴上的点只能表示分数C数轴上的点只能表示有理数D所有有理数都可以用数轴上的点表示出来4、①比-3大的负整数是_______; ②已知m是整数且-4<m<3,则m为_______________。
③有理数中,最大的负整数是 ,最小的正整数是 。
最大的非正数是 。
④与原点的距离为三个单位的点有_ _个,他们分别表示的有理数是 _和_ _。
5、在数轴上点A 表示-4,如果把原点O 向负方向移动1个单位,那么在新数轴上点A 表示的数是( ) A.-5, B.-4 C.-3 D.-26、画出数轴,把下列各组数分别在数轴上表示出来,并按从大到小的顺序排列,用“>”连接起来:⑴ 1,-2,3,-4 ⑵31,0,3,-0.2三、相反数1、像2和-2、-5和5、2.5和-2.5这样,只有 不同的两个数叫做互为相反数。
0的相反数是 。
一般地:若a 为任一有理数,则a 的相反数为-a2、相反数的相关性质:a 、相反数的几何意义:表示互为相反数的两个点(除0外)分别在原点O 的两边,并且到原点的距离相等。
初一数学上册第一章有理数复习教案最新3篇

初一数学上册第一章有理数复习教案最新3篇篇一:数学《有理数》教案篇一一、教材分析:(一)教材的地位和作用:本节课的内容是《新人教版七年级数学》教材中的第一章第四节,“有理数的乘除法”是把“有理数乘法”和“有理数除法”的内容进行整合,在“有理数的加减混合运算”之后的一个学习内容。
在本章教材的编排中,“有理数的乘法”起着承上启下的作用,它既是有理数加减的深入学习,又是有理数除法、有理数乘方的基础,在有理数运算中有很重要的地位。
“有理数的乘法”从具体情境入手,把乘法看做连加,通过类比,让学生进行充分讨论、自主探索与合作交流的形式,自己归纳出有理数乘法法则。
通过这个探索的过程,发展了学生观察、归纳、猜测、验证的能力,使学生在学习的过程中获得成功的体验,增强了自信心。
所以本节课的学习具有一定的现实地位。
(二)学情分析:因为学生在小学的学习里已经接触过正数和0的乘除法,对于两个正数相乘、正数与0相乘、两个正数相除、0与正数相除的情况学生已经掌握。
同时由于前面学习了有理数的加减法运算,学生对负数参与运算有了一定的认识,但仍还有一定的困难。
另外,经过前一阶段的教学,学生对数学问题的研究方法有了一定的了解,课堂上合作交流也做得相对较好。
(三)教学目标分析:基于以上的学情分析,我确定本节课的教学目标如下1、知识目标:让学生经历学习过程,探索归纳得出有理数的乘除法法则,并能熟练运用。
2、能力目标:在课堂学习过程中,使学生经历探索有理数乘除法法则的过程,发展观察、猜想、归纳、验证、运算的能力,同时在探索法则的过程中培养学生分类和归纳的数学思想。
3、情感态度和价值观:在探索过程中尊重学生的学习态度,树立学生学习数学的自信心,培养学生严谨的数学思维习惯。
4、教学重点:会进行有理数的乘除法运算。
5、教学难点:有理数乘除法法则的探索与运用。
确定教学目标的理由依据是:新课标中指出课堂教学中应体现知识与技能、过程与方法、情感态度与价值观的三维目标,同时也基于本节内容的地位与作用。
初一数学《有理数的混合运算》知识点精讲

知识点总结知识点1 常规计算有理数混合运算的运算顺序:1、先乘方,再乘除,最后加减;2、同级运算,从左到右进行;3、如有括号,先做括号内的运算,按小括号、中括号、大括号的顺序依次进行.【方法总结】根据有理数的混合运算顺序和运算法则计算即可.本题主要考查有理数的混合运算,熟练掌握有理数的混合运算的顺序和法则是解题的关键.注意:绝对值符号有括号的作用.知识点2 运算律、规律计算有理数的混合运算中,常用的运算律有:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法对加法的分配律、加法对乘法的分配律. 【方法总结】本题主要考察了有理数混合运算的运算顺序和分配律的使用,(1)和(3)是乘法分配律的正用,(2)是乘法分配律的逆用,熟练掌握运算律的使用是解本题的关键.知识点3 求代数式的值重要结论:互为相反数的两数和为0,相反数等于自身的数是0;互为倒数的两数积为1,倒数等于自身的数有-1,1,倒数等于自身的自然数是1;最大的负整数是-1,最小的正整数是1,绝对值最小的有理数是0;有理数的混合运算:1.有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算。
2.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化。
有理数混合运算的四种运算技巧:(1)转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算.(2)凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解.(3)分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算.(4)巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.知识要点1.计算的基本法则:包括:有理数的加法、减法、乘法、除法、乘方①加法:同号两数相加,取相同的符号,并把绝对值相加. 异号两数相加,取绝对值大的数的符号,并用较大的绝对值减去较小的绝对值. 一个数同0相加,仍得这个数。
(word完整版)初一数学上册完全辅导——第一章有理数精讲
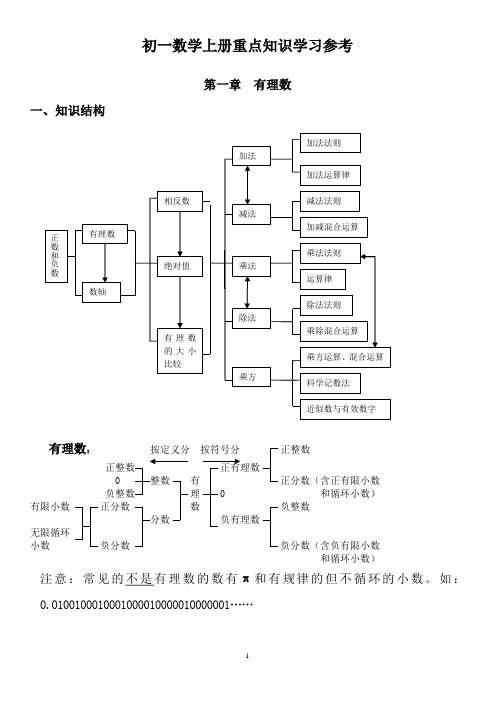
初一数学上册重点知识学习参考第一章 有理数一、知识结构有理数: 按定义分 按符号分正整数 正整数 正有理数0 整数 有 正分数(含正有限小数负整数 理 0 和循环小数)有限小数 正分数 数 负整数分数 负有理数无限循环小数 负分数 负分数(含负有限小数和循环小数)注意:常见的不是有理数的数有π和有规律的但不循环的小数。
如:0.0100100010001000010000010000001……二、掌握要点1、了解有理数的概念(什么是有理数、有理数包含的范围有哪些、有理数之间的大小比较)。
(1)大于0的数叫做正数,如3、1.8、5%等。
(2)在正数前面加上负号“—”的数叫负数,即小于0的数,如-3、-2.5、-5%等。
(3)数0既不是正数,也不是负数。
0除了表示一个也没有以外,是正数和负数的分界,是基准。
(4)在同一个问题中,分别用正数与负数表示的量具有相反的意义。
强调:用正数、负数表示实际问题中具有相反意义的量,而相反意义的量包含两个要素:一是他们的意义相反,如向东与向西、收入与支出;二是他们都是数量,而且是同类的量。
(5)正整数、0、负整数统称整数。
整数可以看作分母为1的分数。
(6)正整数、0、负整数、正分数、负分数都可以写成分数的形式,这样的数称为有理数。
(7)把一些数放在一起,就组成了一个数的集合,简称“数集”。
所有有理数组成的数集叫“有理数集”,所有整数组成的数集叫“整数集”,所有负数组成的数集叫“负数集”……数集一般用圆圈或大括号表示,因为集合中的数是无限的。
(8)有理数可以按不同的标准进行分类,标准不同,分类结果也不同。
问:有理数可分为正数和负数两大类,对吗?为什么?有理数可分为整数和分数两大类,对吗?为什么?2、有理数与数轴上的点一一对应(数轴的三要素、怎样看数轴、掌握应用数轴来进行去绝对值符号的简单运算)。
(1)通常用一条直线上的点表示数,这条直线叫数轴。
数轴三要素:原点、正方向、单位长度原点——在直线上任取一点表示数0,这个点叫原点。
初一数学《有理数的除法》知识点精讲

知识点总结知识点1:有理数除法法则(1) 除以一个数等于乘以这个数的倒数。
即a÷b=a×1/b(b≠0)。
(2) 两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不等于0的数,都得0。
知识点2:有理数的乘除混合运算除转乘,确定符号。
知识点3:有理数的四则混合运算先乘除,后加减,如果有括号,就先算括号里面的。
同级运算中,要按照从左到右的顺序。
知识点4.有理数的除法考点精讲1.4.2有理数的除法1、有理数除法法则1(课本P34)除以一个不等于0的数,等于乘这个数的倒数。
a÷b=a·1/b(b≠0)2、有理数除法法则2(课本P34)两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不等于0的数,都得0。
3、化简分数(课本P35)-45/-12=(-45)÷(-12)=45÷12=15/44、有理数的加减乘除混合运算先乘除,后加减5、用计算器计算计算器的符号键(-)可以用来表示负数的符号。
用计算器计算:(-1.7)×4-(-2.6)÷(-4)-7.45(如图1.4-1)有理数的除法(习题)1.4.2有理数的除法(-6.5)÷0.13(7/4-7/8-7/12)÷(-7)(-7)÷(7/4-7/8-7/12)(-9)×(-11)÷8÷(-125)42×(-2/7)+(-5/4)÷(-0.25)(2)化简下列分数:-42/7,4/-16,-54/-8,-60/25(3)小商店一周的利润是1400元,平均每天的利润是元;小商店一周共亏损840元,平均每天的利润是元。
(4)用“>”“<”或“=”填空:如果a<0,b>0,那么a/b 0,如果a>0,b<0,那么a/b 0,如果a<0,b<0,那么a/b 0,如果a=0,b≠0,那么a/b 0。
初一数学-第七讲 有理数的除法运算

第七讲 有理数的除法运算【知识要点】1.有理数除法法则① 法则一:除以一个数等于乘以这个数的倒数② 法则二:两数相除,同号得正,异号得负,并把绝对值相除。
③ 0除以任何一个非零数,等于0;0不能作除数!2. 1和1-的倒数等于它本身,即倒数等于它本身的有两个,是1±。
3. 1除以非零数,得到它的倒数。
【经典例题】【例1】求下列各数的倒数和负倒数。
①2 ② 431- ③ 20% ④ )0,0(21><-b a ba【例2】计算:① )5()25(-÷- ② )611(431-÷③ )4(4115.2-⨯÷- ④ )85()145()712(-⨯-÷-⑤3)522()213()53(÷-÷-⨯- ⑥3482773⎛⎫⎛⎫÷-⨯÷- ⎪ ⎪⎝⎭⎝⎭⑦ )241()1258343(-÷-- ⑧ )1312()173()1312(1715-÷-+-÷【例3】计算 ① .,14)31415161(m m 求=÷-+- ②11112134---【例4】数学老师布置了一道思考题“计算:⎪⎭⎫ ⎝⎛-+-÷⎪⎭⎫ ⎝⎛-526110132301 ”,小明和小红两位同学经过仔细思考,用不同的方法解答了这个问题: 小明的解法:原式=⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+÷⎪⎭⎫ ⎝⎛-521016132301=⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-2165301 =3301⨯-=101- 小红的解法:原式的倒数=⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-+-301526110132=()30526110132-⨯⎪⎭⎫⎝⎛-+- =-20+3-5+12=-10 故原式=101-①你觉得 的解法更好.②请你用自己喜欢的方法解答下面的问题:计算:⎪⎭⎫⎝⎛-+-÷⎪⎭⎫ ⎝⎛-723214361421。
初一上册数学青岛版有理数的运算知识点归纳

初一上册数学青岛版第三章有理数的运算知识点归纳(史上最全面的总结)一、有理数的加法1.加法法则(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大绝对值减较小绝对值。
(3)互为相反数的两个数相加得零。
(4)一个数与0相加仍得这个数。
2 . 加法运算律(1)加法交换律两个数相加,交换加数的位置,和不变。
a+b=b+a注意事项:对于三个或三个以上的数相加,加法交换律仍使用。
(2)加法结合律三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
(a+b)+c=a+(b+c)注意事项:对于三个以上的数相加,加法结合律仍使用。
(3)常见结合方法a 把正数和负数分别结合。
b 把同分母分数或易通分的分数相结合。
C 把相加得零的几个数相结合。
d 把相加得整数的几个小数相结合。
e几个整数和分数相加,通常整数与分数分别结合。
3.重要结论(1)在有理数范围内,和不一定大于每一个加数。
(2)ba+≠a+b二、有理数的减法1.减法法则减去一个数等于加上它的相反数。
2.数轴上两点间的距离公式设点A表示有理数a,点B表示有理数b,则AB=ba-3.重要结论(1)在有理数范围内,差不一定小于被减数。
(2)任何数减去0仍得这个数。
(3)0减去一个数得这个数的相反数。
(4)ba-≠a-b(5)设a,b为任意有理数a>b ⟺ a-b>0a=b⟺ a-b=0a<b⟺a-b<0三、有理数的乘法1.乘法法则两数相乘,同号得正,异号得负。
并把绝对值相乘。
2.多个数相乘的乘法法则(1)几个不为0的数相乘,积的符号是由负因数的个数决定的,当负因数为偶数个时,积为正。
当负因数的个数为奇数时,积为负,并把绝对值相乘。
(2)几个数相乘,有一个因数为0,积为0.3.乘法运算律(1)乘法交换律两数相乘,交换因数的位置,积不变。
(2)乘法结合律三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
《有理数复习课》公开课教学PPT课件【初中数学人教版七年级上册】

三、巩固练习
计算:
(1)0.125
3
1 4
3
1 8
11
2 3
0.25
(2)( 7 3 5 5 ) (36) 12 4 6 18
(3)(2) ( 1 ) ( 1 ) 12 12
(4)(24
)
(2
2 3
)2
5
1 2
(
1 6
)
(0.5)2
三、巩固练习
解:0.125 (3 1) (3 1) (11 2) 0.25
二、知识要点
4.相反数 只有符号不同的两个数,其中一个是另一个的相反数.
(1)数a的相反数是-a(a是任意一个有理数); (2) 0的相反数是0. (3)若a、b互为相反数,则a+b=0.
练习:(1)如果a=-13,那么-a=______; (2)如果-a=-5.4,那么a=______; (3)如果-x=-6,那么x=______; (4)-x=9,那么x=______.
3
4
2
–3 –2 –1 0 1 2 3 4
(1)数a的绝对值记作︱a︱;
若a>0,则︱a︱= a ; (2) 若a<0,则︱a︱= -a ;
若a =0,则︱a︱= 0 ;
(3)对任何有理数a,总有︱a︱≥0.
二、知识要点
7.有理数大小的比较 (1)可通过数轴比较:
在数轴上的两个数,右边的数总比左边的数大; 正数都大于0,负数都小于0;正数大于一切负数; (2)两个负数,绝对值大的反而小. 即:若a<0,b<0,且︱a︱>︱b︱,则a < b.
三、巩固练习
( 7 3 5 5 ) (36) 12 4 6 18
=( 7 ) (36) 3 (36) 5 (36) 5 (36)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专 家 会 诊
36 1 1 4
36 19
8
☺
☺ ☺
请同学们完成以下程序:
(1)同学们每人在练习本上写四个10以内 的整数;
做 (2)每个同学用你手上的四个数字编一道
一 混合运算的题目;然后把这个题目交给你们
做
组别的同学计算;
(3)计算结束后,编题的同学进行批改。
看谁编的题目 最好!
1、小组内交流:本节课自己给自己
乘 除
(5)(-2) ÷ (-6)= 1
法
3
(6)(4)
(
1) 4
+16
第三关:
乘方关
直接写出结果
(1)32= +9
(2)53 = +125
有 理
(3)(-3)4 = +81 (4)(-3)3 = -27
数
(5) -22 = -4
的 乘 方
(6)
(
2)2 3
=
4 9
(7)(
1)3 3
=
1 27
3 48 22 ( 1) 1 4
(3)22-(-2)2 = 4-4 = 0
(4)-32+2 = -9+2 = -7
要特别注
意运算顺
请 细
(1) 6 2 ( 1)
4
序啊!
心 完 成
(2) -22+2×(-4)2 (3) 3 50 22 ( 1) 1
右
5
边
的
题
目
14 1 5 (3)2 36
解:原式 1 1 5 (9) ☺
有
理
(3) (+3) + (-5)= -2
数 的
(4) -0.3+4.7= +4.4
加 法
(5) (-2)+2= 0
注意应 用运算
法则哦!
计算
(1)(– 14) – (+16)= -30
(2)(+6) – (– 13)= +19
有
(3)(– 7) – (– 10)= +3
理 数
(4)(+5) – (+9)= -4
一去二三里,
数
烟村四五家,
字
诗
亭台六七座,
欣 赏
八九十枝花 。
知 识 结 构 表
加法 减法
运算
乘法
混合运算
除法
有 理
乘方
数
的
运
加法交换律
算
加法结合律
运算律
乘法交换律
简便运算
乘法结合律
乘法分配律
第一关:
加减关
直接写出结果
(1) (-17) + (-15)= -32
(2)(+12)+ (+14)=+26
打多少分,还有哪个需要老师再讲解
小
的地方?
结
2、如何提高有理数运算的准确性,
谈谈你的看法。
1、直接写出答案:
①-17+8= ,②3-6=
,
③(-3)×(
1 6
)=
,
当
④2÷(
1 2
)=
,
堂
⑤-(-3)3=
。
检
2、计算下列各题:
测
(1)5-3÷( 1 )
2
(2)-32+9×(
1 3
)2
解:原式 3 48 4 ( 1) 1
4
例 题
3 12 ( 1) 1 4
331
1
第四关:
混合运算关
解: (1)(-2)×(-3)2 = (-2)×9 = -18
计算:
(1)(-2)×(-3)2 (2)-3÷(-1)2 (3)22-(-2)2 (4)-32+2
(2)-3÷(-1)2 = -3÷1 = -3
的
(5)15 – (– 15)=+30
减 法
(6)0 – 13= -13
(7) – 16 – 38= -54
一个不变, 两个变。
第二关:
乘除关
直接写出结果
(1)4× (-3)= -12
有
(2)(-6) × 0= 0
理 数
(3)(-0.5) × (-9)= +4.5
的
(4)35÷ (-5)= -7
