结构力学_河南工业大学精彩试题
结构力学考试题及答案

结构力学考试题及答案一、单项选择题(每题2分,共10分)1. 梁的弯曲正应力公式为:A. σ=M/IB. σ=M/yIC. σ=M/IyD. σ=M/Iz答案:C2. 梁的剪力图在梁的某一段上是一条水平线,则该段梁的弯矩为:A. 零B. 常数C. 线性变化D. 非线性变化答案:A3. 梁在纯弯矩作用下,其截面上的最大正应力出现在:A. 截面中心B. 截面边缘C. 截面中性轴D. 截面中心与边缘之间答案:B4. 以下哪种情况下梁的挠度最大?A. 固定梁B. 简支梁C. 悬臂梁D. 连续梁答案:C5. 梁的剪力和弯矩之间的关系是:A. 线性关系B. 二次关系C. 一次关系D. 非线性关系答案:B二、计算题(每题10分,共20分)1. 某简支梁,长度为L,两端均受集中载荷P作用,求梁的最大弯矩和最大挠度。
答案:最大弯矩Mmax=PL/4,最大挠度vmax=PL^3/48EI。
2. 某悬臂梁,长度为L,自由端受集中载荷P作用,求梁的固定端弯矩和自由端挠度。
答案:固定端弯矩M=PL,自由端挠度v=PL^3/3EI。
三、简答题(每题5分,共10分)1. 什么是梁的剪力和弯矩?它们在梁的受力分析中有何作用?答案:梁的剪力是指梁上任意截面两侧外力的代数和,它反映了梁在该截面处的受剪情况。
弯矩是指梁上任意截面两侧外力力矩的代数和,它反映了梁在该截面处的受弯情况。
在梁的受力分析中,剪力和弯矩是描述梁受力状态的基本量,通过它们的分布规律可以判断梁的受力情况,进而计算梁的应力和变形。
2. 梁的挠度和转角与哪些因素有关?如何减小梁的挠度?答案:梁的挠度和转角与梁的载荷大小、分布方式、支承条件、截面形状、材料性质等因素有关。
减小梁的挠度可以通过以下方法:增加梁的截面惯性矩、选用弹性模量较大的材料、合理布置支点、增加梁的截面高度、采用预应力等。
《结构力学》试题带答案
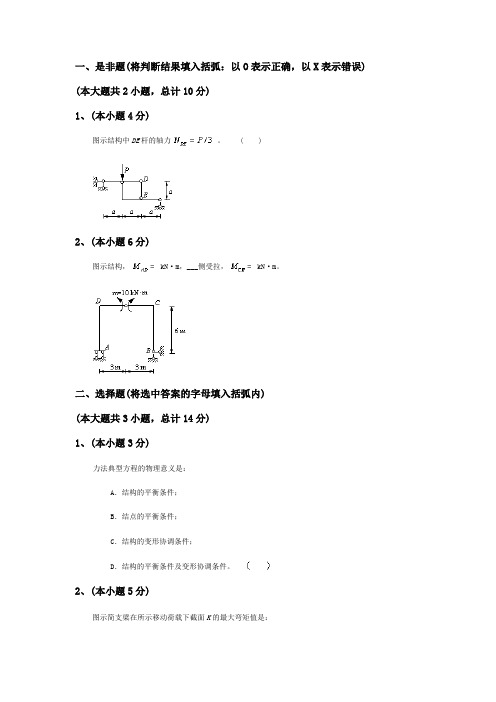
一、是非题(将判断结果填入括弧:以O表示正确,以X表示错误) (本大题共2小题,总计10分)1、(本小题4分)图示结构中DE杆的轴力。
( )2、(本小题6分)图示结构, kN·m,___侧受拉, kN·m。
二、选择题(将选中答案的字母填入括弧内)(本大题共3小题,总计14分)1、(本小题3分)力法典型方程的物理意义是:A.结构的平衡条件;B.结点的平衡条件;C.结构的变形协调条件;D.结构的平衡条件及变形协调条件。
2、(本小题5分)图示简支梁在所示移动荷载下截面K的最大弯矩值是:A.140kN·m;B.160kN·m;C.180kN·m;D.150kN·m。
( )3、(本小题6分)原结构及温度变化下的M图如下所示。
若材料的有关特性改为,且,以外侧受拉为正,则:A.;B.;C.;D.。
三、填充题(将答案写在空格内)(本大题共3小题,总计14分)1、(本小题4分)在_____________________的条件下,图示结构各杆弯矩为零。
2、(本小题5分)图a和图b所示为结构的两个状态,R与间的关系为_________。
(a)(b)3、(本小题5分)图示结构常数,在给定荷载作用下, =___________。
四、(本大题4分)分析图示体系的几何组成。
五、(本大题4分)根据位移法基本原理,草绘图示结构最后弯矩图形状为:六、(本大题6分)图示状态一与状态二,试证明功的互等定理对于该情况不成立。
(a)第一状态 (b)第二状态七、(本大题6分)试确定图示结构位移法基本未知量数目和基本结构。
两根链杆a和b需考虑轴向变形。
八、(本大题7分)求图示桁架杆1和杆2的轴力。
九、(本大题7分)用位移法作图示结构的M图,已知。
十、(本大题10分)用力法计算,并作图示结构由于支座移动引起的M图。
EI=常数,不考虑链杆的轴向变形。
十一、(本大题18分)试用力矩分配法作图示刚架的弯矩图。
结构力学考试题及答案
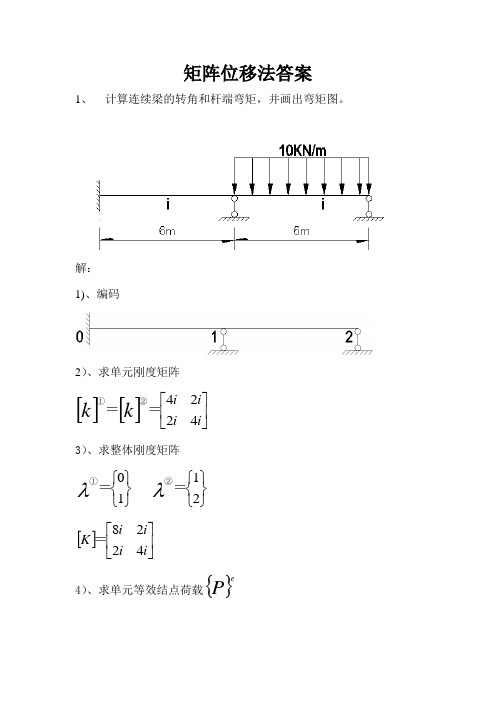
矩阵位移法答案1、 计算连续梁的转角和杆端弯矩,并画出弯矩图。
解: 1)、编码2)、求单元刚度矩阵[][]⎥⎦⎤⎢⎣⎡i i i i k k 4224==②①3)、求整体刚度矩阵⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧2110==②①λλ[]⎥⎦⎤⎢⎣⎡i i i i K 4228=4)、求单元等效结点荷载{}P e{}{}m KN q q P P l l F F ⋅⎭⎬⎫⎩⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=⎭⎬⎫⎩⎨⎧=30301211210022②①{}{}{}F P P P eee-=={}{}m KN P P ⋅⎭⎬⎫⎩⎨⎧-⎭⎬⎫⎩⎨⎧303000==②①5)、集成结构等效结点荷载向量{}P{}m KN P ⋅⎭⎬⎫⎩⎨⎧-=30306)、解方程[]{}{}P K =∆ii i i i 717545303042282121⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎥⎦⎤⎢⎣⎡ 7)、求各杆的杆端内力{}F e{}[]{}{}F k F P e e e e +∆=单元① {}m KN i i i i i F ⋅⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=71.2586.120074504224①单元② {}m KN i i i i i i F ⋅⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=071.2530307757454224-②8)、做M 图2、 求图示刚架的M 、Q 、N 图。
解:1)、整理原始数据及编码2)、求局部坐标系中的单元刚度矩阵{}K e2442101.2,300,20,100cm KN E cm I cm A cm L ⨯====mKN LEI m KN L EI KN L EI m KN LEI m KN L EA ⋅⨯=⨯=⨯=⋅⨯=⨯=2232222106.122106.7512108.376102.2541042003)、计算整体坐标系中的单元刚度矩阵{}k e单元①和单元③单元②{}{}{}2102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200⨯===⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------k k k ③②①[][]I T =,= 0α[][][][]②②①①=,=kk k k90=α[]⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--=100000001000010000000100000001000010T [][][][]2102.2508.376.1208.370420000420008.3716.758.3706.756.1208.372.2508.370420*********.3706.758.3706.75⨯==⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------T k T k T ②②4)、用单元集成法形成整体刚度矩阵{}K⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧000321000321321000===③②①λλλ {}2106.7508.3702.435108.3706.8475⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=K5)、求单元等效结点荷载{}P e{}{}[]833.050833.050-=-=TF P P①①{}{}[]833.050833.050-=TP P ①①=6)、用单元集成法形成整体结构的等效结点荷载{}P{}[]TP 833.050-=7)、形成整体结构的综合结点荷载{}[]TF 402000={}{}[]TP F 167.392500=+8)、解方程[]{}{}{}0F P K +=∆[][]I T =,= 0α⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--167.39250106.7508.3702.435108.3706.84753212 432110924.51575.0232.0-⨯⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆ 9)、求各杆的杆端内力{}F e{}[][]{}{}F T k F P e e e e +∆=单元①{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧----+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=700.13193.24744.9492.5193.14744.9833.050833.05010924.51575.0232.000010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=①①①①F T k F P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=455.6452.19150.24997.12452.19150.2400000010000924.51575.0232.010421000010000100000001000000010000102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=②②②②F T kF P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=760.6062.20744.9302.13062.20744.900000010000924.51575.0232.010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=③③③③F T k F P结构动力学作业答案1、求图示结构的自振频率。
结构力学考试题及答案

结构力学考试题及答案一、选择题1. 结构力学中,下列哪项不是结构的基本概念?A. 结构的刚度B. 结构的稳定性C. 结构的强度D. 结构的美观性答案:D2. 简支梁受均布荷载作用时,最大弯矩出现在:A. 跨中B. 支点处C. 任意截面D. 四分之三跨长处答案:A3. 在结构力学中,剪力和弯矩的方向约定为:A. 剪力向上为正,弯矩顺时针为正B. 剪力向下为正,弯矩逆时针为正C. 剪力向上为正,弯矩逆时针为正D. 剪力向下为正,弯矩顺时针为正答案:B4. 确定结构的内力分布情况通常采用的方法是:A. 能量法B. 虚功原理C. 弯矩分配法D. 刚度法答案:D5. 连续梁与简支梁相比,其特点是:A. 刚度更高B. 跨越能力更强C. 造价更低D. 所有上述选项答案:D二、填空题1. 结构力学中的__________是指结构在荷载作用下不发生位移的能力。
答案:刚度2. 结构的__________是指结构在荷载作用下不发生翻转的能力。
答案:稳定性3. 在进行结构分析时,通常首先需要确定结构的__________和反力。
答案:内力4. 结构力学中,__________是指构件截面上所有外力的集合效果。
答案:截面剪力5. 对于简支梁,当荷载作用在离支点一定距离处时,该点处的弯矩可以通过__________计算得出。
答案:剪力乘以距离三、简答题1. 请简述结构力学中的虚功原理及其应用。
答:虚功原理是指在一个平衡系统中,任何微小的位移或变形所对应的虚功等于该系统内力对该变形所做的功。
这个原理在结构力学中用于分析静不定结构,通过假设结构的位移或变形,计算出相应的虚功,然后根据虚功原理建立平衡方程,求解未知的反力或内力。
2. 描述简支梁受集中荷载作用时的弯矩图和剪力图。
答:简支梁受集中荷载作用时,弯矩图在荷载作用点会出现一个突变,即弯矩值突然增大到最大值,然后随着距离的增加逐渐减小回到零。
剪力图则显示在荷载作用点两侧的剪力值相反,一边为正值,另一边为负值,且随着距离的增加,剪力值逐渐减小到零。
大学结构力学试题及答案

大学结构力学试题及答案一、单选题(每题2分,共20分)1. 以下哪项不是结构力学研究的主要内容?A. 静力分析B. 动力分析C. 材料力学D. 稳定性分析答案:C2. 梁的剪力图和弯矩图是:A. 线性关系B. 非线性关系C. 无关D. 正比关系答案:B3. 悬臂梁的自由端受到一个向上的力,其弯矩图将:A. 向上弯曲B. 向下弯曲C. 保持直线D. 无法确定答案:A4. 简单支撑梁在均布荷载作用下的支座反力是:A. 荷载的一半B. 荷载的两倍C. 荷载的四分之一D. 荷载的三分之一答案:A5. 桁架结构中,节点的平衡方程数通常与:A. 节点数相等B. 杆件数相等C. 节点数减一D. 杆件数减二答案:D二、填空题(每题2分,共20分)1. 结构力学中,__________是分析结构内力的基本方法之一。
答案:弯矩分配法2. 当梁的跨度增加时,其最大弯矩会__________。
答案:增加3. 连续梁的支座反力可以通过__________方法求解。
答案:弯矩分配法4. 梁的剪力和弯矩之间存在__________关系。
答案:微分5. 悬臂梁在自由端受到向下的集中荷载时,其支座处的弯矩为__________。
答案:负值三、简答题(每题10分,共30分)1. 简述结构力学中静定结构和超静定结构的区别。
答案:静定结构是指在静力作用下,结构的内力和位移可以通过静力平衡方程和几何方程直接确定的结构。
超静定结构则是指在静力作用下,结构的内力和位移不能仅通过静力平衡方程和几何方程直接确定,需要使用其他方法如弯矩分配法、力法或位移法等来求解的结构。
2. 描述梁的剪力和弯矩之间的关系。
答案:梁的剪力和弯矩之间存在微分关系。
具体来说,梁的弯矩是剪力的积分,而剪力是弯矩的导数。
在连续梁或悬臂梁上,任意截面的弯矩可以通过对剪力图进行积分得到,反之,任意截面的剪力可以通过对弯矩图进行微分得到。
3. 悬臂梁和简支梁在受力特点上有何不同?答案:悬臂梁的特点是一端固定,另一端自由,因此它在自由端会产生较大的弯矩和剪力。
2020河南工业大学结构设计原理试题

一.计算题(本题30分)某钢筋混凝土构件矩形截面,其短边尺寸b=300mm,长边尺寸h=600mm。
截面上承担的弯矩组合设计值M d=175KN.m,剪力组合设计值V d=155KN,扭矩组合设计值T d=13.95KN.m。
采用C30级的混凝土(f cd=13.8MPa,f cu,k=30MPa,ftd=1.39MPa),箍筋采用R235级钢筋(f sd=195MPa),纵向钢筋采用HRB335级钢筋(fsd=280MPa,x b=0.56).I类环境条件,安全等级为二级。
试进行截面的配筋设计,并给出截面的配筋图。
提示:(1)假定纵筋的a s=40mm,箍筋内表皮至构件表面的距离为30mm(2)取纵筋与箍筋的配筋强度比为1.3二.计算题(本题40分)一根预应力混凝土简支梁,计算跨径l = 28.66m。
预应力钢筋为低松弛钢绞线,抗拉强度标准值f pk = 1860MPa,张拉控制应力σcon = 0.75f pk =1395MPa,弹性模量E p=1.95×105N/mm2。
共配置3束钢绞线,A p=2520mm2。
非预应力钢筋采用HRB400钢筋,A s =1272.5mm2,跨中断面a s =45mm。
主梁混凝土采用C50,弹性模量E c=3.45×104N/mm2。
采用后张法施工,锚具采用夹片式群锚,两端张拉。
钢束竖弯采用直线接圆弧线的方式,三根钢束N1、N2和N3竖向总的弯起角度均为θ =8°,如下图所示,图中单位均为mm。
试求:(1)钢束N1在跨中断面的预应力损失σl 1和σl 2; (说明:1. σl 1 = σcon [1-e-(μθ+k x)], 方程中的转角单位应为弧度,取μ=0.25,k =0.0015;2.反向摩擦影响长度f l 张拉端的锚具变形量取l ∆∑= 4mm )(2)对跨中断面,两阶段的预应力损失量分别为σl I = 121.33MPa ,σl II =102.66MPa ,现若对跨中截面做持久状况下的应力验算,试给出预应力钢筋和非预应力钢筋通过预加力效应对截面施加的综合等效力N pII ,及该等效力的偏心距e p 。
结构力学试题及答案

结构力学复习题一、填空题。
1、在梁、刚架、拱、桁架四种常见结构中,主要受弯的是和,主要承受轴力的是和。
2、选取结构计算简图时,一般要进行杆件简化、简化、简化和简化。
3、分析平面杆件体系的几何组成常用的规律是两刚片法则、和二元体法则。
4、建筑物中用以支承荷载的骨架部分称为,分为、和三大类。
5、一个简单铰相当于个约束。
6、静定多跨梁包括部分和部分,内力计算从部分开始。
7、刚结点的特点是,各杆件在连接处既无相对也无相对,可以传递和。
8、平面内一根链杆自由运动时的自由度等于。
二、判断改错题。
1、三刚片用三个铰两两相联必成为几何不变体系。
()2、对静定结构,支座移动或温度改变会产生内力。
()3、力法的基本体系必须是静定的。
()4、任何三铰拱的合理拱轴都是二次抛物线。
()5、图乘法可以用来计算曲杆。
()6、静定结构的影响线全部都由直线段组成。
()7、多跨静定梁若附属部分受力,则只有附属部分产生内力。
()8、功的互等定理成立的条件是小变形和线弹性。
()9、力法方程中,主系数恒为正,副系数可为正、负或零。
()三、选择题。
1、图示结构中当改变B点链杆方向(不能通过A铰)时,对该梁的影响是()A、全部内力没有变化B、弯矩有变化C、剪力有变化D、轴力有变化2、图示桁架中的零杆为()A、DC, EC, DE, DF, EFB、DE, DF, EFC、AF, BF, DE, DF, EFD、DC, EC, AF, BFAqBDB ACEF3、右图所示刚架中A 支座的反力A H 为( ) A 、PB 、2P -C 、P -D 、2P4、右图所示桁架中的零杆为( )A 、CH BI DG ,,B 、BI AB BG DC DG DE ,,,,,C 、AJ BI BG ,,D 、BI BG CF ,,5、静定结构因支座移动,( ) A 、会产生内力,但无位移 B 、会产生位移,但无内力 C 、内力和位移均不会产生 D 、内力和位移均会产生6、对右图所示的单跨超静定梁,支座A 产生逆时针转角θ,支座B 产生竖直沉降c ,若取简支梁为其基本结构,则力法方程为( )A 、θδ=+a cX B 、θδ=-a cXC 、θδ-=+a cXD 、θδ-=-acX7、下图所示平面杆件体系为( ) A 、几何不变,无多余联系 B 、几何不变,有多余联系 C 、瞬变体系 D 、常变体系PBAEICEI 2EIDBAEI aEIBAXAB CD E F G H I J2P8、图示梁中的轴力( ) A 、全部为拉力 B 、为零 C 、全部为压力D 、部分为拉力,部分为压力9、用图乘法求位移的必要条件之一是( ) A 、单位荷载下的弯矩图为一直线 B 、结构可分为等截面直杆段 C 、所有杆件EI 为常数且相同 D 、结构必须是静定的四、对下图所示平面杆件体系作几何组成分析。
结构力学试题及答案

结构力学试题及答案
试题1
题目
一根长度为L的均匀杆,两端固定,其自由悬挑端有质量为m
的物体悬挂,求杆上的内力分布。
解答
根据结构力学的原理,对于静力平衡的条件,杆上的内力分布
可以通过平衡方程求解。
以物体悬挂端点为起点,沿杆的长度方向建立坐标系。
设杆的
一小段长度为ds,杆的质量线密度为σ,杆上内力的水平分量为N,垂直分量为V。
根据平衡方程,可以得出以下两个方程:
1. 在杆的水平方向上,根据牛顿第二定律,有:dN = -σgds
2. 在杆的竖直方向上,杆上的内力必须平衡,有:dV = -σgds
通过求解上述方程组,可以得到杆上的内力分布情况。
试题2
题目
一根弹性悬挂的杆,水平放置在两个固定的支点上,两端各有质量为m的物体,求悬挂杆上的弯曲曲率。
解答
根据弹性力学的原理,弹性杆的弯曲曲率可以通过弯曲方程求解。
设悬挂杆的长度为L,其弹性模量为E,截面面积为A,力学矩形矩为I,以及弯曲曲率为κ。
根据悬挂杆的受力分析,可以得到弯曲方程:
EκI = M
其中,M是悬挂杆在某一截面上的弯矩。
根据受力平衡条件,可以得到弯矩M为:
M = mgL/4
将上述方程代入弯曲方程中求解,即可得到悬挂杆上的弯曲曲率。
注意:以上解答仅为示例,实际的解答过程可能因具体问题的条件不同而有所变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南工业大学试题纸20 ~20 学年第学期级专业结构力学试题学号::……………………………………密…………封……………线…………………………………一二三四五六七八九总分15分1、如果体系的计算自由度小于或等于零,那么体系一定是几何不变体系。
( )2、外力作用在基本部分上时,附属部分的力、变形和位移均为零。
( )3、简支梁跨任意截面K的弯矩的影响到响线的物理意义是:单位力P=1作用在截面K时整个梁的弯矩图形。
4、如果静定结构的一组力解答满足所有的平衡方程,则这组力解答就是唯一正确的力解答。
( )5、在图1所示两结构中,(a)中拉杆的轴力N与(b)中的水平反力X的关系B是:当拉杆的刚度EA=有限值时,N<XB;当拉杆的刚度EA=无穷大时,N=XB。
()图16、在图2所示结构中若增大柱子的EI值,则梁跨中截面弯矩值减少。
( )图2 图37、对图3(a)所示结构,选(b)为基本体系,则力法典型方程为。
8、结构发生了变形,必然会引起位移,反过来,结构有位移必然有变形发生。
( )9、已知连续梁的M 图如图4所示,则结点B 的转角θB =4/i.( )10、如特殊单元是几何不变体系,其单元刚度矩阵一定是非奇异矩阵.( )二、单项选择题(每小题1.5分,共15分) 1、三刚片组成无多余约束的几何不变体系,其联结方式是()图4A 以任意的三个铰相联B 以不在一条线上三个铰相联C 以三对平行链杆相联D 以三个无穷远处的虚铰相联2、 图5所示结构有多少根零杆( ) A 5根 B 6根 C 7根 D 8根图5 图6 3、图6所示两结构相同的是 ( )A 弯矩B 剪力C 轴力D C 点竖向位移4、设同跨度的三铰拱和曲梁,在相同荷载作用下,同一位置截面的弯矩1K M (三铰拱)和1K M (曲梁)之间的关系为( )A 、1K M >1K M A 、1K M =1K M C 、1K M <1K M D 、条件不够,无法确定5、图7所示虚拟力状态可求出什么( ) A A ,B 两截面的相对位移B A,B两截面的相对转角C A,B两截面相对转动的m倍D A,B两点连线的转动6、力法方程中的系数δki表示的是基本体系由()A Xi 产生的Xk方向的位移 B Xi=1产生的Xk方向的位移C Xi =1产生的Xi方向的位移 D Xk=1产生的Xi方向的位移7、下列关于图8所示结构位移法基本未知量的论述,正确的是图7A 三个基本未知量θA ,θB,Δ B 两个基本未知量θA =θB,ΔC θA =θB= 0,只有一个未知量Δ D θA=θB=Δ/a,只有一个未知量Δ图8 图98、图9所示四结构固定端处的弯矩M A的关系是A M Aa> M Ab > M Ac> M AdB M Aa=MAb= M Ac= M AdC M Ab> M Aa= M Ac> M AdD M Aa<M Ab< M Ac< M Ad9、如图10所示结构的多束约束的个数为()A 6B 8C 10D 1210、在力矩分配法中,一般说来,结点不平衡力矩总等于图10A 交于该结点的各杆端的固断弯矩之和B 传递弯矩C 附加刚臂中的约束力矩D 结点集中力偶荷载三、填空题(每小题3分,共30分)1、如图11(a)所示结构,各杆的EI 为常数,用位移法求解时,取如图(b)年示基本结构,则=P F 1 ,=P F 2 ,2、如图12所示桁架分别承受如图(a)、(b)所示的两种荷载,二者力相同的杆件号有(a ) (b) (a ) (b) 图11 图123、如图13中图(a)所示结构,若取图(b)所示的基本体系,则在力法方程中的副系数 等于零,自由项 等于零。
图134、如图14所示各杆的长度和EI 值相等,若结点A 产生顺时针的单位转角时,在A 点使加的力矩=M图14 图155、已知图15所示连续梁BC 跨的弯矩图,则AB 杆A 端的弯矩=四、作图计算题(共50分)1、如图15所示的刚架,各杆的EI为常数,试作:(1) 刚架的力图(5分)。
(2) 只考虑弯曲变形的影响,求刚架B点的水平位移△。
(5分)2、试作如图16所示梁的Mc及FQD的影响线(10分)3、作所示组合结构中受弯杆的弯矩图,并求二力杆的轴力。
(10分)4、用位移法计算 (a)所示刚架,并绘制弯矩图。
各杆EI为常数。
(10分)llAlB CM B CM BAM BDF QBA F QBCDAAllCE1ABEIC1XBq q5、用力矩分配法计算下图所示对称刚架,并绘制弯矩图。
各杆EI相同且为常数。
6m4mB18kN/mFD4m18kN/mA C E6m4mB18kN/mA C一、判断题:(每小题1.5分,共15分)1 ×2 ×3 ×4 √5 √6 √7 ×8 ×9 √10 √二、选择题(每小题1.5分,共15分)1 B2 D3 A4 C5 C6 B7 C8 C9 C 10 A三、填空题(每小题3分,共4.5分)1、0,P F-2、23、34、36、67、69、27、493、3113δδpp21∆∆4、i85、-30KN*m四、作图计算题(共55分)1、解(1)求支反力()←==∑qaFFxAx()↑==∑20qaFMyBA()↓==∑20qaFFyAy(1分)(2)求杆端弯矩()右边受拉202qaMMCAAC==()下边受拉202qaMMCBBC==(1分)力图如下:(3分)(3)作单位荷载作下的M图如下(2分)2123243241333lqllqllqlEIdsEIMMp⨯+⨯+⎥⎦⎤⎢⎣⎡⨯==∆∑⎰()→EIql834(3分)2解:梁M c和F QD的影响线如下M c的影响线(5分)(1分)qA BCACBqEIE1A llX1qA BCACBqEIE1A llX1X12ql 2l1X12ql 2l(3)计算系数及自由项画出1M和pM图。
并易知11N=F,0NP=F。
(2分)系数和自由项分别为∑⎰∑+=ds EI M EA l F ii 22N 11δ⎪⎭⎫ ⎝⎛⨯⨯⨯+=l l l EI A E l 322111EI l A E l 331+= (2分)(2分)(4)解力法方程,求出基本未知量 将11δ、p1∆代入第⑵步写出的力法方程,得0834131=++EI ql X EI l A E l解方程,得EI l A E l EI ql X 3831411P11+-=∆-=δ (2分)(5)作弯矩图、轴力图 多余未知力求出后,可按叠加原理确定控制截面的弯矩值,再进一步作出弯矩图 由式:p11M X M M +=知 0=BA M21828224234P 11ql lEI ql ql l l EI ql l M X M M AB++-=++-⨯=+=(2分4结(1分)⑵设线刚度为lEI i =,则转角位移方程为:(3分)VB 33∆-=l i i M B BA θ VBB BC64∆+=l i i M θVB 62∆+=l i i M B CB θ 832qli M B BD-=θ⑶由刚结点B 的力矩平衡条件求B θ0=∑B M ,0=++BC BA BD M M M0643383VB V B 2=∆++∆-+-l i i l i i ql i BB B θθθ083102V B =-∆+ql l ii B θ ⑴(2分)取DB 部分隔离体,根据隔离体力的平衡条件计算VB ∆:0=∑Y ,0Q Q =-BC BA F F其中()V B 2Q 331∆+-=+-=l i l i M M l F B AB BA BA θ()⎪⎭⎫⎝⎛∆++∆+-=+-=V B V B Q 626411l i i l i i l M M lF B B CB BC BC θθ V B2126∆--=l i l i B θ代入上式得012633V B 2V B 2=∆++∆+-l il i l i l i B B θθ153V B 2=∆+l i l i B θ ⑵(2分)⑷解由方程⑴与方程⑵组成的方程组,得i ql B 37652=θi ql 3763VB-=∆ (1分)⑸将B θ和V B ∆代入转角位移方程:23205.0376337653ql i ql l i i ql i M BA =⎪⎪⎭⎫⎝⎛-⨯-⨯= 23204.0376637654ql i ql l i i ql i M BC=⎪⎪⎭⎫⎝⎛-⨯+⨯=23201.0376637652ql i ql l i i ql i M CB=⎪⎪⎭⎫⎝⎛-⨯+⨯=22209.0837653ql ql i ql i M BD-=-⨯=EI EI S AB 3264=⨯=,EI EIS AC =⨯=44(1分)4.03232=+=EIEI EI μAB ,6.032=+=EI EI EIμAB(1分)m kN 54126181222F⋅=⨯==ql MAB,mkN 54126181222F⋅-=⨯-=-=ql MBA(1分)⑶计算各杆的杆端弯矩结点B AC 杆端BAABACCA分配系数 0.4 0.6 固端弯矩 -54 54 0 0 分配弯矩 传递弯矩 -10.8 -21.6 -32.4 -16.2 最后杆端弯矩-64.8 32.4 -32.4 -16.2(单位:kN·m) (3分)⑷绘制弯矩图。
(2分)6m4m18k N /m F E河南工业大学试题纸20 ~20 学年第学期级专业试题学号::……………………………………密…………封……………线…………………………………一.单项选择题(每小题2分,共12分。
在每小题的四个备选答案中选出一个正确答案,并将其代号填在题干后面的括号。
不选、错选或多选者,该题无分。
)1.在无多余约束的几何不变体系上增加二元体后构成()A可变体系B瞬变体系C无多余约束的几何不变体系55.位移法典型方程中的主系数恒为正值,付系数恒为负值。
()6.支座位移引起的超静定结构力,与各杆刚度的相对值有关()7.三铰拱水平推力的大小,不仅与拱高f有关,而且与拱轴线形状有关()1。
()F Q AB= 。
y D表示单位移动荷载作用在D点时产生的值。
3.力法的基本未知量是多余未知力,其典型方程是根据多余未知力处的4.567.8.判断图3所示桁架结构有根零杆。
,根据其半边结构完成下列各1、取等代结构2、选择力法的基本未知量;画出相应的力法的基本体系;3、写出力法的基本方程;M图;4、画出相应的M、P5、求出力法方程中的系数和自由项并计算出基本未知量结构力学试题答案一.单项选择题(每小题2分,共12分)1.c2. d3. d4. b5.d6. c二、判断题(每小题1,共8分)M图 2分(3)M,P(4)k11=8i F1P= -16kN·m 2分2。
