大学物理实验等厚干涉
等厚干涉原理与应用实验报告doc

等厚干涉原理与应用实验报告篇一:等厚干涉实验—牛顿环和劈尖干涉等厚干涉实验—牛顿环和劈尖干涉要观察到光的干涉图象,如何获得相干光就成了重要的问题,利用普通光源获得相干光的方法是把由光源上同一点发的光设法分成两部分,然后再使这两部分叠如起来。
由于这两部分光的相应部分实际上都来自同一发光原子的同一次发光,所以它们将满足相干条件而成为相干光。
获得相干光方法有两种。
一种叫分波阵面法,另一种叫分振幅法。
1.实验目的(1)通过对等厚干涉图象观察和测量,加深对光的波动性的认识。
(2)掌握读数显微镜的基本调节和测量操作。
(3)掌握用牛顿环法测量透镜的曲率半径和用劈尖干涉法测量玻璃丝微小直径的实验方法(4)学习用图解法和逐差法处理数据。
2.实验仪器读数显微镜,牛顿环,钠光灯3.实验原理我们所讨论的等厚干涉就属于分振幅干涉现象。
分振幅干涉就是利用透明薄膜上下表面对入射光的反射、折射,将入射能量(也可说振幅)分成若干部分,然后相遇而产生干涉。
分振幅干涉分两类称等厚干涉,一类称等倾干涉。
用一束单色平行光照射透明薄膜,薄膜上表面反射光与下表面反射光来自于同一入射Rre(a)(b)图9-1 牛顿环装置和干涉图样光,满足相干条件。
当入射光入射角不变,薄膜厚度不同发生变化,那么不同厚度处可满足不同的干涉明暗条件,出现干涉明暗条纹,相同厚度处一定满足同样的干涉条件,因此同一干涉条纹下对应同样的薄膜厚度。
这种干涉称为等厚干涉,相应干涉条纹称为等厚干涉条纹。
等厚干涉现象在光学加工中有着广泛应用,牛顿环和劈尖干涉就属于等厚干涉。
下面分别讨论其原理及应用:(1)用牛顿环法测定透镜球面的曲率半径牛顿环装置是由一块曲率半径较大的平凸玻璃透镜和一块光学平玻璃片(又称“平晶”)相接触而组成的。
相互接触的透镜凸面与平玻璃片平面之间的空气间隙,构成一个空气薄膜间隙,空气膜的厚度从中心接触点到边缘逐渐增加。
如图9-1(a)所示。
当单色光垂直地照射于牛顿环装置时(如图9-1),如果从反射光的方向观察,就可以看到透镜与平板玻璃接触处有一个暗点,周围环绕着一簇同心的明暗相间的内疏外密圆环,这些圆环就叫做牛顿环,如图9-1(b)所示.在平凸透镜和平板玻璃之间有一层很薄的空气层,通过透镜的单色光一部分在透镜和空气层的交界面上反射,一部分通过空气层在平板玻璃上表面上反射,这两部分反射光符合相干条件,它们在平面透镜的凸面上相遇时就会产生干涉现象。
等厚干涉实验牛顿环大学物理实验课件

大学物理实验
主要内容
简介
牛顿环是一种光的等厚干涉现象。牛顿 对牛顿环作了精确的定量测定,可以说已 经走到了光的波动说的边缘,但由于过分 偏爱他的微粒说,始终无法正确解释这个 现象。直到19世纪初,英国科学家托马斯⋅ 杨才用光的波动说完满的解释了牛顿环现象。
实验目的
• 观察牛顿环干涉条纹的特点,加深对光的 波动性的认识。
成一个厚度随直径变化的空
气隙。
空气隙的等厚干涉条纹
是一组明暗相间的同心环。
该干涉条纹最早被牛顿发现,
所以称为牛顿环( Newton -
ring)
牛顿环
返回
仪器介绍
• 读数显微镜 • 钠灯 • 平凸透镜
ห้องสมุดไป่ตู้
读数显微镜
读数标尺
读数盘
目镜 上下移动旋钮 物镜 水平移动旋钮
钠灯
钠光灯是一种气体放电灯。在放电管内 充有金属钠和氩气。开启电源的瞬间,氩 气放电发出粉红色的光。氩气放电后金属 钠被蒸发并放电发出黄色光。
•调节目镜清晰地看到十字叉丝,然后由下向上 移动显微镜镜筒(为防止压坏被测物体和物镜, 不得由上向下移动!),看清牛顿干涉环。
测量牛顿环直径
•取m=30 ,n=15。横向改变显微镜筒位置,使叉 丝由第30圈外向第30圈移动直至叉丝交点与之重 合,读取C30 ,继续朝同一方向移动叉丝至第15圈 读取C15 ;仍按原方向移动叉丝(为防止产生空程 差),越过中央暗环,按同样方法读取C'15 、C‘30。 •将牛顿环旋转若干角度,重复以上测量。
半波损失
波传播过程中,遇到波疏介质反 射,反射点入射波与反射波有相同的 相位。波由波密介质反射,反射点入 射波与反射波的相位差π ,光程差为 λ/2 ,即产生了半波损失。
(完整版)光的等厚干涉实验报告

大连理工大学大 学 物 理 实 验 报 告院(系) 材料学院 专业 材料物理 班级 0705 姓 名 童凌炜 学号 200767025 实验台号 实验时间 2008 年 11 月 04 日,第11周,星期 二 第 5-6 节实验名称 光的等厚干涉教师评语实验目的与要求:1. 观察牛顿环现象及其特点, 加深对等厚干涉现象的认识和理解。
2. 学习用等厚干涉法测量平凸透镜曲率半径和薄膜厚度。
3. 掌握读数显微镜的使用方法。
实验原理和内容: 1. 牛顿环牛顿环器件由一块曲率半径很大的平凸透镜叠放在一块光学平板玻璃上构成, 结构如图所示。
当平行单色光垂直照射到牛顿环器件上时, 由于平凸透镜和玻璃之间存在一层从中心向外厚度递增的空气膜, 经空气膜和玻璃之间的上下界面反射的两束光存在光程差, 它们在平凸透镜的凸面(底面)相遇后将发生干涉, 干涉图样是以接触点为中心的一组明暗相间、内疏外密的同心圆, 称为牛顿环(如图所示。
由牛顿最早发现)。
由于同一干涉圆环各处的空气薄膜厚度相等, 故称为等厚干涉。
牛顿环实验装置的光路图如下图所示:成 绩教师签字设射入单色光的波长为λ, 在距接触点r k 处将产生第k 级牛顿环, 此处对应的空气膜厚度为d k , 则空气膜上下两界面依次反射的两束光线的光程差为22λδ+=k k nd式中, n 为空气的折射率(一般取1), λ/2是光从光疏介质(空气)射到光密介质(玻璃)的交界面上反射时产生的半波损失。
根据干涉条件, 当光程差为波长的整数倍时干涉相长, 反之为半波长奇数倍时干涉相消, 故薄膜上下界面上的两束反射光的光程差存在两种情况:2)12(2222λλλδ+=+=k k d k k由上页图可得干涉环半径r k , 膜的厚度d k 与平凸透镜的曲率半径R 之间的关系222)(k k r d R R +-=。
由于dk 远小于R , 故可以将其平方项忽略而得到22k k r Rd =。
等厚干涉实验报告记录

等厚干涉实验报告记录————————————————————————————————作者:————————————————————————————————日期:大学物理实验报告(等厚干涉)一、实验目的:1.、观察牛顿环和劈尖的干涉现象。
2、了解形成等厚干涉现象的条件极其特点。
3、用干涉法测量透镜的曲率半径以及测量物体的微小直径或厚度。
二、实验原理:1.牛顿环牛顿环器件由一块曲率半径很大的平凸透镜叠放在一块光学平板玻璃上构成,结构如图所示。
当平行单色光垂直照射到牛顿环器件上时,由于平凸透镜和玻璃之间存在一层从中心向外厚度递增的空气膜,经空气膜和玻璃之间的上下界面反射的两束光存在光程差,它们在平凸透镜的凸面(底面)相遇后将发生干涉,干涉图样是以接触点为中心的一组明暗相间、内疏外密的同心圆,称为牛顿环(如图所示。
由牛顿最早发现)。
由于同一干涉圆环各处的空气薄膜厚度相等,故称为等厚干涉。
牛顿环实验装置的光路图如下图所示:设射入单色光的波长为λ,在距接触点r k处将产生第k级牛顿环,此处对应的空气膜厚度为d k,则空气膜上下两界面依次反射的两束光线的光程差为22λδ+=kknd式中,n为空气的折射率(一般取1),λ/2是光从光疏介质(空气)射到光密介质(玻璃)的交界面上反射时产生的半波损失。
根据干涉条件,当光程差为波长的整数倍时干涉相长,反之为半波长奇数倍时干涉相消,故薄膜上下界面上的两束反射光的光程差存在两种情况:2)12(2222λλλδ+=+=kkdkkK=1,2,3,…K=0,1,2,…由上页图可得干涉环半径r k,膜的厚度d k与平凸透镜的曲率半径R之间的关系222)(kkrdRR+-=。
由于dk远小于R,故可以将其平方项忽略而得到22kkrRd=。
结合以上的两种情况公式,得到:λkRRdrkk==22,暗环...,2,1,0=k由以上公式课件,r k与d k成二次幂的关系,故牛顿环之间并不是等距的,且为了避免背光因素干扰,一般选取暗环作为观测对象。
大学物理实验实验十六等厚干涉及应用

或薄纸片的厚度 d 为:
d=Nλ 2
(11)
由于 N 数目很大,为了简便,可先测出单位长度的暗条纹数 N0 ,再测出两玻璃板 交线处至金属丝或薄纸片的距离 L ,则
N = N0L
即得
d
=
N0L
λ 2
(12)
由(12)式可知,如果已知入射光波长 λ ,并测出 N0 和 L ,则可求出细金属丝直径或
薄片厚度。
图 1 牛顿环的干涉原理及干涉条纹
156
因此产生两束具有一定光程差的相干光,当它们相遇后就产生干涉现象。由于空气膜厚
度相等处是以接触点为圆心的同心圆,即以接触点为圆心的同一圆周上各点的光程差相
等,故干涉条纹是一系列以接触点为圆心的明暗相间的同心圆,如图 1(b)所示。这种 干涉现象最早为牛顿所发现,故称为牛顿环。
六、注意事项
1.使用读数显微镜时,为避免引进螺距差,移测时必须向同一方向旋转,中途不可 倒退。
2.调节牛顿环厚度时,螺旋不可旋得过紧,以免接触压力过大引起透镜弹性形变。 3.实验完毕应将牛顿环仪上的三个螺旋松开,以免牛顿环变形。 4.在测量劈尖干涉条纹的间距L0时,纵丝每次应与明、暗条纹的交界线重合;测量
射光形成的条纹有何不同?
2.实验中为什么要测牛顿环直径,而不测其半径? 3.在使用读数显微镜时,怎样判断是否消除了视差?使用时最主要的注意事项是 什么? 4.实验中如果用凹透镜代替凸透镜,所得数据有何异同? 5.如何用劈尖干涉检验光学平面的表面质量?
160
δ
=
2hk
+
λ 2
=
⎧ ⎪ ⎨ ⎪⎩(2k
kλ + 1) λ
2
k = 1, 2,3,L(明纹) k = 0,1, 2, 3,L(暗纹) (9)
大学物理实验--等厚干涉

⼤学物理实验--等厚⼲涉实验名称:等厚⼲涉⼀.实验⽬的:1. 理解⽜顿环和劈尖⼲涉条纹的成因与等候⼲涉的含义:2. 学会⽤等候⼲涉法测量薄膜厚度和透镜曲率半径,并熟练运⽤逐差法处理实验数据3. 学习正确使⽤读数显微镜的⽅法。
⼆. 实验仪器测量显微镜、⽜顿环、钠光灯、劈尖装置和待测细丝。
三.实验原理当⼀束单⾊光⼊射到透明薄膜上时,通过薄膜上下表⾯依次反射⽽产⽣两束相⼲光。
如果这两束反射光相遇时的光程差仅取决于薄膜厚度,则同⼀级⼲涉条纹对应的薄膜厚度相等,这就是所谓的等厚⼲涉。
本实验研究⽜顿环和劈尖所产⽣的等厚⼲涉。
1. 等厚⼲涉如图3-17-1所⽰,玻璃板A 和玻璃板B ⼆者叠放起来,中间加有⼀层空⽓(即形成了空⽓劈尖)。
设光线1垂直⼊射到厚度为d 的空⽓薄膜上。
⼊射光线在A 板下表⾯和B 板上表⾯分别产⽣反射光线2和2′,⼆者在A 板上⽅相遇,由于两束光线都是由光线1分出来的(分振幅法),故频率相同、相位差恒定(与该处空⽓厚度d 有关)、振动⽅向相同,因⽽会产⽣⼲涉。
我们现在考虑光线2和2′的光程差与空⽓薄膜厚度的关系。
显然光线2′⽐光线2多传播了⼀段距离2d 。
此外,由于反射光线2′是由光密媒质(玻璃)向光疏媒质(空⽓)反射,会产⽣半波损失。
故总的光程差还应加上半个波长2/λ,即2/2λ+=?d 。
根据⼲涉条件,当光程差为波长的整数倍时相互加强,出现亮纹;为半波长的奇数倍时互相减弱,出现暗纹。
因此有:=+=?22λd+?2)12(22λλK K 出现暗纹,,,出现亮纹 210,3,2,1==K K 光程差?取决于产⽣反射光的薄膜厚度。
同⼀条⼲涉条纹所对应的空⽓厚度相同,故称为等厚⼲涉。
2. ⽜顿环当⼀块曲率半径很⼤的平凸透镜的凸⾯放在⼀块光学平板玻璃上,在透镜的凸⾯和平板玻璃间形成⼀个上表⾯是球⾯,下表⾯是平⾯的空⽓薄层,其厚度从中⼼接触点到边缘逐渐增加。
离接触点等距离的地⽅,厚度相同,等厚膜的轨迹是以接触点为中⼼的圆。
等厚干涉实验报告
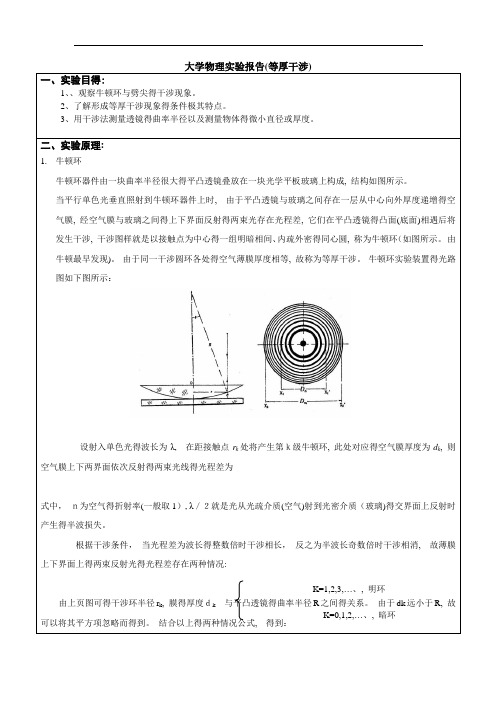
一、实验目得:1、、观察牛顿环与劈尖得干涉现象。
2、了解形成等厚干涉现象得条件极其特点。
3、用干涉法测量透镜得曲率半径以及测量物体得微小直径或厚度。
二、实验原理:1.牛顿环牛顿环器件由一块曲率半径很大得平凸透镜叠放在一块光学平板玻璃上构成, 结构如图所示。
当平行单色光垂直照射到牛顿环器件上时,由于平凸透镜与玻璃之间存在一层从中心向外厚度递增得空气膜, 经空气膜与玻璃之间得上下界面反射得两束光存在光程差, 它们在平凸透镜得凸面(底面)相遇后将发生干涉, 干涉图样就是以接触点为中心得一组明暗相间、内疏外密得同心圆, 称为牛顿环(如图所示。
由牛顿最早发现)。
由于同一干涉圆环各处得空气薄膜厚度相等, 故称为等厚干涉。
牛顿环实验装置得光路图如下图所示:设射入单色光得波长为λ,在距接触点r k处将产生第k级牛顿环, 此处对应得空气膜厚度为d k, 则空气膜上下两界面依次反射得两束光线得光程差为式中,n为空气得折射率(一般取1), λ/2就是光从光疏介质(空气)射到光密介质(玻璃)得交界面上反射时产生得半波损失。
根据干涉条件,当光程差为波长得整数倍时干涉相长,反之为半波长奇数倍时干涉相消,故薄膜上下界面上得两束反射光得光程差存在两种情况:由上页图可得干涉环半径r k, 膜得厚度dk与平凸透镜得曲率半径R之间得关系。
由于dk远小于R, 故可以将其平方项忽略而得到。
结合以上得两种情况公式,得到:K=1,2,3,…、, 明环K=0,1,2,…、, 暗环,由以上公式课件, r k与d k成二次幂得关系,故牛顿环之间并不就是等距得, 且为了避免背光因素干扰, 一般选取暗环作为观测对象。
而在实际中由于压力形变等原因, 凸透镜与平板玻璃得接触不就是一个理想得点而就是一个圆面; 另外镜面沾染回程会导致环中心成为一个光斑, 这些都致使干涉环得级数与半径无法准确测量。
而使用差值法消去附加得光程差,用测量暗环得直径来代替半径,都可以减少以上类型得误差出现。
等厚干涉(干涉法测微小量)

姓名:;学号;班级;教师________;信箱号:______ 预约时间:第_____周、星期_____、第_____~ _____节;座位号:_______预习操作实验报告总分教师签字一、实验名称等厚干涉二、实验目的(1) 观察和研究等厚干涉的现象及其特点 .(2) 练习用干涉法测量透镜的曲率半径、微小厚度 ( 或直径 ).三、实验原理(基本原理概述、重要公式、简要推导过程、重要图形等;要求用自己的语言概括与总结,不可照抄教材)利用透明薄膜上、下两表面对入射光的依次反射,入射光的振幅将分解成有一定光程差的几个部分.这是一种获得相干光的重要途径,被多种干涉仪所采用若两束反射光在相遇时的光程差取决于产生反射光的薄膜厚度,则同一干涉条纹所对应的薄膜厚度相同.这就是所谓的等厚干涉。
(见右图)总的光程差为:(1)当△满足条件:(2)时,发生相长干涉,出现第K级亮纹。
而当:(3)时,发生相消干涉,出现第k级暗纹。
因为同一级条纹对应着相同的膜厚,所以干涉条纹是一组等厚度线。
可以想见,干涉条纹是一组以C点为中心的同心圆,这就是所谓的牛顿环。
如图所示,设第k级条纹的半径为rk,对应的膜厚度为ek ,则:(4)在实验中,R的大小为几米到十几米,而ek的数量级为毫米,所以R >>ek ,ek2相对于2Rk 是一个小量,可以忽略,所以上式可以简化为(5)如果rk是第k级暗条纹的半径,由式(1)和(3)可得:(6)代入式(5)得透镜曲率半径的计算公式(7)对给定的装置,R为常数,暗纹半径(8)和级数k的平方根成正比,即随着k的增大,条纹越来越细。
由于从劈尖的上下表面反射的两条光线来自同一条入射光线,它们满足相干条件并在劈尖的上表面相遇而产生干涉,干涉后的强度由相遇的两条光线的光程差决定,由图可见,二者的光程差等于劈尖厚度的两倍,即n = 0时,,即在两玻璃片交线处为零级暗条纹。
如果在细丝处呈现n = N级条纹,则待测细丝直径为(9)四、实验内容和步骤(要求用自己的语言概括与总结,不可照抄教材)1. 观察牛顿环。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r mR
2 m
r nR
2 n
r r d d R ( m n) 4( m n)
2 m 2 n 2 m 2 n
实验仪器
读数标尺
读数显微镜
目镜
上下移动旋钮
物镜 读数盘
水平移动旋钮
读数显微镜的读数方法
主尺的分度值为1mm,测微鼓轮共有100个刻度,其 份度值为0.01mm,可估读到0.001mm。
n 1 U p cS P c ( Pi P) 2 n(n 1) i 1
c=2 (置信概率 P=95.5%)
3.计算R 的总不确定度
Up R 2 2 UR ( ) U p P 4(m n)
4.相对不确定度E
UR E 100 % R
5.结果表示:
R R U R E=
d nL
2
2.测细丝直径
(1)将被测细丝夹在两块平板玻璃的一端,另一端直 接接触,形成劈尖,然后置于显微镜的载物台上,将调 节螺丝朝下,如图2所示。
(2)调节显微镜和钠光灯位置,能看清十字叉丝、 干涉条纹、玻璃板交线和细丝,并将读数显微镜的 镜筒调至主尺读数范围的一侧边缘。 注意叉丝移动方向要垂直于干涉条纹方向 (3)测出玻璃板交线到细丝的长度L。 (4)再次将镜筒调回至玻璃板交线附近,测出50条 暗纹的长度,重复测量五次,将数据填入表格2中。 5)计算细丝直径的平均值d和不确定度Ud。
d
5.实验结果: d d U d , E ?(P 95.5%)
_
思考题:牛顿环中心斑在什么情况下是暗的?在什么情况下是亮的?
注意事项
1.应等待入射光电源工作几分钟后,处稳定状 态,
再进行实验。 2.为保护实验仪器,聚焦前,应先使物镜接近被测 物,然后使镜筒慢慢向上移直至聚焦。 3.测量读数时,目镜中的十字叉丝的横丝应与读数 标尺相平行,纵丝应与各暗环相切; 4.测量读数时,为避免转动部件的螺纹间隙产生的 空程误差,测微鼓轮只能向一个方向旋转。
主尺 15 mm 最后读数为: 15.506mm
副尺 0.506mm 来自实验步骤】 1.牛顿环测量平凸透镜的曲率半径
S (1)点亮钠光灯,对钠光灯进行预热, 处稳定状态再进行实验。 (2)将读数显微镜的镜筒调至中央附近。 将45度平面镜调成如图1所示的位置,使光 垂直照在平凸透镜装置上。边调节平板玻 璃角度,边移动钠光灯的位置。 此时通过目镜可以看到明亮的 黄色背景;
(3)转动目镜,使十字叉丝最清晰,移动牛顿环,使 牛顿环圆心与十字叉丝中心重合,纵丝应与各暗环相切。 (4) 将牛顿环按图所示放在显微镜的平台上,将显微 镜目镜调到最低,注意不要碰到显微镜,然后由下向上 缓慢移动显微镜镜筒,直至看清干涉条纹为止.
(5)转动测微鼓轮,先使镜筒由牛顿环中心向左移动, 顺序数到第32个暗环,再反向移动到第30暗环并记录, 依次记录30-26、10-6的暗环位置的读数。再继续向右 移动,使十字叉丝经过圆心再依次测出右侧第6-10、 26-30暗环位置的读数。将数据填入表1中。 (6)求出透镜的曲率半径R及其不确定度UR。
3、劈尖
玻 璃 板 交 线 L=43.56mm
细 丝 ( 头 发 丝 )
【数据记录表表格】
玻璃板到细丝的长度L=
次数i 条数
(mm)
起点xi(mm) 终点x’i(mm) ∆i=xi- x’i(mm) ni=50/∆i(条/mm) 50条暗纹长度 单位长度的暗纹 数
1
2 3
50条
50条 50条
【数据处理】
【数据记录表格】
次数 环级
Xi (mm) (左)
Xi ′(mm) (右)
Di=xi-xi′ (mm) (直径)
Di2(mm)2
Pi=|Di+52 - Di2|(mm)2
1
2 3
30
29 28
4
5 6
27
26 10
7
8 9 10
9
8 7 6
1.计算平凸透镜的曲率半径 (m-n=20) 2.计算
Dm 2 Dn2 P R 4(m - n) 4(m n)
1.计算 n
2.计算
d nL
_
_
2
3.计算
k _ 1 U n c cS _ c ( ni n ) n k (k 1) i 1
,
c=2 (置信概率 P=95.5%)
Ud
_
4.计算
Ud
d 2 ( )2U n L U n n 2
E
100 %, ( p 95 .5%)
一、实验目的
1、加深对光的等厚干涉原理的理解 2、掌握用牛顿环测量曲面曲率半径的 原理和方法 3、掌握用劈尖干涉法测量细丝直径 4、学会用读数显微镜
实验内容
1.用牛顿环测透镜的曲率半径 2、用劈尖测细丝直径
1、用牛顿环测透镜的曲率半径原理
2h
2h
2
2
k
明纹
R 暗纹
2
2
2
( 2k 1)
2
2
r R ( R h) 2R h h
o
r
h
R h 2R h h 2 rm R m
2
这样,若测量出第m级暗环的半 径,且已知所用单色光波的波长,就 可计算出透镜的曲率半径R。
dm dn
考虑到玻璃的弹性形变及环心位置不易确定, 本实验测量中透镜半径为:
(P=95.5%)
2、用劈尖测细丝直径 k
2ek
暗纹 ek k
2 ( 2k 1) 2 k 0,1,2 暗条纹
ek
k 1,2,3 明条纹
d
2 相邻两暗纹对应的厚度差暗纹
e
2 若单位长度上的暗纹条数为n,玻璃板交线到 细丝的距离为L,则细丝直径为
