线性系统理论--考试资料
线性系统理论复习题纲
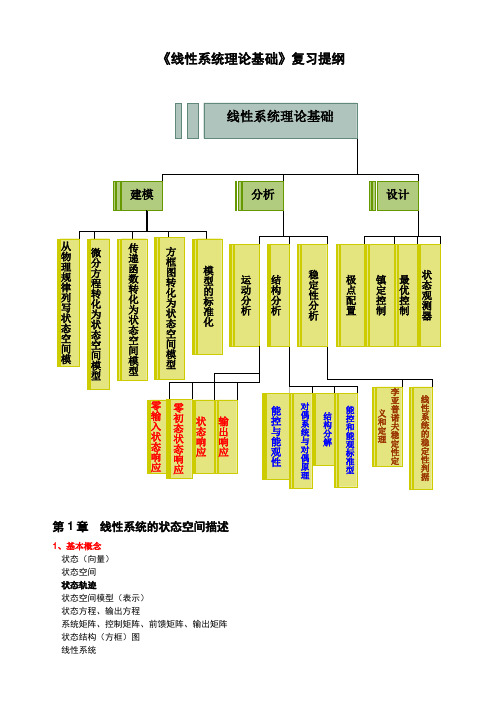
《线性系统理论基础》复习提纲第1章线性系统的状态空间描述1、基本概念状态(向量)状态空间状态轨迹状态空间模型(表示)状态方程、输出方程系统矩阵、控制矩阵、前馈矩阵、输出矩阵状态结构(方框)图线性系统时不变(定常)系统、时变系统连续时间系统、离散时间系统 状态线性变换矩阵的特征值、矩阵的特征向量 对角线标准型、约当标准型 模态标准型 正则型矩阵 范德蒙矩阵 传递函数矩阵2、知识要点%%知识点1:根据物理规律建立状态空间模型♦ 简单机械系统 ♦简单电气系统参考例题:例2.1.1,例2.1.2(P8)%%知识点2:微分方程模型转化为状态空间模型♦微分方程中不含输入导数项给定 ()(1)110n n n y a ya y a y bu --++++=&L ,选取状态向量12(1)n n x y x y x y -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦&M M , 则有状态方程: 1122011010010n n n x x x x u x a a a x b -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦&&M O M M M&L输出方程: []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x y M Λ21001 例2.1.3 (注意:方框图在没有要求时可以不画出) ♦微分方程中包含输入函数导数项,且m n <给定()(1)()(1)110110n n m m n m m ya y a y a yb u b u b u b u ----++++=++++&&L L ,m n <,将其转化为()(1)110()(1)110n n n m m m m y a y a y a y u y b yb y b y b y ----⎧++++=⎪⎨=++++⎪⎩&%%%%L &%%%%L ,选取状态向量12(1)n n x yx y x y-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦%&%M M %,则有状态方程 120110100101n n x x u x a a a -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦&&M O M M &L 输出方程 12011[,,,,0,,0]m n m n x x y b b b x --⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L 123M例2.1.4 ♦ 微分方程中包含输入函数导数项,且n m =若()(1)()(1)110110n n n n n n n ya y a y a yb u b u b u b u ----++++=++++&&L L ,让n y y b u =-%,则转化为如下微分方程的形式()(1)(1)(1)110111100()()()n n n n n n n n n y a y a y a y b a b u b a b u b a b u -----++++=-++-+-%%%%&L L 。
(完整word版)《线性系统理论》试卷及答案

R C 2《线性系统理论》试卷及答案1、(20分)如图所示RLC 网络,若e(t )为系统输入变量r (t),电阻R 2两端的电压为输出量y(t),选定状态变量为 x 1(t)=v 1(t ),x 2(t )=v 2(t),x 3(t)=i (t)要求列写出系统的状态空间描述。
2、(15分)求出下面的输入输出描述的一个状态空间描述。
y (4)+4y (3)+3y (2)+7y (1)+3y=u (3)+ 2u (1)+ 3u3、(15分)计算下列线性系统的传递函数。
[]210X 13101X y -⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦=4、(10分)分析下列系统的能控性.0111X X u a b •⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦5、(10分)分析下列系统的能观性。
[]1110a X X y Xb •⎡⎤==-⎢⎥⎣⎦6、(15分)判断下列系统的原点平衡状态x e 是否大范围渐近稳定。
12221123x x x x x x==--7、(15分)已知系统的状态方程为221012000401X X u •--⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦试确定一个状态反馈阵K,使闭环极点配置为λ1*=—2、λ2*=-3、λ3*=—4.答案:1、(20分)如图所示RLC 网络,若e (t )为系统输入变量r (t ),电阻R 2两端的电压为输出量y (t ),选定状态变量为 x 1(t)=v 1(t),x 2(t )=v 2(t ),x 3(t)=i (t )要求列写出系统的状态空间描述。
2、(15分)求出下面的输入输出描述的一个状态空间描述。
列出向量表示形式解出解出解出r x x x L R x x x rx LR x x x xx x C R x x x C xC x r x R x L L LL⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--=-=+=+==++1321113211311132122222112211333113000xy x xLy (4)+4y (3)+3y (2)+7y (1)+3y=u (3)+ 2u (1)+ 3u[]得出了状态空间表达式列出向量表示形式,就求导,有选取状态变量令有令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=++=⎪⎪⎩⎪⎪⎨⎧+----=========⎩⎨⎧++==++++++++=++++++===43211025233375y ~y ~x y ~x y ~...y ~x y ~x y ~3y ~2y ~y ~3y ~7y ~3y ~4y ~u 3734p 1y ~3734p 32p y d/dtp 4214321(4)43(2)22(1)1(3)4(1)21(1)(3)(1)(2)(3)(4)2342343x x x x x x x y u x x x x x x x x y u p p p u p p p p(完整word 版)《线性系统理论》试卷及答案3、(15分)计算下列线性系统的传递函数.[]Xy u X 10103112X =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=[][][]计算得出传递函数⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-------=-=⎥⎦⎤⎢⎣⎡-------=⎥⎦⎤⎢⎣⎡--=--==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--==⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=----1021131)3)(2(110)()(21131)3)(2(13112)()()(1010311210103112X 1111s s s s B A Is C s G s s s s s s A Is BA Is C s G CB A Xy u X(完整word 版)《线性系统理论》试卷及答案4、(10分)分析下列系统的能控性。
《线性系统理论》课程练习题

《线性系统理论》课程练习题《线性系统理论》课程练习题姓名___________ 学号__________ 专业__________ 1. 根据下列单输入单输出线性定常系统的微分方程或传递函数描述:(1)(3)(2)(1)(2)(1)23532 y y y y u u u +++=++(2)332287 (s)524s sgs s s++=+++列写其状态空间表达式.2.关于矩阵指数函数的性质与计算:(1) 列举矩阵指数函数Ate的基本性质(至少5条);(2) 若已知22222222t t t tAtt t t te e e eee e e e----------= ?--,试计算矩阵A.3.给定一个连续时间线性定常系统,设其约当规范形为2100021002040200731000311030412 02010010011042011001x x uy x=+ ? ? ? ?- ? ?- ? ?-= ? ???试判断其能控性与能观性.4.关于连续时间定常系统的稳定性判据:(1) 描述下列连续时间定常系统的特征值判据与李亚谱诺夫判据;0,(0),0x A x x x t ==≥ (2) 判别下列自治系统平衡状态的渐近稳定性.1123x x -??= ?-??5. 关于极点配置定理与算法:(1) 简述单输入n 维连续时间定常系统的极点配置定理;(2) 描述单输入连续时间定常系统的状态反馈极点配置算法.。
线性系统理论(2013.7.26)
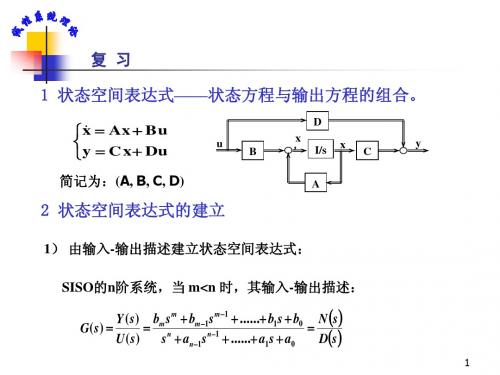
定义 Φ(t ) e At L1[(sI A)1 ] 为系统状态转移矩阵
解状态方程的关键——求状态转移矩阵 。
13
已知状态方程及初始条件:x1(0)=1,x2(0)=0,求解该齐次方程。
1 0 x x 1 1
解:
(sI A)-1
1 s 1 0 (s - 1)2 1 s - 1
系统结构图:
U1(s) G1/s 11(s) Y1(s)
0 G21(s)
1/s(s+2) G12(s)
U2(s)
1 y1 s y 2 0
1 s( s 2) u1 1 u2 s2
1/(s+2) G22(s)
y c1m c1,m 1 c12 c11 X
2) 由系统结构图建立状态空间表达式
4
例 系统如图,试建立起状态空间表达式。 u
—
k x3 1 x2 1 s1 s2 s
x1
yHale Waihona Puke 解:由结构图X 1 ( s) 1 X 2 ( s) s
x1 x2
X 2 ( s) 1 X 3 ( s) s 2
y x1
5
5 矩阵的特征方程、特征值
1)方阵A的特征方程与特征值 设A 为n×n的方阵,如有一未知量λ ,则: 0 a11 a12 ... a1n a11 a12 a 21 a22 ... a 2 n a21 a 22 I A ... ... ... ... ... ... an1 an 2 ... ann an1 a n 2 0
线性系统理论考点汇总

4
系统运动的稳定性
考点 4.1. 渐进稳定: 对特征多项式det(sI − A)运用劳斯判据。 特 征 多 项 式 系 数 都 大 于0是 渐 进 稳 定 的的 必 要 条 件。 BIBO稳定: 传递函数的极点均具有负实部。 考点 4.2. 大范围渐进稳定。 步骤:1、V (x)c。 ˙ (x)负定。或V ˙ (x)半负定,系统状态方程的解 2、V 只有平衡状态(导数不恒为0)。 3、||x|| → ∞,V (x) → ∞ 考点 4.3. P A + AT P = Q,Q = −I 。 若P对称正定,则大范围渐进稳定。
考点 3.1. 系统是否能控/能观。 若A无特定形式:采用秩判据。 若A为 约 旦 规 范 形: 不 同 特 征 值 的 约 旦 块 末 行(首 列)非 零。 相 同 特 征 值 的 约 旦 块 末 行(首 列)线 性 无 关。 考点 3.2. 判断连续时间线性线性时变系统是否完 全能控。 M0 (t) = b(t) 0 (t) M1 (t) = −AM0 (t) + dM dt 对于任意的t,rank M0 (t) M1 (t) 满秩,系统完 全能控。 考点 3.3. 求线性时不变系统的能控性指数和能观 性指数。 使能控性判别阵rank B AB . . . 满秩。 A的最小幂次为α。能 控性指 数u=α+1 C 使能观性判别阵rank CA 的满秩。 ... A的最小幂次为β 。能观性指数v=β +1 考点 3.4. 已知状态空间表达式, 求能控规范性及 其变换阵。 步骤:1、列出特征多项式det(sI − A) 1 0 0 2、变换阵P = A2 B AB B a2 1 0 a1 a2 1 −1 −1 3、A = P AP , B = P B , C = CP 能观规范形形式上对偶。 考点 3.5. 定出三阶龙伯格能控规范形。 取能控性判别阵线性无关的三列,构造变换阵P −1 。 由P的块末行导出变换阵S −1 。 基于状态变换x = S −1 x,导出变换后系统的系数矩 阵。 考点 3.6. 传递函数的能控规范形实现。 提 出 直 接 传 递 矩 阵 化 简 后 分 母 必 须 为严 真 首 一 多 项式。 考 点 3.7. G(s)的 行 列 维 数 为 能 观 块 维 数 和 能 控 块 维数。 考点 3.8. 传递函数矩阵的最小实现。 考点 3.9. 按能控性分解。 取 能 控 性 判别 阵 的 非 零 向Q量q1 ,另取 线 性 无 关 非 零向量q2 ,构成变换矩阵Q。 基于状态变换x = Q−1 x,导出变换后系统的系数矩 阵 考点 3.10. 定出能控能观子系统。
线性系统理论试题

x&1 x&2
=
−7
0
x&3 0
0 −5 0
0 x1 0
0
x2
+
4
−1 x3 7
0
0 5
u1 u2
解:由于对角规范型中 B 包含元素全为零的行,故系统不完全能控。
3.(约当规范形判据的应用)判断下面系统的能控性和能观性
1 1 0 0 0 1
x&
=
0 0
1 0
0 1
u = e(t),输出变量 y = uc。
解:
e
=
uc
+
R
⋅C
duc dt
, x& = − 1 x + 1 u RC RC
, y=x
2.(由输入输出描述建立状态空间描述)系统的传递函数如下,求系统的状态空 间描述
G(s)
=
s3
s2 + s + 5 + 6 s2 + 12 s
+
4
0 解:可控标准形, x& = 0
s −1 0 1 det(sI − A) = 0 s −1 0 = (s −1)2 (s − 2) = 0
0 0 s−2
则系统特征值为 λ1 = 1( λ1 的代数重数 σ1 = 2 ), λ2 = 2 ( λ2 的代数重数 σ 2 = 1 )。 (2)有重特征值,判断是否可以化为对角规范形
对于 2 重特征值 λ1 = 1,它所对应的特征矩阵
1 0
υ11
= 1,υ22
= 1 ,得到
2
个属于二重特征值 λ1
= 1的特征向量υ1
=
0
江苏大学线性系统理论(现代控制理论)考试必备--第3章

有限时刻 , t f , t0对 t时f 刻J 的非零t0初始状态
x(t0 ) , x可0 找到一个无约束的容许控制u(t),能在一个有限
的时间间隔内 t ,[t0使,t f某] 一状态轨线在 时刻为t f
,则
称此x(状t f )态在0 时刻为完全能控t的0 。
tf
定义2 如果存在一个无约束的容许控制u(t),能在一个有
【例1】 判别下1 0
x1 x2
0 1
u
解:首先确定出系统的能控判别阵U,并判别阵U的秩。
rankU rank[B
AB]=rank
0 1
1 0
2
显然,由于 rankU n 2 ,因此该系统完全能控。
第3章 线性控制系统的能控性与能观测性
江苏大学电气学院
状态变量是系统的一个内部变量,能否通过系统输入、 输出这一对外部变量来建立或确定系统的初始状态,这是 系统能控性、能观性问题所要研究的内容,也即研究系统 这个“黑箱”的内部状态能否由输入来加以影响和控制以 及能否由输出来加以反映。
第3章 线性控制系统的能控性与能观测性
江苏大学电气学院
如果系统内部的所有状态的运动能够由输入来加以影响 和控制,就称系统是完全能控的,否则系统就称为不完全 能控的或不能控的。同样,如果系统内部所有状态变量的 任意运动形式均可由输出完全地反映出来,则称系统为完 全能观的,否则就称系统为不完全能现的或不能观的。
第3章 线性控制系统的能控性与能观测性
江苏大学电气学院
对于线性定常系统的状态方程可写为:
x Ax Bu , x(0) x0 , t 0
记为{A,B},其中:x为n×1状态向量;u为p×1输入向量; A为n×n常值矩阵;B为n×p常值矩阵。 线性定常系统能控性的常用判据 1. 格拉姆矩阵判据 定理1 线性定常系统{A,B}完全能控的充分必要条件是,存 在一个有限时刻 tf > 0,使如下定义的格拉姆(Gram)矩阵
线性系统复习题—答案 - 副本

1、已知线性定常系统状态方程为:Ax x =.其中,⎥⎦⎤⎢⎣⎡-=2310A (1)采用线性变换化A 为对角型;32231det )det(2-+=⎥⎦⎤⎢⎣⎡+--=-s s s s A SI 特征值:1,321=-=λλ鉴于系统矩阵是能控规范型,且特征值互异,故取变化矩阵⎥⎦⎤⎢⎣⎡-=1311P ⎥⎦⎤⎢⎣⎡-==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=--13,41434141 11AP P A P 故有则(2)求出状态转移矩阵)(t Φ;⎥⎦⎤⎢⎣⎡+--=-231)(s sA SI⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-++-++--++--++=⎥⎦⎤⎢⎣⎡+-+=--=--141343143343141341143341312)1)(3(1)()()(1s s s s s s s s s s s s A SI A SI adj A SI (主对换,负变号)()[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+-+=-=Φ∴------t t tt t t tt e e e e e e e e A SI L t 4143434341414341)(333311 (3)初始状态T x ]10[)0(=时,写出系统齐次状态方程)(t x 。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-=Φ==--t t t t Ate e e e X t X e t X 41434141)0()()0()(332、已知系统方程为:[]x y u x x 110,121201112201=⋅⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⋅⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⋅(1)写出对偶系统的状态空间描述;;(2)写出原系统的能控矩阵c Q 、能观矩阵o Q ;(3)写出对偶系统的能控矩阵c Q 、能观矩阵o Q ;(4)运用对偶原理,判断原系统及其对偶系统的状态能控、能观测性。
原系统 :能控性: 能观测性:rank( )=3=n即原系统属于完全能控和完全能观系统。
对偶系统 : 根据对偶原理完全能控 完全能观测 完全能观测 完全能控推出,对偶系统属于完全能控和完全能观系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为非奇异,可进行解耦。
则有
(四)全维状态观测器算法: 1.计算对偶系数矩阵 A = AT , B = CT 2.设 K = [k11,k12,...k1n ] ,由α (s)=det(sI-A + BK)=sn + k11sn−1 + ... + k1n 及 α *(s)= ∏ (s-λi*)=α (s) 求得 K
5.计算变换矩阵
6.求Q=P-1 7. 所求增益矩阵 K = KQ
(二)多输入极点配置算法:
则系统的原点平衡状态是大范围渐近稳定。
李亚普诺夫判据:
线性定常系统的零平衡状态Xe =0为渐近稳定的充分必要条件,是
对任意给定的一个正定对称矩阵,如下形式的李பைடு நூலகம்普诺夫矩阵方程:
ATP+PA=-Q
有唯一正定对称矩阵解P。
第二章 线性系统的状态空间描述
(一):例1:下图所示简单电路,电路各组成元件的参数为已知,输入 变量取为电压源e(t),输出变量取为电阻R2的端电压Ur2.
(二):一个单输入—单输出线性定常系统,令y和u分别为其输出变量 和输入变量,则可用单变量的高阶微分方程来描述:
解:确定状态变量,最多2个线性无关的变量,取Uc和 iL 作为状态变量。
或传递函数 m<n(严真情)
m=n(真情)
特征多项式:a(s)= det(sI-A)= sn + an−1sn−1 + ... + a1s + a0
特征矩阵:(sI-A)
预解矩阵: (sI − A)−1
特征值定义为特征方程 det(sI-A)=0 的根
(三)状态方程的约当规范型:
由状态空间描述导出传递函数矩阵:G(s)=C(sI-A)-1B+D 系统状态空间描述在坐标变换下的特性:A=P-1AP,B=P-1B,C=CP,D=D
(一)能控秩判据: 约当规范形判矩:线性定常系统为完全能控的充分必要条件是: ⑴当矩阵A的特征值为两两相异时,对角线规范形
中, B 不包含元素全为零的行。 ⑵当矩阵A的特征值为 λ 1(σ 1重), λ 2(σ 2重)… λ l(σ l重) 且(σ 1+σ 2+…+σ l)=n时,约当规范形
其中
定出 都是行线性无关的,完全能控。
例:给定连续时间的定常系统: 易知,x1=0和x2=0为其唯一的平衡状态. 现取V(x)为状态的一个二次型
V(x)为正定。
V(x) 为负定。
此系统的原点平衡状态是大范围渐近稳定的。 结论3:定常系统,如果存在一个具有连续一阶导数的标量函数V(x), V(0)=0,并且对状态空间X中的一切非零点x满足如下的条件: (1)V(x)为正定。
第5章 线性反馈系统的时间域综合
(一)单输入极点配置算法: 1.判断(A,b)能控性。 2.计算A的特征多项式 3.计算由期望闭环特征值所决定的特征多项式
4.计算 k = [a0* − a0 ,...an*−1 − an−1]
解:先求出 期望的闭环系统矩阵应为:
利用矩阵A和上述得到的矩阵(A-BK),可得
3.取L= K T 4.求(A-LC)
5.全维观测器为: xˆ = ( A − LC)xˆ + Bu + Ly
第七章 线性系统的复频域理论
线性系统的复频域理论,是以传递函数矩阵作为系统描述。 现代复频域理论的特点是,采用传递函数的矩阵分式描述作为系统 数学模型,并以多项式矩阵方法作为系统分析和综合的基本工具。
(二)能观测性秩判据:
约当规范形判矩:
(三)能控规范形: 特征多项式为
构造如下的变换阵
可导出其能控规范形为: 其中:
(四)能观测规范形: 特征多项式为:
变换阵为:
其中:
(五)线性系统的结构分解: (按能控性的结构分解)
(按能观测性的结构分解)
系统结构按能观测性分解的规范形表达式
第4章 系统运动的稳定性
子系统的并联:
子系统的串联:
子系统的反馈联接:
第三章 线性系统的运动分析
(一)矩阵指数函数的算法: 1.特征值法: A的n个特征值为两两相异, P = [v1v2....vn ]为特征向量组成的矩阵
2.预解矩阵法:
(二)零初态响应: 系统的状态运动规律:
第4章 线性系统的能控性与能观测性
能控性:状态是否可由输入影响 线性时变系统,如果对取定初始时刻,t0∈ J的一个非零初始状态x0,
存在一个时刻t1∈ J,t1>t0,和一个无约束的容许控制u(t),t∈ [t0,t1],使状态由x0 转移到x(t1)=0,则称此是在时刻t0为能控的。 能观测性:状态是否可由输出反映。
线性时变系统,如果对取定初始时刻,t0∈ J的一个非零初始状态x0, 存在一个有限时刻t1∈ J,t1>t0,使对所有t ∈ [t0,t1],有y(t)=0,则称此x0在时 刻t0是不能观测的。
李亚普诺夫主稳定性定理: 对于定常系统,如果存在一个具有连续一阶导数的标量函数
V(x),V(0)=0,并且对状态空间X中的一切非零点x满足如下的条件: (1)V (x)为正定。 (2)V(x) = dV (x) / dt 为负定。 (3)当 x → ∞ 时,有V (x) → ∞ 则系统的原点平衡状态是大范围渐近稳定。
(三)可解耦条件和算法:
第1步:计算{di, i=1,2, …p}和
第2步: 若是,可解耦,进入下一步。若否,不能解耦。
第3步:计算E-1和
第4步:取
为:
导出积分型解耦系统 例:给定双输入—双输出的线性定常受控系统为:
解:系统能控且能观测。
②判断可解耦性 可解耦性判别矩阵: ③导出积分型解耦系统 定出
