(整理)材料力学中国建筑工业出版社第四章弯曲内力答案
工程力学(静力学与材料力学)第四版习题答案
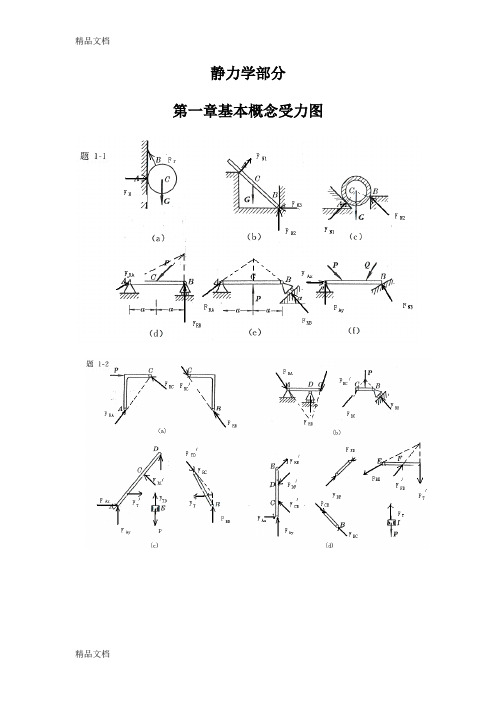
静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故：161.2R F N ==1(,)arccos 2944RY R R F F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑ 13sin 45sin 450RY F Y P P ==-=∑ 故：3R F KN == 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：0X =∑ sin 300AC AB F F -=0Y =∑ cos300AC F W -=0.577AB F W =（拉力） 1.155AC F W =（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑ sin 700AB F W -=1.064AB F W =（拉力）0.364AC F W =（压力）（c ） 由平衡方程有：0X =∑ cos 60cos300AC AB F F -=0Y =∑ sin 30sin 600AB AC F F W +-=0.5AB F W = (拉力)0.866AC F W =（压力）（d ） 由平衡方程有：0X =∑ sin 30sin 300AB AC F F -=0Y =∑ cos30cos300AB AC F F W +-=0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解：（a ）受力分析如图所示：由0x =∑cos 450RA F P -=15.8RA F KN ∴=由0Y =∑sin 450RA RB F F P +-=7.1RB F KN ∴=(b)解：受力分析如图所示：由x =∑cos 45cos 450RA RB F F P --=0Y =∑sin 45sin 450RA RB F F P -=联立上二式，得： 22.410RA RB F KNF KN ==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN = （压力） 5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由0x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解：受力分析如图所示，取左半部分为研究对象由0x =∑ cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CB RA F F '-= 联立后，解得： 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力） 列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q -=联立方程后解得：RD F =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得：RA F =2RB F Q P=+（3）取BCE 部分。
(整理)工程力学(静力学与材料力学)第四版习题答案
静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：161.2R F N==1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 3R F KN== 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)由x =∑cos 450RA F P -=15.8RA F KN∴=由Y =∑sin 450RA RB F F P +-=7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑cos 45cos 450RA RB F F P --=0Y =∑sin 45sin 450RA RB F F P -=联立上二式，得：22.410RA RB F KN F KN==三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解：受力分析如图所示，取左半部分为研究对象由x=∑cos45cos450RA CBP F F--= 0Y=∑sin45sin450CB RAF F'-=联立后，解得：0.707RAF P=0.707RBF P=由二力平衡定理0.707 RB CB CBF F F P'===2-8解：杆AB，AC均为二力杆，取A点平衡由x=∑cos60cos300AC ABF F W⋅--= 0Y=∑sin30sin600AB ACF F W+-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及 ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力） 列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q -=联立方程后解得：RD F =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得：RA F =2RB F Q P=+（3）取BCE 部分。
材料力学弯曲变形答案
第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法，适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设，可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设，可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力ζ与切应力η必相互垂直。
( ) 1.8 同一截面上各点的正应力ζ必定大小相等，方向相同。
( ) 1.9 同一截面上各点的切应力η必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形，则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零，则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中，AD 杆发生的变形为弯曲与压缩的组合变形。
( )1.16 题1.16图所示结构中，AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ，以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ，变形特征是 。
1.3 剪切的受力特征是 ，变形特征是 。
1.4 扭转的受力特征是 ，变形特征是 。
B题1.15图题1.16图1.5 弯曲的受力特征是 ，变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 ， 和 三个方面。
1.8 所谓 ，是指材料或构件抵抗破坏的能力。
所谓 ，是指构件抵抗变形的能力。
所谓 ，是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 ， ， 。
(完整word版)(整理)工程力学(静力学与材料力学)第四版习题答案
静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P Nθ==+=∑ 12sin 140RY F Y P P N θ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故：223R RX RY F F F KN=+= 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：0X =∑ sin300ACAB FF -= 0Y =∑ cos300ACFW -=0.577AB F W =（拉力） 1.155AC F W =（压力）（b ） 由平衡方程有：0X =∑ cos700ACAB FF -= 0Y =∑ sin700ABFW -=1.064AB F W =（拉力）0.364AC F W =（压力）（c ） 由平衡方程有：0X =∑ cos60cos300ACAB FF -= 0Y =∑ sin30sin600ABAC FF W +-=0.5AB F W = (拉力)0.866AC F W =（压力）（d ） 由平衡方程有：0X =∑ sin30sin300ABAC FF -=0Y =∑ cos30cos300ABAC FF W +-=0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解：（a ）受力分析如图所示：由x =∑22cos 45042RA F P -=+15.8RA F KN ∴=由Y =∑22sin 45042RA RB F F P +-=+7.1RB F KN ∴=(b)解：受力分析如图所示：由x =∑cos 45cos 45010RA RB F F P --= 0Y =∑sin 45sin 45010RA RB F F P +-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN = （压力） 5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑ cos45cos450RA CB P F F --=0Y =∑ sin 45sin 450CBRA F F '-=联立后，解得： 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑ cos60cos300AC AB F F W ⋅--=0Y =∑ sin30sin600ABAC FF W +-=联立上二式，解得： 7.32AB F KN =-（受压）27.3AC F KN =（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑ sin cos 0DB T W αα-=0DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑ sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑ cos sin sin 0BC DC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BC BC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CE F F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑ sin75sin750AB AD F F -=0Y =∑ cos75cos750ABAD FF P +-=联立后可得：2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑ cos5cos800AD ND F F '-=cos5cos80ND ADF F '=⋅由对称性及 AD AD F F '=cos5cos5222166.2cos80cos802cos75N ND AD PF F F KN'∴===⋅=2-12解：整体受力交于O点，列O点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得： 2.92RAF KN=1.33DCF KN=（压力）列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得： 1.67ACF KN=（拉力）1.0BCF KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '-= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q2RE F Q '=（2）取ABCE 部分，对C 点列平衡x =∑ cos450RE RA F F -=0Y =∑ sin 450RBRA FF P --=且 RE RE F F '=联立上面各式得： 22RA F Q =2RB F Q P =+（3）取BCE 部分。
材料力学第四版课后答案课件
02 材料力学基础知识
CHAPTER
详细描述
材料力学是工程学科中的一门基础学科，主要研究材料在力作用下的行为，包括材料的 变形、断裂、疲劳等。对于工程师来说，了解材料力学的基本原理和知识是必不可少的
，因为这些原理和知识被广泛应用于各种工程领域，如建筑、机械、航空航天等。
材料力学的基本假设与原理
总结词
材料力学基于一些基本假设和原理，如连续性、均匀 性、各向同性等，通过这些假设和原理来描述材料的 力学行为。
材料力学第四版课后答案课件
目录
CONTENTS
• 材料力学概述 • 材料力学基础知识 • 材料力学基本分析方法 • 材料力学中的能量方法 • 材料力学的应用实例 • 材料力学第四版课后答案解析
01 材料力学概述
CHAPTER
材料力学的定义与重要性
总结词
材料力学是研究材料在力作用下变形、破坏和恢复的学科，对于工程设计和安全至关重 要。
材料力学的发展历程
• 总结词：材料力学的发展经历了多个阶段，从最早的实验观察到现代的数值模拟和智能化技术应用。
• 详细描述：材料力学的发展历程可以追溯到古代，当时的人们通过实践经验积累了一些关于材料性质的认识。然而，真正的材料力学研究始于18世纪，当时的一些科学家开始系统地研 究材料的力学行为。随着科学技术的发展，材料力学的研究也不断深入，涉及到更广泛的应用领域。现代的材料力学研究已经与数学、物理、化学等多个学科交叉融合，形成了许多新 的研究方向和应用领域。同时，随着计算机技术和数值模拟方法的快速发展，现代的材料力学研究也更加依赖于计算机模拟和智能化技术。这些技术的发展为材料力学的研究提供了更 广阔的空间和更深入的认识。
详细描述
材料力学的研究基于一些基本假设和原理。连续性假 设认为材料可以被看作连续的介质，而不是由单个原 子或分子组成。均匀性假设则认为在材料的宏观尺度 上，材料的性质是均匀的，不会因位置的不同而有所 变化。是相同的，不会因方向的不同而有所变化。这些 基本假设和原理为材料力学的研究提供了基础。
《材料力学》第4章弯曲内力 课后答案
0 ； FS−C
= b F， a+b
M
− C
=
ba a+b
F
FS+C
=
−a a+b
F
，
M
+ C
=
ba a+b
F ； FSB
=
−A a+b
F
,MB
=
0
d解
图（d1）， ∑ Fy
=
0，F
=
1 2
ql
，
∑
M
A
= 0，M A
=
− 3 ql 2 8
仿题 a 截面法得
FSA
=
1 2
ql
，MA
=
−
3 8
ql
2
；
FS−C
FS (x) = −F
⎜⎛ 0 < x < l ⎟⎞
⎝
2⎠
M (x) = −Fx ⎜⎛0 ≤ x ≤ l ⎟⎞
⎝
2⎠
FS (x) = F
⎜⎛ l < x < l ⎟⎞
⎝2
⎠
45
M (x) =
FA x +
FB
⎜⎛ ⎝
x
−
l 2
⎟⎞ ⎠
，
FB
= 2F
M (x) = Fx − Fl ⎜⎛ l ≤ x ≤ l ⎟⎞
( ) 解
∑MB
=
0 ， FA
⋅l
+
ql 2
×
3l 4
− ql 2
=
0
， FA
=
5 ql 8
↑
( ) ∑ Fy
= 0 ， FB
材料力学-北京交通大学-4章答案
第四章弯曲内力4.4 设已知题4.4图(a)~(p)所示各梁的载荷 F 、q 、e M 和尺寸a ，(1)列出梁的剪力方程和弯矩方程；(2)作剪力图和弯矩图；(3)确定maxSF 及max M 。
解：(a)如题4.4图(a)所示。
剪立如题4.4图(a 1)所示坐标系。
(1)列剪力方程和弯矩方程。
应用题4.1(a)解法二提供的列剪力方程和弯矩方程的方法。
AC 段 ()()20S F x F x a =<<()()()20M x F x a x a =-<≤CB 段 ()()02S F x a x a =≤≤()()2M x Fa a x a =≤<(2)作剪力图、弯矩图，如题4.4图(a 2)所示。
(3)梁的最大剪力和弯矩为max2SF F =， max M Fa =(b) 如题4.4图(b)所示。
解法同4.4(a)。
剪立题4.4图(b 1)所示坐标系。
(1)列剪力方程和弯矩方程。
AC 段 ()()0S F x qx x a =-≤≤()()2102M x qx x a =-≤≤CB 段 ()()2S F x qa a x a =-≤<()()22a M x qa x a x a ⎛⎫=--≤< ⎪⎝⎭(2) 作剪力图、弯矩图，如题4.4图(b 2)所示。
(3) 梁的最大剪力和弯矩为maxSF qa =， 2max32Mqa =(c) 如题4.4图(c)所示。
解法同4.4(a)。
剪立题4.4图(c 1)所示坐标系。
(1)列剪力方程和弯矩方程。
CB 段 ()()023S F x a x a =≤≤()()223M x qa a x a =≤<AC 段 ()()()202S F x q a x x a =-<≤()()()2212022M x q a x qa x a =--+<≤(2) 作剪力图、弯矩图，如题4.4图(c 2)所示。
工程力学（静力学材料力学）第四版习题答案
静力学部分第一章基本概念受力图工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学汤2-1 解：由解析法，23co s 80R X F X P P Nθ==+=∑12sin 140R Y F YP P Nθ==+=∑故：161.2R F N==1(,)a rc c o s 2944R Y R RF F P F '∠==工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123co s 45co s 453R X F X P P P K N==++=∑13sin 45sin 450R Y F YP P ==-=∑故：3R F K N== 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：X =∑sin 300A C AB F F -=Y=∑co s 300A C F W -=0.577A B F W=（拉力）1.155A C F W=（压力）（b ） 由平衡方程有：X =∑co s 700A C AB F F -=Y=∑sin 700A B F W -=1.064A B F W=（拉力）0.364A CF W=（压力）（c ） 由平衡方程有：X =∑co s 60co s 300A C AB F F -=Y=∑sin 30sin 600A B A C F F W +-=0.5A B F W= (拉力)0.866A C F W=（压力）（d ） 由平衡方程有：X =∑sin 30sin 300A B A C F F -=Y=∑co s 30co s 300A B A C F F W +-=0.577A B F W= (拉力)0.577A C F W= (拉力)工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2-4 解：（a ）受力分析如图所示：由x =∑4c o s 450R A F P ⋅-=15.8R A F K N∴=由0Y =∑s in 450R A R B F F P ⋅+-=7.1R B F K N∴=(b)解：受力分析如图所示：由x =∑c o s 45c o s 450R A R B F F P ⋅--=Y=∑s in 45s in 450R A R B F F P ⋅+-=联立上二式，得：22.410R A R B F K N F K N==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5R A F K N= （压力）5R B F K N=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2A C F G =由x =∑c o s 0A C r F F α-=12c o s G G α∴=由0Y =∑s in 0A C N F F W α+-=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2s in N F W G W α∴=-⋅=-2-7解：受力分析如图所示，取左半部分为研究对象由x =∑co s 45co s 450R A C B P F F --=Y=∑sin 45sin 450C B R A F F '-=联立后，解得：0.707R A F P=0.707R B F P=由二力平衡定理0.707R B C B C B F F F P'===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑co s 60co s 300A C AB F F W ⋅--=Y=∑sin 30sin 600A B A C F F W +-=联立上二式，解得： 7.32A BF K N=-（受压）27.3A CF K N=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑s in c o s 0D B T W αα-=D B T W c tg α∴==（2）取B 点列平衡方程：由Y=∑s in c o s 0B D T T αα'-=230B D T T ctg W ctg K Nαα'∴===2-10解：取B 为研究对象：工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理由Y=∑s in 0B C F P α-=sin B C P F α∴=取C 为研究对象：由x =∑c o s s in s in 0B C D C C E F F F ααα'--=由0Y =∑s in c o s c o s 0B C D C C E F F F ααα--+=联立上二式，且有B C B CF F '= 解得：2c o s 12s in c o s C E P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象：由0Y =∑c o s 0N H C E F F α'-=C E C EF F '= 故有：22c o s 1c o s 2s in c o s 2s in N H P P F ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750A B A D F F -=Y=∑co s 75co s 750A B A D F F P +-=联立后可得： 2c o s 75A D AB P F F ==取D 点平衡，取如图坐标系：x =∑co s 5co s 800AD N D F F '-=c o s 5c o s 80N D A DF F '=⋅由对称性及A D A DF F '=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理c o s 5c o s 5222166.2c o s 80c o s 802c o s 75N N D A D P F F F K N'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑co s co s 300R A D C F F P α+-=Y=∑sin sin 300R A F P α-=联立上二式得：2.92R A F K N=1.33D C F K N=（压力）列C 点平衡x =∑405D C A C F F -⋅=Y=∑305B C A C F F +⋅=联立上二式得：1.67A C F K N=（拉力）1.0B CF K N=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑R D R E F F '=Y =∑R D F Q =联立方程后解得：R D F =2R E F Q'=（2）取ABCE 部分，对C 点列平衡x =∑co s 450R E R A F F -=Y=∑sin 450R B R A F F P --=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理且 R ER EF F '=联立上面各式得：R AF =2R B F Q P=+（3）取BCE 部分。
材料力学第五版课后习题答案
二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：；；（b）解：；；（c）解：；。
(d)解：。
2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
解：2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
解：2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。
如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。
解：2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。
如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。
解：（压）（压）2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。
解：横截面上的线应变相同因此2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。
试求C点的水平位移和铅垂位移。
解：（1）受力图（a），。
（2）变形协调图（b）因，故=（向下）（向下）为保证，点A移至，由图中几何关系知；第三章扭转3-1 一传动轴作匀速转动，转速，轴上装有五个轮子，主动轮Ⅱ输入的功率为60kW，从动轮，Ⅰ，Ⅲ，Ⅳ，Ⅴ依次输出18kW，12kW,22kW和8kW。
材料力学中国建筑工业出版社第四章弯曲内力答案
解：分别先后用1-1、2-2、3-3截面将杆切开，取右边部分研究，整个构件是平衡的，则脱离体也应该平衡。
受力如图(b)、(c)、(d)所示。
内力一定要表标成正方向，剪力绕脱离体内任一点有顺时转动趋势；而表弯矩时，可视杆内任点为固定，使下侧纤维受拉的变矩为正。
如图（b ）:如图（c ）:如图（d ）:4-1c 求指定截面的剪力和弯矩。
4-2cfh 写出下列各梁的剪力方程、弯矩方程，并作剪力图和弯矩图。
题4-2cV MkN ·题4-2f·题4-2h230q l 27(a )(b )M P 111110000()0O Y V qa V qa M qa M M F ⎧=-==⎧⎧⎪→→⎨⎨⎨-⋅∆===⎩⎩⎪⎩∑∑2(e )M (d )a(c )a333233000()0O Y V qa V qa M qa a M qa M F ⎧==-=⎧⎧⎪⎪→→⎨⎨⎨+⋅==-=⎪⎩⎩⎪⎩∑∑222220000()0O Y V qa V qa M M qa a M M F ⎧=-==⎧⎧⎪→→⎨⎨⎨--⋅===⎩⎩⎪⎩∑∑4-3dfgh 用微分关系作下列各梁的剪力图和弯矩图4kN ·m+题4-3d10.25MkN ·m)VkN)--1243.5-10.25-+322+-题4-3fM 图85Pl 83Pl 16Pl P/4-43.5--12MkN ·m)V kN)24++-26.257.57.5题4-3g5P/4+P=15kN+-24313.875313.875qaM 图V 图2qa +-2+-2+-qa2qa题4-3hMkN ·V kN)3.1254-6 起吊一根自重为q （N/m ）的等截面钢筋混凝土梁，问起吊点的合理位置x 应为多少（令梁在吊点处和中点处的最大正负弯矩的绝对值相等）MkN ·m)V kN)题4-6+2ql(l-2x)/4-q l /8qx/22qx/2qx ql/2-qx ql/2-qxqx--+--+q22qx/8qx/82题4-74-7天车梁上小车轮距为c ，起重量为P ，问小车走到什么位置时，梁弯矩最大？并求出最大弯矩。
材料力学习题册答案-弯曲内力
第四章梁的弯曲内力判断题1. 若两梁的跨度、承受载荷及支承相同，但材料和横截面面积不同，则两梁的剪力图和弯矩图不一定相同。
（X ）2. 最大弯矩必然发生在剪力为零的横截面上。
（X ）3. 若在结构对称的梁上作用有反对称载荷,（V ）4. 简支梁及其承载如图4-1所示，假想沿截面m-m将梁截分为二。
若取梁左段为研究对象，则该截面上的剪力和弯矩与q、M无关；若以梁右段为研究对象，则该截面上的剪力和弯矩与F无关。
（X ）则截面C上的剪力F SC=F ,弯矩M C =2Fa3. 梁段上作用有均布载荷时，剪力图是一条斜直线，而弯矩图是一条抛物线。
4. 当简支梁只受集中力和集中力偶作用时，则最大剪力必发生在集中力作用处c1. 梁在集中力偶作用的截面处，它的内力图为（ C ）cA Fs图有突变，M图无变化;B Fs图有突变，M图有转折;C M 图有突变，Fs图无变化;D M图有突变，Fs图有转折。
填空题2•图4-3所示外伸梁ABC，承受一可移动载荷 F ,若F、I均为已知，为减小梁的最大弯矩值，则外伸段的合理长度a= _J/3 ________ 。
图4-2 图4-3则该梁具有对称的剪力图和反对称的弯矩图。
1•图4-2所示为水平梁左段的受力图,选择题2. 梁在集中力作用的截面处，它的内力图为（B ）cA Fs有突变，M图光滑连续;B Fs有突变，M图有转折;C M图有突变，凡图光滑连续；D M图有突变，Fs图有转折。
3. 在图4-4所示四种情况中，截面上弯矩M为正，剪力Fs为负的是（B ）cf s (C)图4-44.梁在某一段内作用有向下的分布力时，则在该段内，M 图是一条(A )。
A 上凸曲线；B 下凸曲线；C 带有拐点的曲线 ；D 斜直线。
5•多跨静定梁的两种受载情况分别如图4-5 ( a )、( b )所示，以下结论中( A )是正确的。
力 F靠近铰链。
tli ＞弯矩图 图4-6F. FsI A)A C 6. 图4-5Fs 图和M 图完全相同Fs 图不同，M 图相同 两者的两者的 若梁的剪力图和弯矩图分别如图AB 段有均布载荷 AB；D4-6 ( a ) Fs 相同对图不同； Fs 图和M 图均不相同。
材料力学答案4弯曲内力
O
0.89
M (kN.m)
1.5m
2kN
1.5m
1.5m
1.11
(+)
(-)
FBY
＝1.11 kN
建立 系
FS－x
和
M－x
坐标
4．应用截面法确定控制 x 面上的剪力和弯矩值，并
将其标在 FS－ x和 M－x
坐标系中。
5．根据微分关系连图线
O (-)
(-)
x
0.335
1.335
1.67
18
Mb / l
CB FS x2 ＝M / l 0 x2 b
M x2 ＝ Mx2 / l 0 x2 b
3. 依方程画出剪力图和弯矩图。
10
内力、内力方程与内力图
简支梁受均布载荷作用
y
q
试写出剪力和弯矩方程，并画
A xC
B 出剪力图和弯矩图。
x
FAy
l
FBy 解：1．确定约束力
1kN.m
4．从A截面左侧开始画
A
C D B 弯矩图。
FAY
1.5m
1.5m
2kN
1.5m
FBY
Fs（ kN）
0.89 M（ kN.m）
1.11
（+）
（-）
0.330
（-） （-）
1.330
1.665
从A左到A右 从A右到C左 从C左到C右 从C右到D左 从D左到D右 从D右到B左 从B左到B右
20
材料力学课程
第4章 弯曲内力
第4章 弯曲内力
弯曲的概念和实例 内力、内力方程与内力图 平衡微分方程 平面刚架和曲杆的内力 习题分析
工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析
![工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析](https://img.taocdn.com/s3/m/4718b41a3c1ec5da50e2705a.png)
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。
解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。
解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。
解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
材料力学——4梁的弯曲内力
2. 梁：以弯曲变形为主的 构件通常称为梁。
3.对称弯曲：作用于杆件上的所有外力都在纵向对称面内时， 弯曲变形后的轴线也将是位于这个对称面内的一 条曲线。
F
q
M
轴线
弯曲后梁的轴线（挠曲线）
纵向对称面
工程中常见的梁，其横截面均有对称轴，例如：
应点处的载荷集度q。
F=qa
q
C
A
B
a
2a
dFS (x) q(x) dx
3
FS
qa
2
(+)
(-)
-qa
M
FS 图
(-)
由此式知：剪力图曲
x 线上一点处的斜率等于
E
1 qa2
(-)
1 qa 2
梁上相应点处的载荷集
8
度q。
(+)
x
qa2
M (x)
FS (x) dFS
FS (x)
M (x) dM
7KN
1m
P=2KN
F D
1m
B左 截面：
FSB左 Fy (左侧) FAy q 3 3KN
MB左
MB (左侧)
FAy
4
M0
q3
3 2
5KN.m
M0 8KN.m
q=2KN/m
P=2KN
A
E
C
F
B
D
1m 1m
3KN FAy
B右截面：
2m
FBy
7KN
1m
1m
与 B左截面相比，该截面的内力只增加了约束反力 FBy，故有：
材料力学第4章第5章
X1 A 1m 35kN
15
20
kN
20
10kN m
4m
2.5
FS x1 20kN
X2
B
0 x1 1
25kN
M x1 20x1
0 x1 1
FS x2 25 10x2
25
M
x2
25
0
x2
x2
10
4
x22 2
0 x2 4
20 31.25
kNm
例4-11 外伸梁AB承受荷载如图所示，作该梁旳内
AC段 ：
BC段 ：
3） 作剪力图与弯矩图
例4-7 如图所示外伸梁，F、a已知，试作其 、Mz图。
解：1） 求约束反力并验算
2) 分段列内力方程 CA段 ：
DB段 ：
AD段 ： 3）画出梁旳剪力图和弯矩图
例4-8 如图所示简支梁承受均布载荷作用，载荷集度为 q，梁 旳长度为l，试作梁旳 、Mz图解。： 1） 求约束反力并验算
叠加法作弯矩图
F
q
F
q
A
BA
＋
B
A
B
l
l
l
F
F+qL
1/2qL2+FL
FL
qL
1/2qL2
第五章 弯曲应力
§1 纯弯曲
F
F
a
a
A
B
F F
Fa
纯弯曲：梁受力弯曲
F
后，如其横截面上只有弯
矩而无剪力，这种弯曲称
为纯弯曲。
AC段： 剪力弯曲
CB段：
纯弯曲
pure bending
试验现象：
F
mn
(完整版)工程力学(静力学与材料力学)第四版习题答案
静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故： 22161.2R RX RY F F F N =+=1(,)arccos 2944RY R R F F P F '∠==o v v2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN ==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故： 223R RX RY F F F KN =+= 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：0X =∑ sin 300AC AB F F -=o0Y =∑ cos300AC F W -=o0.577AB F W =（拉力） 1.155AC F W =（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=o0Y =∑ sin 700AB F W -=o1.064AB F W =（拉力）0.364AC F W =（压力）（c ） 由平衡方程有：0X =∑ cos 60cos300AC AB F F -=o o0Y =∑ sin 30sin 600AB AC F F W +-=o o0.5AB F W = (拉力)0.866AC F W =（压力）（d ） 由平衡方程有：0X =∑ sin 30sin 300AB AC F F -=o o0Y =∑ cos30cos300AB AC F F W +-=o o0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解：（a ）受力分析如图所示：由0x =∑ 22cos 45042RA F P -=+o15.8RA F KN ∴= 由0Y =∑ 22sin 45042RA RB F F P +-=+o7.1RB F KN ∴=(b)解：受力分析如图所示：由 0x =∑ cos 45cos 45010RA RB F F P --=o o0Y =∑sin 45sin 45010RA RB F F P -=o o联立上二式，得： 22.410RA RB F KNF KN ==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN = （压力） 5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由0x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由0x =∑ cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CB RA F F '-=o o 联立后，解得： 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '=Q 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联立后可得： 2cos 75AD AB PF F ==o取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=⋅oo由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N NDADP F F F KN '∴===⋅=o o o o o2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联立上二式得：2.92RA F KN=1.33DC F KN=（压力） 列C 点平衡x =∑405DC AC F F -⋅=Y=∑305BC ACF F+⋅=联立上二式得： 1.67ACF KN=（拉力）1.0BCF KN=-（压力）2-13解：（1）取DEH部分，对H点列平衡x=∑05RD REF F'=Y=∑05RDF Q-=联立方程后解得：5RDF Q=2REF Q'=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。
材料力学题库讲解
材料力学重点难点、习题解析与实战训练目录第二章轴向拉伸与压缩 (1)第三章扭转 (9)第四章弯曲应力 (12)第五章梁弯曲时的位移 (29)第六章简单的超静定问题 (34)第七章应力状态和强度理论 (38)第八章组合变形及连接部分的计算 (48)第九章压杆稳定 (57)附录截面的几何性质 (62)第三章能量法 (67)总复习题 (71)模拟试题 (78)第二章轴向拉伸与压缩【重点难点】(1) 用截面法求内力时总是假设内力是正的。
画轴力图时正值画在x轴上方，负值画在x轴下方。
(2) 直杆斜截面应力中，α=0时有最大正应力，其值为σmax=σ＝N /A；α=45°时有最大切应力，其值为τmax=σ/2。
(3) 对于变截面杆或轴力为变数杆，利用虎克定律计算杆件轴向变形时，应分段计算变形，然后代数相加得全杆变形。
(4) 求解拉压超静定问题的关键是根据结构的变形协调条件列出变形几何方程。
在列变形几何方程时，注意所假设的杆件变形应是杆件可能发生的变形，假设的内力方向应与变形一致。
(5) 拉伸试验中出现的四个阶段，三个强度特征值σp、σs及σb是静载、常温下低碳钢的重要性质。
“冷作硬化”是低碳钢类塑性材料的一个重要现象。
(6) 低碳钢类塑性材料的抗拉压性质相同，铸铁类脆性材料的抗压强度远大于抗拉强度。
【习题解析】例2-1试画出图直杆的轴力图。
（图2-1）解：此直杆在A、B、C、D点承受轴向外力。
先求AB段轴力。
在段内任一截面1-1处将杆件截开，考察左段（图2-1b）。
在截面上设出正轴力N1。
由此段的平衡方程∑X＝0得N1－6＝0，N1＝＋6kNN1得正号说明原先假设拉力是正确的，同时也就表明轴力是正的。
AB段内任一截面的轴力都等于+6kN。
再求BC段轴力，在BC段任一截面2-2处将杆件截开，仍考察左段（图2-1c），在截面上仍设正的轴力N 2，由∑X ＝0得－6＋18＋N 2＝0N 2＝－12kNN 2得负号说明原先假设拉力是不对的（应为压力），同时又表明轴力N 2是负的。
工程力学材料力学第四完整版本习题答案解析
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。
解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。
解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。
解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：分别先后用1-1、2-2、3-3截面将杆切开，取右边部分研究，整个构件是平衡的，则脱离体也应该平衡。
受力如图(b)、(c)、(d)所示。
内力一定要表标成正方向，剪力绕脱离体内任一点有顺时转动趋势；而表弯矩时，可视杆内任点为固定，使下侧纤维受拉
的变矩为正。
如图（b ）:
如图（c ）:
如图（d ）:
4-1c 求指定截面的剪力和弯矩。
4-2cfh 写出下列各梁的剪力方程、弯矩方程，并作剪力图和弯矩图。
题4-2c
V M
kN ·
M
V 题4-2f
·
题4-2h
2
30q l 27
(a )(b )
M P 1111
10
000()0O Y V qa V qa M qa M M F ⎧=-==⎧⎧⎪→→⎨
⎨⎨-⋅∆===⎩⎩⎪⎩∑∑2(e )
M (d )
(c )
3332
33000()0O Y V qa V qa M qa a M qa M F ⎧==-=⎧⎧⎪⎪→→⎨⎨⎨+⋅==-=⎪⎩⎩⎪⎩
∑∑
2222
20
000()0O Y V qa V qa M M qa a M M F ⎧=-==⎧⎧⎪→→⎨
⎨⎨--⋅===⎩⎩⎪⎩∑∑
4-3dfgh 用微分关系作下列各梁的剪力图和弯矩图
4kN ·m
+
题4-3d
10.25
M
kN ·m)
V
kN)-
-
1243.5-1
0.25
-
+
3
2
2
+
-题4-3f
M 图
8
5Pl 8
3Pl 16
Pl P/4
-43.5
--12
M
kN ·m)
V kN)
24+
+
-
26.25
7.57.5
题4-3g
5P/4
+
P=15kN
+-24
313.875
3
13.875
qa
M 图
V 图2
qa +
-
2
+
-2qa
+-qa
2qa
题4-3h
M
kN ·V kN)
3.125
4-6 起吊一根自重为q （N/m ）的等截面钢筋混凝土梁，问起吊点的合理位置x 应为多少（令梁在吊点处和中点处的最大正负弯矩的绝对值相等）
M
kN ·m)
V kN)
题4-6
+
2
ql(l-2x)/4-q l /8
qx/2
2
qx/2qx ql/2-qx ql/2-qx
qx
-
-+
--
+
q
2
2
qx/8
qx/8
2
题4-7
4-7天车梁上小车轮距为c ，起重量为P ，问小车走到什么位置时，梁弯矩最大？并求出最大弯矩。
解：（1）求反力
⎪⎪⎩⎪⎪⎨⎧⋅+⋅=⋅-⋅-=→⎪⎪⎩⎪⎪⎨⎧
=+-⋅-⋅=--+-+⋅-→⎪⎩⎪⎨
⎧==∑∑c l P x l P Y c l P x l P P Y c x P x P l Y c x l P x l P l Y F m F m B A B A A B 220)(220)(2)(20)(0)(
由于
022
=+⨯-
=∑B A Y P
Y Y ，故所求反力无误。
（2）求最大弯矩
最大弯矩只可能出现在两轮子所到之处。
由对称性只算C 轮便可。
⎥
⎦⎤⎢⎣⎡-+-+-=--⋅⎪⎭⎫ ⎝⎛⋅+⋅=--⋅=⎥
⎦⎤⎢⎣⎡---+-=-+-=⋅⎪⎭⎫ ⎝⎛
⋅-⋅-=⋅=22)23()(2)()24()24()2(222222c cl x c l x l P c x l c l P x l
P
c x l Y M l c l c x l P lx x c x l P x c l P x l P P x Y M B D A C
令c l x c l x l P M D 4
3
20)232('
-=→=-+-=， 当4
2c l x -=
时，22max ,)2(4)24(0l c
l P l c l P M C -=⎥⎦⎤⎢⎣⎡---=
当4
3242c l c c l x +=+-=
时，22max ,)2(4)24(0l c
l P l c l P M D -=⎥⎦⎤⎢⎣⎡---=
4-8用叠加法绘制下列各梁的剪力图和弯矩图。
0.5P
0.5P
题4-8a
M
kN V 图(kN)
5
15
-+
V 图
+
+
-5
题4-8b
+
20
题4-8c
题4-10b
M V 图
8=
M
kN ·m)
V 图
4-10b 作图示连续梁的剪力图和弯矩图。