18年高考真题——理科数学(全国1卷)
2018高考真题全国1卷

2018年普通高等学校招生全国统一考试理科综合能力测试注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H 1 Li 7 C 12 N 14 O 16 Na 23 S 32 Cl 35.5 Ar 40 Fe 56 I 127 一、选择题:本题共13个小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.生物膜的结构与功能存在密切的联系。
下列有关叙述错误的是A.叶绿体的类囊体膜上存在催化ATP合成的酶B.溶酶体膜破裂后释放出的酶会造成细胞结构的破坏C.细胞的核膜是双层膜结构,核孔是物质进出细胞核的通道D.线粒体DNA位于线粒体外膜上,编码参与呼吸作用的酶2.生物体内的DNA常与蛋白质结合,以DNA—蛋白质复合物的形式存在。
下列相关叙述错误的是A.真核细胞染色体和染色质中都存在DNA—蛋白质复合物B.真核细胞的核中有DNA—蛋白质复合物,而原核细胞的拟核中没有C.若复合物中的某蛋白参与DNA复制,则该蛋白可能是DNA聚合酶D.若复合物中正在进行RNA的合成,则该复合物中含有RNA聚合酶3.下列有关植物根系吸收利用营养元素的叙述,错误的是A.在酸性土壤中,小麦可吸收利用土壤中的N2和NO-3B.农田适时松土有利于农作物根细胞对矿质元素的吸收C.土壤微生物降解植物秸秆产生的无机离子可被根系吸收D.给玉米施肥过多时,会因根系水分外流引起“烧苗”现象4.已知药物X对细胞增值有促进作用,药物D可抑制药物X的作用。
某同学将同一瓶小鼠皮肤细胞平均分为甲、乙、丙三组,分别置于培养液中培养,培养过程中进行不同的处理(其中甲组未加药物),每隔一段时间测定各组细胞数,结果如图所示。
2022年成人高考数学(理科)真题试卷及答案

2022年成人高等学校招生全国统一考试数学理科试题第Ⅰ卷 选择题共85分一.选择题(本大题共17小题;每小题5分,共85分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合{}12<-=x x M ,{}2|>=x x N ,则=N M ( ).A.{}|13x x <<B.{}|2x x >C.{}|23x x <<D.{}|12x x <<2.设函数2()1f x x =-,则(1)f x +=( ).A.221x x ++B.22x x +C.12+xD.2x 3.函数2lg(43)y x x =-+的定义域为( ).A.{}|31x x -<<B.{}|31x x x <->-或C.{}|13x x <<D.{}|13x x x <>或4.下列函数中,为奇函数的是( ).A.2cos y x =B.sin y x =C.2x y -=D.1y x =+ 5.下列函数中,为减函数的是( ).A.cos y x =B.3x y =C.13log y x=D.231y x =-6.设α是第三象限角,若cos 2α=-,则sin α=( ).A.2B.12C.2-D.12- 7.函数21(0)y x x =+≤的反函数是( ).A.1)y x =≥B.1)y x =≥C.1(0)y x =≥D.1(0)y x =-≥8.过点()2,2-,与直线350x y +-=平行的直线是( ).A.340x y +-=B.340x y ++=C.380x y ++=D.380x y -+=9.已知1sin cos 5αα-=,则sin 2α=( ). A.2425- B.725- C.725 D.242510.设甲:ABC ∆∽'''A B C ∆,乙:ABC ∆≌'''A B C ∆,则( ). A.甲是乙的必要条件但不是充分条件B.甲是乙的充分条件但不是必要条件C.甲是乙的充要条件D.甲既不是乙的充分条件,也不是乙的必要条件11.已知空间向量,,i j k 为两两垂直的单位向量.向量23a i j mk =++,若a =则m =( ).A.-2B.-1C.0D.1 12.()223i -=( ).A.136i -B.1312i -C.56i --D.512i --13.中心在坐标原点,对称轴为坐标轴,且一个顶点为()3,0,虚轴长为8的双曲线方程为( ). A.221916y x -= B.221916x y -= C.221649y x -= D.221964x y -= 14.521()x x+的展开式中,2x 的系数为( ). A.20 B.10 C.5 D.115.已知直线:3230l x y --=,圆22:(1)(1)4C y x ++=-,则C 上到l 的距离为1的点共有( ).A.1个B.2个C.3个D.4个16.袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则其中恰有一个红球的概率为( ). A.815 B.415 C.215 D.11517.给出下列两个命题:①如果一条直线与一个平面垂直,则该直线与该平面内的任何一条直线垂直②以二面角棱上的任意一点为端点,在二面角的两个面内分别作射线,则这两条射线所成的角为该二面角的平面角.则( )A.①②都为真命题B.①为真命题,②为假命题B.①为假命题,②为真命题 D.①②都为假命题第Ⅱ卷 非选择题共65分二.填空题(本大题共4小题;每小题4分,共16分)18.点()4,5关于直线y x =的对称点的坐标为 .19.长方体的长、宽、高分别为2,3,6,则该长方体的对角线长为 . 20.某校学生参加一次科技知识竞赛,抽取了其中8为同学的分数作为样本,数据如下:90,90,75,70,80,75,85,75则该样本的平均数为: .21.设函数()sin f x x x =,则'()f x = .三.解答题(本大题共4小题,共49分.解答应写出推理.演算步骤.)22.本小题满分12分.在ABC ∆中,120O B =,4BC =,ABC ∆的面积为求AC .23.本小题满分12分.已知,,a b c 成等差数列,,,1a b c +成等比数列,若6b =,求a 和c .24.本小题满分12分.已知直线l 的斜率为1,l 过抛物线21:2C x y =的焦点,且与C 交于,A B 两点. (1).求l 与C 的准线的交点坐标;(2).求AB .25.本小题满分13分.设函数()ln f x x x x =+.(1).求曲线()y f x =在点(1(1))f ,处的切线方程.(2).求()f x 的极值.2022年成人高等学校招生全国统一考试数学(理科)试题参考答案一.选择题1.C 2.B 3.D 4.B 5.C 6.D 7.A 8.A 9.D 10.A 11.C 12.D 13.B 14.C 15.D 16.A 17.B二.填空题18.【参考答案】()5,419.【参考答案】720.【参考答案】8021.【参考答案】sin cos x x x +三.解答题共4小题,12+12+12+13分,共49分.22.【参考答案】解:ABC ∆的面积为:01sin1202AB BC ⨯⨯⨯= 所以4AB =.因此2222cos12048o AC AB BC AB BC =+-⨯⨯⨯=.所以AC =23.【参考答案】 解:由已知得12(1)36a c a c +=⎧⎨+=⎩解得48a c =⎧⎨=⎩或93a c =⎧⎨=⎩ 24.【参考答案】解:(1).C 的焦点为1(0,)8,准线为18y =-. 由题意得l 的方程为81+=x y . 因此l 与C 的准线的交点坐标为11(,)48--. (2).由2182y x y x⎧=+⎪⎨⎪=⎩得21208x x --= 设11(,)A x y ,22(,)B x y ,则12121113,2244x x y y +=+=+=. 因此12114AB y y =++=. 25.【参考答案】解:(1).(1)1f =,'()2ln f x x =+,故'(1)2f = 所以曲线()y f x =在点(1(1))f ,处的切线方程为21y x =-.(2).令'()0f x =解得2x e -=.当20x e -<<时,'()0f x <;当2x e ->时,'()0f x >.故()f x 在区间2(0,)e -单调递减,在区间2(,)e -+∞单调递增. 因此()f x 在2x e -=处取得极小值()22e f e --=-.。
2018年高考真题理科数学(全国乙卷) 含解析

说明:非官方版正式答案,答案和解析有可能存在少量错误,仅供参考使用。
2018年新课标I 高考数学(理科)答案与解析1. {}{}243013A x x x x x =-+<=<<,{}32302B x x x x ⎧⎫=->=>⎨⎬⎩⎭. 故332AB x x ⎧⎫=<<⎨⎬⎩⎭.故选D .2. 由()11i x yi +=+可知:1x xi yi +=+,故1x x y =⎧⎨=⎩,解得:11x y =⎧⎨=⎩.所以,x yi + 故选B .3. 由等差数列性质可知:()1959599292722a a a S a +⨯====,故53a =, 而108a =,因此公差1051105a a d -==-∴100109098a a d =+=. 故选C .4. 如图所示,画出时间轴:8:208:107:507:408:308:007:30小明到达的时间会随机的落在图中线段AB 中,而当他的到达时间落在线段AC 或DB 时,才能保证他等车的时间不超过10分钟 根据几何概型,所求概率10101402P +==. 故选B .5. 222213x y m n m n-=+-表示双曲线,则()()2230m n m n +->∴223m n m -<<由双曲线性质知:()()222234c m n m n m =++-=,其中c 是半焦距 ∴焦距2224c m =⋅=,解得1m = ∴13n -<< 故选A .6. 原立体图如图所示:是一个球被切掉左上角的18后的三视图表面积是78的球面面积和三个扇形面积之和2271=42+32=1784S πππ⨯⨯⨯⨯ 故选A .7. ()22288 2.80f e =->->,排除A()22288 2.71f e =-<-<,排除B0x >时,()22x f x x e =-()4x f x x e '=-,当10,4x ⎛⎫∈ ⎪⎝⎭时,()01404f x e '<⨯-=因此()f x 在10,4⎛⎫⎪⎝⎭单调递减,排除C故选D .8. 对A : 由于01c <<,∴函数c y x =在R 上单调递增,因此1c c a b a b >>⇔>,A 错误对B : 由于110c -<-<,∴函数1c y x -=在()1,+∞上单调递减,∴111c c c c a b a b ba ab -->>⇔<⇔<,B 错误对C : 要比较log b a c 和log a b c ,只需比较ln ln a c b 和ln ln b c a ,只需比较ln ln c b b 和ln ln ca a,只需ln b b 和ln a a构造函数()()ln 1f x x x x =>,则()'ln 110f x x =+>>,()f x 在()1,+∞上单调递增,因此()()110ln ln 0ln ln f a f b a a b b a a b b>>⇔>>⇔<又由01c <<得ln 0c <,∴ln ln log log ln ln a b c cb c a c a a b b<⇔<,C 正确 对D : 要比较log a c 和log b c ,只需比较ln ln c a 和ln ln cb而函数ln y x =在()1,+∞上单调递增,故111ln ln 0ln ln a b a b a b>>⇔>>⇔<又由01c <<得ln 0c <,∴ln ln log log ln ln a b c cc c a b>⇔>,D 错误故选C .9.输出32x =,6y =,满足4y x = 故选C .10. 以开口向右的抛物线为例来解答,其他开口同理设抛物线为22y px =()0p >,设圆的方程为222x y r +=,题目条件翻译如图:设(0A x,2p D ⎛- ⎝,点(0A x 在抛物线22ypx =上,∴082px =……①点2p D ⎛- ⎝在圆222x y r +=上,∴2252p r ⎛⎫+= ⎪⎝⎭……②点(0A x 在圆222x y r +=上,∴2208x r +=……③ 联立①②③解得:4p =,焦点到准线的距离为4p =.故选B .11. 如图所示:111∵11CB D α∥平面,∴若设平面11CB D 平面1ABCD m =,则1m m ∥又∵平面ABCD ∥平面1111A B C D ,结合平面11B D C 平面111111A B C D B D =∴111B D m ∥,故11B D m ∥ 同理可得:1CD n ∥故m 、n 的所成角的大小与11B D 、1CD 所成角的大小相等,即11CD B ∠的大小. 而1111BC BD CD ==(均为面对交线),因此113CD B π∠=,即11sin CD B ∠=. 故选A .F12. 由题意知:12π+π 4ππ+π+42k k ωϕωϕ⎧-=⎪⎪⎨⎪=⎪⎩ 则21k ω=+,其中k ∈Z()f x 在π5π,1836⎛⎫⎪⎝⎭单调,5π,123618122T ππω∴-=≤≤接下来用排除法若π11,4ωϕ==-,此时π()sin 114f x x ⎛⎫=- ⎪⎝⎭,()f x 在π3π,1844⎛⎫ ⎪⎝⎭递增,在3π5π,4436⎛⎫⎪⎝⎭递减,不满足()f x 在π5π,1836⎛⎫⎪⎝⎭单调若π9,4ωϕ==,此时π()sin 94f x x ⎛⎫=+ ⎪⎝⎭,满足()f x 在π5π,1836⎛⎫⎪⎝⎭单调递减故选B .13. 由已知得:()1,3a b m +=+∴()22222222213112a b a b m m +=+⇔++=+++,解得2m =-.14. 设展开式的第1k +项为1k T +,{}0,1,2,3,4,5k ∈∴()5552155C 2C 2k kkkkkk T x x---+==.当532k -=时,4k =,即454543255C 210T x x --== 故答案为10.15.由于{}n a 是等比数列,设11n n a a q -=,其中1a 是首项,q 是公比.∴2131132411101055a a a a q a a a q a q ⎧+=+=⎧⎪⇔⎨⎨+=+=⎪⎩⎩,解得:1812a q =⎧⎪⎨=⎪⎩. 故412n n a -⎛⎫= ⎪⎝⎭,∴()()()()21174932 (472)22412111...222n n n n n a a a ⎡⎤⎛⎫-+-++----⎢⎥ ⎪⎝⎭⎢⎥⎣⎦⎛⎫⎛⎫⎛⎫⋅⋅⋅=== ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭当3n =或4时,21749224n ⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦取到最小值6-,此时2174922412n ⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦⎛⎫⎪⎝⎭取到最大值62.所以12...n a a a ⋅⋅⋅的最大值为64.16. 设生产A 产品x 件,B 产品y 件,根据所耗费的材料要求、工时要求等其他限制条件,构造线性规则约束为 **1.50.51500.3905360000x y x y x y x y x N y N⎧+⎪+⎪⎪+⎪⎪⎨⎪⎪⎪∈⎪∈⎪⎩≤≤≤≥≥ 目标函数2100900z x y =+作出可行域为图中的四边形,包括边界,顶点为(60,100)(0,200)(0,0)(90,0)在(60,100)处取得最大值,210060900100216000z =⨯+⨯=17.⑴ ()2cos cos cos C a B b A c +=由正弦定理得:()2cos sin cos sin cos sin C A B B A C ⋅+⋅=()2cos sin sin C A B C ⋅+=∵πA B C ++=,()0πA B C ∈、、, ∴()sin sin 0A B C +=>∴2cos 1C =,1cos 2C = ∵()0πC ∈, ∴π3C =⑵ 由余弦定理得:2222cos c a b ab C =+-⋅221722a b ab =+-⋅()237a b ab +-=1sin 2S ab C =⋅∴6ab = ∴()2187a b +-=5a b +=∴ABC △周长为5a b c ++=18.⑴ ∵ABEF 为正方形∴AF EF ⊥ ∵90AFD ∠=︒ ∴AF DF ⊥ ∵=DFEF F∴AF ⊥面EFDCAF ⊥面ABEF∴平面ABEF ⊥平面EFDC⑵ 由⑴知60DFE CEF ∠=∠=︒∵AB EF ∥AB ⊄平面EFDC EF ⊂平面EFDC∴AB ∥平面ABCDAB ⊂平面ABCD∵面ABCD 面EFDC CD = ∴AB CD ∥ ∴CD EF ∥∴四边形EFDC 为等腰梯形以E 为原点,如图建立坐标系,设FD a =()()000020E B a ,,,,()02202a C A a a ⎛⎫⎪ ⎪⎝⎭,,,()020EB a =,,,22a BC a ⎛⎫=- ⎪ ⎪⎝⎭,,()200AB a =-,, 设面BEC 法向量为()m x y z =,,. 00m EB m BC ⎧⋅=⎪⎨⋅=⎪⎩,即111120202a y a x ay z ⋅=⎧⎪⎨⋅-+⋅=⎪⎩11101x y z ===-,()301m =-,,设面ABC 法向量为()222n x y z =,, =00n BC n AB ⎧⋅⎪⎨⋅=⎪⎩.即222220220a x ay ax ⎧-=⎪⎨⎪=⎩ 22204x y z ===,()034n =,设二面角E BC A --的大小为θ. cos 3m n m nθ⋅===+⋅ ∴二面角E BC A --的余弦值为19.⑴ 每台机器更换的易损零件数为8,9,10,11记事件i A 为第一台机器3年内换掉7i +个零件()1,2,3,4i = 记事件i B 为第二台机器3年内换掉7i +个零件()1,2,3,4i =由题知()()()()()()1341340.2P A P A P A P B P B P B ======,()()220.4P A P B == 设2台机器共需更换的易损零件数的随机变量为X ,则X 的可能的取值为16,17,18,19,20,21,22()()()11160.20.20.04P X P A P B ===⨯=()()()()()1221170.20.40.40.20.16P X P A P B P A P B ==+=⨯+⨯=()()()()()()()132231180.20.20.20.20.40.40.24P X P A P B P A P B P A P B ==++=⨯+⨯+⨯=()()()()()()()()()14233241190.20.20.20.20.40.2P X P A P B P A P B P A P B P A P B ==+++=⨯+⨯+⨯0.20.40.24+⨯=()()()()()()()243342200.40.20.20.40.20.20.2P X P A P B P A P B P A P B ==++=⨯+⨯+⨯=()()()()()3443210.20.20.20.20.08P x P A P B P A P B ==+=⨯+⨯= ()()()44220.20.20.04P x P A P B ===⨯=⑵ 要令()0.5P x n ≤≥,0.040.160.240.5++<,0.040.160.240.240.5+++≥ 则n 的最小值为19⑶ 购买零件所需费用含两部分,一部分为购买机器时购买零件的费用,另一部分为备件不足时额外购买的费用当19n =时,费用的期望为192005000.210000.0815000.044040⨯+⨯+⨯+⨯= 当20n =时,费用的期望为202005000.0810000.044080⨯+⨯+⨯= 所以应选用19n =BE AC ∥,则C EBD =∠∠,由,AC AD D C ==则∠∠,EBD D ∴=∠∠,则EB ED = 4AE EB AE ED AD ∴+=+==所以E 的轨迹为一个椭圆,方程为22143x y +=,(0y ≠);⑵ 221:143x y C +=;设:1l x my =+,因为PQ l ⊥,设():1PQ y m x =--,联立1l C 与椭圆 221143x my x y =+⎧⎪⎨+=⎪⎩得()2234690m y my ++-=;()2212134m m +=+;圆心A 到PQ 距离d ==所以||PQ =,()2212111||||2234MPNQm S MN PQ m +⎡∴=⋅=⋅==⎣+21.⑴ 由已知得:()()()()()'12112x x f x x e a x x e a =-+-=-+① 若0a =,那么()()0202x f x x e x =⇔-=⇔=,()f x 只有唯一的零点2x =,不合题意;② 若0a >,那么20x x e a e +>>,所以当1x >时,()'0f x >,()f x 单调递增 当1x <时,()'0f x <,()f x 单调递减 即:故()f x 在()1,+∞上至多一个零点,在(),1-∞上至多一个零点 由于()20f a =>,()10f e =-<,则()()210f f <, 根据零点存在性定理,()f x 在()1,2上有且仅有一个零点. 而当1x <时,x e e <,210x -<-<,故()()()()()()()222212111x f x x e a x e x a x a x e x e =-+->-+-=-+--则()0f x =的两根11t =,21t =+, 12t t <,因为0a >,故当1x t <或2x t >时,()()2110a x e x e -+-->因此,当1x <且1x t <时,()0f x >又()10f e =-<,根据零点存在性定理,()f x 在(),1-∞有且只有一个零点. 此时,()f x 在R 上有且只有两个零点,满足题意.③ 若02ea -<<,则()ln 2ln 1a e -<=,当()ln 2x a <-时,()1ln 210x a -<--<,()ln 2220a x e a e a -+<+=,即()()()'120x f x x e a =-+>,()f x 单调递增; 当()ln 21a x -<<时,10x -<,()ln 2220a x e a ea -+>+=,即()()()'120x f x x e a =-+<,()f x 单调递减;当1x >时,10x ->,()ln 2220a x e a e a -+>+=,即()'0f x >,()f x 单调递增.即:而极大值()()()(){}22ln 22ln 22ln 21ln 2210f a a a a a a a -=---+--=--+<⎡⎤⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎣⎦故当1x ≤时,()f x 在()ln 2x a =-处取到最大值()ln 2f a -⎡⎤⎣⎦,那么()()l n 20fx f a -<⎡⎤⎣⎦≤恒成立,即()0f x =无解 而当1x >时,()f x 单调递增,至多一个零点 此时()f x 在R 上至多一个零点,不合题意.④ 若2ea =-,那么()ln 21a -=当()1ln 2x a <=-时,10x -<,()ln 2220a x e a ea -+<+=,即()'0f x >,()f x 单调递增当()1ln 2x a >=-时,10x ->,()ln 2220a x e a ea -+>+=,即()'0f x >,()f x 单调递增又()f x 在1x =处有意义,故()f x 在R 上单调递增,此时至多一个零点,不合题意.⑤ 若2ea <-,则()ln 21a ->当1x <时,10x -<,()ln 212220a x e a e a ea -+<+<+=,即()'0f x >,()f x 单调递增当()1ln 2x a <<-时,10x ->,()ln 2220a x e a ea -+<+=,即()'0f x <,()f x 单调递减当()ln 2x a >-时,()1ln 210x a ->-->,()ln 2220a x e a ea -+>+=,即()'0f x >,()f x 单调递增 即:故当()ln 2x a -≤时,()f x 在1x =处取到最大值()1f e =-,那么()0f x e -<≤恒成立,即()0f x =无解当()ln 2x a >-时,()f x 单调递增,至多一个零点 此时()f x 在R 上至多一个零点,不合题意.综上所述,当且仅当0a >时符合题意,即a 的取值范围为()0,+∞.⑵ 由已知得:()()120f x f x ==,不难发现11x ≠,21x ≠,故可整理得:()()()()121222122211x x x e x e a x x ---==--设()()()221xx e g x x -=-,则()()12g x g x = 那么()()()2321'1x x g x e x -+=-,当1x <时,()'0g x <,()g x 单调递减;当1x >时,()'0g x >,()g x 单调递增. 设0m >,构造代数式:()()111222*********m m m m m m m m g m g m e e e e m m m m +-----+-⎛⎫+--=-=+ ⎪+⎝⎭设()2111mm h m e m -=++,0m >则()()2222'01m m h m e m =>+,故()h m 单调递增,有()()00h m h >=.因此,对于任意的0m >,()()11g m g m +>-.由()()12g x g x =可知1x 、2x 不可能在()g x 的同一个单调区间上,不妨设12x x <,则必有121x x <<令110m x =->,则有()()()()()1111211112g x g x g x g x g x +->--⇔->=⎡⎤⎡⎤⎣⎦⎣⎦而121x ->,21x >,()g x 在()1,+∞上单调递增,因此:()()121222g x g x x x ->⇔-> 整理得:122x x +<.22.⑴ 设圆的半径为r ,作OK AB ⊥于K∵120OA OB AOB =∠=︒,∴30sin302OAOK AB A OK OA r ⊥∠=︒=⋅︒==,, ∴AB 与O ⊙相切 ⑵ 方法一:假设CD 与AB 不平行CD 与AB 交于F2FK FC FD =⋅① ∵A B C D 、、、四点共圆∴()()FC FD FA FB FK AK FK BK ⋅=⋅=-+ ∵AK BK =∴()()22FC FD FK AK FK AK FK AK ⋅=-+=-② 由①②可知矛盾 ∴AB CD ∥方法二:因为,,,A B C D 四点共圆,不妨设圆心为T ,因为,OA OB TA TB ==,所以,O T 为AB 的中垂线上,同理,OC OD TC TD ==,所以OT CD 为的中垂线,所以AB CD ∥.23.⑴ cos 1sin x a ty a t =⎧⎨=+⎩(t 均为参数)∴()2221x y a +-= ①∴1C 为以()01,为圆心,a 为半径的圆.方程为222210x y y a +-+-= ∵222sin x y y ρρθ+==, ∴222sin 10a ρρθ-+-= 即为1C 的极坐标方程⑵ 24cos C ρθ=:两边同乘ρ得22224cos cos x y x ρρθρρθ==+=,224x y x ∴+= 即()2224x y -+= ②3C :化为普通方程为2y x =由题意:1C 和2C 的公共方程所在直线即为3C ①—②得:24210x y a -+-=,即为3C ∴210a -= ∴1a =24.⑴ 如图所示:⑵ ()4133212342x x f x x x x x ⎧⎪--⎪⎪=--<<⎨⎪⎪-⎪⎩,≤,,≥()1f x >当1x -≤,41x ->,解得5x >或3x <1x -∴≤当312x -<<,321x ->,解得1x >或13x < 113x -<<∴或312x <<当32x ≥,41x ->,解得5x >或3x <332x <∴≤或5x > 综上,13x <或13x <<或5x >()1f x >∴,解集为()()11353⎛⎫-∞+∞ ⎪⎝⎭,,,。
高考全国甲卷:《理科数学》2018年考试真题与答案解析

高考精品文档高考全国甲卷理科数学·2018年考试真题与答案解析同卷地区贵州省、四川省、云南省西藏自治区、广西自治区高考全国甲卷:《理科数学》2018年考试真题与答案解析一、选择题本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则( )A .B .C .D .答案:C2.( )A .B .C .D .答案:D3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( ){}|10A x x =-≥{}012B =,,A B = {}0{}1{}12,{}012,,()()1i 2i +-=3i--3i-+3i-3i+A .B .C .D .答案:A4.若,则()A.B .C .D .答案:B 1sin 3α=cos 2α=897979-89-5.的展开式中的系数为( )A .10B .20C .40D .80答案:C6.直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是( )A .B .C .D .答案:A7.函数的图像大致为( )A.B.522x x ⎛⎫+ ⎪⎝⎭4x 20x y ++=x y A B P ()2222x y -+=ABP △[]26,[]48,⎡⎣422y x x =-++C.D.答案:D8.某群体中的每位成员使用移动支付的概率都为,各成员的支付方式相互独立,设为该群体的10位成员中使用移动支付的人数,,,则( )。
A .0.7B .0.6C .0.4D .0.3答案:B9.的内角的对边分别为,,,若的面积为,则( )A .B .C .D .p X 2.4DX =()()46P X P X =<=p =ABC △A B C ,,a b c ABC △2224a b c +-C =π2π3π4π610.设是同一个半径为4的球的球面上四点,为等边三角形且其面积为则三棱锥体积的最大值为A .B .C .D .答案:B11.设是双曲线()的左,右焦点,是坐标原点.过作的一条渐近线的垂线,垂足为.若的离心率为AB .2CD答案:C12.设,,则A .B .C .D .A B C D ,,,ABC △D ABC -12F F ,22221x y C a b-=:00a b >>,O 2F C P 1PF =C 0.2log 0.3a =2log 0.3b =0a b ab +<<0ab a b <+<0a b ab+<<0ab a b<<+二、填空题本题共4小题,每小题5分,共20分。
2018年高考全国卷2理科数学真题(附含答案解析)
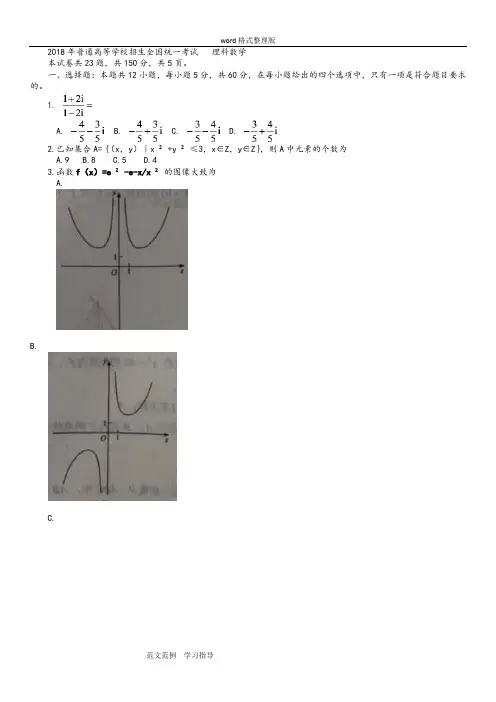
2018年普通高等学校招生全国统一考试理科数学本试卷共23题,共150分,共5页。
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.A. B. C. D.2.已知集合A={(x,y)|x ²+y ²≤3,x∈Z,y∈Z},则A中元素的个数为A.9B.8C.5D.43.函数f(x)=e ²-e-x/x ²的图像大致为A.B.C.D.4.已知向量a,b满足∣a∣=1,a·b=-1,则a·(2a-b)=A.4B.3C.2D.05.双曲线x ²/a ²-y ²/b ²=1(a﹥0,b﹥0)的离心率为,则其渐进线方程为A.y=±xB.y=±xC.y=±D.y=±6.在中,cos=,BC=1,AC=5,则AB=A.4B.C.D.27.为计算s=1-+-+…+-,设计了右侧的程序框图,则在空白框中应填入A.i=i+1B.i=i+2C.i=i+3D.i=i+48.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。
哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23,在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是A. B. C. D.9.在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=则异面直线AD1与DB1所成角的余弦值为A. B.10.若f(x)=cosx-sinx在[-a,a]是减函数,则a的最大值是A. B. C. D. π11.已知f(x)是定义域为(-∞,+∞)的奇函数,满足f(1-x)=f(1+x)。
若f(1)=2,则f(1)+ f(2)+ f(3)+…+f(50)=A.-50B.0C.2D.5012.已知F1,F2是椭圆C: =1(a>b>0)的左、右焦点,A是C的左顶点,点P在过A且斜率为的直线上,△PF1F2为等腰三角形,∠F1F2P=120°,则C的离心率为A..B.C.D.二、填空题:本题共4小题,每小题5分,共20分。
“学科核心素养”在“高考真题”的体现

“学科核心素养”在“高考真题”的体现作者:叶剑平来源:《中学课程辅导·教师教育》 2018年第10期引言事物发展总是有渊源,将来高考的前身就是现行的“全国卷”和“试点卷”。
下面就“全国卷高考题”来看“核心素养”的体现。
从历史高考卷的命制过程的立意看,大致可分“知识立意”、“知识技巧立意”、“能力立意”这三个阶段。
试题包括立意,情境和设问三个方面。
其中以能力立意命题,就是先确立试题在能力方面的考查目标,然后根据能力考查的要求,选择适宜的考查内容,设计恰当的设问方式。
以能力立意命题,不仅是命题方式的变化,更是命题理念和原则的变化。
下面就《数学课程标准》的核心素养中的直观想象、数学建模的说明与近年全国卷试题来比较,尝试说明两者的关联。
一、首先,《数学课程标准》对于直观想象是这样说明的:是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程,主要包括:借助空间认识事物的数量关系,形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系;构建数学问题的直观模型探索解决问题的思路。
2018年高考对此是这样考察的:(2018年全国理科数学1卷第12题)已知正方体的棱长为1,每条棱所在的直线与平面α所成的角都相等,则α与此正方体所得截面面积的最大值为()本题情境来自于新课标《案例11.正方体截面的探究》,直接考查了学生的直观想象能力和数学探究的能力。
学生要先从“每条棱所在的直线与平面α所成的角都相等”这一条件中直观想象到这样一个平面是要与体对角线垂直的。
用运动和变化的观点发现:此平面与正方体所得截面为“三角形→六边形→三角形”这一变化过程,再注意到截面经过六条棱的中点时截面面积最大。
最后运算求出面积的最大值!整个问题的解决过程,直观想象能力起到关键作用。
类似题还有本卷的第7题、第18题;II卷的16题;III卷的第3题,第10题!二、再来看《数学课程标准》对于数学建模是这样说明:是对现实进行数学抽象,用数学语言表达问题,用数学知识与方法构建模型解决问题的过程,主要包括:在实际情境中从数学的视角发现问题、提出问题、分析问题,构建模型,求解结论,验证结果并改进模型,最终解决实际问题。
历年高考数学真题(全国卷整理版)
参考公式:如果事件A 、B 互斥,则球的外表积公式如果事件A 、B 相互独立,则其中R 表示球的半径()()()P A B P A P B =球的体积公式如果事件A 在一次试验中发生的概率是p ,则334V R π=n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径普通高等学校招生全国统一考试一、选择题1、 复数131ii-++= A 2+I B 2-I C 1+2i D 1- 2i 2、集合A ={1.3. m },B ={1,m} ,AB =A, 则m=A 0或3B 0或3C 1或3D 1或3 3 椭圆的中心在原点,焦距为4 一条准线为*=-4 ,则该椭圆的方程为A 216x +212y =1B 212x +28y =1C 28x +24y =1D 212x +24y =1 4 正四棱柱ABCD- A 1B 1C 1D 1中,AB=2,CC 1=22 E 为CC 1的中点,则直线AC 1与平面BED 的距离为A 2B 3C 2D 1〔5〕等差数列{a n }的前n 项和为S n ,a 5=5,S 5=15,则数列的前100项和为(A)100101 (B) 99101 (C) 99100 (D) 101100〔6〕△ABC 中,AB 边的高为CD ,假设a ·b=0,|a|=1,|b|=2,则(A)〔B 〕 (C) (D)〔7〕α为第二象限角,sin α+sin β=33,则cos2α=(A)5-3〔B 〕5-9 (C)59 (D)53〔8〕F1、F2为双曲线C:*²-y²=2的左、右焦点,点P在C上,|PF1|=|2PF2|,则cos∠F1PF2=(A)14〔B〕35 (C)34 (D)45〔9〕*=lnπ,y=log52,12z=e,则(A)*<y<z 〔B〕z<*<y (C)z<y<* (D)y<z<*(10) 函数y=*²-3*+c的图像与*恰有两个公共点,则c=〔A〕-2或2 〔B〕-9或3 〔C〕-1或1 〔D〕-3或1〔11〕将字母a,a,b,b,c,c,排成三行两列,要求每行的字母互不一样,梅列的字母也互不一样,则不同的排列方法共有〔A〕12种〔B〕18种〔C〕24种〔D〕36种〔12〕正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=73。
专题1.1 年全国1卷理科第16题-刷百题不如解透一题之高考真题数学小题大做
一、典例分析,融合贯通典例【2018年全国1卷理科第16题】已知函数f(x)=2sinx+sin2x ,则f(x)的最小值是______. 解法一:引导:首先对函数进行求导,化简求得,从而确定出函数的单调区间,减区间为,增区间为,确定出函数的最小值点,从而求得代入求得函数的最小值.点评:该题考查的是有关应用导数研究函数的最小值问题,在求解的过程中,需要明确相关的函数的求导公式,需要明白导数的符号与函数的单调性的关系,确定出函数的单调增区间和单调减区间,进而求得函数的最小值点,从而求得相应的三角函数值,代入求得函数的最小值. 解法二:()=2sin +sin2=2sin (1+cos )f x x x x x22222()=4sin (1+cos )4(1-cos )(1+cos )f x x x x x ∴=4(3-3cos )(1+cos )(1+cos )(1+cos )3x x x x = 443-3cos +1+cos +1+cos +1+cos )34x x x x ⎛⎫≤ ⎪⎝⎭44327324⎛⎫=⨯= ⎪⎝⎭ ()f x 易知是奇函数1cos = 332(),23sin =2x f x x ⎧⎪⎪∴≥-⎨⎪-⎪⎩当时可以取等号,33().2f x ∴-的最小值是 点评:另辟蹊径,联系均值不等式求最值(和定积最小)。
解法三:解法3:公式搭桥,函数领路,导数建功。
解法四:()=2sin +sin2f x x x ,tan 2xt R =∈令则22234182sin(1cos)(1)1112t ty x xt t t tt-=+=+=++++,31t2,t ttϕ=++令()4222221321t32,0t tt tt tϕμ+-'=+-==≥()令,原式得;(1)(31),μμμ+-=显然13μ=时,取tϕ()到极值经检验当3t=-时,tϕ()有最大值,则y有最小值得:min833.1()3yϕ==--解法4:替换消元,导数建功。
圆锥曲线全国卷高考真题解答题(含解析))
圆锥曲线全国卷高考真题解答题一、解答题1,2019年全国统一高考数学试卷(理科)(新课标Ⅲ)已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点: (2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.2.2019年全国统一高考数学试卷(理科)(新课标Ⅰ) 已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程; (2)若3AP PB =,求|AB |.3.2014年全国普通高等学校招生统一考试理科数学(新课标Ⅰ)已知点A (0,-2),椭圆E :22221x y a b += (a >b >0)F 是椭圆E 的右焦点,直线AF ,O 为坐标原点. (1)求E 的方程;(2)设过点A 的动直线l 与E 相交于P ,Q 两点.当△OPQ 的面积最大时,求l 的方程.已知椭圆222:9(0)C x y m m +=>,直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .(Ⅰ)证明:直线OM 的斜率与l 的斜率的乘积为定值; (Ⅱ)若l 过点(,)3mm ,延长线段OM 与C 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时l 的斜率,若不能,说明理由.5.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ带解析)在直角坐标系xoy 中,曲线C :y=24x与直线(),0y kx a a =+>交与M,N 两点,(Ⅰ)当k =0时,分别求C 在点M 和N 处的切线方程;(Ⅱ)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM =∠OPN ?说明理由.6.2016年全国普通高等学校招生统一考试文科数学(新课标3) 已知抛物线:的焦点为,平行于轴的两条直线分别交于两点,交的准线于两点.(Ⅰ)若在线段上,是的中点,证明;(Ⅱ)若的面积是的面积的两倍,求中点的轨迹方程.7.2016年全国普通高等学校招生统一考试理科数学(新课标2卷)已知椭圆E:2213x y t +=的焦点在x 轴上,A 是E 的左顶点,斜率为k (k > 0)的直线交E 于A ,M 两点,点N 在E 上,MA ⊥NA . (Ⅰ)当t=4,AM AN =时,求△AMN 的面积; (Ⅱ)当2AM AN =时,求k 的取值范围.设圆的圆心为A ,直线l 过点B (1,0)且与x 轴不重合,l 交圆A于C ,D 两点,过B 作AC 的平行线交AD 于点E . (I )证明为定值,并写出点E 的轨迹方程;(II )设点E 的轨迹为曲线C 1,直线l 交C 1于M ,N 两点,过B 且与l 垂直的直线与圆A 交于P ,Q 两点,求四边形MPNQ 面积的取值范围.9.2017年全国普通高等学校招生统一考试理科数学(新课标2卷)设O 为坐标原点,动点M 在椭圆C 22:12x y +=上,过M 作x 轴的垂线,垂足为N ,点P 满足2NP NM =.(1)求点P 的轨迹方程;(2)设点Q 在直线3x =-上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F .10.2018年全国卷Ⅲ理数高考试题文已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点,线段AB 的中点为()()10M m m >,. (1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:FA ,FP ,FB 成等差数列,并求该数列的公差.已知椭圆C :2222=1x y a b +(a>b>0),四点P 1(1,1),P 2(0,1),P 3(–1P 4(1中恰有三点在椭圆C 上. (Ⅰ)求C 的方程;(Ⅱ)设直线l 不经过P 2点且与C 相交于A ,B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1,证明:l 过定点.12.2018年全国普通高等学校招生统一考试理数(全国卷II )设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =. (1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.13.2018年全国普通高等学校招生统一考试理科数学(新课标I 卷)设椭圆22:12x C y +=的右焦点为F ,过F 的直线l 与C 交于,A B 两点,点M 的坐标为(2,0).(1)当l 与x 轴垂直时,求直线AM 的方程; (2)设O 为坐标原点,证明:OMA OMB ∠=∠.14.2018年全国普通高等学校招生统一考试文科数学(新课标I 卷)设抛物线22C y x =:,点()20A ,,()20B -,,过点A 的直线l 与C 交于M ,N 两点. (1)当l 与x 轴垂直时,求直线BM 的方程; (2)证明:ABM ABN ∠=∠.15.2018年全国卷Ⅲ文数高考试题已知斜率为k 的直线l 与椭圆22143x y C +=:交于A ,B 两点.线段AB 的中点为(1,)(0)M m m >.(1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:2FP FA FB =+.16.2017年全国普通高等学校招生统一考试文科数学(新课标1卷)设A 、B 为曲线C :24x y =上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM BM ⊥,求直线AB 的方程.17.2017年全国普通高等学校招生统一考试文科数学(新课标2卷)设O 为坐标原点,动点M 在椭圆C 22:12x y +=上,过M 作x 轴的垂线,垂足为N ,点P 满足2NP NM =.(1)求点P 的轨迹方程;(2)设点Q 在直线3x =-上,且1OP PQ ⋅=.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F .18.2017年全国普通高等学校招生统一考试文科数学(新课标3卷)在直角坐标系xOy 中,曲线22y x mx =+-与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题:(1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.19.(2016新课标全国卷Ⅰ文科)在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :22(0)y px p =>于点P ,M 关于点P 的对称点为N ,连结ON 并延长交C 于点H . (Ⅰ)求OH ON;(Ⅱ)除H 以外,直线MH 与C 是否有其它公共点?说明理由.20.2015年全国普通高等学校招生统一考试文科数学(新课标Ⅱ)已知椭圆2222:1(0)x y C a b a b +=>>的离心率为2,点在C 上(1)求C 的方程(2)直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点,A B ,线段AB 的中点为M .证明:直线OM 的斜率与直线l 的斜率的乘积为定值.21.2019年全国统一高考数学试卷(文科)(新课标Ⅲ)已知曲线2:,2x C y D =,为直线12y上的动点,过D 作C 的两条切线,切点分别为,A B .(1)证明:直线AB 过定点: (2)若以50,2E ⎛⎫⎪⎝⎭为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求该圆的方程.22.2014年全国普通高等学校招生统一考试理科数学(全国Ⅱ卷带解析)设1F , 2F 分别是椭圆C : 22221(0)x y a b a b+=>>的左、右焦点, M 是C 上一点且2MF 与x 轴垂直,直线1MF 与C 的另一个交点为N . (1)若直线MN 的斜率为34,求C 的离心率; (2)若直线MN 在y 轴上的截距为2,且15MN F N =,求a , b .23.2014年全国普通高等学校招生统一考试文科数学(新课标Ⅰ) 已知点,圆:,过点的动直线与圆交于两点,线段的中点为,为坐标原点.(1)求的轨迹方程;(2)当时,求的方程及的面积24.2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)已知过点A (0,1)且斜率为k 的直线l 与圆C :(x -2)2+(y -3)2=1交于M ,N 两点. (1)求k 的取值范围;(2)若OM ON ⋅=12,其中O 为坐标原点,求|MN |.一、解答题1,2019年全国统一高考数学试卷(理科)(新课标Ⅲ)已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点: (2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.【答案】(1)见详解;(2) 3或【分析】(1)可设11(,)A x y ,22(,)B x y ,1(,)2D t -然后求出A ,B 两点处的切线方程,比如AD :1111()2y x x t +=-,又因为BD 也有类似的形式,从而求出带参数直线AB 方程,最后求出它所过的定点.(2)由(1)得带参数的直线AB 方程和抛物线方程联立,再通过M 为线段AB 的中点,EM AB ⊥得出t 的值,从而求出M 坐标和EM 的值,12,d d 分别为点,D E 到直线AB的距离,则12d d ==,结合弦长公式和韦达定理代入求解即可.【详解】(1)证明:设1(,)2D t -,11(,)A x y ,则21112y x =. 又因为212y x =,所以y'x =.则切线DA 的斜率为1x , 故1111()2y x x t +=-,整理得112210tx y -+=. 设22(,)B x y ,同理得222210tx y -+=.11(,)A x y ,22(,)B x y 都满足直线方程2210tx y -+=.于是直线2210tx y -+=过点,A B ,而两个不同的点确定一条直线,所以直线AB 方程为2210tx y -+=.即2(21)0tx y +-+=,当20,210x y =-+=时等式恒成立.所以直线AB 恒过定点1(0,)2.(2)由(1)得直线AB 的方程为12y tx =+. 由2122y tx x y ⎧=+⎪⎪⎨⎪=⎪⎩,可得2210x tx --=, 于是2121212122,1,()121x x t x x y y t x x t +==-+=++=+212|||2(1)AB x x t =-==+.设12,d d 分别为点,D E 到直线AB的距离,则12d d ==.因此,四边形ADBE 的面积()(2121||32S AB d d t =+=+设M 为线段AB 的中点,则21,2M t t ⎛⎫+⎪⎝⎭, 由于EM AB ⊥,而()2,2EM t t =-,AB 与向量(1,)t 平行,所以()220t t t +-=,解得0t =或1t =±.当0t =时,3S =;当1t =±时S =因此,四边形ADBE 的面积为3或. 【点睛】此题第一问是圆锥曲线中的定点问题和第二问是求面积类型,属于常规题型,按部就班的求解就可以.思路较为清晰,但计算量不小. 2.2019年全国统一高考数学试卷(理科)(新课标Ⅰ) 已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程; (2)若3AP PB =,求|AB |. 【答案】(1)12870x y --=;(2【分析】(1)设直线l :32y x m =+,()11,A x y ,()22,B x y ;根据抛物线焦半径公式可得1252x x +=;联立直线方程与抛物线方程,利用韦达定理可构造关于m 的方程,解方程求得结果;(2)设直线l :23x y t =+;联立直线方程与抛物线方程,得到韦达定理的形式;利用3AP PB =可得123y y =-,结合韦达定理可求得12y y ;根据弦长公式可求得结果. 【详解】(1)设直线l 方程为:32y x m =+,()11,A x y ,()22,B x y 由抛物线焦半径公式可知:12342AF BF x x +=++= 1252x x ∴+= 联立2323y x m y x ⎧=+⎪⎨⎪=⎩得:()229121240x m x m +-+= 则()2212121440m m ∆=--> 12m ∴<121212592m x x -∴+=-=,解得:78m =-∴直线l 的方程为:3728y x =-,即:12870x y --= (2)设(),0P t ,则可设直线l 方程为:23x y t =+联立2233x y t y x⎧=+⎪⎨⎪=⎩得:2230y y t --= 则4120t ∆=+> 13t ∴>-122y y ∴+=,123y y t =-3AP PB = 123y y ∴=- 21y ∴=-,13y = 123y y ∴=-则AB ===【点睛】本题考查抛物线的几何性质、直线与抛物线的综合应用问题,涉及到平面向量、弦长公式的应用.关键是能够通过直线与抛物线方程的联立,通过韦达定理构造等量关系. 3.2014年全国普通高等学校招生统一考试理科数学(新课标Ⅰ)已知点A (0,-2),椭圆E :22221x y a b += (a >b >0)的离心率为2,F 是椭圆E 的右焦点,直线AF ,O 为坐标原点.(1)求E 的方程;(2)设过点A 的动直线l 与E 相交于P ,Q 两点.当△OPQ 的面积最大时,求l 的方程.【答案】(1)2214x y += (2)2y x =-【解析】试题分析:设出F ,由直线AFc ,结合离心率求得a ,再由隐含条件求得b ,即可求椭圆方程;(2)点l x ⊥轴时,不合题意;当直线l 斜率存在时,设直线:2l y kx =-,联立直线方程和椭圆方程,由判别式大于零求得k 的范围,再由弦长公式求得PQ ,由点到直线的距离公式求得O 到l 的距离,代入三角形面积公式,化简后换元,利用基本不等式求得最值,进一步求出k 值,则直线方程可求. 试题解析:(1)设(),0F c ,因为直线AF,()0,2A -所以23c =,c =又222,2c b a c a ==- 解得2,1a b ==,所以椭圆E 的方程为2214x y +=.(2)解:设()()1122,,,P x y Q x y 由题意可设直线l 的方程为:2y kx =-,联立221{42,x y y kx +==-,消去y 得()221416120k x kx +-+=,当()216430k ∆=->,所以234k >,即k <或k > 1212221612,1414k x x x x k k+==++. 所以PQ ==214k =+ 点O 到直线l的距离d =所以12OPQS d PQ ∆==0t =>,则2243k t =+,244144OPQ t S t t t∆==≤=++, 当且仅当2t =2=,解得k =时取等号, 满足234k >所以OPQ ∆的面积最大时直线l的方程为:2y x =-或2y x =-. 【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形最值的.4.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅱ)已知椭圆222:9(0)C x y m m +=>,直线l 不过原点O 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .(Ⅰ)证明:直线OM 的斜率与l 的斜率的乘积为定值; (Ⅱ)若l 过点(,)3mm ,延长线段OM 与C 交于点P ,四边形OAPB 能否为平行四边形?若能,求此时l 的斜率,若不能,说明理由.【答案】(Ⅰ)详见解析;(Ⅱ)能,47-或47+. 【解析】试题分析:(1)设直线:l y kx b =+(0,0)k b ≠≠,直线方程与椭圆方程联立,根据韦达定理求根与系数的关系,并表示直线OM 的斜率,再表示;(2)第一步由 (Ⅰ)得OM 的方程为9y x k=-.设点P 的横坐标为P x ,直线OM 与椭圆方程联立求点P 的坐标,第二步再整理点的坐标,如果能构成平行四边形,只需,如果有值,并且满足0k >,3k ≠的条件就说明存在,否则不存在.试题解析:解:(1)设直线:l y kx b =+(0,0)k b ≠≠,11(,)A x y ,22(,)B x y ,(,)M M M x y .∴由2229y kx b x y m=+⎧⎨+=⎩得2222(9)20k x kbx b m +++-=, ∴12229M x x kbx k +==-+,299M M b y kx b k =+=+. ∴直线OM 的斜率9M OM M y k x k==-,即9OM k k ⋅=-. 即直线OM 的斜率与l 的斜率的乘积为定值9-. (2)四边形OAPB 能为平行四边形. ∵直线l 过点(,)3mm ,∴l 不过原点且与C 有两个交点的充要条件是0k >,3k ≠ 由 (Ⅰ)得OM 的方程为9y x k=-.设点P 的横坐标为P x . ∴由2229,{9,y x k x y m =-+=得,即将点(,)3m m 的坐标代入直线l 的方程得(3)3m k b -=,因此2(3)3(9)M mk k x k -=+.四边形OAPB 为平行四边形当且仅当线段AB 与线段OP 互相平分,即2P M x x = 239k =+2(3)23(9)mk k k -⨯+.解得147k =247k =.∵0,3i i k k >≠,1i =,2,∴当l 的斜率为47-或47+时,四边形OAPB 为平行四边形. 考点:直线与椭圆的位置关系的综合应用【一题多解】第一问涉及中点弦,当直线与圆锥曲线相交时,点是弦的中点,(1)知道中点坐标,求直线的斜率,或知道直线斜率求中点坐标的关系,或知道求直线斜率与直线OM 斜率的关系时,也可以选择点差法,设,,代入椭圆方程,两式相减,化简为,两边同时除以得,而,,即得到结果,(2)对于用坐标法来解决几何性质问题,那么就要求首先看出几何关系满足什么条件,其次用坐标表示这些几何关系,本题的关键就是如果是平行四边形那么对角线互相平分,即2P M x x =,分别用方程联立求两个坐标,最后求斜率.5.2015年全国普通高等学校招生统一考试理科数学(新课标Ⅰ带解析)在直角坐标系xoy 中,曲线C :y=24x与直线(),0y kx a a =+>交与M,N 两点,(Ⅰ)当k =0时,分别求C 在点M 和N 处的切线方程;(Ⅱ)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM =∠OPN ?说明理由. 【答案】(Ⅰ0ax y a --=0ax y a ++=(Ⅱ)存在 【详解】试题分析:(Ⅰ)先求出M,N 的坐标,再利用导数求出M,N.(Ⅱ)先作出判定,再利用设而不求思想即将y kx a =+代入曲线C 的方程整理成关于x 的一元二次方程,设出M,N 的坐标和P 点坐标,利用设而不求思想,将直线PM ,PN 的斜率之和用a 表示出来,利用直线PM ,PN 的斜率为0,即可求出,a b 关系,从而找出适合条件的P 点坐标. 试题解析:(Ⅰ)由题设可得(2,)M a a ,(2,)N a -,或(22,)M a -,,)N a a .∵12y x '=,故24x y =在x =2a a C 在(22,)a a 处的切线方程为(2)y a a x a -=-,即0ax y a --=.故24x y =在x =-22a 处的导数值为-a ,C 在(22,)a a -处的切线方程为(2)y a a x a -=-+,即0ax y a ++=.故所求切线方程为0ax y a --=或0ax y a ++=. (Ⅱ)存在符合题意的点,证明如下:设P (0,b )为复合题意得点,11(,)M x y ,22(,)N x y ,直线PM ,PN 的斜率分别为12,k k . 将y kx a =+代入C 得方程整理得2440x kx a --=. ∴12124,4x x k x x a +==-. ∴121212y b y b k k x x --+=+=1212122()()kx x a b x x x x +-+=()k a b a+.当=-b a 时,有12k k +=0,则直线PM 的倾斜角与直线PN 的倾斜角互补, 故∠OPM=∠OPN ,所以(0,)P a -符合题意.考点:抛物线的切线;直线与抛物线位置关系;探索新问题;运算求解能力 6.2016年全国普通高等学校招生统一考试文科数学(新课标3) 已知抛物线:的焦点为,平行于轴的两条直线分别交于两点,交的准线于两点.(Ⅰ)若在线段上,是的中点,证明;(Ⅱ)若的面积是的面积的两倍,求中点的轨迹方程.【答案】(Ⅰ)见解析;(Ⅱ).【解析】试题分析:设的方程为.(1)由在线段上,又;(2)设与轴的交点为(舍去),.设满足条件的的中点为.当与轴不垂直时.当与轴垂直时与重合所求轨迹方程为.试题解析:由题设,设,则,且.记过两点的直线为,则的方程为.............3分(1)由于在线段上,故,记的斜率为的斜率为,则,所以..................5分(2)设与轴的交点为,则,由题设可得,所以(舍去),.设满足条件的的中点为.当与轴不垂直时,由可得.而,所以.当与轴垂直时,与重合,所以,所求轨迹方程为.........12分考点:1.抛物线定义与几何性质;2.直线与抛物线位置关系;3.轨迹求法.7.2016年全国普通高等学校招生统一考试理科数学(新课标2卷)已知椭圆E:2213x y t +=的焦点在x 轴上,A 是E 的左顶点,斜率为k (k > 0)的直线交E 于A ,M 两点,点N 在E 上,MA ⊥NA . (Ⅰ)当t=4,AM AN =时,求△AMN 的面积; (Ⅱ)当2AM AN =时,求k 的取值范围. 【答案】(Ⅰ)14449;(Ⅱ))2.【解析】试题分析:(Ⅰ)先求直线AM 的方程,再求点M 的纵坐标,最后求AMN 的面积;(Ⅱ)设()11,M x y ,写出A 点坐标,并求直线AM 的方程,将其与椭圆方程组成方程组,消去y ,用,t k 表示1x ,从而表示AM ,同理用,t k 表示AN ,再由2AM AN =及t 的取值范围求k 的取值范围.试题解析:(Ⅰ)设()11,M x y ,则由题意知10y >,当4t =时,E 的方程为22143x y +=,()2,0A -.由已知及椭圆的对称性知,直线AM 的倾斜角为4π.因此直线AM 的方程为2y x =+. 将2x y =-代入22143x y +=得27120y y -=.解得0y =或127y =,所以1127y =.因此AMN 的面积AMNS11212144227749=⨯⨯⨯=.(Ⅱ)由题意3t >,0k >,()A .将直线AM的方程(y k x =代入2213x y t +=得()22222330tk xx t k t +++-=.由(221233t k tx tk -⋅=+得)21233tk x tk-=+,故1AM x =+=.由题设,直线AN 的方程为(1y x k =-+,故同理可得AN ==,由2AM AN =得22233k tk k t=++,即()()32321k t k k -=-. 当32k =时上式不成立,因此()33212k k t k -=-.3t >等价于()()232332122022k k k k k k k -+-+-=<--, 即3202k k -<-.由此得320{20k k ->-<,或320{20k k -<->,解得322k <<. 因此k 的取值范围是()32,2.【考点】椭圆的性质,直线与椭圆的位置关系【名师点睛】由直线(系)和圆锥曲线(系)的位置关系,求直线或圆锥曲线中某个参数(系数)的范围问题,常把所求参数作为函数值,另一个元作为自变量求解.8.2016年全国普通高等学校招生统一考试理科数学(新课标1卷) 设圆的圆心为A ,直线l 过点B (1,0)且与x 轴不重合,l 交圆A于C ,D 两点,过B 作AC 的平行线交AD 于点E . (I )证明为定值,并写出点E 的轨迹方程;(II )设点E 的轨迹为曲线C 1,直线l 交C 1于M ,N 两点,过B 且与l 垂直的直线与圆A 交于P ,Q 两点,求四边形MPNQ 面积的取值范围. 【答案】(Ⅰ)答案见解析;(Ⅱ).【解析】试题分析:(Ⅰ)利用椭圆定义求方程;(Ⅱ)把面积表示为关于斜率k 的函数,再求最值。
(19)2022年高考真题——理科数学(全国乙卷)答案(1)
11.双曲线C的两个焦点为 ,以C的实轴为直径的圆记为D,过 作D的切线与C交于M,N两点,且 ,则C的离心率为()
A. B. C. D.
【答案】C
【解析】
【分析】依题意不妨设双曲线焦点在 轴,设过 作圆 的切线切点为 ,可判断 在双曲线的右支,设 , ,即可求出 , , ,在 中由 求出 ,再由正弦定理求出 , ,最后根据双曲线的定义得到 ,即可得解;
在 中, ,所以 .
以 为坐标原点建立如图所示的空间直角坐标系 ,
则 ,所以 ,
设平面 的一个法向量为 ,
则 ,取 ,则 ,
又因为 ,所以 ,
所以 ,
设 与平面 所成的角的正弦值为 ,
所以 ,
所以 与平面 所成的角的正弦值为 .
19.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位: )和材积量(单位: ),得到如下数据:
所以当 时, ,当 时, ,
若 时,
当 时, ,
则此时 ,与前面矛盾,
故 不符合题意,
若 时,
则方程 的两个根为 ,
即方程 的两个根为 ,
即函数 与函数 的图象有两个不同的交点,
令 ,则 ,
设过原点且与函数 的图象相切的直线的切点为 ,
则切线的斜率为 ,
故切线方程为 ,
则有 ,
解得 ,
则切线的斜率为 ,
联立得, ,
所以 的图像关于点 中心对称,因为函数 的定义域为R,
所以
因为 ,所以 .
所以 .
故选:D
【点睛】含有对称轴或对称中心的问题往往条件比较隐蔽,考生需要根据已知条件进行恰当的转化,然后得到所需的一些数值或关系式从而解题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p1, p2 , p3 ,则( ) (A) p1 p2
(B) p1 p3
(C) p2 p 3
p1 p2 p 3
(D)
11.已知双曲线C :
x2 3
y2
1
O 为坐标原点, F 为 C 的右焦点,过 F 的直线与C 的两条渐近线
,
的交点分别为 M , N 。若 OMN 为直角三角形,则| MN | ( )
2018 年普通高等学校招生全国统一考试
数 学(理)(全国 I 卷)
一.选择题(共 12 小题,每小题 5 分,共 60 分。在每小题列出的四个选项中,选出符合题目要求的一
项)
1.设 z
1i 1i
2i ,则| z | (
) D) 2
2.已知集合 A x | x2 x 2 0
3 (A) 2
(B)3
(C) 2 3
(D)4
12.已知正方体的棱长为 1,每条棱所在直线与平面 所成的角相等,则 截此正方体所得截面面积
的最大值为(
) (A) 3 3 4
(B) 2 3 3
(C) 3 2 4
(D) 3 2
二.填空题(共 4 小题,每小题 5 分,共 20 分)
x 2y 2 0 13.若 x, y 满足约束条件 x y 1 0 ,则 z 3x 2 y 的最大值为________。
19.(本小题 12 分)设椭圆 C : x2 y2 1的右焦点为 F ,过 F 的直线 l 与
2
C 交于 A, B 两点,点
M 的坐标为
。⑴当 l与
OMA OM2B,0。
x 轴 垂 直 时 , 求 直 线 AM 的 方 程 ; ⑵ 设 O 为 坐 标 原 点 , 证 明 :
20.(本小题12分)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作
2, 0
且斜率为
2 3 的直线与
C 交于 M , N 两点,则 FM FN ( ) (A)5
(B)6
(C)7
(D)8
第1页共6页
9.已知函数 f x
ex x 0 ,g x
ln x x 0
f x x a 。若 g x 存在 2 个零点,则 a 的取值范围
是( ) (A) 1,0
(B) 0,
(C) 1,
三.解答题(共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题,每个试题考
生都必须作答。第 22、23 题为选考题,考生根据要求作答) (一)必考题:60 分。
17.(本小题 12 分)在平面四边形 ABCD 中, ADC 900 , A 450 , AB 2 , BD 5 。
(D) 1,
10.下图来自古希腊数学家希波克拉底所研究的几何图形。此图由三个半
圆构成,三个半圆的直径分别为直角三角形 ABC 的斜边 BC ,直角边
AB, AC 。 ABC 的三边所围成的区域记为 I,黑色部分记为 II,其余部分记
为 III。在整个图形中随机取一点,此点取自 I,II,III 的概率分别记为
检验,如检验出不合格品,则更换为合格品。检验时,先从这箱产品中任取20件作检验,再根据检验结果
决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为 p 0 p 1 ,且各件产品是否为
不合格品相互独立。⑴记20件产品中恰有2件不合格品的概率为 f p ,求 f p 的最大值点 p0 ;⑵现对
4
4
(B) 1 AB 3 AC
4
4
(C) 3 AB 1 AC
4
4
(D) 1 AB 4
7.已知正方体的棱长为 1,每条棱所在直线与平面 所成的角相等,则
截此正方体所得截面面积的最大值为( )
3 AC 4
(A) 3 3 4
(B) 2 3 3
(C) 3 2 4
(D) 3 2
8.设抛物线C : y2
4x 的焦点为 F ,过点
(C)10
(D)12
5.设函数 f x x3 a 1 x2 ax,若 f x 为奇函数,则曲线 y f x 在点 0,0 处的切线方
程为( ) (A) y 2x
(B) y x
(C) y 2x
(D) y x
6.在 ABC 中, AD 为 BC 边上的中线, E 为 AD 的中点,则 EB ( )
(A) 3 AB 1 AC
21.(本小题 12 分)已知函数 f x
1 x a ln x 。⑴讨论 f x 的单调性;⑵若 f x 存在两个极 x
(A)新农村建设后,种植收入减少
(B)新农村建设后,其他收入增加了一倍以上 (C)新农村建设后,养殖收入增加了一倍
(D)新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
4.设 Sn 为等差数列 an 的前 n 项和,若3S3 S2 S4 , a1 2 ,则 a5 ( )
(A) 12
(B) 10
ðA ( )
R
,则
(A) x | 1 x 2 (B) x | 1 x 2 (C) x | x 1
x|x 1 3.某地区x经| 过x 一2年的新农村建设,
x | x 2 (D)
农村的经济收入增加了一倍,实现翻番。
为更好地了解该地区农村的经济收入变化
情况,统计了该地区新农村建设前后农村
的经济收入构成比例,得到如右饼图。则 下面结论中不正确的是( )
⑴求 cos ADB ;⑵若 DC 2 2 ,求 BC 。
18.(本小题 12 分)如图,四边形 ABCD 为正方形, E, F 分别
第2页共6页
为 AD, BC 的中点,以 DF 为折痕把 DFC 折起,使点C 到达点 P 的
位置,且 PF BF 。⑴证明:平面 PEF 平面 ABFD ;⑵求 DP 与平面 ABFD 所成角的正弦值。
一箱产品检验了20件,结果恰有2件不合格品,以⑴中确定的 p0 作为 p 的值。已知每件产品的检验费用为
2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用。①若不对该箱余下的
产品作检验,这一箱产品的检验费用与赔偿费用的和记为 X ,求 EX ;②以检验费用与赔偿费用和的期望
值为决策依据,是否该对这箱余下的所有产品作检验?
y0
14.记 Sn 为数列 an 的前 n 项和,若 Sn 2an 1 ,则 S6 _____________。
15.从 2 位女生,4 位男生中选 3 人参加科技比赛,且至少有 1 位女生入选,则不同的选法共有 _____________种。(用数字填写答案)
16.已知函数 f x 2sin x sin 2x ,则 f x 的最小值是__________。
