工大出版社杯第16届西北工业大学数模竞赛一等奖论文
数学建模优秀论文模板(全国一等奖模板)
Haozl觉得数学建模论文格式这么样设置版权归郝竹林所有，材料仅学习参考版权：郝竹林备注☆※§等等字符都可以作为问题重述左边的。
一级标题所有段落一级标题设置成段落前后间距13磅二级标题设置成段落间距前0.5行后0.25行图和表的标题采用插入题注方式题注样式在样式表中设置居中五号字体Excel中画出的折线表字体采用默认格式宋体正文10号图标题在图上方段落间距前0.25行后0行表标题在表下方段落间距前0行后0.25行行距均使用单倍行距所有段落均把4个勾去掉注意Excel表格插入到word的方式在Excel中复制后，粘贴，word2010粘贴选用使用目标主题嵌入当前Dsffaf所有软件名字第一个字母大写比如E xcel所有公式和字母均使用MathType编写公式编号采用MathType编号格式自己定义公式编号在右边显示农业化肥公司的生产与销售优化方案摘 要 要求总分总本文针对储油罐的变位识别与罐容表标定的计算方法问题，运用二重积分法和最小二乘法建立了储油罐的变位识别与罐容表标定的计算模型，分别对三种不同变位情况推导出的油位计所测油位高度与实际罐容量的数学模型，运用matlab 软件编程得出合理的结论，最终对模型的结果做出了误差分析。
针对问题一要求依据图4及附表1建立积分数学模型研究罐体变位后对罐容表的影响，并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
我们作图分析出实验储油罐出现纵向倾斜 14.时存在三种不同的可能情况，即储油罐中储油量较少、储油量一般、储油量较多的情况。
针对于每种情况我们都利用了高等数学求容积的知识，以倾斜变位后油位计所测实际油位高度为积分变量，进行两次积分运算，运用MATLAB 软件推导出了所测油位高度与实际罐容量的关系式。
并且给出了罐体倾斜变位后油位高度间隔为1cm 的罐容标定值（见表1），最后我们对倾斜变位前后的罐容标定值残差进行分析，得到样本方差为4103878.2-⨯，这充分说明残差波动不大。
数学建模竞赛论文模板
数码相机定位模型（题目）摘要此处为摘要正文一定要写好。
主要写三个方面：1. 解决什么问题（一句话）2. 采取什么方法（引起阅卷老师的注意，不能太粗，也不能太细）3. 得到什么结果（简明扼要、生动、公式要简单、必要时可采用小图表）关键词：差分近似，误差补偿算法，Simpson积分公式3-5关键词即可目录1.问题重述 .............................................................................................................. 错误!未定义书签。
2.模型假设 .............................................................................................................. 错误!未定义书签。
3.符号说明 .............................................................................................................. 错误!未定义书签。
……………………………说明：目录页可以没有，如果内容比较多，可以有目录页一问题重述二问题分析三模型假定四问题分析五模型建立与求解六模型检验七模型评价八模型推广结合社会实际问题九参考文献[1] 吕显瑞等,数学建模竞赛辅导教材,长春：吉林大学出版社,2002。
[2] 刘来福,曾文艺,数学模型与数学建模北京：北京师范大学出版社，1997。
[3] 陈如栋,于延荣,数学模型与数学建模，北京：国防工业出版社,2006。
[4] 姜启源,谢金星,叶俊,数学模型（第三版），北京：高等教育出版社,2003。
[5] 梁炼，数学建模。
华东理工大学大学出版社 2005.3。
[6] 周义仓，赫孝良，西安交通大学出版社，1998.8。
电工杯数模竞赛论文
答卷编号：论文题目：锅炉的优化问题姓名专业、班级有效联系电话参赛队员1 钱刘宸参赛队员2 王亚堃参赛队员3 李新宇指导教师：参赛学校：西北工业大学证书邮寄地址及收件人：答卷编号：阅卷专家1 阅卷专家2 阅卷专家3 专家签字摘要锅炉是火力发电厂的关键设备之一，在现代电站中，锅炉效率是反映锅炉运行状况好坏的主要性能指标,但是由于设备和运行的原因，锅炉的实际热效率只能达到设计效率的80%左右，大大降低了能源的利用率。
本文主要针对如何提升锅炉效率，促进锅炉节能降耗这个问题进行了分析与讨论，并在此基础上提出使其优化的方法。
在问题一中，我们通过图1可以发现，q2与α成正相关，q3、q4与α成负相关，因此，我们考虑（补充上证明函数式运用的方法），分别求出q2、q3、q4与α之间的函数表达式，由于q=q1+q2+q3占全部热损失的80%左右，因此可以认为，当q最小时，即是锅炉运行中的最佳过量空气系数α，根据函数求导法则可以计算出α的值为（？）。
一、问题重述锅炉是火力发电厂的关键设备之一，其效率直接影响电厂的经济性。
在现代电站中，反映锅炉运行状况好坏的主要性能指标是锅炉效率。
按照中华人民共和国国家标准的电站性能试验规程（GB PTC ），电厂锅炉采用反平衡计算锅炉效率，即：）－（6543211100100q q q q q Q Qq rgl ++++=⨯==η，％ （1） 式中）（6,,2,1 =⨯=i Q Qq ri i 100分别表示有效利用热1q 、排烟热损失2q 、化学不（或可燃气体未）完全燃烧热损失3q 、机械（或固体）不完全燃烧热损失4q 、散热损失5q 和灰渣物理热损失6q 。
促进锅炉节能降耗的重要手段之一是对锅炉机组热力系统进行在线监测与分析，进而优化其运行参数。
锅炉的运行是一个涉及化学反应、传热传质的复杂过程，影响参数众多，主要包括煤质参数、运行参数、设备状况和运行环境等。
目前，在国内常常利用在线监测数据进行偏差（或耗差）分析，来提高锅炉运行的经济性。
2016全国大学生数学建模竞赛获奖名单
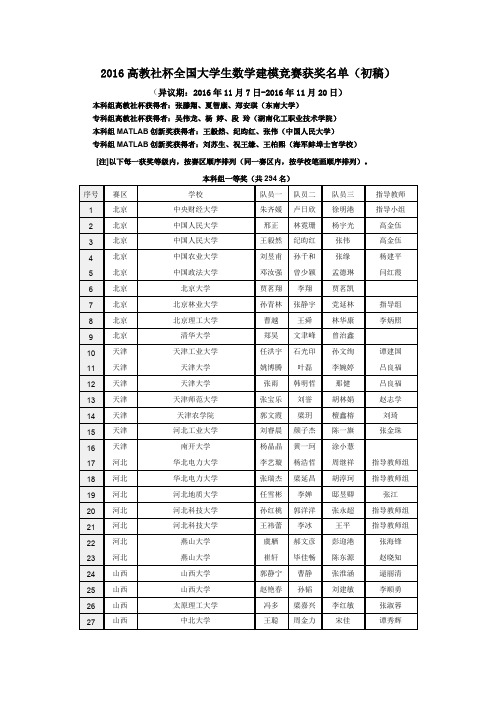
2016高教社杯全国大学生数学建模竞赛获奖名单（初稿）（异议期：2016年11月7日-2016年11月20日）
本科组高教社杯获得者：张滕翔、夏智康、郑安琪（东南大学）
专科组高教社杯获得者：吴伟龙、杨婷、段玲（湖南化工职业技术学院）
本科组MATLAB创新奖获得者：王毅然、纪昀红、张伟（中国人民大学）
专科组MATLAB创新奖获得者：刘苏生、祝王缘、王柏熙（海军蚌埠士官学校）
[注]以下每一获奖等级内，按赛区顺序排列（同一赛区内，按学校笔画顺序排列）。
本科组一等奖（共294名）
本科组二等奖（共1621名）
曹小
专科组一等奖（共60名）。
关于组织工大正禾杯西北工业大学数学建模竞赛暨.
关于组织““工大正禾杯”西北工业大学数学建模竞赛暨全国大学生数学建模竞赛选拔赛”的通知各学院及相关职能(部)处：数学建模竞赛是提高大学生建立数学模型与运用计算机技术解决实际问题的综合能力，开拓知识面，培养大学生创新精神及合作意识的典型创新竞赛活动项目，活动的开展对推动我校数学系列课程教学体系、教学内容和教学方法的改革有着十分重要的作用。
为了推动创新实践教育的深入开展，让尽可能多的学生参与这项有益的活动，同时为我校参加国际、国内各项数学建模竞赛选拔参赛队员，根据西北工业大学校教字[2006]521号文件精神，现决定举办“工大正禾杯”西北工业大学大学生数学建模竞赛暨全国大学生数学建模竞赛选拔赛”。
现将有关事项通知如下，请各学院及相关单位遵照执行。
1、参赛对象为全校在校本科生，参赛人数不限。
各院指定一名领队，负责本院的竞赛组织与协调工作。
2、参赛大学生每3人为一个参赛队；跨院参赛队由其中一个学院负责管理。
3、各学院应为本院参赛学生（包括友谊校区和长安校区）提供参赛所需的竞赛场地、微机、打印机以及有关消耗材料。
竞赛耗材由各学院教学经常费支付。
4、对于组织工作优秀的学院，学校将设立优秀组织奖，颁发证书，并作为对学院教学工作进行考核的依据。
5、竞赛组委会将聘请专家组成评阅委员会，评选出特等奖1个、一等奖、二等奖、三等奖以及成功参赛奖各若干（附件二）。
各学院应督促所有参赛队按时依据相关要求交卷，各学院未交卷队的数目将与该学院获奖学生获奖等级挂钩。
6、对学生和学院的奖励与考核按照校教字[2006]521号文件执行。
学校向获得各奖项的学生颁发证书并按规定计入相应学分；对竞赛成绩优秀的学生依据相关规定，学生处与各学院在评选优秀学生、奖学金时予以认可；对领队教师的辛勤劳动予以表彰并记入适当工作量。
7、我校参加国内、国际数学建模竞赛的队员将主要从校内竞赛成绩优秀的学生中选拔。
8、竞赛期间学校将对各学院竞赛组织情况进行检查。
2016西北工业大学校赛数模论文
目录1.问题重述 (2)1.1问题背景 (2)1.2题目概述 (2)2.模型假设 (2)3.模型建立 (2)3.1任务一 (2)3.2任务二 (7)3.3任务三 (10)4.结果分析与检验 (12)5.参考文献 (13)6.附录 (14)代码一 (14)代码二 (15)一、问题重述1.1问题背景对于高考考生来说，合理填报志愿是一个非常关键的问题，目前实行平行志愿投档方案（考生知道考分后填报六所高校作为平行志愿），大大降低了考生填报志愿的风险性，减少了高分学生落选的可能。
但每年由于考生定位不准确，志愿高校间没有拉开差距，导致落选或者错报志愿的事情仍然时有发生。
1.2题目概述陕西某高考理科考生2015年考试成绩为630分，他倾向于在本省上大学，该名学生从小喜爱机械，车辆，飞机模型。
在参考以上因素下，协助考生填报志愿。
1.2.1任务一:根据以往几年数据，考虑可能影响的因素建立数学模型，用该模型预测陕西省几个高校理工科一本招生的平均录取线。
1.2.2任务二：建立一个基于已有数据和预测数据的概率评估模型，该评估模型被任务一预测得到平均录取线的高校录取概率。
1.2.3任务三：基于已有的录取分数概率模型和概率评估模型，将报考高校范围扩大到全国高校，根据该生的分数和爱好，协助该生制定一个报考方案，对六个志愿进行合理排序，以保证该生不落榜的前提下选到心仪的高校。
二、模型假设1. 运用灰色预测模型来处理朦胧，关系复杂的数据2. 现行的平行志愿投档方案中，考生在填报志愿时已知本省投档线，所以以录取线差直接作为研究对象．3.. 由于陕西省与2010年开始实行平行志愿录取方法，所以不统计2010年以前的数据信息．4. 采用各高校在某省录取情况的平均录取线作为基本数据，同时预测该校在改省招生的平均录取线．5. 假设2015年较上年未发生大的高考改革变化6. 假设高校并未明显扩招或是缩小招生规模．7.假设考生的成绩符合正态分布。
“工大出版社杯”第十五届西北工业大学数学建模B题论文
“工大出版社杯”第十五届西北工业大学数学建模竞赛暨全国大学生数学建模竞赛选拔赛题目B题剪切线学院第队摘要本文主要研究主要食品价格的波动特点及食品价格与CPI的关联度问题，通过对食品进行分类，建立模型，分析价格波动特点，预测2014年5月主要食品价格的变化走势，同时，分析食品价格与CPI指数的关系，找到价格与CPI指数关联度大的食品，从而达到仅仅通过监测尽量少的食品种类价格即能相对准确地计算、预测居民消费者价格指数，简化统计难度的效果。
问题一针对食品价格波动特点，由于不同食品价格变化可能具有较大差别，我们搜集了2013年全年的主要食品价格，将涉及到的食品分为谷物、油脂、畜肉、禽蛋、水产、果蔬六类，建立价格标准，以2013年1月的食品价格为1，进行无量纲化处理，通过对食品与价格的简化与抽象建立模型，通过与标准参数比较，分别做出各种食品价格变动图表以及各类食品均值变化图表，综合对比，分析异同，从而得出各类食品的价格的季节性、周期性波动特点。
问题二针对预测下月食品价格走势的问题，通过第一问的数据，分析出其属于预测问题。
我们首先采用了处理两个变量之间关系的最简单的方法一元线性回归预测法进行预测。
得出结果后，我们对结果进行了检验，发现一元线性回归预测法的精度不高，考虑到灰色预测法对于数据的要求不高，且精度较好，所以我们改用灰色预测法进行预测。
我们建立GM（1,1）模型，利用第一问的数据，预测出5月的食品价格走势（2013年1月1-10日的价格=1）为：谷物类油脂类畜肉类禽蛋类水产类果蔬类2014.5.1-10 1.0081 0.9938 0.9166 0.9933 0.9706 0.9681 2014.5.11-20 1.0093 0.9928 0.9058 0.9924 0.9661 0.9625 2014.5.21-30 1.0104 0.9919 0.8951 0.9915 0.9617 0.9569 问题三针对各个食品价格与CPI的关联度不同，我们运用灰色关联分析法进行建模，计算各类食品与CPI的关联度。
八队数模A题
“工大出版社杯”第十六届西北工业大学数学建模竞赛暨全国大学生数学建模竞赛选拔赛题目A题剪切线自动化学院第八十八队目录电阻率数据插值加密及成像问题摘要实际中一个形状不规则，质量和密度不均匀物体内部和表面的每一个点的电阻率很难或不能实际测量，这对我们研究物理问题形成了阻碍，为了解决显示的物理问题，我们必须知道或估测出很接近的某一点的电阻率数值，因此，本题意欲通过数学建模求出特定点的电阻率数值，并且证明插值后的极值在同一个位置求得，进而求得加密后的每一点电阻率数据和原网格及其加密后网格的平均值和标准差并对两种算法进行评估，然后对加密后的进行颜色图示表示，观察与原图的对比，最后对两种方法的效果进行定量表示。
第一问建立三次线性插值模型和反加权插值模型计算出定点的电阻率数值，然后通过数学证明得到极值点未发生移动。
第二问运用matlab软件进行插值拟合，将步距由10调成1，借助计算机求得与原数据每一个点对应的电阻率数值，并进而求得插值前后的平均值和标准差，以及进行评估。
第三问运用matlab进行绘图，并分别令z=0和50,得到平面二维的颜色图示，直观地看出电阻率在整个物体以及一个界面上变化情况。
第四问建立结果和定值的关系，定量的分析这两个加密方法的优缺。
关键字：MATLAB软件数据插值曲线插值拟合三维模型插值法颜色图示一模型分析1．问题背景物体的电阻是一个很常用的物理量，有很大的运用价值，尤其是在物理学中，它涉及到很多方面，因此知道物体的电阻率很重要，但是实际物体通常呈现不规则形装和不均匀的质量和密度，导致我们很难知道整个物体各个地方的电阻率，因此迫切地需要一种办法来计算出物体各个地方的电阻率，此题便是基于这个问题所提出来的。
2. 问题分析对于问题一，用附件中给出的数据，用matlab插值法建立三维模型，对于问题二，基于问题一给出的两种方法，在matlab里计算出网格大小为1*1*1时的电阻率数据，再用均值法计算出加密前后的平均值和标准差。
数学建模竞赛 数学建模论文
承诺书我们仔细阅读了数学建模竞赛选拔的规则.我们完全明白，在做题期间不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人研究、讨论与选拔题有关的问题。
我们知道，抄袭别人的成果是违反选拔规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守选拔规则，以保证选拔的公正、公平性。
如有违反选拔规则的行为，我们将受到严肃处理。
我们选择的题号是（从A/B/C中选择一项填写）： C队员签名：1. 徐磊2. 陈立3. 张麒日期： 2012 年 8 月 19 日编号专用页评阅编号（评阅前进行编号）：数学建模竞赛成绩的排名与预测一、摘要自一九九二年数学建模竞赛开展以来，逐渐成为全国高校角逐应用数学能力的舞台。
值此二十年周年之际，我们有必要对以往的成绩进行总结和对未来的发展做出预测。
本文主要解决广东省各高校数学建模成绩的排名与预测、全国各院校自建模竞赛活动开展以来建模成绩的科学、合理的排序两个问题。
针对问题一我们通过“建模水平Q ”这样一个数学指标来对各校的建模成绩进行排名，Q 的确定利用了综合评判的原理，以层次分析法为依据得出国家一、二等奖和省级一、二、三等奖对于Q 的权重ω1=（0.5192,0.2704,0.1136,0.0575,0.0393），由统计得出广东省各高校获奖情况，用向量()c C k 11=（k=1,2,3,4,5）表示。
由()()4,3,2,1111=∙=t C t Q ω求的各高校每年的建模水平，继而对广东省各高校进行一年度的排名。
因为数学建模成绩排名应该贴切的反应一个院校的当前数学建模的综合实力，所以各年的成绩对综合排名的影响也有差异，需要对四年的成绩再次加权，用层次分析法求得：ω2=(),0.0954772,0.16010.4673,0.2；继而求出建模水平ω21)(∙=t Q Q 进行综合排名，排名见附录;对于各广东省各高校2012年数学建模成绩的预测，这里建立了灰色模型预测，得出了建模水平)(1t Q 的预测方程的预测方程ee Q tt t 3709.0)1(3709.08597.98597.9)1(1-+-+-=+,继而把t=5代入方程求出2012年建模水平；部分预测值部分如下；更多可见附表。
数模竞赛成绩
方常靖06020902
程可朋06020902
丁力06020902
6院
王月兴06020901
邱晓星04020902
李洵04020904
6院
王丛飞06010901
傅超06010901
陆勇俊06010901
7院
张志刚7191
郑兴博7191
于悦洋7102
7院
张宝龙7193
于涵7193
张少博7193
7院
韩津易7291
1院
庄文铮01010901
刘凤仙01010901
李家乐01010901
1院
龚煦01010901
王亚星01050901
马鸿01040901
1院
肖自磊01010901
延浩01010901
杨昌发01010901
1院
李耀01010902
周运强01010902
李阳01010902
1院
王龙01010902
卢瑞明01010902
刘中元JS000902
吕永玺JS000902
教育实验学院
张艳霞JS000902
孙海洋JS000904
任仲靖JS000902
教育实验学院
刘思奇JS000902
张睿文JS000905
于树印JS000901
教育实验学院
姜坤JS000902
冯帅JS000902
刘通JS000902
教育实验学院
郭振JS000902
黄立05030801
5院
罗春琦05010804
侯宇戡05010804
陈亚胜05010804
5院
张学振050Байду номын сангаас0804
2015西北工业大学数模竞赛 HK13 my work
装订线“工大出版社杯”第十六届西北工业大学数学建模竞赛暨全国大学生数学建模竞赛选拔赛题目(C)题剪切线航空学院第13 队目录摘要 (2)问题重述 (3)基本假设 (5)符号说明 (5)模型建立 (5)模型求解 (13)参考文献 (20)①摘要本文讨论了西安城轨14号线支线由西北工业大学长安校区起至西太路，正太路一线与14号主线相接的问题。
针对问题一以及问题二，我们设计假设三种方案，并结合实际以及长安区未来发展规划，比较几种方案造价以及效益，得出最优解。
针对问题三，我们通过调查数据计算出通车后，对西工大的科研，教育，经济等方面的有利影响。
对于问题四，我们根据实际情况以及其他城市城轨运行方案给出了一种运行方案。
关键词:轻轨线路，费用预算，综合效益。
一、问题重述:1.0规划线路中西留村沿正太、西太路一线通至草堂科技产业基地。
其间西太路线路距西北工业大学长安校区最短距离约 3.8k m，现在要在西留村至草堂科技产业基地两站点间选定一点，支路直通至西北工业大学长安校区。
请从线路中标定一点，设计出一条线路。
1.1 计算该线路采用地面和高架两种方式铺设的费用。
费用主要包括民房拆迁，征地和工程建设等费用。
可参考其它地方修建的相关费用，并结合实地考察。
最后给出费用最小的道路及施工方式，费用预算。
1.2 该线路一旦修建成功，预测其给全校学生带来的便利，对学校交通费用产生的直接影响。
以及对学校教学、科研、学生培养等综合效益的影响。
1.3 还有什么可以研究的问题？你有何建议？（例如：运营方式的建议）问题分析：轻轨的轨道有地面线、高架线和地下线三种形式,其土建费的比例大致是1 : 2 : 3.4.影响工程造价的主要因素是设备费和土建费两大部分。
根据我国实践, 前者约占工程总投资的25 ~ 30 % ,后②者占35 ~ 4 5 %。
综合提出的问题与西北工业大学长安校区环境条件、人为背景、便利条件、以及轻轨的造价和适合的条件，我们分析了影响和决定整个工程的环境因素、人为因素、路线因素以及资金因素。
2016年全国大学生数学建模竞赛获奖论文
小区开放对道路通行的影响评价模型摘要本文针对小区开放对道路的影响进行了研究，建立了层次分析模型、通行能力评价模型，使用了MATLAB、EXCEL等软件，得出小区开放在不同条件下会对道路交通产生不同的影响。
首先运用层次分析法，分析得出整体一般情况下小区开放有利于周边道路交通的结论。
之后构建了不同类型的小区，并分析得出小区开放的效果与小区结构及周边道路结构、车流量有关，因此小区开放不能盲目采取，要因地制宜。
最后根据分析结果，从交通通行的角度，向城市规划和交通管理部门提出了关于小区开放的合理化建议。
本文的突出特点是使用了层次分析法定量的比较了小区开放前后道路合理性，构建了对于研究该问题具有代表性的三种类型的小区，并建立了影响评估模型，客观的对不同小区结构及周边道路结构、车辆通行的影响进行评价。
针对问题一，首先查阅相关资料选取影响道路通行的指标，并对选取的指标进行筛选，然后运用各项指标进行层次分析，通过小区开放和小区封闭对道路交通和理性的判断来分析小区开放对道路通行的影响最后得出从整体看来，小区开放有利于道路通行。
针对问题二，通过查阅有关道路通行能力的相关资料建立了通行能力评价模型，首先根据模型求出道路基本通行能力的表达式，基本通行能力是理想状态下的通行能力，与实际情况分析对比存在差异。
因此基于差异，通过各实际因素对道路通行能力的影响进行修正，得到实际道路通行能力的数据。
最终计算出小区开放前后实际通行能力的相对系数。
针对问题三，构建了三种类型的小区，不同类型的小区具有不同的结构及不同的周边道路结构、车流量，应用问题二建立的模型分别对三种小区开放和封闭条件下周边道路的实际通行能力进行了计算，通过相对系数评价不同类型的小区开放对道路通行的影响，分析得出小区开放与地理位置、内部结构等因素有关，不能一概而论。
针对问题四，结合前述模型结果分析结果，从交通出行角度对城市规划部门和交通管理部门提出了合理化意见。
小区开放要合理的实施以体现小区开放的意义。
数学建模论文案例.
“工大出版社杯”第十六届西北工业大学数学建模竞赛暨全国大学生数学建模竞赛选拔赛题目A题剪切线机电学院第8 队目录一、摘要二、问题一1.提出问题分析2.定义符号说明3.提出假设4.数学推理证明三、问题二1.提出问题2.问题分析3.定义符号说明4.模型建立5.具体情况模型求解6.模型检验与分析7.模型的评价四、问题三1.提出问题2.问题分析3.定义符号说明4.模型建立5.模型求解6.模型的评价五、参考文献一、摘要五子棋在中国文化里可谓是博大精深，蕴含着深刻的数学思想，而本文就对五子棋中的五连珠问题做出一些研究，在棋盘上的每个小方格中都放上棋子，从中取出一些棋子，使得棋盘上剩下的棋子，没有五个在一条直线（横、竖、斜方向）上依次相连，求满足条件的取出最少的棋子数。
对于这道题目而言，三个问题从特殊到一般，从二维平面到三维空间。
对于二维特殊问题的求解，可以根据简单的数学推理与图形演示来表达。
而对于二维平面和三维空间这个一般问题而言，就不能通过简单的图示来表示，只能够通过计算机编程与优化进行讨论，而对于解法，我们则采用回溯法和递归的思想。
针对问题一，在6*7的棋盘上取出一些棋子，我们采用数学推理证明的思想得出答案，通过画图找到一种取出8个棋子满足，之后我们通过在一些规律下的逻辑推理证明7个确实不满足要求，所以8个为最终解。
针对问题二，则是相对问题一的一般情况，将棋盘的大小扩充到m*n的情况，此时利用数学推理证明的思想是行不通的，我们的想法是首先采用0和1的思想，将需要取出的棋子的位置标为0，有棋子的位置标为1 。
每一个棋盘的位置点可以用一个二维数组char[row][column]来表示。
通过对题目的数学理解，我们发现此题与“八皇后问题”十分类似，都采用“马走日”的思想。
但对于“五子连珠”问题，每行每列可以有多个“0”元素，显然较之复杂。
但是我们可以将其抽象为“五皇后”问题，然后进行5*5矩阵的叠加与和递归的想法，首先把第一行处理，然后其他行列根据第一行进行排列，最后输出整个矩阵与所求k值。
2013年西北工业大学数学建模竞赛特等奖论文-朱斌_崔雄一_张文.供应链物流网络与破坏研
目
摘
录
要 ......................................................................................................................... I
一、问题引入 ............................................................................................................... 1 二、问题分析 ............................................................................................................... 1 2.1. 问题一供应链网络设施决策问题分析......................................................... 2 2.2. 问题二、三供应量网络破坏问题分析......................................................... 2 2.2.1 问题二（确定性破坏）分析................................................................ 3 2.2.2 问题三（随机性破坏）分析................................................................ 3 三、基本假设 ............................................................................................................... 4 四、名词解释与符号系统 ........................................................................................... 4 4.1. 名词解释......................................................................................................... 4 4.2. 符号系统......................................................................................................... 5 五、模型的建立与求解 ............................................................................................... 5 5.1. 0-1 规划模型决策供应链网络建设（问题一） ........................................... 5 5.1.1 需求点和供应点间最短距离矩阵........................................................ 5 5.1.2 0-1 规划模型 ....................................................................................... 6 5.1.3 问题一求解.......................................................................................... 7 5.2. 确定性破坏（问题二）................................................................................. 9 5.2.1 供应链破坏损失评估............................................................................ 9 5.2.2 最小破坏数的规划模型...................................................................... 10 5.2.3 最小破坏规划模型求解...................................................................... 11 5.3. 随机性破坏（问题三）............................................................................... 13 5.3.1 随机性破坏规划决策........................................................................... 13 5.3.2 随机性破坏决策................................................................................... 14 5.3.3 随机性破坏决策模型的拓展（普遍破坏模型）............................... 16 六、模型的检验与评价 ............................................................................................. 17 5.1. 模型的检验................................................................................................... 17 5.2. 模型的优点................................................................................................... 17 5.3. 模型的缺点................................................................................................... 17 七、模型的推广 ......................................................................................................... 18 参考文献 ..................................................................................................................... 19 附 录 ........................................................................................................................... 20
西北工业大学竞赛获奖推荐免试名单
17
134
12.69%
606
535
10
11
113
9.73%
467
455
11 12 13
明瑞晨 柴源
2013302155 2013300684
自动化学院 航天学院
自动化
09011302
男 女
第十七届全国机器人锦标赛宠物机器人智能化创 国家级一等奖 新设计一等奖 2016年美国大学生数学建模竞赛二等奖 国际级二等奖
2
7 32 34
27 68 134
25.92% 47.00% 25.37%
565 500 590
457 413 548
郭靖 韩昌富
2013300611 2013301659
航天学院
男 男
1 2
41 42
动力与能源学 飞行器动力 07011302 院 工程 电子信息学院 电磁场与无 08051302 线技术
37
杨鸿杰 苏秀中
2013300576 2012301054
航天学院 机电学院
男 男
1 3
14 47
44 97
31.80% 48.50%
476 525
437 464
38 39 40
张茜
2013300384
航空学院
女
中国国际飞行器设计挑战赛暨科研类全国航空航 国家级一等奖 天模型锦标赛 限时载运空投项目 15、16年美国大学生数学建模竞赛二等奖 2015中国机器人大赛暨robocup公开赛（自创异 形）一等奖冠军 2015中国机器人大赛暨robocup公开舞蹈机器人 （自创多足异形）冠军 国际级二等奖 国家级冠军
6
27
22.20%
2016年数学建模竞赛A题优秀论文
对于问题 2，根据题目所给的数据信息及要求，可以利用问题 1 中的数学模 型，求解出海面风速为 36m/s 时，钢桶和各节钢管的倾斜角度，链条形状和浮标 的游动区域。要求调节重物球的质量，使得钢桶的倾斜角度不超过 5 度，最后一 节锚链与海床的夹角不超过 16 度。对此，以钢桶的倾斜角度和最后一节锚链与 海床的夹角为约束条件，逐步增加重物球的质量，采用二分法，对海水深度进行 求解，当计算值与实际深度相等时，重物球的质量即所需的最小质量。
5.1 模型一的建立与求解
5.1.1 模型一的建立 由题可知，近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统
组成（如图 1 所示），对此，我们可建立力学分析模型，依次对浮标、钢管、钢 桶和锚链的受力平衡和力矩平衡进行分析，将浮标与第一节钢管的结点记为 1， 以此类推将倒数第一节与倒数第二节锚链链接点记为 n；同理，将第一节钢管记 为 1，最后一节锚链记为 n，因此：
西工大数学建模竞赛中取得佳绩
西工大在2011年全国研究生数学建模竞赛中取得佳绩
作者：周玮来源：研究生院发布时间：2011-11-22
10:11 阅读次数：693次发表
评论
西工大新闻网11月22日电日前，2011年全国研究生数学建模竞赛成绩揭晓。
西北工业大学在此次竞赛中，共荣获全国一等奖2项、全国二等奖3项、全国三等奖3项的优异成绩。
根据竞赛章程，此次竞赛全国一等奖比例仅为
3.21%，全国二等奖比例为17.24%。
2011年全国研究生数学建模竞赛于九月顺利举行，包括全国31个省、市、自治区的242所高校和全国各研究院在内的2245支代表队报名参赛，其中有博士生300多名。
西工大此次派出10支代表队参赛，参赛规模为近8年来之首，获奖等级以及数量也均为历史最好，成绩位居全国高校前列。
全国研究生数学建模竞赛的宗旨是提高我国研究生的培养质量，增强研究生解决实际问题的能力，培养研究生在工作中的科学态度和严谨的学风。
2011年全国研究生数学建模竞赛获奖名单
（编辑：袁旭霞）相关链接：
·明德学院宋士贤主编的《工科物理教程》获陕西高校优秀教材一等奖·我校荣获2011年度“陕西省民族团结进步创建活动先进集体”称号
·明德学院在2011年全国健美操推广普及赛（陕西赛区）中取得佳绩
·翱翔之声男声合唱团在“第三届全国大学生艺术展演”中创佳绩。
西北工业大学校内数学建模竞赛试题集锦
西北工业大学校内数学建模竞赛试题集锦(总9页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除西北工业大学校内数学建模竞赛试题集锦2001年试题A最优控制设计在计算机控制过程中，一条计算机子令往往可以控制几个计算机部件，反过来，一个部件一般由几条指令控制。
一个基本的问题是，在指令集合里寻找最少的指令，使得所有的部件得到控制；另一个问题是，当给定每条指令的长度时，在指令集合里，寻找总长度最小的若干指令，使得他们可以控制全部部件。
1、建立解决上述两个问题的的数学模型；2、设计模型的求解算法，用表一所列数据给出求解结果；3、分析所设计算法的复杂性和计算所得到结果。
附表一：指令控制的部件和指令的长度B题：大学教师综合水平与业绩测评模型通过对校、系有关部门的调研，建立“大学教师综合水平与业绩测评模型”。
要求：1、建议考虑如下指标：主持参加的科研项目数及到款金额，科研项目种类；科研获奖情况；发表论文数，发表论文被引用和索引情况；发表论文刊物级别；教学时数；课程难易程度；指导研究生数；教课门数；教学获奖情况；学位状况等2、通过建立模型与相应的指标体系，编制实用程序，输入若干位教师的相应数据，可给出量化分，并排序；3、给出一实例分析，讨论模型的区分程度及优缺点；4、要求附软盘、相关数据以及程序、程序运行环境的详细说明。
2002年试题A:汉江安康站最大、最小泾流量的数学模型气候是重要的环境因素，研究我国干旱和半干旱地区的气候变化规律，对确定陕西的经济发展战略，制定发展规划具有重要意义。
1．请根据陕南汉江安康站统计的最大、最小泾流量数据表1，分析这些数据之间的关系；2．建立最大、最小泾流量适当的数学模型，并检验模型的合理性；3．利用您所建立的模型，对1998，1999，2000，2001，2002年汉江安康站的最大、最小泾流量进行预报，并与实际情况进行比较。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
使用符号
符号说明
S
猩猩或人中易感群数量
E
猩猩或人中潜伏群数量
I
猩猩或人中感染群数量
R
猩猩或人中退出群数量
猩猩或人退出群中死亡的数量
猩猩或人退出群中自愈（治愈）的数量
潜伏者日接触率,即当易感者和感染者有效接触时,成为潜伏者比率
感染者日接触率,即当易感者和感染者有效接触时,成为感染者比率
潜伏群的发病率
从图像我们可以分析出，在开始统计的பைடு நூலகம்11周-100周的时间内，每一周存在的感染者与潜伏者在逐渐减小，但是同时，因病死亡与自愈康复的猩猩数量都在较快的增长，说明这段时间疫情仍然较为严重。
在大约第120周以后，感染者、潜伏者、死亡与自愈者都已经基本达到自己的稳定值，这是说明疫情已经基本上得到控制，猩猩已经基本不再感染埃博拉病毒。
本题希望同学们通过数学建模的方法量化埃博拉病毒的传播规律，深刻认识该病毒的危害，并分析隔离措施的严格执行和药物治疗效果的提高等措施对控制疫情的作用。
假设某地区有20万居民和3000只猩猩。人能以一定的概率接触到所有的猩猩，当接触到有传播能力的猩猩后有一定概率感染病毒，而人发病之后与猩猩的接触可以忽略。人与猩猩的潜伏期都为2周。请你根据相关信息，研究回答以下问题：
1）潜伏者日接触率 (t)：
(3)
2）感染者日接触率 (t):
(4)
3）退出率 ：
(5)
4）潜伏群发病率 ：
= (6)
由我们整理出来的数据带入以上公式，估算得：
求出微分方程的参数后，我们根据整理出来的数据特点进行判断，选取第11周时的S、E、I、R值作为初值，即：
利用MATLAB编写程序（程序源代码见附录2），将参数以及初始值导入微分方程组（1）进行求解，预测出的S、E、I、R四个群的数量变化分别如下：
潜伏群体
处于发病状态
累计自愈
累计因病死亡
第80周
4
8
257
515
第120周
1
2
272
545
第200周
0
0
275
551
问题二
针对描述埃博拉病毒在人群与猩猩群中相互传播特性以及预测人和猩猩中疫情变化的问题，本题中假设了病毒只能由猩猩传染到人。问题一中的SEIR模型虽然是对一种物种内部的传染模型，但我们认为传播模型是可以推广的,即在某一物种内部,埃博拉病毒的传播应该有着相同的规律；另外,在多个物种之间,埃博拉病毒的传播也应有类似的规律。因此，我们就以问题一的SEIR模型为基础进行改进,引入猩猩群对人群的影响因子，建立跨物种传播的SEIR模型，建立微分方程组求解出如下结果：
3、假设在第41周，外界的专家开始介入，并立即严格控制了人类与猩猩的接触，且通过某种特效药物将隔离治疗人群的治愈率提高到了80%。请预测接下来疫情在“虚拟人类种群”的发展情况，对比第2问的预测结果说明其作用和影响，给出“虚拟人类种群”在第45周、第50周、第55周的相关数据；
4、请依据前述数学模型，分析各种疫情控制措施的严格执行和药物（包括防疫药物、检疫药物和治疗药物等）效果的提高等措施对控制疫情的作用。
1.2.4 问题四
问题四需要我们分析各种疫情控制措施的严格执行和药物（包括防疫药物、检疫药物和治疗药物等）效果的提高等措施对控制疫情的作用。那我们就需要利用没有控制措施时的疫情情况与控制时的疫情相比较，得出采取的措施对于控制疫情的作用。
二、问题假设
2.1、假设附件中提供的采样数据准确无误且具有充分的代表性
图6猩猩死亡群（R1）与自愈群（R2）数量的实测值
将附件一中的死亡群与自愈群带入方程组（2）可以求得每周死亡数量与每周自愈数量的相关度：
r=0.869
说明死亡群组与自愈群组的相关度很高，即我们可以视为每周死亡数量与自愈数量的变化是同步的，因此他们各自占退出群的比例可以视为保持不变。
通过计算我们得知第一问题的结果 ：
因此，我们改进SIR模型，加入潜伏群，建立更加适应于埃博拉病毒传播特点的SEIR模型，利用SEIR模型建立起微分方程组，利用微分方程解出的函数对题目要求的进行预测。
1.2.2 问题二的分析
第二个问题需要我们建立“虚拟种群”相互感染的疾病传播模型，描述人和猩猩疫情的发展，预测接下来疫情在这两个群体中的发展情况。这实际上是两个变量之间的关联度描述与预测问题。
表1“虚拟猩猩种群”群体数量预测结果（单位：只）
潜伏群体
处于发病状态
累计自愈
累计因病死亡
第80周
4
8
257
515
第120周
1
2
272
545
第200周
0
0
275
551
4.1.3
根据模型求解结果我们发现，易感群、感染群与潜伏群的变化趋势基本一样。通常在疫情爆发时，感染群数量和潜伏群数量都是呈指数型增长，因此本题中给出的数据应该是在疫情已经爆发了一段时间以后，这时疫情已经由于生态系统自身的调节能力而得到控制，因此感染者与潜伏者数量会逐渐下降最终趋于平缓，而退出群虽然会逐渐增加，但是由于最后疫情得到控制，感染者与潜伏者趋于平缓，那么退出群也会逐渐趋于平缓直到达到上限。
由于我们没有病毒在单一人群中传播的原始数据，这样我们无法利用SEIR模型进行预测。理论上，我们应该在第二问的基础上，计算出与猩猩接触而成为潜伏者和感染者的人数Bt，然后用已知总数减去Bt，得到病毒在人群中单一传播时的数据，以此为依据对问题进行求解。
实际上，由于易感人群数高达10E6数量级，而猩猩感染群只有10数量级，差距非常大，因此猩猩感染群对于人群的传染作用在此问题中可以忽略，我们可以直接用题目中的数据对人的SEIR群变化进行预测。
图2猩猩易感群（S）数量的实测值与预测值
图3猩猩潜伏群（E）数量的实测值与预测值
图4猩猩感染群（I）数量的实测值与预测值
图5猩猩退出群（R）数量的实测值与预测值
以上我们分别预测出了处于S、E、I、R四个群中的猩猩数量，现在我们需要将退出群（R）分解成两部分即分别还需要求解出死亡猩猩（R1）和自愈猩猩（R2）的数量。根据附件一，我们作出死亡群（R1）与自愈群（R2）的图像如下：
2.2、假设短期内猩猩与人类的出生率死亡率对种群数量影响不大
2.3、假设死亡后的猩猩与人类不再具有感染能力
2.4、假设易感者一旦和感染者进行有效接触就会被感染成为潜伏者
2.5、假设单位时间内一个感染者能传染的数量与易感群数量成正比
2.6、假设所有自愈或治愈者不再复发
2.7、假设所有潜伏期病人都会在两周后发病
另外，题目中要求的是退出群中死亡与自愈分别是多少，我们的模型中的退出群是两个之和，似乎无法得出题目要求的值，但是我们通过分析能够发现退出群中自愈量与死亡量是存在关系的，我们可以通过选取死亡群组（R1）作为参考数列，建立灰色关联度模型求解死亡群组（R1）与自愈群组（R2）的关系：
(2)
4.1.2
现在我们根据建立的模型利用已知数据进行求解，我们将题目中给出的数据进行整理，得出我们建模求解需要的S、E、I、R四个群的猩猩数量（见附录1），并且利用整理出的已知数据对微分方程组中的参数进行求解：
1、建立一个病毒传播模型，动态描述病毒在“虚拟猩猩种群”中的传播，并预测接下来的在猩猩中的疫情变化，并给出“虚拟猩猩种群”在第80周、第120周、第200周的相关数据；
2、建立“虚拟种群”相互感染的疾病传播模型，综合描述人和猩猩疫情的发展，并预测接下来疫情在这两个群体中的发展情况，并给出 “虚拟人类种群”在第80周、第120周、第200周的相关数据；
1.2 问题的分析
1.2.1 问题一
问题一需要我们根据猩猩的发病数量和死亡数量，建立一个病毒传播模型，动态描述病毒在“虚拟猩猩种群”中的传播，并预测接下来的在猩猩中的疫情变化，这其实是一个数学上的预测问题。
针对预测问题，我们可以采用常用的时间序列模型或者灰度预测模型，但是针对病毒的传播，其自身有更加贴近实际的SIR模型，但由于SIR模型通常不考虑潜伏群的影响以及变化，而此题要求我们对潜伏群进行研究。
一、问题的重述与分析
1.1 问题的重述
埃博拉病毒有传染性，主要是通过病人的血液、唾液、汗水和分泌物等途径传播。病毒的潜伏期通常只有5天至10天，感染后2～5天出现高热，6～9天死亡。埃博拉病毒只有病人在出现埃博拉症状以后才具有传染性。存在似乎天生就对埃博拉免疫的人，痊愈之后的人也会对入侵他们的那种埃博拉病毒有了免疫能力。
潜伏人群
处于发病状态
隔离治疗
累计治愈
累计因病死亡
第80周
105.4
17.53
12.5
1164.4
2985.6
第120周
101.7
5.491
4.3
1330.5
3448.5
第200周
100.9
0.4208
0.3
1397.0
3621.0
问题三
针对此问中采取隔离与治愈感染者的措施后，要求预测疫情在人类中的发展情况、并与问题二结果作比较的问题，我们利用问题二的结论排除猩猩对人的影响后，此时病毒是在单物种内传播，适用于我们建立的单物种SEIR模型。利用排除猩猩影响后得到的数据，建立微分方程解得：
传染群的退出率(包括死亡和治愈)
r
死亡群数量数列与自愈(或治愈)群数量数列的相关度
λ(t)
B物种与A物种接触群日增长率
p(t)
B物种接触群到潜伏群的比率
q(t)
B物种接触到感染群的发病率
四、模型的建立与求解
4.1 问题一
4.1.1
图1猩猩中S、E、I、R关系图
在本题中，我们将未被感染过的健康猩猩作为易感群（S），易感群与感染者有效接触后，并不会立刻成为感染者，而是全都是进入潜伏期，且所有潜伏期患者都是两周后开始发病，因此，每一周的潜伏群E（t）就等于之后两周感染群的和I(t+1)+I(t+2)。同时因为死亡与自愈的猩猩不会再对别的猩猩产生影响，因此我们把死亡与自愈的猩猩同时都计入退出群。由此我们建立以下微分方程组：