工程力学(静力学与材料力学)第五章空间任意力系详解
工程力学(静力学与材料力学)单辉祖5

Generated by Foxit PDF Creator © Foxit Software For evaluation only.
工程力学电子教案
第五章 空间任意力系
X 0, TA TB cos60 0
T A TB cos60 3 1 80 11.5 ( N ) 6 2
Z F cos F sin
力沿坐标轴分解
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
由式(*)知 合力的大小:
* 合力的方向:
空间汇交力系的合力与方向余弦为:
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
力对轴的矩的概念
P39--P40
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
[例] 已知:P=2000N, C点在Oxy平面内。求:力P对坐标轴的矩。
解:
Pz Psin45 Pxy Pcos45 Px Pcos45sin60 Py Pcos45cos60
力对轴的矩的解析式
mx ( F ) yFz zFy m y ( F ) zFx xFz mz ( F ) xFy yFx
力对轴的矩的解析式
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
工程力学(一)重点考点及试题解析

《工程力学(一)》串讲讲义】课程介绍一、课程的设置、性质及特点《工程力学(一)》课程,是全国高等教育自学考试机械等专业必考的一门专业课,要求掌握各种基本概念、基本理论、基本方法,包括主要的各种公式。
在考试中出现的考题不难,但基本概念涉及比较广泛,学员在学习的过程中要熟练掌握各章的基本概念、公式、例题。
本课程的性质及特点:1.一门专业基础课,且部分专科、本科专业都共同学习本课程;2.工程力学(一)课程依据《理论力学》、《材料力学》基本内容而编写,全面介绍静力学、运动学、动力学以及材料力学。
按重要性以及出题分值分布,这几部分的重要性排序依次是:材料力学、静力学、运动学、动力学。
二、教材的选用工程力学(一)课程所选用教材是全国高等教育自学考试指定教材(机械类专业),该书由蔡怀崇、张克猛主编,机械工业出版社出版(2008年版)。
三、章节体系依据《理论力学》、《材料力学》基本体系进行,依次是第1篇理论力学第1章静力学的基本概念和公理受力图第2章平面汇交力系第3章力矩平面力偶系第4章平面任意力系第5章空间力系重心第6章点的运动第7章刚体基本运动第8章质点动力学基础第9章刚体动力学基础第10章动能定理第2篇材料力学第11章材料力学的基本概念第12章轴向拉伸与压缩第13章剪切第14章扭转第15章弯曲内力第16章弯曲应力第17章弯曲变形第18章组合变形第19章压杆的稳定性第20章动载荷第21章交变应力●静力学公理和物体受力分析静力学公理:二力平衡公理:作用在刚体上的二力使刚体平衡的充要条件是:大小相等、方向相反、作用在一条直线上。
应用此公理,可进行简单的受力分析。
加减平衡力系公理:在作用于刚体的已知力系中加上或减去任何平衡力系,并不改变原力系对刚体的效应。
力的平行四边形法则:作用于物体上某一点的两力,可以合成为一个合力,合力亦作用于该点上,合力的大小和方向可由这两个力为邻边所构成的平行四边形的对角线确定。
力的可传性原理:作用于刚体上的力可沿其作用线移至同一刚体内任意一点,并不改变其对于刚体的效应。
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
工程力学(静力学与材料力学)(第2版)教学课件第5章 空间任意力系

分力对同一点(或轴)之矩的矢量和(或代数和)。
工程力学(静力学与材料力学)
6
例题:在棱长为 b 的正方体上,作用一力 F,试求该力 对三坐标轴以及OA轴之矩。
解:
M x (F ) Fb
M y(F)Mz(F)0
MO (F ) Fbi
设沿OA的单位矢量为s,则
3bs bi bj bk
s 3(i jk) 3
cos(MO ,i)
MOx MO
M x (F ) MO
cos(MO
,
j)
MOy MO
M y (F MO
)
cos
(MO
,k
)
MOz MO
M z M
(F
O
)
MO Mx 2 M y 2 Mz 2
工程力学(静力学与材料力学)
10
§3 空间任意力系的平衡条件
空间任意力系的平衡条件
空间任意力系平衡的必要充分条件是:力系的主矢与 对任一点O的主矩均为零。
[MO (F )]y zFx xFz
[MO (F )]z
xFy
yFx
[MO (F )]x [MO (F )]y
M M
x y
(F (F
) )
[MO (F )]z M z (F )
力对点之矩矢在该点任意轴上的投影,等于此力对
该轴之矩,称为力矩关系定理。
工程力学(静力学与材料力学)
5
合力矩定理一般表述
Fx 0, Fy 0, Fz 0,
FAx Fx 0 FAy Fy 0 FAz Fz 0
FAx Fx FAy Fy FAz Fz
M x (F)0, M Ax Fzr0 M Ax Fzr
M y (F )0, M Ay Fzl 0 M Ay Fzl
工程力学课后知识题目解析
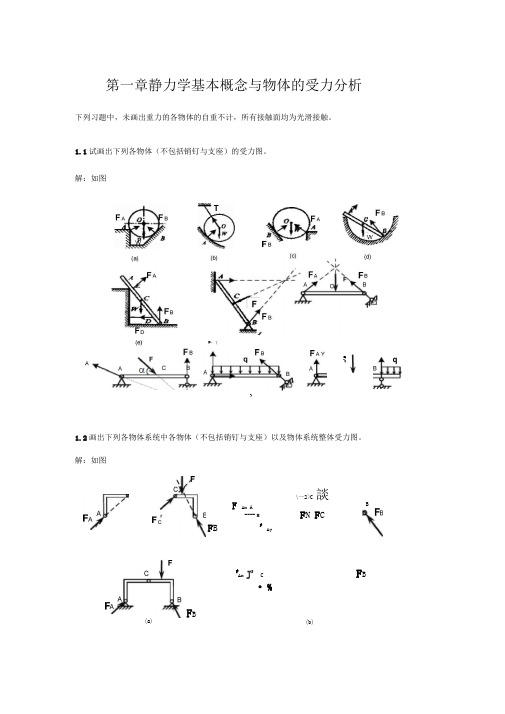
第一章静力学基本概念与物体的受力分析下列习题中,未画出重力的各物体的自重不计,所有接触面均为光滑接触。
1.1试画出下列各物体(不包括销钉与支座)的受力图。
解:如图1.2画出下列各物体系统中各物体(不包括销钉与支座)以及物体系统整体受力图。
解:如图F B F Ax A---- M\—2>C 談F N F CFAyBF B (a) FAx J' CF B• %(b)x-7丫AFaFC(d)(C)(e) (f)(g)(h)OAF12 ◎F F(i)1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成,如题 1.3图所示。
在定滑轮上吊有重为W的物体H。
试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。
解:如图1.4题1.4图示齿轮传动系统,O i为主动轮,旋转方向如图所示。
试分别画出两齿轮的受力图。
解: Bxo2y1.5结构如题1.5图所示,试画出各个部分的受力图。
解:第二章汇交力系2.1在刚体的A点作用有四个平面汇交力。
其中F i = 2kN , F2=3kN , F3=lkN , F4=2.5kN , 方向如题2.1图所示。
用解析法求该力系的合成结果。
F1 = 1kN , F2=2kN , F3=|.5kN。
求该力系解F RX=' X = F J COS300 F4 COS450 - F2 COS600 - F3 COS450 = 1.29KN F R y 八丫=F1 sin300 -F4cos450 F2 sin600 - F3 cos450 = 2.54KNF R - F RX F Ry =2.85KN(F R,X)二arctan^ =63.0702.2题2.2图所示固定环受三条绳的作用,已知的合成结果。
解:2.2图示可简化为如右图所示F R^ \ X -F2 F3COS60° =2.75KNF Ry 二'丫二F i —F s Sin600= —0.3KNF R— F RX F Ry =2.77KNF3FRy 0W(F R ,X)二 arctan6.2F Rx2.3力系如题2.3图所示。
工程力学(静力学与材料力学) 单祖辉 谢传峰合编 课后习题答案
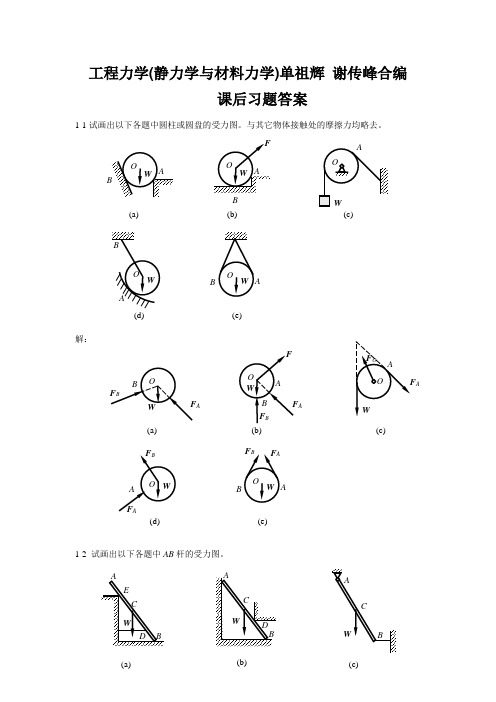
工程力学(静力学与材料力学)单祖辉 谢传峰合编课后习题答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a)(b)c)(d)A(e) A(a)(b) A(c)A(d)A(e)工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)DBF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
(d)FC(e)WB(f)F FBC(c)(d)(b)e)解:(a)(b)(c)(d)(e)ATF BAFCAA C’CDDC’B2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
工程力学课后习题答案(静力学和材料力学)
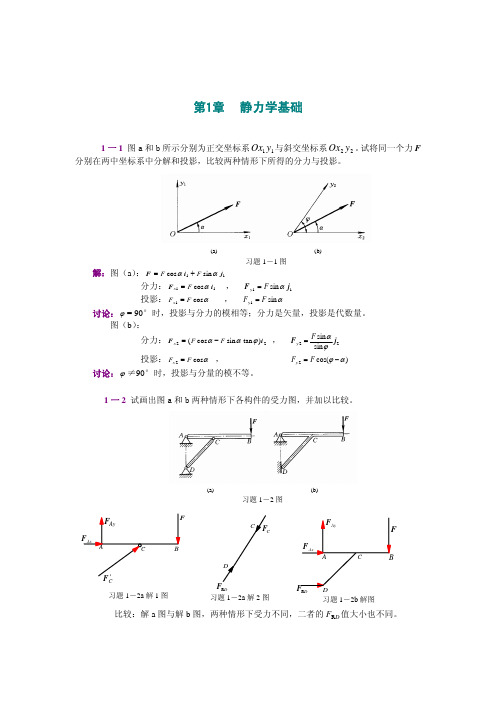
1 一 3 试画出图示各构件的受力图。
F
D
习题 1-3 图
C
F
D
C
A
B
FA
FB
习题 1-3a 解 1 图
F Ax
A
B
FAy
FB
习题 1-3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1-3b 解 2 图
W
FAx
FAy
习题 1-3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1-3d 解 2 图
FB2 x
B
FDy
C FB2 y
F Dx D
W
习题 1-4b 解 2 图
F'B1
B
F'B2x
F'B2 y F1
A B
F'B2x
习题 1-4c 解 1 图
F1 F'B2 y
FDx D FDy
F'B2x B
C
F'B2 y
W
F'B2 B
习题 1-4c 解 2 图
习题 1-4b 解 3 图
FA
A
B
F B1
习题 1-4d 解 1 图
可推出图(b)中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1-12 解 1 图
F AB 习题 1-12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点,滚子搁置在倾斜的光滑刚性平面上,如
工程力学重点

1、物体系统平衡问题; 2、速度、加速度分析问题; 3、组合变形
总复习
提醒
1、带着作图工具和计算器; 2、计算题需作图旳必须作图; 3、做题环节要规范。
总复习
总复习
6、拉伸(压缩)与弯曲旳组合 横截面旳最大拉压正应力
F M
AW
当外力作用线与杆旳轴线平行但不重叠时,将引起 轴向拉伸(压缩)和平面弯曲两种基本变形。也称为 偏心拉(压)——单向应力状态。
总复习
7、弯曲与扭转旳组合 用内力表达旳圆杆弯曲和扭转组合变形强度条件
r3
1 W
r4
1 W
M 2 T 2 [ ] M 2 0.75T 2 [ ]
总复习
第6章 扭转
1、切应力互等定理
2、剪切胡克定律
G
3、外力偶矩
Pk
Pk
总复习
4、扭矩图旳画法 5、圆轴扭转时旳应力和强度条件
T
I p
max
TR IP
T IP
T Wt
R
max
T Wt
[ ]
(1) 切应力分布规律
(2) 抗扭截面系数旳计算
(3) 低碳钢圆轴扭转破坏是沿横截面剪切破坏,铸铁圆轴 扭转破坏是沿与轴线成45º旳斜面被拉断。
(3) 两个强度指标: s及b。
(4) 两个塑性指标:
l l 100%
l
A A 100%
A
(5)几种材料拉伸时旳力学性能比较。
总复习
5、交变应力和疲劳破坏旳概念。 6、剪切与挤压旳实用计算 (1) 注意有两个剪切面旳双剪对剪力旳影响。
(2) 剪切计算面积为实际受剪面积;挤压面计算面积,如挤 压面是平面,按实际挤压面积计算。当挤压面为曲面时 取挤压面在挤压力方向旳投影面积。对挤压面为半圆柱 面,如铆钉等,其挤压计算面积为直径乘被连接件厚度: d×t 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i
j
k
M O (F ) r F x y z X Y Z
=(yZ-zY )i + (zX - xZ)j + (xY -yX )kz§5-1Fra bibliotek力对轴的矩
力对轴之矩是力对 绕该定轴转动的物体作 用效果的度量
门上作用一个力 F 假定门绕 z 轴旋转 将力 F 向 z 轴和 xy 面分解成两个分力 Fz 和
3、空间力系简化为力螺旋的情形
主矢R’ ≠ 0;主矩MO ≠ 0
MO O R O R , MO O MO O
且
R
M O∥ R ’
R MO
右螺旋
左螺旋
力螺旋就是由一个力和一个力偶组成的力 系,其中的力垂直于力偶作用面 力螺旋的力作用线称为力螺旋的中心轴 力螺旋由两个力学基本要素组成,不能进 一步合成
R ( X ) 2 ( Y ) 2 ( Z ) 2
cos(R, i ) X / R; cos(R, j ) Y / R; cos(R, k ) Z / R
M O [ M x (F )]2 [ M y (F )]2 [ M z (F )]2
cos(M O , i ) M x (F ) / M O ; cos(M O , j ) M y ( F ) / M O ; cos(M O , k ) M z (F ) / M O
当主矩MO与主矢R’即不平行也不正交时
R’ R’
α
R’ M ’O M”O M ’O
MO
O
O
O d
M”O = MO sinα ;M’O = MO cosα M’O和R’组成力螺旋,其中心轴距O点的距离为: M O sin MO d R R
4、空间力系简化为平衡的情形
主矢R’ = 0;主矩M
§5 - 2
F2
空间力系向一点简化
F1
M1
F2
O
, ,
F1 ,
Mo O
R,
F3
MF 2 3
O M3
O : 简化中心
R = F1 + F2 + F3 ;
M o = M1 + M2 + M3 ;
R
——
F
i 1
n
i
MO
——
M
i 1
n
O
( Fi )
力系的主矢
力系对简化中心主矩
结论
空间任意力系向一点简化,可得一力和一个力 偶。这个力的大小和方向等于该力系的主矢,作用 线通过简化中心O;这个力偶的矩矢等于该力系对 简化中心的主矩。 主矢与简化中心无关;主矩与简化中心的位置 有关。
z
( F ) = M
y
(BC) = - Fl cosα
M
z
( F ) = M
z
( Fx ) = -F
x
(AB+CD) = -F ( l + a )sinα
解法2
直接套用力对轴 之矩的解析表达式: 力在 x、y、z轴 的投影为 X = F sin α Y = 0 Z = - F cos α
z
A Fx x B
F Fz Fxy
Fxy。
分力 Fxy 使门绕 z 轴 旋转。
y x
力对轴的矩之定义
力对轴的矩是一个代 数量,其绝对值等于该力在 垂直于该轴的平面上的投影 对于此平面与该轴的交点的 矩的大小。顶着坐标轴看力 使物体绕轴逆时针旋转为正。 正负可以按右手法则确定 即 ① ②
z
F
Fz Fxy
B h
O
F A xy
可得 [ M [ M [ M
O O
O
( F ) ] ( F ) ] ( F ) ]
x y
z
= = =
M M M
x y
( F ( F
) )
z
( F )
结论: 力对点的矩 矢在通过该 点的某轴上 的投影,等 于力对该轴 的矩。
力对点O的矩的大小为
M O ( F ) [ M x ( F )]2 [ M y ( F )]2 [ M z ( F )]2
力对点O的矩的方向余弦为
M x (F ) cos M O (F )
cos
M y (F ) MO (F )
M z (F ) cos MO (F )
5-1 图中力F的大小为10kN,求的力 F 在 x、 y、z三坐标轴的投影,以及对三坐标轴的矩和对 O点的矩。(长度单位为m) 解: z 1、先求F的三个方向余弦
cos(i , M O (F )) Mx 0.82 M O (F )
2
2
2
cos( j, MO (F ))
My MO (F )
0.51
Mz cos(k , M O ( F )) 0.25 MO (F )
手柄 ABCE 在平面 Axy内,在D 处作用 例 5-2 一个力F,它垂直y轴,偏离铅垂线的角度为α ,若 CD = a,BC∥x轴,CE ∥y轴,AB = BC = l。求力F 对x、y和z三轴的矩。
空间力系的简化结果分析
1、空间力系简化为一个合力偶
主矢R’ = 0;主矩MO≠ 0 主矩与简化中心无关。
2、空间力系简化为一个合力
① 主矢R’ ≠ 0;主矩MO = 0 ② 主矢R’ ≠ 0;主矩MO ≠ 0 且 MO⊥ R’
MO
O
取
R
d= |MO| / R
O d
R”
R R
O
R
MO
O
合力矩定理
R
空间力系平衡的充分必要条件: 所有力在三个坐标轴中的每一个轴上的投影 的代数和等于零,以及这些力对于每一个坐标轴 的矩的代数和也为零。 除了上述的基本方程,还有所谓的 4 力矩、 5力矩和 6 力矩式。
几种特殊情形平衡规律
[Ⅰ] 汇交力系 有三个平衡方程:
∑X = 0,∑Y= 0,∑Z = 0
[Ⅱ] 平行力系(假定力的作用线平行 z 轴) ∵ ∑X≡0,∑Y≡0 ,∑Mz ≡ 0 ∴ 平行力系有三个平衡方程:
O
= 0
§5 - 3 空间任意力系的平衡方程
由: R ( X ) 2 ( Y ) 2 ( Z ) 2 0
M O [ M x (F )]2 [ M y (F )]2 [ M z ( F )]2 0
X 0; Y 0; Z 0 得: M x ( F ) 0; M y ( F ) 0; M z ( F ) 0
,
R”
O d
R R
,
O
R
R =∑Fi ,d= |MO| / R ∵力偶(R,R’’)的矩MO等于R 对O点的矩,即 MO = MO(R) ,而又有 MO = ∑MO(F) ∴得关系式 MO( R ) = ∑MO(F )
即:空间任意力系的合力对于任意一点的矩等于 各分力对同一点的矩的矢量和。 将上式向任意轴投影(如 z 轴)得: Mz ( R ) = ∑M z( F )
∑Z = 0,∑M
x
= 0 ,∑M
y
= 0
[Ⅲ] 平面一般力系(假定力的作用面为Oxy面) ∵ ∑Z≡0 ,∑Mx ≡ 0 ,∑My ≡ 0 ∴平面一般力系有三个平衡方程:
∑X = 0,∑Y= 0,∑M
z
= 0
例 5-3 均质长方形薄板重 W = 200N,用球形铰
链A和蝶形铰链 B 固定在墙上,并用二力杆 EC 将板维持水平。求 EC 杆的拉力和铰链的反力。
力对轴的矩等于零的情形:
M z( F ) = M O ( Fxy ) = ± Fxy h = ± 2△OAB
力与轴相交( h = 0 ) 力与轴平行( Fxy = 0
一句话: 只要力与轴共面, 力对轴的矩等于零。
力对轴的矩之解析表达式
设空间中有一个力 F 力作用点 A的坐标为(x,y,z )
z
Z
F
M z (F ) xY yX 4 (5 2 ) 9 (4 2 ) 16 2 (kN m)
4、求力F对O点的矩
由 M O (F ) = M
x
i + M
y
j + M
z
k 得:
MO (F ) 52 2i 32 2 j 16 2k
即
M O (F ) M x M y M z 89.26(kN m)
z
解:受力分析如图
E
60°
ZA XA D x A
30°
YA B
W T C XB
ZB
y
a
b
W = 200N
∑X = 0, XA + XB-T cos30º sin30 º = 0 ∑Y = 0, YA - T cos30 º cos30 º = 0
z E ZA XA A 30 ° a 60 ° YA B W T C XB b y ZB
1、回顾力在直角坐标轴上的投影
X = F cosα
z Z
F
γ β
Y = F cosβ Z = F cosγ
z Z
γ
α
Y y
X
x
F
Y
X
x
φ
y
X = F sinγ cosφ Y = F sinγ sinφ Z = F cosγ
2.
回顾力对点的矩
n z r A O h y B F MO(F)
力F 对点O的矩矢为定位矢量
力对点的矩和力对轴的矩的关系
• 力对点的矩矢量可以写成:
M O( F ) = [M O ( F )]x i + [M O ( F )]y j + [M O ( F )]z k = ( yZ - zY )i + ( zX - xZ )j + ( xY - yX )k
