理论力学模拟试题
理论力学期末模拟试卷8套
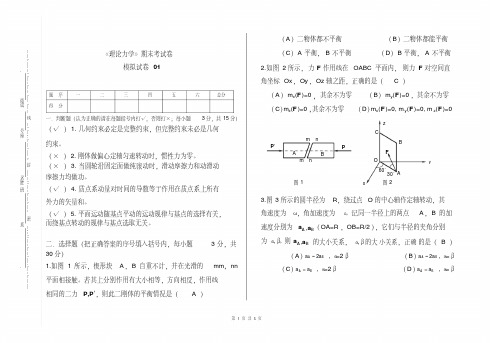
B
D
a
FgR
A mg FD
F Ax
F Ay
第 4页共 5页
B
h= 1m
a
l
D 30° A
解:以杆为研究对象 , 受力如图,虚加惯性力
M A (F ) 0
点系的mg达l c朗os3伯0 原FD理l FgR l sin 30 0
2
2
2
FgR= - ma, 则由质
FD m( g cos30 a sin30 )
( D )M1 点科氏加速度大小为 2 v1 sin ,方向垂直纸面向里
解:( 研究 AB,已知
的方向,因此可确定出 P 点为速度瞬心
v A l , AP l AB v A / AP l / l
vB BP AB
2l ( )
四.一根直杆和一个圆盘焊接组成的系统, 它们的质量均为 8 kg, 可绕 O 点转动,当 OA 处于水平位置时 , 系统具有角速度 =4rad/s 。求该瞬时轴承 O的反力。( 15 分)
( B)其它同( A ),但其中 LQ 1 ml 2
12
( C)仅为作用于杆质心的一个力: RQ 1 ml
2
( D )仅为作用于图面内的一个力偶:
LQ 1 ml 2 3
M 2 点科氏加速度为 0
A
C
9. 两个相同的定滑轮如下图示,开始时都处于静止,问下面描述
正确的是( A ) ( A ) A B, A B ( C) A B , A B
外力的矢量和。
(√ ) 5. 平面运动随基点平动的运动规律与基点的选择有关, 而绕基点转动的规律与基点选取无关。
二.选择题(把正确答案的序号填入括号内,每小题 30 分) 1.如图 1 所示,楔形块 A , B 自重不计,并在光滑的
理论力学试题库及答案(通用篇)

理论力学试题库及答案(通用篇)一、理论力学试题库(通用篇)试题一:已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3,y = 4t² - t + 1。
求该质点在t = 2s 时的速度和加速度。
试题二:一质点沿圆周运动,其半径为 r,角速度为ω,角加速度为α。
求质点在任意时刻 t 的速度和加速度。
试题三:一质点从静止开始沿直线运动,受到恒力F 的作用。
求质点在任意时刻 t 的速度和位移。
试题四:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的速度和加速度。
试题五:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移。
试题六:一质点在重力作用下做自由落体运动,求质点在任意时刻 t 的速度和位移。
试题七:一质点在水平地面上受到一斜向上的拉力F,拉力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和加速度。
试题八:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的切向加速度和法向加速度。
试题九:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移和速度。
试题十:一质点在水平地面上受到一恒力 F 的作用,力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和位移。
二、答案答案一:t = 2s 时,速度 v = (4t, 8t - 1) = (8, 15) m/s;加速度 a = (8, 8) m/s²。
答案二:质点在任意时刻 t 的速度v = (rω, 0),加速度a = (0, rα)。
答案三:质点在任意时刻 t 的速度 v = (F/m)t,位移 s = (F/m)t²/2。
答案四:质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt)),加速度 a = (-rω²sin(ωt), rω²cos(ωt))。
理论力学期末试卷-模拟试卷03(带答案)

《理论力学》期末考试模拟试卷03题 序 一 二 三 四 五 六 总分 得 分一. 填空题(每空3分, 共30分)1.已知力 沿直线AB 作用, 其中一个分力的作用线与AB 成30°角, 若欲使另一个分力的大小在所有分力中为最小, 则此二分力间的夹角..9. 度。
2.已知力 的大小为60(N ),则力 对x 轴的矩.160(N ·cm.;对z 轴的矩.100(N ·cm )。
3.设一质点的质量为m, 其速度 与x 轴的夹角为 , 则其动量在x 轴上的投影为mv.=mvcos 。
4.图示结构受矩为M=10KN.m 的力偶作用。
若a=1m, 各杆自重不计。
则固定铰支座D 的反力的大小为 10kN , 方向 水平向右 。
5.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
6.已知A 重100kN ,B 重25kN ,A 物与地面间摩擦系数为0.2。
端铰处摩擦不计。
则物体A 与地面间的摩擦力的大小.. 1.k.....。
二. 选择题(把正确答案的序号填入括号内, 每小题3分, 共15分)1. 作用在一个刚体上的两个力 A 、 B ,满足 A=- B 的条件,则该二力可能....... 。
(A )作用力和反作用力或一对平衡的力; (B )一对平衡的力或一个力偶; (V )一对平衡的力或一个力和一个力偶; (D )作用力和反作用力或一个力偶。
2. 某平面任意力系向O 点简化, 得到如图所示的一个力 (和一个力偶矩为Mo 的力偶, 则该力系的最后合成结果... ... 。
(A )作用在O 点的一个合力; (B )合力偶;(C )作用在O 点左边某点的一个合力;(D )作用在O 点右边某点的一个合力。
3.一动点在圆盘内运动, 同时圆盘又绕直径轴x 以角速度ω转动, 若AB ∥OX, CD ⊥OX, 则当动点....运动时, 可使科氏加速度恒等于零。
理论力学xia模拟试题及答案

理论力学xia模拟试题及答案理论力学模拟试题及答案一、选择题(每题2分,共20分)1. 在经典力学中,牛顿第一定律描述的是:A. 物体的加速度与作用力成正比B. 物体的加速度与作用力成反比C. 物体在没有外力作用下保持静止或匀速直线运动D. 物体在任何情况下都有惯性2. 根据牛顿第二定律,力的量度是:A. 质量B. 加速度C. 动量D. 质量与加速度的乘积3. 以下哪一项不是牛顿第三定律的内容:A. 作用力与反作用力大小相等B. 作用力与反作用力方向相反C. 作用力与反作用力同时产生D. 作用力与反作用力作用在不同物体上4. 在圆周运动中,角速度的大小是:A. 线速度与半径的比值B. 线速度与时间的比值C. 弧长与时间的比值D. 半径与时间的比值5. 动量守恒定律适用于:A. 只有重力作用的系统B. 只有摩擦力作用的系统C. 只有外力作用的系统D. 系统所受外力之和为零的系统二、填空题(每题2分,共20分)6. 牛顿第一定律也被称为______定律。
7. 牛顿第二定律的数学表达式是______。
8. 当物体受到多个力作用时,合力的作用效果与______力的效果相同。
9. 角动量守恒定律适用于______。
10. 一个物体的动能与其______的平方成正比。
三、简答题(每题10分,共30分)11. 简述牛顿运动定律的基本内容。
12. 解释什么是角动量守恒,并给出一个实际应用的例子。
13. 描述动量守恒定律在碰撞问题中的应用。
四、计算题(每题15分,共30分)14. 一个质量为2kg的物体在水平面上以5m/s的速度匀速运动,受到一个10N的水平拉力作用。
求物体的动量变化率。
15. 一个质量为3kg的物体从静止开始,在竖直方向上受到一个恒定的力作用,力的大小为50N。
如果物体在2秒内上升了10米,请计算物体的最终速度。
参考答案:一、选择题1. C2. D3. D4. A5. D二、填空题6. 惯性7. F = ma8. 一个等效9. 系统所受外力之和为零10. 速度三、简答题11. 牛顿运动定律包括:第一定律(惯性定律),第二定律(动力定律),第三定律(作用与反作用定律)。
理论力学模拟题

《理论力学》模拟题(补)一. 单项选择题1、如图1.1所示,四本相同的书,每本重均为P ,设书与书间的摩擦因数为0.1,书与手间的摩擦因数为0.25,欲将四本书一起抱起,则两侧手应加的压力至少大于( )。
A 、 10PB 、 8PC 、 6PD 、 4P2、如图1.2所示,重Q=200N 的三角形板,用等长杆O 1A ,O 2B 支持着。
设O 1O 2=AB ,杆重及摩擦不计。
若能使三角形板在角α=300时保持平衡,则水平力P 的大小应为( )。
A 、P=115.47B 、P=200C 、P=364ND 、P=173NFF21O O BAQPα图 1.1 图 1.23、平面杆机构如图1.3示,各杆重量不计,AB =CD =a 。
已知AB 杆上作用一力偶M1,如在CD 杆上作用一力偶M2。
则机构平衡时,M1与M2之间的大小为( )。
A 、 M1=M2B 、 M1=3M2C 、 M1=33M2D 、 M1=23M24、物块重P ,与水面的摩擦角o20m ϕ=,其上作用一力Q ,且已知P=Q ,方向如图,则物块的状态为( )。
A 、 静止(非临界平衡)状态B 、 临界平衡状态C 、 滑动状态D 、 不能确定21M M DCBA30°图 1.3 图 1.45、如图1.5所示,两齿条分别以速度v 1、v 2,沿相反向运动,两齿条之间夹有一齿轮,其半径为R ,设v 1>v 2,则齿轮中心O 点的速度大小应为( )。
A 、221v v - B 、21v v - C 、221v v + D 、21v v + 6、如图1.6所示,已知F 1、F 2、F 3、F 4为作用于刚体上A 、B 、C 、D 四点的平面一般力系,其力矢关系如图2.1所示为平行四边形,由此可知( )。
A 、力系可合成为一个力偶B 、力系可合成一个力C 、 力系可简化为一个力和一个力偶D 、力系的合力为零,力系平衡2图1.67、刚体作平面运动,在任一瞬时,若选A 点为基点,则B 点绕A 点运动的速度为v BA , 若选B 点为基点,则A 点绕B 点运动的速度为v AB ,对于v BA 与v AB , 以下正确的说法是( )。
理论力学模拟题计算题

理论力学模拟题计算题1、图示梁,已知m=20 kN.m,q= 10 kN/m , l=1m,求固定端支座A的约束力。
2、如图所示三铰刚架,已知P=20kN,m=10kN.m,q=10kN/m不计自重,计算A、B、C的束力。
3、多跨梁在C点用铰链连接。
已知均布荷载集度q =10 kN/m,CD上作用一力偶,力偶矩为M=40kN·m,l=2m。
试求A、B、 D处约束力。
4、平面曲柄摆杆机构如图所示,曲柄OA的一端与滑块A用铰链连接。
当曲柄OA以匀角速度ω绕固定轴O转动时,滑块在摇杆O1B上滑动,并带动摇杆O1B绕固定轴O1摆动。
设曲柄长OA= r,两轴间距离OO1=l。
求当曲柄OA在水平位置时摇杆的角速度和角加速度。
5、图示四连杆机构,O1B=l, AB=1.5 l 且C点是AB 中点,OA 以角速度ω转动,在图示瞬时,求B、C 两点的速度和加速度,刚体AB 的角速度ABω6、在图示四连杆机构中,已知:曲柄OA= r =0.5 m ,以匀角速度rad/s 40=ω转动,r AB 2=,r BC 2=;图示瞬时OA 水平,AB 铅直, 45=ϕ。
试求(1)该瞬时点B 的速度;(2)连杆AB 的角速度。
7、图示摇杆机构,折杆AB 以等速度υ向右运动。
摇杆长度OC =a ,用点的合成运动知识求当︒=45ϕ(距离l OA =)时C 点的速度、加速度。
8、刨床的急回机构如图所示。
曲柄OA 以匀角速度ω绕O 作定轴转动,滑块在摇杆B O 1上滑动,并带动杆B O 1绕定轴1O 摆动。
设曲柄长为r OA =,在图示位置时OA 水平,1OO 铅垂,30=ϕ。
求:该瞬时摇杆B O 1角速度和角加速度。
9、质量为m 1和m 2的两重物,分别挂在两条绳子上,绳又分别绕在半径为1r和2r 并装在同一轴的两鼓轮上,已知两鼓轮对于转轴O 的转动惯量为I ,系统在重力作用下发生运动,求鼓轮的角加速度。
(m 1<m 2)10、已知均质圆轮绕轴O 转动,轮的重量为P ,半径为R ,其上作用一主动力偶M ,重物的质量为m ,计算重物上升的加速度a 。
理论力学测试题及答案

理论力学测试题及答案一、单项选择题(每题2分,共10分)1. 牛顿第一定律描述的是:A. 物体在没有外力作用下的运动状态B. 物体在受到平衡力作用下的运动状态C. 物体在受到非平衡力作用下的运动状态D. 物体在任何力作用下的运动状态答案:A2. 以下哪个不是惯性参考系的特点?A. 牛顿第一定律在其中成立B. 牛顿第二定律在其中成立C. 牛顿第三定律在其中成立D. 物体在其中不受任何力的作用答案:D3. 动量守恒定律适用于:A. 只有重力作用的系统B. 只有弹力作用的系统C. 只有摩擦力作用的系统D. 只有保守力作用的系统答案:D4. 以下哪个是矢量?A. 质量B. 速度C. 时间D. 温度答案:B5. 以下哪个是标量?A. 力B. 位移C. 功D. 速度答案:C二、填空题(每空1分,共10分)1. 牛顿第二定律的数学表达式为:\[ F = ma \],其中\( F \)代表______,\( m \)代表______,\( a \)代表______。
答案:力;质量;加速度2. 根据牛顿第三定律,作用力和反作用力大小相等,方向______,作用在______。
答案:相反;不同物体上3. 动量的定义是质量与______的乘积。
答案:速度4. 功的定义是力与力的方向上的______的乘积。
答案:位移5. 动能的定义是\( \frac{1}{2}mv^2 \),其中\( m \)代表______,\( v \)代表______。
答案:质量;速度三、简答题(每题10分,共20分)1. 简述牛顿第二定律的物理意义。
答案:牛顿第二定律表明,物体的加速度与作用在物体上的合外力成正比,与物体的质量成反比,即力是改变物体运动状态的原因。
2. 描述动量守恒定律在碰撞过程中的应用。
答案:在没有外力作用的系统中,两个或多个物体发生碰撞时,碰撞前后系统的总动量保持不变。
这意味着碰撞前后各物体动量的矢量和相等。
四、计算题(每题15分,共30分)1. 一辆质量为1500kg的汽车以20m/s的速度行驶,突然刹车,经过5秒后停止。
《理论力学》模拟试题答案.docx
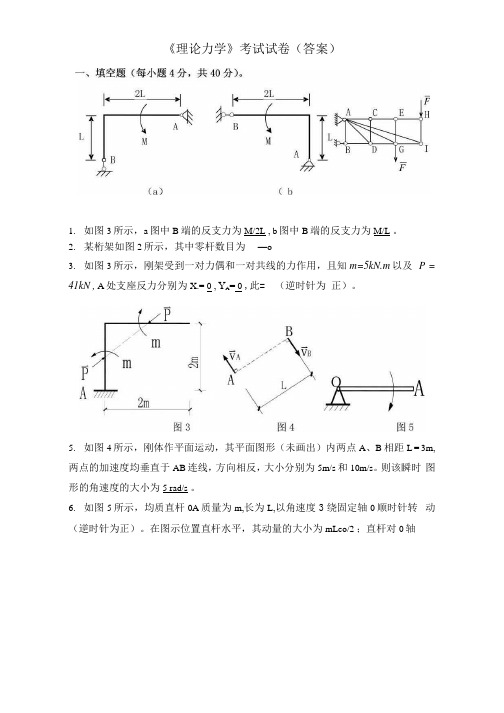
《理论力学》考试试卷(答案)1.如图3所示,a图中B端的反支力为M/2L , b图中B端的反支力为M/L 。
2.某桁架如图2所示,其中零杆数目为—o3.如图3所示,刚架受到一对力偶和一对共线的力作用,且知m=5kN.m以及P = 41kN , A处支座反力分别为X.= 0 ,Y A= 0 ,此= (逆时针为正)。
5.如图4所示,刚体作平面运动,其平面图形(未画出)内两点A、B相距L = 3m, 两点的加速度均垂直于AB连线,方向相反,大小分别为5m/s和10m/s。
则该瞬时图形的角速度的大小为5 rad/s 。
6.如图5所示,均质直杆0A质量为m,长为L,以角速度3绕固定轴0顺时针转动(逆时针为正)。
在图示位置直杆水平,其动量的大小为mLco/2 ;直杆对0轴动量矩的大小为ml? 3/3 ,杆动能大小为ml; 3 76。
二、计算题(共60分)。
1.如图所示,梁AC用三根链杆支承,梁受集中力P和均布荷载作用,已知P=40kN, q=5kN/m,试求各链杆的内力。
(本题15分)解:受力分析如图所示:2.桁架如图所示,试求杆件CD, CE和EF的内力。
(本题15分)解:由图分析可知CD杆为0杆。
……(1分)1)先取整体分析,如图所示分别对A点和B点取矩:Am尸)=o-2x10-4x10-6x10-8x5 + 8x7? = 0D2>*)=°2x10 + 4x10 + 6x10 + 8x5-8x7?^ =0解得:R A =20kN, R B =20kN如图取I - I截面左半部分对A点取矩,取II-11截面右部分对B点取矩£ 〃很了)= 0-2xl0-2x S CE sin(cif)-lx S CE cos(o) = 0£ 〃七(了)= o8X7?A +8X5+6X10+4X10+6X S CE sin(。
)-lx S CE cos(。
)+ 4x S FE = 0上式解得:S^=—11.18KN, S FF = 1QKNCc r Zi3,图示机构中,曲柄04长为r,绕。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考试题型:
一、根据力学公理作受力图。
[2×5分=10分] 二、求约束反力。
[2×10分=20分]
三、轴向拉压杆强度、变形、超静定问题。
[20分] 四、扭转强度、刚度。
[20分] 五、作弯曲内力图。
[10分] 六、弯曲正应力强度问题。
[20分]
一、作受力图。
(a )
(b )
(c )
(d )
(e )
(f )
二、求约束反力。
1,AB 梁受如图所示约束和荷载,已知40F kN =,10/q kN m =,20.M kN m =1a m =。
求两端所受的约束反力。
(15分)
2,求约束反力大小。
(g ) (h )
(i )
题1图
题1图
题2图
三、轴向拉压杆强度、变形、超静定问题。
1,如题图所示圆截面直杆,已知直径10d mm =,1000a mm =,材料的弹性模量
200E GPa =,[]80MPa σ=。
(1)作直杆的轴力图;(2)对AC 杆进行强度校核;(3)题2图
求杆AC 的总变形。
(15分)
2、
如题图所示杆系结构,已知BD 杆为圆截面钢板,直径20d mm =,长度1l m =,
200E GPa =;BC 杆为方截面木杆,边长100a mm =,12E GPa =;荷载50F kN =。
(a)求各杆的内力;(b )求B 点的位移。
(15分)
3,图示结构中。
若1、2两杆的EA 相同,则节点A 的竖向位移∆Ay =
,水平位
移为∆Ax = 。
4,正方形结构受力如图,P =50 kN ,各杆横截面积A =2000 mm 2
,求各杆的正应力。
5,图示木制桁架受水平力P 作用,已知P =80 kN ,许用拉、压应力分别为:[ σ t
]=8 MPa ,[ σc ]=10 MPa ,设计AB 杆和CD 杆的横截面面积。
题图
题图
P A 2 1
l
30º
P P
①②③
④A D B C ⑤
6,钢质圆杆的直径d =10 mm ,P =5 kN ,弹性模量E =210 GPa 。
求杆内最大应变和杆的总伸长。
7,如图所示,杆ABC 为刚杆,①、②、③各杆E 、A 、l 均相同,求各杆内力值。
8,静不定结构如图所示。
AB 为刚体,1、2杆的EA 相同,试列出求解两杆内力F N1和F N2的方程式。
9,图示杆系结构,已知F =10kN,杆长l =2m ,杆径d =25mm,=30°,材料的弹性模量E =210Gpa,求结点A 的位移A
B P
A
C D
30° 60° 30° d A B C
D 2P
2P P A B C P ③ ② ① a a l a a a A B α 2 1
l
P
10,已知22113322E A E A E A ==,2L l =,分别求1、2、3杆的内力。
11,如图上所示,刚性杆AB 的左端铰支,①、②两杆为长度相等,横截面面积相等的等直杆,其弹性模量分别为E 1和E 2,且有E 1=2E 2,求1、2杆的内力及B 的位移。
12,图示为一简单托架,BC 杆为圆钢,横截面直径d =20mm ,BD 杆为8号槽钢。
若试校核托架的强度,并求B 点的位移。
设F =60KN ,[]22160/,200/MN m E GN m σ==。
四、扭转强度、刚度。
1,一受扭圆轴,横截面上的最大切应力τmax
=40MPa ,如图
所示,则横截面上a 点的切应力τa
α α
1
2 3
P
A
a
a
a
P
A
B
C D
②
①
(mm )
τa
25
a
τmax
= 。
2,阶梯轴尺寸及受力如图所示,AB 段的最大切应力τmax1与BC 段的最大切应力τmax2之比
τmax1 / τmax2= 。
3,图示阶梯形圆轴受扭转力偶作用,材料的切变模量为G ,则相对扭转角ΦAC
= ,在m 1单独作用时,ΦAB = 。
4,作图所示轴的扭矩图。
5,直径为60 mm 的实心圆轴,其强度恰好满足要求。
在受力不变的条件下,若改用内外径比0.8α=的空心圆轴,求轴的外直径D 。
2
(kN ·m)
6,直径为100 mm 的圆轴,材料的G =80 GPa ,其表面上的纵向线在扭转力偶作用时倾斜角0
0.0065α=,求:(1)外力偶矩m 的值;(2)若[ τ ] = 70 MPa ,校核其强度。
7,阶梯圆轴AB ,受力如图所示,已知m 、a 、G I p ,试作AB 轴的扭矩图,并计算B 截面相对于A 截面的扭转角ΦAB 。
8,如图所示,已知作用在变截面钢轴上的外力偶矩m 1= kN ·m ,m 2=·m 。
试求最大切应力和两截面间相对扭转角。
材料的G =80 GPa 。
9,阶梯圆轴受力如图所示。
已知D =2 d ,材料的切变模量为G ,试求:
(1) 轴的最大切应力;
(2) A 、C 两截面的相对扭转角; (3) 最大单位长度扭转角。
五、作弯曲内力图。
m
p
六,弯曲强度
1,两材料相同的圆截面梁,载荷如图所示,若二梁内最大应力相等,则
D 1:D 2= 。
q
2
2、某抗弯构件的截面为T 形,如图所示,为使截面上的最大拉应力max ()t σ和最大压应力
max ()c σ同时分别达到材料的[ σ t ]和[ σc ],应将1y 和2y 的比值设计为 。
(C 为形心)
3,图示外伸梁,受均布载荷作用,已知:q =10 kN / m ,4m a =,[]160MPa σ=, 试
4、16号工字钢截面的尺寸及受力如图所示。
[]160MPa σ=,试校核正应力强度条件。
5、圆形截面简支梁受力如图,已知[]12MPa σ=,直径为d ,若直径增加一倍,则载荷q 最大可增加到多少
下压
I z =×107mm 4
=160mm
z
y
mm )
2
100
6、图示为一铸铁梁,P 1 =9 kN , P 2 =4 kN ,许用拉应力[ σ t ]=30 MPa ,许用压应力[ σc ]=60 MPa ,647.6310m y I -=⨯,试校核此梁的强度。
7、试确定图示箱式截面梁的许用载荷q ,已知[]160MPa σ=。
(kN ·
.m
80。
