勾三股四弦五-勾股定理介绍
勾股定理知识点+对应类型
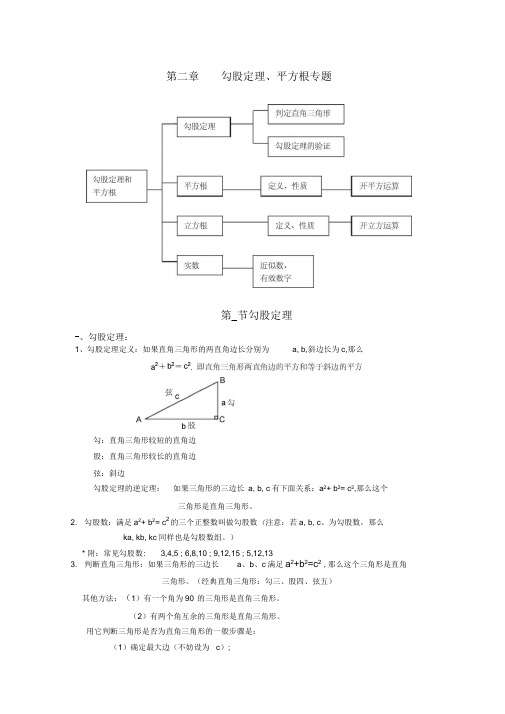
第二章勾股定理、平方根专题第_节勾股定理-、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a, b,斜边长为c,那么勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a, b, c有下面关系:a2+ b2= c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+ b2= c2的三个正整数叫做勾股数(注意:若a, b, c、为勾股数,那么ka, kb, kc同样也是勾股数组。
)* 附:常见勾股数: 3,4,5 ; 6,8,10 ; 9,12,15 ; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2) 若c2= a2+ b2,则^ ABC是以Z C为直角的三角形;若a2 + b2v c2,则此三角形为钝角三角形(其中c为最大边);若a2 + b2> c2,则此三角形为锐角三角形(其中c为最大边)4. 注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的(3) 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1) 已知直角三角形的两边求第三边。
(2) 已知直角三角形的一边,求另两边的关系。
(3) 用于证明线段平方关系的问题。
(4) 利用勾股定理,作出长为际的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a,那么这个数就叫做a的平方根。
(也称为二次方根),也就是说如果x2=a,那么x就叫做a的平方根。
勾股定理的公式,勾、股、弦的介绍

勾股定理的公式,勾、股、弦的介绍
勾股定理的公式是a²+b²=c²,其中a和b是直角三角形的两条直角边,c是斜边。
在勾股定理的公式中,“勾”、“股”、“弦”分别指的是:
勾:在直角三角形中,较短的直角边被称为“勾”。
它代表了直角三角形的一个直角边,是勾股定理中的重要组成部分。
股:直角三角形中,较长的直角边被称为“股”。
它也是直角三角形的一个直角边,与“勾”共同构成了直角三角形的两条直角边。
弦:直角三角形的斜边被称为“弦”。
它是直角三角形中最长的一条边,与直角相对。
在勾股定理中,斜边的平方等于两直角边的平方和。
勾股定理

勾股定理勾股定理在西方又称“毕达哥拉斯定理”,就是指三角形两直角边的平方和等于斜边的平方。
中国古代称两直角边为勾(一般指较短直角边)和股、斜边为弦,所以也称此定理为勾股定理。
我国最早的数学文献《周髀算经》(约成书于公元前157年前)中记述了周公(击武王弟弟)与古代数学家商高的一段对话,首先提出了勾股形的问题。
商高说:“故折矩,以为勾广三,股修四,径隅五”。
意思说,如果直角三角形两直角边长是3和4,那么它的斜边必定是5。
这是勾股定理的一个特例。
商高时代,约比古希腊数学家毕达哥拉斯早500年。
我国对于勾股定理的证明,最早的形式见于公元3世纪吴国人赵爽(字君卿)所著《勾股圆方图注》,在这篇短文中,赵爽用割补法画了一张所谓的“弦图”(见图),其中每一个直角三角形称为“朱实”,中间的一个小正方形叫“中黄实”,以弦为边的正方形ABEF 叫“弦实”。
由于四个朱实加上一个中黄实就等于弦实,所以有下式成立:4×21ab+(b-a ) 2=c 2 化简后即得a 2+b 2=c 2这个证法通过图形的分割、移补,精霖总结了我国东汉以前在勾股定理方面的光辉成就。
赵爽的证法与印度数学家婆斯伽罗在公元1150年的证法相似,婆氏也曾作出类似的图形。
世界上对勾股定理的证明方法很多,1940年有人出了一本勾股定理证明专集,其中收集了365种证法,当然,证法还不止这些。
1876年,加菲尔德(1881年任美国总统)想出了一个相当精采的证明: 如图,梯形面积=2b a ×(a+b ) =21(a 2+2ab+ b 2). 又可得梯形面积=21c 2+21ab+21ab =21(c 2+2ab ) 比较两式,可得a 2+b 2=c 2 。
勾股定理定义

勾股定理定义
勾股定理,是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。
勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。
在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他们用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
勾股定理与平方根的数学知识点

勾股定理与平方根的数学知识点一、勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
我国古代把直角三角形中,较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦。
结论为:勾三股四弦五a2+b2=c21、如果三角形的三边长a、b、c满足a+b=c,那么这个三角形是直角三角形。
2、满足a+b=c的3个正整数a、b、c称为勾股数。
(例如,3、4、5是一组勾股数)。
利用勾股数可以构造直角三角形。
二、平方根1、定义一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也称为二次方根。
也就是说,如果x2=a,那么x就叫做a的平方根。
2、一个正数有2个平方根,它们互为相反数;0只有一个平方根,它是0本身;负数没有平方根。
3、求一个数a的平方根的运算,叫做开平方。
4、正数a有两个平方根,其中正的平方根,也叫做a的算术平方根。
例如:4的平方根是2,其中2叫做4的算术平方根,记作=2;2的平方根是其中2的算术平方根。
0只有一个平方根,0的平方根也叫做0的算术平方根,即三、立方根1、定义一般地,如果一个数的立方等于a,那么这个数叫做a的立方根,也称为三次方根。
也就是说,如果x=a,那么x就叫做a的立方根,数a的立方根记作,读作三次根号a。
2、求一个数a的立方根的运算,叫做开立方。
3、正数的立方根是正数,负数的立方根是负数,0的立方根是0。
四、实数1、无限不循环小数称为无理数。
2、有理数和无理数统称为实数。
3、每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点都表示一个实数,实数与数轴上的点是一一对应的。
五、近似数与有效数字1、例如,本册数学课本约有100千字,这里100是一个近似似数。
2、对一个近似数,从左边第一个不是0的数字起,到末位数字止,所有的数字都称为这个近似数的有效数字。
初二数学勾股定理知识点勾股定理在任何一个直角三角形(Rt△)中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方,这就叫做勾股定理。
勾股定理

勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方。
这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉斯定理”或者“百牛定理“(毕达哥拉斯发现了这个定理后,即斩了百头牛作庆祝,因此又称“百牛定理”),法国、比利时人又称这个定理为“驴桥定理”。
他们发现勾股定理的时间都比我国晚,我国是最早发现这一几何宝藏的国家。
目前初二学生学,教材的证明方法采用赵爽弦图。
勾股定理是一个基本的几何定理,它是用代数思想解决集几何问题的最重要的工具之一,是数形结合的纽带之一。
勾股定理指出:直角三角形两直角边(即“勾”“股”短的为勾,长的为股)边长平方和等于斜边(即“弦”)边长的平方。
也就是说,设直角三角形两直角边为a和b,斜边为c,那么a的平方+b的平方=c的平方a^2+b^2=c^2周髀算经》记载了勾股定理的公式与证明,相传是在商代由商高发现,故又有称之为商高定理;三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释,又给出了另外一个证明[1]。
法国和比利时称为驴桥定理,埃及称为埃及三角形。
我国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦。
我国是发现和研究勾股定理最古老的国家之一。
我国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理。
在公元前1000多年,据记载,商高(约公元前1120年)答周公曰“故折矩,以为句广三,股修四,径隅五。
既方之,外半其一矩,环而共盘,得成三四五。
两矩共长二十有五,是谓积矩。
”因此,勾股定理在我国又称“商高定理”。
在公元前7至6世纪一中国学者陈子,曾经给出过任意直角三角形的三边关系即“以日下为勾,日高为股,勾、股各乘并开方除之得邪至日。
在法国和比利时,勾股定理又叫“驴桥定理”。
还有的国家称勾股定理为“平方定理”。
西欧对此定理戏称为“笨蛋的难关(Asses' Bridge)”,照原文直译,就是“驴桥”,因此,我国也有将此命题译作“驴桥定理”的。
勾三股四弦五I

第七讲.勾三股四弦五I【教学目标】1.复习直角三角形及勾股定理;2.掌握勾股定理的直接应用;3.掌握构造勾股定理法;4.掌握勾股定理的综合应用。
【知识、方法梳理】1. 勾股定理定义:如果直角三角形的两直角边长分别为a ,b ,斜边长为c ,那么222a b c +=. 即直角三角形两直角边的平方和等于斜边的平方ABCa b c弦股勾勾:直角三角形较短的直角边 股:直角三角形较长的直角边 弦:斜边勾股定理的逆定理:如果三角形的三边长,,a b c 有下面关系:222a b c +=,那么这个三角形是直角三角形.2. 勾股数:满足222a b c +=的三个正整数叫做勾股数(注意:若,,a b c 为勾股数,那么,,ka kb kc 同样也是勾股数组.)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长,,a b c 满足222a b c +=,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90的三角形是直角三角形. (2)有两个角互余的三角形是直角三角形.用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c );(2)若222c a b =+,则ABC ∆是以C ∠为直角的三角形; 若222a b c +<,则此三角形为钝角三角形(其中c 为最大边); 若222a b c +>,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30,那么它所对的直角边等于斜边的一半.(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边. (2)已知直角三角形的一边,求另两边的关系.(3)用于证明线段平方关系的问题. (4)利用勾股定理,作出长为n 的线段【典例精讲】类型一:勾股定理的直接用法例1.在Rt ABC ∆中,90C ∠=(1)已知6a =, 10c =,求b , (2)已知40a =,9b =,求c ; (3)已知25c =,15b =,求a .【思路点拨】: 写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用. 【解析】:(1) 在ABC ∆中,90C ∠=,6a =, 10c =,228b c a =-=(2) 在ABC ∆中,90C ∠= ,40a =,9b =,2241c a b =+=(3) 在ABC ∆中,90C ∠=,25c =,15b =,2220a c b =-=类型二:勾股定理的构造应用例2.如图,已知:在ABC ∆中,607030B AC AB ∠===,,。
勾股定理的详细讲解

勾股定理的详细讲解
勾股定理,是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。
中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦,所以称这个定理为勾股定理,也有人称商高定理。
勾股定理现约有500种证明方法,是数学定理中证明方法最多的定理之一。
勾股定理是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。
在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他们用演绎法证明了直角三角形斜边平方等于两直角边平方之和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾三股四弦五——《勾股定理》
在中国古代,大约是公元前十一世纪战国时期,西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。
商高说:“…故折矩,勾广三,股修四,经隅五。
”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。
以后人们就简单地把这个事实说成“勾三股四弦五”。
这就是著名的勾股定理,也称为“商高定理”。
数学家刘徽(公元263年)作《九章算术注》时,依据其“割补术”为证勾股定理另辟蹊径而作“青朱出入图”。
刘徽描述此图,“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不动也,合成弦方之幂。
开方除之,即弦也。
”上述内容直白表达就是,青朱两个正方形经过分割、拼合成以弦长为边长的新正方形,重点在于新形成的正方形是在原来两个正方形基础上
拼合而成,这就完全适合直角三角形两条直
角边的平方和等于斜边平方的判定原则。
用勾(a)和股(b)相乘(a×b)等于
两块红色三角形的面积,乘以二(2ab)即为
四块红色三角形的面积,以勾(a)股(b)
的差(b-a)再平方即为中间的黄色正方形,
所有四个红色三角形的面积加这个黄色正方形的面积,即为弦(c)为边长的正方形的面积。
数学表达式为:c2=(a-b)2+2ab=a2+b2-2ab+2ab=a2+b2。
