实验设计与数据处理习题练习
课后作业试验设计与数据处理
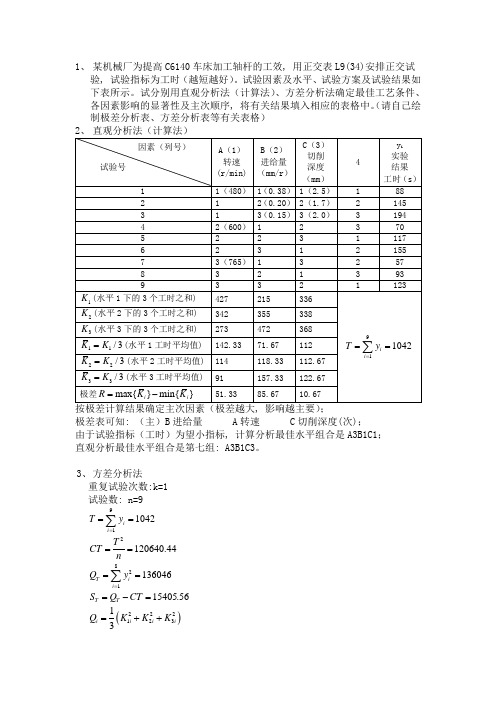
1、 某机械厂为提高C6140车床加工轴杆的工效, 用正交表L9(34)安排正交试验, 试验指标为工时(越短越好)。
试验因素及水平、试验方案及试验结果如下表所示。
试分别用直观分析法(计算法)、方差分析法确定最佳工艺条件、各因素影响的显著性及主次顺序, 将有关结果填入相应的表格中。
(请自己绘制极差分析表、方差分析表等有关表格)极差表可知: (主)B 进给量 A 转速 C 切削深度(次); 由于试验指标(工时)为望小指标, 计算分析最佳水平组合是A3B1C1; 直观分析最佳水平组合是第七组: A3B1C3。
3、 方差分析法重复试验次数:k=1 试验数: n=9911042i i T y ===∑2120640.44T CT n ==821136046T i i Q y ===∑15405.56T T S Q CT =-=()22212313i i i i Q K K K =++i i S Q CT =-自由度: 819=-=T f2134=-====f f f f C B A方差:1925.69/==T T T f S V 1983.45/==A A A f S V 5518.78/==B B B f S V 107.11/==C C C f S V 93.45/444==f S V 第一类误差: 89.18641==S S e 241==f f e 第二类误差:∑∑∑∑=====⎪⎪⎭⎫ ⎝⎛-=n i k j ij ni kj ij e y k y S 121112201 0)1(2=-=k n f e89.186421==+=S S S S e e e 221=+=e e e f f f93.45/===f S V V方差表可知: (主)B进给量 A转速 C切削深度(次)。
由于试验指标(工时)为望小指标, 方差分析最佳水平组合是A3B1C1。
实验设计与数据处理

13125916机电硕1308班周晓易1.某工厂进行技术改造,以减少工业酒精中甲醇含量的波动。
原工艺生产的工业酒精中甲醇含量的总体方差为0.35.技术改造后,进行抽样检验,样品数为25个,结果样品甲醇含量的样本方差为0.15。
问技术改造后工业酒精中甲醇含量的波动性是否更小?(α=0.05)答:检验技术改造后工业酒精中甲醇含量的波动性是否更小,要使用χ2单侧(左侧)检验。
已知σ2=0.35,n=25,s2=0.15。
当α=0.05时,χ20.95(24)=CHIINV(0.95,24)=13.848,而χ2=24*0.15/0.35=10.286,χ20.95(24)>χ2,说明技术改革后产品中甲醇含量的波动较之前有显著减少。
2. A与B两人用同一种分析方法测定金属钠中铁的含量,测试结果分别为:A:8.0,8.0,10.0,10.0,6.0,6.0,4.0,6.0,6.0,8.0B:7.5,7.5,4.5,4.0,5.5,8.0,7.5,7.5,5.5,8.0试问A、B二人测定的铁的精密度是否有显著性差异?(α=0.05)解答如图:这里F>1,为右侧检验,这时F 单尾临界值>1,对于右侧检验,如果F<F 单尾临界,或者P(F<=f) 单尾>α,就可以认为第一组数据较第二组数据的方差没有显著增大,否则就认为第一组的数据较第二组的数据的方差有显著增大。
在本例中,由于P>0.05,所以A、B 二人测定的铁的精密度无显著性差异。
3. 用新旧工艺冶炼某种金属材料,分别从两种产品中抽样,测定试样中的杂质含量,结果如下:旧工艺:2.69, 2.28, 2.57, 2.30, 2.23, 2.42, 2.61, 2.64, 2.72, 3.02, 2.45, 2.95, 2.51新工艺:2.26, 2.25, 2.06, 2.35, 2.43, 2.19, 2.06, 2.32, 2.34试问新工艺是否更稳定,并检验两种工艺之间是否存在系统误差?(α=0.05)解答:由于s21<s22,故新工艺比旧工艺更稳定;又因为F<1,所以为左侧检验。
实验设计与数据处理大作业及解答
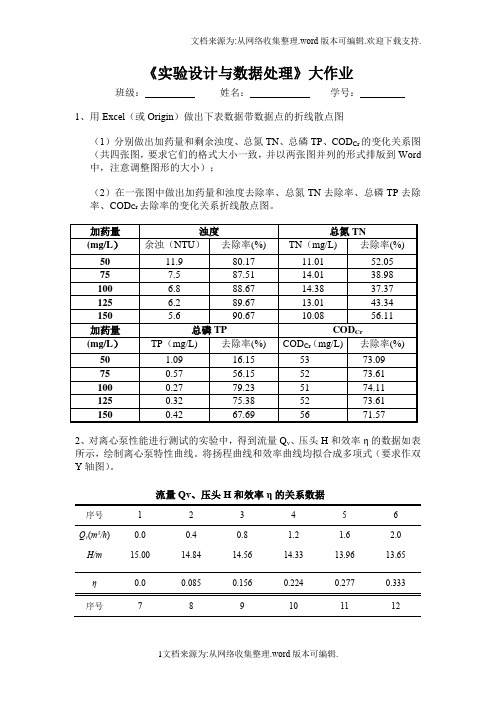
《实验设计与数据处理》大作业班级:姓名:学号:1、用Excel(或Origin)做出下表数据带数据点的折线散点图(1)分别做出加药量和剩余浊度、总氮TN、总磷TP、COD Cr的变化关系图(共四张图,要求它们的格式大小一致,并以两张图并列的形式排版到Word 中,注意调整图形的大小);(2)在一张图中做出加药量和浊度去除率、总氮TN去除率、总磷TP去除率、COD Cr去除率的变化关系折线散点图。
2、对离心泵性能进行测试的实验中,得到流量Q v、压头H和效率η的数据如表所示,绘制离心泵特性曲线。
将扬程曲线和效率曲线均拟合成多项式(要求作双Y轴图)。
流量Qv、压头H和效率η的关系数据序号123456Q v(m3/h) H/m0.015.000.414.840.814.561.214.331.613.962.013.65η0.00.0850.1560.2240.2770.333序号789101112Q v(m3/h) H/mη2.413.280.3852.812.810.4163.212.450.4463.611.980.4684.011.300.4694.410.530.4313、用分光光度法测定水中染料活性艳红(X-3B)浓度,测得的工作曲线和样品溶液的数据如下表:(1)列出一元线性回归方程,求出相关系数,并绘制出工作曲线图。
(2)求出未知液(样品)的活性艳红(X-3B)浓度。
4、对某矿中的13个相邻矿点的某种伴生金属含量进行测定,得到如下一组数据:试找出某伴生金属c与含量距离x之间的关系(要求有分析过程、计算表格以及回归图形)。
提示:⑴作实验点的散点图,分析c~x之间可能的函数关系,如对数函数y=a+blgx、双曲函数(1/y)=a+(b/x)或幂函数y=dx b等;⑵对各函数关系分别建立数学模型逐步讨论,即分别将非线性关系转化成线性模型进行回归分析,分析相关系数:如果R≦0.553,则建立的回归方程无意义,否则选取标准差SD最小(或R最大)的一种模型作为某伴生金属c与含量距离x之间经验公式。
数据处理与实验设计考试卷

数据处理与实验设计考试卷一、单选题(每题3分,共30分)1. 在数据处理中,以下哪种统计量可以反映数据的集中趋势?()A. 方差。
B. 标准差。
C. 平均数。
D. 极差。
2. 对于一组数据12,15,18,20,25,其中位数是()。
A. 18.B. 19.C. 20.D. 15.3. 在实验设计中,以下哪种设计可以同时研究多个因素对实验结果的影响?()A. 完全随机设计。
B. 随机区组设计。
C. 析因设计。
D. 拉丁方设计。
4. 当我们想要检验两个总体均值是否相等时,通常使用()。
A. t检验。
B. F检验。
C. 卡方检验。
D. 秩和检验。
5. 在数据收集过程中,如果样本存在偏差,可能会导致()。
A. 结果的准确性提高。
B. 结果的可靠性降低。
C. 结果不受影响。
D. 实验更容易进行。
6. 数据的离散程度可以用()来衡量。
A. 众数。
B. 中位数。
C. 方差。
D. 平均数。
7. 在实验设计中,控制组的作用是()。
A. 作为实验处理的对象。
B. 与实验组进行对比,排除无关因素的影响。
C. 增加实验的样本量。
D. 确定实验的变量。
8. 以下关于标准差的说法正确的是()。
A. 标准差越大,数据越集中。
B. 标准差越小,数据越分散。
C. 标准差是方差的平方根。
D. 标准差与数据的集中趋势无关。
9. 若要研究施肥量和灌溉量对农作物产量的影响,最合适的实验设计是()。
A. 单因素实验设计。
B. 双因素实验设计。
C. 多因素实验设计。
D. 重复测量设计。
10. 在进行数据分组时,分组的组数一般()。
A. 越多越好。
B. 越少越好。
C. 根据数据的特点和研究目的确定。
D. 固定为5组。
二、多选题(每题5分,共25分)1. 以下属于数据处理步骤的有()。
A. 数据收集。
B. 数据整理。
C. 数据分析。
D. 数据解释。
E. 数据删除。
2. 在实验设计中,影响实验结果的因素包括()。
A. 自变量。
B. 因变量。
C. 控制变量。
实验设计与数据处理第五章例题及课后习题答案

习题5.1、
优选过程:
1、首先在试验范围0.618处做第一个实验,这一点的温度为:x1=340+(420-340)×
0.618=389.44.
2、在这点的对称点,即0.382处做一个实验,这一点的温度为:x2=420-(420-340)×0.618=370.56.
3、比较两次的实验结果,发现第一点比第二点的合成率高,故舍去370.56以下部分,在
370.56-420之间,找x1的对称点:x3=420-(420-370.56)×0.618=389.44608.
4、比较两次的实验结果,发现第一点比第三点的合成率高,故舍去389.44608以下部分,
在389.44608-420之间,找x1的对称:x4=420-(420-389.44608)×0.618=401.11767744. 5、比较两次的实验结果,得到最佳点为401.1177。
习题5.2、
优选过程:
1、首先在试验范围3/5处做第一个实验,这一点加入的白砂糖桶数为:
x1=3+3/5*(8-3)=6桶
2、在这点的对称点,即2/5处做一个实验,这一点加入的白砂糖桶数为:
x2=8-3/5*(8-3)=5桶
3、比较两次的实验结果,发现第一点比第二点的实验结果好,故舍去5以下的部分,在5-8之间,找x1的堆成点
习题5.3
目标函数。
实验设计与数据处理4计算题

三、计算题1、随机抽测了10只兔的直肠温度,其数据为:38.7、39.0、38.9、39.6、39.1、39.8、μ=39.5(℃),试检验38.5、39.7、39.2、38.4(℃),已知该品种兔直肠温度的总体平均数μ是否存在显著差异?该样本平均温度与(10 分)抽测5个不同品种的若干头母猪的窝产仔数,结果见下表,试检验不同品种母猪平均窝产仔数的差异是否显著。
(不必进行多重比较) F0.05(4,20)=2.87, F0.01(4,20)=4.432、11只60日龄的雄鼠在x射线照射前后之体重数据见下表(单位:g):检验雄鼠在照射x射线前后体重差异是否显著?3、某鸡场种蛋常年孵化率为85%,现有100枚种蛋进行孵化,得小鸡89只,问该批种蛋的孵化结果与常年孵化率有无显著差异?4、在同样饲养管理条件下,三个品种猪的增重如下表,试对三个品种增重差异是否显著进行检验。
品种增重x(kg)ijA116 12 18 18 13 11 15 10 17 18A210 13 11 9 16 14 8 15 13 8A311 8 13 6 7 15 9 12 10 115、为了比较4种饲料(A)和猪的3个品种(B),从每个品种随机抽取4头猪(共12头)分别喂以4种不同饲料。
随机配置,分栏饲养、位置随机排列。
从60日龄起到90日龄的时期内分别测出每头猪的日增重(g),数据如下,试检验饲料及品种间的差异显著性。
4种饲料3个品种猪60~90日龄日增重A1A2A3A4 B1505 545 590 530B2490 515 535 505B3445 515 510 4956、两对相对性状杂交子二代A—B—,A—bb,aaB—,aabb 4种表现型的观察次数依次为:315、108、101、32,问是否符合9∶3∶3∶1的遗传比例?7、某生物药品厂研制出一批新的鸡瘟疫苗,为检验其免疫力,用200只鸡进行试验,某中注射100只(经注射后患病的10只,不患病的90只),对照组(注射原疫苗组)100只(经注射后患病的15只,不患病的85只),试问新旧疫苗的免疫力是否有差异。
实验设计与数据处理习题集

水平号12345678序号AB112478224857336336448715551284663663775142887521y5.86.34.95.444.533.6SUMMARY OUTPU回归统计Multiple R 0.99970596265R Square 0.99941201175Adjusted R Sq 0.99917681646标准误差0.03240370349190230180220170210137.5138138138.5139139.5140底水量(x 1)/g 2202302404.0,4.5,3.0,3.6。
已知试验指标与两因素之间成二元线性关系,试用回归分析法139.5140吸氨时间(x 2)/min 136.5137吸氨时间(x 2)/min 选用均匀表U 8*(85)安排实验,8个试验结果(吸氨量/g)依次为:5.8,6.3,4.9,5.4,出较好工艺条件,并预测该条件下相应的吸氨量。
138.5139170180190200210137240第七章 均匀设计1、在啤酒生产的某项工艺实验中,选取了底水量(A)和吸氨时间(B)两个因素都取了8个水平,进行试验设计,因素水平如下。
试验指标为吸氨量,越大越好。
137.5回归方程模型为y =a+b 1x 1+b 2x 2136.5200底水量(x 1)/g观测值8方差分析dfSS MS F Significance F 回归分析28.9235 4.461754249.285714288.38342726421残差50.005250000000.00105总计78.92875Coefficients 标准误差t Stat P-value Lower 95%Intercept 96.52583333331.4768020536165.36138888561.5871169308092.7295928008底水量(x1)/-0.69666666660.010********-66.7626010421.42755955001-0.7234906467吸氨时间(x2)0.021*********.0005217491941.84641500741.470141026900.020********RESIDUAL OUTP 观测值预测 y 残差15.797500000000.0024999999926.32250000000-0.022******** 4.88250.017499999994 5.4075-0.00750000005 3.967500000000.032499999996 4.49250.007500000007 3.0525-0.052500000083.577500000000.022********观测值预测 y15.7975000000026.322500000003 4.88254 5.40755 3.967500000006 4.49257 3.052583.57750000000R=0.99 和Significance F=8.38342726421806E-09<0.01,说明该回归方程非常显y=96.5-0.70X 1+0.02X 2个因素,越好。
试验设计与数据处理作业

试验设计与数据处理作业(二)
无机122班罗远方通过正交试验对对木犀草素的β-环糊精包合工艺进行优化,需要考察的因数及水平如下:
试验指标有两个:包合率和包含物收率,这两个指标都是越大越好。
用正交表L9(34)安排试验,将3个因素依次放在1,2,3列上,不考虑因素间的交互作用,9次试验结果依次如下:
包合率/%:
,,,,,,,,
包合物收率/%:
,,,,,,,,
这两个指标的重要性不相同,如果化成数量,包合率和包含物收率重要性之比为3:2,试通过综合评分法确定有方案。
解:依题意,这是一个3因素3水平的试验,由于不考虑交互作用,所以可选用正交表L9(34)来安排试验。
表头设计、试验方案及实验结果如下表所示:
试验方案及其试验结果
如上表,采用综合评分法来确定优方案,试验结果具体计算过程:有两个指标:包合率和包合物收率,将其分别转换成它们的隶属度,用隶属度来表示分数。
指标隶属度=(指标值-指标最小值)/(指标最大值-指标最小值)因两个指标的重要性不一样,如果化成数量,包合率和包含物收率重要性之比为3:2,故有:
综合分数=包合率隶属度×+包合物收率隶属度×
依次求得9次试验的综合分数后,再分别计算它们所对应的K1,K2,K3,从而确定优方案:
通过正交试验对对木犀草素的β-环糊精包合工艺进行优化,试验指标包合率和包合物收率要越大越好。
A因素列:K1>K2>K3
B因素列:K2>K3>K1
C因素列:K3>K2>K1
所以有综合评分法确定优方案为A1B2C3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
09印刷工程5班方桂森 0
1、某饮料生产企业研制出一种新型饮料。
饮料的颜射共有四种,分别为橘黄色、
粉色、绿色和物色透明。
随机从超市市场收集了前一期该种饮料的销售量(万元),如下表所示,试问饮料的颜色是否对销售产生影响。
答:实验数据处理如下表:
实验分析:其中F-crit是显着性水平为时F的临界值,也就从F分布表中查到的(3,16),在本次试验中,F=>F-crit=,所以颜色因素对实验指标销售有显着影响,而P-value=<,说明颜色因素对销售有显着影响,因为P-value表示的是因素对实验结果无显着影响的概率。
2、在用原子吸收分光光度法测定镍电解液中微量杂质铜时,研究了乙炔和空气流量变
化对铜在某波长上吸光度的影响,得到下表所示的吸光度数据。
试根据表中数据分
析乙炔和空气流量的变化对铜吸光度的影响。
答:实验数据分析如下表:
实验分析:表中行代表的是乙炔流量,列代表的是空气流量。
在乙炔流量因素中,我们可以看到,F=> F-crit=且P-value=<,所以乙炔流量这个因素对铜吸光度的影响非常显着,而在空气流量中F< F-crit且P-value>,所以空气因素对铜吸光度的影响不大。
3、为了研究铝材材质的差异对于它们在高温水中的腐蚀性能的影响,用三种不同的铝
材在去离子水和自来水中于170°C进行了一个月的腐蚀试验,测得的深蚀率(μm)如下表所示。
试由下表所述结果考察铝材材质和水质对铝材腐蚀的影响。
试验数据处理结果:
试验数据分析:表中样本表示铝材材质,列表示去不同液体,交互表示的是两个因素的交互作用,从表中可以看到,样本的F> F-crit=和列F> F-crit=的以及交互的F > F-crit=,同时样本的P-value和列的P-value以及交互的P-value都远远小于,所以我们可以读出结论,铝材材质和不同液体对实验结果铝材腐蚀的影响较大,同时铝材材质和不同液体的交互作用对铝材腐蚀有显着影响。
