弯曲钻柱轴向力计算及强度校核
钻柱弯曲计算(kk)资料
qm
s in
r
)
与Dowson的处理方法相同，令： Fcr 0
1
n
n
L
qm
s in
4
8EIr
可得：
求得：
Fhel 2 2
EIqm sin
r
钻柱的纵弯（屈曲 讲
定向井中钻柱的失稳屈曲：
6. 吴疆（Jiang Wu）等人对水平井眼内钻柱曲屈的研究，得出：
Fsin 2
EIqm r
Fhel 2(2
r—视半径；r 0.5(Dh Dc )
α—井斜角；
Fcrit
2.93(
E
I
)0.479
q 0.522 m
(
s
in r
)0.436
钻柱的纵弯（屈曲 讲
定向井中钻柱的失稳屈曲：
4. 1984年Dowson首次提出倾斜井眼内钻柱发生正弦屈曲的载荷计算 公式，又称Dowson公式：
Fcr (n)
EI
Fsin 2
EIqm sin
r
这就是著名的Dowson公式，在工程上得到了广泛应用。
钻柱的纵弯（屈曲 讲
定向井中钻柱的失稳屈曲：
5. 1989年，Yu-che Chen等人，提出在斜直井眼和水平井眼中钻柱 发生螺旋屈曲的临界轴向压力计算公式：
Fcr (n)
4EI
2
L2
(n2
1 n2
L4
8 4EI
I—钻铤截面轴惯性矩ft4，；
I
64
(Dc4o
Dc4i）
r—视半径，ft ；
r 0.5(Dh Dc )
α—井斜角；
钻柱的纵弯（屈曲） 讲
定向井中钻柱的失稳屈曲：
钻柱力学计算
钻柱力学计算一、不带工具接头的管材在斜井段临界弯曲力的计算：式中：F c －临界弯曲力；lb ； E －杨氏模量，30 ⨯1000000 psi(钢材)； I －管材的惯性矩， in 4；W m －管材在钻井液中的重量，lb/in ； R －管材与井眼的径向间隙，in ； θ－井斜角，︒；二、带工具接头的管材在斜井段临界弯曲力的计算：式中：F c －临界弯曲力；lb ；W A －管材在空气中的重量，lb/in ； I －管材的惯性矩， in 4；A S －管材的横截面积，in 2；M W －钻井液密度，lb/gal ；D H －井眼直径，in ；D TJ －工具接头外径，in ；θ－井斜角，︒；2/1sin 2⎥⎦⎤⎢⎣⎡∙∙∙⨯=R W I E F m c θ()2/1sin 5.65550⎥⎦⎤⎢⎣⎡-∙-∙⨯=TJ H W A c D D M W I F θ()2216ID OD A I S +=三、摩擦扭矩的估算：钻具在斜直井段的摩擦扭矩：钻具在水平段的摩擦扭矩：钻具在90︒的弯曲井段中，如果钻压<0.33W M R 则：如果钻压>0.33W M R 则：式中：T －斜井段中的摩擦扭矩，ft-lb; T H －在水平井段中未接触井底旋转时的摩擦扭矩， ft-lb; T O －在90︒弯曲造斜井段造斜时的摩擦扭矩，ft-lb; OD －旋转钻具的接头外径或钻铤外径，in; L －钻具长度，ft;F －摩擦系数，在估算公式中取0.33; θ－井斜角，︒；W m －管材在钻井液中的重量，lb/in ； R －总的造斜曲率半径，ft;WOB －钻压，lb 。
24sin θ∙∙∙∙=F L W OD T M 72LW OD T M H ∙∙=72RW OD T M o ∙∙=()R W WOB OD R W OD T M M D 33.04672-+∙∙=四、钻具阻力计算：a. 钻具下入时的阻力估算：钻具在稳斜段中：钻具在水平段中：钻具在90︒弯曲造斜段：式中：D －斜井段中的摩擦阻力，lb; D H －在水平井段中的摩擦阻力，lb; D B －在90︒弯曲造斜井段的摩擦阻力，lb; W m －钻具在钻井液中的重量，lb/in ； L －钻具长度，ft;F －摩擦系数，在估算公式中取0.33; θ－井斜角，︒；R －造斜曲率半径，ft;WOB －钻压，lb 。
石油工程钻井钻柱力学-第四章 第3节-钻柱螺旋弯曲基本概念
o
3）、qn——由 钻组在泥浆 中的重量 q 产生的分布载 荷（沿半径指向外）；
NPT
4）、ƒn——法向反力（方 向沿半径指向中心）。
5）、此外，还受弯曲、扭 矩剪切、轴向拉、压力； 振动等。NPT—中和点； 当坐标原点选在中和点街 面上，Z轴平行于井眼轴线 （方向向下为正）时，取 出的距离原点 Z 的单元体 所对应的 角可认为其上 的螺旋角等于常数。 12
a L L Lab b x F
t
KL
t
Pa
图 2
T
图6 13
弯曲井段钻柱受力计算举例
如果已知狗腿严重度 = 5°/ 100 Ft，井段长度 L = 100Ft， 钻柱所受轴向拉力 T =105 Lbf。
试问：拉力 T 使钻柱对井壁产生的侧向压力 F = ?
[ Lbf、KN、t（吨）]—1Lbf = 4.448（N）。 如图（6）所示。 解： 1、由几何关系知道： x
— —（3）； 2 2 2 p 4 r 2 S
9
4）、再由曲率定义；得螺旋弯曲钻柱任意点处的曲率 计算公式：k p dx dy dz （4） ——— ds ds ds
2 2 2
5）、若将（3）式的二阶导数代入（4）式，并经过简化，可得至于螺距 （P）和圆柱半径（r）有关的曲率公式： k 4 2 r p 4 r
解：由题意：kb = 5/304.8m、 L = 1219.2/2 = 609.6cm、
6
Ap =74.79cm2、 Wp = 1112.06kN、 Wp =44.48kN。 I = /64(Dp4 - Di4) = 5086.74cm4、Dp = 24.447cm k = （64.5158 Wp / EI）0.5 = 8.25 10-3 kL = 8.25 609.6 10-3 = 5.0292 Tanh（0.3937kL）=Tanh（0.39375.0292）=0.96259 所以得答案：Qw = 1113.60kN
弯曲变形的强度条件和强度计算
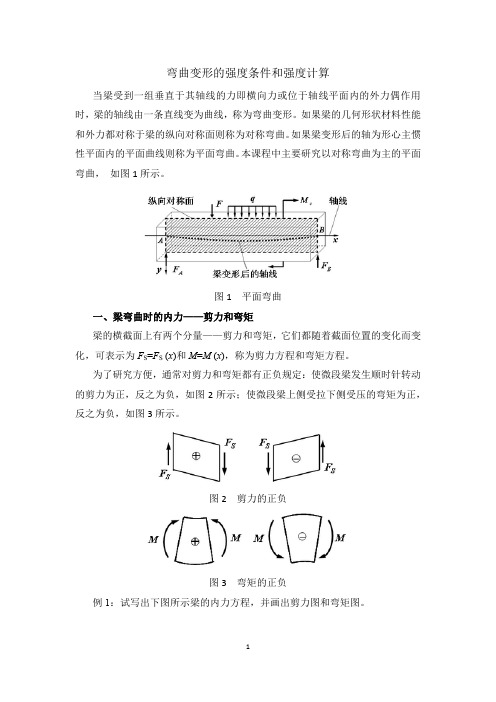
弯曲变形的强度条件和强度计算当梁受到一组垂直于其轴线的力即横向力或位于轴线平面内的外力偶作用时，梁的轴线由一条直线变为曲线，称为弯曲变形。
如果梁的几何形状材料性能和外力都对称于梁的纵向对称面则称为对称弯曲。
如果梁变形后的轴为形心主惯性平面内的平面曲线则称为平面弯曲。
本课程中主要研究以对称弯曲为主的平面弯曲，如图1所示。
图1 平面弯曲一、梁弯曲时的内力——剪力和弯矩梁的横截面上有两个分量——剪力和弯矩，它们都随着截面位置的变化而变化，可表示为F S=F S(x)和M=M (x)，称为剪力方程和弯矩方程。
为了研究方便，通常对剪力和弯矩都有正负规定：使微段梁发生顺时针转动的剪力为正，反之为负，如图2所示；使微段梁上侧受拉下侧受压的弯矩为正，反之为负，如图3所示。
图2 剪力的正负图3 弯矩的正负例1：试写出下图所示梁的内力方程，并画出剪力图和弯矩图。
解：（1）求支反力=∑C M：0310126=⨯--⋅AyF，kN7=AyF=∑Y：010=-+ByAyFF，kN3=ByF（2）列内力方程剪力：⎩⎨⎧<<-<<=63kN33kN7)(S xxxF弯矩：⎩⎨⎧≤≤≤≤⋅-⋅-=633mkN)6(3mkN127)(xxxxxM（3）作剪力图和弯矩图二、梁弯曲时的正应力在一般情况下，梁的横截面上既有弯矩又有剪力。
若梁上只有弯矩没有剪力，称为纯弯曲。
本讲主要讨论纯弯曲时横截面上的应力——正应力。
梁横截面上的正应力大小与该点至中性轴的距离成正比，即正应力沿截面宽度均匀分布，沿高度呈线性分布，如图4所示。
图4 梁弯曲时的正应力分布图即有yIxMz)(=σ（1）中性轴把截面分成受拉区和受压区两部分，且最大拉应力和最大压应力发生在上下边缘处，其值为max max y I Mz=σ。
令max y I W z z=，即有：zW M =max σ （2）式中，W z 称为抗弯截面系数，它与横截面的几何尺寸和形状有关，量纲为[长度]3，常用单位为mm 3或m 3。
2第4章钻柱弯曲-屈曲理论
m3
EI qm
钻杆断面轴惯性 矩，m4
钻柱在泥ቤተ መጻሕፍቲ ባይዱ中每 米重力，N/m
钻柱的纵弯（屈曲）
讲
Lubinski 的垂直井眼内钻柱弯曲 微分方程的建立
建立微分方程的目的：
• 研究钻柱在自重作用下去失稳屈曲的弯 曲形状时什么样？ • 用数学方程表示弯曲形状； • 受压长度与弯曲形状的关系，受压长度 对弯曲形状的影响；
r b tg (1.02 ) m r 1 b tg (1.5 ) m
1
b tg 1 (0.44
• 二次弯曲时的钻头倾角， 显然小于一次弯曲的倾角。 于是有人想将此原理用于 打直井。 • 60年代初到80年代中期， 此理论曾充斥我国钻井现 场
r ) m
实际情况不可能出现二次弯曲： 1. 钻铤上多带有扶正器； 2. 井眼不可能绝对垂直； 3. 钻柱是不断旋转的； 实际将出现螺旋弯曲。
钻柱的纵弯 （屈曲）
Lubinski 的垂直井眼内钻柱弯曲微分方 程的建立
W2 F2 W Qs Fs 0
分离体处在静力平衡状态下，所有力的合 力（矢量合）等于零。
将所有力投影到MN所在的断面上，则在 MN方向上，所有力的合力也应该等于零。
W2 sin F2 cos W sin Qs 0 Qs (W2 W ) sin F2 cos （1）
1
Dh—井眼直径； Dc—钻柱直径；
钻柱的纵弯（屈曲）
讲
Lubinski 的垂直井眼 内钻柱弯曲微分方程的 建立
弯曲状态 一次临界弯曲 二次弯曲出现 前的瞬间 二次临界弯曲
石油工程钻井钻柱力学-第五章钻柱一般设计方法与螺弯受力精品PPT课件
式中： PCIN——井深为 DW1处套管的内压力 ,MPa; D D0——上覆岩层压
力剃度，MPa/m； DW-——井深，m； DW1——-计算点井深处的压力
剃度， MPa/m ；GDg——天然气的压力剃度， MPa/m ；
7
二、钻柱设计的一般试验内容（条件）
1、 额定极限试验——如图 1A、B所示。
17
第三步：如果不满足公式（1-7）的任何一项试验要求，初 选壁厚是不使用的。需要用下列步骤进行计算。 （1）、如果所选择的tm是制造厂家壁厚列表中最后的，当 前设计就是失败的。 （2）、如果所哦选择tm不是制造厂家壁厚列表中最后的， 然后，从制造厂家壁厚列表中选择下一个壁厚tm+1。采用第 1-5 步重新进行设计。
2、大位移井钻柱设计方法步骤
设计过程需从井眼底部（端面）向上到井口逐渐（即从底 端的第“Ei”各单元）开始，按上述内容）逐一进行计算，
15
未设计好钻柱单元
节点（I+1）
tm E(I)设计单元
已设计好单元
0.000 1000 TVD 2000 英 3000 尺 4000 5000
井眼轨迹（二维剖面）
14
三、 钻柱的一般设计方法步骤
1、大位移井钻柱设计所需剖面（如图 3）
1）、井身剖面——认为井身剖面是由钻柱是由许多不连续 的节点组成的。
2）、钻柱剖面——是和井身剖面一样的网络形式。即节点 数相同、节点之间有相同的长度。
3）、设计任务——用制造厂家的钻柱管材壁厚表，确定钻 柱剖面上每个单元的近似壁厚。
当增大压缩比。对于高压缩比情况，想通过增大压缩比（13 ）来增加延伸长度（L）是无效的。由（9）式可以说明：
把最大压缩比用于钻柱设计上，将会减小钻柱的延伸长度。 2、压缩比（）大表示钻柱所受载荷大，相当于强度变差 或薄弱），从作业安全性来件，钻柱的（max）也要受限 制。主要原因在于：严重的螺旋弯曲是容易使钻柱产生其它 形式的破坏（如螺旋麻花状破坏）。因此在进行钻井作业时 ，要求保持低的压缩比。 3、式（9）中的最大压缩比（max）通常需要借助两个系 数加以确定。钻柱的下井深度（H）和作业的安全系数。在 实际应用，max一般限定到 10。
钻柱弯曲计算(kk)
钻柱的纵弯（屈曲）
定向井钻柱屈曲试验研究与理论研究的对比
Fhel
弯曲井眼内钻柱屈曲失稳的试验研究
• 两种理论模型计算结果与实验结果对比 ： 曲率 半径 (m)
试件类 型 5×0.5
正弦屈曲载荷(N) 实验值 Wu 于永南
325.23
429.68 2041.76 2438.23 2497.39 3509.79
临界长度：
• 受压长度较短时，钻柱不发生弯曲； • 受压长度达到一定值时，开始发生一次 弯曲，将此受压长度称作“临界长度”； • 临界长度的顶点，乃是“中性点”；
截面法：在受压段上，任取一点S，S 点所在断面为MN断面。从此处断开， 进行研究
钻柱的纵弯（屈曲
讲
定向井中钻柱的失稳屈曲：
1. 美国人Woods在与 Lubinski研究直井钻柱屈曲 时，也研究了倾斜井眼内钻 柱的屈曲问题，给出了倾斜 井眼中由于钻柱自重引起的 螺旋弯曲的临界公式：
2
2
求得：
EIqm sin Fhel 2 2 r
钻柱的纵弯（屈曲
讲
定向井中钻柱的失稳屈曲：
6. 吴疆（Jiang Wu）等人对水平井眼内钻柱曲屈的研究，得出：
EIqm Fsin 2 r EIqm Fhel 2(2 2 1) r
7. Mitchell通过对非线性微分方程的求解，得出了倾斜井眼内出现螺 旋屈曲的临界压力计算公式：
一次弯曲的临界受压长度
m3
EI qm
钻杆断面轴惯性 矩，m4
钻柱在泥浆中每 米重力，N/m
钻柱的纵弯（屈曲）
讲
Lubinski 的垂直井眼内钻柱弯曲 微分方程的建立
钻柱受力分析及强度校核
1
钻柱的工作状态
一、起下钻
整个钻柱被悬挂起来，在自重力的作 用下，处于拉伸的直线稳定状态
二、正常钻进
在部分自重压力、公转离心力和旋转 扭矩等因素的作用下，钻柱处于弯曲状态。
2
钻柱的受力分析
钻柱承受的基本载荷主要有以下几种：
（1）轴向力和压力： 钻柱在垂直井眼中处于悬挂状态，由于其自身的重量 ，钻柱受到拉伸，最下端的拉力最小（等于 0），最上端 的拉力最大。当井眼内充满钻井液时，钻柱还受到钻井液 对其产生的浮力，而作用在钻柱内外表面的侧向静液压力 ，虽然合力为零，但对钻柱管体形成侧向挤压作用，两种 力综合作用相当于使钻柱的线重减轻。 正常钻进时，部分钻柱的重力加到钻头上作为钻压。 钻压使钻柱的轴向拉力都减小一个相应数值，且下部钻柱 受压缩应力的作用。鲁宾斯基在此提出了中性点的概念
y d p Ks d p Ks 1 t 2 LS 2 LS
2
1 2
12
钻柱的强度校核
三是拉力余量法。考虑钻柱被卡时的上提解卡力，以钻柱 的最大允许静拉力小于最大安全拉伸力的一个合适余量来确保 钻柱不被拉断。
Fa FP MOP
4
钻柱的受力分析
1、钻柱的轴向应力计算 （1） 钻柱在空气中悬空时（图a） 分析：受重力、拉力 任一截面的拉力： ……………………（1） 式中： Fo——空气中任一截面上的拉力，kN； qp、qc——分别为钻杆、钻铤单位长度的重力，kN； Lc、——钻铤长度，m； Lp——截面以下钻杆长度，m；
5
9
钻柱的受力分析
6、纵向振动 n 在中性点处会产生交变的轴向应力； n 当纵向振动的周期和钻柱本身固有的振动周期相同（或成整 数倍时），就会产生共振，称之为“跳钻”。后果是严重的。 7、扭转振动
第5章钻柱
第五章 钻柱第一节 钻柱的工作状态及受力分析一、工作状态起下钻时：钻柱处于悬持状态－－受拉伸(自重)，直线稳定状态正常钻进：Ｐ＜Ｐ1 直线稳定Ｐ1≤Ｐ＜Ｐ2 一次弯曲Ｐ2≤Ｐ＜Ｐ3 二次弯曲钻柱旋转→扭矩离心力→下部弯曲半波缩短上部弯曲半波增长（上部受拉）结论：变节距的空间螺旋弯曲曲线形状钻柱在井内可能有4种旋转形式：(P96)a.自转：b.公转：沿井壁滑动。
c.自转和公转的结合：沿井壁滚动。
d.整个钻柱作无规则的摆动：二、钻柱在井下的受力分析(1) 轴向拉应力与压应力拉应力：由钻柱自重产生，井口最大，起钻和卡钻时产生附加拉力。
压应力：由钻压产生，井底最大。
应力分布(P97，图3-2) 轴向力零点：钻柱上即不受拉也不受压的一点。
中和点：该点以下钻柱在液体中的重量等于钻压。
(2) 剪应力(扭矩)：旋转钻柱和钻头所需的力，井口最大。
(3) 弯曲应力：钻柱弯曲并自转时产生交变的拉压应力。
井眼弯曲→钻柱弯曲 132(4) 纵向、横向、扭转振动(5) 其他外力：起下钻动载（惯性）,井壁磨擦力，钻柱旋转时因离心力引起的弯曲。
综合以上分析：工况不同，应力作用不同，需根据实际工况确定应力状态。
(1) 钻进时钻柱下部：轴向压力、扭矩、弯曲力矩、交变应力；(2) 钻进和起下钻时井口钻柱：拉力、扭力最大＋动载(3) 钻压、地层岩性变化引起中和点位移产生交变载荷。
第二节 钻井过程中各种应力的计算一、轴向应力计算（一）上部拉应力计算1、钻柱在泥浆中空悬浮力：αρ⋅⋅⋅⋅=F L g B mα——考虑钻杆接头和加厚影响的重量修正系数，1.05～1.10 钻柱在空气中的重力：αρ⋅⋅⋅⋅=F L g Q s a井口拉力：B Q Q a -=a f Q K Q ⋅=浮力系数：)1(s m f K ρρ-=ρs －－钢的密度，7.85 g/cm 3拉应力：FQ t =σ 注意计算井口以下任一截面上的拉力不能直接用浮力系数法计算。
钻柱强度计算新方法
钻柱强度计算新方法韩志勇（石油大学石油工程系，山东东营257062）摘要 提出了一种钻柱强度计算新方法。
可用于钻柱的强度设计和强度校核。
新方法和传统方法相比，有以下五个特点：（1）对钻柱每一个断面都进行强度校核；（2）对管的内壁和外壁分别进行强度校核；（3）利用计算机进行断面上有关内力的计算；（4）用“液压系数”处理液压环境对钻柱轴向力的影响；（5）考虑液压环境引起的附加剪应力的影响。
作者认为，“浮力系数”一次不甚恰当，应该用“液压系数”。
详细地给出了各种液压环境下钻柱液压系数的计算公式及算例。
并指出了新方法所属概念和共识的适用范围。
主题词 钻柱力学；钻井设计；强度；计算 0 引言对钻柱在垂直井眼、倾斜井眼、弯曲井眼内，以及在循环条件下的轴向力计算问题，以有详细的论述和相关计算公式[1～4]。
但对一些问题的论述和钻柱强度计算公式的推导，还有不完善的地方，本文对此作进一步阐述。
文中给出的所有公式，均可按法定计量单位运算。
使用常用单位时，应进行换算。
1 钻柱强度计算公式1．1 安全系数和相当应力计算公式微段的上断面的内缘处： N i =σs/σei)(3)(222ni mi bi a ei ττσσσ+++=微段的上断面的外缘处： N o =σs/σeo)(3)(222no mo bo a eo ττσσσ+++=式中，Ni 和No —分别为钻柱计算断面内缘、外缘处的强度安全数；σs —钻柱钢材的最小屈服极限；σei 和σeo —分别为钻柱计算断面内、外缘处的相当应力；σa —钻柱计算断面上的轴向应力；σbi 和σbo —分别为钻柱计算断面内、外缘处的弯曲应力；τmi 和τni —分别为钻柱计算断面内缘处的扭应力和附加剪应力；τmO 和τnO —分别为钻柱计算断面外缘处的扭应力和附加剪应力；1．2 轴向应力σa 的计算 σa =σz +σf +σp式中，σz —由重力和液压力引起的轴向力； σf —钻柱轴向运动摩阻力引起的轴向应力； σp —钻压引起的轴向应力； 1．3 弯曲应力σbo 和σbi 的计算若已知断面上的弯矩，可用下式计算：)(3244i o ib bi D D D M −=πσ )(3244i o ob bo D D D M −=πσ若已知井眼曲率，可用下式计算： K ED i bi 21=σK ED o bo21=σ 若考虑接头影响，可用下式计算：)tanh(2U UK ED i bi =σ)tanh(2U UKED o bo =σ其中，ρ⋅∆=L U 21EIF z=ρ 式中，M b —计算断面的弯矩；E —钻柱钢材的杨氏弹性模量； I —计算断面的极惯性矩；K —计算断面所在的井眼曲率；D i 和D o —分别为计算断面的内径和外径； F z —由钻柱重力和液压力引起的轴向力； U 和ρ—计算的过渡参数。
钻柱力四
2、斜井螺弯钻杆无因次参数表达形式； 斜井螺弯钻杆无因次参数表达形式；
1
实际上，钻杆有效重量是向下的， 实际上，钻杆有效重量是向下的，其侧向分量对井壁上半 部分并不起作用，接触力也是不均匀和不连续的； 部分并不起作用，接触力也是不均匀和不连续的；因此井 壁下半部分支撑着全部的侧向分量， 壁下半部分支撑着全部的侧向分量，而且在下井壁上转换 为摩擦阻力。假设形成螺旋弯曲的钻杆有多个螺距， 为摩擦阻力。假设形成螺旋弯曲的钻杆有多个螺距，与井 壁的接触力是均匀和连续的。因此， 壁的接触力是均匀和连续的。因此，有重量的钻杆和井壁 之间的接触力由（ 两部分组成。 之间的接触力由（we，wn）两部分组成。即：We + Wi - Wo r× (x)/(4×EI)组成的 组成的， （ ）为未知轴向压载： 和 Wn = r×F2(x)/(4×EI)组成的，F（x）为未知轴向压载：
F ( x) = Fo + µWe Sinα ⋅ dl − WeCosα ⋅ dl ——（4-1）
y
0
0
斜井眼
α Fƒ
We Sinα α
F(x)
x
Fo
螺旋弯曲钻杆
图（4-1） 斜井内螺旋弯曲钻杆轴向力示意图 ）
5
1
dL
We Sinα α
上井壁
We Cosα α
α
We
下井壁 有重量钻杆和井壁的接触力 NA A
rf EIWe Ao x W A rf + Arctg F Fa ( x ) = 2 tg e o o EIWe Ao rf 4 EI —（4-6b）
石油钻井用钻柱弯曲计算
2
2
式中，n为钻柱变形的半波数。n的大小与钻柱长度L有关。显然， 临界屈曲载荷应该是上式计算的最小值。为求得最小临界值， Dowson将n看作是连续变量，即认为钻柱长度为无限长。则根据 一阶导数等于零，可求得：
L qm sin n EIr
1 4
则得：
EIqm sin Fsin 2 r
I
64
4 4 ( Dco Dci ）
r—视半径，ft ；
r 0.5( Dh Dc )
α—井斜角；
钻柱的纵弯（屈曲）
讲
定向井中钻柱的失稳屈曲：
2. 20世纪50年代，Lubinski和 Woods在研究钻柱弯曲问题时，对倾 斜井眼内钻柱的失稳屈曲，进行了实 验研究。根据试验曲线，回归了发生 屈曲的临界压力计算公式：
左边式中， W—钻压,lb； qm—钻铤线浮重，lb/ft； m—一个无因次单位的长度，ft； E—钢材弹性模量，4176x106 lb/in2； I—钻铤截面轴惯性矩ft4，；
W m sin 2 m qm r
0.511115
• 值得注意的是，该公式重的 W乃是钻压，即钻柱的自重 形成的轴向压力。这与后来 一些研究者用Fcrit 作为两端 轴向力研究失稳屈曲，是有 差别的。
这就是著名的Dowson公式，在工程上得到了广泛应用。
钻柱的纵弯（屈曲
讲
定向井中钻柱的失稳屈曲：
5. 1989年，Yu-che Chen等人，提出在斜直井眼和水平井眼中钻柱 发生螺旋屈曲的临界轴向压力计算公式：
qm sin 1 L4 Fcr (n) 4 EI 2 (n 2 4 ) L n 8 EI r Fcr 0 与Dowson的处理方法相同，令： n 1 L qm sin 4 n 可得： 8EIr
石油钻井行业钻柱力学计算
石油钻井行业钻柱力学计算一、 不带工具接头的管材在斜井段临界弯曲力的计算：式中：F c －临界弯曲力；lb ；E －杨氏模量，30 ⨯1000000 psi(钢材)； I －管材的惯性矩， in 4；W m －管材在钻井液中的重量，lb/in ； R －管材与井眼的径向间隙，in ； θ－井斜角，︒；二、 带工具接头的管材在斜井段临界弯曲力的计算：式中：F c －临界弯曲力；lb ；W A －管材在空气中的重量，lb/in ； I －管材的惯性矩， in 4；A S －管材的横截面积，in 2； M W －钻井液密度，lb/gal ； D H －井眼直径，in ； D TJ －工具接头外径，in ； θ－井斜角，︒；2/1sin 2⎥⎦⎤⎢⎣⎡∙∙∙⨯=R W I E F m c θ()2/1sin 5.65550⎥⎦⎤⎢⎣⎡-∙-∙⨯=TJ H W A c D D M W I F θ()2216ID OD A I S+=三、 摩擦扭矩的估算：钻具在斜直井段的摩擦扭矩：钻具在水平段的摩擦扭矩：钻具在90︒的弯曲井段中，如果钻压<0.33W M R 则：如果钻压>0.33W M R 则：式中：T －斜井段中的摩擦扭矩，ft-lb;T H －在水平井段中未接触井底旋转时的摩擦扭矩， ft-lb; T O －在90︒弯曲造斜井段造斜时的摩擦扭矩，ft-lb; OD －旋转钻具的接头外径或钻铤外径，in; L －钻具长度，ft;F －摩擦系数，在估算公式中取0.33; θ－井斜角，︒；W m －管材在钻井液中的重量，lb/in ； R －总的造斜曲率半径，ft; WOB －钻压，lb 。
24sin θ∙∙∙∙=F L W OD T M 72LW OD T M H ∙∙=72RW OD T M o ∙∙=()R W WOB ODR W OD T M M D 33.04672-+∙∙=四、 钻具阻力计算：a. 钻具下入时的阻力估算： 钻具在稳斜段中：钻具在水平段中：钻具在90︒弯曲造斜段：式中：D －斜井段中的摩擦阻力，lb; D H －在水平井段中的摩擦阻力，lb; D B －在90︒弯曲造斜井段的摩擦阻力，lb; W m －钻具在钻井液中的重量，lb/in ； L －钻具长度，ft;F －摩擦系数，在估算公式中取0.33; θ－井斜角，︒； R －造斜曲率半径，ft; WOB －钻压，lb 。
优选钻柱弯曲屈曲理论
钻柱的纵弯（屈曲）
Lubinski 的垂直井眼内钻柱弯曲微分方程的建立
m是一个根据公式导出的单位。根据：X m x Y m y 可得：
dY d (my) mdy dy dX d (mx) mdx dx d 2Y d ( dY ) d ( dY ) 1 d ( dy ) 1 d 2 y dX 2 dX dX d (mx) dX m dx dx m dx2 d 3Y d ( d 2Y ) d ( 1 d 2 y ) 1 d ( d 2 y ) 1 d 3 y dX 3 dX dX 2 d (mx) m dx2 m2 dx dx2 m2 dx3
• 研究钻柱在自重作用下去失稳屈曲的弯 曲形状时什么样？
• 用数学方程表示弯曲形状； • 受压长度与弯曲形状的关系，受压长度
对弯曲形状的影响；
临界长度：
• 受压长度较短时，钻柱不发生弯曲； • 受压长度达到一定值时，开始发生一次
弯曲，将此受压长度称作“临界长度”；
• 临界长度的顶点，乃是“中性点”；
截面法：在受压段上，任取一点S，S 点所在断面为MN断面。从此处断开， 进行研究
钻柱的纵弯（屈曲）
Lubinski 的垂直井眼内钻柱弯曲 微分方程的建立
MN断面处钻柱轴线的倾斜角为α；
• 建立坐标系0-XY，微段长度的关 系：
tg dY dL dY 2 dX 2
dX
研究断面以下分离体的受力状况：
– 如何理解无因次量的单位m？ • 有一表示时间的量Y(小时)，1小时=60分，Y小时=ym，y=1，m=60分； • X、Y坐标原单位为米，先将X、Y坐标用mx、my代替，其中x、y代表量值， m代表单位。例如：X=50米，Y=60米，假设m=5米，则x=10，y=12； • x、y是无因次量；m是无因次量的单位。
轴的弯扭合成强度计算
轴的弯扭合成强度计算在初步完成轴的结构设计之后，对上面的草图略加修改，即可进行强度的校核计算了。
前面提到过，多数情况下，轴的工作能力一般主要取决于轴的强度。
此时只做强度计算，以防止或检验断裂和塑性变形。
而对于刚度要求高的轴和受力大的细长轴，还应该进行刚度计算，防止产生过大的线性变形。
对于高速运转的轴，还应该进行振动稳定性计算。
以防止产生共振破坏。
在进行轴的强度校核计算时，应根据轴的具体载荷和应力情况，采用相应的计算方法，并恰当的选择其许用应力。
根据计算原则，对于传动轴（仅仅或主要承受扭矩）按照扭矩强度条件进行计算，对于心轴（只承受弯矩）应该按照弯曲疲劳强度进行计算，对于该主轴，既承受扭矩还承受弯矩，是一个转轴，所以必须进行弯扭合成强度条件进行计算，需要时还应该进行疲劳强度的精确校核。
先按照弯扭合成强度条件进行计算：通过对该主轴的结构设计，轴的主要结构尺寸，轴上的零件的位置以及外载荷和支反力的作用位置已经确定。
轴上的载荷可以求得，因此可以按弯扭合成强度条件对该主轴进行强度的校核计算，其计算步骤如下：①做出轴的计算简图（力学模型）轴上受的载荷是由轴上的零件传来的，所以，计算时，可以将轴上的分布载荷情况简化为集中力。
其作用点可以一律简化，取为分布载荷的中点，作用在轴上的扭矩，一般从传动件轮毂宽度的中点算起，通常把当作置于铰链支座上的梁，支反力的作用点与轴承的类型和布置方式有关。
在做计算简图时，应该先求出轴上的受力零件的载荷（若为空间力系，图4 主轴再分解为水平分力和垂直分力。
然后求出各支承的水平反力和垂直反力），如图6所示。
②做弯矩图：根据前面的简图，分别按水平面和垂直面计算各力产生的弯矩图，并按计算结果分别作出水平面上的弯矩HM图和垂直面上的弯矩图上F M ，然后按照后面的公式推导出总弯矩，并作出M 图，如图6所示。
22VHMMM +=③作出扭矩图，如图5所示： ④作出计算弯矩图根据已经作出的总弯矩图和扭矩图，求出计算弯矩αc M ，并做出αc M图。
某井钻柱强度校核
某井钻柱强度校核某井钻柱强度校核摘要：由于某井是一口5110米的深井水平井，水平位移680米，水平段距离380米。
在钻井过程中不可避免地要遇到卡钻、弊钻、处理事故等过扭矩操作。
因此钻杆的抗扭强度是关键参数。
钻杆接头的抗扭强度是一个多变量函数，这些变量包括钢材强度、接头尺寸、螺纹形式、导程、锥度以及配合面螺纹或台肩的预紧力及摩擦系数等。
钻杆接头的外径和内径，在一定程度上决定了接头的抗扭强度，对钻杆的抗扭强度进行校核，保证管体的抗扭屈服强度。
钻杆的结构设计决定了钻杆的性能，在同样材料，同样工况，钻杆外径相同的情况下，不同结构尺寸的钻杆所表现出的性能也不一样，因此，通过对钻杆结构设计进行强度计算和校核不仅仅有着实际应用的意义，更可以从另一种角度，例如结合钻杆失效等问题，来探索研究更合理的钻杆结构设计，本文依据API给出的标准，在前人研究结果的基础上，对某厂的S135钻杆进行理化性能分析和结构设计的强度计算与校核。
目前在钻杆的使用中,失效问题是钻杆研究中的重要课题,基于钻杆的失效分析,从失效的角度来分析优化钻杆在结构设计上应注意的问题,为今后的钻杆结构设计提出一些理论依据。
具体内容如下：1. 油田钻具失效现状调研；2. 某公司 S135 钻杆材料理化性能分析；3. 某公司 S135 钻杆强度分析计算；关键词：钻柱；强度计算；设计；校核；钻具失效A well drilling column strength checkAbstract: Due to a well of 5110 is an one mouthful of horizontal Wells rice. Horizontal displacement is 680 meters. Horizontal distance is 3.8 meters. In drilling process, accident treatment and disadvantages will be inevitably stucked, such as torque operation. Therefore pipe wrest resistant strength is thekey parameters. Drill pipe joints wrest resistant intensity is a multivariate function. These variables include steel strength, connector size, thread form, palpitation, taper and surface thread or pre-tightening force and friction coefficient, etc. Drill pipe diameter and inner fittings, in certain extent determine the joints of drill pipe wrest resistant intensity. The intensity checking wrest resistant ensure the hose body wrest resistant yield strength.Pipe structure design decision was designed. Simulated performance, in the same materials , conditions ,and pipe diameter in the same case, different structure size of drill pipe showed what performance is not the same. Therefore, through the structure design of drill pipe calculated and checked the strength that is not just the meaning of practical application. For example, with the pipe failure to explore more reasonable drill pipe research, which is based on the structure design are given in the standard API, based on the results of previous studies. The S135 of a factory for drill physical-chemical properties of the analysis and structural design strength calculation and checking. To drill pipe structure design, currently has a decisive impact performance in use of pipe.Failure is an important subject in the research of drill pipe, which is based on the drill pipe failure analysis that from the perspective of failure in the structural design optimization drill problems that should be paid attention to on the drill pipe structure, in order to put forward some theoretical basis for design . Specific content as follows :1. Oilfield drilling tools failure situation investigation;2. A company S135 pipe materials; chemical performance analysis;3. A company S135 pipe strength calculation and analysis ;keyword:drill column, Strength calculation, Design, Check, Drilling tools, failure目录绪论 (1)1. 课题的意义 (1)2. 国内外研究现状 (2)1 钻柱 (5)1.1 钻柱的工作状态 (5)1.2 钻柱的受力分析 (8)1.3 钻井过程中各种应力的计算 (11)1.3.1 钻柱轴向应力的计算 (11)1.3.2 钻柱下部压力（Compressive stress）的计算 (14)1.3.3 钻柱剪应力（Shear stress）的计算 (15)1.3.4 钻柱弯曲应力（Bending stress）的计算 (17)1.3.5 钻柱抗挤（collapse Resistance）计算 (19)2 钻具失效现状及分析 (23)2.1 钻具主要失效类型 (23)2.2.1 过量变形 (23)2.2.2 断裂 (23)2.2.3 表面损伤 (24)2.2 钻具失效的原因 (25)2.3 预防钻具失效的措施探讨 (26)3 某公司S135钻杆理化性能分析 (28)3.1 管体化学成分 (28)3.2 接头化学成分 (28)3.3 管体、加厚对焊区的机械性能 (28)3.4 工具接头的机械性能 (29)4 某公司S135 钻杆强度分析计算 (30)4.1 钻杆抗拉强度计算 (30)4.2 钻杆抗扭屈服强度计算 (31)4.2.1 钻杆管体的抗扭强度关 (31)4.2.2 旋接接头扭矩计算 (33)4.3 钻杆抗挤强度计算 (34)4.3.1 屈服强度挤毁压力计算公式 (34)4.3.2 塑性挤毁压力公式 (35)4.3.3 过渡挤毁压力公式 (37)4.3.4 弹性挤毁压力公式 (38)4.4 钻杆抗内压强度计算 (40)4.5 对焊区的强度计算 (40)4.5.1 对焊区抗拉强度的计算 (40)4.5.2 对焊区抗扭强度的计算 (41)4.5.3 对焊区抗挤毁强度的计算 (41)4.5.4 对焊区抗内压强度计算 (41)4.6 某水平井钻柱设计 (42)4.6.1 一开钻具组合 (42)4.6.2 二开钻具组合 (42)4.6.3 三开钻具组合 (42)4.6.4 四开钻具组合 (43)4.7 钻具强度校核 (43)4.7.1 抗拉强度校核 (43)4.7.2 抗扭强度校核 (43)4.8 校核结果 (45)5 总结 (46)参考文献 (47)致谢 ................................................................................................... 错误！未定义书签。
椭圆钻杆强度校核
椭圆钻杆强度校核
钻杆连接如下，套管一端与连接杆热压连接成总成，总成之间用限位螺栓连接：
上图中：
外面套管材料为优质碳素结构钢（45#），
抗拉强度δb≥600Mpa，屈服强度δs≥355Mpa，
弹性模量E=200～220Gpa，泊松比μ=0.24～028；
里面连接杆材料为球墨铸铁（QT500-7），
抗拉强度δb≥500Mpa，屈服强度δs≥320Mpa，
弹性模量E=151～160Gpa，泊松比μ=0.25～029；
限位螺栓材料为合金结构钢（35CrMo），
抗拉强度δb≥985Mpa，屈服强度δs≥835Mpa，
弹性模量E=210Gpa，泊松比μ=0.25～0.3；
一、螺栓强度分析
用Ansys仿真模拟，螺栓与套管螺纹连接，假设刚性，沿套管轴向加力，受力如下图：
可知，当施加力达到65748N（约6.6T）时，螺栓达到屈服极限835Mpa，如图中螺栓根部（红色部分）。
二、套管扭矩分析
假设连接杆固定，对套管施加扭矩，受力如下图：
可知，当施加扭矩达到636201N.m 时，螺栓达到屈服极限355Mpa ，如图中钻杆螺栓孔根部（红色部分）。