二次函数根的分布
高中高考数学:二次函数根的分布

2
分析:①由 f (−3) ⋅ f (0) < 0 ,即 (14m + 15)( m + 3) < 0 ,得出 −3 < m < − 15 ;
14
②由 ∆ = 0 即16m
2
− 4 ( 2m + 6 ) = 0 得出 m = −1 或 m =
3 , 2
当 m = −1 时,根 x = −2 ∈ ( −3, 0 ) ,即 m = −1 满足题意; 当 m = 3 时,根 x = 3 ∉ ( −3, 0 ) ,故 m = 3 不满足题意;
2
所以 mx − ( m + 2 ) x + 2 = ( x − 1)( mx − 2 ) ,另一根为 2 ,由1 < 2 < 3 得 2 < m < 2 即为所求; m m 3
2
方程有且只有一根,且这个根在区间 (m, n ) 内,即 ∆ = 0 ,此时由 ∆ = 0 可以求出参数的值,然后再将参数的 值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数. 如:已知方程 x − 4mx + 2m + 6 = 0 有且一根在区间 ( −3, 0 ) 内,求 m 的取值范围.
两根都在 (m, n ) 内
两根有且仅有一根在 (m, n ) 一根在 (m, n ) 内,另一根在 内,另一根在 [m, n] 之外
m n x
( p, q ) 内, m < n < p < q
n
p q
m
x
m
n
x
得出的结论
∆>0 f (m) > 0 f (n) > 0 b m < − <n 2a
微专题11 二次函数根的分布问题(解析版)

微专题11二次函数根的分布问题【方法技巧与总结】1、实系数一元二次方程20(0)ax bx c a ++=≠的实根符号与系数之间的关系(1)方程有两个不等正根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=->⎨⎪⎪=>⎪⎩(2)方程有两个不等负根12,x x ⇔212124000b ac b x x a c x x a ⎧⎪∆=->⎪⎪+=-<⎨⎪⎪=>⎪⎩(3)方程有一正根和一负根,设两根为12,x x ⇔120cx x a=<2、一元二次方程20(0)ax bx c a ++=≠的根的分布问题一般情况下需要从以下4个方面考虑:(1)开口方向;(2)判别式;(3)对称轴2bx a=-与区间端点的关系;(4)区间端点函数值的正负.设12,x x 为实系数方程20(0)ax bx c a ++=>的两根,则一元二次20(0)ax bx c a ++=>的根的分布与其限定条件如表所示.根的分布图像限定条件12m x x <<02()0b m a f m ∆>⎧⎪⎪->⎨⎪⎪>⎩12x m x <<()0f m <12x x m<<02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪>⎩在区间(,)m n 内没有实根∆<12120x x m x x m∆==≤=≥或02()0b m a f m ∆>⎧⎪⎪-<⎨⎪⎪≥⎩02()0b n a f n ∆>⎧⎪⎪->⎨⎪⎪≥⎩()0()0f m f n ≤⎧⎨≤⎩在区间(,)m n 内有且只有一个实根()0()0f m f n >⎧⎨<⎩()0()0f mf n<⎧⎨>⎩在区间(,)m n内有两个不等实根2()0()0bm naf mf n∆>⎧⎪⎪<-<⎪⎨⎪>⎪>⎪⎩【题型归纳目录】题型一:正负根问题题型二:根在区间的分布问题题型三:整数根问题题型四:范围问题【典型例题】题型一:正负根问题例1.(2022·河南·郑州市回民高级中学高一阶段练习)已知m为实数,命题甲:关于x的不等式240mx mx+-<的解集为R;命题乙:关于x的方程22200x mx m-++=有两个不相等的负实数根.若甲、乙至少有一个为真命题,求实数m的取值范围为_______.【答案】(20,0]-【解析】由命题甲:关于x的不等式240mx mx+-<的解集为R,当0m=时,不等式40-<恒成立;当0m≠时,则满足2160mm m<⎧⎨∆=+<⎩,解得160m-<<,综上可得160m-<≤.由命题乙:关于x的方程22200x mx m-++=有两个不相等的负实数根,则满足2121244(20)020200m m x x m x x m ⎧∆=-+>⎪+=<⎨⎪=+>⎩,整理得2200020m m m m ⎧-->⎪<⎨⎪>-⎩,所以45020m m m m <->⎧⎪<⎨⎪>-⎩或,解得204m -<<-.所以甲、乙至少有一个为真命题时,有160m -<≤或204m -<<-,可得200m -<≤,即实数m 的取值范围为(20,0]-.故答案为:(20,0]-.例2.(2022·全国·高一单元测试)关于x 的方程2210ax x ++=的实数根中有且只有一个负实数根的充要条件为____________.【答案】0a ≤或1a =【解析】若方程2210ax x ++=有且仅有一个负实数根,则当0a =时,12x =-,符合题意.当0a ≠时,方程2210ax x ++=有实数根,则440a ∆=-≥,解得1a ≤,当1a =时,方程有且仅有一个负实数根1x =-,当1a <且0a ≠时,若方程有且仅有一个负实数根,则10a<,即0a <.所以当0a ≤或1a =时,关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根.综上,“关于x 的方程2210ax x ++=的实数根中有且仅有一个负实数根”的充要条件为“0a ≤或1a =”.故答案为:0a ≤或1a =.例3.(2022·甘肃·兰化一中高一阶段练习)若一元二次方程2330kx kx k ++-=的两根都是负数,求k 的取值范围为___________.【答案】125k ≤-或3k >【解析】首先0k ≠,设方程2330kx kx k ++-=的两根为12,x x ,则12121200,00x x x x x x +<⎧<<⇔⎨>⎩,所以2Δ94(3)03030k k k kkk k⎧⎪=--≥⎪⎪-<⎨⎪-⎪>⎪⎩,又0k ≠,解得125k ≤-或3k >.故答案为:125k ≤-或3k >.例4.(2022·全国·高一专题练习)已知关于x 的二次方程2(21)210m x mx m +-+-=有一正数根和一负数根,则实数m 的取值范围是_____.【答案】112m -<<【解析】由题意知,二次方程有一正根和一负根,得2101021m m m +≠⎧⎪-⎨<⎪+⎩,解得112m -<<.故答案为:112m -<<例5.(2022·河南·高一阶段练习)(1)若不等式210ax bx +-<的解集是113x x ⎧⎫-<<⎨⎬⎩⎭∣,求,a b 的值;(2)若31b a =--,且关于x 的方程210+-=ax bx 有两个不同的负根,求a 的取值范围.【解析】(1)由题意可得1-和13是方程210+-=ax bx 的两个实根,则11,31113b a a ⎧-+=-⎪⎪⎨-⎪-⨯=⎪⎩解得3,2a b ==.(2)因为31b a =--,所以()23110ax a x -+-=,由题可知Δ0>,则1a <-或19a >-,由题意,方程有两个负根,即310,10,a a a +⎧<⎪⎪⎨-⎪>⎪⎩解得103-<<a .综上,实数a 的取值范围是109aa ⎧⎫-<<⎨⎬⎩⎭∣.例6.(2022·辽宁·沈阳市第八十三中学高一阶段练习)已知1x 、2x 是一元二次方程24410kx kx k -++=的两个实数根.(1)若1x 、2x 均为正根,求实数k 的取值范围;(2)是否存在实数k ,使得()()12123222x x x x --=-成立?若存在,求出k 的值;若不能存在,请说明理由.【解析】(1)由题意,一元二次方程有两个正根1x 、2x 故20,(4)16(+1)0k k k k ≠∆=-≥,即0k ≤,且121210104x x k x x k +=>⎧⎪+⎨=>⎪⎩,解得:1k <-.(2)由题意,当0∆≥,即0k ≤时,有121211,4k x x x x k++==()()2221212121212129(1)93222+252()92442k k x x x x x x x x x x x x k k ++--=-=+-=-=-=-解得:95k =,与0k ≤矛盾.故不存在实数k ,使得()()12123222x x x x --=-成立题型二:根在区间的分布问题例7.(2022·全国·高一专题练习)已知一元二次方程x 2+ax +1=0的一个根在(0,1)内,另一个根在(1,2)内,则实数a 的取值范围为________.【答案】5(,2)2--【解析】设f (x )=x 2+ax +1,由题意知(0)10(1)20(2)520f f a f a =>⎧⎪=+<⎨⎪=+>⎩,解得-52<a <-2.故答案为:5(,2)2--.例8.(2022·全国·高一课时练习)已知关于x 的方程220x x a -+=.(1)当a 为何值时,方程的一个根大于1,另一个根小于1?(2)当a 为何值时,方程的一个根大于1-且小于1,另一个根大于2且小于3?(3)当a 为何值时,方程的两个根都大于0?【解析】(1)二次函数22y x x a =-+的图象是开口向上的抛物线,故方程220x x a -+=的一个根大于1,另一个根小于1,则2120a -+<,解得1a <,所以a 的取值范围是{}1a a <.(2)方程220x x a -+=的一个根大于1-且小于1,另一个根大于2且小于3,作满足题意的二次函数22y x x a =-+的大致图象,由图知,120120440960a a a a ++>⎧⎪-+<⎪⎨-+<⎪⎪-+>⎩,解得30a -<<.所以a 的取值范围是{}30a a -<<.(3)方程220x x a -+=的两个根都大于0,则Δ4400a a =-≥⎧⎨>⎩,解得01a <≤,所以a 的取值范围是{}01a a <≤.例9.(2022·全国·高一专题练习)已知关于x 的一元二次方程2220x ax a -++=,当a 为何值时,该方程:有不同的两根且两根在(1,3)内.【解析】令2()22f x x ax a =-++,因为方程2220x ax a -++=有不同的两根且两根在(1,3)内,所以213Δ44(2)0(1)30(3)1150a a a f a f a <<⎧⎪=-+>⎪⎨=->⎪⎪=->⎩,解得1125<<a ,故答案为:112,5⎛⎫⎪⎝⎭例10.(2022·江苏·高一专题练习)已知二次函数()2221R y x tx t t =-+-∈.(1)若该二次函数有两个互为相反数的零点,解不等式22210x tx t -+-≥;(2)若关于x 的方程22210x tx t -+-=的两个实根均大于2-且小于4,求实数t 的取值范围.【解析】(1)设二次函数()2221y x tx t t =-+-∈R 的两个零点分别为1x ,2x ,由已知得120x x +=,而122x x t +=,所以20t =,故0=t ,不等式22210x tx t -+-≥即210x -≥,解得1≥x 或1x ≤-,故不等式的解集为{1x x ≥或}1≤-x .(2)因为方程22210x tx t -+-=的两个实根均大于2-且小于4,所以()()()()222222Δ2t 4t 102t 422t 2t 1042t 4t 10⎧=---≥⎪⎪-<<⎨⎪--⨯-+->⎪-⨯+->⎩,即2240244308150t t t t t ≥⎧⎪-<<⎪⎨++>⎪⎪-+>⎩,解得:13t -<<,即实数t 的取值范围为{}13t t -<<.例11.(2022·全国·高一单元测试)求实数m 的范围,使关于x 的方程()221 260.x m x m +-++=(1)有两个实根,且一个比2大,一个比2小;(2)有两个实根 αβ,,且满足014αβ<<<<;(3)至少有一个正根.【答案】(1)1m <-(2)7554m -<<-(3)1m ≤-【分析】设()()22126y f x x m x m ==+-++,一元二次方程根的分布主要从对称轴、判别式、端点值、开口方向这几个方面来确定.(1)设()()22126y f x x m x m ==+-++.依题意有()20f <,即()441260m m +-++<,得1m <-.(2)设()()22126y f x x m x m ==+-++.依题意有()()()02601450410140f m f m f m ⎧=+>⎪=+<⎨⎪=+>⎩,解得7554m -<<-.(3)设()()22126y f x x m x m ==+-++.方程至少有一个正根,则有三种可能:①有两个正根,此时可得()()Δ0002102f m ⎧⎪≥⎪⎪>⎨⎪-⎪>⎪-⎩,即153.311m m m m m ≤-≥⎧⎪>-∴-<≤-⎨⎪<⎩或.②有一个正根,一个负根,此时可得()00f <,得3m <-.③有一个正根,另一根为0,此时可得()6203210m m m +=⎧∴=-⎨-<⎩,.综上所述,得1m ≤-.例12.(2022·上海市七宝中学高一阶段练习)方程()2271320x a x a a -++--=的一个根在区间()0,1上,另一个根在区间()1,2上,则实数a 的取值范围为___________.【答案】()()2,13,4--【解析】令()()227132f x x a x a a =-++--,因为程()2271320x a x a a -++--=的一个根在区间()0,1上,另一个根在区间()1,2上,所以()()()001020f f f ⎧>⎪<⎨⎪>⎩,即()22220713202821320a a a a a a a a ⎧-->⎪--+--<⎨⎪-++-->⎩,解得21a -<<-或34a <<,所以实数a 的取值范围为()()2,13,4--.故答案为:()()2,13,4--.例13.(2022·全国·高一专题练习)关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根,则实数a 的取值范围是_____.【答案】16(5,]3【解析】关于x 的方程()2140x a x --+=在区间[]1,3内有两个不等实根,令()()214f x x a x =--+,则有()()()2Δ1160113216031630a a f a f a ⎧=-->⎪-⎪<<⎪⎨⎪=-≥⎪=-≥⎪⎩,解得1653a <≤,所以实数a 的取值范围是16(5,]3.故答案为:16(5,]3例14.(2022·全国·高一单元测试)方程()2250x a x a --+-=的两根都大于2,则实数 a 的取值范围是_____.【答案】54a -<≤-【解析】由题意,方程()2250x a x a +=---的两根都大于 2,令()()225f x x a x a =+---,可得()020222f a⎧⎪≥⎪>⎨⎪-⎪>⎩,即2165024a a a ⎧≥⎪+>⎨⎪->⎩,解得54a <≤--.故答案为:54a -<≤-.例15.(2022·全国·高一专题练习)已知关于x 的方程220ax x ++=的两个实根一个小于0,另一个大于1,则实数a 的取值范围是_____.【答案】()3,0-【解析】显然0a ≠,关于x 的方程220ax x ++=对应的二次函数()22f x ax x =++当0a >时,二次函数()22f x ax x =++的图象开口向上,因为220ax x ++=的两个实根一个小于0,另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0,另一个大于1,所以()()0010f f ⎧<⎪⎨<⎪⎩,即2030a <⎧⎨+<⎩,解得a ∈∅;②当0a <时,二次函数()22f x ax x =++的图象开口向下,因为220ax x ++=的两个实根一个小于0,另一个大于1等价于二次函()22f x ax x =++的图象与x 轴的两个零点一个小于0,另一个大于1,所以()()0010f f ⎧>⎪⎨>⎪⎩,即2030a >⎧⎨+>⎩,解得30a -<<.;综上所述,实数a 的范围是()3,0-.故答案为:()3,0-.例16.(2022·全国·高一专题练习)已知方程()()22110x a x a a -+++=的两根分别在区间()0,1,()1,3之内,则实数a 的取值范围为______.【答案】()0,1.【解析】方程()()()()2211010x a x a a x a x a ⎡⎤+++=⇒--+=⎣⎦-∴方程两根为12,1x a x a ==+,若要满足题意,则01113a a <<⎧⎨<+<⎩,解得01a <<,故答案为:()0,1.例17.(2022·上海·高一专题练习)方程2240x ax -+=的两根均大于1,则实数a 的取值范围是_______【答案】5[2,)2【解析】2240x ax -+=的两个根都大于121520Δ4160a a a >⎧⎪∴->⎨⎪=-≥⎩,解得522a ≤<可求得实数a 的取值范围为5[2,2故答案为:5[2,)2例18.(2022·湖北·华中师大一附中高一开学考试)关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ,且121x x <<,那么a 的取值范围是()A .2275a -<<B .25a >C .27a <-D .2011a -<<【答案】D【解析】当0a =时,()2290ax a x a +++=即为20x =,不符合题意;故0a ≠,()2290ax a x a +++=即为22190x x a ⎛⎫+++= ⎪⎝⎭,令2219y x x a ⎛⎫=+++ ⎪⎝⎭,由于关于x 的方程()2290ax a x a +++=有两个不相等的实数根12,x x ,且121x x <<,则()229y ax a x a =+++与x 轴有两个交点,且分布在1的两侧,故1x =时,0y <,即211190a ⎛⎫++⨯+< ⎪⎝⎭,解得211a<-,故2011a -<<,故选:D例19.(2022·全国·高一课时练习)关于x 的方程()22210x m x m +-+-=恰有一根在区间()0,1内,则实数m 的取值范围是()A .13,22⎡⎤⎢⎥⎣⎦B .12,23⎛⎤ ⎥⎝⎦C .1,22⎡⎫⎪⎢⎣⎭D.{12,623⎛⎤⋃- ⎥⎝⎦【答案】D【解析】方程2(2)210x m x m +-+-=对应的二次函数设为:()2(2)21f x x m x m =+-+-因为方程2(2)210x m x m +-+-=恰有一根属于(0,1),则需要满足:①()()010f f ⋅<,()()21320m m --<,解得:1223m <<;②函数()f x 刚好经过点()0,0或者()1,0,另一个零点属于(0,1),把点()0,0代入()2(2)21f x x m x m =+-+-,解得:12m =,此时方程为2302x x -=,两根为0,32,而()30,12∉,不合题意,舍去把点()1,0代入()2(2)21f x x m x m =+-+-,解得:23m =,此时方程为23410x x -+=,两根为1,13,而()10,13∈,故符合题意;③函数与x 轴只有一个交点,横坐标属于(0,1),()2(2)4210m m ∆=---=,解得6m =±当6m =+2(2)210x m x m +-+-=的根为2-若6m =-2(2)210x m x m +-+-=2,符合题意综上:实数m的取值范围为{12,623⎛⎤⋃- ⎥⎝⎦故选:D题型三:整数根问题例20.(2022·上海市实验学校高一开学考试)已知12,x x 是一元二次方程24410kx kx k -++=的两个实数根.(1)是否存在实数k ,使得()()12123222x x x x --=-成立?若存在,求出k 的值;若不存在,请说明理由;(2)求使12212x x x x +-的值为整数的实数k 的整数值.【解析】(1)假设存在实数k ,使得()()12123222x x x x --=-成立,一元二次方程24410kx kx k -++=的两个实数根,()2400Δ(4)441160k k k k k k ≠⎧∴⇒<⎨=--⋅+=-⎩,(不要忽略判别式的要求),由韦达定理得1212114x x k x x k +=⎧⎪+⎨=⎪⎩,()()()()2221212121212129322252942k x x x x x x x x x x x x k +∴--=+-=+-=-=-,95k ⇒=但0k <,∴不存在实数k ,使得()()12123222x x x x --=-成立.(2)()22212121221121244224411x x x x x x k x x x x x x k k +++-==-=-=-++,∴要使其值是整数,只需要1k +能被4整除,故1124k +=±±±,,,即021335k =---,,,,,,0k <,235k ∴=---,,.例21.(2022·上海·高三专题练习)已知,a Z ∈关于x 的一元二次不等式260x x a -+≤的解集中有且仅有3个整数,则所有符合条件的a 的值之和是()A .13B .18C .21D .26【答案】C【解析】设2()6f x x x a =-+,其图象为开口向上,对称轴为3x =的抛物线,根据题意可得,3640a ∆=->,解得9a <,因为()0f x ≤解集中有且仅有3个整数,结合二次函数的对称性可得(2)0(1)0f f ≤⎧⎨>⎩,即4120160a a -+≤⎧⎨-+>⎩,解得58a <≤,又,a Z ∈所以a =6,7,8,所以符合题意的a 的值之和6+7+8=21.故选:C例22.(多选题)(2022·全国·高一课时练习)已知a ∈Z ,关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数,则a 的值可以是()A .5B .6C .7D .9【答案】BC【解析】设()26f x x x a =-+,函数图象开口向上,且对称轴为3x =,因此关于x 的一元二次不等式x 2-6x +a ≤0的解集中有且仅有3个整数时,需满足()()2010f f ⎧≤⎪⎨>⎪⎩,即2226201610a a ⎧-⨯+≤⎨-⨯+>⎩,解得58a <≤,又因为a ∈Z ,所以6a =或7或8,故选:BC.例23.(2022·全国·高一专题练习)若方程()22460x kx x --+=有两个不相等的实根,则k 可取的最大整数值是______.【答案】1【解析】方程化为()221860k x x --+=,由()Δ6424210k =-->,12k ≠解得116k <,所以k 最大整数值是1.故答案为:1.题型四:范围问题例24.(2022·上海·高一专题练习)已知t 是实数,若a ,b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根,则()()2211a b --的最小值是___________.【答案】3-【解析】a ,b 是关于x 的一元二次方程2210x x t -+-=的两个非负实根,∴可得2a b +=,10ab t =-≥,1t ∴≥,又()4410t ∆=--≥,可得2t ≤,12t ∴≤≤,又()()()()()()222222211121a b ab a b ab a b ab --=-++=-+++()()()()2221114211a b t t ∴--=--+-+,24t =-,又12t ≤≤,2340t ∴-≤-≤,故答案为:3-.例25.(2022·吉林省实验中学高一阶段练习)设方程240x mx m -+=的两实根分别为12,x x .(1)当1m =时,求1211+x x 的值;(2)若120,0x x >>,求实数m 的取值范围及124x x +的最小值.【解析】(1)当1m =时,方程为2410x x -+=,2(4)4120∆=--=>,所以12124,1x x x x +=⋅=,122112114x x x x x x ∴+⋅+==.(2)因为240x mx m -+=两根120,0x x >>,所以21212Δ1640400m m x x m x x m ⎧=-≥⎪+=>⎨⎪⋅=>⎩,解得14m ≥.因为12124x x x x +=,120,0x x >>,所以12114x x +=,所以211212121241111194(4)()(5)54444x x x x x x x x x x ⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭,当且仅当21124x x x x =,即1233,48x x ==时等号成立,此时91324m =>符合题意,124x x ∴+的最小值为94.例26.(2022·北京海淀·高一期末)已知函数()22f x x bx c =++(b ,c 为实数),()()1012f f -=.若方程()0f x =有两个正实数根1x ,2x ,则1211+x x 的最小值是()A .4B .2C .1D .12【答案】B【解析】因为函数()22f x x bx c =++(b ,c 为实数),()()1012f f -=,所以1012200288b c b c +=++-,解得4b =-,所以()224f x x x c -+=,因为方程()0f x =有两个正实数根1x ,2x ,所以()Δ168000c f c =-≥⎧⎨=>⎩,解得02c <≤,所以121212112422x x c x x x x c =++==≥,当c =2时,等号成立,所以其最小值是2,故选:B例27.(2022·江苏·高一)已知关于x 的方程230x kx k -++=有两个正根,那么两个根的倒数和最小值是()A .-2B .23C .89D .1【答案】B【解析】由题意可得∆2()4(3)0k k =--+ ,解得6k 或2k ≤-,设两个为1x ,2x ,由两根为正根可得12120·30x x k x x k +=>⎧⎨=+>⎩,解得0k >,综上知,6k .故两个根的倒数和为12121211x x x x x x ++=1331k k k==++,6k ,∴1106k < ,3102k < ,故33112k <+,∴12331k+,故两个根的倒数和的最小值是23.故选:B例28.(2022·上海·华师大二附中高一期中)已知实数a b <,关于x 的不等式()210x a b x ab -+++<的解集为()12,x x ,则实数a 、b 、1x 、2x 从小到大的排列是()A .12a x x b <<<B .12x a b x <<<C .12a x b x <<<D .12x a x b<<<【答案】A【解析】由题可得:12x x a b +=+,121x x ab =+.由a b <,12x x <,设1x a m =+,则2x b m =-.所以212()()()1a m b m ab m b a m ab x x =+-=+--=+,所以2()1m b a m --=,21m m b a+=-.又a b <,所以0b a ->,所以0m >.故1x a >,2x b <.又12x x <,故12a x x b <<<.故选:A.例29.(2022·福建厦门·高一期末)已知函数()()11f x x x a =-⋅--,a R ∈.(1)若0a =,解不等式()1f x <;(2)若函数()f x 恰有三个零点1x ,2x ,3x ,求123111x x x ++的取值范围.【解析】(1)当0a =时,原不等式可化为()120x x -⋅-<…①.(ⅰ)当0x ≥时,①式化为220x x --<,解得12x -<<,所以02x ≤<;(ⅱ)当0x <时,①式化为220x x -+>,解得x ∈R ,所以0x <.综上,原不等式的解集为(),2-∞.(2)依题意,()()()2211,11,x a x a x af x x a x a x a ⎧-++--<⎪=⎨-++-≥⎪⎩.因为()10f a =-<,且二次函数()211y x a x a =-++-开口向上,所以当x a ≥时,函数()f x 有且仅有一个零点.所以x a <时,函数()f x 恰有两个零点.所以()()()21,21410,10.a a a a f a +⎧<⎪⎪⎪=+-+>⎨⎪=-<⎪⎪⎩解得3a >.不妨设123x x x <<,所以1x ,2x 是方程()2110x a x a -++--=的两相异实根,则12121,1x x a x x a +=+⎧⎨=+⎩,所以121212111x x x x x x ++==.因为3x 是方程()2110x a x a -++-=的根,且312a x +>,由求根公式得3x =因为函数()g a ()3,+∞上单调递增,所以()332x g >=31012x <<-.所以123111x x x ++.所以a 的取值范围是21,22⎛- ⎝⎭.【过关测试】一、单选题1.(2022·江苏·高一专题练习)已知p :a m <(其中R a ∈,m ∈Z ),q :关于x 的一元二次方程2210ax x ++=有一正一负两个根.若p 是q 的充分不必要条件,则m 的最大值为()A .1B .0C .1-D .2【答案】C【解析】因为2210ax x ++=有一正一负两个根,所以224010a a ⎧∆=->⎪⎨<⎪⎩,解得0a <.因为p 是q 的充分不必要条件,所以0m <,且m ∈Z ,则m 的最大值为1-.故选:C2.(2022·江苏·高一专题练习)已知方程2(2)50x m x m +-+-=有两个不相等的实数根,且两个实数根都大于2,则实数m 的取值范围是()A .(5,4)(4,)--+∞B .(5,)-+∞C .(5,4)--D .(4,2)(4,)--+∞【答案】C【解析】令()2(2)5mf x m x x =+-+-由题可知:()()()()2Δ02450442222242250520m m m m m m m m m m f >⎧⎧--⨯->><-⎧⎪⎪-⎪⎪>⇒<-⇒<-⎨⎨⎨⎪⎪⎪+-⨯+->>-⎩>⎩⎪⎩或则54m -<<-,即(5,4)m ∈--故选:C3.(2021·北京·北师大实验中学高一期中)设方程2610x x -+=的两个不等实根分别为12,x x ,则12||x x -=()A .3B .6C.D.【答案】D【解析】2610x x -+=,364320∆=-=>,故121261x x x x +=⎧⎨=⎩,12||x x -===.故选:D.4.(2021·江苏·高一课时练习)设a 为实数,若方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解,则a 的取值范围是().A .(,0)(1,)-∞⋃+∞B .(1,0)-C .1,03⎛⎫- ⎪⎝⎭D .1,0(1,)3⎛⎫-+∞ ⎪⎝⎭【答案】C【解析】令2()2g x x ax a =-+,由方程220x ax a -+=在区间(1,1)-上有两个不相等的实数解可得244011(1)0(1)0a a a g g ⎧∆=->⎪-<<⎪⎨->⎪⎪>⎩,即011131a a a a <⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩或111131a a a a >⎧⎪-<<⎪⎪⎨>-⎪⎪<⎪⎩,解得103-<<a ,故选:C5.(2022·全国·高一课时练习)一元二次方程()22100ax x a ++=≠有一个正实数根和一个负实数根的一个充分不必要条件是()A .0a <B .0a >C .1a <-D .2a <【答案】C【解析】由题意,不妨设2()21f x ax x =++,因为(0)10=>f ,且()22100ax x a ++=≠有一个正实数根和一个负实数根,所以2()21f x ax x =++的图像开口向下,即0a <,故对于选项ABCD ,只有C 选项:1a <-是0a <的充分不必要条件.故选:C.6.(2021·四川·树德中学高一阶段练习)设集合{}2320A x x x =-+<,集合{}2210B x ax x =--=,若A B ⋂≠∅,则实数a 的取值范围是()A .34,43⎡⎫⎪⎢⎣⎭B .5,34⎛⎫ ⎪⎝⎭C .3,4⎡⎫+∞⎪⎢⎣⎭D .(1,)+∞【答案】B【解析】由题意,{}2320{|12}A x x x x x =-+<=<<若AB ⋂≠∅,即方程2210ax x --=存在根在区间(1,2)(1)若102102a x x =∴--=∴=-,不成立;(2)若0a ≠,由于0x =不为方程的根,故0x ≠,则222221211210(1)1x ax x a x x x x+--=⇔==+=+-由于21115(1,2)(,1)(1)1(,3)24x x x ∈∴∈∴+-∈综上,实数a 的取值范围是5,34⎛⎫⎪⎝⎭故选:B7.(2022·全国·高一课时练习)要使关于x 的方程()22120x a x a +-+-=的一根比1大且另一根比1小,则实数a 的取值范围是()A .{}12a a -<<B .{}21a a -<<C .{}2a a <-D .{}1a a >【答案】B【解析】由题意可得()2211220a a a a +-+-=+-<,解得21a -<<.故选:B.8.(2021·甘肃·天水市第一中学高一阶段练习)已知一元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ,2x ,且12013x x <<<<,则m 的值为()A .4-B .5-C .6-D .7-【答案】A【解析】因为元二次方程2(1)10()x m x m Z +++=∈有两个实数根1x ,2x ,且12013x x <<<<,令2()(1)1f x x m x =+++,则由题意可得(0)0(1)0(3)0f f f >⎧⎪<⎨⎪>⎩,即10,30,1330,m m >⎧⎪+<⎨⎪+>⎩解得1333m -<<-,又m Z ∈,可得4m =-.故选:A 二、多选题9.(2022·江苏南通·高一开学考试)已知不等式20(0)x ax b a ++>>的解集是{}|x x d ≠,则下列四个结论中正确的是().A .24a b=B .若不等式2+x ax b c +<的解集为(3,1)-,则7a b c ++=C .若不等式20x ax b +-<的解集为12(,)x x ,则120x x >D .若不等式2x ax b c ++<的解集为12(,)x x ,且12||4x x -=,则4c =【答案】ABD【解析】由题意,不等式20(0)x ax b a ++>>的解集是{}|x x d ≠,所以240a b ∆=-=,24a b ∴=,所以A 正确;对于B :2+x ax b c +<变形为2+0x ax b c +-<,其解集为(3,1)-,所以231 314 a b c a b -+=-⎧⎪-⨯=-⎨⎪=⎩,得214a b c =⎧⎪=⎨⎪=⎩,故7a b c ++=成立,所以B 正确;对于C :若不等式20x ax b +-<的解集为12(,)x x ,由韦达定理知:21204a x xb =-=-<,所以C 错误;对于D :若不等式2x ax bc ++<的解集为12(,)x x ,即20x ax b c ++-<的解集为12(,)x x ,由韦达定理知:21212,4a x x a x x b c c +=-=-=,则12||4x x -==,解得4c =,所以D 正确.故选:D.10.(2021·江苏·海安高级中学高一阶段练习)一元二次方程240x x m -+=有正数根的充分不必要条件是()A .4m =B .5m =C .1m =D .12=-m 【答案】ACD【解析】设()24f x x x m =-+,则二次函数()f x 的图象的对称轴为2x =.当4m =时,方程即()224420x x x -+=-=,求得2x =,满足方程有正根,但由方程240x x m -+=有正数根,可得()240f m =-≤,即4m ≤,故4m =是方程240x x m -+=有正数根的充分不必要条件,故A 满足条件;当5m =时,方程即()224521x x x -+=-=-,求得x ∈∅,不满足方程有正实数根,故5m =不是方程240x x m -+=有正数根的充分条件,故排除B .当1m =时,方程即()224123x x x -+=-=,求得2=±x 但由方程240x x m -+=有正数根,可得()240f m =-≤,即4m ≤,故1m =方程240x x m -+=有正数根的充分不必要条件,故C 满足条件;当12=-m 时,方程即24120x x --=,求得2x =-,或6x =,满足方程有正根,但由方程240x x m -+=有正数根,可得()240f m =-≤,即4m ≤,故12=-m 方程240x x m -+=有正数根的充分不必要条件,故D 满足条件,故选:ACD .11.(2022·湖南湖南·高一期末)若方程220x x λ++=在区间()1,0-上有实数根,则实数λ的取值可以是()A .3-B .18C .14D .1【答案】BC【解析】由题意22x x λ=--在(1,0)-上有解.∵(1,0)x ∈-,∴222(1)1(0,1)x x x λ=--=-++∈,故选:BC .12.(2021·全国·高一专题练习)已知关于x 的方程()230x m x m +-+=,则下列结论中正确的是()A .方程()230x m x m +-+=有一个正根一个负根的充要条件是{}0m m m ∈<B .方程()230x m x m +-+=有两个正实数根的充要条件是{}01m m m ∈<≤C .方程()230x m x m +-+=无实数根的充要条件是{}1m m m ∈>D .当m =3时,方程()230x m x m +-+=的两个实数根之和为0【答案】AB【解析】对A ,当0x =时,函数2(3)y x m x m =+-+的值为m ,由二次函数的图象知,方程有一正一负根的充要条件是{}|0m m m ∈<,故A 正确;对B ,若方程()230x m x m +-+=有两个正实数根1x ,2x ,即()2121234030,0,m m x x m x x m ⎧∆=--≥⎪+=->⎨⎪=>⎩解得:01m <≤,故B 正确;对C ,方程()230x m x m +-+=无实数根,即()2340m m ∆=--<,解得:19m <<,方程()230x m x m +-+=无实数根的充要条件是{}19m m m ∈<<,故C 错误;对D ,当3m =时,方程为230x +=,无实数根,故D 错误.故答案为:AB.13.(2021·江苏·高一专题练习)已知一元二次方程()()21102x m x m Z +++=∈有两个实数根12,x x ,且12013x x <<<<,则m 的值为()A .-2B .-3C .-4D .-5【答案】BC 【解析】设()()2112f x x m x =+++,由12013x x <<<<,可得()()()()10200110110230193102f f m f m ⎧>⎪⎧>⎪⎪⎪<⇒+++<⎨⎨⎪⎪>⎩⎪+++>⎪⎩,解得:25562m -<<-,又因为m Z ∈,得3m =-或4m =-,故选:BC.三、填空题14.(2022·安徽省蚌埠第三中学高一开学考试)关于x 的方程210x ax ++=的一根大于1,一根小于1,则a 的取值范围是:__________________.【答案】a <-2【解析】∵关于x 的方程210x ax ++=的一根大于1,另一根小于1,令2()1=++f x x ax ,则(1)20f a =+<,求得2a <-,故答案为:2a <-15.(2021·北京师大附中高一期中)若关于x 的一元二次方程2240x ax -+=有两个实根,且一个实根小于1,另一个实根大于2,则实数a 的取值范围是________.【答案】(52,+∞)【解析】设2()24f x x ax =-+,由题意2Δ4160(1)1240(2)4440a f a f a ⎧=->⎪=-+<⎨⎪=-+<⎩,解得52a >,故答案为:5(,)2+∞.16.(2021·上海·复旦附中高一期中)若关于x 的方程220x kx -+=的一根大于-1,另一根小于-1,则实数k 的取值范围为______.【答案】(),3-∞-【解析】由题意,关于x 的方程220x kx -+=的一根大于-1,另一根小于-1,设()22f x x kx =-+,根据二次函数的性质,可得()130f k -=+<,解得3k <-,所以实数k 的取值范围为(),3-∞-.故答案为:(),3-∞-.17.(2020·上海·高一专题练习)已知集合()(){}2|320,A x x x x x R =-+-≤∈,{}2|120,B x x ax x R =--≤∈,若A B ⊆,则实数a 的取值范围是______________.【答案】[]1,1-【解析】由()()2320x x x -+-≤,得23020x x x ⎧-≥⎪⎨+-≤⎪⎩或23020x x x ⎧-≤⎪⎨+-≥⎪⎩,解得13x ≤≤,所以集合{|31A x x =-≤≤-或}13x ≤≤,因为A B ⊆,令()212f x x ax =--,则()()3030f f ⎧-≤⎪⎨≤⎪⎩,即9312093120a a +-≤⎧⎨--≤⎩,解得11a -≤≤,所以实数a 的取值范围是[]1,1-故答案为:[]1,1-四、解答题18.(2022·全国·高一期中)命题:p 关于x 的方程20x x m ++=有两个相异负根;命题():0,q x ∃∈+∞,2390x mx -+<.(1)若命题q 为假命题,求实数m 的取值范围;(2)若这两个命题有且仅有一个为真命题,求实数m 的取值范围.【解析】(1)若命题q 为假命题,则对()0,x ∀∈+∞,2390x mx -+≥为真命题;239mx x ∴≤+,即93m x x ≤+;96x x +≥(当且仅当9x x =,即3x =时取等号),36m ∴≤,解得:2m ≤,∴实数m 的取值范围为(],2-∞.(2)由(1)知:若命题q为真命题,则2m >;若命题p 为真命题,则Δ1400m m =->⎧⎨>⎩,解得:104m <<;若p 真q 假,则104m <<;若p 假q 真,则2m >;综上所述:实数m 的取值范围为()10,2,4⎛⎫+∞ ⎪⎝⎭.19.(2022·湖南·高一课时练习)若一元二次方程2570x x a --=的一个根在区间()1,0-内,另一个根在区间()1,2内,求实数a 的取值范围.【解析】令2()57f x x x a =--,则根据题意得(1)057012(0)000(1)0202(2)0201406f a a f a a f a a f a a ->⇒+->⇒<⎧⎪<⇒-⇒⎪⎨<⇒--⇒-⎪⎪>⇒-->⇒<⎩,∴06a <<.故实数a 的取值范围(0,6).20.(2021·辽宁·昌图县第一高级中学高一期中)1.已知()()2213f x x a x =+-+.(1)如果方程()0f x =在()0,3有两个根,求实数a 的取值范围;(2)如果[]1,2x ∃∈,()0f x >成立,求实数a 的取值范围.【解析】(1)()()2213f x x a x =+-+的对称轴为1x a=-要想方程()0f x =在()0,3有两个根,需要满足()()()100001330f a f a f ⎧-<⎪>⎪⎨<-<⎪⎪>⎩解得:(1,1a ∈--(2)[]1,2x ∃∈,()22130x a x +-+>成立,即3122x a x ⎛⎫->-+ ⎪⎝⎭在[]1,2x ∈上有解,只需1a -大于()322x g x x ⎛⎫=-+ ⎪⎝⎭的最小值,其中()322x g x x ⎛⎫=-+ ⎪⎝⎭为对勾函数,在x ⎡∈⎣上单调递增,在)x ∈上单调递减,又()131222g ⎛⎫=-+=- ⎪⎝⎭,()2372244g ⎛⎫=-+=- ⎪⎝⎭,所以最小值为()12g =-故12a ->-,解得:1a >-,实数a 的取值范围为()1,-+∞21.(2021·上海市七宝中学高一阶段练习)设二次函数()2f x ax bx c =++,其中R a b c ∈、、.(1)若()21,94b a c a =+=+,且关于x 的不等式()28200-+<x x f x 的解集为R ,求a 的取值范围;(2)若Z a b c ∈、、,且()()01f f 、均为奇数,求证:方程()0f x =无整数根;(3)若21,21,a b k c k ==-=,当方程()0f x =有两个大于1的不等根时求k 的取值范围.【解析】(1)∵()22820440x x x -+=-+>∴()()221940f x ax a x a =++++<在R 上恒成立∵0a ≠,则()()20Δ414940a a a a <⎧⎪⎨=+-+<⎪⎩,解得12a <-综上所述:a 的取值范围为1,2⎛⎫-∞- ⎪⎝⎭.(2)∵()()0,1f c f a b c ==++,则c 为奇数,a b +为偶数当Z x ∈时,则有:1.若a b 、均为偶数时,则2ax bx +为偶数∴()20f x ax bx c =++≠,即方程()0f x =无整数根2.若a b 、均为奇数时,则有①若x 为偶数时,则2ax bx +为偶数∴()20f x ax bx c =++≠,即方程()0f x =无整数根②若x 为奇数时,则()2ax bx x ax b +=+为偶数∴()20f x ax bx c =++≠,即方程()0f x =无整数根综上所述:方程()0f x =无整数根(3)()()2221f x x k x k =+-+由题意可得()()222Δ21402112120k k k f k k ⎧=-->⎪-⎪->⎨⎪=+>⎪⎩,解得2k <-则k 的取值范围为(),2∞--.。
二次方程根的分布情况归纳(教师版)

二次方程根的分布与二次函数在闭区间上的最值归纳21、一元二次方程ax bx c 0根的分布情况设方程ax bx c 0 a 0的不等两根为X|,X2且X i x?,相应的二次函数为f x ax bx c 0,方程的根即为二次函数图象与x轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)根在区间上的分布还有一种情况:两根分别在区间夕卜,即在区间两侧为2,(图形分别如下)需满足的条件是f n 0 f n 0对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在 m, n 有以下特殊情况:1 若f m 0或f n 0,则此时f mg f n 0不成立,但对于这种情况是知道了方程有一根为 m 或n ,可以求出另外一根, 然后可以根据另一根在区间 m,n ,从而可以求出参数的值。
如方程mx 2 m 2 x 2 0、 2 2 2在区间1,3上有一根,因为f 10,所以mx m 2 x 2 x 1 mx 2,另一根为 ,由13m m2得 m 2即为所求;3 2方程有且只有一根,且这个根在区间m, n ,即 0,此时由 0可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给疋的区间, 如右不在,舍去相应的参数。
如方程x 4mx 2m 6 0有且 一根在区间 3,0 ,求m 的取值围。
分析:①由f 3gf 0 0 即 14m 15 m3 0得出 3 15 m;②由0即 16m 2 4 2m146 0得出m 31 或 m —,2 当m1时,根x23,0 ,即m31满足题意;当m 时,根x 323,0,故 m-不满足题意; 2综上分析,得出3 m至或14m1根的分布练习题例1、已知二次方程 2m 1 x 2 2mx m 1 0有一正根和一负根,数 m 的取值围。
1解:由 2m 1 gf 0 0即 2m 1 m 1 0,从而得m 1即为所求的围。
二次方程根的分布口诀

二次方程根的分布口诀二次方程根的分布口诀,那可是数学学习中的一把“利器”!咱们先来说说啥是二次方程。
就比如说$ax^2 + bx + c = 0$($a ≠ 0$)这样的式子就是二次方程。
那根的分布是啥呢?简单说,就是研究这个方程的根在某个区间内的情况。
这根的分布口诀啊,就像是一个神秘的魔法咒语,掌握了它,解决问题就能事半功倍。
比如说“左负右正中间零,左正右负两边零”,这口诀听起来是不是有点像绕口令?别着急,咱们慢慢解释。
“左负右正中间零”意思是,如果二次函数的图像与$x$轴的交点在左边是负数,右边是正数,那么对称轴就在中间,也就是对称轴对应的$x$值是零。
“左正右负两边零”呢,就是反过来,如果左边是正数,右边是负数,那根就在对称轴的两边,也就是对称轴对应的$x$值是零。
我记得有一次给学生讲这个知识点,有个小家伙一脸懵地看着我,嘴里嘟囔着:“老师,这也太难懂啦!”我就耐心地给他举了个例子。
假设咱们有个二次方程$x^2 - 3x + 2 = 0$,咱们先把它变成二次函数$y = x^2 - 3x + 2$,然后画出它的图像。
这图像就像一个弯弯的彩虹,对称轴是$x = \frac{3}{2}$。
当$x = 1$和$x = 2$的时候,函数值为零,这两个点就是方程的根。
这时候你看,左边的根$1$是负数,右边的根$2$是正数,这不就符合“左负右正中间零”嘛!还有啊,像“大于取两边,小于取中间”这个口诀也很有用。
比如说方程$(x - 1)(x - 2) > 0$,要找它的解集,就是$x < 1$或者$x > 2$,这就是“大于取两边”。
要是方程$(x - 1)(x - 2) < 0$,解集就是$1 <x < 2$,这就是“小于取中间”。
学习这根的分布口诀,可不能死记硬背,得结合实际例子多练习。
有一回,我布置了一道关于二次方程根的分布的作业题。
有个学生做得一塌糊涂,我把他叫到办公室,一点点给他分析。
二次函数根的分布

二次函数根的分布二次函数是二次多项式的函数,其一般形式为y=ax^2+bx+c(其中a≠0)。
首先,我们需要了解二次函数的图像特点。
对于二次函数y=ax^2+bx+c,a决定了二次函数的开口方向和开口大小,a>0时开口向上,a<0时开口向下;b决定了二次函数的对称轴位置,对称轴的方程为x=-b/2a;c决定了二次函数与y轴的交点。
其次,我们来探讨二次函数的根的分布。
二次函数的根即方程的解,即使二次方程的解的个数以及位置。
对于一元二次方程ax^2+bx+c=0,我们可以利用判别式来判断解的情况:判别式Δ=b^2-4ac。
1.当Δ>0时,方程有两个不相等的实根。
实根的个数与开口方向无关,只与判别式Δ有关。
-当Δ>0时,方程有两个不相等的实根。
-当Δ=0时,方程有一个实根,这个实根称为方程的重根。
-当Δ<0时,方程无实根,但可以有两个共轭虚根。
值得注意的是,只有在a≠0时,方程为一元二次方程,才能求解二次函数的根。
接下来,我们来分析二次函数根的分布。
1.当Δ>0时,方程有两个不相等的实根。
此时,二次函数与x轴交于两个不同的点,也就是有两个实根。
这两个实根的位置由二次函数的对称轴决定,对称轴的方程为x=-b/2a。
假设根的位置为x1和x2,那么有以下三种情况:-当x1和x2均小于对称轴的x坐标时,二次函数开口向上,根的位置为x1>x2-当x1和x2均大于对称轴的x坐标时,二次函数开口向下,根的位置为x1<x2-当x1小于对称轴的x坐标,x2大于对称轴的x坐标时,一个根位于对称轴的左侧,一个根位于对称轴的右侧。
2.当Δ=0时,方程有一个实根,这个实根称为方程的重根。
此时,二次函数与x轴有且仅有一个交点,也就是有一个实根。
这个实根的位置正好位于二次函数的对称轴上,对称轴的方程为x=-b/2a。
3. 当Δ<0时,方程无实根,但可以有两个共轭虚根。
此时,二次函数与x轴没有交点,也就是无实根。
二次函数根的分布

二次函数根的分布二次函数根的分布是二次函数中的重要内容。
这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用。
下面我们将主要结合二次函数图象的性质,分两种情况系统地介绍二次函数根的分布的充要条件及其运用。
一.一元二次方程根的基本分布——零分布所谓一元二次方程根的零分布,指的是方程的根相对于零的关系。
比如二次方程有一正根,有一负根,其实就是指这个二次方程一个根比零大,一个根比零小,或者说,这两个根分布在零的两侧。
设一元二次方程02=++c bx ax (0≠a )的两个实根为1x ,2x ,且21x x ≤。
【定理1】⎪⎪⎪⎩⎪⎪⎪⎨⎧>=>-=+≥-=∆>>00040,02121221a c x x a bx x ac b x x ,则例1若一元二次方程0)1(2)1(2=-++-m x m x m 有两个正根,求m 的取值范围。
【定理2】⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<-=+≥-=∆<<00040,02121221a c x x a bx x ac b x x ,则【定理3】0021<<<ac x x ,则例3 k 在何范围内取值,一元二次方程0332=-++k kx kx 有一个正根和一个负根?【定理4】 1)01=x ,02>x ⇔0=c 且0<a b;2)01<x ,02=x ⇔0=c 且0>ab。
例4若一元二次方程03)12(2=-+-+k x k kx 有一根为零,则另一根是正根还是负根?二.一元二次方程的非零分布——k 分布设一元二次方程02=++c bx ax (0≠a )的两实根为1x ,2x ,且21x x ≤。
k 为常数。
则一元二次方程根的k 分布(即1x ,2x 相对于k 的位置)有以下若干定理。
【定理1】⎪⎪⎪⎪⎨⎧>->≥-=∆≤<k ab k af ac b x x k 20)(04221,则【定理2】⎪⎪⎪⎪⎨⎧<->≥-=∆<≤k ab k af ac b k x x 20)(04221,则【定理3】21x k x <<⇔0)(<k af【定理4】有且仅有11x k <(或2x )2k <⇔0)()(21<k f k f【定理5】221211p x p k x k <<≤<<⇔⎪⎪⎪⎩⎪⎪⎪⎨⎧><<>>0)(0)(0)(0)(02121p f p f k f k f a 或⎪⎪⎪⎩⎪⎪⎪⎨⎧<>><<0)(0)(0)(0)(02121p f p f k f k f a 此定理可直接由定理4推出,请自证。
二次方程根的分布情况归纳(完整版)
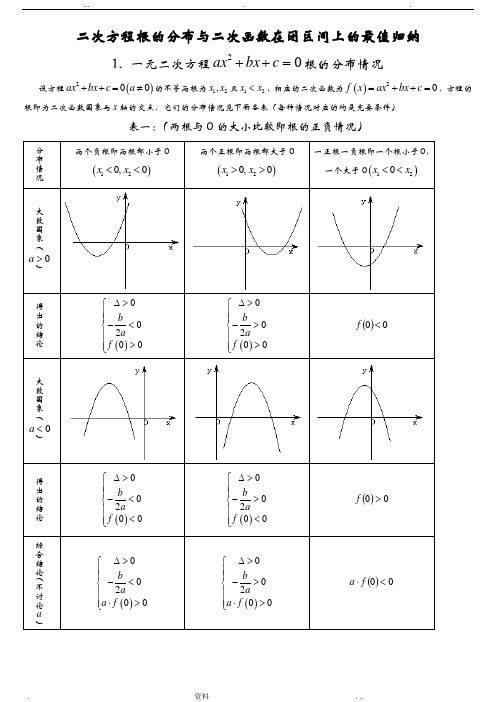
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0,一个大于0()120x x <<大致图象(>a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象(<a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论(不讨论a)()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ,一个大于k 即21x k x <<大致图象(>a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象(<a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论(不讨论a )()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()n m ,两根有且仅有一根在()n m ,(图象有两种情况,只画了一种) 一根在()n m ,,另一根在()q p ,,q p n m <<<大致图象(>a )得出的结论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 大致图象(<a )得出的结论()()0002f m f n b m na ∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000fm f n f p f q ⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩综合结论(不讨论a)——————()()0<⋅n f m f()()()()⎪⎩⎪⎨⎧<<00q f p f n f m f 根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,,从而可以求出参数的值。
二次函数根的分布和最值
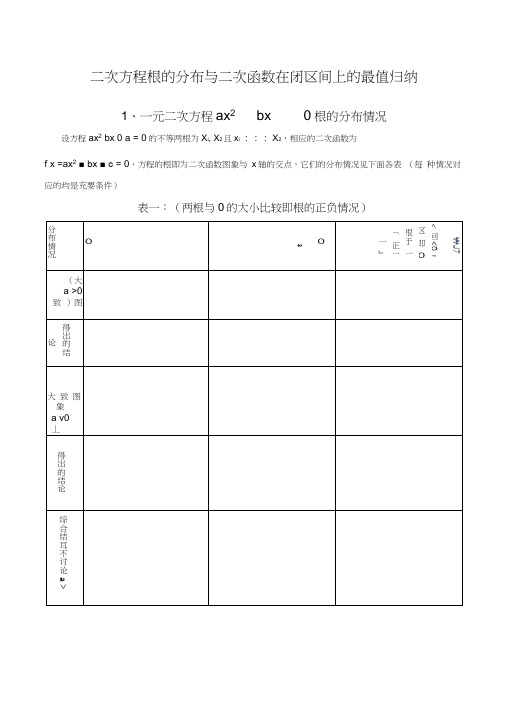
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程ax2bx 0根的分布情况设方程ax2 bx 0 a = 0的不等两根为X i, X2且x i :::X2,相应的二次函数为f x =ax2■ bx ■ c = 0,方程的根即为二次函数图象与x轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)根在区间上的分布还有一种情况:两根分别在区间m,n夕卜,即在区间两侧为:::m,x2• n ,(图形分别如下)需满足的条件是对以上的根的分布表中一些特殊情况作说明: (1) 两根有且仅有一根在 m,n 内有以下特殊情况:1 若f m =0或f n =0,贝眦时f m|_f n :: 0不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间 m,n 内,从而可以求出参数的值。
如方 程 mx 2-m ・2x ・2=0在区间 1 , 3E 有一根,因为 f1=0 , 所以222mx 2 - m2x ^ x-1 mx-2,另一根为一,由13得 m ::: 2即为所求; mm 32 方程有且只有一根, 且这个根在区间 m,n 内,即丄=0,此时由厶=0可以求出参数的值, 然后 再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程x 2 -4 m x 2 m 6 = 0有且一根在区间-3,0内,求m 的取值范围。
分析:①由15f -3Lf 0 :: (即卩 14m 15 m 3 :: 0得出 -3 :: m ;②由• ; -0即 16m 2-4 2m 6;=0得 143 3出m~-1或m ,当m = -1时,根x=-2三i 3。
,即m=-1满足题意;当m 时,根2 23 15-3, 0,故m 不满足题意;综上分析,得出 -3:::m 或m=-1』 2 14根的分布练习题例1、已知二次方程 2m 1 x 2 -2mx ■ m -1 =0有一正根和一负根,求实数 m 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0,一个大于0()120x x <<大致图象(>a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象(<a )得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论(不讨论a)()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即 k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ,一个大于k 即21x k x <<大致图象(>a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象(<a )得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论(不讨论a)()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()nm,内两根有且仅有一根在()nm,内(图象有两种情况,只画了一种)一根在()nm,内,另一根在()qp,内,qpnm<<<大致图象(0 > a)得出的结论()()2f mf nbm na∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅nfmf()()()()f mf nf pf q⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()f m f nf p f q<⎧⎪⎨<⎪⎩大致图象(0 < a)得出的结论()()2f mf nbm na∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅nfmf()()()()f mf nf pf q⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()f m f nf p f q<⎧⎪⎨<⎪⎩综合结论(不讨论a )——————()()0<⋅nfmf()()()()⎪⎩⎪⎨⎧<<qfpfnfmf根在区间上的分布还有一种情况:两根分别在区间()外,即在区间两侧12,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明:(1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求;2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
解:由 ()()2100m f +< 即 ()()2110m m +-<,从而得112m -<<即为所求的范围。
例2、已知方程()2210x m x m -++=有两个不等正实根,求实数m 的取值范围。
解:由()()0102200m f ∆>⎧⎪-+⎪->⎨⎪>⎪⎩⇒ ()218010m m m m ⎧+->⎪>-⎨⎪>⎩ ⇒ 3223220m m m ⎧<->+⎪⎨>⎪⎩或⇒ 0322m <<-322m >+即为所求的范围。
例3、已知二次函数()()()222433y m x m x m =+-+++与x 轴有两个交点,一个大于1,一个小于1,求实数m 的取值范围。
解:由 ()()210m f +< 即 ()()2210m m ++< ⇒ 122m -<<即为所求的范围。
例4、已知二次方程()22340mx m x +-+=只有一个正根且这个根小于1,求实数m 的取值范围。
解:由题意有方程在区间()0,1上只有一个正根,则()()010f f < ⇒ ()4310m +< ⇒ 13m <-即为所求范围。
(注:对于可能出现的特殊情况方程有且只有一根且这个根在()0,1内,由0∆=计算检验,均不复合题意,计算量稍大)1.二次函数及图象设有一元二次函数y=ax2+bx+c(a≠0),判别式Δ=b2-4ac,当Δ>0时y=f(x)与x轴有二交点;当Δ=0时,y=f(x)与x轴仅有一交点;当Δ<0时,y=f(x)与x轴无交点.当Δ>0时,设y=f(x)图象与x轴两交点为x1<x2.一元二次函数y=f(x)与x轴交点x1,x2就是相应一元二次方程f(x)=0的两根.观察图象不难知道.图像为观察图象不难知道△=0,a>0 , △=0,a<0当△<0时,y=f(x)图象与x轴无公共点,其图象为观察图象不难知道.a>0时,绝对不等式f(x)>0解为x∈R.a<0时,绝对不等式f(x)<0解为x∈R.2.讨论一元二次方程的根的分布情况时,往往归结为不等式(组)的求解问题,其方法有3种:(1)应用求根公式;(2)应用根与系数关系;(3)应用二次函数图象.在进行转化时,应保证这种转化的等价性.就这三种方法而言,应用二次函数图象和性质应是比较简捷的一种方法.设f(x)=ax2+bx+c(a>0),方程ax2+bx+x=0的个根为α,β(α≤β),m,n为常数,且n<m,方程根的分布无外乎两种情况:②α,β同居一区间时,不但要考虑端点函数值的符号,还要考虑三、好题解给你 (1)预习题 1. 设有一元二次函数y=2x2-8x+1.试问,当x∈[3,4]时,随x变大,y的值变大还是变小?由此y=f(x)在[3,4]上的最大值与最小值分别是什么?解:经配方有y=2(x-2)2-7 ∵对称轴x=2,区间[3,4]在对称轴右边,∴y=f(x)在[3,4]上随x变大,y的值也变大,因此y max=f(4)=1. y min=f(3)=-5.2.设有一元二次函数y=2x2-4ax+2a2+3.试问,此函数对称轴是什么?当x∈[3,4]时,随x变大,y的值是变大还是变小?与a取值有何关系?由此,求y=f(x)在[3,4]上的最大值与最小值.解:经配方有y=2(x-a)2+3.对称轴为x=a.当a≤3时,因为区间[3,4]在对称轴的右边,因此,当x∈[3,4]时,随x变大,y的值也变大.当3<a<4时,对称轴x=a在区间[3,4]内,此时,若3≤x≤a,随x变大,y的值变小,但若a≤x≤4,随x变大,y的值变大.当4≤a时,因为区间[3,4]在对称轴的左边,因此,当x∈[3,4]时,随x变大,y的值反而变小.根据上述分析,可知.当a≤3时,y max=f(4)=2a2-16a+35.y min=f(3)=2a2-12a+21.当3<a<4时,y min=f(a)=3.其中,a≤3.5时,y max=f(4)=2a2-16a+35.a≥3.5时,y max=f(3)=2a2-12a+21.当a≥4时,y max=f(3)=2a2-12a+21.y min=f(4)=2a2-16a+35.(1)(2)基础题例1.设有一元二次方程x2+2(m-1)x+(m+2)=0.试问:(1)m为何值时,有一正根、一负根.(2)m为何值时,有一根大于1、另一根小于1.(3)m为何值时,有两正根.(4)m为何值时,有两负根.(5)m为何值时,仅有一根在[1,4]内?解:(1)设方程一正根x2,一负根x1,显然x1、x2<0,依违达定理有m+2<0.∴ m<-2.反思回顾:x1、x2<0条件下,ac<0,因此能保证△>0.(2)设x1<1,x2>1,则x1-1<0,x2-1>0只要求(x1-1)(x2-1)<0,即x1x2-(x1+x2)+1<0.依韦达定理有 (m+2)+2(m-1)+1<0.(3)若x1>0,x2>0,则x1+x2>0且x1,x2>0,故应满足条件依韦达定理有(5)由图象不难知道,方程f(x)=0在[3,4]内仅有一实根条件为f(3)·f(4)<0,即[9+6(m-1)+(m+2)]·[16+8(m-1)+(m+2)]<0.∴(7m+1)(9m+10)<0.例2. 当m为何值时,方程有两个负数根?解:负数根首先是实数根,∴,由根与系数关系:要使方程两实数根为负数,必须且只需两根之和为负,两根之积为正.由以上分析,有即∴当时,原方程有两个负数根.(3)应用题例1. m取何实数值时,关于x的方程x2+(m-2)x+5-m=0的两个实根都大于2?解:设f(x)=x2+(m-2)x+5-m,如图原方程两个实根都大于2所以当-5<m≤-4时,方程的两个实根大于2.例2.已知关于x方程:x2-2ax+a=0有两个实根α,β,且满足0<α<1,β>2,求实根a的取值范围.解:设f(x)=x2-2ax+a,则方程f(x)=0的两个根α,β就是抛物线y=f(x)与x轴的两个交点的横坐标,如图0<α<1,β>2的条件是:<1,β>2.例3.m为何实数时,关于x的方程x2+(m-2)x+5-m=0的一个实根大于2,另一个实根小于2.解:设f(x)=x2+(m-2)x+5-m,如图,原方程一个实根大于2,另一个实根小于2的充要条件是f(2)<0,即4+2(m-2)+5-m<0.解得m<-5.所以当m<-5时,方程的一个实根大于2,另一个实根小于2.(2)(4)提高题例1.已知函数的图象都在x轴上方,求实数k的取值范围.解:(1)当,则所给函数为二次函数,图象满足:,即解得:(2)当时,若,则的图象不可能都在x轴上方,∴若,则y=3的图象都在x轴上方由(1)(2)得:反思回顾:此题没有说明所给函数是二次函数,所以要分情况讨论.例2.已知关于x的方程(m-1)x2-2mx+m2+m-6=0有两个实根α,β,且满足0<α<1<β,求实数m的取值范围.解:设f(x)=x2-2mx+m2+m-6,则方程f(x)=0的两个根α,β,就是抛物线y=f(x)与x轴的两个交点的横坐标.如图,0<α<1<β的条件是解得例3.已知关于x的方程3x2-5x+a=0的有两个实根α,β,满足条件α∈(-2,0),β∈(1,3),求实数a的取值范围.解:设f(x)=3x2-5x+a,由图象特征可知方程f(x)=0的两根α,β,并且α∈(-2,0),β∈(1,3)的解得-12<a<0.四、课后演武场 1.已知方程(m-1)x2+3x-1=0的两根都是正数,则m的取值范围是( B )A.B.C.D.2.方程 x 2+(m 2-1)x +(m -2)=0的一个根比1大,另一个根比-1小,则m 的取值范围是( C ) A .0<m <2 B .-3<m <1 C .-2<m <0 D .-1<m <1 3.已知方程 有两个不相等的实数根,则k 的取值范围是( C )A .B .C .D .4.已知关于x 的方程3x 2+(m-5)x +7=0的一个根大于4,而另一个根小于4,求实数m 的取值范围.可知方程f (x )=0的一根大于4,另一根小于4的充要条件是:f (4)<0)5.已知关于x 的方程x 2+2mx +2m +3=0的两个不等实根都在区间(0,2)内,求实数m 的取值范围.征可知方程f (x )=0的两根都在(0,2)内的充要条件是2、二次函数在闭区间[]n m ,上的最大、最小值问题探讨设()()002>=++=a c bx ax x f 则二次函数在闭区间上的最大、最小值有如下的分布情况:ab n m 2-<< n a b m <-<2即[]n m ab ,2∈- n m ab<<-2 图象最大、最小值()()()()n f x f m f x f ==min max()()(){}()⎪⎭⎫ ⎝⎛-==a b f x f m f n f x f 2,max minmax()()()()m f x f n f x f ==min max(1)若[]n m a b ,2∈-,则()()()⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛-=n f a b f m f x f ,2,max max ,()()()⎭⎬⎫⎩⎨⎧⎪⎭⎫⎝⎛-=n f a b f m f x f ,2,min min ; (2)若[]n m ab,2∉-,则()()(){}n f m f x f ,m ax max =,()()(){}n f m f x f ,m in min = 另外,当二次函数开口向上时,自变量的取值离开对称轴越远,则对应的函数值越大;反过来,当二次函数开口向下时,自变量的取值离开对称轴轴越远,则对应的函数值越小。
