罐区盘点必备的卧式容器液位体积计算器
卧式油罐液位体积的计算

卧式油罐液位体积的计算
设卧式油罐截面半径为R,液面高度为h,油罐长为L.则液位为h时所盛液体的体积
V=[R²arccos(1-h/R)-(R-h)√()]L
求法:
作出卧式油罐的一个截面圆O,作出液面AB(假设AB低于圆心O),过O作AB的垂线交AB于D,交圆周于C.DC=h
则由弦AB和弧ACB围成的面积为
S=S扇形OACB-S三角形OAB
=R²arccos(1-h/R)-(R-h)√(2Rh-h²)
液体的体积V=液体的底面积S*液体的长度L
得V=[R²arccos(1-h/R)-(R-h)√(2Rh-h²)]L
注:上式虽然是在液面低于圆心的情况下推导出的,但也适用于液面于圆心相平以及液面高于圆心的情况
卧式储罐不同液位下的容积(质量)计算

卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h:对应h高度卧罐内储液体积(m3);m h:对应h高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为V1=h yi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式椭圆封头容器不同液位的体积计算

符号
L(m)R t(m)h(m)hi(m)(E3-D3)/D3Vt(m3)Vf(m3)V(m 3)数值2100.0001000.0001000.000500.0000.0003298672230.000523598766.6673822270996.667卧式椭圆形封头容器不同液位的体积计算
Dt ——筒体内径,m Rt——筒体或球形封头内半径,m h ——液面高度,m V——卧式容器体积,m3hi ——封头曲面深度,m (标准型:hi=1/2Rt ) Vt——筒体部分体积,m3
L ——筒体长度(含封头直边高度),m Vf——封头部分体积,m3
1、 筒体内液体体积计算(如上图):
筒体的截面积方程:X 2+Y 2=Rt 2 故:X=(Rt 2-Y 2)1/2
因此:液面高度为h 时筒体内液体的体积:
2、椭圆封头内液体体积计算(如上图):
椭圆封头的椭球面方程:
]2
arcsin 2)^(1[2^2^2^2π+-+--∙-∙=-=⎰--Rt Rt h Rt Rt h Rt Rt h Rt L dy
y Rt L Vt Rt
h Rt 2^2^2^)/(12
^2^2^2^2^y x Rt Rt hi z hi z Rt y x --=∴=++
因此:当容器内的液面高度为h 时,封头内液体的体积:
]33^233)^()(2^[22^2^2^22^2^0Rt Rt h Rt h Rt Rt hi dx y x Rt dy Rt hi zdxdy
Vf y Rt Rt h Rt
f ----=--==⎰⎰⎰⎰---π。
最新卧式储罐不同液位下的容积计算(精品收藏)
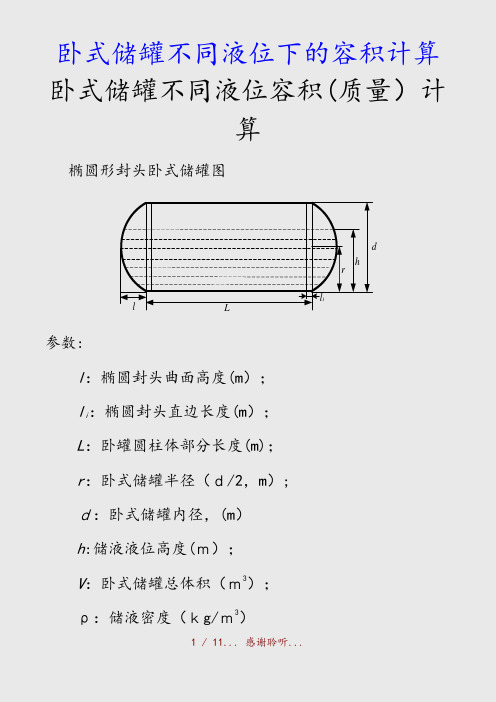
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图h drl Ll i参数:l:椭圆封头曲面高度(m);l i:椭圆封头直边长度(m);L:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V h :对应h 高度卧罐内储液体积(m 3); m h:对应h 高度卧罐内储液重量(kg);椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体.简化模型图如下.ohr以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)ρr L h V h m h液体密度储罐半径圆柱体部分长度储液液位高度储液体积 储液重(kg/m 3)ﻫ(m) (m )(m )(m 3)量 (kg )备注:该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
ohrh 尺以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c ++=垂直于y轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=h yi aS dy-⎰22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为222yj S a y dy=-则筒体部分容积为:2hyj a V S -=⎰222haL a y dy -=-⎰22222(arcsin )2h h La a h a a π=+-+(arcsin)22h a ππ-≤≤(3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++22222(arcsin )2h h La a h a a π+-+此公式中液位高度h是以储罐内径中心为原点,其中a=b=r化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h 实例:某热电厂液氨罐尺寸为:储罐体积50m3,直段筒体长度L 1=8480m m,封头直段长度L 2=40mm (圆柱体部分长度为(L 1+L 2/2)=8580mm),筒体半径R=a =b =1300mm,封头高度c=650m m ρV r l L h h尺 Vh m h误差液体密度(kg/m3)储罐总体积ﻫ(m3)储罐半径ﻫ(m)封头高度ﻫ(m)圆柱体部分长度(m)储液液位高度(中点为坐标原点)(m)实际标尺刻度储液体积(m3)储液重量(kg)不同液高下计算得到的体积与实际储液体积间误差1501.30.658。
卧式椭圆封头储罐液位体积对照表

生产中经常会遇到贮槽内液体体积的计算问题,立式容器都比较好计算,而卧式椭圆形封头贮槽内液体体积的计算,尤其是任意高度时液体体积的计算非常因难。
为了能够及时迅速的计算出实
际液体体积,本人用EXCEL 制作了一个200个分度的《卧式椭圆封头储罐液位体积对照表》,不敢
吃独食,拿出来献丑,广告说了:“大家好才是真的好!”
说明:1、计算公式采用的是积分运算,精度极高。
2、只需输入直筒长度(含封头直筒部分)和罐内径两个数据,表中所有数据都自动生成。
3、标题可随意编辑,可以写上您需要的内容,打印出来备查。
4、无计量单位,如果计算超大或超小的容器,只需按公里或毫米输入数据即可,计算结果就是立方公里或立方毫米。
5、可复制到其他工作表中粘贴,重新编辑格式。
6、如果觉得好,就在使用的时候大喊三声:“真是好人呐!”我就知足了。
各类储罐不同液位的体积计算

各类储罐不同液位的体积计算储罐是用来存储各种液体物质的设备,常见的储罐有圆柱形储罐、球形储罐、锥形储罐等。
不同液位下的体积计算对于工业生产和储罐设计具有重要意义。
下面将分别介绍不同液位下的储罐体积计算方法。
1.圆柱形储罐圆柱形储罐是最常见的一种储罐类型,其体积计算相对简单。
如果液位高度小于罐的半径,体积计算公式为:V=hπr²其中V为液体体积,h为液位高度,r为罐的半径。
当液位高度超过罐的半径时,体积计算公式为:V=(πr²L)+(πr²/2)(h-L)其中L为圆柱形储罐底部与液体接触的长度。
2.球形储罐球形储罐是体积计算相对复杂的一种储罐类型。
当液位高度小于罐的球冠高度时,体积计算公式为:V=(2/3)πr³-h(π/3)(3r²-h²)^(1/2)当液位高度超过罐的球冠高度时,体积计算公式为:V=(2/3)πr³+(π/6)(3r²h-h³)3.锥形储罐锥形储罐是一种底面为圆锥形的储罐,体积计算相对复杂。
体积计算公式为:V=(π/3)(R²+Rr+r²)H其中V为液体体积,R为锥形储罐顶面的半径,r为锥形储罐底面的半径,H为液位高度。
需要注意的是,上述三种储罐类型的体积计算公式均为理想情况下的计算值,不考虑储罐内部构造、口径、接口等因素。
实际情况下,储罐的形状和内部结构会对液位与体积之间的关系造成一定影响,因此在实际应用中还需要进行修正和校正。
此外,还有其他一些特殊形状的储罐,如椭球形储罐、水平圆筒体形储罐等,其体积计算公式较为复杂,需要根据具体情况进行推导和计算。
总之,储罐液位与体积之间的关系是储罐设计和储存液体物质的重要参数之一,不同类型储罐的体积计算方法也有所差异。
在实际应用中,需要根据具体储罐的形状和内部结构,选择合适的体积计算方法,并进行相应的修正和校正。
卧式储罐不同液位下的容积计算

椭圆形封头卧式储罐图参数:l:椭圆封头曲面高度(m);l:椭圆封头直边长度(m);iL:卧罐圆柱体部分长度(m);r:卧式储罐半径(d/2,m);d:卧式储罐内径,(m)h:储液液位高度(m);V:卧式储罐总体积(m3);ρ:储液密度(kg/m3)V:对应h高度卧罐内储液体积(m3);hm:对应h高度卧罐内储液重量(kg);h椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=表1 卧式储罐不同液位下容积(重量)该计算公式推导过程如下卧式储罐不同液位下的容积简化计算公椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高(1)椭圆球体部分该椭圆球体符合椭圆球体公式:2222221x y z a b c ++= 其中a=b=r ,则有222221x y z a c++= 垂直于y 轴分成无限小微元,任一微元面积为:22()yi cS a y aπ=-当液面高度为h 时,椭圆球体内液氨容积为 V1=hyi a S dy -⎰ 22()haca y dy aπ-=-⎰3322()33ch a a h a π=-+ (2)直段筒体部分:筒体的纵断面方程为222x y a +=任一微元的面积为yj S = 则筒体部分容积为:2hyj a V S -=⎰ha L -=⎰2(arcsin )2h La a π=+(arcsin)22h a ππ-≤≤ (3)卧式储罐储液总体积总容积为V=V1+V2,V=23242()33ch a a h a π-++2(arcsin )2h La a π+ 此公式中液位高度h 是以储罐内径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212222πh r r h r h Lr L r V h若液位高度h 以卧罐底部为起点,如下图则卧式储罐内储液总体积计算公式:()()()⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212222πr h r r r h r r h Lr L r V h若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=其它方法如下:第一种方法卧式储罐不同液位下的容积简化计算公卧式储罐内储液总体积计算公式:)]arcsin(2)[(]3)(1)[(222232rr h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐内储液总重量为:hh V m ρ=此方式用到参数较多ρ、V 、r 、l 、L 、h 。
卧式储罐不同液位下的容积计算

卧式储罐不同液位下的容积计算卧式储罐是一种常见的用于储存液体的设备,其容积计算是用户在使用储罐过程中需要了解的重要参数之一、液位与容积之间存在着一定的关系,可以通过液位的变化来计算储罐在不同液位下的容积。
下面我将详细介绍卧式储罐不同液位下容积计算的方法。
卧式储罐通常由圆筒和两个半球形的端部组成,液位的高低会直接影响到储罐内液体的容积。
根据液位位置的不同,可以将储罐分为以下三种情况进行计算:液位位于下半球内、液位位于上半球内、液位位于圆筒部分内。
第一种情况:液位位于下半球内。
在这种情况下,液位与半球的接触面形成的是一个锥形体。
首先需要计算出液体在锥形体中的体积,然后再加上液体在半球形部分的体积。
液体在锥形体中的体积可以通过以下公式计算:V=πh^2(3R-h)/3其中,V为液体在锥形体中的体积,h为液位高度,R为半球的半径。
第二种情况:液位位于上半球内。
在这种情况下,液位位于圆筒和半球的交界处。
容积的计算可以分为两部分进行:液体在半球形部分的容积和液体在圆筒部分的容积。
首先计算液体在半球形部分的容积,可以使用以下公式:V1=(2/3)πh^2(3R-h)其中,V1为液体在上半球内的容积,h为液位高度,R为半球的半径。
然后计算液体在圆筒部分的容积,可以使用以下公式:V2=πR^2h其中,V2为液体在圆筒内的容积,h为液位高度,R为半球的半径。
最后将液体在半球形部分和圆筒部分的容积相加,即可得到液位位于上半球内时的总容积。
第三种情况:液位位于圆筒部分内。
在这种情况下,液体仅填充了圆筒的部分。
容积的计算可以直接使用以下公式:V=πR^2h其中,V为液体在圆筒内的容积,h为液位高度,R为半球的半径。
通过以上三种情况的容积计算方法,可以得出卧式储罐在不同液位下的容积。
用户可以根据储罐的实际情况和液位高度来进行相应的计算,从而获取准确的容积数值。
这些容积数值对于储罐的管理和使用都具有重要的参考价值,可以帮助用户更好地进行液体的储存和运输计划。
