频谱分析(完整版)
第3章-频谱分析

周期信号分解为一系列虚指数函数的离散和或连续和。 利用
信号的正弦分解思想, 系统的响应则可表示为不同频率正弦分 量产生响应的叠加。
第3章 连续时间系统的频域分析
3.1.2 傅立叶级数 1. 周期信号的三角级数表示 在电子技术、 通信工程、 自动控制等领域, 除了正弦
信号外, 非正弦周期信号也经常遇到。 把非正弦周期信号分 解为傅立叶级数是法国科学家傅立叶所做出的巨大贡献。 1807年, 傅立叶以他惊人的洞察力大胆断言: 任何周期函数都 可以用收敛的正弦级数表示。 他的关于把信号分解为正弦分 量的思想对后来的自然科学等领域产生了巨大的影响。
【例 3-4】 画出图3-4所示矩形周期信号f(t)的双边频谱图
形。
第3章 连续时间系统的频域分析
解 由
Fn
1 T
T /2 f t ejn1t dt 1 2sinn π/ 4
T / 2
4 n π/ 4
得:
F0=0.25 F±1=0.225 F±2=0.159 F±3=0.075 F±4=0 F±5=-0.045 F±6=0.053 F±7=-…
12 e jn1t dt
0
2
j4n1
e
jn 2
1
1
jn
jn
e4
e
j
n 4
jn
e 4
2
jn
e4
sin
n
n
4
故f(t)展开为指数形式的傅立叶级数为
f
t
(
2
jn
e4
sቤተ መጻሕፍቲ ባይዱn
n
) e jn1t
n
4
第3章 连续时间系统的频域分析
3.2 周期信号的频谱及特点
频谱分析(完整版)

Matlab 信号处理工具箱 帮助文档 谱估计专题翻译:无名网友 & Lyra频谱分析Spectral estimation (谱估计)的目标是基于一个有限的数据集合描述一个信号的功率(在频率上的)分布。
功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信号的检测。
从数学上看,一个平稳随机过程n x 的power spectrum (功率谱)和correlation sequence (相关序列)通过discrete-time Fourier transform (离散时间傅立叶变换)构成联系。
从normalized frequency (归一化角频率)角度看,有下式()()j mxx xxm S R m eωω∞-=-∞=∑注:()()2xx S X ωω=,其中()/2/2lim N j n n N N X x e ωω=-=∑πωπ-<≤。
其matlab 近似为X=fft(x,N)/sqrt(N),在下文中()L X f 就是指matlab fft 函数的计算结果了使用关系2/s f f ωπ=可以写成物理频率f 的函数,其中s f 是采样频率()()2/sjfm f xx xxm S f R m eπ∞-=-∞=∑相关序列可以从功率谱用IDFT 变换求得:()()()/22//22sss f jfm f j m xx xx xx sf S e S f e R m d df f πωππωωπ--==⎰⎰序列n x 在整个Nyquist 间隔上的平均功率可以表示为()()()/2/202ss f xx xx xx sf S S f R d df f ππωωπ--==⎰⎰ 上式中的()()2xx xx S P ωωπ=以及()()xx xx sS f P f f =被定义为平稳随机信号n x 的power spectral density (PSD)(功率谱密度) 一个信号在频带[]1212,,0ωωωωπ≤<≤上的平均功率可以通过对PSD 在频带上积分求出从上式中可以看出()xx P ω是一个信号在一个无穷小频带上的功率浓度,这也是为什么它叫做功率谱密度。
频谱分析

一个信号的频谱告诉我们这个信号包含哪些正弦函数。
比如,信号X(t)=2sin(3t).它的频谱只有一个点:(3,2).也就是说,这个信号它只包含了一个正弦函数,角频率为3,幅值为2。
傅立叶定理指出:任何一个周期函数都可以分解为很多正弦函数的和。
进而我们可以把一个非周期函数看作是一个周期为无限大的周期函数。
傅立叶定理有着非常广泛的应用。
加窗在进行离散傅立叶dft变换时,为了减小频谱泄漏现象要进行加窗处理比如使用海宁窗等,实际上是对序列的边界点进行了平滑处理以使得以此序列进行周期拓展时边界点是连续的.对于一已知序列在时域不加窗(或加矩形窗)和加海宁窗再进行dft,所得结果肯定不一致.在实际工程应用领域,例如电气工程中的谐波分析等不加窗后进行dft所得结果的物理意义是显而易见的.但加了窗后反而使结果没什么意义了. 从另外一种角度出发,假设序列是同步采样得到的结果,也就是边界点上没有出现跳变,自然也无需再加窗平滑处理,那此时再进行加窗处理相当于改变了输入序列的值,变换结果与原先不同也是自然的了. 是不是加窗变换后还要进行一些处理才能得到与实际意义(比如物理意义)相符的结果?通常做的ft应该都是加窗处理了的,只不过采用了一个矩形窗而你没有注意到而已。
加窗就是信号乘以窗函数,相应于频域就是离散信号的频谱与窗函数频谱的卷积。
离散的数字信号频谱是以采样率为周期的从负无穷到正无穷的周期性谱,而有限长度的时间窗对应于无限长度的频率响应,因此它与信号频谱的卷积自然也是无限长度的,也就是产生了频谱的混迭,信号带宽越宽混迭的影响就更大。
自然dtf采样到的-pi到+pi的频谱也存在了混迭,除了一些解析解信号的频谱有可能由这些频谱中推算出原始1)信号加窗与分帧是两个不同的概念.2)一首歌首先要经过分帧,下一步才是加窗.3)音频信号属于"短时平稳过程" 每一帧信号视为平稳过程,即统计特性平稳.4)因为傅立叶变换对应的是无限信号,信号经过分帧后变成有限信号,分帧的信号再进行傅立叶变换后,高频部分将有"泄露",所以要加窗.5)窗函数的拼谱都是在某高频部分截止,所以每帧信号加窗后的傅立叶变化,频谱基本"泄露"6)详细内容请参考<信号与系统>卷积中文名称:卷积英文名称:convolution定义:数学中关于两个函数的一种无穷积分运算。
频谱分析(完整版)

翻译:无名网友 & Lyra
频谱分析
Spectral estimation(谱估计)的目标是基于一个有限的数据集合描述一个信号的功 率(在频率上的)分布。功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信 号的检测。 从数学上看,一个平稳随机过程 xn 的 power spectrum(功率谱)和 correlation sequence(相关序列)通过 discrete-time Fourier transform(离散时间傅立叶变换) 构成联系。从 normalized frequency(归一化角频率)角度看,有下式
ˆ f P xx k
其中
X L fk fs L
2
, fk
kf s , k 0,1, , N 1 N
L 1
X L f k xL n e 2 jkn / N
n 0
选择 N 是大于 L 的下一个 2 的幂次是明智的, 要计算 X L f k 我们直接对 xL n 补零到 长度为 N。假如 L>N,在计算 X L f k 前,我们必须绕回 xL n 模 N。 作为一个例子,考虑下面 1001 元素信号 xn ,它包含了 2 个正弦信号和噪声 randn('state',0); fs = 1000; % Sampling frequency t = (0:fs)/fs; % One second worth of samples A = [1 2]; % Sinusoid amplitudes (row vector) f = [150;140]; % Sinusoid frequencies (column vector) xn = A*sin(2*pi*f*t) + 0.1*randn(size(t)); 注意:最后三行表明了一个方便的表示正弦之和的方法,它等价于: xn = sin(2*pi*150*t) + 2*sin(2*pi*140*t) + 0.1*randn(size(t)); 对这个 PSD 的周期图估计可以通过产生一个周期图对象(periodogram object)来计算 Hs = spectrum.periodogram('Hamming'); 估计的图形可以用 psd 函数显示。 psd(Hs,xn,'Fs',fs,'NFFT',1024,'SpectrumType','twosided')
2 信号分析基础(频谱分析)
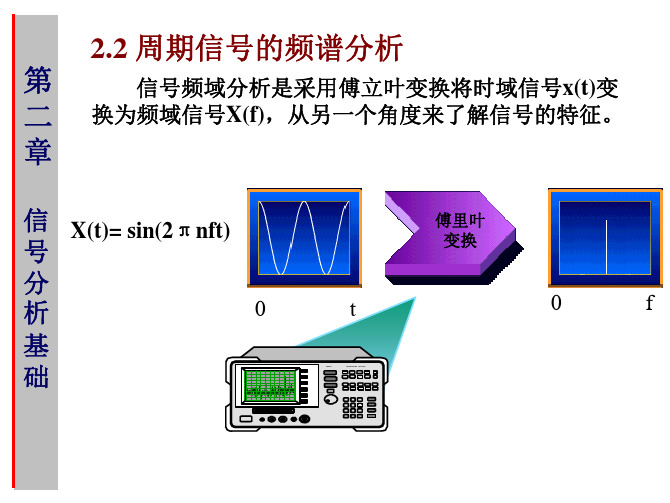
(2.69)
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
式2.68称为 x t 的傅立叶变换,称式2.69为 X 的 傅立叶逆变换,两者称为傅立叶变换对,可记为
x t X
IFT
FT
2 f 代入傅立叶积分式中,则式2.68, 2.69变为
X f x t e j 2 ft dt
Im[X ( f )] ( f ) arctgRe[ X ( f )]
x (t ) 1 X ( )e jt d 2 X ( ) x (t )e jt dt
X f 连续幅值谱
f
连续相位谱
X 频谱密度函数
2.2 周期信号的频谱分析 第 二 章
信号频域分析是采用傅立叶变换将时域信号x(t)变 换为频域信号X(f),从另一个角度来了解信号的特征。
信 X(t)= sin(2πnft) 号 分 0 析 基 础
傅里叶 变换
t
8563A
SPECTRUM ANALYZER 9 kHz - 26.5 GHz
0
f
频域分析的概念 周 期 信 号 的 频 谱 分 析
傅 里 叶 变 换 与 非 周 期 信 号 的 分 解
T0 T0 , 设有一个周期信号x(t)在区间 2 2
以傅立叶级数表示为
x t
n
ce
n
jn0t
1 式中 cn T0
T0 2 T 0 2
x t e
jn0t
dt
将其代入上式则得
n n
幅频谱 相频谱
频谱图的概念 周 期 信 号 的 频 谱 分 析
典型信号的频谱分析

典型信号的频谱分析一、试验目的在理论学习的基础上,通过本实验熟悉典型信号的频谱特征,能够从信号频谱中读取所需的信息,也就是具备读谱图的能力。
二、试验原理1. 正弦波、方波、三角波和白噪声信号是实际工程测试中常见的典型信号,这些信号时域、频域之间的关系很明确,并且都具有一定的特性,通过对这些典型信号的频谱进行分析,可以掌握信号的特性,熟悉信号的分析方法。
2. 信号的频谱可分为幅值谱、相位谱、功率谱、对数谱等。
傅立叶变换是信号频谱分析中常用的一个工具,它把一些复杂的信号分解为无穷多个相互之间具有一定关系的正弦信号之和,并通过对各个正弦信号的研究来了解复杂信号的频率成分和幅值。
3. 信号频谱分析是采用傅立叶变换将时域信号x(t)变换为频域信号X(f),从而帮助人们从另一个角度来了解信号的特征。
时域信号x(t)的傅氏变换为:x(t)=a0/2+ a1*sin(2πf0t)+b1*cos(2πf0t)+ a2*sin(2πf0t)+b2*cos(2πf0t)+.........用Cn画出信号的幅值谱曲线,从信号幅值谱判断信号特征。
三、试验内容a)白噪声信号幅值谱特性b)正弦波信号幅值谱特性c)方波信号幅值谱特性d)三角波信号幅值谱特性e)拍波信号幅值谱特性f)正弦波信号+白噪声信号幅值谱特性四、程序及波形1.%white noiset=0:0.01:1A=rand(size(t))Afft=abs(fft(A))/5122.%ssin savet=0:0.01:1y1=sin(2*pi*5*t)fs=0:1:100y2=abs(fft(y1))/512plot(fs,y2)3.%fang wavet = 0:0.0001:0.0625y = SQUARE(2*pi*30*t) fs=0:16:10000Y=abs(fft(y))/512plot(fs,Y)4.%sanjiao wavef=100width=0.3t4=0:0.001:0.1c=2*pi*f*t4y4=sawtooth(c,width)fs=0:1/0.001:10Y4=abs(fft(y4))/512plot(fs,Y4)5.%pai wavet=0:0.01:1m1=sin(2*pi*5*t)m2=sin(2*pi*6*t)M1=m1+m2fs=0:0.1:100M2=abs(fft(M1))/512plot(t,M2)6.%white +sinet=0:0.001:1;%采样周期为0.001s,即采样频率为1000Hz;%产生噪声污染的正弦波信号;x=sin(2*pi*100*t)+sin(2*pi*200*t)+rand(size(t));Y=fft(x,512);%对x进行512点的幅里叶变换;f=1000*(0:256)/512;%设置频率轴(横轴)坐标,1000为采样频率;plot(f,Y(1:257));%画出频域内的信号;五、结论1.可以从受噪声污染的信号中鉴别出有用的信号;由最后一个图知道,从受污染信号的时域形式中,很难看出正弦波的成分。
频谱分析
1. FFT的提出 DFT在18世纪就已经被提出,但是一直到20世纪,都没有被真正用 于实际的谱分析和信号处理。 直到1965年IBM的T.W.Cooley和MIT的J.W.Tuky提出了基2FFT算法 之后,使DFT算法的运算效率提高了1个数量级以上。
F (m )
N 1
f ( k )W N
6.3.1 离散傅里叶变换(DFT)
DFT的应用举例:
subplot(3,2,1);plot(wk,abs(Xk));
例:对长度为26的三角形序列x (n),编写matlab程序验证频 率采样定理。 close all;clear all;clc; M=27;N=32;n=0:M; xa=0:floor(M/2); xb= ceil(M/2)1:-1:0; xn=[xa,xb]; Xk=fft(xn,1024); X32k=fft(xn,32) x32n=ifft(X32k ); X16k=X32k(1:2:N); x16n=ifft(X16k,N/2); ) subplot(3,2,2);stem(n,xn,'.');bo x on k=0:1023;wk=2*k/1024;
(a)FT[X(n)] 200
(b) 三 角 波 序 列 ;x(n) 20 15
|X(ej )|
x(n)
100 0 0 0.5 / (c) 16点 频 域 采 样 200 1
10 5 0
0
5
10
15 n
20
25
30
(d) 16点 IDFT[X16(k)] 20
|X16(k)|
信号时域特性与频域特性的关系
频谱分析

频谱分析利用傅里叶变换的方法对振动的信号进行分解,并按频率顺序展开,使其成为频率的函数,进而在频率域中对信号进行研究和处理的一种过程,称为频谱分析。
怎样进行频谱分析:利用频谱分析仪进行测量,输入信号不能有失真,因此要按特定应用的要求设置频谱分析仪和优化测量步骤,以达到最好的技术指标。
下面的测量提示对这些步骤有详细的说明。
1. 选择最好的分辨率带宽 (RBW)必须认真考虑分辨率带宽 (RBW)的设置,因为他关系到频谱成分的分离,适宜的噪声基底的设置和信号的解调。
通过低电平信号的测量,可以看到使用窄RBW的优点。
在使用窄RBW时,频谱分析仪显示出较低的平均噪声级 (DANL),且动态范围增加,灵敏度有所改进。
在图3中,把RBW从100kHz改变到10kHz 将能更好地分辨-95dBm的信号。
但并非任何情况都是最窄的RBW最好。
对于调制信号,RBW一定要设置得足够宽,使它能将信号边带包括在内。
如果忽略这一点,测量将是极不精确的。
窄RBW设置的一项重要缺点是扫频速度。
更宽的RBW设置在给定频率范围内允许更快的扫频。
图4和图5比较了在200MHz频率范围内,10kHz和 3kHzRBW的扫频时间。
一定要知道RBW 选择时所必须的基本权衡因素,使得用户在明白哪些参数最为重要的时候,给以适当的优化。
但在权衡不可避免时,现代频谱分析仪可为您提供弱化,甚至消除这些因素的方法。
通过使用数字信号处理,频谱分析仪在实现更精确的测量的同时还提供更高的速度,即使是使用窄RBW。
2. 改进测量精度在进行任何测量前,必须了解有哪些可以改进幅度和频率测量精度的技术。
自校准功能可用来产生误差校正系数 (例如幅度改变—分辨率带宽),分析仪随后用它校正测量数据,得到更好的幅度测量结果,并使您能在测量过程中更灵活地改变控制。
当被测装置接到经校准的分析仪时,信号传输网络可能会使感兴趣信号减弱或变形,必须在测量中排除这一影响,见图6。
一种方法是使用分析仪的内置幅度校正功能,一个信号源以及一个功率表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通过最小化前向预测误差做时间序列的自回 spectrum.cov, pcov 归(AR)谱估计 通过最小化前向及后向预测误差做时间序列 spectrum.mcov, pmcov 的自回归(AR)谱估计 多重信号分类 虚谱估计 spectrum.music, pmusic spectrum.eigenvector, peig
P 1 ,2
2 1
Pxx d
1 2
Pxx d
从上式中可以看出 Pxx 是一个信号在一个无穷小频带上的功率浓度,这也是为什么 它叫做功率谱密度。 PSD 的单位是功率(e.g 瓦特)每单位频率。在 Pxx 的情况下,这是瓦特/弧度/抽 或只是瓦特/弧度。在 Pxx f 的情况下单位是瓦特/赫兹。PSD 对频率的积分得到的单位是 瓦特,正如平均功率 P , 所期望的那样。
% Sampling frequency % One second worth of samples % Sinusoid amplitudes (row vector)
f = [150;140]; % S inusoid frequencies (column vector) xn = A*sin(2*pi*f*t) + 0.1*randn(size(t)); 注意:最后三行表明了一个方便的表示正弦之和的方法,它等价于: xn = sin(2*pi*150*t) + 2*sin(2*pi*140*t) + 0.1*randn(size(t)); 对这个 PSD 的周期图估计可以通过产生一个周期图对象(periodogram object)来计算 Hs = spectrum.periodogram('Hamming'); 估计的图形可以用 psd 函数显示。 psd(Hs,xn,'Fs',fs,'NFFT',1024,'SpectrumType','twosided')
Nonparametric Methods 非参数法
下面讨论 periodogram, modified periodogram, Welch, 和 multitaper 法。同时 也讨论 CPSD 函数,传输函数估计和相关函数。
Periodogram 周期图法
一个估计功率谱的简单方法是直接求随机过程抽样的 DFT ,然后取结果的幅度的平方。 这样的方法叫做周期图法。 一个长 L 的信号 xL n 的 PSD 的周期图估计是
Power Spectral Density Estimate via Periodogram 0 -10 -20
Power/frequency (dB/Hz)
-30 -40 -50 -60 -70 -80
0
0.1
0.2
0.3
0.4 0.5 0.6 Frequency (kHz)
0.7
0.8
0.9
1 2
对实信号,PSD 是关于直流信号对称的,所以 0 的 Pxx 就足够完整的描述 PSD 了。然而要获得整个 Nyquist 间隔上的平均功率,有必要引入单边 PSD 的概念:
0 0 Ponesided 2 Pxx 0
ˆ f P xx k
其中
X L fk fs L
2
, fk
kf s , k 0,1,, N 1 N
X L f k xL n e2 jkn / N
n 0
L 1
选择 N 是大于 L 的下一个 2 的幂次是明智的, 要计算 X L f k 我们直接对 xL n 补零到 长度为 N。假如 L>N,在计算 X L f k 前,我们必须绕回 xL n 模 N。 作为一个例子,考虑下面 1001 元素信号 xn ,它包含了 2 个正弦信号和噪声 randn('state',0); fs = 1000; t = (0:fs)/fs; A = [1 2];
xL n x n wR n
因为时域的乘积等效于频域的卷积,所以上式的傅立叶变换是
1 XL f fs
fs / 2
fs / 2
X WR f d
前文中导出的表达式
ˆ f P xx
XL f fs L
2
说明卷积对周期图有影响。 正弦数据的卷积影响最容易理解。假设 x n 是 M 个复正弦的和
S xx
m
R m e
xx
j m
注: S xx X ,其中 X lim
2
N
1 N
n N /2
N /2
xn e jn 。其 matlab
近似为 X=fft(x,N)/sqrt(N),在下文中 X L f 就是指 matlab fft 函数的计算结果了 使用关系 2 f / f s 可以写成物理频率 f 的函数,其中 f s 是采样频率
ˆ f P xx
XL f fs L
2
注:这里 X L f 运用的是 matlab 里面的 fft 的定义不带归一化系数,所以要除以 L 其中
X L f xL n e2 jfn / f s
n 0
L 1
实际对 X L f 的计算可以只在有限的频率点上执行并且使用 FFT。实践上大多数周期 图法的应用都计算 N 点 PSD 估计
S xx f
m
R m e
xx
2 jfm / f s
相关序列可以从功率谱用 IDFT 变换求得:
Rxx m
s S xx e jm S f e2 jfm / f s d xx df 2 f s fs / 2
f /2
M
x n Ak e jk n
k 1
其频谱是
X f f s Ak f f k
k 1
M
对一个有限长序列,就变成了
XL f
1 fs
fs / 2
fs / 2
f s Ak f k WR f d AkWR f f k
Parametric methods (参量类方法) 这类方法是假设信号是一个由白噪声驱动的线性系统的输 出。这类方法的例子是 Yule-Walker autoregressive (AR) method 和 Burg method 。这些方法先估计假设的 产生信号的线性系统的参数。 这些方法想要对可用数据相对较少的情况产生优于传统非参数 方法的结果。 Subspace methods (子空间类) 又称为 high-resolution methods (高分辨率法)或者 super-resolution methods (超分辨率方法) 基于对自相关矩阵的特征分析或者特征值分解产生信号的频率分量。 代表 方 法 有 multiple signal classificat ion (MUS IC) method 或 eigenvector (EV) method。这类方法对线谱(正弦信号的谱)最合适,对检测噪声下的正弦信号很有效,特 别是低信噪比的情况。 方法 周期图 Welch 多椎体 Yule-Walker AR Burg Covariance (协方差) 修正协方差 MUSIC 特征向量法 PSD 估计 重叠,加窗的信号段的平均周期图 多个正交窗(称为锥)的组合做谱估计 时间序 列的 估计 的自 相关函 数计 算自 回归 (AR)谱估计 通过最小化线性预测误差计算自回归( AR) 谱估计 描述 函数 spectrum.periodogram, periodogram spectrum.welch, pwelch, cpsd, tfestimate, mscohere spectrum.mtm, pmtm spectrum.yulear, pyulear spectrum.burg, pburg
序列 xn 在整个 Nyquist 间隔上的平均功率可以表示为
Rxx 0
上式中的
Hale Waihona Puke s S xx S f d xx df 2 fs fs / 2
f /2
Pxx
S f S xx 以及 Pxx f xx 2 fs
被定义为平稳随机信号 xn 的 power spectral density (PSD)(功率谱密度) 一个信号在频带 1 , 2 ,0 1 2 上的平均功率可以通过对 PSD 在频带上积分 求出
k 1 k 1
M
M
所以在有限长信号的频谱中,Dirac 函数被替换成了形式为 WR f f k 的项,该项对 应于矩形窗的中心在 f k 的频率响应。 一个矩形窗的频率响应形状是一个 sinc 信号,如下所示
矩形窗在物理频率上的功率谱密度 0 -10 -20
PSD dB watt/Hz
Matlab 信号处理工具箱 帮助文档 谱估计专题
翻译:无名网友 & Lyra
频谱分析
Spectral estimation(谱估计)的目标是基于一个有限的数据集合描述一个信号的功 率(在频率上的)分布。功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信 号的检测。 从数学上看,一个平稳随机过程 xn 的 power spectrum(功率谱)和 correlation sequence(相关序列)通过 discrete-time Fourier transform(离散时间傅立叶变换) 构成联系。从 normalized frequency(归一化角频率)角度看,有下式
平均功率通过用下述求和去近似积分 求得 [Pxx,F] = psd(Hs,xn,fs,'twosided'); Pow = (fs/length(Pxx)) * sum(Pxx) Pow = 2.5059 你还可以用单边 PSD 去计算平均功率 [Pxxo,F] = psd(Hs,xn,fs,'onesided'); Pow = (fs/(2*length(Pxxo))) * sum(Pxxo) Pow = 2.5011 周期图性能 下面从四个角度讨论周期图法估计的性能:泄漏,分辨率,偏差和方差。 频谱泄漏 考虑有限长信号 xL n ,把它表示成无限长序列 x n 乘以一个有限长矩形窗 wR n 的 乘积的形式经常很有用:
