长方体和正方体知识梳理思维导图
2017长方体和正方体知识梳理思维导图
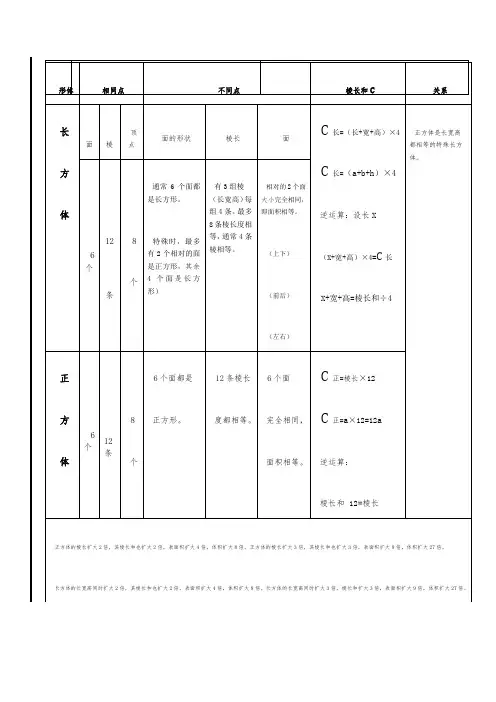
S长=2ab+2ah+2bh
逆运算：设长X
x×宽×2+x×高×2+宽×高×2=表面积
面积进率100
平方米
m2
平方分米
dm2
平方厘米
cm2
长方体或正方体6个面的总面积，叫做它的表面积。
V长=长×宽×高=abh
V长=底面积×高=Sh
=左面积×长=Sa
=前面积×宽=Sb
逆运算：设长X
X×宽×高=长方体体积
长方体体积÷（宽×高）
长方体体积÷底面积=高
体积进率1000
立方米m3
立方分米（升）
dm3L
立方厘米（毫升）
cm3mL
体积
容积
物体所占空间的大小叫做物体的体积。
（从外面量长、宽、高。）
箱子、油桶、仓库、水池等所能容纳物体的体积，通常叫做他们的容积。（从里面量长、宽、高。）
正
方
体
底面积×高
或：长×宽×（升高-原高）
3.游泳池、鱼缸等：表面积减1上面
4.包装问题：商标、衣柜、喷漆等。
5.抽纸盒类型：六个面面积减去缺口面积。
6.占地面积问题：只求底面面积。
7.立体图形的切割：切割会使表面积增加，
将长方体的最大面组合，表面积减少的最多，
将长方体的最小面组合，表面积减少的最少。
8.立体图形的拼合：组合只会使表面积减少，
4.看问题是让求什么？（棱长和、表
面积、体积、容积、长、价钱、
瓷砖块等）
5.确定公式并计算（顺逆）
6.换算单位（体积变容积；大变小）
7.价钱（单价×数量=总价；
每份数×份数=总数）
8.瓷砖块（大面积÷小面=块数，
长方体和正方体知识梳理思维导图
2017长方体和正方体知识梳理思维导图(总2页)--本页仅作为文档封面，使用时请直接删除即可--叫做它的表面积。
长方体或正方体6个面的总面积，形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C 长方体 =（长+宽+高）×4C 长方体 =（a+b+h ）×4逆运算：（方程法）设长X（X +宽+高）×4 = C 长X +宽+高 =棱长和÷4 （算术法）长=棱长和÷4-长-宽正方体是长宽高都相等的特殊长方体。
6个12 条 8 个有6个面都是长方形。
有时，最多有2个相对的面是正方形，其余4个面是完全相同的长方形）有3组棱（长宽高）每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
（上 下） （前 后） （左 右）正 方 体6个12条8 个6个面都是 正方形。
12条棱长 度都相等。
6个面 完全相同， 面积相等。
C 正 = 棱长×12 C 正 = a ×12= 12a逆运算：棱长和÷ 12 = 棱长正方体的棱长扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
形体S 表面积（6面）V 体积（容积）计算公式单位定义计算公式 常用单位定义长方 体 S 表=（长×宽+ 长×高+ 宽×高）×2 S 表=（ab + ah + bh ）×2 S 表=S 表= 2ab + 2ah +2bh 逆运算：设长X(x ×宽+x ×高+宽×高)×2表面积x×宽+x ×高+宽×高 =表面积÷2面积每相邻单位间进率为100平方米m2平方分米 dm 2 平方厘米cm 2V 长 = 长×宽×高 =abh V 长= 底面积×高 =Sh（=左面积×长=Sa =前面积×宽=Sb ）逆运算： 设长X X ×宽×高 =长方体体积 长方体体积÷（宽×高） 长方体体积÷底面积=高 体积进率1000立方米m 3立方分米（升）1dm 3=1L立方厘米（毫升）1cm 3 =1mL体积容积正 方 体S 正= 棱长×棱长×6 S 正=任意一个面的面积×6= 6×a ×a =6a 2逆运算：一个面的面积= 表面积 ÷ 6V 正 = 棱长×棱长×棱长 V 正 =a ×a ×a =a 3m 2 100 dm 2 100 cm 2m 3 1000 dm 3 1000 cm 3进率：大变小×进率（+0或向右移动小数点）；小变大 ÷ 进率 （-0或向左移动小数点） L1000mL解决思路题型物体所占空间的大小叫做物体的体积。
长方体和正方体知识梳理思维导图
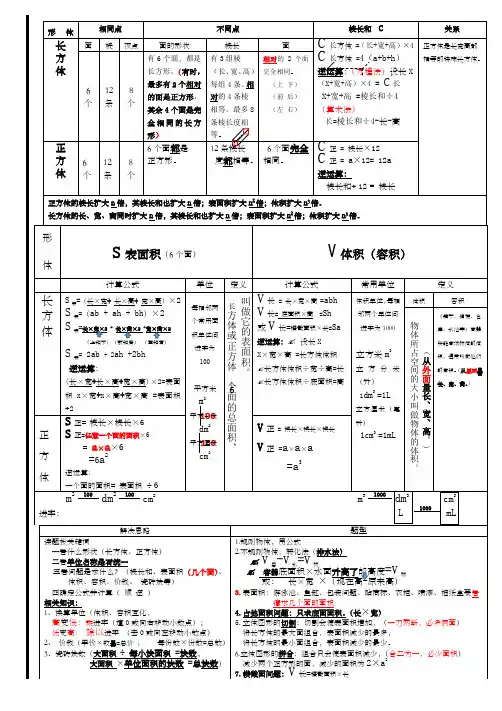
立方分米 （升）
1dm3 =1L
立方厘米（毫 升）
1cm3 =1mL
体积
容积
物 体 所 占（ 空从 间外 的面 大量 小长 叫、 做宽 物、 体高 的。 体） 积 。
（箱子、油桶、仓 库、水池等）容器 所能容纳物体的体 积，通常叫做他们 的容积。（从里面量 长、宽、高。）
dm m3 1000
全 相 同 的 长 方 条棱长度相
形）
等。
6 个面都是
12 条棱长
6 个面完全
正方形。
度都相等。 相同。
棱长和 C
C 长方体 =（长+宽+高）×4 C 长方体 =4（a+b+h）
逆运算：（方程法）设长 X
（X+宽+高）×4 = C 长
X+宽+高 =棱长和÷4 （算术法）
长=棱长和÷4-长-高
C 正 = 棱长×12 C 正 = a×12= 12a
形体
长 方 体
正 方 体
相同点 面 棱 顶点
6 12 8 个条 个
6 12 8 个条 个
不同点
面的形状
棱长
面
有 6 个面，都是 有 3 组棱
相对的 2 个面
长方形。（有时， （长、宽、高） 完全相同。
最多有 2 个相对 每组 4 条。相 （上 下）
的面是正方形， 对的 4 条棱
（前 后）
其余 4 个面是完 相等。最多 8 （左 右）
或 正 方 体
叫 做 它 的 表 面 积 。
长 = 长×宽×高 =abh 长= 底面积×高 =Sh 或 长=横截面积×长=Sa 逆运算： 设长 X
X×宽×高 =长方体体积 长方体体积÷宽÷高=长
长方体和正方体知识梳理思维导图
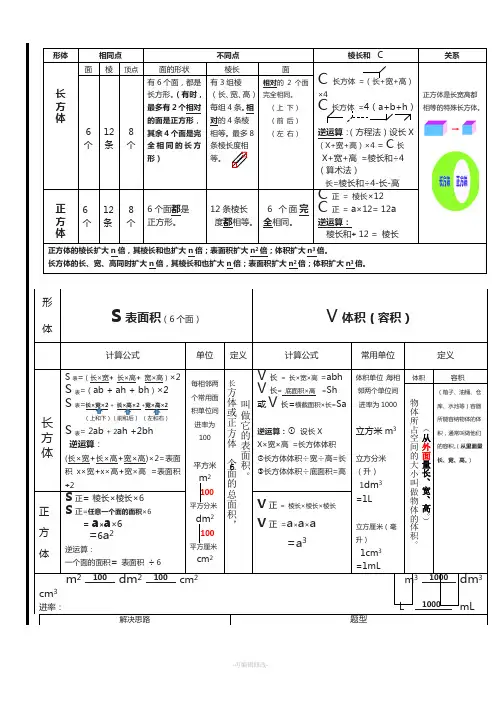
100 叫做它的表面积。
长方体或正方体个面的总面积，100形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C长方体 =（长+宽+高）×4C 长方体 =4（a+b+h ）逆运算：（方程法）设长X（X+宽+高）×4 = C 长X+宽+高 =棱长和÷4 （算术法）长=棱长和÷4-长-高正方体是长宽高都相等的特殊长方体。
6个12 条 8 个有6个面，都是长方形。
（有时，最多有2个相对的面是正方形，其余4个面是完全相同的长方形）有3组棱（长、宽、高）每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
（上 下） （前 后） （左 右）正 方 体6个12条 8 个6个面都是 正方形。
12条棱长度都相等。
6个面完全相同。
C 正 = 棱长×12C 正 = a ×12= 12a逆运算：棱长和÷ 12 = 棱长正方体的棱长扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
形体S 表面积（6个面）V 体积（容积）计算公式单位定义计算公式 常用单位定义长方 体 S 表=（长×宽+ 长×高+ 宽×高）×2S 表=（ab + ah + bh ）×2 S 表=长×宽×2 + 长×高×2 +宽×高×2（上和下）（前和后） （左和右）S 表= 2ab + 2ah +2bh 逆运算：(长×宽+长×高+宽×高)×2=表面积x ×宽+x ×高+宽×高 =表面积÷2每相邻两个常用面积单位间进率为 100平方米 m 2平方分米 dm 2平方厘米cm 2V 长 = 长×宽×高 =abh V 长= 底面积×高 =Sh 或V 长=横截面积×长=Sa逆运算：① 设长XX ×宽×高 =长方体体积②长方体体积÷宽÷高=长 ③长方体体积÷底面积=高 体积单位，每相邻两个单位间进率为1000立方米m 3立方分米（升） 1dm 3=1L立方厘米（毫升）1cm 3=1mL体积容积（箱子、油桶、仓库、水池等）容器所能容纳物体的体积，通常叫做他们的容积。
长方体和正方体思维导图
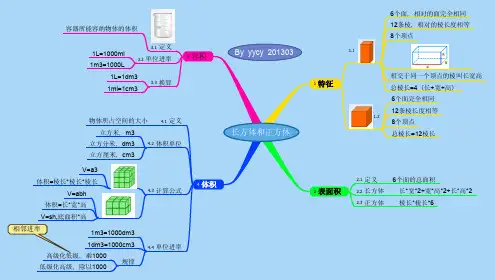
8个顶点 总棱长=12棱长
2 表面积2.1 定义 2.2 长方体 Nhomakorabea.3 正方体
6个面的总面积 长*宽*2+宽*高*2+长*高*2 棱长*棱长*6
体积=长*宽*高
V=sh,底面积*高
相邻进率
1m3=1000dm3
1dm3=1000cm3
高级化低级，乘1000 低级化高级，除以1000
规律
4.3 计算公式 4.4 单位进率
4 体积
长方体和正方体
6个面，相对的面完全相同 12条棱，相对的棱长度相等 8个顶点
1.1
1 特征
相交于同一个顶点的棱叫长宽高 总棱长=4（长+宽+高） 6个面完全相同 12条棱长度相等
容器所能容纳物体的体积
1L=1000ml 1m3=1000L
3.1 定义 3.2 单位进率
1L=1dm3 1ml=1cm3
3.3 换算
3 容积
By yycy 201303
物体所占空间的大小 4.1 定义 立方米，m3
立方分米，dm3 4.2 体积单位 立方厘米，cm3
V=a3
体积=棱长*棱长*棱长
V=abh
数学长方体和正方体知识梳理思维导图
数学长⽅体和正⽅体知识梳理思维导图形体相同点不同点棱长和C关系长⽅体⾯棱顶点⾯的形状棱长⾯C长=（长+宽+⾼）×4C长 =（a+b+h）×4逆运算：设长X（X +宽+⾼）×4 = C长X +宽+⾼ =棱长和÷4正⽅体是长宽⾼都相等的特殊长⽅体。
6个12条8个通常6个⾯都是长⽅形。
特殊时，最多有2个相对的⾯是正⽅形，其余4个⾯是长⽅形）有3组棱（长宽⾼）每组4条。
最多8条棱长度相等，通常4条棱相等。
相对的2个⾯⼤⼩完全相同，即⾯积相等。
（上下）（前后）（左右）正⽅体6个条8个6个⾯都是正⽅形。
12条棱长度都相等。
6个⾯完全相同，⾯积相等。
C正= 棱长×12C正=a×12= 12a逆运算：棱长和÷12 = 棱长正⽅体的棱长扩⼤2倍，其棱长和也扩⼤2倍，表⾯积扩⼤4倍，体积扩⼤8倍。
正⽅体的棱长扩⼤3倍，其棱长和也扩⼤3倍，表⾯积扩⼤9倍，体积扩⼤27倍。
长⽅体的长宽⾼同时扩⼤2倍，其棱长和也扩⼤2倍，表⾯积扩⼤4倍，体积扩⼤8倍。
长⽅体的长宽⾼同时扩⼤3倍，棱长和扩⼤3倍，表⾯积扩⼤9倍，体积扩⼤27倍。
形体S表⾯积（6⾯）V体积（容积）计算公式单位定义计算公式常⽤单位定义长⽅体S长=（长×宽+ 长×⾼+ 宽×⾼）×2S长=（ab + ah + bh）×2S长=长×宽×2 + 长×⾼×2 +宽×⾼×2（上下）（前后）（左右）S长= 2ab+ 2ah +2bh逆运算：设长Xx×宽×2 + x×⾼×2 +宽×⾼×2 =表⾯积⾯积进率100平⽅⽶m2平⽅分⽶平⽅厘⽶cm2长⽅体或正⽅体6个⾯的总⾯积，叫做它的表⾯积。
V长= 长×宽×⾼=abhV长= 底⾯积×⾼ =Sh=左⾯积×长=Sa=前⾯积×宽=Sb逆运算：①设长XX ×宽×⾼ =长⽅体体积②长⽅体体积÷（宽×⾼）③长⽅体体积÷底⾯积=⾼体积进率1000⽴⽅⽶m3⽴⽅分⽶（升）dm3 L⽴⽅厘⽶（毫升）cm3 mL体积容积物体所占空间的⼤⼩叫做物体的体积。
2017长方体和正方体知识梳理思维导图
叫做它的表面积。
长方体或正方体6个面的总面积，形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C 长方体 =（长+宽+高）×4 C 长方体 =（a+b+h ）×4逆运算：（方程法）设长X（X +宽+高）×4 = C 长X +宽+高 =棱长和÷4 （算术法）长=棱长和÷4-长-宽正方体是长宽高都相等的特殊长方体。
6个 12 条 8 个有6个面都是长方形。
有时，最多有2个相对的面是正方形，其余4个面是完全相同的长方形）有3组棱（长宽高）每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
（上 下） （前 后） （左 右）正 方 体6个12条 8 个6个面都是 正方形。
12条棱长度都相等。
6个面 完全相同， 面积相等。
C 正 = 棱长×12 C 正 = a ×12= 12a逆运算：棱长和÷ 12 = 棱长正方体的棱长扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
形体S 表面积（6面）V 体积（容积）计算公式单位定义计算公式 常用单位定义长方 体 S 表=（长×宽+ 长×高+ 宽×高）×2 S 表=（ab + ah + bh ）×2 S 表=长×宽×2 + 长×高×2 +宽×高×2（上和下）（前和后） （左和右）S 表= 2ab + 2ah +2bh 逆运算：设长X(x ×宽+x ×高+宽×高)×2=表面积x ×宽+x ×高+宽×高 =表面积÷2面积每相邻单位间进率为 100平方米m2平方分米 dm 2 平方厘米cm 2V 长 = 长×宽×高 =abh V 长= 底面积×高 =Sh（=左面积×长=Sa =前面积×宽=Sb ）逆运算：① 设长X X ×宽×高 =长方体体积 ②长方体体积÷（宽×高） ③长方体体积÷底面积=高 体积进率1000立方米m3立方分米（升）1dm 3=1L立方厘米（毫升）1cm 3 =1mL体积容积箱子、油桶、仓库、水池等所能容纳物体的体积，通常叫做他们的容积。
长方体和正方体知识梳理思维导图教学内容
长方体和正方体知识梳理思维导图收集于网络，如有侵权请联系管理员删除100 叫做它的表面积。
长方体或正方体 个面的总面积，形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C长方体 =（长+宽+高）×4C 长方体 =4（a+b+h ）逆运算：（方程法）设长X（X+宽+高）×4 = C 长X+宽+高 =棱长和÷4 （算术法）长=棱长和÷4-长-高正方体是长宽高都相等的特殊长方体。
6个12 条8 个有6个面，都是长方形。
（有时，最多有2个相对的面是正方形，其余4个面是完全相同的长方形）有3组棱（长、宽、高）每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
（上 下） （前 后）（左 右） 正 方 体6个12条8 个6个面都是 正方形。
12条棱长 度都相等。
6个面完全相同。
C 正 = 棱长×12 C 正 = a ×12= 12a逆运算：棱长和÷ 12 = 棱长正方体的棱长扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
形体S 表面积（6个面）V 体积（容积）计算公式单位定义计算公式常用单位定义长 方 体 S 表=（长×宽+ 长×高+ 宽×高）×2S 表=（ab + ah + bh ）×2S表=长×宽×2 + 长×高×2 +宽×高×2（上和下）（前和后） （左和右）S表= 2ab + 2ah +2bh逆运算：(长×宽+长×高+宽×高)×2=表面每相邻两个常用面积单位间进率为 100平方米 m2V 长 = 长×宽×高 =abhV 长= 底面积×高 =Sh 或V 长=横截面积×长=Sa 逆运算：① 设长X X ×宽×高 =长方体体积 ②长方体体积÷宽÷高=长 体积单位，每相邻两个单位间进率为1000立方米m 3立方分米（升） 体积 容积（箱子、油桶、仓库、水池等）容器所能容纳物体的体积，通常叫做他们的容积。
数学长方体和正方体知识梳理思维导图
形体相同点不同点棱长和C关系长方体面棱顶点面的形状棱长面C长=（长+宽+高）×4C长 =（a+b+h）×4逆运算：设长X（X +宽+高）×4 = C长X +宽+高 =棱长和÷4正方体是长宽高都相等的特殊长方体。
6个12条8个通常6个面都是长方形。
特殊时，最多有2个相对的面是正方形，其余4个面是长方形）有3组棱（长宽高）每组4条。
最多8条棱长度相等，通常4条棱相等。
相对的2个面大小完全相同，即面积相等。
（上下）（前后）（左右）正方体6个12条8个6个面都是正方形。
12条棱长度都相等。
6个面完全相同，面积相等。
C正= 棱长×12C正=a×12= 12a逆运算：棱长和÷12 = 棱长正方体的棱长扩大2倍，其棱长和也扩大2倍，表面积扩大4倍，体积扩大8倍。
正方体的棱长扩大3倍，其棱长和也扩大3倍，表面积扩大9倍，体积扩大27倍。
长方体的长宽高同时扩大2倍，其棱长和也扩大2倍，表面积扩大4倍，体积扩大8倍。
长方体的长宽高同时扩大3倍，棱长和扩大3倍，表面积扩大9倍，体积扩大27倍。
形体S表面积（6面）V体积（容积）计算公式单位定义计算公式常用单位定义长方体S长=（长×宽+ 长×高+ 宽×高）×2S长=（ab + ah + bh）×2S长=长×宽×2 + 长×高×2 +宽×高×2（上下）（前后）（左右）S长= 2ab+ 2ah +2bh逆运算：设长Xx×宽×2 + x×高×2 +宽×高×2 =表面积面积进率100平方米m2平方分米dm2平方厘米cm2长方体或正方体6个面的总面积，叫做它的表面积。
V长= 长×宽×高=abhV长= 底面积×高 =Sh=左面积×长=Sa=前面积×宽=Sb逆运算：①设长XX ×宽×高 =长方体体积②长方体体积÷（宽×高）③长方体体积÷底面积=高体积进率1000立方米m3立方分米（升）dm3 L立方厘米（毫升）cm3 mL体积容积物体所占空间的大小叫做物体的体积。
长方体与正方体(人教版五年级数学下册思维导图)
三、长方体与正方体（二）长方体与正方体的表面积（三）长方体与正方体的体积（一）长方体与正方体的认识长方体体积和体积单位正方体（立方体）正方体是长、宽、高都相等的长方体体积单位间的进率容积和容积单位通过观察和讨论可知：长方体一般是由6个长方形围成的立体图形。
在一个长方体中，相对的面完全相同，相对的棱长度相等棱长是1cm （dm 、m ）的正方体，体积是1cm³（dm³、m³）1L=1000mL, 1L=1dm³, 1mL=1cm³长方体或正方体6个面的总面积，叫做它的表面积（例题注意没有底面或没有盖的物体的表面积计算）容积单位1m³=1000dm³，1dm³=1000cm³正方体：是由6个完全相同的正方形围成的立体图形，所有的棱长度相等相交于一个顶点的三条棱的长度分别叫长、宽、高棱面面和面相交的线段顶点棱和棱的交点长方体体积体积单位正方体体积体积物体所占空间的大小叫做物体的体积计量体积要用体积单位，常用的体积单位有立方厘米、立方分米、立方米，分别可以写作cm³、dm³、m³V=abh （a 、b 、h 代表长、宽、高） 也可以表示为V=Sh （S 为长方体底面积）V=aaa=a³，a³读作a 的立方，也可以写成 V=Sh （S 为正方体底面积）6个面（都是长方形，也有可能顶对面是正方形），12条棱，8个顶点6个面（都是正方形），12条棱，8个顶点长方体表面积：（长x 宽+长x 高+宽x 高）x2——S=2（ab+ah+bh ）正方体表面积：棱长x 棱长x6——S=a²长度——米、分米、厘米——相邻两个单位间的进率为10面积——平方米、平方分米、平方厘米——相邻两个单位间的进率为100体积——立方米、立方分米、立方厘米——相邻两个单位间的进率为1000容积箱子、油桶、仓库等所能容纳物体的体积，通常叫做它们的容积计量单位，一般就用体积单位。
长方体和正方体复习思维导图
长方体和正方体展
开
图
共11种：1+4+1，6种；3+3，一种；2+2+2，一种；1+3+2，3种
规律：只要所给的图形出现田字格形，凹字格形，就不能拼成长方体或正方体
特
征
都有6个面，8个顶点，12条棱，相对的面完全相同，相对的棱长度相
等。
正方体是特殊的长方体：所有棱长都相等，所有面都相同
至少要8个小正方体才能拼成一个大的正方体
表
面
积
长方体：（长×宽+长×高+宽×高）×2
用字母表示：S=(ab+ac+bc)×2
正方体：边长×边长×6，用字母表示S=6a2
长宽高同时扩大几倍，表面
积就扩大倍数的平方倍
体
积
长方体和正方体体积统一公式：
体积=底面积×高
长方体：长×宽×高
正方体：边长×边长×边长
长宽高同时扩大几倍，体积就扩大
倍数的立方倍
棱
长
之
和
长方体：（长+宽+高）×4
正方体：边长×12
长宽高同时扩大几倍，棱长之和就扩大几倍
容
积
容器所能容纳的物体的体积，叫做它的容积
容积
的计
算
1，和长方体，正方体的计算方法相同
2，排水法：被沉
物体的体积等于上
升部分水的体积
方法一：容器的底面积×上升部分水的高度
方法二：放入物体后的体积—原来水的体积容积或体积单位1L=1dm3 1ml=1cm3 1L=1000ml 1dm3 =1000cm3
长方体或正方体截成若干个小立方体后，体积不变，表面积增加了。
长方体和正方体知识梳理思维导图76828
叫做它的表面积。
长方体或正方体6个面的总面积，形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C 长方体 =（长+宽+高）×4C 长方体 =（a+b+h ）×4逆运算：（方程法）设长X（X +宽+高）×4 = C 长X +宽+高 =棱长和÷4 （算术法）长=棱长和÷4-长-宽正方体是长宽高都相等的特殊长方体。
6个12 条8 个有6个面都是长方形。
有时，最多有2个相对的面是正方形，其余4个面是完全相同的长方形）有3组棱（长宽高）每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
（上 下）（前 后）（左 右） 正 方 体6个12条8 个6个面都是 正方形。
12条棱长度都相等。
6个面完全相同， 面积相等。
C 正 = 棱长×12 C 正 = a ×12= 12a逆运算：棱长和÷ 12 = 棱长正方体的棱长扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
形体S 表面积（6面）V 体积（容积）计算公式单位定义计算公式常用单位定义长 方 体 S 表=（长×宽+ 长×高+ 宽×高）×2S 表=（ab + ah + bh ）×2S表=长×宽×2 + 长×高×2 +宽×高×2（上和下）（前和后） （左和右）S表= 2ab + 2ah +2bh逆运算：设长X(x ×宽+x ×高+宽×高)×2=表面积x ×宽+x ×高+宽×高 =表面积÷2面积每相邻单位间进率为 100平方米m 2 平方分米dm2V 长 = 长×宽×高 =abhV 长= 底面积×高 =Sh （=左面积×长=Sa =前面积×宽=Sb ） 逆运算：① 设长X X ×宽×高 =长方体体积 ②长方体体积÷（宽×高） ③长方体体积÷底面积=高体积进率1000 立方米m 3立方分米（升）1dm 3=1L体积 容积箱子、油桶、仓库、水池等所能容纳物体的体积，通常叫做他们的容积。
《长方体和正方体》思维导图
相同点
不同点
棱长和
关系
长
方
体
面
棱
顶点
面的形状
棱长
面的大小（面积）
正
方
体
3-1
长
方
体
正
方
体
的
认
识
形体
表面积
体积（容积）
计பைடு நூலகம்公式
常用单位
定义
计算公式
常用单位
定义
长
方
体
正
方
体
进
率
3-2
3-3
长
方
体
正
方
体
的
表面积
体积
容积
所有公式
解题思路
题型
解
决
问
题
形体
相同点
不同点
棱长和
关系
长
方
体
面
棱
顶点
面的形状
棱长
面的大小（面积）
正
方
体
3-1
长
方
体
正
方
体
的
认
识
形体
表面积
体积（容积）
计算公式
常用单位
定义
计算公式
常用单位
定义
长
方
体
正
方
体
进
率
3-2
3-3
长
方
体
正
方
体
的
表面积
体积
容积
所有公式
解题思路
题型
解
决
问
题
2017长方体和正方体知识梳理思维导图
（上下）（前后）（左右）
S长=2ab+ 2ah +2bh
逆运算：设长X
x×宽×2 + x×高×2 +宽×高×2 =表面积
面积进率100
平方米
m2
平方分米
dm2
平方厘米
cm2
长方体或正方体6个面的总面积，叫做它的表面积。
V长=长×宽×高=abh
V长=底面积×高=Sh
=左面积×长=Sa
=前面积×宽=Sb
逆运算：设长X
X×宽×高=长方体体积
长方体体积÷（宽×高）
长方体体积÷底面积=高
体积进率1000
立方米m3
立方分米（升）
dm3L
立方厘米（毫升）
cm3mL
体积
容积
物体所占空间的大小叫做物体的体积。
（从外面量长、宽、高。）
箱子、油桶、仓库、水池等所能容纳物体的体积，通常叫做他们的容积。（从里面量长、宽、高。）
大面积小面积二维平面c长方形长宽2c正方形边长4s长方形长宽s正方形边长边长高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率高级单位进率高级单位的数低级单位低级单位的数进率
相对的2个面大小完全相同，即面积相等。
（上下）
（前后）
（左右）
正
2017长方体和正方体知识梳理思维导图
（上下）（前后）（左右）
S长=2ab+ 2ah +2bh
逆运算：设长X
x×宽×2 + x×高×2 +宽×高×2 =表面积
面积进率100
平方米
m2
平方分米
dm2
积，叫做它的表面积。
V长=长×宽×高=abh
V长=底面积×高=Sh
4.看问题是让求什么？（棱长和、表
面积、体积、容积、长、价钱、
瓷砖块等）
5.确定公式并计算（顺逆）
6.换算单位（体积变容积；大变小）
7.价钱（单价×数量=总价；
每份数×份数=总数）
8.瓷砖块（大面积÷小面=块数，
如果小面积没告诉，需要再计算
小面积）
1.规则物体，用公式
2.不规则物体：排水法
V总-V水=V物
减少两个正方形的面，减少的面积为2×a2
9.横截面问题：看成底面积
10.大箱装小盒：大面积÷小面积
二
维
平
面
C长方形=（长+宽）×2
C正方形=边长×4
S长方形=长×宽
S正方形=边长×边长
长方体的长宽高同时扩大2倍，其棱长和也扩大2倍，表面积扩大4倍，体积扩大8倍。长方体的长宽高同时扩大3倍，棱长和扩大3倍，表面积扩大9倍，体积扩大27倍。
形体
S表面积（6面）
V体积（容积）
计算公式
单位
定义
计算公式
常用单位
定义
长
方
体
S长=（长×宽+长×高+宽×高）×2
S长=（ab + ah + bh）×2
=左面积×长=Sa
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
100 叫
做它的表面积。
长
方体或正方体
个面的总
面
积
，
100
形体
相同点 不同点
棱长和 C
关系
长 方 体
面
棱
顶点
面的形状 棱长 面
C 长方体 =（长+宽+高）×4
C 长方体 =4（a+b+h ）
逆运算：（方程法）设长X
（X+宽+高）×4 = C 长
X+宽+高 =棱长和÷4 （算术法）
长=棱长和÷4-长-高
正方体是长宽高都相等的特殊长方体。
6个 12 条 8 个
有6个面，都是长方形。
（有时，最多有2个相对的面是正方形，其余4个面是完全相同的长方形）
有3组棱（长、宽、高）每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面
完全相同。
（上 下） （前 后） （左 右）
正 方 体
6个
12条 8 个
6个面都是 正方形。
12条棱长
度都相等。
6个面完全
相同。
C 正 = 棱长×12 C 正 = a ×12= 12a
逆运算：
棱长和÷ 12 = 棱长
正方体的棱长扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍，其棱长和也扩大n 倍；表面积扩大n 2倍；体积扩大n 3倍。
形
体
S 表面积（6个面）
V 体积（容积）
计算公式
单位
定义
计算公式
常用单位
定义
长
方 体 S 表=（长×宽+ 长×高+ 宽×高）×2 S 表
=（ab + ah + bh ）×2 S 表=长×宽×2 + 长×高×2 +宽×高×2
（上和下）（前和后） （左和右）
S 表
= 2ab + 2ah +2bh 逆运算：
(长×宽+长×高+宽×高)×2=表面
积x ×宽+x ×高+宽×高 =表面积
÷2
每相邻两个常用面积单位间
进率为 100
平方米 m 2
平方分米 dm 2
平方厘米
cm 2
V 长 = 长×宽×高 =abh V 长= 底面积×高 =Sh 或V 长=横截面积×长=Sa
逆运算：① 设长X X ×宽×高 =长方体体积 ②长方体体积÷宽÷高=长 ③长方体体积÷底面积=高 体积单位，每相邻两个单位间
进率为1000
立方米m 3
立方分米
（升）
1dm 3
=1L
立方厘米（毫
升） 1cm 3 =1mL
体积 容积
（箱子、油桶、仓库、水池等）容器所能容纳物体的体
积，通常叫做他们的容积。
（从里面量长、宽、高。
）
正 方 体
S 正= 棱长×棱长×6 S 正=任意一个面的面积×6
= a ×a ×6 =6a 2
逆运算：
一个面的面积= 表面积 ÷ 6
V 正 = 棱长×棱长×棱长 V 正 =a ×a ×a =a 3
m 2 100 dm 2 100 cm 2 m 3 1000 dm 3 cm 3
进率：
L
1000
mL
解决思路
题型
物
体所占空间的大小叫做物体的体
积。
（从外面量长、宽、高。
）
6。