勾股数序列
100以内的勾股数

100以内的勾股数:i=3j=4k=5i=5j=12k=13i=6j=8k=10i=7j=24k=25i=8j=15k=17i=9j=12k=15i=9j=40k=41i=10j=24k=26i=11j=60k=61i=12j=16k=20i=12j=35k=37i=13j=84k=85i=14j=48k=50i=15j=20k=25i=15j=36k=39i=16j=30k=34i=16j=63k=65i=18j=24k=30i=18j=80k=82i=20j=21k=29i=20j=48k=52i=21j=28k=35i=21j=72k=75i=24j=32k=40i=24j=45k=51i=24j=70k=74i=25j=60k=65i=27j=36k=45i=28j=45k=53i=30j=40k=50i=30j=72k=78i=32j=60k=68i=33j=44k=55i=33j=56k=65i=35j=84k=91i=36j=48k=60i=36j=77k=85i=39j=52k=65i=39j=80k=89i=40j=42k=58i=40j=75k=85i=42j=56k=70i=45j=60k=75i=48j=55k=73i=48j=64k=80i=51j=68k=85i=54j=72k=90i=57j=76k=95i=60j=63k=87i=65j=72k=97勾股数的常用套路所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(a,b,c)。
即a^2+b^2=c^2,a,b,c∈N又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数n得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c互质的勾股数组。
关于这样的数组,比较常用也比较实用的套路有以下两种:1、当a为大于1的奇数2n+1时,b=2*n^2+2*n,c=2*n^2+2*n+1。
勾 股 数 序 列

勾股数序列山东定陶一中刘述省序言两千多年前,中国人和希腊人发现了勾股定理,当是数学史上的伟大创举。
a=2mn,b=m²-n²,c=m²+n²则是近代中国人在数论领域的又一重大成就,它将勾股数的一般求法表述得如此简捷。
然而迄今为止,未见一个具体详细的勾股数序列表。
这是因为,用现代数学家的眼光来看,找素勾股数是一件很困难的事,更不用说全部勾股数的序列表了。
2002年,本人找到了一种极其初等的方法。
初中学生即可做,可以将所有勾股数按照一定的顺序一个不漏地列出来,制作成表。
(当然,由于勾股数的无限多,只能列出一定范围内的)。
此成果获得中国管理科学研究院颁发的中国新时期人文科学优秀成果一等奖。
学校有了自己的网站,给我们广大师生建立了互相交流的平台。
自己多年的一点点积累,也很想与大家一起交流学习。
下面的正文力图深入浅出,另有勾股数序列表一并附上。
并指望有一天,看到有高手通过编程法打印出可观的勾股数序列表,学生人手一册。
真正让勾股定理走进普通人之中。
正文先找素勾股数,即勾a,股b,弦c三数互质(无公约数)的勾股数。
故约定:a<b<c . a² + b² = c²且a b c 互质。
因a² = (c-b) (c+b) ,突破口选在c-b上。
并记满足c-b=k的素勾股数为d k 勾股数。
(论文在后面将d k勾股数的倍数形成的勾股数叫做d k倍勾股数)以下将按照k的取值从小到大依次探求结论。
k=1时,a²=k(b+c)=b+c=2b+1.知a是大于1的奇数。
设a = 2m +1,则b = (a²-1) / 2 , c=b+1.m依次从1开始取值,即得到d1素勾股数序列如下:a b c 说明:1. a列从上到下依次多2 ,b列从上到下依次多加4 .3 4 55 12 13 2. 各列个位数五个数一循环。
7 24 259 40 41 3. 拟人法比喻,c为姐,b为弟,a 为妹。
勾股数规律的探究

勾股数的规律能够组成一个直角三角形的三边长的正整数,叫做勾股数。
如“勾三股四弦为五”(3,4,5)再如常见的(6,8,10)(5,12,13)、(7,24,25),熟记一些勾股数利于我们更快、更准的解决于直角三角形有关的实际问题。
下面就勾股数的三个正整数之间的规律进行探究:规律一:在勾股数(3,4,5)、(5,12,13)、(7,24,25)(9,40,41)中,我们发现由(3,4,5)有: 32=9=4+5由(5,12,13)有: 52=25=12+13由(7,24,25)有: 72=49=24+25由(9,40,41)有: 92=81=40+41.即在一组勾股数中,当最小边为奇数时,它的平方刚好等于另外两个连续的正整数之和。
其论证如下:数a为大于1的正数,则2a+1为奇数数,则有∵(2a+1)2=4a2+4a+1=(2a2+2a)+(2a2+2a+1)∴(2a +1)2+(2a 2+2a)2=(2a2+2a+1)2因此,我们把它推广到一般,从而可得出勾股数公式一:(2a+1,2a2+2a,2a2+2a+1)(a为正整数)或整理为:对于一个大于1的整奇数m,构成的勾股数为(m,,)规律二:在勾股数(6,8,10)、(8,15,17)、(10,24,26)中,我们发现由(6,8,10)有: 62=36=2×(8+10)由(8,15,17)有: 82=64=2×(15+17)由(10,24,26)有: 102=100=2×(24+26)即在一组勾股数中,当最小边为偶数时,它的平方刚好等于两个连续且相差为2的整数之和的二倍。
其论证如下:数a为大于1的正数,则2a为偶数,则有∵(2a)2=4a2=2[(a2-1)+(a2+1)]∴(2a)2+(a2-1)2=(a2+1)2(a≥2且a为正整数)因此,我们把它推广到一般,从而可得出勾股数公式二:(2a,a2-1,a2+1)(a≥2且a为正整数)或整理为:对于一个大于1的整偶数m,构成的勾股数为(m,,)。
九宫格中的勾股数理

九宫格中的勾股数理
九宫格是由九个格子组成的方形网格,它们被编号为1到9。
在数学中,勾股数是指满足勾股定理的三个正整数。
勾股定理是指在一个直角三角形中,斜边的平方等于另外两边平方和。
在九宫格中,可以构造出许多勾股数。
其中最常见的是3-4-5三元组,也就是说在九宫格中,如果将1、2、3编号为第一行,4、5、6编号为第二行,7、8、9编号为第三行,那么在同一行或同一列或同一对角线上取出任意三个数,如果它们的平方和等于另一个数的平方,那么这三个数就是一个勾股数。
例如,取出第一行的1、2、3,它们的平方和为14,而第二行的5的平方是25,所以1、2、3和5就是一个勾股数。
再例如,取出第一列的1、4、7,它们的平方和为66,而第三行的9的平方是81,所以1、4、7和9就是一个勾股数。
通过在九宫格中不断寻找勾股数,可以发现许多有趣的规律和性质。
例如,九宫格中可以构造出无穷多个勾股数,而且每个勾股数都可以被唯一地表示为不同三元组的平方和。
此外,九宫格中还存在着一些特殊的勾股数,如5-12-13和7-24-25等,它们在勾股数中起到了重要的作用。
因此,九宫格中的勾股数理具有很高的研究价值和教育意义,它不仅可以帮助学生深入理解勾股定理,还可以启发学生的数学思维和创新能力。
- 1 -。
勾股数的第n个规律公式

勾股数的第n个规律公式勾股数是指满足勾股定理的三个正整数(a,b,c),其中a和b是直角三角形的两条直角边,c是斜边。
勾股定理可以表示为a^2 + b^2 = c^2。
根据勾股定理的规律,我们可以推导出勾股数的一些特征和公式。
在这篇文章中,我们将探讨勾股数的第n个规律公式。
我们来看一下勾股数的前几个规律。
最简单的勾股数是(3, 4, 5),接下来是(5, 12, 13),然后是(8, 15, 17),(7, 24, 25),(9, 40, 41),以及(11, 60, 61)等等。
可以观察到,这些勾股数的斜边c都是一个奇数,并且a和b之间的差距逐渐增大。
我们可以通过数学推导来得出勾股数的第n个规律公式。
假设第n 个勾股数为(a, b, c),其中a和b都是奇数,c是一个奇数。
根据前面的观察,我们可以假设 a = 2m + 1,b = 2m + 2n + 1,c = 2m + 2n + 2,其中m和n都是非负整数。
根据勾股定理,我们可以得到(a, b, c)满足的条件:(2m + 1)^2 + (2m + 2n + 1)^2 = (2m + 2n + 2)^2。
将这个等式展开并化简,可以得到4n^2 + 4n + 1 = 4m(m + n + 1)。
进一步化简得到n(n + 1) = m(m + n + 1)。
通过观察我们可以发现,当m = n时,等式成立。
所以,第n个勾股数的规律公式可以表示为(a, b, c) = (2n + 1, 2n + 2n + 1, 2n + 2n + 2),其中n为非负整数。
通过这个规律公式,我们可以计算出任意一个勾股数。
例如,当n = 1时,我们可以得到(3, 4, 5);当n = 2时,我们可以得到(5, 12, 13);当n = 3时,我们可以得到(7, 24, 25)。
通过逐步增加n的值,我们可以计算出更多的勾股数。
勾股数的规律公式不仅可以用于计算勾股数,还可以用于解决一些几何问题。
100以内的勾股数规律整理
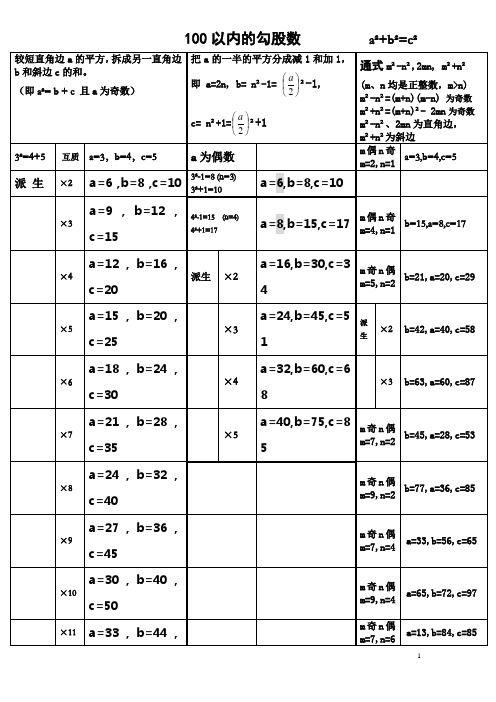
派 生
×2 ×3 ×4 ×5 ×6 ×7 ×8 ×9 ×10 ×11 ×12 ×13 ×14 ×15 ×16 ×17 ×18 ×19
a=6,b=8, a=6,b=8,c=10 a=9,b=12, a=9,b=12,c=15
3²-1=8 (n=3) 3²+1=10
(n=4 4²-1=15 (n=4) 4²+1=17 +1=17
生
a=32,b=60, a=32,b=60,c=68 32,b=60 a=40,b=75, a=40,b=75,c=85 40,b=75
m奇n偶 b=45,a=28,c=53 45,a=28,c= b=45,a=28,c=53 m=7,n=2 m奇n偶 77,a=36,c= ,a=36,c=85 b=77,a=36,c=85 m=9,n=2 m奇n偶 a=33,b=56,c=65 33,b=56,c= a=33,b=56,c=65 m=7,n=4 m奇n偶 a=65,b=72,c=97 65,b=72,c= a=65,b=72,c=97 m=9,n=4 m奇n偶 a=13,b=84,c=85 13,b=84,c= a=13,b=84,c=85 m=7,n=6 奇数±奇数= ∵奇数±奇数=偶数 偶数±偶数= 偶数±偶数=偶数 奇数±偶数= 奇数±偶数=奇数 奇数×偶数= 奇数×偶数=偶数 奇数×奇数= 奇数×奇数=奇数 又∵ =(m+n)² 斜边 m²+n²=(m+n)²- 2mn 直角边 2mn 为偶数 =(m+n)(m直角边 m²-n²=(m+n)(m-n) 三边不能同偶 同偶基本勾 同偶, 三边不能 同偶 , 同偶基本勾 股数就不互质了 就不互质了, 股数就不互质了, m+n≠ 即 m+n≠偶数 不能同奇数、不能同偶 ∴m、n 不能同奇数、不能同偶 ∴m、n 为一奇一偶
勾股数的规律

所谓勾股数,就是当组成一个直角三角形的三边长都为正整数时,我们就称这一组数为勾股数;
那么,组成一组勾股数的三个正整数之间,是否具有一定的规律可寻呢下面我们一起来观察几组勾股数:
规律一:在勾股数3,4,5、5,12,13、7,24,259,40,41中,我们发现
由3,4,5有:32=9=4+5
由5,12,13有:52=25=12+13
由7,24,25有:72=49=24+25
由9,40,41有:92=81=40+41.
即在一组勾股数中,当最小边为奇数时,它的平方刚好等于另外两个连续的正整数之和;因此,我们把它推广到一般,从而可得出以下公式:
∵2n+12=4n2+4n+1=2n2+2n+2n2+2n+1
∴2n+12+2n2+2n2=2n2+2n+12n为正整数
勾股数公式一:2n+1,2n2+2n,2n2+2n+1n为正整数
规律二:在勾股数6,8,10、8,15,17、10,24,26中,我们发现
由6,8,10有:62=36=2×8+10
由8,15,17有:82=64=2×15+17
由10,24,26有:102=100=2×24+26
即在一组勾股数中,当最小边为偶数时,它的平方刚好等于两个连续整数之和的二倍,推广到一般,从而可得出另一公式:∵2n2=4n2=2n2-1+n2+1
∴2n2+n2-12=n2+12n≥2且n为正整数
勾股数公式二:2n,n2-1,n2+1n≥2且n为正整数
利用以上两个公式,我们可以快速写出各组勾股数;。
100以内的勾股数

100以内的勾股数100以内的勾股数:i=3 j=4 k=5i=5 j=12 k=13i=6 j=8 k=10i=7 j=24 k=25i=8 j=15 k=17i=9 j=12 k=15i=9 j=40 k=41i=10 j=24 k=26i=11 j=60 k=61i=12 j=16 k=20i=12 j=35 k=37i=13 j=84 k=85i=14 j=48 k=50i=15 j=20 k=25i=15 j=36 k=39i=16 j=30 k=34i=16 j=63 k=65i=18 j=24 k=30i=18 j=80 k=82i=20 j=21 k=29i=20 j=48 k=52i=21 j=28 k=35i=21 j=72 k=75i=24 j=32 k=40i=24 j=45 k=51i=24 j=70 k=74i=25 j=60 k=65i=27 j=36 k=45i=28 j=45 k=53i=30 j=40 k=50i=30 j=72 k=78i=32 j=60 k=68i=33 j=44 k=55i=33 j=56 k=65i=35 j=84 k=91i=36 j=48 k=60i=36 j=77 k=85这是最经典的一个套路,而且由于两个连续自然数必然互质,所以用这个套路得到的勾股数组全部都是互质的。
2、当a为大于4的偶数2n时,b=n2-1, c=n2+1也就是把a的一半的平方分别减1和加1,例如:n=3时(a,b,c)=(6,8,10)n=4时(a,b,c)=(8,15,17)n=5时(a,b,c)=(10,24,26)n=6时(a,b,c)=(12,35,37)... ...这是次经典的套路,当n为奇数时由于(a,b,c)是三个偶数,所以该勾股数组必然不是互质的;而n为偶数时由于b、c是两个连续奇数必然互质,所以该勾股数组互质。
所以如果你只想得到互质的数组,这条可以改成,对于a=4n (n>= 2), b=4*n^2-1, c=4*n^2+1,例如:n=2时(a,b,c)=(8,15,17)n=3时(a,b,c)=(12,35,37)n=4时(a,b,c)=(16,63,65)... ...========Edward补充========对于N 为质因数比较多的和数时还可以参照其质因数进行取相应的勾股数补充,即1个N会有多对的勾股数,例如:n=9时(a,b,c)=(9,24,25)or (9,12,15) --------3* (3,4,5)n=12时(a,b,c)= (12,35,37) or (12,16,20) ----- 4*(3,4,5)=========ShangJingbo补充=======还有诸如此类的勾股数,20、21、29;119、120、169;696、697、985;4059、4060、5741;23660、23661、33461;137903 137904 195025803760 803761 11366894684659 4684660 6625109常见的几种通式:(1) (3,4,5), (6,8,10)… …3n,4n,5n (n是正整数)第3 / 4页(2) (5,12,13),(7,24,25), (9,40,41)… …2n +1, 2n^2 +2n, 2n^2 +2n +1 (n是正整数)(3) (8,15,17), (12,35,37) … …2^2*(n+1),[2(n+1)]^2-1,[2(n+1)]^2+1 (n是正整数)(4)m^2-n^2,2mn,m^2+n^2 (m、n均是正整数,m>n)观察分析上述的勾股数,可看出它们具有下列二个特点:1、直角三角形短直角边为奇数,另一条直角边与斜边是两个连续自然数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股数序列山东定陶一中刘述省序言两千多年前,中国人和希腊人发现了勾股定理,当是数学史上的伟大创举。
a=2mn,b=m2-n2,c=m2+n2 则是近代中国人在数论领域的又一重大成就,它将勾股数的一般求法表述得如此简捷。
然而迄今为止,未见一个具体详细的勾股数序列表。
这是因为,用现代数学家的眼光来看,找素勾股数是一件很困难的事,更不用说全部勾股数的序列表了。
2002年,本人找到了一种极其初等的方法。
初中学生即可做,可以将所有勾股数按照一定的顺序一个不漏地列出来,制作成表。
(当然,由于勾股数的无限多,只能列出一定范围内的)。
此成果获得中国管理科学研究院颁发的中国新时期人文科学优秀成果一等奖。
学校有了自己的网站,给我们广大师生建立了互相交流的平台。
自己多年的一点点积累,也很想与大家一起交流学习。
下面的正文力图深入浅出,另有勾股数序列表一并附上。
并指望有一天,看到有高手通过编程法打印出可观的勾股数序列表,学生人手一册。
真正让勾股定理走进普通人之中。
正文先找素勾股数,即勾a,股b,弦c三数互质(无公约数)的勾股数。
故约定:a<b<c . a2 + b2 = c2且a b c 互质。
因a2 = (c-b) (c+b) ,突破口选在c-b上。
并记满足c-b=k的素勾股数为d k 勾股数。
(论文在后面将d k勾股数的倍数形成的勾股数叫做d k倍勾股数)以下将按照k的取值从小到大依次探求结论。
k=1时,a2=k(b+c)=b+c=2b+1.知a是大于1的奇数。
设a = 2m +1,则b = (a2 -1) / 2 , c=b+1.m依次从1开始取值,即得到d1素勾股数序列如下:a b c 说明:1. a列从上到下依次多2 ,b列从上到下依次多加4 .3 4 55 12 13 2. 各列个位数五个数一循环。
7 24 259 40 41 3. 拟人法比喻,c为姐,b为弟,a为妹。
可编口诀如下:11 60 6113 84 85 妹妹方一方,姐弟和相当;15 112 11317 144 145 姐大弟一年,三人勾股弦。
19 180 181.。
k=2时,a2=2(b+c)=2(2b+2)=4(b+1).设a=2m,则b=m2-1,c=b+2.得出通项公式后,还要注意考虑两点。
第一,要保证a b c 互质。
这里a 已经确定是偶数,b 就不能再是偶数,所以知m 是偶数。
第二,要保证b >a 。
这里换算为m2 —1 >2m 。
得到m >1+2。
以上两点结合起来,就确定了m 的取值。
m为大于等于4的偶数。
m从4开始依次取偶数,即得到d2素勾股数序列如下:a b c8 15 17 说明:1. a列从上到下依次多4 , b 列从上到下依次多加8.12 35 3716 63 65 2. 各列个位数五个数一循环。
20 99 10124 143 145 3. b 比m 2 少1 ,c 比m 2 多1 .28 195 19732 255 25736 323 32540 399 401.。
k =3时,d3素勾股数不存在。
因为如果k=3,则a b c 有公约数3. 推导如下:若a2 = 3(2b+3),则a中有3因子,设a =3m,则b =(3m2-3)/2, b 中也有3因子,c = b + 3 自然也有3因子。
于是a b c 有公约数3. 于之前的约定a b c 是素勾股数相矛盾,故知d3 素勾股数不存在仿照上面的方法很容易推导出,k取4,5,6,7时,相应的d4,d5,d6,d7素勾股数均不存在。
k = 8时, a 2 = 8 (2 b + 8) = 16 (b + 4) . 设a = 4 m , 则b = m2 -4,c=b+8.仍然注意考虑两点:第一,保证abc互质,知m为奇数.第二,保证b>a,即解m2-4>4m,得m>2(1+2).所以m从5开始依次取奇数,就得到d8素勾股数序列如下:abc20 21 29 说明:1. a 列从上到下依次多8 ,b 列从上到下依次多加8 .28 45 5336 77 85 2. 各列个位数五个数一循环。
44 117 12552 165 173 3. b 比m 2 少4 ,c 比m 2 多4 .60 221 22968 285 29376 357 36584 437 445.。
k=9时,a2=9(2b+9).设a=3m,b=(m2-9)/2,c=b+9.仍要考虑两点:第一,保证abc互质。
即b中不含3因子且b是正整数,故知m为奇数且不含3因子。
第二,保证b>a ,即解m2-9>6m.得m>3(1+2).所以m依次取大于等于9的奇数同时还要去掉3的倍数.就得到d9素勾股数序列如下: abc33 56 65 说明:1. a 列从上到下本来应该依次多6,由于隔两行去掉了m 是3的倍数那一行,39 80 89 所以依次多6,12,6,12 。
b 列的规律也因此而变。
57 176 18569 260 269 2. 各列个位数五个数一循环也随之而变。
75 308 31787 416 425 3. b 的2倍 比 m 2 少9 ,c 的2 倍比 m 2 多 9 .93 476 485。
由于k 取10,11,12,13,14,15,16,17均不能保证a b c 的互质性,所以d10一直到d17素勾股数都不存在。
推导方法与d3的推导方法类似,不再 赘述。
k =18时,读者可以自己推导d18素勾股数的通项公式了吧?a =6m,b=m2-9,c=b+18.其中m从8开始取不含3因子的偶数。
k从19到24.又不存在相应的素勾股数序列了。
至此,本文最关键的问题已经显现,首先需要解决k 的取值要求,以确保dk 素勾股数存在;其次要解决dk 素勾股数的一般求法。
定理1 当k 中含有偶数个偶素数因子时,dk 素勾股数不存在。
证明:设k =n 22m . (m 中不含2因子, n 为正整数), 则由a2=k(2b+k)=n 22m(2b+n 22m),设a=n 2t,t2=2m(b+122 n m)。
知t 为偶数,再设t=2s,s2=m(b/2+-2n 22m).从而知b 也必须是偶数。
c 是偶数。
a b c不互质。
故dk 素勾股数不存在。
定理2 当k 中含有奇数个某奇素数因子时,dk 素勾股数不存在。
证明:设k= 2n-1pm .(m中不含p因子,p是奇素数,n为正整数),则由a2=k(2b+k)=2n-1pm(2b+2n-1pm),可设a=npt得到 t2=m(2b+2n-1pm)/p,从而b 中含有p 因子,a b c 有公因子p . 不互质, 故dk 素勾股数不存在.以上两个定理说明了:k 可以取1,另外k 只能取2的奇数次方,取3,5,7,11等奇素数的偶次方,以及它们之间的乘积。
在不超过200的k 的可取值共有17个。
它们是1,2,8,9,18,25,32,49,50,72,81,98,121,128,162,169,200.再表述的具体严谨些:k 的取值中若有2因子,只能有奇数个2因子;若有奇素数因子,只能有偶数个某奇素数因子。
例如32,25,23*2,2435*3*2.由于k=1时通项已经给出 ,下面分三种具体情况给出知k 的值如何求dk 素勾股数的公式。
第一种情况:k =122-n (n 为正整数)时,由a2 = k (2b + k) =122-n (2b+122-n )=n 22 (b +222-n ),可设 a =n 2 m ,则 b = m 2 - 222-n ,c=b+k=b+122-n .公式已经给出,在具体取值中要注意两点:第一,要保证abc互质,因为a 是偶数,而b 与c 同奇偶,故要求b 不能为偶数,即m 2 -222-n不能为偶数。
可知 n = 1 时,m 取偶数。
n >1 时,m 取奇数。
第二,要保证b > a ,即m 2 -222-n >n 2 m ,解得 m >1n 2-(1 +2).第二种情况:k = p 2 (p 是大于1的奇数 )时,由a 2 = k ( 2 b + k )= p 2 ( 2 b + p 2 ),可设a = p m ,则b = ( m 2 -p2)/ 2 , c = b +p 2 . 公式已经给出,在具体取值中要注意两点:第一,要保证abc互质, 因为a 中含有p 的所有因子,c 与b 之差是p 2,故要求b 中不能含有p 的任何素因子,进而知m 首先是奇数,其次m 中也不能含有p 的任何素因子。
第二,要保证b > a ,即 m 2 -p2> 2 p m ,解得 m > p (1 +2).第三种情况:k =122-n p 2 (n 为正整数, p 为大于1 的奇数)时, 由a2 = k (2b + k) =122-n p 2(2b+122-n p 2)=n22p 2 (b +222-n p 2 ), 可设 a =n 2p m ,则 b = m 2 - 222-n p 2 ,c=b+k=b+122-n p 2 .公式已经给出,在具体取值中要注意两点:第一,要保证abc互质,因为a 是偶数,且a中含有p 的所有因子,c 与b 之差是122-n p 2,故要求b 不能为偶数,并且要求b 中不能含有p 的任何素因子, 进而知首先当n = 1 时m 是偶数,当n >1时m 是奇数,其次m 中也不能含有p 的任何素因子。
第二,要保证b > a ,即m 2 -222-n p 2 >n 2p m ,解得 m >p n 12-(1 +2).好了! 问题已经圆满解决,可以轻松一下试一试了。
例如 k=200=235*2仿照上面第三种情况可知,设a = 20 m ,b = m 2 -100 ,c=b+200 . m 取奇数并且不能取5的倍数。
又有m >10 (1 +2),于是m 可以依次取值 27, 29 , 31, 33 , 37, 39 ,41, 43 ,47,……….(记住一定要将5的倍数的奇数去掉) ,分别带入上面的公式,就得到了d200素勾股数序列了。
( 第一组数是 540 629 829 并且a 列至少递进40 才到下一组数)尾 声最后的工作是如何制作一个勾股数序列表。
首先规定:排列顺序以a 的从小到大排列,a 相同时以b 的从小到大排列。
a<b<c ,a2+b2=c2 .其次由于勾股数是无限的,故列表应选择一个适当的范围。
下面就a 不超过100的勾股数序列表的制作过程说明如下。
第一步,先将范围内的所有素勾股数全部列出来 ,即d1 ,d2 ,d8 ,d9 ,d18 ,d25 ,d32 素勾股数满足a≤100的全部列出。
第二步,再将范围内的所有素勾股数的倍数形成的新勾股数满足a≤100的全部列出。
第三步,将以上所有勾股数按照规定的顺序排列出来,就得到了符合你所选范围内的一个不漏的勾股数序列表。
