2017级广西大学硕士研究生弹性力学试卷

弹性力学历届考试试题

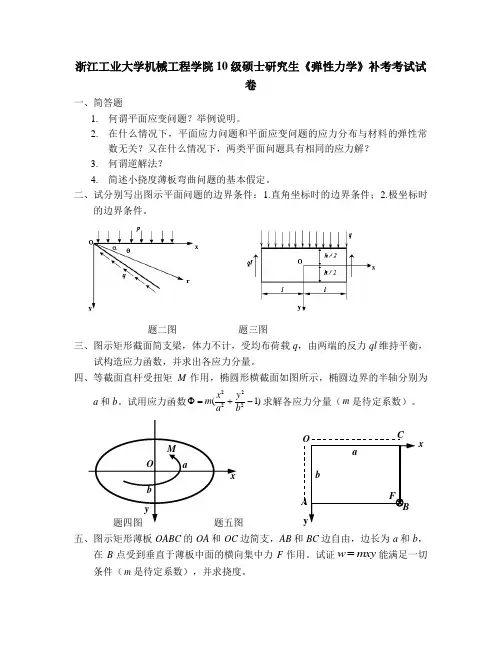
卷一、简答题1. 何谓平面应变问题？举例说明。

2. 在什么情况下，平面应力问题和平面应变问题的应力分布与材料的弹性常数无关？又在什么情况下，两类平面问题具有相同的应力解？ 3. 何谓逆解法？4. 简述小挠度薄板弯曲问题的基本假定。

二、试分别写出图示平面问题的边界条件：1.直角坐标时的边界条件；2.极坐标时的边界条件。

题二图题三图三、图示矩形截面简支梁，体力不计，受均布荷载q ，由两端的反力ql 维持平衡，试构造应力函数，并求出各应力分量。

四、等截面直杆受扭矩M 作用，椭圆形横截面如图所示，椭圆边界的半轴分别为a 和b 。

试用应力函数2222(1)x y m a bΦ=+-求解各应力分量（m 是待定系数）。

五、图示矩形薄板OABC 的OA 和OC 边简支，AB 和BC 边自由，边长为a 和b ，在B 点受到垂直于薄板中面的横向集中力F 作用。

试证w mxy =能满足一切条件（m 是待定系数），并求挠度。

OA CxOA Cx卷六、简答题5. 何谓平面应力问题？举例说明。

6. 何谓轴对称问题？举例说明。

7. 何谓半逆解法？8. 何谓圣维南原理？圣维南解的价值何在？七、设Airy 应力函数为3cx =Φ，其中c 为常数。

试在图中绘出边界上的面力。

题二图题三图八、设有矩形截面的长梁，其长度为l ，深度为h ，宽度为b ，三者之间的关系为b h l >>>>。

在两端的集中力偶M 作用下（不计体力），梁发生纯弯曲变形。

试用Airy 应力函数求解应力分量。

九、等截面直杆的椭圆形横截面如图所示，椭圆边界的半轴分别为a 和b 。

试用应力函数2222(1)x y m a bΦ=+-求解各应力分量（m 是待定系数）。

十、图示矩形薄板OABC 的OA 和OC 边简支，AB 和BC 边自由，边长为a 和b ，在B 点受到垂直于薄板中面的横向集中力F 作用。

试证w m xy =能满足一切xx 条件（m 是待定系数），并求挠度。

硕士研究生入学考试弹性力学试题

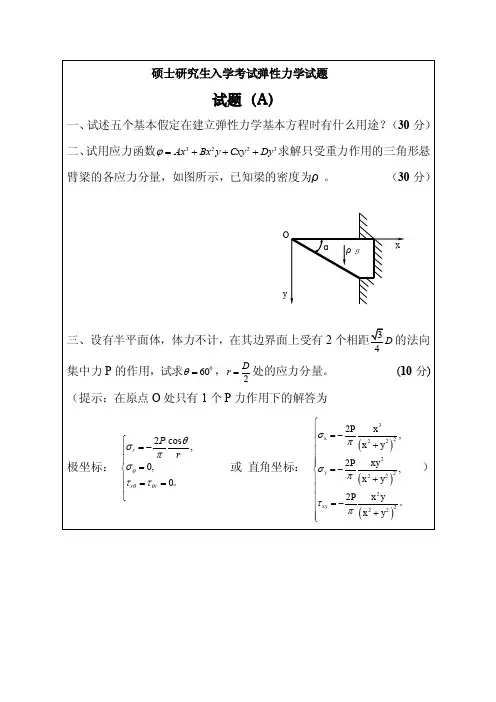
（50 分）
1、悬臂梁在端部受集中力
M、F，上面受有分布载荷 q0
l x
，下面受有均布剪力 0
；
2、楔形体在一面受有均布压力 q 和楔顶受有一集中载荷 P 的作用。
y
o
P
q
r
x
三、试推导出按位移求解弹性力学问题时所用的基本微分方程（Lame 方程）。（30 分）四、在已知扭矩 M 的作用下，半径为 a 的圆截面扭杆，有半径为 b 的圆弧槽，取坐
硕士研究生入学考试弹性力学试题
试题（A）
一、试述五个基本假定在建立弹性力学基本方程时有什么用途？（30 分）
二、试用应力函数 Ax3 Bx2 y Cxy2 Dy3 求解只受重力作用的三角形悬
臂梁的各应力分量，如图所示，已知梁的密度为ρ 。
（30 分）
O
α ρɡ
x
y
三、设有半平面体，体力不计，在其边界面上受有 2 个相距 3 D 的法向
y q
O q
α /2
α /2
x
2、矩形薄板，三边固定，一边受有均布压力 q
q
x o
b a
b a
y
（40 分）
试题（B）
一、如图所示为平面应力状态下的细长薄板条，上下边界受均布力 q 的作用，其余边
界上均无面力作用，试说明 A，B，C 点处的应力状态。 q
（20 分）
C o
B y
q
A
x
二、试给出如图所示平面应力问题的定解条件
a
a
a
O
x
a
ρg
y
4
集中力 P 的作用，试求 600 ，r D 处的应力分量。
2
(10 分)

弹性力学考研试题及答案

弹性力学考研试题及答案1. 弹性力学基本概念- 弹性力学是研究物体在外力作用下发生形变，当外力消失后物体能否恢复原状的学科。

2. 弹性力学的基本原理- 胡克定律：在弹性限度内，物体的形变与外力成正比。

- 弹性模量：描述材料抵抗形变的能力。

3. 弹性力学的数学描述- 应力：单位面积上的内力。

- 应变：物体形变的程度。

- 应力-应变关系：描述应力与应变之间的数学关系。

4. 弹性力学的分类- 线弹性：应力与应变成正比。

- 非线性弹性：应力与应变不成正比。

5. 弹性力学的应用- 结构工程：预测和设计结构的承载能力。

- 材料科学：研究材料的力学性质。

6. 弹性力学的计算方法- 有限元分析：通过数值方法求解弹性力学问题。

- 能量法：利用能量原理求解弹性力学问题。

7. 弹性力学的实验方法- 拉伸试验：测量材料的弹性模量。

- 压缩试验：测量材料的抗压能力。

8. 弹性力学的典型问题- 梁的弯曲：分析梁在弯曲力作用下的应力和应变分布。

- 薄壳理论：研究薄壳结构在外力作用下的变形。

9. 弹性力学的前沿研究- 智能材料：研究具有自适应能力的新型材料。

- 纳米力学：研究纳米尺度下的力学行为。

答案1. 弹性力学基本概念- 正确。

2. 弹性力学的基本原理- 正确。

3. 弹性力学的数学描述- 正确。

4. 弹性力学的分类- 正确。

5. 弹性力学的应用- 正确。

6. 弹性力学的计算方法- 正确。

7. 弹性力学的实验方法- 正确。

8. 弹性力学的典型问题 - 正确。

9. 弹性力学的前沿研究 - 正确。

弹性力学试题

西安电子科技大学
研究生课程考试试题
考试科目：课程编号：
考试日期：年月日考试时间：120 分考试方式：(闭卷) 任课教师：班号
学生姓名：学号：
概念题（30分，每题6分）
1．试叙述弹性力学的基本假定及这些基本假定在建立弹性力学基本方程时的作用。

2．何为一点的应力、应变状态？为什么可以用应力分量、应变分量来表示一点的应力、应变状态？
3. 叙述平面应力和平面应变问题在结构形状、所受外力、应力、应变等方面有何特
点？
4．简述圣维南原理,并说明圣维南原理在弹性力学中的作用及使用时注意要点。

5．写出按位移求解空间轴对称问题的基本方程及求解步骤。

计算题（70分）
1．题1图示构件，试写出其应力边界条件。

（15分）
题1图
O
2．如题1图示，楔形体在两侧受有均布剪应力q ，如图所示。

试求其应力分量。

（20
分）
3．如下图所示之悬臂梁，在端部受集中力P 作用，试用应力函数33cy Bxy Axy ++=ϕ ，求其应力分量（不计体力）。

（20分）
题3图
4．如题4图示，设圆筒从某一均匀温度加热，内面（a r =）增温a T ，外面（b r =）0=∂θ），求稳定后（0=∂∂t T ）圆增温b T ，无热源（0=W ，绝热温升率：筒内的热应力。

（15分）
题4图。

广西大学考研真题材料力学模拟

广西大学考研真题材料力学模拟----e901a290-715d-11ec-9153-7cb59b590d7d材料力学模拟卷一如果任何图形对正交坐标轴的惯性积为零，那么这对坐标轴就是。

a形心轴；b对称轴；c主惯性轴；d形心主惯性轴。

直径为D=16cm的圆钢筋AB与B处的刚性折叠钢筋BCD铰接。

当D受到水平力P时，测量钢筋AB的线应变ε=9×10^-4。

已知钢的弹性模量为e=210gpa。

试着找出（1）P力的大小。

（2）材料力学模拟第二卷d点的水平位移。

如果等效圆管在弹性范围内轴向拉伸，则外径和内径将变为。

① 外径和内径均增大；② 外径和内径均减小；③ 外径减小，内径增大；④ 外径增大，内径减小。

在下列说法中，________是正确的。

a、当悬臂梁只承受集中力时，梁内无弯矩；当悬臂梁只承受集中力偶时，梁中没有基础；c、当简支梁只承受集中力时，梁内无弯矩；d、当简支梁只承受集中力偶时，梁内吴剪力。

材料力学模拟第三卷图中应力圆a、b、c表示的应力状态非别为（）a、二向应力状态、纯剪切应力状态、三向应力状态；b、单向拉应力状态、单向压应力状态和三维应力状态；c、单向压应力状态、纯剪应力状态和单向拉应力状态；d、单向拉应力状态、单向压应力状态和纯剪应力状态。

t形截面铸铁梁，设各个截面的弯矩均为正值，则将其截面按图1-4______所示的方式不知，梁的强度最高。

薄壁圆管在扭转作用下的剪应力公式为（R为圆管的平均半径，t为壁厚）。

那就对了a、该剪应力公式可根据平衡关系到处；b、剪切应力公式可以从平衡、几何和物理条件中推导出来；c、剪应力公式符合“平面假设”；d、剪应力公式适用于T“R”的圆管。

a、a，c；b、a，d；c、b，c；d、a，b，c，d材料力学模拟第四卷轴向拉、压杆，由截面法求得同一截面的左、右两部分的轴力，则两轴力大小相等，而（）a、方向相同，符号相反b、方向相反，符号相同c、方向相同，符号相反d、方向相反，符号相反铸铁梁承受集中的电偶M。

研究生弹性力学考试模拟试题

主要研究弹性物体的应力、应变、位移等物理量之间的关系，以及物体在外力作用下的变是工程学科中的重要基础学科，广泛应用于土木工程、机械工程、航空航天等领域。
弹性力学的基本假设
物体是连续的
弹性力学认为物体是由连续分布的物质组成，没有原子或分
子的离散性。
物体是线性的
CHAPTER 03
弹性力学中的应变分析
应变状态与几何方程
应变状态
描述物体在受力后形状和尺寸的变化，包括线应变和角应变。
几何方程
描述应变与位移之间的关系，是弹性力学中的基本方程之一。
应变协调方程与相容性条件
应变协调方程
确保应变在物体内部连续变化，没有应变奇异点。
相容性条件
确保物体在不同点上的应变能够相互协调，满足整体连续性的要求。
题，可以更容易地求解该方程。在弹性力学中，变分法被广泛应用于求
解弹性体的应力、应变和位移等问题。
02
弹性力学中的变分方程
在弹性力学中，变分法将求解弹性体的应力、应变和位移的问题转化为
求解变分方程的问题。通过选择不同的变分条件和边界条件，可以得到
不同的变分方程。
03
变分法的应用范围
除了在弹性力学中应用外，变分法还广泛应用于其他领域，如流体力学
边界条件和初始条件
描述物体边界上的受力情况和初始状态。
CHAPTER 02
弹性力学中的应力分析
应力状态与平衡方程
总结词
理解应力状态与平衡方程是解决弹性力学问题的关键。
详细描述
应力状态描述了物体内部各点处应力的方向和大小，平衡方程则表达了物体内部各点应力的平衡关系。通过平衡方程，我们可以求解出物体内部的应力分布。
中，需要考虑边界条件和载荷条件，并采用适当的数值方法进行求解。

弹性力学试卷2017上学期答案及评分标准

2016-2017第二学期弹性力学考试答案及评分标准概念问答题1、以应力作未知量，应满足什么方程及什么边界条件？答：以应力作为未知量应满足平衡微分方程、相容方程及边界条件。

2、平面问题的未知量有哪些？方程有哪些？答：平面问题有X、y、xy、x、y、xy、U、V八个，方程有两个平衡方程,个几何方程，三个物理方程。

（5分）3、已知x200Pa ，y100Pa，xy50Pa 及r100Pa，100Pa，试分别在图中所示单元体画出应力状态图4、简述圣维南原理答:如果把物体的一小部分边界上的面力，变换为分布不同但静力等效的面力（主矢量相同，对同一点的主矩也相同），那么，近处的应力分量将有显著的改变，但远处所受的影响可以不计。

（5分）5、简述应变协调方程的物理意义。

答：⑴形变协调条件是位移连续性的必然结果。

连续体一位移连续-几何方程一形变协调条件。

（2分）⑵形变协调条件是与形变对应的位移存在且连续的必要条件。

形变协调一对应的位移存在一位移必然连续；形变不协调—对应的位移不存在—不是物体实际存在的形变—微分体变形后不保持连续。

（3分）&刚体位移相应于什么应变状态。

答：刚体位移相应于零应变状态，对平面问题为x= y= xy=0 （5 分）7、简述最小势能原理，该原理等价于弹性力学的哪些基本方程？答：由位移变分方程可得（2分）（5 分）300Pa，Xu Yv Zw dxdydz Xu Yv Zw dS 0 或Xu Yv Zw dxdydz Xu Yv Zw dS其中为物体得总势能（形变势能和外力势能在之和）， 0称为最小势能原理，它表明物体处于平衡位置时，总势能的一阶变分为零。

可以证明：在线弹性体中，2 0，即在所有几何可能的位移中，实际的位移使总势能取最小值。

最小势能原理等价于平衡微分方程和静力边界条件。

（5分）、已知下述应变状态是物体变形时产生的，试求各系数之间应满足的关系（ 5分）x A 0 A （X 2y 2） 4 4 x yyB 0 Bdx 2 y 2） 44x yxyCGxy （x 2 y 2C2）应变分量存在的必要条件是满足形变相容条件，即为固定边界。

弹性力学考研试题及答案

弹性力学考研试题及答案试题：弹性力学考研模拟试题一、选择题（每题3分，共30分）1. 在弹性力学中，下列哪一项不是胡克定律的假设条件？A. 材料是连续的B. 材料是各向同性的C. 材料是完全弹性的D. 材料是各向异性的答案：D2. 弹性模量E和泊松比ν之间的关系可以表示为：A. E = 2G(1 + ν)B. E = 3K(1 - 2ν)C. E = 3K(1 + ν)D. E = 2G(1 - ν)答案：A3. 在平面应力问题中，最大剪切应力的方向与σx和σy的方向夹角为：A. 45°B. 22.5°C. 0°D. 90°答案：A4. 根据圣维南原理，对于一个弹性体，远离力作用区域的内部应力分布主要取决于：A. 体力B. 面力C. 边界条件D. 材料的弹性常数答案：C5. 在弹性力学中，拉梅常数λ和μ分别代表：A. 第一拉梅常数和第二拉梅常数B. 体积模量和剪切模量C. 泊松比和弹性模量D. 应力和应变的关系常数答案：A6. 对于一个理想的弹性体，其应力-应变关系是：A. 线性的B. 非线性的C. 时间依赖的D. 温度依赖的答案：A7. 在弹性力学中，平面应变问题通常指的是：A. 只有x方向的应变B. 只有y方向的应变C. 垂直于平面方向的位移为零D. 水平面方向的位移为零答案：C8. 根据弹性力学，下列哪一项不是弹性体的边界条件？A. 位移边界条件B. 应力边界条件C. 混合边界条件D. 速度边界条件答案：D9. 在弹性力学中，下列哪一项不是应力函数？A. Airy应力函数B. 位移函数C. 温度场D. 势能函数答案：B10. 在三维弹性力学问题中，位移矢量可以表示为：A. u = ∇ψ + ∇×γB. u = ∇ψ - ∇×γC. u = ∇×ψ + ∇γD. u = ∇×ψ - ∇γ答案：A二、简答题（每题10分，共20分）11. 简述弹性力学中的平面应力和平面应变问题的区别。

弹性力学试题及答案

《弹性力学》试题参考答案（答题时间：100分钟）一、填空题（每小题4分）1．最小势能原理等价于弹性力学基本方程中：平衡微分方程，应力边界条件。

2．一组可能的应力分量应满足：平衡微分方程，相容方程（变形协调条件）。

3．等截面直杆扭转问题中， M dxdy D=⎰⎰2ϕ的物理意义是杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M 。

4．平面问题的应力函数解法中，Airy 应力函数ϕ在边界上值的物理意义为边界上某一点（基准点）到任一点外力的矩。

5．弹性力学平衡微分方程、几何方程的张量表示为：0,=+i j ij X σ ，)(21,,i j j i ij u u +=ε。

二、简述题（每小题6分）1．试简述力学中的圣维南原理，并说明它在弹性力学分析中的作用。

圣维南原理：如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力（主矢与主矩相同），则近处的应力分布将有显著的改变，但远处的应力所受影响可以忽略不计。

作用：（1）将次要边界上复杂的面力（集中力、集中力偶等）作分布的面力代替。

（2）将次要的位移边界条件转化为应力边界条件处理。

2．图示两楔形体，试分别用直角坐标和极坐标写出其应力函数ϕ的分离变量形式。

题二（2）图（a ）⎩⎨⎧=++= )(),(),(222θθϕϕf r r cy bxy ax y x （b ）⎩⎨⎧=+++=)(),(),(33223θθϕϕf r r dy cxy y bx ax y x 3．图示矩形弹性薄板，沿对角线方向作用一对拉力P ，板的几何尺寸如图，材料的弹性模量E 、泊松比已知。

试求薄板面积的改变量S ∆。

题二（3）图设当各边界受均布压力q 时，两力作用点的相对位移为l ∆。

由q E)1(1με-=得，)1(2222με-+=+=∆Eb a q b a l设板在力P 作用下的面积改变为S ∆，由功的互等定理有：l P S q ∆⋅=∆⋅将l ∆代入得：221b a P ES +-=∆μ显然，S ∆与板的形状无关，仅与E 、μ、l 有关。

广西大学材料力学试题及答案完整版

2010～2011年广西大学材料力学考试试卷及答案一、判断题（正确打“√”，错误打“X ”，本题满分为10分）1、拉杆伸长后，横向会缩短，这是因为杆有横向应力的存在。

( )2、圆截面杆件受扭时，横截面上的最大切应力发生在横截面离圆心最远处。

( )3、两梁的跨度、承受载荷及支承相同，但材料和横截面面积不同，因而两梁的剪力图和弯矩图不一定相同。

( )4、交变应力是指构件内的应力，它随时间作周期性变化，而作用在构件上的载荷可能是动载荷，也可能是静载荷。

( )5、弹性体的应变能与加载次序无关，只与载荷的最终值有关。

（）6、单元体上最大切应力作用面上必无正应力。

( )7、平行移轴公式表示图形对任意两个相互平行轴的惯性矩和惯性积之间的关系。

（） 8、动载荷作用下，构件内的动应力与材料的弹性模量有关。

( )9、构件由突加载荷所引起的应力，是由相应的静载荷所引起应力的两倍。

( ) 10、包围一个点一定有一个单元体，该单元体各个面上只有正应力而无切应力。

( )二、选择题（每个2分，本题满分16分）1．应用拉压正应力公式AF N=σ的条件是（）。

A 、应力小于比例极限； B 、外力的合力沿杆轴线； C 、应力小于弹性极限；D 、应力小于屈服极限。

2．梁拟用图示两种方式搁置，则两种情况下的最大弯曲正应力之比 )(m ax )(m axb a σσ 为（）。

A 、1/4； B 、1/16； C 、1/64； D 、163、关于弹性体受力后某一方向的应力与应变关系有如下论述：正确的是。

A 、有应力一定有应变，有应变不一定有应力； B 、有应力不一定有应变，有应变不一定有应力； C 、有应力不一定有应变，有应变一定有应力；(a) (b)D 、有应力一定有应变，有应变一定有应力。

4、火车运动时，其轮轴横截面边缘上危险点的应力有四种说法，正确的是。

A ：脉动循环应力： B ：非对称的循环应力； C ：不变的弯曲应力；D ：对称循环应力5、如图所示的铸铁制悬臂梁受集中力F 作用，其合理的截面形状应为图（）6、对钢制圆轴作扭转校核时，发现强度和刚度均比规定的要求低了20%，若安全因数不变，改用屈服极限提高了30%的钢材，则圆轴的（） A 、强度、刚度均足够；B 、强度不够，刚度足够； C 、强度足够，刚度不够；D 、强度、刚度均不够。

弹性力学2016期末考试B1

西南交通大学研究生2016－2017学年第(一)学期考试试卷B课程代码 51212001 课程名称弹性力学考试时间 120 分钟题号一二三四五总成绩得分阅卷教师签字：一、（20分）概念题1. 等直杆受到扭矩作用时，最大剪应力一般发生在距截面形心最远处的边界上，此话对吗？为什么？（5分）2．试述简述圣维南原理的基本概念。

（5分）3．平面应力问题和平面应变问题的几何特点、受力特点特征和应力特点是什么？（5分） 4．下列平面问题，要使应变分量：（5分）22441224412212()()()()()0x y xy z yz xz A x y x y B x y x y C xy x y C εεγεγγ=+++=+++=++===成为一种可能的应变状态，试确定各常数之间的关系。

二、（20分）矩形截面柱（密度为ρ）的侧面作用着均布剪力q ，如图所示，试求应力分量。

（提示：设0x σ=）第二题院系学号姓名密封装订线密封装订线密封装订线三、（20分）图示楔形体两侧受均布力q 作用，不计体力，试检验)2sin 2cos (2D C B A r +++=θθθϕ能否作为应力函数，如能，求出应力分量。

四、（20分）已知某点的应力张量为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=00000)(ττττσij试确定该点处主应力和最大剪应力值。

五、（20分）带半圆形槽的圆轴是机械中采用半圆键联接的一种传动轴的结构形式，其横截面形状如图所示，圆轴的半径为a ，槽的半径为b 。

，圆槽的方程为0),(221=-=b r r f θ，圆轴的方程为，0cos 2),(2=-=θθa r r f ，若单位长度扭转角为α，试确定的最大剪应力。

（提示：应力函数为)cos 2cos 2(22221θθΦrab ar b r A r f f A +--==）第五题图第三题图。

2017年广西桂林电子科技大学工程力学考研真题A卷

2017年广西桂林电子科技大学工程力学考研真题A 卷1. 如题1图所示，将两个相同的光滑圆柱放在矩形槽内，各圆柱的半径为r=200mm,重P 1=P 2=600N 。

试求接触点 A 、B 、C 的约束力。

(15分)题1图2. 如题2图所示,机构OABO 1在图示位置平衡。

已知OA=400mm,O 1B=600mm,作用在OA 上的力偶矩大小m N M e .11 。

试求力偶矩2e M 的大小和杆AB 所受的力。

各杆的重量及各处摩擦均不计。

（10分）题2图3. 试求题3图中1、2、3、4杆的内力。

（20分）CABm 1，r 1m 2，r 23题3图4. 如题4图，已知均质正方形板重P=100N ，在O 处用球形铰链固定在墙上，B 处用两活动铰支座支撑，通过绳CD 将板保持在水平位置。

试求绳CD 的拉力、支座O 和B 处的约束力。

（20分）题4图5. 两均质滑轮如题5图所示，在重物C 的作用下，轮A 与地面只滚不滑，求重物C 由静止开始下降高度h 时轮A 质心的加速度A a 。

（20分）题5图6. 一根等直圆杆如题6图所示，其直径为d=30mm.已知F=20kN,l =0.9m ，E=5101.2⨯MPa 。

试作轴力图，并求杆端D 的水平位移D ∆以及B 、C 两截面的相对纵向位移BC ∆。

（15分）题6图7. 题7图示一根两端固定的阶梯形圆轴。

它在截面突变处受一大小为e M 的外力偶作用。

若212d d =,试求固定端的约束力偶矩A M 和B M ，并作扭矩图。

（15分）题7图8.题8图所示双跨等截面连续梁。

（1）试求支座约束反力；（2）绘剪力图和弯矩图。

(20分)提示:跨中集中荷载F 作用下跨度为l 的简支梁跨中挠度为EI Fl 48/3题8图9.在一处于平面应力状态下的受力物体中，用三个相互成60o截面取出一个正三角形单元体，其受力状态如题图9所示.试求其主应力及其截面位置。

（15分）题9图。

《弹性力学》课程试卷(A)12级.doc

《弹性力学》课程试卷（A）本试卷用于2012年级土木工程专业本科学生（考试时量：120分钟总分:100分）其他注意事项：1、答案必须真写在答题纸上，填写在试卷上无效。

2、答案必须写明题目序号，并按题序号答题。

3、请保持行距，保持卷面整洁。

一、单项选择题（本大题共10小题，每小题2分，共20分）1、弹性力学建立的基本方程多是偏微分方程，还必须结合（）求解这些微分方程，以求得具体问题的应力、应变、位移。

A）相容方程B）近似方法C）边界条件D）附加假定2、根据圣维南原理，作用在物体一小部分边界上的力系可以用（）的力系代替，则仅在近处应力分布有改变，而在远处所受的影响可以不计。

A）几何等效B）静力等效C）平衡D）任意3、弹性力学平面问题的求解中，平面应力问题与平面应变问题的三类基本方程不完全相同，其比较关系为（）。

A）平衡方程、几何方程、物理方程完全相同B）平衡方程、几何方程相同，物理方程不同C）平衡方程、物理方程相同，几何方程不同D）平衡方程相同，物理方程、几何方程不同4、不计体力，在极坐标中按应力求解平面问题时，应力函数必须满足（）。

①区域内的相容方程；②边界上的应力边界条件；③满足变分方程；④如果为多连体，考虑多连体中的位移单值条件。

A）②④ B）②③④ C）①②③ D）①②③④5、函数= ax4 +bx2y2 +cy4如作力座力函数，各系数之间的关系是（LA）各系数叫取任意值B）b = -3（tz + c）C）b = a+ c D）G +/?+ C =06、已知一平而应变问题内某一点的正应力分量为：o; = 35MPa,= 25MPa, // 二0.3 则f 为多少（）。

A） 15MPa B） 18MPa C） 20MPa D） 22Mpa7、无体力情况下平面问题的应力分量如下，试判断以下两组应力分量可在弹性体中存在的是（）。

其中，A，B, C，D, E，F为常数（1）（7V= Ax + By, <r v = Cx + Dy, r xy = Ex + Fy（2）<T V = A（x2 + y2）,<r v = B（x2 + y2）,r =Cxy•*A）（1） B）（2） C）（1）、（2） D）都不可能存在8、不计体力，下阁所示弹性体的应力函数（）。

弹性力学及有限元课程考试

湖南工业大学研究生课程考试《弹性力学及有限元》答卷本人承诺：本试卷确为本人独立完成，若有违反愿意接受处理。

签名：______________学号：____________________专业：__________________所在院（部）：_________________一、读书报告弹性力学也称弹性理论，主要研究弹性体在外力作用或温度变化等外界因素下所产生的应力、应变和位移，从而解决结构或机械设计中所提出的强度和刚度问题。

在研究对象上，弹性力学同材料力学和结构力学之间有一定的分工。

材料力学基本上只研究杆状构件；结构力学主要是在材料力学的基础上研究杆状构件所组成的结构，即所谓杆件系统；而弹性力学研究包括杆状构件在内的各种形状的弹性体。

弹性力学是固体力学的重要分支，它研究弹性物体在外力和其它外界因素作用下产生的变形和内力，也称为弹性理论。

它是材料力学、结构力学、塑性力学和某些交叉学科的基础，广泛应用于建筑、机械、化工、航天等工程领域.弹性力学的基本假设如下：（一）物体构造的连续性假设，假定组成物体的介质充满了该物体所占有的全部空间，中间没有任何空隙，是连续的密实体。

（二）物体的完全弹性假设，假定除去引起物体变形的外力之后，物体能够完全恢复到未知此外力时的原来形状，而没有任何残余变形（在温度保持不变的条件下），并假定材料服从虎克定律，即应力与应变成正比。

（三）物体的均匀性假设，假定整个物体是由同一种材料组成的。

（四）物体的各向同性假设，假定物体的力学性质在各个方向上都是相同的。

（五）小变形假设，假定物体在受力变形以后，体内所有各点的位移都远远小于物体的原来尺寸，应变和转角远远小于1。

有限元法是一种数值计算的近似方法。

早在40年代初期就已有人提出，但当时由于没有计算工具而搁置，一直到50年代中期，高速数字电子计算机的出现和发展为有限元法的应用提供了重要的物质条件，才使有限元法得以迅速发展。

有限元法的优点很多，其中最突出的优点是应用范围广。

西安交通大学17年3月课程考试《弹性力学》作业考核试题满分答案

##交通大学17年3月课程考试《弹性力学》作业考核试题一、单选题〔共30 道试题,共60 分.〕V 1. 下列关于几何方程的叙述,没有错误的是〔〕A. 由于几何方程是由位移导数组成的,因此,位移的导数描述了物体的变形位移B. 几何方程建立了位移与变形的关系,因此,通过几何方程可以确定一点的位移C. 几何方程建立了位移与变形的关系,因此,通过几何方程可以确定一点的应变分量D. 几何方程是一点位移与应变分量之间的唯一关系标准答案：C2. 弹性力学对杆件分析〔〕A. 无法分析B. 得出近似的结果C. 得出精确的结果D. 需采用一些关于变形的近似假定标准答案：C3. 表示应力分量与体力分量之间关系的方程为〔〕A. 平衡微分方程B. 平衡应力方程C. 物理方程D. 平衡应变方程标准答案：A4. 对于承受均布荷载的简支梁来说,弹性力学解答与材料力学解答的关系是〔〕A. σx的表达式相同B. σy的表达式相同C. τxy的表达式相同D. 都满足平截面假定标准答案：C5. 在平面应变问题中〔取纵向作z轴〕〔〕A. σz=0,w=0,εz=0B. σz≠0,w≠0,εz≠0C. σz=0,w≠0,εz=0D. σz≠0,w=0,εz=0标准答案：D6. 下列哪种材料可视为各向同性材料〔〕A. 木材B. 竹材C. 混凝土D. 夹层板标准答案：C7. 具体步骤分为单元分析和整体分析两部分的方法是〔〕A. 有限差分法B. 边界元法C. 有限单元法的D. 数值法标准答案：C8. 利用有限单元法求解弹性力学问题时,不包括哪个步骤〔〕A. 结构离散化B. 单元分析C. 整体分析D. 应力分析标准答案：D9. 在弹性力学里分析问题,要建立〔〕套方程.A. 一B. 二C. 三D. 四标准答案：C10. 用应力分量表示的相容方程等价于〔〕A. 平衡微分方程B. 几何方程和物理方程C. 用应变分量表示的相容方程D. 平衡微分方程.几何方程和物理方程标准答案：B11. 如果必须在弹性体上挖空,那么孔的形状应尽可能采用〔〕A. 正方形B. 菱形C. 圆形D. 椭圆形标准答案：C12. 关于弹性力学的正确认识是〔〕A. 计算力学在工程结构设计中的作用日益重要B. 弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C. 任何弹性变形材料都是弹性力学的研究对象D. 弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析标准答案：A13. 在弹性力学中规定,线应变〔〕,与正应力的正负号规定相适应.A. 伸长时为负,缩短时为负B. 伸长时为正,缩短时为正C. 伸长时为正,缩短时为负D. 伸长时为负,缩短时为正标准答案：C14. 每个单元的位移一般总是包含着〔〕部分A. 一B. 二C. 三D. 四标准答案：B15. 弹性力学研究〔〕由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移B. 刚体C. 粘性体D. 塑性体标准答案：A16. 弹性力学与材料力学的主要不同之处在于〔〕A. 任务B. 研究对象C. 研究方法D. 基本假设标准答案：B17. 应力不变量说明〔〕A. 应力状态特征方程的根是不确定的B. 一点的应力分量不变C. 主应力的方向不变D. 应力随着截面方位改变,但是应力状态不变标准答案：D18. 平面应变问题的应力、应变和位移与那个〔些〕坐标无关〔纵向为z 轴方向〕〔〕A. xB. yC. zD. x, y, z标准答案：C19. 每个单元的应变包括〔〕部分应变.A. 二B. 三C. 四D. 五标准答案：A20. 设有平面应力状态,σx=ax+by,σy=cx+dy,τxy=?dx?ay?γx,其中a,b,c,d均为常数,γ为容重.该应力状态满足平衡微分方程,其体力是〔〕A. fx=0,fy=0B. fx≠0,fy=0C. fx≠0,fy≠0D. fx=0,fy≠0标准答案：D21. 圆弧曲梁纯弯时,〔〕A. 横截面上有正应力和剪应力B. 横截面上只有正应力且纵向纤维互不挤压C. 横截面上只有正应力且纵向纤维互相挤压D. 横截面上有正应力和剪应力,且纵向纤维互相挤压标准答案：C22. 下列外力不属于体力的是〔〕A. 重力C. 惯性力D. 静水压力标准答案：D23. 用应变分量表示的相容方程等价于〔〕A. 平衡微分方程B. 几何方程C. 物理方程D. 几何方程和物理方程标准答案：B24. 按应力求解〔〕时常采用逆解法和半逆解法.A. 应变问题B. 边界问题C. 空间问题D. 平面问题标准答案：D25. 在弹性力学中规定,切应变以直角〔〕,与切应力的正负号规定相适应.A. 变小时为正,变大时为正B. 变小时为负,变大时为负C. 变小时为负,变大时为正D. 变小时为正,变大时为负标准答案：D26. 关于应力状态分析,〔〕是正确的.A. 应力状态特征方程的根是确定的,因此任意截面的应力分量相同B. 应力不变量表示主应力不变C. 主应力的大小是可以确定的,但是方向不是确定的D. 应力分量随着截面方位改变而变化,但是应力状态是不变的标准答案：D27. 应力状态分析是建立在静力学基础上的,这是因为〔〕A. 没有考虑面力边界条件B. 没有讨论多连域的变形C. 没有涉与材料本构关系D. 没有考虑材料的变形对于应力状态的影响标准答案：D28. 下列材料中,〔〕属于各向同性材料.A. 竹材B. 纤维增强复合材料C. 玻璃钢D. 沥青标准答案：D29. 平面应力问题的外力特征是〔〕A. 只作用在板边且平行于板中面B. 垂直作用在板面C. 平行中面作用在板边和板面上D. 作用在板面且平行于板中面标准答案：A30. 下列问题可简化为平面应变问题的是〔〕A. 墙梁B. 高压管道C. 楼板D. 高速旋转的薄圆盘标准答案：B二、多选题〔共10 道试题,共20 分.〕V 1. 下列对象属于弹性力学研究对象的是〔〕A. 杆件B. 板壳C. 块体D. 质点标准答案：ABC2. 下面不属于平面应力问题的外力特征是〔〕A. 只作用在板边且平行于板中面B. 垂直作用在板面C. 平行中面作用在板边和板面上D. 作用在板面且平行于板中面标准答案：BCD3. 下列材料中,〔〕不属于各向同性材料.A. 竹材B. 纤维增强复合材料C. 玻璃钢D. 沥青标准答案：ABC4. 函数φ<x,y>=axy3+bx3y能作为应力函数,则a与b〔〕A. a与b可取任意值B. a=bC. a=-bD. a=b/2标准答案：ABCD5. 有限单元法的具体步骤分为〔〕两部分A. 边界条件分析B. 单元分析C. 整体分析D. 节点分析标准答案：BC6. 下列哪种材料不能视为各向同性材料〔〕A. 木材B. 竹材C. 混凝土D. 夹层板标准答案：ABD7. 下列力是体力的是：〔〕A. 重力B. 惯性力C. 电磁力D. 静水压力标准答案：ACD8. 下列问题不能简化为平面应变问题的是〔〕A. 墙梁B. 高压管道C. 楼板D. 高速旋转的薄圆盘标准答案：ACD9. 边界条件表示在边界上位移与约束的关系式,它可以分为〔〕边界条件A. 位移B. 内力C. 混合D. 应力标准答案：ACD10. 关于弹性力学的不正确认识是〔〕A. 计算力学在工程结构设计的中作用日益重要B. 弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需对问题作假设C. 任何弹性变形材料都是弹性力学的研究对象D. 弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析.标准答案：BCD三、判断题〔共10 道试题,共20 分.〕V 1. 当问题可当作平面应力问题来处理时,总有σz=τxz=τyz=0.〔〕A. 错误B. 正确标准答案：B2. 三次或三次以下的多项式总能满足相容方程.〔〕A. 错误B. 正确标准答案：B3. 对于应力边界问题,满足平衡微分方程和应力边界条件的应力,必为正确的应力分布〔〕A. 错误B. 正确标准答案：A4. 体力作用在物体内部的各个质点上,所以它属于内力〔〕A. 错误B. 正确标准答案：A5. 当物体可当作平面应变问题来处理时,总有εz=γxz=γyz=0〔〕A. 错误B. 正确标准答案：B6. 孔边应力集中是由于受力面减小了一些,而应力有所增大〔〕A. 错误B. 正确标准答案：A7. 对于多连体位移解答不必满足位移单值条件.〔〕A. 错误B. 正确标准答案：A8. 当物体的形变分量完全确定时,位移分量却不能完全确定.〔〕A. 错误B. 正确标准答案：B9. 物体变形连续的充分和必要条件是几何方程<或应变相容方程>〔〕A. 错误B. 正确标准答案：A10. 按应力求解平面问题,最后可以归纳为求解一个应力函数.〔〕A. 错误B. 正确标准答案：A。

881弹性力学考研真题

881弹性力学考研真题弹性力学是力学的一个分支，研究材料在受力下变形的性质和规律。

作为工程力学和固体力学中的重要学科，弹性力学在工程设计、材料科学、地震工程等领域都有广泛的应用。

本文将从881弹性力学考研真题的角度，探讨弹性力学的基本理论和解题方法。

一、背景知识在回答881弹性力学考研真题之前，我们首先需要掌握弹性力学的基本知识。

弹性力学主要研究材料的弹性变形，即物体在受力时能够恢复原状的性质。

其中，应力和应变是弹性力学中最基本的概念。

应力是物体单位面积上的受力，分为法向应力和剪切应力两种。

法向应力是指力作用于单位面积的垂直分量，剪切应力是指力作用于单位面积的切向分量。

应力的大小可以通过受力及物体截面积的比值来计算。

应变是物体的形变与原始形状之间的相对变化。

根据其定义，应变可以分为正应变和剪切应变两种。

正应变是指物体在受力下沿着受力方向发生的长度变化与原始长度之间的比值，剪切应变是指物体单位长度发生的角度变化。

二、解题方法在回答881弹性力学考研真题时，我们需要灵活运用弹性力学的基本理论和解题方法。

下面以一个例题来说明如何解答弹性力学的考试题目。

例题：一根长为L的悬臂梁在其端部受到均匀分布载荷，载荷强度为q。

在梁的自重和载荷的作用下，梁会发生弯曲。

求梁的最大挠度。

解题思路：根据题目所给条件，我们可以通过弯矩-曲率方程来求解梁的最大挠度。

1. 确定坐标系：假设梁的受力方向为y轴正方向，x轴为梁的长度方向。

2. 建立坐标系中的基本关系：根据弹性力学的基本理论，梁的弯矩和挠度满足以下关系：M = EIεM为弯矩，E为弹性模量，I为截面惯性矩，ε为法向应变，即ε = dy/dx。

3. 求解弯矩分布：根据题目所给条件，可以得到梁在均匀分布载荷作用下的弯矩分布为：M = qLx - 1/2qL^24. 求解挠度方程：将弯矩代入弯矩-曲率方程，并解得挠度方程为：d^2y/dx^2 - (qL/EI)x + 1/2qL^2/EI = 05. 求解最大挠度：对挠度方程进行积分求解，得到最大挠度表达式：y_max = 1/24qL^4/EI通过上述解题方法，我们可以得到悬臂梁在受力下的最大挠度。