习题第17章.doc
九年级物理第17章欧姆定律习题

7.如图5所示电路中,当开关闭合后, 电流表A1、A2的示数比 I1:I2=5;3,则电阻比R1:R2=___, 电流表A1、A3的示数比I1:I3=______。
8.如图2所示的电路中,电压表V1的 示数为9伏,电压表V2的示数为3伏, 那么R1与R2的阻值之比为 A .2 :1 B .1 : 2 C .3 :1 D .1 : 3
9.小娟在探究“电阻上的电流跟两端 电压的关系”时,将记录整理的实验 数据绘制成图7所示I-U关系图像。由 图可得甲的电阻为___Ω,乙的电阻 为_____Ω
10.在某一温度下,两个电路元件A和B中 的电流与两端电压的关系如图6所示。 (1)由图可知,元件______中的电流与 它两端电压之间的关系遵循欧姆定律。另 一元件的电阻随着电压的升高而_____。 (2)将A和B并联 后接在电压为1.0V 的电源两端,元件 A的电阻是____Ω, 元件B的电阻是___Ω。
3、有两个电阻之比R1:R2=2:5, 把它们串联在电路中,通过它们的电 流强度之比I1:I2= ,加在它们 的两端电压之比U1:U2= ;如 果把它们并联在电路中,通过它们的 电流之比I1:I2= ,加在它们两 端的电压之比是U1:U2= .
• 4.两只电阻组成串联电路, R1与R2两端电压之比是4:1, 若将这两只电阻并联,其电流 之比: ( ) • A. 4:1 B.3:1 • C.1:3 D.1:4
图6
11(14义乌)如图所示电路,电源电压不变, 滑动变阻器上标有“2A 20欧姆”字样。以下 四个图像中,能正确表示当开关S闭合后,通 过小灯泡L的电流I与滑动变阻器连入电路的电 阻R的关系的是
。
三.不同规格的灯泡串并联问题 12.两个定值电阻,甲标有“16Ω , 1.5A”,乙标有“22Ω ,0.5A”。现 把它们两个串起来,则该串联电路 两端允许通过的最大电流是 ______A,允许加的最高电压是
2019年初级经济基础知识第十七章练习题

初级经济基础《第十七章汇率与国际收支》共34题1.[多选题]一国货币成为国际货币必须具备的条件有( )。
A该国货币可兑换B该国是发达国家C该国经济金融实力强大D该国货币币值稳定E该国经济增长快参考答案:ACD参考解析:国际货币的条件:首先是可兑换货币,即自由外汇;其次是货币发行国家具备强大的经济金融实力,该货币币值稳定。
美元、欧元、英镑、日元主要是的国际货币。
2.[单选题]某银行挂出的即期汇率是USD1=CNY6.3530 , 6个月远期汇率USD1=CNY6.2895 ,则远期美元( )。
A升值B贬值C贴水D升水参考答案:C参考解析: ( 1 )出现即期和远期字眼,进行期汇(远期汇率)和现汇(即期汇率)比较,选择升水或贴水;不出现即期和远期字眼,光说汇率变化,则选择升值或贬值。
(2)直接看过去,美元期汇比现汇便宜,说明美元远期贴水了。
3.[单选题]银行挂出的人民币对美远的即期汇率是: USD1=CNY7.5865; 3个月远期汇率是: USD1= CNY7.4992。
这表明人民币远期( )。
A升水B贴水C升值D贬值参考答案:A参考解析: ( 1 )出现即期和远期字眼,进行期汇(远期汇率)和现汇(即期汇率)比较,选择升水或贴水;不出现即期和远期字眼,光说汇率变化,则选择升值或贬值。
(2)直接看过去,美元期汇比现汇便宜,说明美元远期贴水了,对应的人民币则远期升水。
4.[单选题]关于汇率的说法中,错误的是( )。
A人民币对美元对的中间价是USD1 =CNY6.6200.这种标价法为间接标价法B一般来说,银行现钞卖出价与外汇卖出价相同C汇率是以一种货币表示另一种货币的价格D中间价是买入汇率和卖出汇率的算术平均数参考答案:A参考解析:本题考查第17章第1节:汇率。
汇率,指不同货币相互兑换的比率,即以一种货币表示另一种货币的价格,C正确;现钞汇率是银行买卖外汇现钞的汇率。
现钞的买卖差价要大于现汇; -般来说,银行的现钞买入价低于外汇买入价,而现钞卖出价与外汇卖出价相同,B正确;中间价(又称中间汇率),买入汇率和卖出汇率的算术平均数,D正确;以一定单位的外国货币作为标准,折算为本国货币来表示汇率。
名校课堂WORD版练习题----第17章--练习题
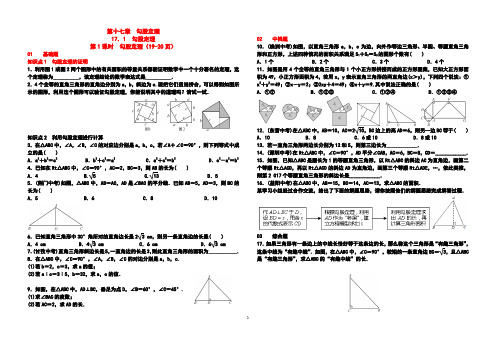
第十七章 勾股定理17.1 勾股定理第1课时 勾股定理(19-20页)01 基础题 知识点1 勾股定理的证明 1.利用图1或图2两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为__________,该定理结论的数学表达式是__________. 2.4个全等的直角三角形的直角边分别为a ,b ,斜边为c.现把它们适当拼合,可以得到如图所示的图形,利用这个图形可以验证勾股定理,你能说明其中的道理吗?请试一试.知识点2 利用勾股定理进行计算3.在△ABC 中,∠A ,∠B ,∠C 的对应边分别是a ,b ,c ,若∠A +∠C =90°,则下列等式中成立的是( )A .a 2+b 2=c 2B .b 2+c 2=a 2C .a 2+c 2=b 2D .c 2-a 2=b 24.已知在Rt △ABC 中,∠C =90°,AC =2,BC =3,则AB 的长为( )A .4 B. 5 C.13 D .55.(荆门中考)如图,△ABC 中,AB =AC ,AD 是∠BAC 的平分线.已知AB =5,AD =3,则BC 的长为( )A .5B .6C .8D .106.已知直角三角形中30°角所对的直角边长是2 3 cm ,则另一条直角边的长是( ) A .4 cm B .4 3 cm C .6 cm D .6 3 cm 7.(甘孜中考)直角三角形斜边长是5,一直角边的长是3,则此直角三角形的面积为___________. 8.在△ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别是a ,b ,c. (1)若b =2,c =3,求a 的值;(2)若a ∶c =3∶5,b =32,求a ,c 的值.9.如图,在△ABC 中,AD ⊥BC ,垂足为点D ,∠B =60°,∠C =45°. (1)求∠BAC 的度数;(2)若AC =2,求AD 的长.02 中档题10.(株洲中考)如图,以直角三角形a ,b ,c 为边,向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足S 1+S 2=S 3的图形个数有( ) A .1个 B .2个 C .3个 D .4个 11.如图是用4个全等的直角三角形与1个小正方形拼接而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x ,y 表示直角三角形的两直角边(x >y),下列四个说法:①x 2+y 2=49;②x -y =2;③2xy +4=49;④x +y =9.其中说法正确的是( ) A .①② B .①②③ C .①②④ D .①②③④12.(东营中考)在△ABC 中,AB =10,AC =210,BC 边上的高AD =6,则另一边BC 等于( ) A .10 B .8 C .6或10 D .8或10 13.若一直角三角形两边长分别为12和5,则第三边长为____________.14.(深圳中考)在Rt △ABC 中,∠C =90°,AD 平分∠CAB ,AC =6,BC =8,CD =____________. 15.如图,已知△ABC 是腰长为1的等腰直角三角形,以Rt △ABC 的斜边AC 为直角边,画第二个等腰Rt △ACD ,再以Rt △ACD 的斜边AD 为直角边,画第三个等腰Rt △ADE ,…,依此类推,则第2 017个等腰直角三角形的斜边长是____________.16.(益阳中考)在△ABC 中,AB =15,BC =14,AC =13,求△ABC 的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.03 综合题 17.如果三角形有一条边上的中线长恰好等于这条边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC 中,∠C =90°,较短的一条直角边BC =3,且△ABC 是“有趣三角形”,求△ABC 的“有趣中线”的长.第2课时勾股定理的应用(21-22页)01 基础题知识点1 勾股定理的实际应用1.如图,一根垂直于地面的旗杆在离地面5 m处折断,旗杆顶部落在离旗杆底部12 m处,旗杆折断之前的高度是( )A.5 m B.12 m C.13 m D.18 m2.如图,要制作底边BC的长为44 cm,顶点A到BC的距离与BC长的比为1∶4的等腰三角形木衣架,则腰AB的长为____________cm.(结果保留根号)3.(东营中考)如图,有两棵树,一棵高12米,另一棵高6米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行____________米.4.八(2)班小明和小亮同学学习了“勾股定理”之后,为了测得如图风筝的高度CE,他们进行了如下操作:(1)测得BD的长度为15米;(注:BD⊥CE)(2)根据手中剩余线的长度计算出风筝线BC的长为25米;(3)牵线放风筝的小明身高1.6米.求风筝的高度CE.知识点2 在数轴上表示无理数5.如图,长方形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于点M,则点M所表示的数为( )A.2 B.5-1 C.10-1 D. 56.在数轴上作出表示5的点(保留作图痕迹,不写作法).知识点3 勾股定理与网格图形7.(淮安中考)如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为( )A.5 B.6 C.7 D.258.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边有( )A.0条 B.1条 C.2条 D.3条9.如图所示,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,BD⊥AC于点D,则BD的长为( )A.455 B.235 C.255 D.43302 中档题10.如图,在水塔O的东北方向32 m处有一抽水站A,在水塔的东南方向24 m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )A.45 m B.40 m C.50 m D.56 m11.小明学了利用勾股定理在数轴上作一个无理数后,于是在数轴上离原点2个单位长度的位置找一个点D,然后过点D作一条垂直于数轴的线段CD,CD为3个单位长度,以原点为圆心,到点C的距离为半径作弧,交数轴于一点,则该点位置大致在数轴上( )A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间12.如图,在7×7的正方形网格中,每个小正方形的边长为1,画一条线段AB=50,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( ) A.1种 B.2种 C.3种 D.4种13.如图,长为8 cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3 cm到点D,则橡皮筋被拉长了____________cm.14.(吉林中考)如图,在平面直角坐标系中,点A,B的坐标分别为(-6,0),(0,8).以点A为圆心,AB长为半径画弧交x轴正半轴于点C,则点C的坐标为____________.15.将一根24 cm的筷子,置于底面直径为15 cm,高8 cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为h cm,则h的取值范围是____________.16.超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?03 综合题17.已知:如图,在Rt△ABC中,∠C=90°,AB=5 cm,AC=3 cm,动点P从点B出发沿射线BC以1 cm/s的速度移动,设运动的时间为t s.(1)求BC边的长;(2)当△ABP为直角三角形时,求t的值.小专题(二) 巧用勾股定理解决折叠与展开问题(23-24页)类型1 利用勾股定理解决平面图形的折叠问题1.如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,求BF的长.2.长方形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,求AB的长.3.如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC 边上的点E处.求D,E两点的坐标.4.有一长方形纸片ABCD,按如图方式折叠,使点B与点D重合,折痕为EF.(1)求证:△DEF是等腰三角形; (2)若AD=3,AB=9,求BE的长.5.有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm.(1)如图1,现将纸片沿直线AD折叠,使直角边AC落在斜边AB上,则CD=________cm;(2)如图2,若将直角∠C沿MN折叠,点C与AB中点H重合,点M,N分别在AC,BC上,则AM2,BN2与MN2之间有怎样的数量关系?并证明你的结论.类型2 利用勾股定理解决立体图形的展开问题6.如图,一圆柱体的底面周长为24 cm,高AB为5 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )A.6 cm B.12 cm C.13 cm D.16 cm 7.如图,在一个长为2 m,宽为1 m的长方形草地上,放着一根长方体的木块,它的棱和草地宽AD平行且棱长大于AD,木块从正面看是边长为0.2 m的正方形,一只蚂蚁从点A处到达点C 处需要走的最短路程是____________m(精确到0.01 m).8.如图,长方体的高为5 cm,底面长为4 cm,宽为1 cm.(1)点A1到点C2之间的距离是多少?(2)若一只蚂蚁从点A2爬到C1,则爬行的最短路程是多少?9.如图,圆柱形玻璃杯高为12 cm,底面周长为18 cm,在杯外离杯底4 cm的点C处有一些蜂蜜,此时一只蚂蚁正好也在杯外壁,离杯上沿4 cm的点A处.(1)求蚂蚁要吃到甜甜的蜂蜜所爬行的最短距离;(2)若将蜂蜜的位置改为在杯内离杯底4 cm的点C处,其余条件不变,请你求出此时蚂蚁吃到蜂蜜所爬行的最短距离.17.2 勾股定理的逆定理(25-26页)01 基础题知识点1 互逆命题1.下列各命题的逆命题不成立的是( )A.两直线平行,同旁内角互补 B.若两个数的绝对值相等,则这两个数也相等C.对顶角相等 D.如果a2=b2,那么a=b2.写出下列命题的逆命题,并判断它们是真命题还是假命题.(1)如果两个三角形全等,那么这两个三角形的面积相等;(2)等腰三角形的两个底角相等.知识点2 勾股定理的逆定理3.下列四组线段中,可以构成直角三角形的是( )A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,64.下列各组数是勾股数的是( )A.3,4,5 B.1.5,2,2.5 C.32,42,52 D.3,4, 5 5.在△ABC中,AB=8,AC=15,BC=17,则该三角形为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形6.三角形的边长之比为:①1.5∶2∶2.5;②4∶7.5∶8.5;③1∶3∶2;④3.5∶4.5∶5.5.其中可以构成直角三角形的有( )A.1个 B.2个 C.3个 D.4个7.如图,分别以三角形三边为直径向外作三个半圆,如果较小的两个半圆面积之和等于较大的半圆面积,那么这个三角形为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.锐角三角形或钝角三角形8.已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,三边分别为下列长度,判断该三角形是不是直角三角形,并指出哪一个角是直角.(1)a=3,b=22,c=5; (2)a=5,b=7,c=9;(3)a=2,b=3,c=7; (4)a=5,b=26,c=1.9.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.(1)求△ABC的周长;(2)判断△ABC是否是直角三角形?为什么?02 中档题10.如图,AD为△ABC的中线,且AB=13,BC=10,AD=12,则AC等于( )A.10 B.11 C.12 D.13 11.已知a,b,c是三角形的三边长,如果满足(a-6)2+b-8+||c-10=0,那么下列说法中不正确的是( )A.这个三角形是直角三角形 B.这个三角形的最长边长是10C.这个三角形的面积是48 D.这个三角形的最长边上的高是4.812.△ABC中∠A,∠B,∠C的对边分别是a,b,c,下列命题中是假命题的是( )A.若∠C-∠B=∠A,则△ABC是直角三角形B.若c2=b2-a2,则△ABC是直角三角形,且∠C=90°C.若(c+a)(c-a)=b2,则△ABC是直角三角形D.若∠A∶∠B∶∠C=5∶2∶3,则△ABC是直角三角形13.一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M,N两点相距100海里,则∠NOF的度数为( )A.50° B.60° C.70° D.80°14.已知两条线段的长为3 cm和2 cm,当第三条线段的长为____________cm时,这三条线段能组成一个直角三角形.15.如图是一个零件的示意图,测量AB=4厘米,BC=3厘米,CD=12厘米,AD=13厘米,∠ABC=90°,根据这些条件,你能求出∠ACD的度数吗?试说明理由.16.已知,如图,四边形ABCD中,AB=BC=1,CD=3,DA=1,且∠B=90°.求:(1)∠BAD的度数;(2)四边形ABCD的面积(结果保留根号).03 综合题17.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且满足c+a=2b,c-a=12b,则△ABC 是什么特殊三角形?章末复习(二) 勾股定理(27-28页)01 基础题知识点1 勾股定理1.如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点在格点上,∠A,∠B,∠C的对边分别为a,b,c,则△ABC的三边长a,b,c的大小关系是( )A.a<b<c B.c<b<a C.a<c<b D.c<a<b 2.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=5,则BC的长为( )A.3-1B.3+1C.5-1D.5+13.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD=____________.知识点2 勾股定理的应用4.(哈尔滨中考)如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )A.60海里 B.45海里 C.203海里 D.303海里5.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面 2 m,则旗杆的高度为(滑轮上方的部分忽略不计)( )A.12 m B.13 m C.16 m D.17 m6.已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4 km,B,C两地的距离是3 km,则A,B两地的距离是_____km;若A地在C地的正东方向,则B地在C地的_______方向.7.(烟台中考)如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连接OC,以O为圆心,CO长为半径画弧交数轴于点M,则点M对应的实数为____________.知识点3 逆命题与逆定理8.命题“互为相反数的两个数和为0”的逆命题是____________________________________.9.“同旁内角互补”的逆命题是________________.它是____________命题.知识点4 勾股定理的逆定理10.在△ABC中,AB=6,AC=8,BC=10,则该三角形为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形11.已知三组数据:①2,3,4;②3,4,5;③1,3,2.分别以每组数据中的三个数为三角形的三边长,能构成直角三角形的有( )A.② B.①② C.①③ D.②③12.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为( )A.90° B.60° C.45° D.30°02 中档题13.如图,在单位正方形组成的网格图中标有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是( )A.CD,EF,GH B.AB,EF,GH C.AB,CD,EF D.GH,AB,CD14.若一个三角形的周长为12 3 cm,一边长为3 3 cm,其他两边之差为 3 cm,则这个三角形是____________.15.如图是由4个边长为1的正方形构成的“田字格”.只用没有刻度的直尺在这个“田字格”中最多可以作出以格点为端点、长度为5的线段________条.16.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为2,5,1,2,则最大的正方形E的面积是____________.17.如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A1处,问梯子底部B将外移多少米?18.小明将一副三角板按如图所示摆放在一起,发现只要知道其中一边的长就可以求出其他各边的长,若已知CD=2,求AC的长.03 综合题19.(广东中考)如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于点D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.单元测试(二) 勾股定理(时间:45分钟 满分:100分)一、选择题(每小题4分,共32分)1.下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( ) A .3,4,5 B .6,8,10 C.3,2, 5 D .5,12,13 2.已知命题:等边三角形是等腰三角形,则下列说法正确的是( ) A .该命题为假命题 B .该命题为真命题 C .该命题的逆命题为真命题 D .该命题没有逆命题 3.如图是一扇高为2 m ,宽为1.5 m 的门框,李师傅有3块薄木板,尺寸如下:①号木板长3 m ,宽2.7 m ;②号木板长2.8 m ,宽2.8 m ;③号木板长4 m ,宽2.4 m .可以从这扇门通过的木板是( )A .①号B .②号C .③号D .均不能通过 4.下面各三角形中,面积为无理数的是()5.已知一个三角形的三个内角的比是1∶2∶1,则这三个内角对应的三条边的比是( )A .1∶1∶ 2B .1∶1∶2C .1∶2∶1D .1∶4∶16.(甘孜中考)如图,点D 在△ABC 的边AC 上,将△ABC 沿BD 翻折后,点A 恰好与点C 重合.若BC =5,CD =3,则BD 的长为( )A .1B .2C .3D .4 7.(黔东南中考)如图,将Rt △ABC 绕点A 按顺时针旋转一定的角度得到Rt △ADE ,点B 的对应点D 恰好落在BC 边上,若AC =3,∠B =60°,则CD 的长为( )A .0.5B .1.5 C. 2 D .18.如图,圆柱的底面周长为6 cm ,高为6 cm ,AC 是底面圆的直径,点P 是母线BC 上的一点,且PC =23BC.一只蚂蚁从点A 出发沿着圆柱体的表面爬行到点P 的最短路程是( )A .(4+6π) cm B .5 cm C .3 cm D .7 cm二、填空题(每小题4分,共24分)9.(无锡中考)写出命题“如果a =b ,那么3a =3b ”的逆命题:____________. 10.在Rt △ABC 中,∠C =90°,∠A =45°,AB =10,BC =____________.11.如图,三个正方形的面积分别为S 1=3,S 2=2,S 3=1,则在分别以它们的一边为边围成的三角形中,∠1+∠2=____________度.12.在平静的湖面上,有一朵红莲,高出水面1 m ,一阵风吹来,红莲被吹到一边,花朵贴到水面,已知红莲移动的水平距离为2 m ,则这里的水深是____________m. 13.如图,在△ABC 中,AB ∶BC ∶CA =3∶4∶5,且周长为36 cm ,点P 从点A 开始沿AB 边向点B 以每秒1 cm 的速度移动;点Q 从点B 沿BC 边向点C 以每秒2 cm 的速度移动,如果同时出发,则过3秒时,△BPQ 的面积为____________cm 2.14.要在街道旁修建一个奶站,向居民区A ,B 提供牛奶,奶站应建在什么地方,才能使A ,B 到它的距离之和最小?小聪根据实际情况,以街道为x 轴,建立了如图所示的平面直角坐标系,并测得A 点的坐标为(0,3),B 点的坐标为(6,5),则A ,B 两点到奶站距离之和的最小值是_______.三、解答题(共44分)15.(10分)如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.(1)求CD的长; (2)求AB的长; (3)判断△ABC的形状.16.(10分)一根直立的旗杆AB长8 m,一阵大风吹过,旗杆从C点处折断,顶部(B)着地,离杆脚(A)4 m,如图,工人在修复的过程中,发现在折断点C的下面1.25 m的D处,有一明显伤痕,如果下次大风将旗杆从D处刮断,则杆脚周围多大范围内有被砸伤的危险?17.(12分)如图所示,四边形ABCD是长方形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.18.(12分)已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图1,若点P在线段AB上,且AC=1+3,PA=2,则:①线段PB=,PC=;②猜想:PA2,PB2,PQ2三者之间的数量关系为____________;(2)如图2,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图2给出证明过程.。
西方经济学习题第十七章总需求总供给模型(习题)

西方经济学习题第十七章总需求总供给模型(习题)第十七章总需求总供给模型一、名词解释总需求总供给利率效应潜在产量二、选择题1、价格水平上升时,会使()A.减少实际货币供给,LM曲线右移B.减少实际货币供给,LM曲线左移C.增加实际货币供给,LM曲线右移D.增加实际货币供给,LM曲线右移2、当()时,总需求曲线更平缓。
A.投资支出对利率变化更平缓B.支出乘数较小C.货币需求对利率变化较敏感D.货币供给量较大3、松货币政策和紧的财政政策搭配能使总需求曲线()A. 向左移动B.向右移动C. 不变D.难以确定4、扩张性财政政策对总需求的影响时()A.同一价格水平对应的总需求增加B.同一总需求水平对应的价格水平下降C.价格水平下降,总需求增加D.价格水平提高,总需求减少5、总供给曲线向上移动的原因是()A 工资提高B 需求C 技术进步 D价格提高6、在水平状的总供给曲线,决定产出增加的主导力量是()A 供给B 需求C 产出D 以上均正确7、在垂直状的总供给曲线,决定价格的主导力量是()A 供给B 需求C 产出D 以上均正确8、总需求曲线是表明(A)同时达到均衡时总需求与价格水平关系的曲线。
()A、商品市场与货币市场;B、商品市场与劳动市场;C、货币市场与劳动市场;D、国外市场与国内市场。
9、总需求曲线向右上方移动的原因是:().A、政府支出的减少;B、货币供给量的增加;C、私人投资减少;D、消费支出的减少。
10、当自发总需求增加时,总需求曲线:(B)。
A、向左平行移动;B、向右平行移动;C、不变;D、向右旋转。
11、当价格水平不变,总供给可以增加的总供给曲线是:()。
A、凯恩斯主义总供给曲线;B、短期总供给曲线;C、长期总供给曲线;D、古典主义总供给曲线。
12、长期总供给曲线表示:().A、经济中已经实现了充分就业;B、经济中的资源还没有得到充分利用;C、在价格不变时,总供给可以无限增加;D、总供给增加,价格不会有变化。
第十七章借款费用习题

第十七章借款费用一、单项选择题1、2×10年5月1日,乙公司为兴建自用仓库从银行借入专门借款6 000万元,借款期限为2年,年利率为10%,借款利息按季支付。
乙公司于2×10年10月1日正式开工兴建厂房,预计工期1年3个月,工程采用出包方式。
乙公司于开工日、2×10年12月31日、2×11年5月1日分别支付工程进度款1 200万元、1 000万元、1 500万元。
因可预见的气候原因,工程于2×11年1月15日至3月15日暂停施工。
厂房于2×11年12月31日达到预定可使用状态,乙公司于当日支付剩余款项800万元。
乙公司自借入款项起,将闲置的借款资金投资于固定收益债券,月收益率为0.5%。
乙公司按期支付前述专门借款利息,并于2×12年5月1日偿还该项借款。
要求:根据上述资料,不考虑其他因素,回答下列问题。
<1>、乙公司专门借款费用开始资本化的时点是()。
A.2×10年4月15日B.2×11年5月1日C.2×10年12月31日D.2×10年10月1日<2>、下列关于乙公司在资本化期间内闲置的专门借款资金取得固定收益债券利息的会计处理中,正确的是()。
A.冲减工程成本B.递延确认收益C.直接计入当期损益D.直接计入资本公积<3>、乙公司于2×11年度应予资本化的专门借款费用是()。
A.370万元B.432万元C.332万元D.250万元<4>、乙公司累计计入损益的专门借款费用是()。
A.180万元B.130万元C.270万元D.200万元2、A公司为增值税一般纳税人,2×11年1月1日开始建设一幢自用厂房。
2×11年及之前未取得专门借款,所发生支出均系占用一般借款。
1~3月期间发生以下支出:1月10日,购买工程物资含税价款为87.75万元;2月1日将企业产品用于建造固定资产,产品成本为15万元,其中材料成本13.5万元,增值税进项税额为2.30万元,该产品计税价格为18万元,增值税销项税额为3.06万元,其中材料价款和增值税进项税额已支付,另外1.5万元为折旧等非付现成本;2月20日支付建造资产的职工薪酬1.5万元;3月10日交纳领用本公司产品所应支付的增值税税额0.76万元;3月20 日支付建造资产的职工薪酬7.5万元。
第17章相对论习题答案

3.在S系中一次爆炸发生在坐标(x,y,z,t) 为(6,0,0,10-8)处,S’系相对S系以0.8c的速 度沿x轴正向运动,在t=t’=0时两参考系的 原点重合,求S’中测得该爆炸的坐标 (6,0,0,-10-8) 。 ____________
x ( x ut ) y y z z u t ( t 2 x ) c
2.设S’系相对S系以匀速u运动,两系原点o’、o重 合时,在原点处发出一光脉冲,则两坐标系观测 到的波面形状分别是( ) A、S系为球面,S’系为椭球面
B、 S系为椭球面,S’系为球面 C、 两系均观测到球面
D、 两系均观测到椭球面
3.狭义相对论中“洛仑兹变换”式的适用条 件是( ) A、两个惯性系相对低速运动 B、两个惯性系相对高速运动 C、任意两个惯性系之间 D、惯性系与非惯性系之间
2. 有一根1m长的杆,当其中点经过照相机的瞬 间,打开照相机快门,连同一根静止的有刻度的 米尺一同拍下,如果杆相对照相机的速度 ,照 片上记录的运动杆长度该是多少?结果与运动的 B 杆缩短相对论效应矛盾吗?A
O O
解答:当杆的中点经过照相机时开始拍照,相 机接收到杆上各点发出的光同时到达相机,但 是这些光并不是同时发出的,距离远的点先发 光,近的后发光。 0.5 对于A端 ct1 0.5 t1 t1 c 对于B端 ct 2 0.5 t 2
(二)填空题
1.迈克耳逊—莫雷实验通过测量 地球相对以太的速度 否定了 绝对参考系 的存在。 2.有一速度为的宇宙飞船沿轴正方向飞行,飞 船头尾各有一个脉冲光源在工作,处于船尾 的观察者测得船头光源发出得光脉冲的传播 速度大小为 c ,处于船头的观察者测得船 尾光源发出得光脉冲的传播速度大小为 c 。
第17章微生物与寄生虫学习题(精)

第17章微生物与寄生虫学习题细菌形态与结构一、名词解释1.微生物2.荚膜3.芽胞4.质粒5.L型细菌二、填空题1.根据微生物的细胞结构及化学组成,可将其分为、、三种类型。
2.细菌物形态多种多样,根据外形可归纳为、和。
3.细菌的基本结构包括、、和等。
4.细菌的特殊结构有、、和。
5.异染颗粒对鉴定有意义。
6.细胞膜的主要功能有、、。
7.核质与细菌的、有着密切的关系。
★8. 溶菌酶的作用机理是切断N-乙酰葡萄糖胺与N-乙酰胞壁酸之间的连结,破坏的骨架,引起革兰阳性菌裂解;青霉素则是干扰之间的连结,使革兰阳性菌不能合成而导致死亡。
★9. 菌体中的RNA均存在于核蛋白体上,当m RNA与核蛋白体连成时,即成为合成蛋白质的场所。
细菌核蛋白体沉降系数为。
由和两个亚基组成,链霉素能与细菌核蛋白体的亚基结合,红霉素能与亚基结合从而干扰蛋白质的合成而致细菌死亡。
三、判断改错题1.细菌是一类含有完整细胞器的单细胞微生物。
()2.芽胞形成是细菌的繁殖方式.( )3.临床上常以杀死细菌的芽胞作为彻底灭菌的指标.( )4.荚膜本身具有毒性,所以有荚膜的细菌毒力强.( )5.鉴别细菌最常用,最重要的染色法是革兰染色法和抗酸染色法.( )6.性菌毛与细菌遗传物质传递及耐药菌形成有关.( )四、选择题1.细菌的测量单位是( )A.nmB. umC. mmD. cm2.细菌细胞壁的共有成分是( )A.多糖B.脂多糖C.肽聚糖D.磷壁酸3.细菌能维持其一定外形是因为( )A.细菌壁的半渗透性B.细胞质是溶胶状物质C.细胞壁坚韧且具有弹性D.细胞浆具有渗透压4.革兰氏染色法的染色步骤是( )A.初染-脱色-复染-媒染B. 初染-复染-媒染-脱色C.初染-脱色-媒染-复染D. 初染-媒染-脱色-复染5.与细菌体内遗传有关的物质是( )A.核糖体B.中介体C.染色体D.质粒6.有关细菌芽胞的正确描述是( )A.是某些细菌的特殊结构B.当环境适宜时可发芽为多个繁殖体C.是细菌保持生命力的一种形式D.根据芽胞的形状,位置及大小有助于鉴别细菌7.细菌涂片标本制作步骤包括有( )A.涂片B.固定C.染色D.干燥五、简答题1.G+菌与G-菌细胞壁的结构主要有何不同?2.简述显微镜油镜的使用及保护法.★3.细菌有哪两种菌毛?各有何功能?4.举例说明微生物与人类的关系.5.列表说明细菌特殊结构的种类及医学意义。
人教新版八年级下册第17章 勾股定理 单元练习题 含答案

第17章勾股定理一.选择题(共10小题)1.下列几组数能作为直角三角形三边长的是()A.3,4,6B.1,1,C.5,12,14D.,2,5 2.勾股定理是人类最伟大的科学发明之一.如图1,以直角三角形ABC的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,三个阴影部分面积分别记为S1,S2,S3,若已知S1=1,S2=2,S3=3,则两个较小正方形纸片的重叠部分(四边形DEFG)的面积为()A.5B.5.5C.5.8D.63.下列各数组中,不是勾股数的是()A.6,8,10B.9,41,40C.8,12,15D.5k,12k,13k(k为正整数)4.如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=16,则S1的值为()A.7B.8C.9D.105.如图,数轴上的点A表示的数是﹣2,点B表示的数是1,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为()A.B.+2C.﹣2D.26.如图,在△ABC中,D是BC上一点,已知AB=13,AD=12,AC=15,BD=5,则DC 的长为()A.13B.12C.9D.87.如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE═∠BAC,则DE的长为()A.cm B.cm C.cm D.1cm8.意大利著名画家达•芬奇用下图所示的方法证明了勾股定理.若设左图中空白部分的面积为S1,右图中空白部分的面积为S2,则下列表示S1,S2的等式成立的是()A.S1=a2+b2+2ab B.S1=a2+b2+abC.S2=c2D.S2=c2+ab9.在△ABC中,AB=AC=10,BD是AC边上的高,DC=2,则BD等于()A.2B.4C.6D.810.如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为()A.B.C.1或D.1或二.填空题(共5小题)11.如图,∠C=∠ADB=90°,AD=1,BC=CD=2,则AB=.12.如图,以AB为斜边的Rt△ABC的每条边为边作三个正方形,分别是正方形ABMN,正方形BCPQ,正方形ACEF,且边EF恰好经过点N.若S3=S4=5,则S1+S5=.(注:图中所示面积S表示相应封闭区域的面积,如S3表示△ABC的面积)13.若点P(a,3)在第二象限,且到原点的距离是5,则a=.14.图1是小慧在“天猫•双11”活动中购买的一张多档位可调节靠椅,档位调节示意图如图2所示,已知两支脚AB=AC=10分米,BC=12分米,O为AC上固定连接点,靠背OD=10分米.档位为Ⅰ档时,OD∥AB.档位为Ⅱ档时,OD'⊥AC.当靠椅由Ⅰ档调节为Ⅱ档时,靠背頂端D向后靠的水平距离(即EF)为分米.15.如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B.最终荡到最高点C处,若∠AOC=90°,点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为米.三.解答题(共5小题)16.如图,图中数字代表正方形的面积,∠ACB=120°,求正方形P的面积.(提示:直角三角形中,30°角所对的直角边等于斜边的一半)17.如图,在四边形ABCD中,AB=1,AD=,BD=2,∠ABC+∠ADC=180°,CD=.(1)判断△ABD的形状,并说明理由;(2)求BC的长.18.如图所示,已知△ABC中,∠B=90°,AB=16cm,AC=20cm,P、Q是△ABC的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为ts.(1)则BC=cm;(2)当t为何值时,点P在边AC的垂直平分线上?此时CQ=;(3)当点Q在边CA上运动时,直接写出使△BCQ成为等腰三角形的运动时间.19.通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形﹣﹣两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?(填“是”或不是);(2)若某三角形的三边长分别为1、、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;(3)在Rt△ABC中,两边长分别为a、c,且a2=50,c2=100,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;探究:在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a2:b2:c2.20.已知,DA,DB,DC是从点D出发的三条线段,且DA=DB=DC.(1)如图①,若点D在线段AB上,连接AC,BC,试判断△ABC的形状,并说明理由.(2)如图②,连接AC,BC,AB,且AB与CD相交于点E,若AC=BC,AB=16,DC =10,求CE和AC的长.参考答案一.选择题(共10小题)1.D.2.D.3.C.4.B.5.C.6.C.7.C.8.B.9.C.10.C.二.填空题(共5小题)11.3.12.5.13.﹣4.14.2.15.4.5.三.解答题(共5小题)16.解:如图,作AD⊥BC,交BC延长线于D,∵∠ACB=120°,∴∠ACD=60°,∠DAC=30°;∴CD=AC=1,∴AD=,在直角三角形ADB中,BD=BC+CD=3+1=4,AD=,根据勾股定理得:AB2=AD2+BD2=3+16=19;∴正方形P的面积=AB2=19.17.解:(1)△ABD是直角三角形.理由如下:在△ABD中,∵AB2+AD2=12+()2=4,BD2=22=4,∴AB2+AD2=BD2,∴△ABD是直角三角形.(2)在四边形ABCD中,∵∠ABC+∠ADC=180°,∴∠A+∠C=180°,由(1)得∠A=90°,∴∠C=90°,在Rt△BCD中,∠C=90°,BC2=BD2﹣CD2=22﹣()2=2,∴BC=.18.解:(1)∵∠B=90°,AB=16cm,AC=20cm ∴==12(cm).故答案为:12;(2)∵点P在边AC的垂直平分线上,∴PC=P A=t,PB=16﹣t,在Rt△BPC中,BC2+BP2=CP2,即122+(16﹣t)2=t2解得:t=.此时,点Q在边AC上,CQ=(cm);故答案为:13cm.(3)①当CQ=BQ时,如图1所示,则∠C=∠CBQ,∵∠ABC=90°,∴∠CBQ+∠ABQ=90°.∠A+∠C=90°,∴∠A=∠ABQ,∴BQ=AQ,∴CQ=AQ=10,∴BC+CQ=22,∴t=22÷2=11秒.②当CQ=BC时,如图2所示,则BC+CQ=24,∴t=24÷2=12秒.③当BC=BQ时,如图3所示,过B点作BE⊥AC于点E,∴,∴=.∴CQ=2CE=14.4,∴BC+CQ=26.4,∴t=26.4÷2=13.2秒.综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.19.解:(1)设等边三角形的边长为a,∵a2+a2=2a2,∴等边三角形一定是奇异三角形;(2)∵,∴该三角形一定是奇异三角形;(3)当c为斜边时,b2=c2﹣a2=50,Rt△ABC不是奇异三角形;当b为斜边时,b2=c2+a2=150,∵50+150=2×100,∴Rt△ABC是奇异三角形;∴a2+b2=2c2,∴Rt△ABC是奇异三角形;拓展:Rt△ABC中,∠C=90°,∴a2+b2=c2,∵c>b>a,∴2c2>b2+a2,2a2<b2+c2,∵Rt△ABC是奇异三角形,∴2b2=a2+c2,∴2b2=a2+a2+b2,∴b2=2a2,∴c2=3c2,∴a2:b2:c2=1:2:3.故答案为:是.20.解:(1)△ABC是直角三角形,理由:∵DA=DB=DC,∴∠A=∠ACD,∠B=∠BCD,∵∠A+∠ACD+∠B+∠BCD=180°,∴∠ACD+∠BCD=90°,∴∠ACB=90°,∴△ABC是直角三角形;(2)∵DA=DB,∴点D在线段AB的垂直平分线上,∵AC=BC,∴点C在线段AB的垂直平分线上,∴CD垂直平分AB,∴∠AEC=∠AED=90°,∵AB=16,DC=10,∴AE=8,AD=CD=10,∴DE==6,∴CE=CD﹣DE=4,∴AC===4.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十七章经济增长和周期理论(本章不作为考试内容,仅用于练习)一、单项选择题1.下列哪一种情况不是贫穷国家经济发展的主要障碍()A.人口增长B.跨国公司的存在C.低储蓄率D.国际债务2.哈罗德- 多马模型认为,长期中实现经济稳定增长的条件是()A.有保证增长率与自然增长率相等B.实际增长率与有保证增长率相等C.实际增长率、有保证增长率、自然增长率相一致D.实际增长率应大于自然增长率3.根据哈罗德- 多马模型,当资本产出率为4,储蓄率为20%时,经济增长率为()A.5%B.80%C.20%D.15%4.若要使经济增长率从5%提高到8%,在储蓄率为20%条件下,根据哈罗德- 多马模型资本产出率应该为()A.4B.2.5C.6D.55.若想把经济增长率从5%提高到7%,在资本产出率等于4的前提下,根据哈罗德- 多马模型,储蓄率应达到()A.28%B.30%C.32%D.45%6.根据哈罗德- 多马模型,当有保证增长率大于实际增长率时,经济将出现()A.均衡增长B.累积性收缩C.累积性扩张D.不能确定7.当实际的资本产出率大于愿意的资本产出率时,厂商的决策是()A.增加投资B.减少投资C.保持原有投资水平D.增雇工人8.多马和哈罗德在以下哪一点上有差别()A.投资在增长过程中的重要性B.使用凯恩斯的分析结构C.增长的中心问题在于保持预期投资持续地与增长的计划储蓄相等D.他们设计投资过程的具体方程9.多马模型意味着()A.为了维持充分就业,投资不仅必须在整个时期内增长,而且必须以一种递增的速度增长B.如果净投资保持不变,则生产能力、总需求都不会增长C.总需求将毫无困难地跟上生产能力D.技术因素在经济增长中具有十分重要的意义10.在哈罗德的增长模型中,有保证增长率和自然增长率的区别在于()A.前者假定资本与劳动的比例不断提高,后者没有B.前者以充分就业为前提,后者没有C.前者是不稳定的,后者是比较稳定的D.以上答案都不对11.新古典增长模型对哈罗德- 多马模型的重要修正是()A.它假定经济中只生产一种产品B.它假定规模收益不变C.它假定生产中的资本与劳动的比率是可变的D.它假定生产中只使用资本与劳动两种要素12. 下面哪一个论断是不正确的()A.新古典增长模型表明,决定经济增长的因素是资本的增加、劳动的增加和技术进步。
B.新古典增长模型强调了经济增长会加剧收入分配不平等C.新古典增长模型考虑到技术进步的情况D.新古典增长模型假定资本与劳动比率是可变的13.根据新古典增长模型,一个国家最终将()A.以一个不断增长的比率增长B.保持一个静止状态C.耗光自然资源难以维持生存D.造成严重的污染使其人民难以生存14.一些经济学家认为,经济增长是有极限的,因为无限增长会出现不良的经济现象()。
A.贸易壁垒B.社会福利下降C.滞胀D.分配不公平15.就整个经济来说,经济增长的主要机会成本是()。
A.未来人们的生活水准将下降B.导致自然资源的短缺C.降低人们目前的消费水准D.必然导致贫穷16.政府关于使储蓄等于投资的政策将()A.导致私人投资越来越少B.抑制增长率C.稳定经济增长率D.导致社会资本过剩,私人生产资本缺乏17.主流经济学家并不认为增长的害处大于好处,但他们认为由增长带来的害处是因为()A.资源有限而人的欲望无限B.某些产品生产导致社会成本大于私人成本C.公司的判断错误D.政府对经济的干预18.在资料充足的情况下,最有意义的而又适用的衡量经济增长的工具是()A.GDP的货币量B.实际的GDPC.人均实际GDPD.人均货币收入19.用乘数-加速原理交互作用,分析投资与产出关系引起经济周期性波动的代表人物是()A.凯恩斯B.亚当斯密C.萨缪尔森D.罗宾逊20.实际经济周期理论认为,经济周期波动的根源是()A.内生的B.外生的C.自发调节的D.有规律的21.通常表示经济周期波动的变量是()A.就业水平B.物价水平C.利率D. 国内生产总值的增长速度22.经济周期可分为两个阶段()A.扩展阶段与收缩阶段B.繁荣阶段与衰退阶段C.萧条阶段与复苏阶段D.以上都不对23.乘数原理和加速原理的联系在于()A.前者说明投资的变化对国民收入的影响,后者说明国民收入的变化对投资产生的影响B.两者都说明投资是怎样产生的C.前者说明了经济如何走向繁荣,后者说明经济怎样陷入萧条D.前者说明了经济如何陷入萧条,后者说明经济如何走向繁荣24.经济周期的中心是()A.价格的波动B.利率的波动C.GDP的波动D.工资的波动25.导致经济周期波动的投资主要是()A.投资存货B.固定资产投资C.愿意投资D.重置投资26.在经济周期里,波动最大的一般是()A.资本品的生产B.农产品的生产C.日用消费品的生产D.没有一定的规律27.按照萨缪尔森的经济周期理论,经济之所以发生周期性波动是因为()A.乘数作用B.加速数作用C.乘数和加速数的交织作用D.外部经济因素作用28.凯恩斯主义认为引起国民收入波动的主要原因是()A.总需求B.总供给C.投资D.充分就业二、多项选择题1.经济增长的源泉是()A.国民收入B.资本C.劳动D.技术进步E.基数效用2.关于经济周期理论,以下正确的说法是()A.经济周期的中心是国民收入的波动B.经济周期在经济中是不可避免的波动C.每次经济周期是相同的D.经济周期都是繁荣与萧条的交替E.科斯定理作用于经济周期3. 经济长期稳定增长的条件是()A.实际增长率等于合意增长率B.实际增长率等于自然增长率C.合意增长率等于自然增长率D.合意增长率等于有保证增长率E.公共物品与私人物品相适应4. 哈罗德- 多马模型的假设包括()A.社会只生产一种产品B.生产中只使用劳动和资本两种生产要素C.规模收益递增D.规模收益不变E.不考虑技术进步5. 哈罗德- 多马模型提出的三个增长率的概念是()A.实际增长率B.技术进步增长率C.有保证增长率D.自然增长率E.边际技术增长率6. 新古典增长模型与哈罗德- 多马模型的差别在于()A.前者考虑生产两种产品,后者考虑生产一种产品B.前者假定生产中资本与劳动的比率是可变的,后者假定不变C.前者假定规模收益递增,后者假定递减D.前者可以考虑技术进步情况,后者没有予以考虑E.前者依据恩格尔曲线,后者依据洛伦兹曲线7. 经济周期繁荣阶段的主要特征是()A.投资增加B.信用增加C.物价上涨D.就业增加E.发散型蛛网8. 加速原理主要使用的经济变量是()A.效用B.国民收入C.投资D.消费E.基尼系数9. 加速数的大小可用以下因素确定()A.投资乘数B.自发消费C.单位产出D.资本量E.等产量曲线10. 经济周期一般呈现的阶段有()A.经济繁荣阶段B.经济衰退阶段C.经济萧条阶段D.经济复苏阶段E.自然垄断阶段三、判断题1. 经济增长可以简单地定义为一国在一定时期内国内生产总值的增长,即总产出量的增加。
2. 经济增长和经济发展是相同的概念。
3.哈罗德- 多马模型表明,当经济处于均衡时,国民收入增长率等于该社会的储蓄率除以资本产出比。
4. 有保证增长率是指经济中实际实现的增长率,它由实际的储蓄率与实际的资本产出所决定。
5.根据哈罗德- 多马模型,当有保证增长率大于实际增长率时,经济将出现均衡增长。
6.在长期内最有可能实现的是有保证增长率。
7.根据哈罗德的定义,自然增长率小于等于实际增长率。
8.新古典增长模型表明,决定经济增长的因素是资本的增加、劳动的增加和技术进步。
9.经济增长的充分条件是制度与意识的相互调整。
10. 加速原理与乘数原理一样,存在一些局限性。
11. 乘数与加速原理的互为因果,互为前提,造成了国民经济由繁荣、衰退、萧条到复苏的周期性波动。
12. 繁荣和萧条是经济周期的过渡阶段。
13. 衰退与复苏是经济周期的主要阶段。
14. 只要国民收入变动,就会引起投资的加速变动。
15.如果经济中存在闲置资源,加速原理就不能充分发挥作用。
16.如果一段时间内国民收入保持稳定,那么,总投资将减少。
17.当经济达到繁荣时,会因加速数下降而转入衰退。
四、概念联线1.经济增长:是指一国商品和劳务总量的增加,即GDP的增加。
2.合意增长率:是指能产生使企业家感到满意的经济活动结果的经济增长率。
3.自然增长率:是指现有人口、资源和技术水平条件下,所允许达到的最大增长率。
4.经济周期:一般把这种经济波动,即经济繁荣和衰退的交替,称为经济周期。
5.加速原理:是说明国民收入或消费量变动与投资变动之间关系的理论。
