2017管综数学真题无水印
2017管综初数详解

2017管综初数真题(详解)一、问题求解(本大题共5小题,每小题3分,共45分)下列每题给出5个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
1、甲从1、2、3中抽取一个数,记为a ;乙从1、2、3、4中抽取一个数,记为b ,规定当a b >或者1a b +<时甲获胜,则甲取胜的概率为( )(A )16 (B )14 (C )13 (D )512 (E )12【答案】E【解析】穷举法: 满足a b >的有(2,1)(3,1)(3,2);满足1a b +<的有(1,3)(1,4)(2,4); 共六组,因此概率为61342=⨯ 2、已知ABC ∆和'''A B C ∆满足''''::2:3AB A B AC AC ==,',A A π∠+∠=则ABC∆和'''A B C ∆的面积比为( )(A 23 (B 35 (C )2:3 (D )2:5 (E )4:9 【答案】E【解析】特值法:假设2,''''3,'2AB AC A B A C A A π====∠=∠=,则11:'22:334:922S S =⨯⨯⨯⨯=3、将6人分成3组,每组2人,则不同的分组方式共有( )(A )12 (B )15 (C )30 (D )45 (E )90 【答案】B【解析】分组分配:均匀分组,注意消序2226423315C C C A ⨯⨯= 4记123,,σσσ分别为甲、乙、丙投中数的方差,则( )(A )123σσσ>> (B )132σσσ>> (C )213σσσ>> (D )231σσσ>> (E )321σσσ>>【答案】B【解析】计算方差、比较大小()()()()()()()()()222122222223255585=563542454=42387479714=733x x x σσσ-+-+-==-+-+-==-+-+-==甲乙丙,,,因此,132σσσ>>5、将长、宽、高分别为12、9、6的长方体切割成正方体,且切割后无剩余,则能切割成相同正方体的最少个数为( ) (A )3 (B )6 (C )24 (D )96 (E )648 【答案】C【详解】正方体的棱长应是长方体棱长的公约数,想要正方体最少,则找最大公约数即3,因此得到的正方体个数为129624333⨯⨯= 6、某品牌电冰箱连续两次降价10%后的售价是降价前的( )(A )80% (B )81% (C )82% (D )83% (E )85% 【答案】B【详解】假设降价前是1,则降价后为()()1110%110%81%⨯--=7、甲、乙、丙三种货车载重量成等差数列,2辆甲种车和1辆乙种车的载重量为95吨,1辆甲种车和3辆丙种车载重量为150吨,则甲、乙、丙分别各一辆车一次最多运送货物为()(A )125. (B )120. (C )115. (D )110. (E )105. 【答案】E【解析】设甲乙丙分别载重量为,,a b c ,由题得2295337245353150b a c a b a c b b b a c =+⎧⎪+=⇒++==⇒=⎨⎪+=⎩,因此 所求3105a b c b ++==8、张老师到一所中学进行招生咨询,上午接到了45名同学的咨询,其中的9位同学下午又咨询了张老师,占张老师下午咨询学生的10%,一天中向张老师咨询的学生人数为()(A )81. (B )90. (C )115. (D )126. (E )135. 【答案】D【解析】上午咨询的老师为45名,下午咨询的老师共90名,其中9名学生上午和下午都咨询了,因此学生总数为45+90-9=1269、某种机器人可搜索到的区域是半径为1米的圆,若该机器人沿直线行走10米,则其搜索出的区域的面积(单位:平方米)为()(A )102π+. (B )10π+. (C )202π+. (D )20π+ . (E )10π.【答案】D【解析】如图,机器人走过的区域为:因此面积是长方形加一个圆:2210120ππ⨯+⨯=+ 10、不等式12x x -+≤的解集为( )(A )(,1]-∞. (B )3(,]2-∞. (C )3[1,]2. (D )[1,)+∞. (E )3[,)2+∞.【答案】B 【解析】121221232x x x x x x x x -+≤⇒-≤-⇒-≤-≤-⇒≤11、在1到100之间,能被9整除的整数的平均值是( ) (A )27 (B )36 (C )45 (D )54 (E )63 【答案】D 【详解】考查整除,19100111k k ≤≤→≤≤,9的倍数有9,18,27,…,99,这些数值的平均数为()9991154211+⨯=⨯12、某试卷由15道选择题组成,每道题有4个选项,其中只有一项是符合试题要求的,甲有6道题是能确定正确选项,有5道能排除2个错误选项,有4道能排除1个错误选项,若从每题排除后剩余的选项中选一个作为答案,则甲得满分的概率为( )(A )451123⋅(B )541123⋅(C )541123+ (D )541324⎛⎫⎪⎝⎭(E )541324⎛⎫+ ⎪⎝⎭【答案】B【详解】5道题可排除2个错误选项,因此答对每题的概率为12,5道题目全部做对的概率为512;4道题目可排除1个错误选项,因此答对每题的概率为13,4道题目全部做对的概率为413,因此概率为512⋅41313.某公司用1万元购买了价格分别为1750和950的甲、乙两种办公设备,则购买的甲、乙办公设备的件数分别为( ) (A )3,5(B )5,3(C )4,4(D )2,6(E )6,2 【答案】A 【详解】考查不定方程,设甲种办公设备为x ,乙种办公设备为y ,列方程为1750950100003519200x y x y +=→+=,系数中有5直接看个位,35x 的个位必为0或者5,由于19y 的个位不为0,因此19y 的个位为5,那么35x 的个位必为5,因此y=5,x=3 14.如图,在扇形AOB 中,,14AOB OA π∠==, AC 垂直于OB ,则阴影部分的面积为( )11111(A )- (B )- (C )- (D )- (E )-8488424448πππππ【答案】A 【详解】2OCA 1111=11=82284S S S ππ∆=-⋅⋅-⋅⋅-阴影扇形15.老师问班上50名同学周末复习情况,结果有20人复习过数学,30人复习过语文,6人复习过英语,且同时复习过数学和语文的有10人,同时复习过语文和英语的有2人,同时复习过英语和数学的有3人.若同时复习过这三门课的人为0,则没有复习过这三门课程的学生人数为( ) (A )7 (B )8 (C )9 (D )10 (E )11 【答案】C【详解】复习数学的看做A ,复习语文的看做B ,复习英语的看做C ,复习数学和语文的看做AB ,复习数学和英语的看做AC ,复习语文和英语的看做BC ,全部都复习的没有,三科全部都没有复习的看做D ,因此列式为:502030610239A B C AB AC BC D D D Ω=++---+→=++---+→= 二.条件充分性判断:第16-25小题,每小题3分,共30分。
2017年考研管综真题试题及解析(全套)

2017全国硕士研究生入学统一考试管理类专业学位联考综合能力试题一、问题求解(本大题共5小题,每小题3分,共45分)下列每题给出5个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
1、甲从1、2、3中抽取一个数,记为a ;乙从1、2、3、4中抽取一个数,记为b ,规定当a b >或者1a b +<时甲获胜,则甲取胜的概率为( )(A )16 (B )14 (C )13 (D )512 (E )12【答案】E【解析】穷举法: 满足a b >的有(2,1)(3,1)(3,2);满足1a b +<的有(1,3)(1,4)(2,4); 共六组,因此概率为61342=⨯ 2、已知ABC ∆和'''A B C ∆满足''''::2:3AB A B AC AC ==,',A A π∠+∠=则ABC∆和'''A B C ∆的面积比为( )(A (B (C )2:3 (D )2:5 (E )4:9 【答案】E【解析】特值法:假设2,''''3,'2AB AC A B A C A A π====∠=∠=,则11:'22:334:922S S =⨯⨯⨯⨯=3、将6人分成3组,每组2人,则不同的分组方式共有( )(A )12 (B )15 (C )30 (D )45 (E )90 【答案】B【解析】分组分配:均匀分组,注意消序2226423315C C C A ⨯⨯= 4记123,,σσσ分别为甲、乙、丙投中数的方差,则( )(A )123σσσ>> (B )132σσσ>> (C )213σσσ>> (D )231σσσ>> (E )321σσσ>>【答案】B【解析】计算方差、比较大小()()()()()()()()()222122222223255585=563542454=42387479714=733x x x σσσ-+-+-==-+-+-==-+-+-==甲乙丙,,,因此,132σσσ>>5、将长、宽、高分别为12、9、6的长方体切割成正方体,且切割后无剩余,则能切割成相同正方体的最少个数为( ) (A )3 (B )6 (C )24 (D )96 (E )648 【答案】C【详解】正方体的棱长应是长方体棱长的公约数,想要正方体最少,则找最大公约数即3,因此得到的正方体个数为129624333⨯⨯= 6、某品牌电冰箱连续两次降价10%后的售价是降价前的( )(A )80% (B )81% (C )82% (D )83% (E )85% 【答案】B【详解】假设降价前是1,则降价后为()()1110%110%81%⨯--=7、甲、乙、丙三种货车载重量成等差数列,2辆甲种车和1辆乙种车的载重量为95吨,1辆甲种车和3辆丙种车载重量为150吨,则甲、乙、丙分别各一辆车一次最多运送货物为()(A )125. (B )120. (C )115. (D )110. (E )105. 【答案】E【解析】设甲乙丙分别载重量为,,a b c ,由题得2295337245353150b a c a b a c b b b a c =+⎧⎪+=⇒++==⇒=⎨⎪+=⎩,因此 所求3105a b c b ++==8、张老师到一所中学进行招生咨询,上午接到了45名同学的咨询,其中的9位同学下午又咨询了张老师,占张老师下午咨询学生的10%,一天中向张老师咨询的学生人数为()(A )81. (B )90. (C )115. (D )126. (E )135.【答案】D【解析】上午咨询的老师为45名,下午咨询的老师共90名,其中9名学生上午和下午都咨询了,因此学生总数为45+90-9=1269、某种机器人可搜索到的区域是半径为1米的圆,若该机器人沿直线行走10米,则其搜索出的区域的面积(单位:平方米)为()(A )102π+. (B )10π+. (C )202π+. (D )20π+. (E )10π.【答案】D【解析】如图,机器人走过的区域为:因此面积是长方形加一个圆:2210120ππ⨯+⨯=+ 10、不等式12x x -+≤的解集为()(A )(,1]-∞. (B )3(,]2-∞. (C )3[1,]2. (D )[1,)+∞. (E )3[,)2+∞.【答案】B 【解析】121221232x x x x x x x x -+≤⇒-≤-⇒-≤-≤-⇒≤11、在1到100之间,能被9整除的整数的平均值是() (A )27(B )36(C )45(D )54 (E )63 【答案】D 【详解】考查整除,19100111k k ≤≤→≤≤,9的倍数有9,18,27,…,99,这些数值的平均数为()9991154211+⨯=⨯12、某试卷由15道选择题组成,每道题有4个选项,其中只有一项是符合试题要求的,甲有6道题是能确定正确选项,有5道能排除2个错误选项,有4道能排除1个错误选项,若从每题排除后剩余的选项中选一个作为答案,则甲得满分的概率为()(A )451123⋅(B )541123⋅(C )541123+ (D )541324⎛⎫ ⎪⎝⎭(E )541324⎛⎫+ ⎪⎝⎭【答案】B【详解】5道题可排除2个错误选项,因此答对每题的概率为12,5道题目全部做对的概率为512;4道题目可排除1个错误选项,因此答对每题的概率为13,4道题目全部做对的概率为413,因此概率为512⋅41313.某公司用1万元购买了价格分别为1750和950的甲、乙两种办公设备,则购买的甲、乙办公设备的件数分别为( ) (A )3,5(B )5,3(C )4,4(D )2,6(E )6,2 【答案】A 【详解】考查不定方程,设甲种办公设备为x ,乙种办公设备为y ,列方程为1750950100003519200x y x y +=→+=,系数中有5直接看个位,35x 的个位必为0或者5,由于19y 的个位不为0,因此19y 的个位为5,那么35x 的个位必为5,因此y=5,x=3 14.如图,在扇形AOB 中,,14AOB OA π∠==,AC 垂直于OB ,则阴影部分的面积为( )11111(A )- (B )- (C )- (D )- (E )-8488424448πππππ【答案】A 【详解】2OCA 1111=11=82284S S S ππ∆=-⋅⋅-⋅⋅-阴影扇形15.老师问班上50名同学周末复习情况,结果有20人复习过数学,30人复习过语文,6人复习过英语,且同时复习过数学和语文的有10人,同时复习过语文和英语的有2人,同时复习过英语和数学的有3人.若同时复习过这三门课的人为0,则没有复习过这三门课程的学生人数为( ) (A )7(B )8(C )9(D )10(E )11 【答案】C 【详解】复习数学的看做A ,复习语文的看做B ,复习英语的看做C ,复习数学和语文的看做AB ,复习数学和英语的看做AC ,复习语文和英语的看做BC ,全部都复习的没有,三科全部都没有复习的看做D ,因此列式为:502030610239A B C AB AC BC D D D Ω=++---+→=++---+→= 二.条件充分性判断:第16-25小题,每小题3分,共30分。
2017年管理类联考真题(完整整理版)

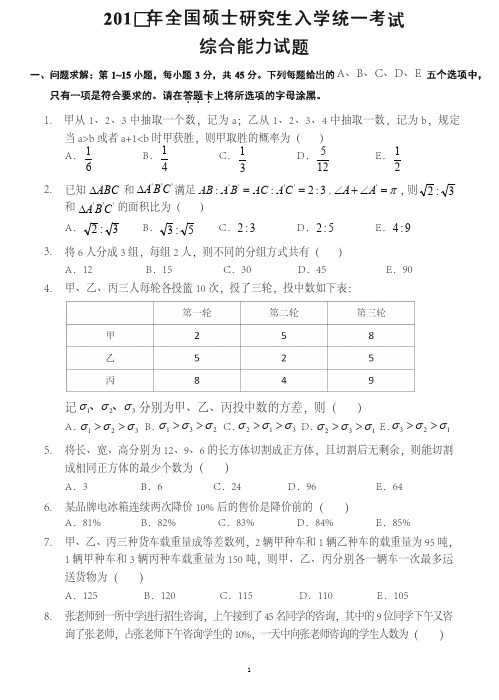
2017年管理类联考真题及答案解析一、问题求解:(第1~15小题,每小题3分,共45分,下列每题给出的A 、B 、C 、D 、E 五个选项中,只有一项是符合试题要求的,请在答题卡上将所选项的字母涂黑。
)1.甲从1、2、3中抽取一个数,记为a ;乙从1、2、3、4中抽取一数,记为b ,规定当b a >或者b a <+1时甲获胜,则甲取胜的概率为( ) (A )61(B )41(C )31(D )125(E )21 2.已知ABC Δ和C B A Δ满足π,3:2::='∠+∠='=''A A C A AC B A AB ,则ABC Δ和C B A Δ的面积比为( )(A )3:2(B )5:3(C )3:2(D )5:2(E )9:4 3.将6人分成3组,每组2人,则不同的分组方式共有( ) (A )12(B )15(C )30(D )45(E )904.甲、乙、丙三人每轮各投篮10次,投了三轮,投中数如下表:设321,,σσσ分别为甲,乙,丙投中数的方差,则(A )321σσσ>>(B )231σσσ>>(C )312σσσ>>(D )132σσσ>>(E )123σσσ>>5.将长、宽、高分别是12,9和6的长方体切割成正方体,且切割后无剩余,则能切割成相同正方体的最少个数为A3 B6 C24 D96 E6486. 某品牌电冰箱连续两次降价10%后的售价是降价前的( ) (A )80%(B )81%(C )82%(D )83%(E )85%7. 甲、乙、丙三种货车载重量成等差数列,2辆甲种车和1辆乙种车的载重量为95吨,1辆甲种车和3辆丙种车载重量为150吨,则甲、乙、丙分别各一辆车一次最多运送货物为( ) (A )125(B )120(C )115(D )110(E )1058. 张老师到一所中学进行招生咨询,上午接到了45名同学的咨询,其中9位同学下午又咨询了张老师,占张老师下午咨询学生的10%,一天中向张老师咨询的学生人数为( ) (A )81(B )90(C )115(D )126(E )1359. 某种机器人可搜索到的区域是半径为1米的圆,若该机器人沿直线行走10米,则其搜索出的区域的面积(单位:平方米)为( )(A )210π+(B )π+10(C )220π+(D )π+20(E )π1010. 不等式21≤+-x x 的解集为( )(A )(]1,∞-(B )⎥⎦⎤ ⎝⎛∞-23,(C )⎥⎦⎤⎢⎣⎡23,1(D )[)+∞,1(E )⎪⎭⎫⎢⎣⎡+∞,2311. K40733 9F1D 鼝622511 57EF 埯32780 800C 而31803 7C3B 簻21702 54C6 哆21256 5308 匈 12.13. 在1到100之间,能被9整除的整数的平均值是( ) (A )27(B )36(C )45(D )54(E )6314. 某试卷由15道选择题组成,每道题有4个选项,只有一项是符合试题要求的,甲有6道题是能确定正确选项,有5道能排除2个错误选项,有4道能排除1个错误选项,若从每题排除后剩余的选项中选一个作为答案,则甲得满分的概率为()(A )543121⋅(B )453121⋅(C )453121+(D )544321⎪⎭⎫ ⎝⎛⋅(E )544321⎪⎭⎫ ⎝⎛+15. 某公司用1万元购买了价格分别为1750和950的甲、乙两种办公设备,则购买的甲、乙办公设备的件数分别为()(A )3,5(B )5,3(C )4,4(D )2,6(E )6,216. 如图,在扇形AOB 中,,,1,4OB OC OA AOB ⊥==∠π则阴影部分的面积为( )(A )418-π(B )818-π(C )214-π(D )414-π(E )814-π 17. 老师问班上50名同学周末复习的情况,结果有20人复习过数学、30人复习过语文、6人复习过应用,且同时复习了数学和语文的有10人、语文和英语的有2人、英语和数学的有3人。
全国硕士研究生考试-管理类联考备考2017数学真题

(E)
1 24
3 + 4
5
13、甲、乙、丙三种货车的载重量成等差数列,2 辆甲种车和 1 辆乙种车满载量为 95 吨,1 辆甲种车满载量为 150 吨,则用甲、乙、丙各 1 辆车一次最多运送货物( ). (A) 125吨 (B) 120吨 (C) 115吨 (D) 110吨 (E) 105吨
1 (A) 8 4
1 (B) 8 8
1 (C) 4 2
1 (D) 4 4
1 (E) 4 8
10、老师问班上 50 名同学周末复习的情况,结果有 20 人复习过数学,30 人复习过语 文, 6 人复习过英语,且同时复习了数学和语文的有 10 人,同时复习了语文和英语的 有 2 人,同时复习了英语和数学的有 3 人,若同时复习了这三门课的人数为0,则没复 习过这三门课程的学生人数为( ). (A)7 (B) 8 (C)9 (D) 10
18、直线 y ax b 与抛物线 y x 2 有两个交点. ( 1)a 2 4b; (2)b 0.
19、能确定某企业产值的月平均增长率. ( 1)已知一月份的产值; (2)已知全年的总产值.
20、圆 x 2 y 2 ax by c 0 与 x 轴相切,则能确定 c 的值. ( 1)已知 a 的值; (2)已知 b 的值.
全国硕士研究生考试 管理类联考备考 2017 数学真题
一、问题求解(本大题共 15 小题,每小题 3 分,共 45 分)下列每题给出的五个选项中, 只有一个符合要求,请在答题卡上将所选择的字母涂黑.
1、甲从 1、、 2 3 中抽取一个数,设为 a ; 乙从 1、、、 2 3 4 中抽取一个数,设为b ;规定当 a b 或 a 1 b 时甲获胜,则甲获胜的概率为( ). (A) 1 6 (B) 1 4 1 (C) 3 5 (D) 12 (E) 1 2
管综数学真题无水印精选文档

管综数学真题无水印精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-2017年数学真题一、问题求解:1、甲从1、2、3中抽取一个数,设为a ;乙从1、2、3、4中抽取一数,设为b ,规定当a b >或者1a b +<时甲获胜,则甲取胜的概率为( ) (A )16 (B )14 (C )13 (D )512 (E )122.已知ABC ∆和C B A '''∆满足''''::2:3AB A B AC AC==,π='∠+∠A A ,则ABC ∆和C B A '''∆的面积比为( )(A )3:2 (B )5:3 (C )2 : 3 (D )2 : 5 (E )4 : 9 3.将6人分成3组,每组2人,则不同的分组方式共有( )(A ) 12 (B )15 (C )30 (D )45 (E )904. 甲、乙、丙三人每轮各投篮10次,投了3轮,投中数如下表:记321,,σσσ分别为甲、乙、丙投中数的方差,则( )(A )321σσσ>> (B )231σσσ>> (C )312σσσ>> (D )132σσσ>> (E )123σσσ>>5、张老师到一所中学进行招生咨询,上午接到了45名学生的咨询,其中的9位同学下午又咨询了张老师,占张老师下午咨询学生的10%,一天中向张老师咨询的学生人数为( )(A ) 81 (B )90 (C )115 (D )126 (E )1356、某品牌电冰箱连续两次降价10%后的售价是降价前的()(A ) 80% (B )81% (C )82% (D )83% (E )85%7、甲乙丙三种货车载重量成等差数列,2辆甲种车和1辆乙种车的载重量为95吨,1辆甲种车和3辆丙种车载重量为150吨,则甲、乙、丙分别各一辆车一次最多运货物为( )(A ) 125 (B )120 (C )115 (D )110 (E )1058、某公司用1万元购买了价格分别为1750和950的甲、乙两种办公设备,则购买甲、乙办公设备的件数 分别为( )(A )3 ; 5 (B )5 ; 3 (C )4 ; 4 (D )2 ; 6 (E )6 ; 29、如图1,在扇形AOB 中,4π=∠AOB ,1=OA ,OB AC ⊥,则阴影部分的面积为( )(A )418-π(B )818-π(C )214-π(D )414-π(E )814-π10、老师问班上50名同学周末复习的情况,结果有20人复习过数学、30人复习过语文、6人复习过英语,且同时复习了数学和语文的有10人、语文和英语的有2人、英语和数学的有3人。
2017年管理类联考真题(完整整理版)

2017年管理类联考真题及答案解析一、问题求解:(第1~15小题,每小题3分,共45分,下列每题给出的A 、B 、C 、D 、E 五个选项中,只有一项是符合试题要求的,请在答题卡上将所选项的字母涂黑。
)1.甲从1、2、3中抽取一个数,记为a ;乙从1、2、3、4中抽取一数,记为b ,规定当b a >或者b a <+1时甲获胜,则甲取胜的概率为( ) (A )61(B )41(C )31(D )125(E )21 2.已知ABC Δ和C B A Δ满足π,3:2::='∠+∠='=''A A C A AC B A AB ,则ABC Δ和C B AΔ的面积比为( ) (A )3:2(B )5:3(C )3:2(D )5:2(E )9:4 3.将6人分成3组,每组2人,则不同的分组方式共有( ) (A )12(B )15(C )30(D )45(E )904.甲、乙、丙三人每轮各投篮10次,投了三轮,投中数如下表:设321,,σσσ分别为甲,乙,丙投中数的方差,则(A )321σσσ>>(B )231σσσ>>(C )312σσσ>>(D )132σσσ>>(E )123σσσ>> 5.将长、宽、高分别是12,9和6的长方体切割成正方体,且切割后无剩余,则能切割成相同正方体的最少个数为A3 B6 C24 D96 E6486. 某品牌电冰箱连续两次降价10%后的售价是降价前的( ) (A )80%(B )81%(C )82%(D )83%(E )85%7. 甲、乙、丙三种货车载重量成等差数列,2辆甲种车和1辆乙种车的载重量为95吨,1辆甲种车和3辆丙种车载重量为150吨,则甲、乙、丙分别各一辆车一次最多运送货物为( ) (A )125(B )120(C )115(D )110(E )1058. 张老师到一所中学进行招生咨询,上午接到了45名同学的咨询,其中9位同学下午又咨询了张老师,占张老师下午咨询学生的10%,一天中向张老师咨询的学生人数为( ) (A )81(B )90(C )115(D )126(E )1359. 某种机器人可搜索到的区域是半径为1米的圆,若该机器人沿直线行走10米,则其搜索出的区域的面积(单位:平方米)为( ) (A )210π+(B )π+10(C )220π+(D )π+20(E )π1010. 不等式21≤+-x x 的解集为( )(A )(]1,∞-(B )⎥⎦⎤ ⎝⎛∞-23,(C )⎥⎦⎤⎢⎣⎡23,1(D )[)+∞,1(E )⎪⎭⎫⎢⎣⎡+∞,2311. 在1到100之间,能被9整除的整数的平均值是( ) (A )27(B )36(C )45(D )54(E )6312. 某试卷由15道选择题组成,每道题有4个选项,只有一项是符合试题要求的,甲有6道题是能确定正确选项,有5道能排除2个错误选项,有4道能排除1个错误选项,若从每题排除后剩余的选项中选一个作为答案,则甲得满分的概率为()(A )543121⋅(B )453121⋅(C )453121+(D )544321⎪⎭⎫ ⎝⎛⋅(E )544321⎪⎭⎫ ⎝⎛+13. 某公司用1万元购买了价格分别为1750和950的甲、乙两种办公设备,则购买的甲、乙办公设备的件数分别为()(A )3,5(B )5,3(C )4,4(D )2,6(E )6,2 14. 如图,在扇形AOB 中,,,1,4OB OC OA AOB ⊥==∠π则阴影部分的面积为( )(A )418-π(B )818-π(C )214-π(D )414-π(E )814-π 15. 老师问班上50名同学周末复习的情况,结果有20人复习过数学、30人复习过语文、6人复习过应用,且同时复习了数学和语文的有10人、语文和英语的有2人、英语和数学的有3人。
2017管理类联考综合真题(含答案)
)
B.120 C.115 D.110 E.105
8.
张老师到一所中学进行招生咨询,上午接到了 45 名同学的咨询,其中的 9 位同学下午又咨 询了张老师,占张老师下午咨询学生的 10%,一天中向张老师咨询的学生人数为(
1
)
A.81
B.90
C.115
D.126
E.135
9.
某种机器人可搜索到的区域是半径为 1 米的圆,若该机器人沿直线行走 10 米,则 其搜索出的区域的面积(单位:平方米)为( A. B. C.
25. 设 a、b 是两个不相等的实数,则函数
(1)1,a,b 成等差数列; (2)1,a,b 成等比数列。
的最小值小于零。
三、逻辑推理:本大题共 30 小题,每小题 2 分,共 60 分。下面每题所给出 的五 个选项中,只有一项是符合试题要求的。请在答题卡上将所选项的字母涂黑。 26. 倪教授认为,我国工程技术领域可以考虑与国外先进技术合作,但任何涉及核心技
。
23. 某机构向 12 位教师征题,共征集到 5 种题型 52 道,则能确定供题教师的人数
(1)每位供题教师提供试题数相同; (2)每位供题教师提供的题型不超过 2 种。
3
24. 某人参加资格考试,有 A 类和 B 类选择,A 类的合格标准是抽 3 道题至少会做 2 道,
B 类的合格标准是抽 2 道题需都会做,则此人参加 A 类合格的机会大。 (1)此人 A 类题中有 60% 会做; (2)此人 B 类题中有 80% 会做。
19. 某人从 A 地出发,先乘时速为 220km 的动车,后转乘时速为 100km 的汽车到达 B 地,
则 A、B 两地的距离为 960km。 (1)乘动车的时间与乘汽车的时间相等; (2)乘动车的时间与乘汽车的时间之和为 6 小时。
2017年管理类联考真题

2017届管理类专业硕士研究生全国联考真题一、问题求解:第1—15小题,每小题3分,共45分. 下列每题给出的A 、B 、C 、D 、E 五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1. 某品牌的电冰箱连续两次降价10%后的售价是降价前的()(A )80% (B )81% (C )82% (D )83% (E )85%2. 张老师到一所中学进行招生咨询,上午接受了45名同学的咨询,其中的9人下午又咨询了张老师,占他下午咨询学生的10%,一天张老师咨询的学生人数为()(A )81 (B )90 (C )115 (D )126 (E )1353. 甲、乙、丙三种货车的载重量成等差数列,2辆甲种车和1辆乙种车满载量为95吨,1辆甲种车和3辆丙种车满载量为150吨,则甲、乙、丙各1辆载满货物为多少?(A )125吨 (B )120吨 (C )115吨 (D )110吨 (E )105吨4. 12x x -+≤成立,则的取值范围。
(A )(]-1∞, (B )3-2,⎛⎤∞ ⎥⎝⎦ (C )31,2,⎡⎤⎢⎥⎣⎦(D )(]1+∞, (E )3+2,⎡⎫∞⎪⎢⎣⎭ 5. 某机器人可搜索到的区域是半径为1米的圆,若该机器人沿直线行走10米,则其搜索区域的面积(平方米)为( )(A )102π+ (B )10+π (C )202π+ (D )20+π (E )10π 6.某试卷由15道选择题组成,每道题有4个选项,只有一项是符合试题要求的,甲有6道能确定正确选项,有5道题能排除2个错误选项,有4道题能排除1个错误选项,若从每道题排除后剩余的选项中选1个作为答案,则甲得满分的概率为() (A )112⋅453 (B )112⋅543 (C )11254+3 (D )12⎛⎫⋅ ⎪⎝⎭5434 (E )12⎛⎫ ⎪⎝⎭543+4 7.某公司用1万元购买了价格分别是1750元和950元的甲乙两种办公设备,则购买的甲、乙办公设备的件数分别为()(A )3,5 (B )5,3 (C )4,4 (D )2,6 (E )6,28.老师问班上50名同学周末复习的情况,结果有20人复习过数学,30人复习过语文,6人复习过英语,且同时复习了数学和语文的有10人,语文和英语的有2人,英语和数学的有3人,若同时复习过这三门课的人数为0,则没复习过这三门课程的学生人数为()(A )7 (B )8 (C )9 (D )10 (E )119.如图1,在扇形AOB中,π∠⊥AOB=,OA=1,ACOB,4则阴影部分的面积为()(A )1π-84 (B )1π-88 (C )1π-42 (D )1π-44 (E )1π-48 10.在1和100之间,能被9整除的整数的平均值是()(A )27 (B )36 (C )45 (D )54 (E )63【参考答案】D11.已知ABC ∆和A B C '''∆满足:'''''∠∠πAB:AB=AC:AC=23,A+A=,则ABC ∆与A B C '''∆的面积之比为()(A 2:3 (B 3:5 (C )2:3 (D ):25(E )4:9 12.甲从1,2,3中抽取一数,记为a,乙从1,2,3,4中抽取一数,记为b,规定当a>b或a+1<b时甲获胜,则甲获胜的概率为() (A )16 (B )14 (C )13 (D )251 (E )1213.将长、宽、高分别是12,9和6的长方体切割成正方体,且切割后无剩余,则能切割成相同的正方体的最少个数为() (A )3 (B )6 (C )24 (D )96 (E )648第一轮 第二轮 第三轮 甲2 5 8 乙5 2 5 丙 8 4 9记σσσ123,,分别为甲、乙、丙投中数的方差,则()(A )σσσ123>>(B )σσσ132>>(C )σσσ213>> (D )σσσ231>>(E )σσσ321>>15.将6人分为3组,每组2人,则不同的分组方式共有 ()(A )12种 (B )15种 (C ) 30种 (D )45种 (E )90种二、条件充分性判断:第16—25小题,每小题3分,共30分.要求判断每题给出得条件(1)和(2)能否充分支持题干所陈述的结论. A 、B 、C 、D 、E 五个选项为判断结果, 请选择一项符合试题要求得判断, 在答题卡上将所选项得字母涂黑.16. 某人需要处理若干份文件,第一小时处理了全部文件的15,第二小时处理了剩余文件的14,则此人需要处理的文件共25份。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年数学真题
一、问题求解:
1、甲从1、
2、3中抽取一个数,设为a ;乙从1、2、
3、4中抽取一数,设为b ,规定当a b >或者1a b +<时甲获胜,则甲取胜的概率为( ) (A )
16 (B )14 (C )13 (D )512 (E )12
2.已知ABC ∆和C B A '''∆满足''
''
::2:3AB A B AC AC ==,π='∠+∠A A ,则ABC ∆和
C B A '''∆的面积比为( )
(A )3:2 (B )5:3 (C )2 : 3 (D )2 : 5 (E )4 : 9 3.将6人分成3组,每组2人,则不同的分组方式共有( )
(A ) 12 (B )15 (C )30 (D )45 (E )90
4. 甲、乙、丙三人每轮各投篮10次,投了3轮,投中数如下表:
记321,,σσσ分别为甲、乙、丙投中数的方差,则( )
(A )321σσσ>> (B )231σσσ>> (C )312σσσ>> (D )132σσσ>> (E )123σσσ>>
5、张老师到一所中学进行招生咨询,上午接到了45名学生的咨询,其中的9位同学下午又
咨询了张老师,占张老师下午咨询学生的10%,一天中向张老师咨询的学生人数为( ) (A ) 81 (B )90 (C )115 (D )126 (E )135
6、某品牌电冰箱连续两次降价10%后的售价是降价前的()
(A ) 80% (B )81% (C )82% (D )83% (E )85%
7、甲乙丙三种货车载重量成等差数列,2辆甲种车和1辆乙种车的载重量为95吨,1辆甲种车和3辆丙种 车载重量为150吨,则甲、乙、丙分别各一辆车一次最多运货物为( )
(A ) 125 (B )120 (C )115 (D )110 (E )105
8、某公司用1万元购买了价格分别为1750和950的甲、乙两种办公设备,则购买甲、乙办公设备的件数 分别为( )
(A )3 ; 5 (B )5 ; 3 (C )4 ; 4 (D )2 ; 6 (E )6 ; 2
9、如图1,在扇形AOB 中,4
π
=
∠AOB ,1=OA ,OB AC ⊥,则阴影部分的面积为( )
(A )
41
8-π
(B )818-π
(C )214-π
(D )41
4-π
(E )8
14-π
10、老师问班上50名同学周末复习的情况,结果有20人复习过数学、30人复习过语文、
6人复习过英语,且同时复习了数学和语文的有10人、语文和英语的有2人、英语和数学的有3人。
若同时复习过这三门课的人数为0,则没复习过这三门课程的学生人数为( ) (A )7 (B )8 (C )9 (D )10 (E )11
11、某种机器人可搜索的区域是半径为1m 的圆,若该机器人沿直线行走10m ,则其搜索
出的区域的面积(单位:2m )为( ) (A )2
10π
+
(B )π+10 (C )2
20π
+
(D )π+20 (E )π10
12、不等式
21≤+-x x 的解集为()
(A )(,1]-∞ (B )3(,]2-∞ (C )3[1,]2 (D )[1,)+∞ (E )3[,)2
+∞
13、某试卷由15道选择题组成,每道题有4个选项,只有一项是符合试题要求的,甲有6
道题能确定正确选项,有5道题能排除2个错误选项,有4道题能排除1个错误选项,若从每题排除后剩余的选项中选一个作为答案,则甲得满分的概率为( )
(A )543121⋅ (B )453121⋅ (C )453121+ (D )544321⎪⎭⎫ ⎝⎛⋅ (E )5
44321⎪
⎭
⎫ ⎝⎛+
14、在1到100之间,能被9整除的整数的平均值是( )
(A )27 (B )36 (C )45 (D )54 (E )63
15、将长、宽、高分别是12,9和6的长方体切割成正方体,且切割后无剩余,则能切割
成相同正方体的最少个数为( )
(A )3 (B )6 (C )24 (D )96 (E )648
二、条件充分性判断:
A 、 条件(1)充分,但条件(2)不充分
B 、 条件(2)充分,但条件(1)不充分
C 、 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分
D 、 条件(1)充分,条件(2)也充分
E 、 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来也不充分
16、某人需要处理若干分文件,第1小时处理了全部文件的
5
1
,第2小时处理了剩余文件的4
1
,则此人需要处理的文件数为25份。
(1)前两小时处理了10份文件 (2)第二小时处理了5份文件
17、某人从A 地出发,先乘时速为220千米的动车,后转乘时速为100千米的汽车到达B
地,则A ,B 两地的距离为960千米。
(1)乘动车时间与乘汽车的时间相等。
(2)乘动车时间与乘汽车的时间之和为6小时。
18、直线
b ax y +=与抛物线2x y =有两个交点。
(1)b a 42> (2)0>b
19、能确定某企业产值的月平均增长率
(1)已知一月份的产值 (2)已知全年的总产值
20、圆022
=+--+c by ax y x
与x 轴相切,则能确定c 的值
(1)已知a 的值 (2)已知b 的值
21、如图2,一个铁球沉入水池中,则能确定铁球的体积。
(1)已知铁球露出水面的高度
(2)已知水深及铁球与水面交线的周长。
22、已知c b a ,,为三个实数,则{}5,,min
≤---c a c b b a
(1)5,5,5≤≤≤c b a (2)15=++c b a
23、某人参加资格证考试,有A 类和B 类选择,A 类的合格标准是抽3道题至少会做2道,
B 类的合格标准是抽2道题需要都会做,则此人参加A 类合格的机会大。
(1)此人A 类题中有60%会做 (2)此人B 类题中有80%会做
24、某机构向12位教师征题,共征集到5种题型的试题52道,则能确定提供教师的人数。
(1)每位供题教师提供试题数相同 (2)每位供题教师提供的题型不超过2种
25、设b a ,是两个不相等的实数,则函数
()b ax x x f ++=22的最小值小于零。
(1)b a ,,1成等差数列 (2)b a ,,1成等比数列。
