2018年攻读工商管理硕士学位全国联考数学真题
可知有无穷多解，所以选 E。
【考点】应用题。
25.设函数 f (x) x2 ax ，则 f (x) 最小值与 f ( f (x)) 的最小值相等 （1） a 2 （2） a 0
【答案】（D）
【解题过程】 f (x) x2 ax 与 f [ f (x)] x2 ax 2 a x2 ax 最小值相等，又知当 x a 时， 2
（1） | a b | 1 a2
（2） | a b | 1 a2
【答案】（A） 【解题过程】要使圆与直线不相交，两者的关系是相离的，即圆心到直线的距离大于圆的半径。圆
心为（0,1），半径为 1，直线方程的一般形式为 x ay b 0 ，则 d
a b 1。 1 a2
【考点】解析几何问题。 22.如甲公司年终奖总额增加 25%，乙公司年终奖减少 10%，两者相等，则能确定两公司的员工人数
6.6 张不同卡片两张一组分别装入甲、乙、丙 3 个袋中，指定两张要在同一组，不同装法有（ ）
种
A.12
B.18
C.24
D.30
E.36
【答案】（B） 【解题过程】 C24C22 3 2 1 18 。
2
【考点】分步计数原理和分组分排问题。
7.四边形 A、B、C、D 是平行四边形，A2B2C2D2 是 A1B1C1D1 四边的中点，A3B3C3D3 是 A2B2C2D2 四 边的中点，依次下去，得到四边形序列 AnBnCnDn（n=1,2,3,…）。设 AnBnCnDn 面积为 Sn，且 S1=12， 则 S1+S2+S3+…=（ ） A.16 B.20 C.24 D.28 E.30
（A）条件（1）充分，但条件（2）不充分 （B）条件（2）充分，但条件（1）不充分 （C）条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分 （D）条件（1）充分，条件（2）也充分 （E）条件（1）和条件（2）单独都不充分，条件（1）和条件（2）联合起来也不充分
16.
{an
}
为等差数列，则能确定a 1
【答案】（A）
【解题过程】设甲、乙、丙三人的年收入分别为 a, b, c ，则 b2 ac 。对于条件（1），由 b ac a c 2
可得，当 a c 的值确定时，即可确定 b 的最大值，充分；对于条件（2），已知 a c 的值，则 b 的
值是确定的，不充分。 【考点】均值不等式问题。
f (x) 取 得 最 小 值 为 a 2 a a ， 由 整 体 性 可 知 当 x2 ax a 时 ，
2 2
2
f [ f (x)] a 2 a a 等于 f (x) 。即 x2 ax a 有根，由根的判别式 a2 2a 0 可
A. π 3 B. π 6 C. π 3 3 2
D. 2π 3 3
E. π 3
【答案】（D）
【解题过程】截掉部分的底面积为 1 π 22 3 22 2 π 3 ，体积等于底面积乘以高（高为 3），
6
4
3
可得体积为 2π 3 3 。
【考点】立体几何问题。
15.羽毛球队 4 名男运动员 3 女足动员，从中选出 2 对参加混双比赛，不同选派方式有（
总平均年龄为 32 3 27 2 30 。 5
【考点】平均值问题。
3.某单位分段收费收网站流量（单位：GB）费：每日 20（含）GB 以内免，20 到 30（含）每 GB 收 1
元，30 到 40（含）每 GB 3 元，40 以上每 GB 5 元，小王本月用 45GB 该交费（ ）元
A.45
的 3 名人员再进行分配共有 3×2×1=6 种方法，由分步原理知共有 12 种方法。
【考点】全错位排列，分步计数原理。 13.从标号 1 到 10 中的 10 张卡片中随机抽 2 张，而它们的标号之和能被 5 整除的概率为（ ）
1
1
2
2
7
A.
B.
C.
D.
E.
5
9
9
15
45
【答案】（A）
【解题过程】从 10 张卡片中选 2 张，共有 C120 45 ，分母为 45；分子为两张卡片上的数字之和被 5
之比 （1）甲公司的人均年终奖与乙公司相同 （2）两公司的员工数之比与两公司年终奖总额之比相等
【答案】（D）
【解题过程】设去年甲乙两公司的年终奖总额分别为 a, b ，由题意知 25%a 10%b a : b 2 : 5 ， 而今年的年终奖总额之比为125%a : 90%b 125 2 : 90 5 ，比值确定。对于条件（1），人均年
a 2
a 的值 9
（1）已知 a1 的值
（2）已知 a5 的值
【答案】（B）
【解题过程】对于条件（1），显然不充分；对于条件（2）， S9 9a5 ，故充分。
【考点】等差数列问题。
17.设 m, n 为正整数，则能确定 m n 的值 （1） 1 3 1 mn
（2） 1 2 1 mn
【答案】（D）
E.0.6
【答案】（C）
【解题过程】通过分析，甲要赢得比赛，必须在第二和第三局全胜，概率为 0.6×0.6=0.36。 【考点】概率的独立性。
9.圆 C : x2 ( y a)2 b ，若圆 C 在点（1, 2）处的切线与 y 轴交点为（0, 3），则 ab =（ ）
A.-2
B.-1
C.0
【答案】（E）
1y 1
【答案】（A）
x y 2 x2 2xy y2 2 x2 y2 4
【解题过程】对于（1），
，条件（1）充分；对于条件（2）,
x y 2.
取 x 为 10， y 为 1/10，而 x y 10 ，条件（2）不充分。
A.19
B.18
C.24
D.36
E.72
【答案】（D）
）种
【解题过程】从 4 名男运动员和 3 名女运动员各选取 2 名共有 C24 C32 中方法，再配成两对，共有 2
种选择，故有 C24 C32 2 36 种方式。
【考点】分步计数原理。
二、条件充分性判断：第 16~25 小题，每小题 3 分，共 30 分。要求判断每题给出的条件（1）和条 件（2）能否充分支持题干所陈述的结论。A、B、C、D、E 五个选项为判断结果，请选择一项符合 试题要求的判断，在答题卡上将所选的字母涂黑。
整除，通过穷举法共有{1,4}，{1,9}，{2,3}，{2,8}，{3,7}，{4,6}，{5,10}，{7,8}，{6,9}共 9 组数据
能被 5 整除。
【考点】古典概率问题。
14.圆柱体底面半径为 2，高为 3，垂直于底面的平面截圆柱体所得截面为矩形 ABCD，若弦 AB 所对
圆心角是 π ，则截去部分（较小那部分）体积为（ ） 3
可得 r 1，圆的面积为 π 。
【考点】平面几何求面积问题。
5.实数 a, b 满足
，
，则 a2 b2 （ ）
a3 b3 26 a b 2
A.30B.22 C.15
D.13
E.10
【答案】（E）
【解题过程】由已知条件可知 a 3, b 1，则 a2 b2 10 。
【考点】整式分式问题。
2018 年攻读工商管理硕士学位全国联考数学真题
一、问题求解：本大题共 15 小题，每小题 3 分，共 45 分。下列每题给出的五个选项中，只有一项
是符合试题要求的。请在答题卡上将所选的字母涂黑。
1.学科竞赛设一、二、三等奖，比例 1:3:8，获奖率 30%，已知 10 人已获一等奖，则参赛人数为（ ）
【解题过程】对于条件（1），只有 m 2, n 6和m 4, n 4 两个解，故 m n 8 ，充分；对于
条件（2），只有 m 2, n 4和m 3, n 3 两个解，故 m n 6 ，充分。
【考点】整除问题。 18.甲、乙、丙 3 人年收入成等比，则能确定乙的年收入最大值
（1）已知甲、丙两人年收入之和 （2）已知甲、丙两人年收入之积
【考点】函数问题。
12.某单位为检查 3 个印前工作，由这 3 个部门主任和外聘 3 名人员组成检查组，每组 1 名外聘，规 定本部门主任不能检查本部门，则不同的安排方式有（ ）
A.6 种
B.8 种
C.12 种 D.18 种
E.36 种
【答案】（C）
【解题过程】3 个部门的主任均不能够担任本部门的检查工作，全错位排列，共有 2 种方法，外聘
终奖相同，那么人数之比就等于年终奖总额之比，充分；对于（2），员工人数之比等于年终奖总额 之比，充分。 【考点】比例问题 23.已知点 P(m,o)，A(1,3)，B(2,1)，点（x，y）在△PAB 上，则 x-y 的最小值与最大值分别为-2 和 1
（1）m≤1 （2）m≥-2 【答案】（C）
【解题过程】通过画图可以得出，当 2 m 1 时，结论成立。
【考点】线性规划问题。 24.甲购买了若干 A 玩具，乙购买了若干 B 玩具送给幼儿园，甲比乙少花了 100 元，则能确定甲购买 的玩具件数
（1）甲与乙共购买了 50 件玩具 （2）A 玩具的价格是 B 玩具的 2 倍 【答案】（E）
【解题过程】显然单独均不成立，联合考察。设 A、B 玩具数量分别为 x,y，A 玩具的价格 为 a,则
女员工年龄（岁） 23 25 27 27 29 31
据表中数据统计，该公司男员工的平均年龄与全体员工平均年龄分别是（ ）
A.32，30 B.32，29.5 C.32，27
D.30，27
E.29.5，27
【答案】（A）
【解题过程】由表可知，男员工的平均年龄=32，女员工的平均年龄=27，男女员工人数之比=9:6=3:2，
A.70
2018年MBA和MPAcc数学真题解析改最终版本
2018年攻读工商管理硕士学位全国联考数学真题一、问题求解：本大题共15小题，每小题3分，共45分。
下列每题给出的五个选项中，只有一项是符合试题要求的。
请在答题卡上将所选的字母涂黑。
1.学科竞赛设一、二、三等奖，比例1:3:8，获奖率30%，已知10人已获一等奖，则参赛人数为（）A.300 B.400 C.500D.550 E.600【答案】（B ）【解题过程】由总量=分量÷分量百分比，可得参赛总人数为：10÷（30%÷12）=400。
【考点】比例问题应用题。
2.为了解某公司员工年龄结构，按男女人数比例进行随机抽样，结果如下：男员工年龄（岁）232628303234363841女员工年龄（岁）232527272931据表中数据统计，该公司男员工的平均年龄与全体员工平均年龄分别是（）A.32，30 B.32，29.5 C.32，27 D.30，27 E.29.5，27【答案】（A ）【解题过程】由表可知，男员工的平均年龄=32，女员工的平均年龄=27，男女员工人数之比=9:6=3:2，总平均年龄为305227332=⨯+⨯。
【考点】平均值问题。
3.某单位分段收费收网站流量（单位：GB ）费：每日20（含）GB 以内免，20到30（含）每GB 收1元，30到40（含）每GB 3元，40以上每GB 5元，小王本月用45GB 该交费（）元A.45B.65C.75D.85E.135【答案】（B ）【解题过程】应该缴费：10+10×3+5×5=65（元）。
【考点】分段计费。
4.圆O 是△ABC 内切圆△ABC 面积与周长比1:2，则图O 面积（）.A.πB.2πC.3πD.4πE.5π【答案】（A ）【解题过程】设内切圆的半径为r ，△的三边为c b a ,,，则2:1)(:2)(=++⨯++c b a rc b a ，化简可得1r =，圆的面积为π。
【考点】平面几何求面积问题。
2018管理类联考数学真题-张全军
2018届(2017年12月)管理类联考数学真题张全军整理一、问题求解：1.学科竞赛设一等奖、二等奖和三等奖. 比例为1:3:8，获奖率为30％，已知10人获一等奖，则参加竞赛的人数为( ).(A)300 (B)400 (C)500 (D)550 (E)6002.为了解某公司员工的年龄结构，按男女的比例进行随机检查，结果如下：)岁.(A)32, 30 (B)32, 29.5 (C)32, 27 (D)30, 27 (E)29.5, 273.某单位采取分段收费的方式收取网络流量（单位:GB）费用；每月流量20(含)以内免费;流量20-30(含)的每GB收费1元，流量30到40(含)的每GB收费3元，流量40以上的每GB 收费5元. 小王这个月用了45GB的流量，则他应该交费( )元.(A)45 (B)65 (C)75 (D)85 (E)1354.如图，圆O是三角形ABC的内切圆，若三角形ABC的面积与周长的大小之比为1:2，则圆O的面积为( ).(A)π(B)2π(C)3π(D)4π(E)5π5.设实数,a b 满足||2a b −=，33||26a b −=，则22a b +=( ).(A)30(B)22(C)15(D)13(E)106.有96位顾客至少购买了甲、乙、丙三种商品中的一种，经调查：同时购买甲、乙两种商品的有8位，同时购买甲、丙两种商品的有12位，同时购买乙、丙两种商品的有6位，三种同时购买有2位，则仅购买一种商品的顾客有( )位.(A)70(B)72(C)74(D)76(E)827.如图，四边形1A 1B 1C 1D 是平行四边形，2A ,2B ,2C ,2D 分别是1A 1B 1C 1D 四边的中点，3A ,3B ,3C ,3D 分别是2A 2B 2C 2D 四边的中点，依次下去，得到四边形序列m A m B m C mD (m =1，2，3…)，设m A m B m C m D 的面积为m S 且1S =12，则1S +2S +3S +…= ( ).(A)16(B)20(C)24(D)28(E)308.将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中，若指定的两张卡片要在同一组，则不同的袋法有( )种.(A)12(B)18(C)24(D)30(E)369.甲、乙两人进行围棋比赛，约定先胜2盘者赢得比赛；已知每盘棋甲获胜的概率是0.6，乙获胜的概率是0.4，若乙在第一盘获胜，则甲赢得比赛的概率为( ).(A)0.144(B)0.288(C)0.36(D)0.4(E)0.610.已知圆C:2x +2()y a −=b ，若圆C 在点(1,2)处的切线与y 轴的交点为(0,3)，则ab =( ).(A)-2(B)-1(C)0(D)1(E)211.羽毛球队有4名男运动和3名女运动员，从中选出两对参加混双比赛，则不同的选派方式有( )种.(A)9(B)18(C)24(D)36(E)7212.从标号为1到10的10张卡片中随机抽取2张，它们的标号之和能被5整除的概率为( ).(A)15(B)19(C)29(D)215(E)74513.某单位为检查3个部门的工作，由这3个都门的主任和外聘的3名人员组成检查组，2人一组检查工作，每组有1名外聘成员. 规定本部门主任不能检查本部门，则不同的安排方式有 ( )种.(A)6 (B)8(C)12(D)18(E)3614.如图，圆柱体的底面半径为2，高为3，垂直于底面的平面截圆柱体所得截面为矩形ABCD ，若弦AB 所对的圆心角是π３，则截掉部分(较小部分)的体积为( ).(A)3π−(B)26π−(C)2π−(D)2π− (E)π15.函数{}8,max )(22+−=x x x f 的最小值为( ).(A)8 (B)7(C)6(D)5(E)4二、条件充分性判断：16.设为x ，y 实数，则2x y +≤.(1)222x y +≤. (2)1xy ≤.17.设{}n a 为等差数列，则能确定129a a a +++的值.(1)已知1a 的值. (2)已知5a 的值.18.设m ,n 是正整数，则能确定m n +的值.(1)131m n +=. (2)121m n +=.19.甲、乙、丙三人的年收入成等比数列，则能确定乙的年收入的最大值.(1)已知甲、丙两人的年收入之和.(2)已知甲、丙两人的年收入之积.20.如图，在矩形ABCD 中，AE FC =，则三角形AED 与四边形BCFE 能拼接成一个直角三角形.(1)2EB FC =.(2)ED EF =.21.甲购买了若干件A 玩具，乙购买了若干件B 玩具送给幼儿园，甲比乙少花了100元，则能确定甲购买的玩具件数.(1)甲与乙共购买了50件玩具.(2)A 玩具的价格是B 玩具的2倍.22.已知点(,0)1,3(2,1)P m A B ，（），，点(,)x y 在三角形PAB 上，则x y －的最小值与最大值分别为－２和１.(1) 1.m ≤(2) 2.m ≥−23.如果甲公司的年终奖总额增加25%，乙公司的年终奖总额减少10%，两者相等，则能确定两公司的员工人数之比.(1)甲公司的人均年终奖与乙公司的相同.(2)两公司的员工人数之比与两公司的年终奖总额之比相等.24.,a b 为实数,则222x y y +=圆与直线x ay b +=不相交.(1)||a b −>(2)||a b +>25.设函数2()f x x ax =+，则()f x 的最小值与(())f f x 的最小值相等.(1)2a ≥.(2)0a ≤.。
MBA数学历年真题
1997年全国在职攻读工商管理硕士学位入学考试数学试题（本试卷满分为100分，考试时间为180分钟）一、选择题：本大题共20个小题，每小题2.5分,共50分。
1．若某人以1000元购买A 、B 、C 三种商品，且所有金额之比是1∶1.5∶2.5,则他购买A 、B 、C 三种商品的金额（单位：元）依次是A. 100, 300, 600B. 150, 225, 400C. 150, 300, 550D.200, 300, 500E. 200, 250, 5502. 某地连续举办三场国际商业足球比赛, 第二场观众比第一场少了80%, 第三场观众比第二场减少了50%,若第三场观众仅有2500人, 则第一场观众有A. 15000人B. 20000人C. 22500人D. 25000人E. 27500人3. 用一条绳子量井深, 若将绳子折成三折来量, 井外余绳4尺, 折成4折来量, 井外余绳1尺, 则井深是A. 6 尺B. 7尺C. 8尺D. 9尺E. 12尺4. 银行的一年期定期存款利率为10%, 某人于1991年1月1日存入1000元, 1994年1月1日取出, 若按复利计算, 他取出时所得的本金和利息共计是A. 10300元B.10303元C. 13000元D. 13310元E. 14641元 5. 某商品打九折会使销售增加20%, 则这一折扣会使销售额增加的百分比是 A. 18% B. 10% C. 8% D. 5% E. 2%的值是则的几何平均值是的两个实根，若是方程a x x a x x x x ,311076,.621221+=+-A. 2B. 3C. 4D. –2E. –35)23.(7x -的二项展开式中, 3x 的系数是A. –540B. –720C. –160D. 540E. 720 15. 函数xy 4=的一阶导数是A. x4 B. 14-x x C. x xln 4 D. 4ln 4x E. 4ln 4x16. 由方程xy e y=所确定的函数)(x y y =的导数'y 是A. x e y y -B. xe yy + C. y e x y - D. y e x y + E. y x e y -17.=⎰dx xf )3(63' A. )1()2(f f - B. [])1()2(3f f - C. [])1()2(31f f - D.[])1()2(31""f f - E. [])1()2(3""f f - 19. 若A 是3阶矩阵, 且TT A A A +=则,3=A. 6B. 2/3C. 24D. 12E. 9二、计算题：本大题共12小题，前10题每小题4分，后2题每小题5分，共计50分 。
2018年全国硕士研究生入学统一考试数学一试题及答案解析
2018年全国硕士研究生入学统一考试数学一试题及答案解析一、选择题（4分×8）1.下列函数在x = 0处不可导的是 （ ）A 、 ()sin f x x x = B、()f x x = C 、()cos f x x = D、()f x = 解 选D 。
由导数定义或左右导数与导数的关系可知：00sin lim lim 0,x x x x x x x x→→==故A 选项不正确；000x x →→==，故B 选项不正确；2002sin cos 12lim lim 0x x x x x x →→-==，故C 选项不正确；20002sin 12lim lim 2x x x x x x→→→-==-，极限不存在，故D 选项正确。
2. 过点(1,0,0),(0,1,0)，且与曲面22z x y =+相切的平面为 （ ）A 、 01z x y z =+-=与B 、022z x y z =+-=与2C 、1x y x y z =+-=与D 、22x y x y z =+-=与2解 选B 。
由已知，点(1,0,0),(0,1,0)在切平面上，而选项C ，D 显然不满足，故排除C ，D 。
又曲面22z x y =+上任一点(,,)x y z 处的法向量为(2,2,1)x y -，如选项A 正确，1x y z +-=的法向量为(1,1,1)-，可得切点的11,22x y ==，代入曲面方程得12z =，而代入1x y z +-=得0z =，矛盾，故排除A 选项。
3. 023(1)(21)!nn n n +∞=+-=+∑（ ） A 、 sin1cos1+ B 、2sin1cos1+C 、2sin12cos1+D 、2sin13cos1+解 选B 。
因00023212(1)(1)(1)(21)!(21)!(21)!nn n n n n n n n n n +∞+∞+∞===++-=-+-+++∑∑∑ 0011(1)2(1)cos12sin1(2)!(21)!n n n n n n +∞+∞===-+-=++∑∑。
2018联考数学真题答案及详细解析
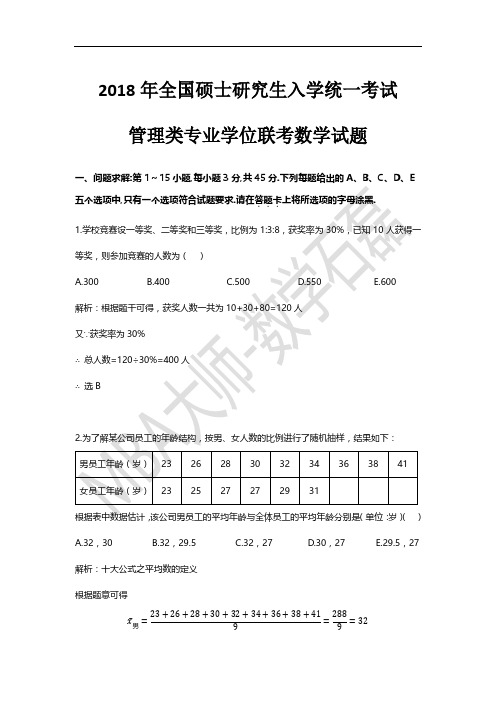
A.30
B.22
C.15
D.13
解析：由题干可得
������ = 3，������ = 1 ∴ ������2 + ������2 = 10 ∴ 选E
E.10
6.有 96 位顾客至少购买了甲、乙、丙三种商品中的一种，经调查：同时购买了甲、乙两种
商品的有 8 位，同时购买了甲、丙两种商品的有 12 位，同时购买了乙、丙两种商品的有 6
������ ������
解析：对于（1），������ = 2, ������ = 6、������ = 4, ������ = 4
对于（2），������ = 2, ������ = 4、������ = 3, ������ = 3
∴ 选D
������ + ������ = 8 ������ + ������ = 6
女员工年龄（岁） 23 25 27 27 29 31
根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是（单位：岁）( )
A.32，30
B.32，29.5
C.32，27
D.30，27
E.29.5，27
解析：十大公式之平均数的定义
根据题意可得
23 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 41 288
∴ 选D
12.从标号为 1 到 10 的 10 张卡片中随机抽取 2 张，它们的标号之和能被 5 整除的概率为
（）
A.1
B.1
5
9
解析：“M-W”模型
C.2
D. 2
E. 7
9
15
2018 年全国硕士研究生招生考试管理类联考综合真题及答案详解
第126页共344页2018年全国硕士研究生招生考试管理类专业学位联考综合能力试题一、问题求解：第1～15小题，每小题3分，共45分。
下列每题给出的A、B、C、D、E 五个选项中，只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
1.学科竞赛设一等奖、二等奖和三等奖，比例为1:3:8，获奖率为30%，已知10人获得一等奖，则参加竞赛的人数为（）.A.300B.400C.500D.550E.6002.为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：男员工年龄（岁）232628303234363841女员工年龄（岁）232527272931根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是（单位：岁）（）.A.32，30B.32，29.5C.32，27D.30，27E.29.5，273.某单位采取分段收费的方式收取网络流量（单位：GB）费用：每月流量20（含）以内免费，流量20到30（含）的每GB 收费1元，流量30到40（含）的每GB 收费3元，流量40以上的每GB 收费5元.小王这个月用了45GB 的流量，则他应该交费（）.A.45元B.65元C.75元D.85元E.135元4.如图1，圆O 是三角形ABC 的内切圆，若三角形ABC 的面积与周长的大小之比为1:2，则圆O 的面积为（）.A.πB.π2 C.π3 D.π4 E.π55.设实数b a ,满足26,233=-=-b a b a ，则=+22b a （）.A.30B.22C.15D.13E.106.将6张不同的卡片2张一组分别装入甲、乙、丙3个袋中，若指定2张卡片要在同一组，则不同的装法有（）.A.12种B.18种C.24种D.30种E.36种7.如图2，四边形1111D C B A 是平行四边形，2222,,,D C B A 分别是1111,,,D C B A 四边的中点，3333,,,D C B A 分别是四边形2222,,,D C B A 的中点，依次下去，得到四边形序列)3,2,1( ，=n D C B A n n n n .设n n n n D C B A 的面积为n S ，且121=S ，则=+++ 321S S S （）.A.16B.20C.24D.28E.308.甲、乙两人进行围棋比赛，约定先胜两局者赢得比赛.已知每盘棋甲获胜的概率为0.6，乙获胜的概率为0.4.若乙在第一局获胜，则甲赢得比赛的概率为（）.A.0.144B.0.288C.0.36D.0.4E.0.69.有96位顾客至少购买了甲、乙、丙三种商品中的一种，经调查:同时购买了甲、乙两种商品的有8位，同时购买了甲、丙两种商品的有12位，同时购买乙、丙两种商品的有6位，同时购买三种商品的有2位.则仅购买一种商品的顾客有（）.A.70位B.72位C.74位D.76位E.82位10.已知圆C ：b a y x =-+22)(.若圆C 在点（1,2）处的切线与y 轴的交点为（0,3），则=ab （）.A.-2B.-1C.0D.1E.211.羽毛球队有4名男运动员和3名女运动员，从中选出两对参加混双比赛，则不同的选派方式有（）.A.9种B.18种C.24种D.36种E.72种12.从标号为1到10的10张卡片中随机抽取2张，它们的标号之和能被5整除的概率为（）.A.51 B.91 C.92 D.152 E.45713.如图3，圆柱体的底面半径为2，高为3，垂直于底部的平面截圆柱体所得截面为矩形ABCD .若弦AB 所对的圆心角是3π，则截掉部分（较小部分）的体积为（）.A.3-π B.62-π C.233-π D.332-π E.3-π14.某单位为检查3个部门的工作，由3个部门的主任和外聘的3名人员组成检查组，分2人一组检查工作，每组有1名外聘成员.规定本部门主任不能检查本部门，则不同的安排方式有（）.A.6种B.8种C.12种D.18种E.36种15.函数{}8,max )(22+-=x x x f 的最小值为（）.A.8B.7C.6D.5E.4二.条件充分性判断：第16～25小题，每小题3分，共30分。
2018年全国硕士研究生入学统一考试《数学》真题及详解
2018年全国硕士研究生入学统一考试《数学》真题
(总分150, 考试时间180分钟)
一、单项选择题：1-8小题，每小题4分，共32分.下列每题给出的四个选项中，只有一个选项符合题目要求的，请将所选项前的字母填在答题卡指定位置上
1. f（x）=sinx/x（）
A 有界，奇
B 有界，偶
C 无界，奇
D 无界，偶
该问题分值: 4
答案:B
2.
A 单减少，凹
B 单减少，凸
C 单增加，凹
D 单增加，凸
该问题分值: 4
答案:D
3.
A 1/e
B 2/e
C 1+e/e2
D 2/e2
该问题分值: 4
答案:B
4. 已知Z=（x-y2）e1+xy，则|dz|（1，-1）=（）
A dx+2dy
B -dx+2dy
C dx-2dy
D -dx-2dy
该问题分值: 4
答案:A
5. 设向量组α1，α2，α3与向量α1，α2等价，则（）
A α1与α2线性相关
B α1与α2线性无关
C α1，α2，α3线性相关
D α1，α2，α3线性无关
该问题分值: 4
答案:C
6.
该问题分值: 4
由于矩阵形式比较简申只需要求解几个代数余子式带入验证即可，由于
7. 设随机变x，y相互独立，且x，y分别服从参数为1，2的泊松分布，则p{2x+y=2} = （）
该问题分值: 4
答案:C
8.
A Q统计量；服从分布t(10)
B Q统计量；服从分布t(9)
C Q不是统计量；服从分布t(10)
D Q统计量；服从分布t(9)
该问题分值: 4
答案:D。
(完整版)MBA历年试题解析
2009年10月在职攻读工商管理硕士学位全国联考综合能力数学试题一.问题求解（第15~1小题，每小题3分，共45分，下例每题给 出A 、B 、C 、D 、E 五个选项中，只有一项是符合试题要求的，请在答题卡上将所选项的字母涂黑）1. 已知某车间的男工人数比女工人数多80%,若在该车间的一次技术考核中全体工人的平均成绩为75分,而女工平均成绩比男工平均成绩高20%,则女工平均成绩为（）分。
（A ）88 （B ）86 （C ）84 （D ）82 （E ）80[点拨]未知量设少的一方容易计算。
解：设女工人数为x ，男工平均成绩为y ，则842.170758.18.12.1=⇒=⇒=+⨯+⨯y y xx x y x y ，选（C ）。
2.某人在市场上买猪肉，小贩称得肉重为4斤，但此人不放心，拿出一个自备的100克重的砝码，将肉与砝码一起让小贩用原秤复称，结果重量为25.4斤，由此可知顾客应要求小贩补猪肉（）两（A ）3 （B ）6 （C ）4 （D ）7 （E ）8[点拨]比例问题，但应先化为同一计量单位。
解：32405.22=⇒=x x ，应要求小贩补猪肉83240=-两。
选（E ）。
3. 甲、乙两商店某种商品的进价都是200元，甲店以高于进价20%的价格出售，乙店以高于进价15%的价格出售，结果乙店的售出件数是甲店的两倍，扣除营业税后乙店的利润比甲店多5400元。
若营业税率是营业额的5%，那么甲、乙两店售出该商品各为（）件（A ）450，900 （B ）500，1000 （C ）550，1100（D ）600，1200 （E ）650，1300[点拨]直接设甲店售出件数，在利用利润差。
解：设甲店售出x 件，则甲店的利润为 x x x 28%52.12002.0200=⨯⨯-⨯， 乙店的利润为 x x x 37%5215.1200215.0200=⨯⨯⨯-⨯⨯，60054002837=⇒=-x x x 。
2018管理类联考真题及答案
2018届管理类专业硕士研究生全国联考真题一、问题求解：第1—15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1、学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30％、已知10人获得一等奖，则参加竞赛的人数为（A）300 （B）400（C）500 （D）550（E）600【答案】B2、为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：根据表中数据估计，该公司男员工的平均年龄与全体员工的平均年龄分别是（单位：岁）（A）32，30 （B）32, 29.5（C）32, 27 （D）30, 27（E）29.5, 27【答案】A3、某单位采取分段收费的方式收取网络流量（单位：GB）费用：每月流量20（含）以内免费，流量20到30（含）的每GB收费1元，流量30到40（含）的每GB收费3元，流量40以上的每GB收费5元，小王这个月用了45GB的流量，则他应该交费（A）45元（B）65元（C）75元（D）85元（E）135元【答案】B4、如图，圆O是三角形ABC的内切圆，若三角形ABC的面积与周长的大小之比为1：2，则圆O的面积为【答案】A（A）π（B）2π（C）3π（D）4π（E）5π5、设实数,满足|-|=2，|-|=26, 则+=（A）30 （B）22（C）15 （D）13（E）10【答案】E6、甲、乙两人进行围棋比赛，约定先胜2盘者赢得比赛。
已知每盘棋甲获胜的概率是0.6，乙获胜的概率是0.4，若乙在第一盘获胜，则甲赢得比赛的概率为（A）0.144 （B）0.288（C）0.36 （D）0.4（E）0.6【答案】C7、如图，四边形平行四边形，, , ,分别是四边的中点，,,,分别是四边的中点，依次下去。
得到四边形序列（m=1，2，3…），设的面积为且=12，则+++…=（A）16 （B）20 （C）24 （D）28 （E）30 【答案】C8、已知圆+=b，若圆C在点（1.2）处的切线与y轴的交点为（0.3），则ab=（A）1-2 （B）-1 （C）0 （D）1 （E）2【答案】E9、有96位顾客至少购买了甲、乙、丙三种商品中的一种，经调查：同时购买甲、乙两种商品的有8位，同时购买甲、丙两种商品的有12位，同时购买乙、丙两种商品的有6位，三种同时购买有2位，则仅购买一种商品的顾客有（A）70位（B）72位（C）74位（D）76位（E）82位【答案】C10、将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中，若指定的两张卡片要在同一组，则不同的袋法有（A）12种（B）18种（C）24种（D）30种（E）36种【答案】B11、某单位为检查3个部门的工作。
2018年12月管理类联考数学真题-张全军
2019届(2018年12月)管理类联考数学真题-张全军张全军 整理一、问题求解1.某车间计划10天完成一项任务，工作3天后因故停工2天，但仍需要按计划完成任务，则工作效率需要提高( ).(A)20%(B)30%(C)40%(D)50%(E)60%2.设函数2()2(0)af x x a x=+> 在(0,)+∞的最小值为0()12f x =，则0x =( ). (A)5(B)4(C)3(D)2(E)13.某影城统计了一季度的观众人数，如图1，则一季度的男女观众人数之比为( ).(A)3:4(B) 5:6(C) 12:13(D)13:12(E) 4:34.设实数,a b 满足6,||||6ab a b a b =++−=，则22a b +=( ). (A)10(B)11(C)12(D)13(E)145.设圆C 与圆22(5)2x y −+=关于2y x =对称，则圆C 的方程为( ).(A)22(3)(4)2x y −+−= (B)22(4)(3)2x y ++−= (C)22(3)(4)2x y −++= (D)22(3)(4)2x y +++= (E)22(3)(4)2x y ++−=6.将一批树苗种在一个正方形花园边上，四角都种，如果每隔3m 种一棵树，那么剩下10棵树苗，如果每隔2m 种一棵，那么恰好种满正方形3条边，则这批树苗有( )棵.(A)54(B)60(C)70(D)82(E)947.在分别标记1、2、3、4、5、6的6张卡片里，甲抽取1张，乙从余下的卡片中再抽取2张，乙的卡片的数字之和大于甲的卡片数字的概率为( ).(A)1160(B)1360(C)4360(D)4760(E)49608.十名同学的语文和数学成绩如下：1212(A)E1>E2, δ1>δ2(B)E1>E2, δ1<δ2(C)E1>E2, δ1=δ2(D)E1<E2, δ1>δ2(E)E1<E2,δ1<δ29.如图，正方体于半径为3m球内，且一面位于球的大圆上，则正方体的表面积最大为( ).(A)12(B)18(C)24(D)30(E)3610.在三角形ABC中，AB=4，AC=6，BC=8，D为BC的中点，则AD=( ).(C)3(D)11.某单位要铺设草坪，若甲乙两公司合作需6天完成，工时费共2.4万元；若甲公司单独做4天后由乙公司接着做9天完成，工时费共计2.35万元；若由甲公司单独完成该项目，则工时费共计( )万元.(A)2.25(B)2.35(C)2.4(D)2.45(E)2.512.如下图，六边形ABCDEF 是平面与棱长为2的正方体所截得到的，若A 、B 、D 、E 分别为相应棱的中点，则六边形ABCDEF 的面积为( ).(A)2(C)(D)(E)13.火车行驶72千米用时1小时，其速度v 与行驶时间t 的关系如图所示，则v 0= ( ).(A)72(B)80(C)90(D)95(E)9614.某中学的5个学科各推荐2名教师作为支教候选人，若从中选派来自不同学科的2人参加支教工作，则不同的选派方式有( ).(A)20(B)24(C)30(D)40(E)4515.设数列{}n a 满足110,21n n a a a +=−=，则100a =( ).(A)9921−(B)992(C)9921+(D)10021−(E)10021+二、条件充分性判断：16.甲、乙、丙三人各自拥有不超过10本图书，甲丙购入2本图书后，他们拥有的图书数量构成等比数列，则能确定甲拥有图书的数量.(1)已知乙拥有的图书数量.(2)已知丙拥有的图书数量.17.有甲、乙两袋奖券，获奖率分别为p 和q ，某人从两袋中各随机抽取1张奖券，则此人获奖的概率不小于34. (1)已知p +q =1.(2)已知14pq =.18.直线y kx =与圆22430x y x +−+=有两个交点.(1)0k <<.(2)02k <<.19.能确定小明年龄.(1)小明年龄是完全平方数.(2)20年后小明年龄是完全平方数.20.关于x 的方程210x ax b ++−=有实根.(1)0a b +=.(2)0a b −=.21.如图，已知正方形ABCD 面积，O 为BC 上一点，P 为AO 的中点，Q 为DO 上一点，则能确定三角形PQD 面积.(1)O 为BC 的三等分点.(2)Q 为DO 的三等分点.22.设n 为正整数，则能确定n 除以5的余数.(1)已知n 除以2的余数. (2)已知n 除以3的余数.23.某校理学院五个系每年的录取人数如下表：(1)数学系录取平均分提高了3分，生物系录取平均分降低了2分. (2)化学系录取平均分提高了1分，地学系录取平均分降低了4分.24.设{}n a 的前n 项和为n S ，则数列{}n a 为等差数列.(1)2=2,1,2,3,n S n n n +=.(2)2=21,1,2,3,n S n n n ++=.25.设三角形区域D 由直线8560x y +−=，6420x y −+=与860kx y k −+−=(0)k <组成，则对于任意的(,)x y D ∈，22lg()2x y +≤.(1)(,1]k ∈−∞−.(2)1[1,)8k ∈−−.。