工程力学(静力学与材料力学)公式整理
工程力学知识点
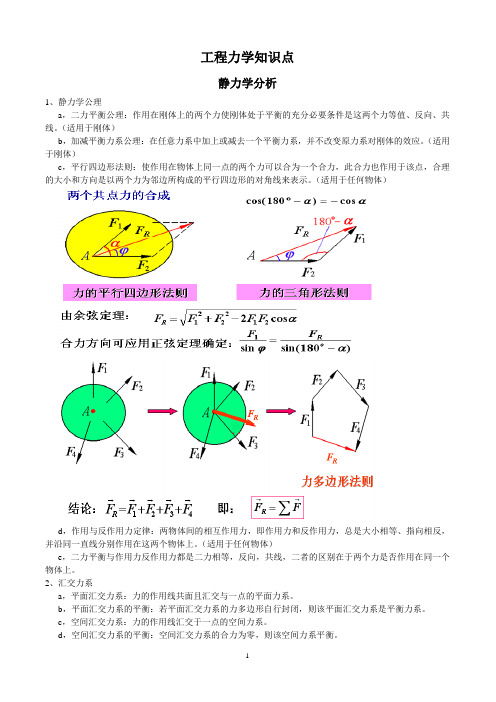
工程力学知识点静力学分析1、静力学公理a，二力平衡公理：作用在刚体上的两个力使刚体处于平衡的充分必要条件是这两个力等值、反向、共线。
（适用于刚体）b，加减平衡力系公理：在任意力系中加上或减去一个平衡力系，并不改变原力系对刚体的效应。
（适用于刚体）c，平行四边形法则：使作用在物体上同一点的两个力可以合为一个合力，此合力也作用于该点，合理的大小和方向是以两个力为邻边所构成的平行四边形的对角线来表示。
（适用于任何物体）d，作用与反作用力定律：两物体间的相互作用力，即作用力和反作用力，总是大小相等、指向相反，并沿同一直线分别作用在这两个物体上。
（适用于任何物体）e，二力平衡与作用力反作用力都是二力相等，反向，共线，二者的区别在于两个力是否作用在同一个物体上。
2、汇交力系a，平面汇交力系：力的作用线共面且汇交与一点的平面力系。
b，平面汇交力系的平衡：若平面汇交力系的力多边形自行封闭，则该平面汇交力系是平衡力系。
c，空间汇交力系：力的作用线汇交于一点的空间力系。
d，空间汇交力系的平衡：空间汇交力系的合力为零，则该空间力系平衡。
3、力系的简化结果a，平面汇交力系向汇交点外一点简化，其结果可能是①一个力②一个力和一个力偶。
但绝不可能是一个力偶。
b，平面力偶系向作用面内任一点简化，其结果可能是①一个力偶②合力偶为零的平衡力系c，平面任意力系向作用面内任一点简化，其结果可能是①一个力②一个力偶③一个力和一个力偶④处于平衡。
d，平面平行力系向作用面内任一点简化，其结果可能是①一个力②一个力偶③一个力和一个力偶④处于平衡。
e，平面任意力系平衡的充要条件是①力系的主矢为零②力系对于任意一点的主矩为零。
4、力偶的性质a，由于力偶只能产生转动效应，不产生移动效应，因此力偶不能与一个力等效，即力偶无合力，也就是说不能与一个力平衡。
b，作用于刚体上的力可以平移到任意一点，而不改变它对刚体的作用效应，但平移后必须附加一个力偶，附加力偶的力偶矩等于原力对于新作用点之矩，这就是力向一点平移定理。
材料力学公式完全版
材料力学公式完全版材料力学是研究材料在外力作用下的力学性质和变形行为的一门学科。
在材料力学中，有很多的公式被广泛应用于计算和分析材料的力学行为。
下面是一些常见的材料力学公式：1. 应力(Stress)：应力是单位面积上的力，通常用σ 表示，计算公式为：σ = F / A，其中 F 是力的大小，A 是面积。
2. 应变(Strain)：应变是物体在受力作用下发生变形的程度，通常用ε 表示，计算公式为：ε = ΔL / L，其中ΔL 是长度的变化量，L 是初始长度。
3. 弹性模量(Young's modulus)：弹性模量是衡量材料抵抗变形的能力的物理量，通常用 E 表示，计算公式为：E = σ / ε。
4. 剪切应力(Shear stress)：剪切应力是垂直方向上的切应力，通常用τ 表示，计算公式为：τ = F / A，其中 F 是切力的大小，A 是垂直于切力方向的面积。
5. 剪切应变(Shear strain)：剪切应变是物体在受剪切力作用下的变形程度，通常用γ 表示，计算公式为：γ = tanθ，其中θ 是切变角度。
6. 泊松比(Poisson's ratio)：泊松比是衡量材料横向收缩相对于纵向伸长的程度的物理量，通常用ν 表示，计算公式为：ν = -ε横 /ε纵。
7. 屈服强度(Yield strength)：屈服强度是材料开始产生塑性变形的临界点，通常用σy 表示。
8. 极限强度(Ultimate strength)：极限强度是材料在破坏前能承受的最大应力，通常用σu 表示。
9. 可延性(Elonagation)：可延性是材料在断裂前的拉伸变形量，通常用δ 表示，计算公式为：δ = (L - L0) / L0。
10. 硬度(Hardness)：硬度是材料抵抗划伤或压痕的能力，常用的硬度测量方法有布氏硬度、维氏硬度等。
11. 柯尔摩根关系(Hooke's law)：柯尔摩根关系是描述弹性固体在小应变下的力学行为的线性关系，计算公式为：σ = Eε，其中 E 是杨氏模量，σ 是应力，ε 是应变。
力学计算公式
力学计算公式Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】常用力学计算公式统计一、材料力学：1.轴力（轴向拉压杆的强度条件）σmax=N max/A≤[σ]其中，N为轴力，A为截面面积2.胡克定律（应力与应变的关系）σ=Eε或△L=NL/EA其中σ为应力，E为材料的弹性模量，ε为轴向应变，EA为杆件的刚度（表示杆件抵抗拉、压弹性变形的能力）3.剪应力（假定剪应力沿剪切面是均匀分布的）τ=Q/A Q其中，Q为剪力，A Q为剪切面面积4.静矩（是对一定的轴而言，同一图形对不同的坐标轴的静矩不同,如果参考轴通过图形的形心，则x c=0，y c=0，此时静矩等于零）对Z轴的静矩S z=∫A ydA=y c A其中：S为静矩，A为图形面积，y c为形心到坐标轴的距离，单位为m3。
5.惯性矩对y轴的惯性矩I y=∫A z2dA其中：A为图形面积，z为形心到y轴的距离，单位为m4常用简单图形的惯性矩矩形：I x=bh3/12，I y=hb3/12圆形：I z=πd4/64空心圆截面：I z=πD4（1-a4）/64，a=d/D（一）、求通过矩形形心的惯性矩求矩形通过形心，的惯性矩I x=∫Ay2dAdA=b·dy，则I x=∫h/2-h/2y2（bdy）=[by3/3]h/2-h/2=bh3/12 （二）、求过三角形一条边的惯性矩I x=∫Ay2dA，dA=b x·dy，b x=b·（h-y）/h则I x=∫h0（y2b（h-y）/h）dy=∫h0（y2b –y3b/h）dy=[by3/3]h0-[by4/4h]h0=bh3/126.梁正应力强度条件（梁的强度通常由横截面上的正应力控制）σmax=M max/W z≤[σ]其中：M为弯矩，W为抗弯截面系数。
7.超静定问题及其解法对一般超静定问题的解决办法是：（1）、根据静力学平衡条件列出应有的平衡方程；（2）、根据变形协调条件列出变形几何方程；（3）、根据力学与变形间的物理关系将变形几何方程改写成所需的补充方程。
材料力学公式大全
材料力学公式大全材料力学是研究材料在外力作用下的变形、破坏和稳定性等力学性能的学科。
在工程实践中，材料力学公式是工程师们进行材料设计、分析和计算的重要工具。
本文将为大家介绍一些常用的材料力学公式，希望能对大家有所帮助。
1. 应力和应变。
在材料力学中，应力和应变是最基本的概念。
应力是单位面积上的内力，通常用σ表示，其公式为：σ = F/A。
其中，F为受力，A为受力面积。
应变是材料单位长度的变形量，通常用ε表示，其公式为：ε = ΔL/L。
其中，ΔL为长度变化量，L为原始长度。
2. 弹性模量。
弹性模量是材料在弹性阶段的应力和应变关系的比例系数，通常用E表示，其公式为：E = σ/ε。
3. 餐极限。
屈服极限是材料在受力作用下开始发生塑性变形的应力值，通常用σy表示。
4. 断裂韧性。
断裂韧性是材料在破坏前所能吸收的能量，通常用K表示，其公式为：K = σ√πc。
其中，σ为应力，c为裂纹长度。
5. 疲劳强度。
疲劳强度是材料在交变应力作用下能够承受的最大应力值，通常用σf表示。
6. 塑性体积变形。
塑性体积变形是材料在塑性变形过程中体积的变化，通常用ΔV表示，其公式为：ΔV = V(ε1-ε2+ε3)。
其中，V为原始体积，ε1、ε2、ε3分别为三个主应变。
7. 岛壳理论。
岛壳理论是用于计算薄壁结构的强度和稳定性的理论，通常用T表示，其公式为：T = P/A。
其中，P为受力，A为受力面积。
8. 塑性流动理论。
塑性流动理论是用于描述金属材料在塑性变形过程中的流动规律的理论，通常用ε表示，其公式为：ε = ln(ε0/εf)。
其中，ε0为初始应变，εf为终止应变。
以上就是一些常用的材料力学公式，希望对大家有所帮助。
在工程实践中，我们可以根据具体情况选择合适的公式进行分析和计算，以保证工程设计的安全可靠性。
材料力学是一个复杂而又有趣的领域，希望大家能够在学习和工作中不断深入研究，提升自己的专业能力。
工程力学公式总结
刚体 力的三要素：大小、方向、作用点静力学公理：1力的平行四边形法则2二力平衡条件3加减平衡力系原理（1）力的可传性原理（2）三力平衡汇交定理4作用与反作用定律约束：柔索约束；光滑面约束；光滑圆柱（圆柱、固定铰链、向心轴承、辊轴支座）；链杆约束（二力杆） 平面汇交力系平衡的必要和充分条件是：力系的合力等于零。
平面汇交力系平衡几何条件：力多边形自行封闭合力投影定理合力在任一轴上的投影，等于各分力在同一轴上投影的代数和。
它表明了合力与分力在同一坐标轴投影时投影量之间的关系。
平面汇交力系平衡条件：∑F ix =0；∑F iy =0。
2个独立平衡方程 第三章 力矩 平面力偶系力矩M 0(F)=±Fh(逆时针为正) 合力矩定理：平面汇交力系的合力对平面上任一点力矩，等于力系中各分力对与同一点力矩的代数和。
Mo(F )=Mo(F1)+Mo(F 2)+...+Mo(F n)=∑Mo(F ) 力偶；由大小相等,方向相反，而作用线不重合的两个平行力组成的力系称为力偶 力偶矩M =±Fd(逆时针为正)力偶的性质：性质1 力偶既无合力，也不能和一个力平衡，力偶只能用力偶来平衡。
性质2 力偶对其作用面内任一点之矩恒为常数，且等于力偶矩，与矩心的位置无关。
性质3 力偶可在其作用面内任意转移，而不改变它对刚体的作用效果。
性质4 只要保持力偶矩的大小和转向不变，可以同时改变力偶中力的大小和力偶臂的长短， 而不改变其对刚体的作用效果。
平面力偶系平衡条件是合力偶矩等于零。
第四章 平面任意力系力的平移定理：将力从物体上的一个作用点,移动到另外一点上,额外加上一个力偶矩,其大小等于这个力乘以2点距离,方向为移动后的力与移动前力的反向力形成的力偶的反方向平面力向力系一点简化可得到一个作用在简化中心的主矢量和一个作用于原平面内的主矩，主矢量等于原力系中各力的矢量和，而主矩等于原力系中各力对点之矩的代数和。
平面任意力系平衡条件：∑F ix =0；∑F iy =0，∑M 0(Fi)=0。
工程力学公式大全-精选.pdf
wmax l
[ w] ， l
max
[]
16、（ 1）轴向载荷与横向载荷联合作用强度：
max ( min )
FN
M ห้องสมุดไป่ตู้ax
A WZ
（ 2）偏心拉伸 (偏心压缩 )： max ( min ) FN F A WZ
（ 3）弯扭变形杆件的强度计算：
r3
1 M 2 T2
1
M y2
M
2 z
T2
[]
WZ
WZ
r4
1 M 2 0.75T 2
6
32
13、 平面弯曲杆件横截面上的最大切应力：
max
FS S * zmax
K FS
bI Z
A
14、 平面弯曲杆件的强度校核： （ 1）弯曲正应力 t max [ t ] ， cmax [ c ]
（ 2）弯曲切应力 max [ ] （ 3）第三类危险点：第三和第四强度理论
15、 平面弯曲杆件刚度校核：叠加法
R
， IP
I
IP
WP
d4 (1
32
4) ，
WP
d3 (1
4 ) ，强度校核： max Tmax [ ]
16
WP
6、单位扭转角：
d dx
T
，刚度校核： max
GI P
T max
GI P
[ ] ，长度为 l 的一段轴两截
面之间的相对扭转角
Tl
，扭转外力偶的计算公式：
GI P
Me 9549 p( KW ) n( r /min)
tan 2 0
10、 第三和第四强度理论： 11、 平面弯曲杆件正应力：
r3
2 4 2 ， r4
工程力学知识点
工程力学知识点静力学分析1、静力学公理a，二力平衡公理：作用在刚体上的两个力使刚体处于平衡的充分必要条件是这两个力等值、反向、共线.（适用于刚体）b，加减平衡力系公理:在任意力系中加上或减去一个平衡力系，并不改变原力系对刚体的效应.（适用于刚体）c，平行四边形法则：使作用在物体上同一点的两个力可以合为一个合力，此合力也作用于该点，合理的大小和方向是以两个力为邻边所构成的平行四边形的对角线来表示。
（适用于任何物体) d，作用与反作用力定律:两物体间的相互作用力，即作用力和反作用力，总是大小相等、指向相反，并沿同一直线分别作用在这两个物体上。
（适用于任何物体）e,二力平衡与作用力反作用力都是二力相等，反向，共线，二者的区别在于两个力是否作用在同一个物体上。
2、汇交力系a，平面汇交力系：力的作用线共面且汇交与一点的平面力系.b,平面汇交力系的平衡：若平面汇交力系的力多边形自行封闭,则该平面汇交力系是平衡力系。
c,空间汇交力系：力的作用线汇交于一点的空间力系。
d，空间汇交力系的平衡：空间汇交力系的合力为零,则该空间力系平衡。
3、力系的简化结果a，平面汇交力系向汇交点外一点简化,其结果可能是①一个力②一个力和一个力偶.但绝不可能是一个力偶。
b，平面力偶系向作用面内任一点简化，其结果可能是①一个力偶②合力偶为零的平衡力系c，平面任意力系向作用面内任一点简化，其结果可能是①一个力②一个力偶③一个力和一个力偶④处于平衡。
d,平面平行力系向作用面内任一点简化,其结果可能是①一个力②一个力偶③一个力和一个力偶④处于平衡。
e，平面任意力系平衡的充要条件是①力系的主矢为零②力系对于任意一点的主矩为零。
4、力偶的性质a,由于力偶只能产生转动效应，不产生移动效应，因此力偶不能与一个力等效，即力偶无合力,也就是说不能与一个力平衡。
b,作用于刚体上的力可以平移到任意一点，而不改变它对刚体的作用效应，但平移后必须附加一个力偶，附加力偶的力偶矩等于原力对于新作用点之矩，这就是力向一点平移定理。
(完整word版)工程力学重点总结
第一章静力学的基本概念和公理受力图一、刚体P2 刚体：在力的作用下不会发生形变的物体。
力的三要素：大小、方向、作用点平衡：物体相对于惯性参考系处于静止或作匀速直线运动。
二、静力学公理1力的平行四边形法则：作用在物体上同一点的两个力，可以合成为仍作用于改点的一个合力，合力的大小和方向由这两个力为边构成的平行四边形的对角线矢量确定。
2二力平衡条件：作用在同一刚体上的两个力使刚体保持平衡的必要和充分条件是：这两个力的大小相等、方向相反，并且作用在同一直线上。
3加减平衡力系原理：作用于刚体的任何一个力系中，加上或减去任意一个平衡力系，并不改变原来力系对刚体的作用。
（1）力的可传性原理：作用在刚体上某点的力可沿其作用线移动到该刚体内的任意一点，而不改变该力对刚体的作用。
（2）三力平衡汇交定理：作用于刚体上三个相互平衡的力，若其中两个力的作用线汇于一点，则此三个力必在同一平面内，且第三个力的作用线通过汇交点。
4作用与反作用定律：两个物体间相互作用的力，即作用力和反作用力，总是大小相等，方向相反，作用线重合，并分别作用在两个物体上。
5 刚化原理：变形体在某一力系作用下处于平衡状态时，如假想将其刚化为刚体，则其平衡状态保持不变。
三、约束和约束反力P7 约束：1柔索约束：柔索只能承受拉力，只能阻碍物体沿着柔索伸长的方向运动，故约束反力通过柔索与物体的连接点，方位沿柔索本身，指向背离物体；2光滑面约束：约束反力通过接触点，沿接触面在接触点的公法线，并指向物体，即约束反力为压力；3光滑圆柱铰链约束：①圆柱、②固定铰链、③向心轴承：通过圆孔中心或轴心，方向不定的力，可正交分解为两个方向、大小不定的力；④辊轴支座：垂直于支撑面，通过圆孔中心，方向不定；4链杆约束（二力杆）：工程中将仅在两端通过光滑铰链与其他物体连接，中间又不受力作用的直杆或曲杆称为连杆或二力杆，当连杆仅受两铰链的约束力作用而处于平衡时，这两个约束反力必定大小相等、方向相反、沿着两端铰链中心的连线作用，具体指向待定。
《材料力学》公式汇总
《材料力学》公式汇总材料力学是研究材料的力学性质和性能的一门学科。
它主要研究材料力学性质的宏观表现以及材料在外界作用下的应力和应变的关系。
以下是一些常见的材料力学公式的汇总。
1.应力和应变的关系应力是指单位面积上的力，可以通过以下公式来计算：σ=F/A其中，σ表示应力，F表示作用在材料上的力，A表示力作用的面积。
应变是指物体长度、体积或形状的变化与原始尺寸之比，可以通过以下公式来计算：ε=ΔL/L其中，ε表示应变，ΔL表示长度的变化量，L表示原始长度。
2.弹性模量弹性模量描述了固体材料在受力后恢复原始形态的能力。
可以通过以下公式计算：E=σ/ε其中，E表示弹性模量，σ表示应力，ε表示应变。
3.轴向应力轴向应力是指作用在物体纵向的应力，可以通过以下公式计算：σ₁=F/A₀其中，σ₁表示轴向应力，F表示作用在材料上的力，A₀表示初始横截面积。
4.泊松比泊松比描述了材料在一方向受拉伸时，在垂直方向上的收缩。
可以通过以下公式计算：v=-ε₂/ε₁其中，v表示泊松比，ε₁表示纵向应变，ε₂表示横向应变。
5.剪切模量剪切模量描述了固体材料抵抗剪切变形的能力。
可以通过以下公式计算：G=τ/γ其中，G表示剪切模量，τ表示剪切应力，γ表示剪切应变。
6. Hooke定律Hooke定律描述了线性弹性材料在小应力下的应力-应变关系：σ=Eε其中，σ表示应力，E表示弹性模量，ε表示应变。
7.横向应力横向应力是指作用在物体横向的应力，可以通过以下公式计算：σ₂=vσ₁其中，σ₂表示横向应力，v表示泊松比，σ₁表示轴向应力。
8.斯特莱克斯公式斯特莱克斯公式描述了固体材料的切变模量和弹性模量的关系：G=E/2(1+v)其中，G表示剪切模量，E表示弹性模量，v表示泊松比。
9.薄壁压力容器的应力对于薄壁压力容器，其轴向应力和周向应力可以通过以下公式计算：σ₈=Pd/2tσ₆=Pd/4t其中，σ₈表示轴向应力，σ₆表示周向应力，P表示内压力，d表示容器的直径，t表示容器的壁厚。
工程力学公式总结
工程力学公式总结《工程力学》〔1〕、〔2〕是广播电视高校开放教育“水利水电工程专业”同学必修的技术基础课。
它包含理论力学〔静力学部分〕、材料力学和结构力学三部分内容。
它以高等数学、线性代数为基础，通过本课程的学习，培育同学具有初步对工程问题的简化技能，肯定的分析与计算技能，是学习有关后继课程和从事专业技术工作的基础。
本课程课内学时70，试验学时4。
通过本课程的学习，使同学掌控物体的受力分析、平衡条件及娴熟掌控平衡方程的应用；掌控基本构件的强度、刚度和稳定性问题的分析和计算；掌控平面杆件结构内力和位移的计算方法。
本课程的文字教材选用李前程、安学敏编著的《建筑力学》，由中国建筑工业出版社出版；并配有6讲电视课。
本课程按两学期开设，2000春开设《工程力学》〔1〕。
本学期的学习内容为该教材的前十章，并辅以“应用力学仿真试验”课件完成试验。
本学期课程的教学基本要求：1、掌控刚体平衡方程的应用。
2、掌控基本构件的强度、刚度和稳定性问题的分析。
3、了解杆件结构的基本组成规章。
4、掌控静定结构的内力和位移的计算方法二、基本内容、要求及学习要点第一章绪论〔一〕基本内容及要求1．结构与构件〔1〕理解结构的概念；〔2〕了解结构按其几何特征的三种分类。
2．刚体、变形体及其基本假设〔1〕了解建筑力学中物体的概念；〔2〕掌控在建筑力学中将物体抽象化为两种计算模型，以及刚体、抱负变形固体的概念及其主要区分。
〔3〕掌控弹性变形与塑性变形的概念。
3．杆件变形的基本形式〔1〕掌控轴向变形或压缩、剪切、扭转、弯曲四种基本变形的变形特点。
4．建筑力学的任务和内容〔1〕了解建筑力学的任务、目的，结构正常工作需要满意的要求；〔2〕掌控强度、刚度、稳定性的概念；〔3〕了解建筑力学的内容。
5．荷载的分类〔1〕掌控荷载的概念；〔2〕了解按荷载作用范围的分类及分布荷载、集中荷载的概念；〔3〕了解按荷载作用时间的分类及恒荷载、活荷载的概念；〔4〕了解按荷载作用性质的分类及静荷载、动荷载的概念及动荷载作用的基本特点。
材料力学基本公式
材料力学基本公式材料力学是研究物质在外力作用下的力学性能和变形规律的学科，是工程学科中的基础学科之一、在材料力学中，有许多基本公式被广泛应用于解决各种工程问题。
以下是材料力学中的一些基本公式。
1.杨氏模量公式：杨氏模量是材料刚度的度量，表示单位应变下单位应力的比例关系。
杨氏模量（E）的计算公式为：E = stress/strain其中stress为应力，strain为应变。
2.材料的胡克定律：胡克定律描述了物质在小应变条件下的弹性变形。
根据胡克定律，应力与应变之间的关系可以表示为：stress = E * strain其中E为杨氏模量。
3.线性弹性模量公式：线性弹性模量也是材料的刚度度量指标，用于描述材料在线弹性阶段的变形特性。
计算线性弹性模量（E）的公式为：E = (stress2 - stress1) / (strain2 - strain1)其中stress1和strain1为初始应力和应变，stress2和strain2为最终应力和应变。
4.泊松比公式：泊松比是一个描述材料在拉伸或压缩过程中沿着一维方向收缩或膨胀的程度的无量纲物理常数。
泊松比（v）的计算公式为：v = - (lateral strain) / (axial strain)其中lateral strain为横向应变，axial strain为轴向应变。
5.拉伸和压缩弹性模量公式：拉伸弹性模量（E）和压缩弹性模量（Ec）是描述材料在拉伸和压缩条件下的弹性变形能力的指标。
计算拉伸弹性模量的公式为：E = (stress2 - stress1) / (strain2 - strain1)计算压缩弹性模量的公式为：Ec = (stress2 - stress1) / (strain2 - strain1)其中stress1和strain1为初始应力和应变，stress2和strain2为最终应力和应变。
6.剪切模量公式：剪切模量用于描述材料在剪切应力作用下的抗剪切能力，是衡量材料的剪切刚度的指标。
工程力学公式总结
工程力学公式总结
哇塞，朋友们！今天咱就来讲讲工程力学公式总结。
你想想看，工程力学就像一个超级大宝藏，而这些公式就是打开宝藏大门的钥匙呀！
先来说说牛顿第二定律吧，F=ma，简单来说就是力等于质量乘加速度。
就好比你推一个大箱子，箱子越重，你得用更大的力才能让它动得快，这不是很明显嘛！比如小明要推动一个大柜子，累得气喘吁吁，就是因为柜子质量大，那需要的力也就大呀。
再看看胡克定律，F=kx，这就像一根弹簧，你拉它的长度变化和力是
成正比的。
你看那些蹦蹦床，人在上面跳来跳去，弹簧的伸缩不就是这个道理嘛！小红在蹦蹦床上玩得可欢了，就是因为弹簧的特性。
还有什么呢？对了，压强公式P=F/S。
压力除以受力面积就是压强啦。
你看我们踩在雪地上，有时候会陷进去，那就是我们对雪地的压强比较大呀。
要是穿上大鞋底，受力面积大了，压强就小啦，不就没那么容易陷进去了嘛。
小李穿着雪地靴在雪地里轻松行走，就是利用了这个道理呢！
还有很多很多其他的公式呢，每个公式都有它独特的用处和意义。
这些公式就像是我们解决问题的秘密武器呀，掌握了它们，我们就能在工程力学的世界里畅通无阻。
工程力学公式真的太重要啦，它们是我们探索和理解这个世界的有力工具，我们一定要好好钻研它们呀，让它们为我们的生活和工作带来更多的便利和惊喜！。
工程力学公式大全
工程力学公式:1、轴向拉压杆件截面正应力N F A σ=，强度校核max []σσ≤2、轴向拉压杆件变形Ni i iF l l EA ∆=∑3、伸长率：1100%l l l δ-=⨯断面收缩率：1100%A A Aψ-=⨯4、胡克定律：E σε=，泊松比：'ευε=-，剪切胡克定律：G τγ=5、扭转切应力表达式：T I ρρτρ=，最大切应力：max P P T T R I W τ==，44(1)32P d I πα=-，34(1)16P d W πα=-，强度校核：max max []PT W ττ=≤6、单位扭转角：P d T dx GI ϕθ==，刚度校核：max max []PT GI θθ=≤，长度为l 的一段轴两截面之间的相对扭转角P Tl GI ϕ=，扭转外力偶的计算公式：()(/min)9549KW r p Me n =7、薄壁圆管的扭转切应力：202TR τπδ=8、平面应力状态下斜截面应力的一般公式：cos 2sin 222x yx yx ασσσσσατα+-=+-，sin 2cos 22x yx ασστατα-=+9、平面应力状态三个主应力：22'()22x yx yx σσσσστ+-=++，22''()22x yx yx σσσσστ+-=-+，'''0σ= 最大切应力22max '''()22x yx σσσσττ--=±=±+，最大正应力方位02tan 2xx yτασσ=--10、第三和第四强度理论：2234r σστ=+，2243r σστ=+11、平面弯曲杆件正应力：Z My I σ=，截面上下对称时，ZM W σ=矩形的惯性矩表达式：312Z bh I =圆形的惯性矩表达式：44(1)64Z d I πα=- 矩形的抗扭截面系数：26Z bh W =，圆形的抗扭截面系数：34(1)32Z d W πα=- 13、平面弯曲杆件横截面上的最大切应力：max max *S z S Z F S F K bI Aτ== 14、平面弯曲杆件的强度校核：（1）弯曲正应力max []t t σσ≤，max []c c σσ≤（2）弯曲切应力max []ττ≤（3）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法max []w w l l≤，max []θθ≤ 16、（1）轴向载荷与横向载荷联合作用强度： max max min ()N ZF M A W σσ=± （2）偏心拉伸(偏心压缩)：max min ()N ZF F A W δσσ=± （3）弯扭变形杆件的强度计算： 22222311[]r y z ZZ M T M M T W W σσ=+=++≤222224110.750.75[]r y z Z Z M T M M T W W σσ=+=++≤。
材料力学基础公式
材料力学基础公式一、轴向拉压。
1. 内力 - 轴力（N）- 截面法：N = ∑ F_外（轴力等于截面一侧外力的代数和，拉力为正，压力为负）2. 应力 - 正应力（σ）- σ=(N)/(A)（A为横截面面积）3. 变形 - 轴向变形（Δ L）- 胡克定律：Δ L=(NL)/(EA)（L为杆件原长，E为弹性模量）- 线应变：varepsilon=(Δ L)/(L)，且σ = Evarepsilon二、扭转。
1. 内力 - 扭矩（T）- 截面法：T=∑ M_外（扭矩等于截面一侧外力偶矩的代数和，右手螺旋法则确定正负，拇指指向截面外法线为正）2. 应力 - 切应力（τ）- 对于圆轴扭转：τ=(Tρ)/(I_p)（ρ为所求点到圆心的距离，I_p为极惯性矩）- 在圆轴表面：τ_max=(T)/(W_t)（W_t为抗扭截面系数）3. 变形 - 扭转角（φ）- φ=(TL)/(GI_p)（G为剪切弹性模量）三、弯曲内力。
1. 剪力（V）和弯矩（M）- 截面法：- 剪力V=∑ F_y（截面一侧y方向外力的代数和）- 弯矩M=∑ M_z（截面一侧对z轴外力矩的代数和）- 剪力图和弯矩图：- 集中力作用处，剪力图有突变（突变值等于集中力大小），弯矩图有折角。
- 集中力偶作用处，弯矩图有突变（突变值等于集中力偶大小），剪力图无变化。
2. 弯曲正应力（σ）- σ=(My)/(I_z)（y为所求点到中性轴的距离，I_z为截面对z轴的惯性矩）- 最大正应力：σ_max=(M)/(W_z)（W_z为抗弯截面系数）3. 弯曲切应力（τ）- 对于矩形截面：τ=(VQ)/(Ib)（Q为所求点以上（或以下）部分面积对中性轴的静矩，b为截面宽度）- 对于圆形截面：τ=(4V)/(3A)（A为圆形截面面积）四、梁的变形。
1. 挠曲线近似微分方程。
- EIfrac{d^2y}{dx^2} = M(x)（y为挠度，x为梁轴线坐标）2. 用叠加法求梁的变形。
材料力学公式总结
材料力学公式总结材料力学是研究材料在外力作用下的力学性质和行为的学科。
它的研究对象包括材料的强度、刚度、塑性变形、断裂等方面的性质。
材料力学公式是用来描述和计算材料力学性质的数学表达式。
下面是材料力学公式的总结。
1. 杨氏模量（Young's modulus）：杨氏模量是衡量材料刚度的指标，表示材料在拉伸或压缩过程中的应力和应变之比。
杨氏模量的计算公式为：E=σ/ε其中，E为杨氏模量，σ为应力，ε为应变。
2. 泊松比（Poisson's ratio）：泊松比是描述材料压缩应变时的纵向收缩和横向膨胀之间的比例关系。
泊松比的计算公式为：ν=-ε横向/ε纵向其中，ν为泊松比，ε横向为横向应变，ε纵向为纵向应变。
3. 斯特劳斯公式（Stress-Strain Curve）：斯特劳斯公式描述了材料的应力和应变之间的关系。
在弹性阶段，应力和应变线性相关，即：σ=E*ε其中，σ为应力，E为杨氏模量，ε为应变。
4. 屈服强度（Yield Strength）：屈服强度是材料在超过弹性极限后开始发生塑性变形的应力。
屈服强度一般用屈服点上的应力值表示。
5. 弹性极限（Elastic Limit）：弹性极限是指材料在不发生塑性变形的最大应力值。
超过弹性极限后，材料将开始发生塑性变形。
6. 拉伸强度（Tensile Strength）：拉伸强度是材料在拉伸过程中最大的抗拉应力，表示材料抵抗破坏的能力。
7. 断裂强度（Fracture Strength）：断裂强度是材料发生破裂时所承受的应力。
它是材料在强度和脆性方面的一个重要指标。
8. 斯特劳斯硬化指数（Strain Hardening Exponent）：斯特劳斯硬化指数描述了材料在塑性变形时硬度增加的速率。
该指数可以通过材料力学实验和测试获得。
9. 塑性应变（Plastic Strain）：塑性应变是材料在超过弹性极限后发生塑性变形的应变量。
10. 线膨胀系数（Linear Expansion Coefficient）：线膨胀系数描述了材料在温度变化下长度变化的比例关系。
材料力学公式大全
材料力学公式大全1. 应力(stress)公式：应力是单位面积上的力，常用符号表示为σ。
在一维情况下，应力公式可以表示为:σ=F/A其中，σ是应力，F是作用力，A是力作用的面积。
2. 应变(strain)公式：应变是用于描述物体形变的量，常用符号表示为ε。
在一维情况下，应变公式可以表示为:ε=ΔL/L0其中，ε是应变，ΔL是变形长度，L0是原始长度。
3. 弹性模量(elastic modulus)公式：弹性模量是衡量材料对外力作用下变形能力的指标，常用符号表示为E。
在一维情况下，弹性模量公式可以表示为:E=σ/ε其中，E是弹性模量，σ是应力，ε是应变。
4. 屈服强度(yield strength)公式：屈服强度是材料在变形过程中开始发生塑性变形的临界应力，常用符号表示为σy。
屈服强度公式可以表示为:σy=Fy/A其中，σy是屈服强度，Fy是屈服点的作用力，A是力作用的面积。
5. 拉伸强度(tensile strength)公式：拉伸强度是材料在拉伸过程中最大的抗拉应力，常用符号表示为σts。
拉伸强度公式可以表示为:σts = Fmax / A其中，σts是拉伸强度，Fmax是最大作用力，A是力作用的面积。
6. 断裂强度(fracture strength)公式：断裂强度是材料在破坏前的最大抗拉应力，常用符号表示为σf。
断裂强度公式可以表示为:σf=Ff/A其中，σf是断裂强度，Ff是破坏点的作用力，A是力作用的面积。
以上是一些常用的材料力学公式，这些公式在材料力学的研究和实际应用中有着重要的作用。
通过对这些公式的使用和理解，我们可以更好地了解材料在受力下的性能和行为，对于材料的设计和实际应用有着重要的指导意义。
工程力学公式大全
扬州科技学院工程力学资料工程力学公式：1、轴向拉压杆件截面正应力N F Aσ=，强度校核max []σσ≤2、轴向拉压杆件变形Ni i iF l l EA ∆=∑3、伸长率：1100%l l l δ-=⨯断面收缩率：1100%A A Aψ-=⨯ 4、胡克定律：E σε=，泊松比：'ευε=-，剪切胡克定律：G τγ= 5、扭转切应力表达式：T I ρρτρ=，最大切应力：max P PT TR I W τ==，44(1)32P d I πα=-，34(1)16P d W πα=-，强度校核：maxmax []PT W ττ=≤ 6、单位扭转角：Pd Tdx GI ϕθ==，刚度校核：max max []PT GI θθ=≤，长度为l 的一段轴两截面之间的相对扭转角PTl GI ϕ=，扭转外力偶的计算公式：()(/min)9549KW r p Me n =7、薄壁圆管的扭转切应力：202TR τπδ=8、平面应力状态下斜截面应力的一般公式：cos 2sin 222x yx yx ασσσσσατα+-=+-，sin 2cos 22x yx ασστατα-=+9、平面应力状态三个主应力：'2x yσσσ+=，''2x yσσσ+='''0σ=最大切应力max '''2σστ-=±=，最大正应力方位02tan 2x x yτασσ=--10、第三和第四强度理论：3r σ=4r σ=11、平面弯曲杆件正应力：ZMy I σ=，截面上下对称时，ZM W σ=矩形的惯性矩表达式：312Z bh I =圆形的惯性矩表达式：44(1)64Z d I πα=-矩形的抗扭截面系数：26Z bh W =，圆形的抗扭截面系数：34(1)32Z d W πα=-13、平面弯曲杆件横截面上的最大切应力：max max *S z SZ F S FK bI Aτ==14、平面弯曲杆件的强度校核：（1）弯曲正应力max []t t σσ≤，max []c c σσ≤（2）弯曲切应力max []ττ≤（3）第三类危险点：第三和第四强度理论15、平面弯曲杆件刚度校核：叠加法max []w wl l≤，max []θθ≤ 16、（1）轴向载荷与横向载荷联合作用强度： maxmax min ()N ZF M A W σσ=±（2）偏心拉伸(偏心压缩)：max min ()N ZF F A W δσσ=±（3）弯扭变形杆件的强度计算：22222311[]r y z Z M T M M T W W σσ=+=++≤222224110.750.75[]r y z ZZM T M M T W W σσ=+=++≤机械制图方面=>齿轮计算公式1 齿轮模数：m=p/π齿轮模数m=齿距p 除以 3.14测绘时的简易计算m=齿顶圆直径（外径）d 除以（齿数z+2）2 齿轮分度圆直径：d=mz分度圆直径d=模数m 乘以齿数z3 齿轮压力角：标准齿轮的压力角为20度压力角标准为20度其他还有14.5度17.5度15度25度和28度4 齿轮变位系数：用范成法加工齿轮时，刀具中心线不与齿轮的分度圆相切，刀具中心与齿轮的分度圆的距离除以模数所得的商就是齿轮的变位系数。