三等厚度轮盘的应力计算
力学专业课程毕业论文高速回转圆盘的应力与应变理论分析

高速回转圆盘的应力与应变理论分析由于结构在真空环境下进行髙速的回转运动,在支撑、阻力的影响都忽略的情况下,首先想到结构是由于离心力的作用而发生的破坏。
目前工程上常用的计算髙速回转圆盘的方法有两种:一种是二次应力法,它是将圆盘简化为平面应力问题来求解,列出力平衡的微分方程;另一种方法是采用有限元法。
一、轮盘应力分析的一般理论回转圆盘的应力应该是三向应力,即径向应力周向应力轴向应力但由于轴向应力通常较径向应力和周向应力小得多,可认为回转圆盘仅受两向应力而把轴向应力 O■。
略去不计。
对于轴向厚度小于外直径1/4的薄圆盘是比较合适的。
图所示圆盘,盘的内半径为心,外半径为尺°,厚度y比外半径要小得多,且随半径r 而变化。
当该盘以角速度回转①在回转圆盘上切岀一个微块,当圆盘以角速度血旋转时,该微块的离心力为dp = dm・厂ar = pdV ・ rco" = pyrco^drdO图x・x变厚度圆盘在离心力作用下受力分析 a)对微元体进行受力分析:微元体所受到的载荷:①上表而径向力小②下表面径向力碍:③轴向载荷久④离心力dpb)对微元体列写平衡方程:de dy d0 7 ?(er,. + —— Jr)(y +—Jr)(r + dr)dO一a r yrdO一2(r&ydrsin ——+ pyrco^drdO = 0 dr dr 2由于是一个微量,所以sin —2 2 整理上式,并略去髙阶微量得E / x E (du咕口7(6*>刁乔七 刃=(% + 〃£)=__r —+“1 一“1一〃 "经化简,并令如得即为任意不等厚回转圆盘在离心力作用下产生变形的微分方程。
二.几种特殊情况2.1等厚度盘对于等厚度盘,尸常量,因此—=0,叫翌=0 dr dr 于是d^it 1 du u一 + ------ -- — = -Ardr r dr 厂几何方程: 物理方程:(2,2)(2,4)f 1 丄〃(In y)) du 'M(ln y) _ 1 L lrdr ) drk rdrr 2 丿(2,5)(2,6)将上式代入式d 2u= -Ar或者1 cl(ur)= -Ar积分得“ =—d/+c/+£i,式中G G为积分常数。
旋转圆盘应力计算

旋转圆盘应力计算一、几何模型及计算相关参数本题用全三维模型计算旋转等温等厚空心圆盘周向应力和径向应力随半径变化规律。
圆盘的计算参数如下:圆盘外半径Ra=0.27m内半径R0=0.1m圆盘厚度2mm材料密度7800kg/m3弹性模量E=2e5泊松比υ =0.3转速盘缘无外载,无温度载荷二、有限元模型有限元全三维模型如下图定义的单元类型为solid186,单元数为121,节点数为972,位移边界条件为:两个关键点施加X方向约束,两个关键点施加Y方向约束,三个节点施加Z方向约束,网格信息如下图:三、计算结果计算后的周向应力和径向应力分布云图如下:设置一条路径,均分20段,XG从0.1变化到0.27。
径向应力SX和轴向应力SY变化如下计算数据XG 0.1 0.1085 0.117 0.1255 0.134 0.1425 0.151 SX 0.00E+00 1.43E+07 3.63E+07 5.82E+07 7.63E+07 8.01E+07 8.39E+07 SY 4.85E+08 4.56E+08 4.25E+08 3.93E+08 3.65E+08 3.48E+08 3.31E+080.1595 0.168 0.1765 0.185 0.1935 0.202 0.21058.77E+07 9.14E+07 9.24E+07 8.68E+07 8.12E+07 7.57E+07 7.02E+073.15E+08 2.98E+08 2.84E+08 2.73E+08 2.61E+08 2.50E+08 2.39E+080.219 0.2275 0.236 0.2445 0.253 0.2615 0.276.47E+07 5.57E+07 4.49E+07 3.40E+07 2.30E+07 1.21E+07 1.04E+062.27E+08 2.17E+08 2.06E+08 1.96E+08 1.86E+08 1.75E+08 1.65E+08四、网格加密收敛性检验加密后网格模型如下定义的单元类型为solid186,单元数为2295,节点数为16650,网格信息如下图:应力随半径变化计算结果如下:同样和上次一样,计算数据如下:XG 9.95E-02 0.10803 0.11655 0.12506 0.13358 0.14209 0.15061 0.15912 SX 83899 2.92E+07 5.07E+07 6.67E+07 7.79E+07 8.54E+07 9.02E+07 9.26E+07 SY 4.83E+08 4.45E+08 4.13E+08 3.87E+08 3.65E+08 3.45E+08 3.28E+08 3.12E+08 0.16764 0.17615 0.18467 0.19318 0.2017 0.21021 0.21873 0.22724 9.28E+07 9.12E+07 8.80E+07 8.36E+07 7.79E+07 7.12E+07 6.35E+07 5.49E+07 2.98E+08 2.84E+08 2.72E+08 2.60E+08 2.49E+08 2.38E+08 2.27E+08 2.16E+08 0.23576 0.24427 0.25279 0.2613 0.26982 4.54E+07 3.52E+07 2.41E+07 1.24E+07 35907 2.06E+08 1.95E+08 1.85E+08 1.74E+08 1.64E+08加密后的网格计算结果在图线上看来更加精确,可以判断出随着网格划分的越精细,有限元计算机误差会更小,故收敛性检验成功。
ANSYS关于等厚旋转圆盘的模拟与验证

ANSYS关于等厚旋转圆盘的模拟与验证
下图引自->弹性力学--第四版--上册--徐芝纶,关于等厚旋转圆盘的径向及环向应力计算公式(第70页),采用ANSYS对其进行模拟与验证以说明等厚旋转圆盘的径向及环向应力计算公式的合理及ANSYS处理问题的强力,图中, 为密度(ANSYS实例取7.85e-9t/mm3), 为角速度(ANSYS实例取10rad/s), 为圆盘外径(ANSYS实例取100mm), 为泊松比(ANSYS实例取0.29)。
图1 等厚旋转圆盘应力计算公式
采用plane183单元,材料为钢材,属性:弹性模量E=2.06E5MPa,泊松比μ=0.29,密度ρ=7.85e-9t/mm3,圆盘有限元模型示意图见图2。
图2 有限元模型示意图
图3为圆盘径向应力图,图4为圆盘环向应力图,选取圆盘中心及边缘位置应力数值模拟值及理论公式计算值进行对比,见表1,二者相差比较小,表明理论公式与数值模拟具有很好的一致性,不得不惊叹于前人的理论功底与ANSYS的强力!
图3 圆盘径向应力云图
图4 圆盘环向应力云图
表1 旋转圆盘有限元模拟及理论计算对比
圆盘中心径向及环向应力值/MPa 圆盘边缘径向
应力值/MPa
圆盘边缘环向
应力值/MPa
理论值0.003228 0 0.001393 模拟值0.003229 -4.756e-6 0.001393。
第6章 高速回转元件的强度和转轴的临界转速讲诉

2 Ra2
R02
Ra2 R02 R2
1 3 3
R2 当R
R0时,内孔处周向应力为最大
t0
27
t0
3
8
2
Ra2
R02
Ra2 R02 R0 2
1 3 3
R0 2
2
4 3600
3
1
8
2、受力分析
1)作用在内表面的径向应力 r
N2 r Rd y 2)作用在外表面的径向应力 r d r
径向力 N1 ( r d r )(R dR)d ( y dy)
3)作用在两侧面的周向应力 t
周向力在垂直方向的分力
F
sin
2
t
(3
) Ra2
(1
) R02
在轮盘外径R=Ra处,
( r )Ra 0
( t )Ra
2 4
(3 )R02 (1 )Ra2
(v)Ra
2 4E
Ra
(3
) R02
(1
) Ra2
r
3 8
2 Ra2
R02 R2
Ra2 R02
ra
R02
Ra2 R2
Ra2
1 R02
r
0
3
8
2 Ra2
R02
Ra2 R02 R2
R2
t
某航空发动机涡轮盘和叶片的强度分析与寿命计算

西北工业人学硕士学位论文第三章(2)采用大枞树形榫头榫槽;(3)涡轮盘的前后端面还有轴向凸边,凸边外缘车有封严蓖齿,在涡轮盘的前面有加装平衡块的径向凸缘,凸缘上钻有小孔。
3.3.2涡轮盘的有限元计算模型1.实体模型的建立为了减少计算时间,提高效率,切去封严蓖齿及凸缘上的小孔。
涡轮盘在结构上呈现旋转周期性(捌,即绕其转轴转动口=2n,/N(N为叶片数)角度后,结构的几何形状和转动前完全一样。
取5.29。
的扇形对称体进行三维有限元计算,这样在该扇区沿周向拷贝68份之后,恰好为整个涡轮盘。
涡轮盘的计算模型在UG中建立,整体轮盘模型如图3.1所示;取其1/68扇形区域如图3.2所示。
计算坐标系采用柱坐标系,其中x轴表示涡轮盘的径向,Y轴表示周向,z轴表示轴向,坐标原点位于轮盘形心。
图3.1整体涡轮盘模型图3.21/68扇形区模型2.有限元网格的划分由于涡轮盘的形状不规则,因而使得对模型进行的有限元划分变得十分困难。
在圆角过渡等区域经常出现包含奇异角的单元,在计算过程中会在造成刚度矩阵奇异.使计算失败,这就需要手工划分来避免奇异单元的产生。
而且,在划分时,容易产生应力集中的区域采用较密的网格,同时为了减少单元的数量,需要进行疏密过渡。
在模型划分好后,仔细检查模型是否有缺陷存在,若塑!!三些查兰堡主兰堡堕塞堑三童模型中包含了不为人知的单元空洞、重合节点等缺陷,会造成计算结果不准确,严重的还会使计算根本偏离了预期方向,甚至使计算进行不下去。
对于涡轮盘的有限元网格均采用六面体八节点单元。
考虑到轮盘比较复杂,为了能够划分六面体单元,对涡轮盘的实体几何模型进行了分割,其中涡轮盘轮缘以E榫槽部分分割为18个体,划分为546个单元,1143个节点,如图3.3所示;轮缘以下部分分割为20个体,划分了1070个单元,1603个节点,如图3.4所示。
(a)儿何模型(b)有限元模型幽3.3涡轮盘榫槽部分有限元模型(a)儿何模型(b)有限元模型图3.4涡轮柱扇区有限元模型3.4涡轮盘的材料参数该型发动机涡轮盘采用GH4169合金材料,它是以体心四方的广和面心立方的/相沉淀强化的镍基高温合金,在一253~700。
滚动轴承的受力分析、载荷计算、失效和计算准则
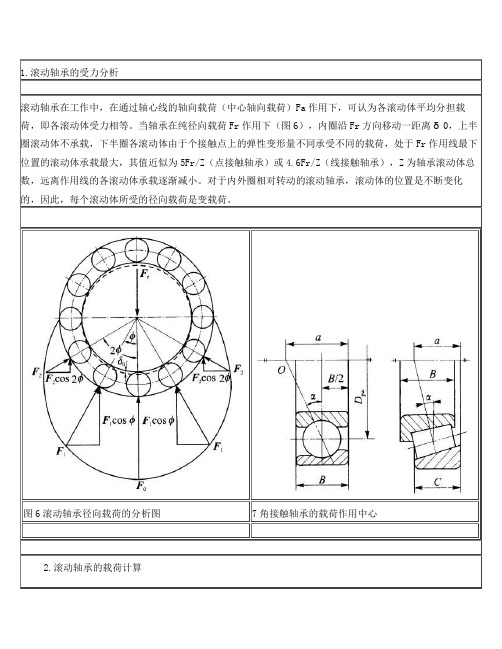
Fr /(2Y)
角接触轴承附加轴向力的方向是由轴承外圈的宽边指向窄边,通过内圈作用于轴上。角接触轴承一般应成对使用。
图9角接触轴承所受的轴向载荷
计算角接触轴承所受的轴向载荷Fa1、Fa2时,要同时考虑附加轴向力FSl、FS2和作用于轴上的其他工作轴向力FA。如图9,若FSl+FA>FS2,由于轴承Ⅱ的右端已固定,轴不能向右移动,根据轴系轴向力的平衡关系,则Fa2= FSl+FA;同理,若FS2>FSl+FA,则Fa2 = FS2。因此,轴承Ⅱ所受的轴向力必然是下列两值中较大者
Fa2 = FS2(2)
Fa2= FSl+FA(-3)
用同样方法分析,可得轴承Ⅰ所受的轴向力是下列两值中较大者
Fa1= FSl(4)
Fa1 = FS2-FA(5)
当轴上轴向力FA与图示方向相反时,FA应取负值。
3.滚动轴承的失效和计算准则
滚动轴承的主要失效形式有:
(1)滚道和滚动体表的疲劳点蚀滚动轴承工作时内、外套圈间有相对运动,滚动体既自转又围绕轴承中心公转,滚动体和套圈分别受到不同的脉动接触应力。工作若干时间后,各元件接触表面上都可能发生接触疲劳点蚀。点蚀会使轴承工作时振动、噪声和发热急剧增大。
计算各种角接触轴承附加轴向力的公式可查表5。表中Fr为轴承的径向载荷;e为判断系数,查表6;Y为圆锥滚子轴承的轴向动载荷系数,查表7。
表-5角接触轴承附加轴向力公式
轴承类型
角接触球轴承
圆锥滚子轴承
70000C(α=15°)
70000AC(α=25°)
70000B(α=40°)
30000
FS
eFr
0.68Fr
角接触轴承受径向载荷Fr时,会产生附加轴向力FS。图8所示轴承下半圈第i个球受径向力Fri。由于轴承外圈接触点法线与轴承中心平面有接触角α,通过接触点法线对轴承内圈和轴的法向反力Fi将产生径向分力Fri;和轴向分力FSi。各球的轴向分力之和即为轴承的附加轴向力FS。按一半滚动体受力进行分析,有
4-72-11 №10 叶轮后盘切应力计算
据
1.2.05 050301-5 4-72-11 №10 风机叶轮后盘最大切应力计算 ( 参考《风机手册》第2版 第五章第三节第一小节 例 (5-5)) 专利代号:ZL 02 2 14256 .8 (安装软件:Excel 2003) 第五章 风机的用途、结构、材料、强度
( 黑三角 ▲ 置换法 )
第三节 风机强度计算
一、通风机的强度计算
例 (5-5) 4-72-11 №10 离心通风机叶轮后盘为钢板制成的等厚圆盘。
在已知圆盘厚度、内外径、叶轮最大转速、单个叶片质量、叶轮中心至
叶片重心的半径、叶片数量等条件下,求叶轮后盘的最大切应力。
(见正文图5-51 图5-52 图5-53)
解 4-72-11 №10 风机叶轮后盘最大切应力计算见下表
( 续 )
( 续 )
ψ
ϕ
ψ
ψ
ϕ
ψ
警示:在上述表中的 ▲ 表示 :
1) 在右侧单元格中用新的数值置换上一次试验时用过的数值
2) 或者默认在右侧单元格中保留了上一次试验时用过的数值,而不需作任何工作。
以下全同。
3) 必须确认上述两项确实实现
4) 一定要重新置换、默认,否则你所见到的是上一次试验时采用过的(这一次应置换)数值残留。
材料
σ
]130
s σ=]180
s σ=
图5-51 等厚圆盘
a)后(中盘)、平前盘 b) 圆锥前盘 c) 圆弧前盘
图5-52 圆盘重心示意图
图5-53 叶片离心力示意图
编写人员:
青岛大学程利荣
大连海事大学袁川广
南方航空樊斌
沈阳鼓风机研究所续魁昌
临沂市风机厂盖京方魏如彬路新艳张京亮孔祥飞。
滚动轴承的校核计算及公式

滚动轴承的校核计算及公式1 基本概念1.轴承寿命:轴承中任一元件出现疲劳剥落扩展迹象前运转的总转数或一定转速下的工作小时数。
批量生产的元件,由于材料的不均匀性,导致轴承的寿命有很大的离散性,最长和最短的寿命可达几十倍,必须采用统计的方法进行处理。
2.基本额定寿命:是指90%可靠度、常用材料和加工质量、常规运转条件下的寿命,以符号L10(r)或L10h(h)表示。
3.基本额定动载荷(C):基本额定寿命为一百万转(106)时轴承所能承受的恒定载荷。
即在基本额定动载荷作用下,轴承可以工作106 转而不发生点蚀失效,其可靠度为90%。
基本额定动载荷大,轴承抗疲劳的承载能力相应较强。
4.基本额定静载荷(径向C0r,轴向C0a):是指轴承最大载荷滚动体与滚道接触中心处引起以下接触应力时所相当的假象径向载荷或中心轴向静载荷。
在设计中常用到滚动轴承的三个基本参数:满足一定疲劳寿命要求的基本额定动载荷Cr(径向)或Ca(轴向),满足一定静强度要求的基本额定静强度C0r(径向)或C0a(轴向)和控制轴承磨损的极限转速N0。
各种轴承性能指标值C、C0、N0等可查有关手册。
2 寿命校核计算公式图17-6滚动轴承的寿命随载荷的增大而降低,寿命与载荷的关系曲线如图17-6,其曲线方程为PεL10=常数其中 P-当量动载荷,N;L10-基本额定寿命,常以106r为单位(当寿命为一百万转时,L10=1);ε-寿命指数,球轴承ε=3,滚子轴承ε=10/3。
由手册查得的基本额定动载荷C是以L10=1、可靠度为90%为依据的。
由此可得当轴承的当量动载荷为P时以转速为单位的基本额定寿命L10为Cε×1=Pε×L10L10=(C/P)ε 106r (17.6)若轴承工作转速为n r/min,可求出以小时数为单位的基本额定寿命h (17.7)应取L10≥L h'。
L h '为轴承的预期使用寿命。
通常参照机器大修期限的预期使用寿命。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2个子午面,所以有:
(D)
由平衡条件得到:
'
d (E) Fr dF Fr 2 F sin( ) 0 2
将(A)、(B)、(C)、(D)代入式(E),并因 为d 很小, sin( d ) d 同时略去高阶微量,整理 2 2 得到:
t d r dB 1 ( ) r R 2 0 dR BdR R R
流体机械现代设计(二)
——强度校核
(安全)
前言
研究内容
1. 叶轮的安全——足够的强度 2. 轴承的安全——振动(临界转速) ——位移(轴向推力)
3. 轴承的承载
第一章 轮盘应力分析及强度计算
• 一. 工作与失效(叶轮) • 1. 工作情况:整个机器(系统)的心脏。靠一定的过 盈或键配在轴上,在转轴的带动下,高速运转,传递 • 能量。 • 2. 受力情况: (1) 整个叶轮:承受离心力 • (2)内孔处:挤压力 • (3)气体压力(一般可忽略) • 3. 失效情况: (1)在离心力的作用下破坏 • (2)在高速下松脱(过盈量的问题)
(1-2a)
且有虎克定律:
E r ( r t ) 2 1
E t ( t r ) 2 1
将(1-2)(1-3)代入式(1-1)得:
(1-2b)
d 2 d (ln B) 1 d d (ln B) 1 2 AR 0 2 R dR RdR dR dR R
(1-1)
上式即为轮盘应力状态的微分方程。
又由材料力学和图1-1知,切向应变和径向应变与径向 变形 之间的关系为: (不考虑热应力)
( R )d Rd C D CD t = Rd R CD
' '
A' B ' AB dR d dR d r AB dR dR
a2 A 2 (1 )a1 (1 ) 2 (1 3 ) R j 8 R j
a1
和
a2
为未知数,解上式,可得:
AR j 1 1 a1 rj tj 2E 2E 4
2
AR j 1 E 2 1 2 a2 R j tj R j rj 2E 2E 8
• 4. 安全可靠的准则: • (1)一般要求:
s :屈服极限(手册)
s k 1.8 max
k: 安全系数(行业标准)
• 5 本章最终研究对象(内容):
max
二. 轮盘(叶轮)应力计算的微分方程
叶轮以角速度
旋转,取一微元体(见书图1-1)
不考虑热应力,则受力分析如下:
1)微元体的离心力
和 a 2 ,即可以求出应力
r
和
t
若以下标“j”表示某轮盘段的内径,则有R j 或 D j 又若已知某轮盘段内径 R j(或 D j )处的应力 rj 和, tj 显然,他们也应满足式(1-5), 所以则应该有:
E rj 1 2
E tj 1 2
上式只有
a2 A 2 (1 )a1 (1 ) 2 (3 ) R j 8 Rj
(1-3)
式中:
1 A E
2
2
——材料的泊松比 E ——材料的弹性模量 ——材料密度
——轮盘旋转角速度
式(1-3)是 用变形来表示的旋转轮盘的基本方程, 解方程,可以得到径向变形,再借助式(1-2a)和 (1-2b))即可求出应力的大小。
三. 等厚度轮盘的应力计算
“厚度”即轴向宽度。等厚度,即轮盘厚度B(R)=常数。
由(1-3)式可知,当B(R)=常数时,式(1-3)变为:
d 1 d 1 2 AR 2 R dR R dR
2
(1-4)
上式可整理为: d 1 d (R) AR
dR R dR
上式积分一次,得: d
A 3 (R) R 2a1 R dR 2
a2 A 2 (1 )a1 (1 ) R 2 (3 ) 8 R
(1-5)
E t 1 2
a2 A 2 (1 )a1 (1 ) R 2 (1 3 ) 8 R
分析上式,可知,只要求出积分常数 a1
2
dF
,方向为径向向外
2
dF dm R BR d dR R
2)在半径为R的圆柱面上均布径向应力 合力为Fr, 方向向内
r
(A)
,其 (B)
Fr r BR d
图1.1
3)在半径为(R+dR)的圆柱面上均布径向应 力
'
r d r
' ,其合力为 Fr ,方向向外:
等 厚 度 轮 盘
a A 3 再积分一次得: R a1 R 2 8 R
上式对R微分一次,得:
(A)
a2 d 3 2 AR a1 2 dR 8 R
(B)
式中:a1、a2为积分常数。
将式(A)、(B)代回式(1-2a),式(1-2a)再代入 (1-2b)得:
E r 1 2
4
解出 a1 和 a 2 后,将上式代回式(1-5)(即任一截 面半径处的应力表达式),且令:
①
Rj
Di x R D
1 x2 ② r t 2
③
1 x2 ,t r 2
(1-6)
c 27.5(3.3 2.6x 2 0.7x 4 )
c 27.5(1.9 2.6x 0.7 x )
Fr ( r d r ) ( B dB) ( R dR) d (C)
4) 夹角为 d 的微元体两侧面为切向应力 t ,其合 力为 F,方向与对应的子午面垂直,大小为:
F t 向向内)
d d F sin( ) t B dR sin( ) 2 2
