7多组定量资料的比较
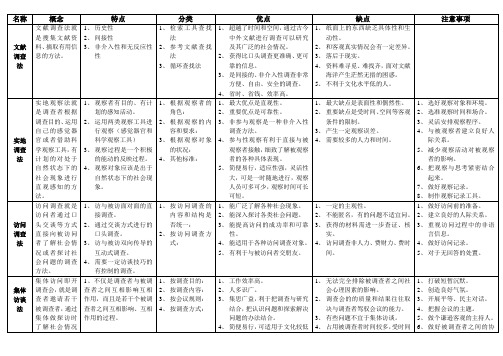
七种调查方法的比较
3、一大特色是匿名性。
4、对调查双方都比较方便。
5、可以排除人际交往中可能产生的种种干扰。
6、节省人力、时间和经费。
1、只能获得书面社会信息,不能得到生动具体的社会情况。
2、缺乏弹性,难做定性调查。
3、自填式问卷可能出现随便敷衍和对问题的不理解。
4、被调查者任意填写或在大众心理驱使下按照主流意识填写。
名称
概念
特点
分类
优点
缺点
注意事项
文献调查法
文献调查法就是搜集文献资料、摘取有用信息的方法。
1、历史性
2、间接性
3、非介入性和无反应性性
1、检索工具查找法
2、参考文献查找法
3、循环查找法
1、超越了时间和空间,通过古今中外文献进行调查可以研究及其广泛的社会情况。
2、获得比口头调查更准确、更可靠的信息。
3、是间接的、非介入性调查非常方便、自由、安全的调查。
1、观察者有目的、有计划的感知活动。
2、运用两类观察工具进行观察(感觉器官和科学观察工具)
3、观察过程是一个积极的能动的反映过程。
4、观察对象应该是出于自然状态下的社会现象。
1、根据观察者的角色:
2、根据观察的内容和要求:
3、根据观察对象的状况:
4、其他标准:
1、最大优点是直观性。
2、重要优点是可靠性。
1、访与被访面对面的直接调查。
2、通过交谈方式进行的口头调查。
3、访与被访双向传导的互动式调查。
4、需要一定访谈技巧的有控制的调查。
1、按访问调查的内容和结构是否统一:
2、按访问调查方式:
1、能广泛了解各种社会现象。
2、能深入探讨各类社会问题。
医学统计学各种资料比较选择方法小结

医学统计学各种资料比较选择方法小结一、两组或多组计量资料的比较1.两组资料:1)大样本资料或服从正态分布的小样本资料(1)若方差齐性,则作成组t检验(2)若方差不齐,则作t’检验或用成组的Wilcoxon秩和检验2)小样本偏态分布资料,则用成组的Wilcoxon秩和检验2.多组资料:1)若大样本资料或服从正态分布,并且方差齐性,则作完全随机的方差分析。
如果方差分析的统计检验为有统计学意义,则进一步作统计分析:选择合适的方法(如:LSD检验,Bonferroni检验等)进行两两比较。
2)如果小样本的偏态分布资料或方差不齐,则作Kruskal Wallis的统计检验。
如果Krus kal Wallis的统计检验为有统计学意义,则进一步作统计分析:选择合适的方法(如:用成组的Wilcoxon秩和检验,但用Bonferroni方法校正P值等)进行两两比较。
二、分类资料的统计分析1.单样本资料与总体比较1)二分类资料:(1)小样本时:用二项分布进行确切概率法检验;(2)大样本时:用U检验。
2)多分类资料:用Pearson c2检验(又称拟合优度检验)。
2. 四格表资料1)n>40并且所以理论数大于5,则用Pearson c22)n>40并且所以理论数大于1并且至少存在一个理论数<5,则用校正c2或用Fisher’s 确切概率法检验3)n£40或存在理论数<1,则用Fisher’s 检验3. 2×C表资料的统计分析1)列变量为效应指标,并且为有序多分类变量,行变量为分组变量,则行评分的CMH c 2或成组的Wilcoxon秩和检验2)列变量为效应指标并且为二分类,列变量为有序多分类变量,则用趋势c2检验3)行变量和列变量均为无序分类变量(1)n>40并且理论数小于5的格子数<行列表中格子总数的25%,则用Pearson c2(2)n£40或理论数小于5的格子数>行列表中格子总数的25%,则用Fisher’s 确切概率法检验4. R×C表资料的统计分析1)列变量为效应指标,并且为有序多分类变量,行变量为分组变量,则CMH c2或Krus kal Wallis的秩和检验2)列变量为效应指标,并且为无序多分类变量,行变量为有序多分类变量,作none zer o correlation analysis的CMH c23)列变量和行变量均为有序多分类变量,可以作Spearman相关分析4)列变量和行变量均为无序多分类变量,(1)n>40并且理论数小于5的格子数<行列表中格子总数的25%,则用Pearson c2(2)n£40或理论数小于5的格子数>行列表中格子总数的25%,则用Fisher’s 确切概率法检验三、Poisson分布资料1.单样本资料与总体比较:1)观察值较小时:用确切概率法进行检验。
第7章 多组定量资料的比较思考与练习参考答案

第7章 多组定量资料的比较思考与练习参考答案一、最佳选择题1. 完全随机设计资料的方差分析中,必然有( C )。
A. 组间SS >组内SSB. 组内组间总MS MS MS +=C. 总ss=组间SS +组内SSD. 组内组间MS MS >E. 组间组内νν> 2. 定量资料两样本均数的比较,可采用( D )。
A. t 检验B.F 检验C. Bonferroni 检验D. t 检验与F 检验均可E. LSD 检验3. 当组数等于2时,对于同一资料,方差分析结果与t 检验结果相比,( C )。
A. t 检验结果更为准确B. 方差分析结果更为准确C. 完全等价且F t =D. 完全等价且t F =E. 两者结果可能出现矛盾4. 若单因素方差分析结果为),(01.021ννF F >,则统计推断是( D )。
A. 各样本均数都不相等B. 各样本均数不全相等C. 各总体均数都不相等D. 各总体均数不全相等E. 各总体均数全相等 5. 完全随机设计资料的方差分析中,组间均方表示( C )。
A. 抽样误差的大小B. 处理效应的大小C. 处理效应和抽样误差综合结果D. N 个数据的离散程度E. 随机因素的效应大小 6. 多样本定量资料比较,当分布类型不清时应选择( D )。
A. 方差分析B. t 检验C. Z 检验D. Kruskal-Wallis 检验E. Wilcoxon 检验 7. 多组样本比较的Kruskal-Wallis 检验中,当相同秩次较多时,如果用H 值而不用校正后的c H 值,则会( C )。
A . 提高检验的灵敏度B .把一些无差别的总体推断成有差别 C. 把一些有差别的总体推断成无差别D.Ⅰ、Ⅱ类错误概率不变E. 以上说法均不对二、思考题1. 方差分析的基本思想和应用条件是什么?答:方差分析的基本思想是,对于不同设计的方差分析,其思想都一样,即均将处理间平均变异与误差平均变异比较。
07多组定量资料的比较(研121009)PPT课件

单 样 本
配 对 设 计
两 多 独 立 样 本
等 级 资 料Biblioteka 前提条件t / Z检验
方差分析
秩和检验
两 多配 组 组对 二 多设 分 分计 类类
四格表 R×C表 配对 四格表
2检验
教学内容
1.1 单因素方差分析 1.2多个样本均数间的两两比较
1.3 Kruskal-Wallis检验
1.5 随机区组设计资料的方差分析
2
S总 S =STS = (xij-x), v总 =vT=N -1
j= 1i= 1
⒉ 组间变异
各处理组的样本均数 X1、 X2、 X3、 X4不等,这 种变异称为组间变异。同理,组间的变异也与 每组的样本含量(自由度)有关。
k
S组 S= 间 SA S = n i(x i- x )2 , v 组= 间 v 1= k- 1 i= 1
i= 1
3. 组内变异:组内离差平方和
k nj
2
S组 S= 内 SES = (xij-xi), v组= 内 vW =N -k
i= 1j= 1
随机误差
三部分变异的关系:
变异的关系:
k nj
2
SS 总 =
( x ij - x )
i=1 j=1
k nj
=
[( x i - x ) ( x ji - x i)] 2
差分析,F=21.142,P <0.001,可认为 4 个总体小白鼠生存时间的均
数不全相同,即至少不两个不同。
附表 4 组小白鼠平均耐缺氧存活时间比较/min
组别
n
体重前后差值(g)
对照组
15
21.54 ±3.43
定量资料常用的组间比较方法选择及案例(二)

定量资料常用的组间比较方法选择及案例(二)哈喽,大家好!我是艾德医讯的小艾。
昨天给大家讲解的是定量资料的两组间比较方法(定量资料常用的组间比较方法选择及案例(一)),今天给大家分享:定量资料三组之间的比较方法。
定量资料三组之间的比较步骤:步骤为五步:①确定变量类型:定量资料还是分类资料?②确定组数:是两组比较,还是多组比较?③检验是否符合正态分布:正态性检验;④方差齐性检验;⑤最终组间比较方法的选择。
如下:案例:还是按步骤走(以JMP软件操作为例):①确定变量类型:定量资料还是分类资料?:定量资料②确定组数:是两组比较,还是多组比较?:三组(多组)③检验是否符合正态分布:正态性检验;打开数据库→分析菜单→分布→将变量选定角色→选择连续拟合→正态,进行正态性检验正态性检验结果显示;三组均符合正态分布④方差齐性检验;点击分析菜单→以x拟合y→方差齐性检验方差齐性检验显示:方差不齐(但此处概率值显示0.02,可以按方差齐来选择方法)⑤最终组间比较方法的选择。
三组正态、方差齐,选择方差分析。
那么,JMP实现方差分析:如果方差分析有统计学意义,可进一步分析具体是哪两组之间有差异。
如果比较组数不是很多(如3组),此时Tukey法和Bonferroni法均可作为首选。
结论:本例分析结果表明,三组的血糖降低值差异总的有统计学意义,两两比较结果显示,对照药与实验药的大剂量组差别有统计学意义,与小剂量组差别无统计学意义。
相关文章链接:关于召开《调查问卷设计和量表设计与评价》实战班的通知观于海者难为水——随手编一个护理基金标书(三)你不努力,谁也给不了你想要的生活。
——量表开发类的文章应如何撰写?护理科研主题怎么选?从0到1SCI-Hub——免费下载收费的SCI文献随手编一个护理基金标书小傻瓜,我来疼你!给你一个样本量计算的小工具(Excel)和案例分享数据分析建模的“天龙八步”。
正确的选择数据统计分析方法:多组数据比较
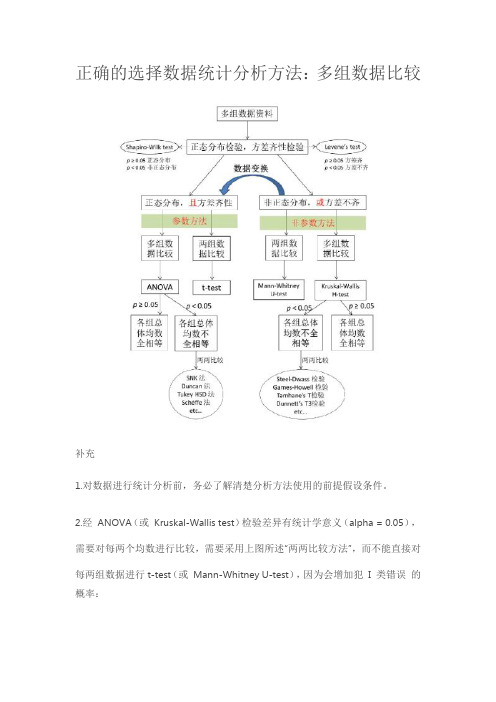
正确的选择数据统计分析方法:多组数据比较补充1.对数据进行统计分析前,务必了解清楚分析方法使用的前提假设条件。
2.经ANOVA(或Kruskal-Wallis test)检验差异有统计学意义(alpha = 0.05),需要对每两个均数进行比较,需要采用上图所述“两两比较方法”,而不能直接对每两组数据进行t-test(或Mann-Whitney U-test),因为会增加犯I 类错误的概率:例如三组数据资料,ANOVA结果显示p < 0.05;然后每两组均数t-test比较一次,则需比较3次,那么比较3次至少有一次犯I 类错误的概率就是alpha’ = 1-0.95^3 = 0.1426 > 0.05。
3.第一型及第二型错误(英语:Type I error & Type II error)或型一错误及型二错误:4.对于双样本t-test讨论:z-test:大样本;>30;z分布;t-test:小样本;<30;t分布;但是,对于> 30 的样本,Z-test检验要求知道总体参数的标准差,在理论上成立,事实上总体参数的标准差未知,实际应用中一般使用t-test.小知识:如何选取两两比较的方法?5-1、SNK 法最为常用,但当两两比较的次数极多时,该方法的假阳性很高,最终可以达到100%。
因此比较次数较多时,不推荐使用;5-2、若存在明显的对照组,要进行的是“验证性研究”,即计划好的某两个或几个组间的比较,宜用LSD 法;5-3、若设计了对照组,要进行k-1 个组与某个对照组之间的比较,宜用Dunnett 法;5-4、若需进行多个均数间的两两比较(探索性研究),且各组人数相等,宜用Tukey法;5-5、根据对所研究领域内相关研究的文献检索,参照所研究领域内的惯例选择适当的方法。
一张图搞明白分类资料的组间比较方法

一张图搞明白分类资料的组间比较方法分类资料的组间比较非常简单,不像定量资料那样,还得看正态性、方差齐性这么烦人的过程。
唯一需要看的就是结局是什么样子。
所以,如果说定量资料你能用错,你还可以说,你不会做正态性检验、不会方差齐性检验。
那么如果分类资料的组间比较你用错的,真的没有什么理由可以找,所以你真的没有任何犯错的理由。
分类资料就是那些可以划分类别的数据,两类和多类均可,只不过需要注意一下多类别的时候可能是有序的,也可能是无序的。
无序的就是没有什么等级高低顺序,就像血型,没有什么理由认为A比B 要高一等或低一等。
有序就是能看出一种天然的顺序,就像疗效,无效、显效、痊愈,给人感觉痊愈就是比显效高一等。
有一种情形要注意,不是看到率或百分比就要认为是分类资料,就要用卡方检验的。
有的率是作为连续资料来分析的。
比如脂肪百分比,虽然也是个比例,但你没法用卡方检验。
因为这个百分比是每个人都有一个这样的数值,你能做的是把每个人的百分比作为一个定量资料,然后进行组间比较。
以前就有人真的这么问过我说:这不是比例吗?比例不是都得用卡方吗?我想这种观念很可能是老师在教学的时候习惯把比例和率跟卡方联系起来,事实上未必,其实用“分类资料”这样的字眼更好一些。
分类资料的比例,说的是一定的数量占所有人的百分比,具体到每个人来说,他只有0或1这样的数值(多分类也可能是0、1、2等),计算的比例是0或1占的比例。
而刚才这种情形是每个人都有一个具体的不同数值,这是完全不同的。
对于分类资料的组间比较,可以通过下面这样一张图来选择方法:从这个图不难看出,分类资料的组间比较只需要注意三点就可以:(1)设计类型。
这个你自己是很清楚的。
大多数情况下,可能我们做的都是基于完全随机设计的。
对于没有设计的,如比较男女之间的发病率,男女分组不是随机设计的,那也采用完全随机设计的方法来分析。
(2)组别数,从小学一年级就应该能数的很清楚了。
(3)重要的是结局的类型,是二分类还是多分类,多分类是有序的还是无序的。
多组定量资料的比较

研究建议
THANKS FOR
WATCHING
感谢您的观看
主题意义
主题介绍
研究目的
描述多组定量资料的基本特征
对各组数据进行描述性统计分析,包括均值、中位数、标准差等指标,以全面了解各组数据的基本特征和分布情况。
比较各组之间的差异
通过统计检验方法,比较各组之间的均值、方差等指标,探究各组之间的差异及其显著性。
解释差异原因
结合实际情境和专业知识,对各组之间的差异进行解释和推断,探究其可能的原因和机制。
研究结论
总结词:研究建议
详细描述:基于研究结论,本研究提出以下建议。首先,建议进一步探究各组间差异的来源,以更深入地理解这些差异背后的机制。其次,针对表现优异的组别,可以尝试复制其成功模式,并应用于其他情境。此外,建议开展更多跨学科和跨领域的研究,以更全面地了解所研究的现象,并为其在实际应用中的推广提供科学依据。同时,加强数据收集和整理工作,确保研究结果的准确性和可靠性也是非常重要的。
协方差分析
总结词
重复测量方差分析适用于具有重复测量数据的多组定量资料比较,能够考虑时间因素的影响,评估组间差异的动态变化。
详细描述
重复测量方差分析(Repeated Measures ANOVA)是一种专门用于具有重复测量数据的多组定量资料比较的方法。它能够考虑时间因素的影响,并评估组间差异在不同时间点的动态变化。通过使用适当的统计模型和假设检验,可以确定组间差异是否随时间而变化,并确定变化的趋势和显著性。
多组定量资料的比较需要专业的统计学知识和经验,对分析人员的要求较高。
01
数据量大
多组定量资料的比较需要处理大量数据,计算复杂,对计算机性能要求较高。
02
对数据质量要求高
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【分析思路】
先对数据进行正态性检验和方差齐性检验:
Tests of Normality 组别 1 2 3 4 Kolmogorov-Smirnova Shapiro-Wilk Statistic df Sig. Statistic df .162 4 . .989 4 .270 6 .195 .889 6 .231 6 .200* .890 6 .307 4 . .729 4 Sig. .952 .314 .316 .024
其中:
MS组间 SS组间 /
MS组内 SS组内 /
三、方差分析的步骤
1.建立假设,确定显著性水平
H0 :1= 2 = 3 =….
H1 :总体均数不等或不全相等
=0.05
2.计算统计量F
3.求概率值P,做出推论
下面以完全随机设计资料为例,说明各部分变异 的计算方法。将N个受试对象随机分为k组,分别 接受不同的处理。归纳整理数据的格式、符号见 下表:
15
31.83 4.54
60
26.07 5.70
【案例解析】
资料类型:定量资料
设计类型:完全随机设计 分析方法:根据正态性检验结果和方差齐
性检验结果来决定采用单因素方差分析还
是秩和检验。
上述资料能否用前面所学两样本t检
验进行两两比较?
1 对照—A 2 对照—B 3 对照—C 4 A-B 5 B-C 6 A-C
应用方差分析解决!!
方差分析也是统 计检验的一种。 由英国著名统计 学家: R.A.FISHER推 导出来的,也叫 F检验。
一、 模型条件
独立性:各样本是相互独立的随机样本
正态性:各样本来自正态分布
方差齐性:各样本方差相等,即方差齐。
二、方差分析的基本思想
将总变异分解为几个组成部分,其
自由度也分解为相应的几部分。
式中 K 为常数,须经尝试得到。若原 始数据中有小值或零时,可用下式:
x' ln(X 1)
对数变换的用途:
①使服从对数正态分布的资料正态化;
②使方差不齐且各组的接近的资料达到方 差齐的要求; ③使曲线直线化,常用于曲线拟合。
2.平方根变换 (square root transformation) 将原始 数据 X 的平方根作为分析变量
二、作用: 1、使资料正态化;
2、使资料方差齐; 3、使曲线直线化。
三、常用数据变换方法
1.对数变换(transformation of
logarithm) 将原始数据X取对数,
以其对数值作为分析变量。
x' log X或x' ln X
还可根据需要用 x' ln(X K ) 或
x' ln(K X )
四、ANOVA 的局限性
在多组定量资料比较时,ANOVA 是一种 常用的方法。但ANOVA只能说明多个总体均数 总得来说有无差别,若想进一步了解到底哪 哪两个组之间有差别,还需做两两比较。
五、方差分析与t检验的关系
当比较两个均数时,从同一资料算得之
F 值与t值有如下关系:
F = t2
可见在两组均数比较时,方差分析 与t检验的效果是完全一样的。
【例7.1】
为研究茶多酚保健饮料对急性缺氧的影响, 将 60 只小白鼠随机分为四组:对照组(蒸馏 水 0.25ml )、低剂量组( 2.0g/kg )、中剂量 组(4.0g/kg)、高剂量组(8.0g/kg),40 天后对小白鼠进行缺氧存活实验,结果如表 7-1,试比较不同剂量的茶多酚保健饮料对延 长小白鼠的平均耐缺氧存活时间有无差别。
6次两样本t检验
4! 43 C 6 2!(4 2)! 2
2 4
第一次比较 第二次比较 第三次比较 ……
α=0.05 α=0.05 α=0.05
哈 哈 !
一类错误概率合计: 1 (1 0.05) 6 0.26
6次比较均不犯 一类错误的概率
因而,多样本均数的比较不能直 接用前面学过的两样本t检验进行!
数据变换
一、意义:参数统计分析方法对资料有 一定的要求,如t检验和方差分析要求样本 来自正态分布总体,并且总体方差齐等。 但实际工作中并非所有的统计资料都能满 足参数统计分析方法的条件;对于不能满 足条件的资料,则不能直接应用参数统计 分析方法,否则有可能导致错误的结论。
此时,一是可通过适当的变量变 换,使之达到方法的要求;二是可选 用非参数统计分析方法。一般情况下, 若能通过变量变换使资料符合参数方 法条件时,应尽量用参数统计方法。
处理组(i) 1 2 3 … … … … …
3j
k
xij
x11 x12
x1n1
n1
x 21 x 22
x 2 n2
…
x 31 x 32
xk1
xk 2
…
…
x3n3
n3
…
x knk
nk
合 计
x
j 1
1j
x
j 1
n2
2j
x
j 1
… …
x
j 1
kj
ni
n1
n2
n3
nk
1.建立假设,确定检验水准 H 0 :1 = 2 = 3 = 4
H1 :总体均数不等或不全相等
α=0.05
组别 对照组
耐缺氧时间 21.31 23.14 27.48 19.54 18.03 24.03 22.82 18.72 23.46 20.34 26.98 19.56 17.39 24.37 16.01
ni
Xi
Si
15
21.54 3.43
低 剂 量 20.16 24.49 21.32 19.46 25.63 28.81 18.74 18.42 组 26.13 25.24 20.23 22.47 29.38 20.16 22.51
P值 >0.05 <0.05 <0.05 <0.05 <0.05 <0.05
按0.05检验水准,除对照组和低剂量组差异无 统计学意义外,其余任何两组差异均有统计学 意义。
单因素方差分析要求各样本均来自正态总体 且总体方差齐,当数据来自偏态分布或总体方差 不齐时,采用变量变换或秩和检验(kruskal-
总变异的分解
组间变异 组内变异
总变异
各种变异的表示方法
• SS总 • 总 • MS总
SS组内 组内 MS组内
SS组间 组间 MS组间
三者之间的关系:
SS总=
总=
SS组内+ SS组间
组内+ 组间
一般,组间变异大于或等于组内变异
组间变异 MS组间 F 组内变异 MS组内
均方
离均差平方和
李琳琳 副教授 郑大公共卫生学院
方差分析
1
教学内容
第一节 单因素方差分析
第二节 多个样本均数间的两两比较 第三节 多个样本均数的秩和检验
学习要求
掌握多样本定量资料平均水平比较的分析思
路 掌握方差分析的基本思想 了解多样本秩和检验的基本步骤
One-way analysis of variance
ni
2
ν组间=g-1=4-1=3
或
ν组内=N-g=60-4=56
SS总 SS组间 898.39
SS组间 MS组间 339.14 组间
MS组内
SS组内
组内
16.04
MS组间 F 21.14 MS组内
表7.3 方差分析表
变异来源 总变异 组间变异 组内变异
SS
15
31.83 4.54
60
26.07 5.70
2 计算统计量
表 7.2 变异来源 总 变 异 组间变异 单因素方差分析的计算公式 自由度 ( ) 均方(MS) N -1 F 离均差平方和(SS)
( X X )2
n (X
i
i
X)
2
g-1 N-g
SS组间
MS组间 MS组内
组间
SS组内
某一对或几对在专业上有特殊意义的均数之差的
总体均数是否为0。
XAXB SX AX B
1 1 MS 误差 ( ) n A nB
1 1 )时,可以认为在 n A nB
LSD t
SX AX B
LSD t t , 时,即 X A X B t , MS误差 (
15
22.88 3.56
中 剂 量 35.07 28.11 24.74 29.79 22.68 23.01 28.32 29.04 组 24.33 33.97 21.86 28.65 25.13 34.44 31.69 Nhomakorabea15
28.06 4.38
高 剂 量 30.23 36.84 38.61 27.13 28.79 33.24 31.68 28.29 组 合计 38.47 35.10 28.01 23.37 28.44 34.22 35.08
组别 对照组
耐缺氧时间 21.31 23.14 27.48 19.54 18.03 24.03 22.82 18.72 23.46 20.34 26.98 19.56 17.39 24.37 16.01
ni
Xi
Si
15
21.54 3.43
低 剂 量 20.16 24.49 21.32 19.46 25.63 28.81 18.74 18.42 组 26.13 25.24 20.23 22.47 29.38 20.16 22.51
wallis) 。
【例7.3】 对按完全随机设计分组的四组大白鼠,给
予不同剂量的某种激素后,测量耻骨间隙宽度的增
