高职对口招生考试模拟试题数学模拟
2023年高职对口招生考试模拟试题数学模拟

对口升学数学模拟试题(第Ⅰ卷)注意事项:1、 答第Ⅰ卷前,考生务必将自己旳姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2、 每题选出答案后,用铅笔把答题卡上对应题目旳答案标号黑,如需改动,用橡皮擦洁净后,再选涂其他答案,不能答在试题卷上。
一、选择题(本大题共20个小题,每题3分,共60分)1、已知集合P={(x ,y )|y = x+1},Q={( x ,y )| x 2+y 2=1},则集合P ∩Q 旳子集旳个数是( )A 、2B 、4C 、6D 、8 2、设命题p :a 2+b 2=0,则⌝p 是( )A 、a=0且b=0,B 、a ≠0且b ≠0,C 、a ≠0或b ≠0,D 、a=0或b=0 3、不等式|x +5|>1旳解集是( )A 、{x|x>-4}B 、{x|-6<x<-4}C 、{x|x<-6或x>-4}D 、{x|x<-6}4、已知奇函数f(x)在(0,+∞)上是增函数,偶函数g(x)在(0,∞)上是减函数,则在 (-∞,0)上,有( )A 、f(x)为减函数,g(x)为增函数;B 、f(x)为增函数,g(x)为减函数;C 、f(x)、g(x)都是增函数;D 、f(x)、g(x)都是减函数 5、已知tan θ=2,则sin θcos θ=( )A 、53B 、52C 、±52D 、±536、已知f (e x)= x ,则f (5)=( )A 、e5B 、5C 、ln5D 、log 5 e7、 将二次函数y= (x -2)2+1 图像旳顶点A 平移向量a = (-2,3)后得到点A ’旳坐标是( )A 、(0, 4)B 、(4, -4)C 、(4, 0)D 、(-4, 4)8、在△ABC 中,若∠A 、∠B 、∠C 成等差数列,且BC= 2,BA=1, 则AC 等于( )A 、332 B 、 1 C 、3 D 、 7 9、若a 与b 都是单位向量,则下列式子恒成立旳是( )A 、a ·b =0;B 、|a |=|b |,C 、a -b =0;D 、a 、b =110、若等差数列{a n }中旳前n 项和为s n =4n 2–n ,则这个数列旳通项公式是( )A 、a n =4n -1B 、a n =8n -5C 、a n =4n+3D 、a n =8n+511、把6本不一样旳书平均放在三只抽屉里,不一样旳放法有( )A 、90B 、45C 、30D 、1512、若(1+x )8展开式旳中间三项依次成等差数列,则x 旳值为( )A 、21或2 B 、21或4 C 、2或4 D 、2或41 13、甲、乙两人同步解答一道题,甲解出旳概率是p ,乙解出旳概率是q ,则这道题被解出旳概率是( )A 、pqB 、p+qC 、p (1-q)+q (1-p)D 、p+q –pq14、对任意实数k,直线(k+1)x -ky -1=0与圆x 2+y 2-2x -2y -2=0旳位置关系是 ( ) A.相交 B.相切 C.相离 D.与k 旳值有关 15、二次函数f(x)=ax 2+bx+c ,满足f(4)=f(1),则( )A、f(2)>f(3) B、f(3)>f(2) C、f(3)=f(2) D、不确定 16、已知抛物线y 2=8x 上一点P 到焦点旳距离为5,则点P 旳横坐标为( )A 、2B 、3C 、5D 、717、双曲线116922=-y x 旳渐近线方程为( )A 、y=x 43±B 、y=x 34±C 、y=43± D 、y=x 34± 18、已知点P (2,a )是第一象限内旳点,且到直线4x -3y+2=0旳距离等于4,则a 旳值为( )A 、4B 、6C 、8D 、1019、洗衣机旳洗衣桶内用清水洗衣服,假如每次能洗去污垢旳32,则要使存留在衣服上旳污垢不超过最初衣服上旳污垢旳2%,该冼衣机至少要清洗旳次数为( )A 、2B 、3C 、4D 、5 20下列四个命题:①平行于同一条直线旳两条直线平行; ②平行于同一条直线旳两个平面平行;③平行于同一种平面旳两条直线平行 ④平行于同一种平面旳两个平面平行。
河南高职对口招生数学冲刺模拟试题三(含答案)

数学试题一、选择题(本题共有12小题,每小题5分, 共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1、下列关系式中,正确的关系式有几个 ( ) 1)2∈Q 2)0∉N 3)∈2{1,2} 4) φ ={0} A .0 B .1 C .2 D .32、二次函数y=x 2-4x+3在区间(1,4]上的值域是 ( ) A .[-1,+∞) B .(0,3] C .[-1,3] D .(-1,3] 3.下面各组函数中是同一函数的是 ( ) A .322y x y x x =-=-与B .2()y x =与||y x =C .11(1)(1)y x x y x x =+⋅-=+-与D .22()21()21f x x x g t t t =--=--与4、.函数x xx y +=的图象是5.、已知函数2()44f x ax ax R a =++的定义域为,则实数的取值范围为( ) A .(]0.1B . (,0][1,)-∞⋃+∞C . ()(,0)1,-∞⋃+∞D .[]0,1 6、已知()2x x af x a +==的图象关于直线=1对称,则实数( )A .-1B . 0C .1D .27、下列各组函数中,表示同一函数的是( )A .2|,|x y x y ==B .4,222-=+⨯-=x y x x yC .33,1xx y y ==D .2)(|,|x y x y ==8、若函数f(x)=x 2+2(a-1)x+2在区间(-∞,4]上是减函数,那么实数a 的取值范围是( )A .a ≥3B .a ≤-3C .a ≤5D .a ≥ -39、已知A 、B 两地相距150千米,某人开汽车以60千米/小时的速度从A 地到达B 地,在B 地停留1小时后再以50千米/小时的速度返回A 地,把汽车离开A 地的距离x 表示为时间t(小时)的函数,则t=5时,x 的值为( )A .300B .150C .-100D .7510、设偶函数f (x )的定义域为R ,对任意的[211,21221()()0,),,0f x f x x x x x x x -∈+∞≠<-有,则(2),(),(3)f f f π--的大小关系是( )A .f(π)>f(-3) >f (-2)B .f(π)>f(-2)>f(-3)C . f(π)<f(-3)<f(-2)D .f(π)<f(-2)<f(-3)11.{1.2.3},,,.I A I B I A B =⊆⊆且非空,其中集合A 中的最大元素小于B 中的最小元素,则满足条件的集合A.B 共有( )组A . 4 B. 5 C . 6 D .7{222(0)22(0)(),()(4)x x x x x x f x f a f a a +≥-+<=>12.已知函数且,则实数的取值范围为().、A .(0,4) B. (-1.1) C .(-∞,0)⋃(4,+∞) D .∅ 二、填空题(本题共4小题, 每小题5分, 共20分)13、{}{}2(,)|,,(,)|,,A x y y x x R B x y y x x R A B ==∈==∈⋂=则14.、函数1()2,x 0xf x R =∈≠(x 且)的值域为15、1037188-⎛⎫⎛⎫-++⎪ ⎪⎝⎭⎝⎭= 。
三校生对口高职单招数学模拟试卷15套6

高职单招数学模拟试卷六姓名:__________ 考号:__________得分:__________一、选择题:(本大题共12小题,每小题7分,共84分)1.设全集{1,3,5,7}U =,集合{3,5}A =,{1,3,7}B =,则()U A B = ( )A .{5}B .{3,5}C .{1,5,7}D .∅2.函数2()23f x x x =--,则(1)f x -= ( ) A .24x -- B .24x - C .2(1)4x --D .24x -3.下列式子正确的是 ( ) A .2020sin 40sin 501+= B .22sin cos sin x x x =- C .2sin 0x += D .22cos2sin sin x x x =-4.从5名男兵和4名女兵中选两人参加上海世博会服务工作,要求必需有男有女,则不同的选法为 ( ) A .9种 B .20种 C .48种D .60种5.数列{}n a 满足11,,n a S n ==则2010a = ( ) A .1 B .2009 C .2010D .20116.圆经过点(3,4),圆心在原点,则圆的方程为 ( ) A .225x y += B .2225x y += C .227x y += D .()()223425x y -+-= 7.方程22193x y k k +=--表示焦点在x 轴上的椭圆,则k 的取值范围为 ( )A .(3,)+∞B .(,9)-∞C .(3,6)D .(,6)-∞8.等比数列{}n a 满足:112n n a a +=,22a =,则5a = ( )A .8B .16C .32D .64 9.函数y =的定义域是 ( )A .[1,1]-B .(1,1)-C .(,1)-∞D .(1,)-+∞10.函数2()(sin 2cos 2)f x x x =-的最小正周期和最大值分别是 ( ) A .π,1B .π,2C .2π,2 D .2π,3 11.不等式211x ≥+的解集是 ( ) A .{/11}x x -<≤ B .{/1}x x ≤ C .{/1}x x >- D .{/11}x x x ≤>-或 12.垂直于x 轴的直线L 交抛物线24y x =与A 、B两点,且AB =,则该抛物线的 焦点到直线L 的距离是 ( ) A . 1B .2C .3D .4二、填空题:(本大题共6小题,每小题7分,共42分)13.已知直线l 过点(0,4)且倾斜角为090,则直线l 的方程是 . 14.已知点(2,)A n 点(,3)B m 关于点(2,2)对称,则m 和n 的值为 . 15.已知1sin()3πα-=,(,)2παπ∈,则tan α= .16.抛物线24y x =上一点P (,)a b 到焦点的距离为2,则b = .17.已知等比数列{}n a 满足1234561,8a a a a a a ++=++=-则{}n a 的公比q = . 18.经过点(0,1)-和(1,0),且圆心在直线1y x =+上的圆的方程是 . 三、解答题:(本大题共6小题,共74分)19.计算(本小题满分12分)23log 2333lg2log 27lg53sin2A π-+-++20.(本小题满分12分)已知二次函数2()f x x bx c =++满足(0)3,(1)(3)f f f =-=. (1)求b ,c 的值; (2)若()0f x ≥求x 的解集.21.(本小题满分12分)若22()cos sin 21f x x x x =-++,求:()f x 的最值及周期.22.(本小题满分12分)ABC ∆中,已知02,4,30a c A ==∠=. (1)求b ,B ,C ; (2)求ABC ∆的面积.23.(本小题满分12分)某商品的价格为40元时,月销售为10000件,价格每提高2元, 月销售量就会减少400件,在不考虑其他因素时, (1)试求这种商品的月销售量与价格之间的函数关系; (2)当价格提高到多少元时,这种商品就会卖不出去.24.(本小题满分14分)已知直线l 的倾斜角α满足cos 2α=,椭圆满足:焦点在x 轴 上,长轴长为4,离心率为双曲线2213y x -=的离心率的倒数。
职高对口高考模拟数学试卷

#### 一、填空题(每空2分,共20分)1. 若函数 \( f(x) = ax^2 + bx + c \) 在 \( x = 1 \) 处取得极值,则 \( a + b + c = \) ________。
2. 在等差数列 \(\{a_n\}\) 中,若 \( a_1 = 3 \),公差 \( d = 2 \),则\( a_5 = \) ________。
3. 已知圆的方程为 \( x^2 + y^2 - 4x - 6y + 9 = 0 \),则该圆的半径为________。
4. 若 \( \cos \alpha = \frac{1}{3} \),则 \( \sin \alpha \) 的值为________。
5. 函数 \( y = \frac{1}{x} \) 的图像关于 ________ 对称。
6. 若 \( \sqrt{a^2 + b^2} = 5 \),\( a = 3 \),则 \( b \) 的值为________。
7. 三个数的和为 12,其中两个数分别为 3 和 5,则第三个数为 ________。
8. 若 \( \triangle ABC \) 中,\( a = 5 \),\( b = 6 \),\( c = 7 \),则\( \cos A \) 的值为 ________。
9. 下列不等式中,正确的是 ________(选项:A. \( 2x > 4 \);B. \( 3x \leq 9 \);C. \( x^2 \geq 4 \);D. \( \frac{1}{x} < 1 \))10. 已知 \( \log_2 8 = 3 \),则 \( \log_2 32 = \) ________。
#### 二、选择题(每题3分,共30分)1. 函数 \( y = x^3 - 3x \) 的图像在 \( x = 0 \) 处的切线斜率为:A. 0;B. -3;C. 3;D. 不存在。
黑龙江高职对口招生考试数学模拟试题一(含答案)
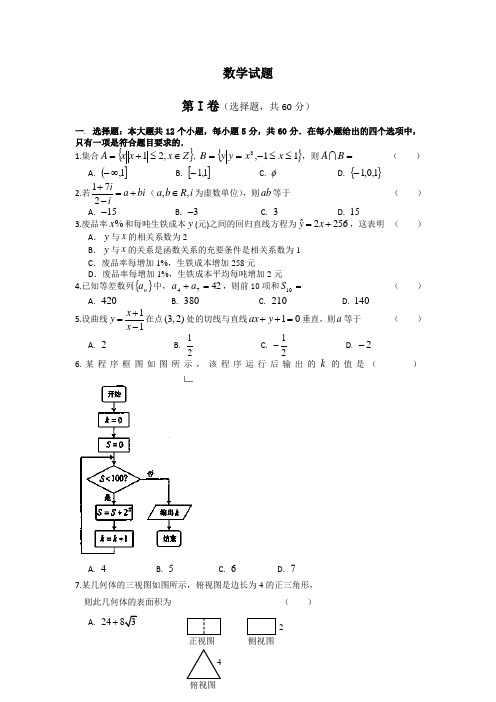
数学试题第I 卷(选择题,共60分)一. 选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}Z x x x A ∈≤+=,21,{}11,3≤≤-==x x y y B ,则=B A ( ) A. (]1,∞-B. []1,1-C. φD. {}1,0,1-2.若172ia bi i+=+-(,,a b R i ∈为虚数单位),则ab 等于 ( ) A. 15- B. 3- C. 3 D. 153.废品率%x 和每吨生铁成本y (元)之间的回归直线方程为ˆ2256y x =+,这表明 ( )A .y 与x 的相关系数为2B .y 与x 的关系是函数关系的充要条件是相关系数为1C .废品率每增加1%,生铁成本增加258元D .废品率每增加1%,生铁成本平均每吨增加2元4.已知等差数列{}n a 中,4274=+a a ,则前10项和=10S ( ) A. 420 B. 380C. 210D. 1405.设曲线11x y x +=-在点(3,2)处的切线与直线10ax y ++=垂直,则a 等于 ( ) A. 2 B. 12 C. 12- D. 2-6.某程序框图如图所示,该程序运行后输出的k 的值是( )A. 4B. 5C. 6D. 7 7.某几何体的三视图如图所示,俯视图是边长为4的正三角形, 则此几何体的表面积为 ( ) A. 2483+ 4正视图侧视图俯视图2B.C. 12+D. 24+8.已知函数()2xf x =的反函数()g x 满足()()4g a g b +=,则11a b+的最小值为 ( ) A. 1 B. 13 C. 12 D. 149.定义运算:12142334a a a a a a a a =-,将函数cos2()sin2xf x x =的图像向左平移m (0m >)个单位,所得图像对应的函数为偶函数,则m 的最小值是 ( )A. 3πB. 32πC. 34πD. 37π10.已知函数2()f x x bx c =++,其中04,04b c ≤≤≤≤,记事件A 为 “函数()f x 满足条件:(2)12(1)1f f ≤⎧⎨-≤⎩”,则事件A 发生的概率为 ( )A. 49B. 13C. 12D. 1911.已知12,F F 分别为双曲线22221x y a b-=(a >0,b >0)的左、右焦点,P 为双曲线左支上的任意一点,若221||||PF PF 的最小值为8a ,则双曲线离心率e 的取值范围是 ( )A. (1,)+∞B. (0,3]C. (1,3]D. (1,2] 12.定义域为R 的偶函数()f x ,对x R ∀∈,有(2)()(1)f x f x f +=+,且当[2,3]x ∈ 时,2()21218f x x x =-+-,若函数()log (1)a y f x x =-+在()0,+∞上至少有三个零点,则a 的取值范围是 ( )A.B.C.D. 第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题~(24)题为选考题,考生根据要求做答.二. 填空题:本大题共4小题,每小题5分,共20分.13.已知圆C 与直线04=--y x 及0=-y x 都相切,且圆心在直线0=+y x 上,则圆C 的方程为 .14.某高中在校学生2000人,高一年级与高二年级人数相同并且都比高三年级多1人,为了响应市教育局“阳光体育”号召,该校开展了跑步和跳绳两项比赛,要求每人都参加而其中::2:3:5a b c =,全校参与跳绳的人数占总人数的5,为了了解学生对本次活动的满意度,采用分层抽样从中抽取一个200人的样本进行调查,则高二年级中参与跑步的同学应抽取 人. 15.已知向量13(,),,22a OA ab OB a b =-=-=+,若OAB ∆是等边三角形,则OAB ∆的面积为 .16.数列{}n a 满足11a =,且对任意的正整数,m n 都有m n m n a a a mn +=++,则12201220131111a a a a ++++= .三. 解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知向量()sin m x x =,()sin ,cos n x x =,设函数()n m x f ⋅=. (Ⅰ)求函数()f x 的解析式,并求()f x 在区间⎥⎦⎤⎢⎣⎡-6,4ππ上的最小值; (Ⅱ)在ABC ∆中,c b a ,,分别是角C B A ,,的对边,A 为锐角,若()()32f A f A +-=, 7b c +=,ABC ∆的面积为32,求a .18.(本小题满分12分)甲、乙两个盒子中各有3个球,其中甲盒中有2个黑球1个白球,乙盒中有1个黑球2个白球,所有球之间只有颜色区别.(Ⅰ)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率; (Ⅱ)将这两个盒子中的球混合在一起,从中任取2个,求取出的2个球中至少有一个黑球的概率. 19.(本小题满分12分) 四棱锥S ABCD -中,底面ABCD 为平行四边形, 侧面SBC ⊥底面ABCD ,E 为SD 的中点,已知452ABC AB BC ∠===,,SB SC == (Ⅰ)求证:SA BC ⊥;(Ⅱ)在BC 上求一点F ,使//EC 平面SAF ; (Ⅲ)求三棱锥D EAC -的体积.20.(本小题满分12分)已知椭圆C 的焦点在x 轴上,离心率2e =,且经过点(2,1)A -. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)斜率为1-的直线l 与椭圆C 相交于,P Q 两点,求证:直线AP 与AQ 的倾斜角互补.21.(本小题满分12分)已知函数()ln f x x a x =-,1(), (R).ag x a x+=-∈(Ⅰ)若1a =,求函数()f x 的极值;(Ⅱ)设函数()()()h x f x g x =-,求函数()h x 的单调区间; (Ⅲ)若在区间[]1,e (e 2.718=)上存在一点0x ,使得0()f x <0()g x 成立,求a 的取值范围.AB C D S E答案一、 选择题:(本大题共12小题,每小题5分,共60分)题号123456789 10 11 12 答案 D B D C D A A C CBCA二、填空题:(本大题共4小题,每小题5分,共20 分) 13. ()()21122=++-y x 14. 36 15.33 16.10072013 三、解答题:(本大题共6小题,共70分。
甘肃兰州市高职对口招生考试数学模拟试题三(含答案)

数学试题一、选择题:(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列命题中的假命题是( ).A. 0lg ,=∈∃x R xB. 1tan ,=∈∃x R xC. 0,3>∈∀x R xD. 02,>∈∀x R x2.“0m n >>”是“方程221mx ny +=”表示焦点在y 轴上的椭圆”的( ).A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3. 设双曲线)0,0(12222>>=-b a by a x 的虚轴长为2,焦距为32,则双曲线的渐近线方程为( ). A.x y 2±= B .x y 22±= C . x y 2±= D.x y 21±= 4.如果方程121||22=---m y m x 表示双曲线,那么实数m 的取值范围是( ). A. 2>m B .1<m 或2>m C . 21<<-m D .11<<-m 或2>m5.已知椭圆2222=+y x 的两焦点为21,F F ,且B 为短轴的一个端点,则21BF F ∆的外接圆方程为()A .4)1(22=+-y x B. 122=+y xC. 422=+y xD. 4)1(22=-+y x6. 已知△ABC 的三边长6,5,3===c b a ,则△ABC 的面积为 ( ). A.14 B .142 C .15 D .1527.等比数列{a n }中,a 2=9,a 5=243,则{a n }的前4项和为( ).A .81B .120C .168D .1928. 不等式220ax bx 的解集是11(,)23,则a b 的值是( ). A. 10 B. 10 C. 14 D. 149.设x x x f ln )(=,若2)(0='x f ,则=0x ( ).A . 2eB . eC . ln 22D .ln 210. 如图,1F 和2F 分别是双曲线12222=-by a x (0,0>>b a )的两个焦点,A 和B 是以O 为圆心,以1OF 为半径的圆与该双曲线左支的两个交点,且AB F 2∆是等边三角形,则双曲线的离心率为( )A .3 B. 5 C.13+ D. 25 11. 设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( )A . 1B .21C . 21-D . 1- 12.函数y =3x 2+6x 2+1的最小值是( ) A .32-3 B .-3 C .6 2 D .62-3二.填空题(每小题5分,共20分)13.抛物线281x y -=的准线方程是 ; 14.函数1)(23+++=mx x x x f 是R 上的单调函数,则m 的取值范围为 ; 15. 过点(1,1)M 作一直线与椭圆22194x y +=相交于B A ,两点,若M 点恰好为弦AB 的中点,则AB 所在直线的方程为 ;16. 设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,则y u x =的取值范围是 .三、解答题:(本大题共6小题,共70分。
高职对口招生联合测试模拟卷

高职对口招生联合测试模拟卷一、语文部分(一)基础知识1. 下列加点字读音完全正确的一项是()A. 拮据(jū)诓骗(kuāng)恪尽职守(gè)B. 狡黠(xiá)抽噎(yē)强聒不舍(guō)C. 恣睢(suī)陨落(yǔn)气吞斗牛(dǒu)D. 栈桥(zhàn)襁褓(qiáng)怒不可遏(è)2. 下列词语书写完全正确的一项是()A. 亵渎断章取义一代天娇重蹈覆辙B. 狡黠孤军奋战红装素裹涕泗横流C. 凌驾黎民百姓无与伦比脑羞成怒D. 襁褓刻骨铭心自知之明郭然无累(二)阅读理解阅读下面的文言文,完成 3 5 题。
《岳阳楼记》庆历四年春,滕子京谪守巴陵郡。
越明年,政通人和,百废具兴。
乃重修岳阳楼,增其旧制,刻唐贤今人诗赋于其上。
属予作文以记之。
予观夫巴陵胜状,在洞庭一湖。
衔远山,吞长江,浩浩汤汤,横无际涯;朝晖夕阴,气象万千。
此则岳阳楼之大观也,前人之述备矣。
然则北通巫峡,南极潇湘,迁客骚人,多会于此,览物之情,得无异乎?若夫淫雨霏霏,连月不开,阴风怒号,浊浪排空;日星隐曜,山岳潜形;商旅不行,樯倾楫摧;薄暮冥冥,虎啸猿啼。
登斯楼也,则有去国怀乡,忧谗畏讥,满目萧然,感极而悲者矣。
至若春和景明,波澜不惊,上下天光,一碧万顷;沙鸥翔集,锦鳞游泳;岸芷汀兰,郁郁青青。
而或长烟一空,皓月千里,浮光跃金,静影沉璧,渔歌互答,此乐何极!登斯楼也,则有心旷神怡,宠辱偕忘,把酒临风,其喜洋洋者矣。
嗟夫!予尝求古仁人之心,或异二者之为,何哉?不以物喜,不以己悲;居庙堂之高则忧其民;处江湖之远则忧其君。
是进亦忧,退亦忧。
然则何时而乐耶?其必曰“先天下之忧而忧,后天下之乐而乐”乎。
噫!微斯人,吾谁与归?3. 下列加点词解释有误的一项是()A. 百废具兴(具:同“俱”,全、皆)B. 属予作文以记之(属:同“嘱”,嘱托)C. 薄暮冥冥(薄:迫近)D. 至若春和景明(景:景色)4. 下列各项中加点词意义和用法相同的一项是()A. 刻唐贤今人诗赋于其上多会于此B. 不以物喜属予作文以记之C. 其喜洋洋者矣其真无马邪D. 然则何时而乐耶望之蔚然而深秀者5. 下列对文章理解有误的一项是()A. 文章第一段叙述事情的本末缘起,第二段描写岳阳楼的大观,三、四段分别写迁客骚人以物喜、以己悲的览物之情。
福建高职对口招生考试数学模拟试题八(含答案)

数学试题第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若i 是虚数单位,则复数i (2i)⋅+在复平面内所对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限2.设全集U =R ,{(3)0}A x x x =+<,{1}B x x =<-,则图中阴影部分表示的集合为A .(3,1)--B .(1,0)-C .[1,0)-D .(,1)-∞-3.某校组织班班有歌声比赛,8个评委为某个班级打出的分数如茎叶图所示,则这些数据的中位数是A .84B .85C .86D .87.54.执行如图所示程序框图所表达的算法,若输出的x 值为48,则输入的x 值为A .3B .6C .8D .125.若0a >,0b >,且1,,,4a b 构成等比数列,则.A .22a b +有最小值4 B .a b +有最小值4C .22a b +无最小值D .a b +有最小值26.圆0422=-+x y x 在点)3,1(P 处的切线方程为 A .023=-+y x B .043=-+y xC .043=+-y xD .023=+-y x 7.下列函数中,既是奇函数又是减函数的是A .13y x =B .x x f tan )(-=C .2()1x f x x =- D .x x x f 22)(-=- 8.设,a b ∈R ,那么“>1a b”是“>>0a b ”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件9.若双曲线()222210,0x y a b a b -=>>的一个焦点在直线20x y a --=上,则其渐近线方程为 A .3y x =±B .33y x =±C .13y x =±D .3y x =± 10.已知()21()cos 3sin cos 02f x x x x ωωωω=-⋅->的图象与1y =的图象的两相邻交点间的距离为π,要得到()y f x =的图象,只须把cos 2y x =的图象A .向左平移3π个单位 B .向右平移3π个单位 C .向左平移6π个单位 D .向右平移6π个单位 11.已知周期函数()f x 的定义域为R ,周期为2,且当11x -<≤时,2()1f x x =-.若直线y x a =-+与曲线()y f x =恰有2个交点,则实数a 的所有可能取值构成的集合为A .3{|24a a k =+或524k +,k ∈Z } B .1{|24a a k =-或324k +,k ∈Z } C .{|21a a k =+或524k +,k ∈Z } D .{|21a a k =+,k ∈Z } 12.如图,在棱长为1的正方体1111ABCD A B C D -的对角线1AC 上任取一点P ,以A 为球心,AP为半径作一个球.设AP x =,记该球面与正方体表面的交线的长度和为()f x ,则函数()f x 的图象最有可能的是.A .B .C .D .x 123y O x 123y O x 123y O x123y O第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.将答案填在答题卡的相应位置.13.已知向量(4,)m =a ,(1,2)=-b,若+=-a b a b ,则实数m 等于 .14.根据2012年初我国发布的《环境空气质量指数AQI 技术规定(试行)》,AQI 共分为六级:(0,50]为优,(50,100]为良,(100,150]为轻度污染,(150,200]为中度污染,(200,300]为重度污染,300以上为严重污染.2013年5月1日出版的《A 市早报》报道了A 市2013年4月份中30天的AQI统计数据,右图是根据统计数据绘制的频率分布直方图. 根据图中的信息可以得出A 市该月环境空气质量优良的总天数为 .15.一水平放置的平面图形OABC ,用斜二测画法画出它的直观图''''O A B C 如图所示,此直观图恰好是一个边长为2的正方形,则原平面图形OABC 的面积为 .16.对于30个互异的实数,可以排成m 行n 列的矩形数阵,右图所示的5行6列的矩形数阵就是其中之一.将30个互异的实数排成m 行n 列的矩形数阵后,把每行中最大的数选出,记为12,,m a a a ⋅⋅⋅,并设其中最小的数为a ;把每列中最小的数选出,记为12,,n b b b ⋅⋅⋅,并设其中最大的数为b .两位同学通过各自的探究,分别得出两个结论如下:①a 和b 必相等; ②a 和b 可能相等;③a 可能大于b ; ④b 可能大于a .以上四个结论中,正确结论的序号是__________________(请写出所有正确结论的序号).三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.在某次模块水平测试中,某同学对于政治、历史、地理这三个学科每个学科是否能达到优秀水平的概率都为12,记政治、历史、地理达到优秀水平的事件分别为1A 、2A 、3A ,未达到优126126126x x x y y y z z z秀水平的事件分别为1A 、2A 、3A .(Ⅰ)若将事件 “该同学这三科中恰有两科达到优秀水平” 记为M ,试求事件M 发生的概率;(Ⅱ)请依据题干信息,仿照(Ⅰ)的叙述,设计一个关于该同学测试成绩情况的事件N ,使得事件N 发生的概率大于%85,并说明理由.18.已知ABC ∆外接圆O 的半径为1,且12OA OB ⋅=-. (Ⅰ)求AB 边的长及角C 的大小;(Ⅱ)从圆O 内随机取一个点M ,若点M 取自ABC ∆内的概率恰为334π,试判断ABC ∆的形状.19.在数列}{n a 和等比数列}{n b 中,01=a ,23=a ,1*2()n a n b n N +=∈.(Ⅰ)求数列{}n b 及}{n a 的通项公式;(Ⅱ)若n n n b a c ⋅=,求数列{}n c 的前n 项和n S .20.已知长方体1111ABCD A B C D -中,底面ABCD 为正方形,1D D ⊥面ABCD ,4AB =,12AA =,点E 在棱11C D 上,且13D E =.(Ⅰ)试在棱CD 上确定一点1E ,使得直线1//EE 平面1D DB ,并证明;(Ⅱ)若动点F 在底面ABCD 内,且2AF =,请说明点F 的轨迹,并探求EF 长度的最小值.21.已知(0,1)F 是中心在坐标原点O 的椭圆C 的一个焦点,且椭圆C 的离心率e 为12. (Ⅰ)求椭圆C 的方程; (Ⅱ)设:11(,)M x y 、22(,)N x y 为椭圆C 上不同的点,直线MN 的斜率为1k ;A 是满足OM ON OA λ+=(0λ≠)的点,且直线OA 的斜率为2k .①求12k k ⋅的值;②若A 的坐标为3(,1)2,求实数λ的取值范围.22.定义域为D 的函数()f x ,其导函数为'()f x .若对x D ∀∈,均有()'()f x f x <,则称函数()f x 为D 上的梦想函数.(Ⅰ)已知函数()sin f x x =,试判断()f x 是否为其定义域上的梦想函数,并说明理由; (Ⅱ)已知函数()1g x ax a =+-(a ∈R ,(0,)x π∈)为其定义域上的梦想函数,求a 的取值范围;(Ⅲ)已知函数()sin 1h x x ax a =++-(a ∈R ,[0,]x π∈)为其定义域上的梦想函数,求a 的最大整数值.答案一、选择题:本大题考查基础知识和基本运算.每小题5分,满分60分.1.B 2.A 3.C 4.B 5.B 6.D7.D 8.B 9.A 10.C 11.C 12.B二、填空题:本大题考查基础知识和基本运算.每小题4分,满分16分.13.2 14.12 15. 16.②③三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.本小题主要考查古典概型等基础知识,考查运算求解能力以及应用意识,考查必然与或然思想等.满分12分.解:(Ⅰ)依题意,总的基本事件有“123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ”,共8种,………………2分 事件M 包含的基本事件有“123(,,)A A A ,123(,,)A A A ,123(,,)A A A ”,共3种,…4分 由于每个基本事件发生的可能性都相等,故事件M 发生的概率83)(=M P .……6分 (Ⅱ)方案一:记“该同学这三科中至少有一科达到优秀水平”的事件为N ,则事件N 发生的概率大于%85.…………8分理由:事件N 包含的基本事件有“123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ”,共7种,……10分 由于每个基本事件发生的可能性都相等,所以%8587)(>=N P .……12分 方案二:记 “该同学参加这次水平测试成绩不全达到优秀水平”的事件为N ,则事件N 发生的概率大于%85.…………8分理由:事件N 包含的基本事件有“123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ,123(,,)A A A ”,共7种,……10分 由于每个基本事件发生的可能性都相等,故%8587)(>=N P .………12分 18.本小题主要考查向量的数量积、几何概型、解三角形等基础知识,考查运算求解能力,考查函数与方程思想等. 满分12分.解:(Ⅰ)依题意1cos 2OA OB OA OB AOB ⋅=⋅⋅∠=-,………………2分 得1cos 2AOB ∠=-,又0AOB π<∠<,故23AOB π∠=,…4分 又AOB ∆为等腰三角形,故AB = …………5分 而123C AOB π∠=∠=或12(2)23C AOB ππ∠=-∠=.………………6分(Ⅱ)依题意,从圆O 内随机取一个点,取自ABC ∆内的概率OABC S S P 圆∆=,可得S 4ABC ∆=.………………8分 设BC a =,AC b =.设23C π∠=,由1sin 24ABC S ab C ∆=⋅⋅=,得3ab =, ……① 由2222cos 3AB a b ab C =+-=,得223a b ab ++=, ……②联立①②得220a b +=,这是不可能的. 所以必有3C π∠=. …………9分由1sin 24ABC S ab C ∆=⋅⋅=,得3ab =, ……① 由2222cos 3AB a b ab C =+-=,得223a b ab +-=,226a b += …②………11分联立①② 解得a b ==所以ABC ∆为等边三角形.………………12分19.本小题主要考查等比数列、数列通项公式、数列求和等基础知识,考查运算求解能力,考查函数与方程思想等. 满分12分.解法一:(Ⅰ)依题意21=b ,8233==b ,………………2分设数列}{n b 的公比为q ,由120n a n b +=>,可知0q >,………3分由822213=⋅=⋅=q q b b ,得42=q ,又0>q ,则2=q ,………4分故n n n n q b b 222111=⋅==--,………5分又由n a n 221=+,得1-=n a n .………………6分(Ⅱ)依题意n n n c 2)1(⋅-=.………………7分n n n n n S 2)1(2)2(2221201321⋅-+⋅-+⋅⋅⋅+⋅+⋅+⋅=- , ①则14322)1(2)2(2221202+⋅-+⋅-+⋅⋅⋅+⋅+⋅+⋅=n n n n n S ②……9分①-②得21231122222(1)2(1)212n n n n n S n n +++--=++⋅⋅⋅+--⋅=--⋅-, …………11分 即12)2(4+⋅-+-=-n n n S ,故12)2(4+⋅-+=n n n S .………………12分解法二:(Ⅰ)依题意}{n b 为等比数列,则q b b n n =+1(常数), 由120n a n b +=>,可知0q >,………………2分由q n n n n a a a a ==-++++1122211, 得q a a n n 21log =-+(常数),故}{n a 为等差数列,…………4分设}{n a 的公差为d ,由01=a ,220213=+=+=d d a a ,得1=d ,故1-=n a n .…………6分(Ⅱ)同解法一.20.本小题主要考查直线与直线、直线与平面的位置关系等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想等.满分12分.解:(Ⅰ)取CD 的四等分点1E ,使得13DE =,则有1//EE 平面1D DB . 证明如下:………1分因为11//D E DE 且11D E DE =,所以四边形11D EE D 为平行四边形,则11//D D EE ,………2分因为1DD ⊂平面1D DB ,1EE ⊄平面1D DB ,所以1//EE 平面1D DB .………4分(Ⅱ)因为2AF =,所以点F 在平面ABCD 内的轨迹是以A 为圆心,半径等于2的四分之一圆弧.………………6分因为11//EE DD ,1D D ⊥面ABCD ,所以1E E ⊥面ABCD , ………………7分故2221114EF E E E F E F =+=+.………………8分 所以当1E F 的长度取最小值时,EF 的长度最小,此时点F为线段1AE 和四分之一圆弧的交点,………………10分即11523E F E A AF =-=-=,所以221113EF E E E F =+=.即EF 长度的最小值为13.………………12分21.本小题主要考查椭圆的标准方程、直线与椭圆等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想等.满分12分.解:(Ⅰ)依题意,可设椭圆C 的方程为22221y x a b+=(0a b >>),………………1分 由1c =,12c e a ==,得2a =, 由222b a c =-,可得23b =,………………3分故椭圆C 的方程为22143y x +=.………………4分 (Ⅱ)解法一:①由11(,)M x y 、22(,)N x y 且1k 存在,得21121y y k x x -=-,………………5分 由OM ON OA λ+=,0λ≠且2k 存在,得21221y y k x x +=+, 则222121211222212121y y y y y y k k x x x x x x +--⋅=⋅=+--.………………6分 ∵11(,)M x y ,22(,)N x y 在椭圆上,∴2211143y x +=,2222143y x +=,………7分 两式相减得22222121043y y x x --+=,2221222143y y x x -=--, ∴1243k k ⋅=-.………………8分②若A 的坐标为3(,1)2,则223k =,由①可得12k =-. 设直线:2MN y x m =-+(m ∈R ), 由222,1,43y x m y x =-+⎧⎪⎨+=⎪⎩得2216123120x mx m -+-=,…….……9分 所以1234m x x +=. ∵OM ON OA λ+=,∴1232x x λ+=,2m λ=. …………10分 又由()()22124163120m m ∆=--⋅⋅->,解得44m -<<,………………11分 ∴22λ-<<且0λ≠.………………12分解法二:①设直线1:MN y k x m =+(m ∈R ),若0m =,则120,x x +=由A 满足OM ON OA λ+=(λ∈R ,0λ≠),得0A x =,∵直线OA 的斜率2k 存在,∴0m ≠. ………5分 由122,1,43y k x m y x =+⎧⎪⎨+=⎪⎩得22211(43)63120k x k mx m +++-=……(*).……………6分 ∵11(,)M x y 、22(,)N x y ,∴11221643k m x x k +=-+. ………7分 ∵12112()2y y k x x m +=++,A 满足OM ON OA λ+=,∴直线OA 的斜率2121211121214323y y k m k k k x x x x k ++==+=-++, 经化简得1243k k ⋅=-. ………9分 ②若A 的坐标为3(,1)2,则223k =,由①可得12k =-. ………10分 ∴方程(*)可化为2216123120x mx m -+-=,下同解法一.22.本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等.满分14分.解:(Ⅰ)函数()sin f x x =不是其定义域上的梦想函数.………………1分理由如下:()sin f x x =定义域D R =,()'cos f x x =,………………2分 存在3x π=,使()'()33f f ππ>,故函数()sin h x x =不是其定义域R D =上的梦想函数.……4分.(Ⅱ)()1g x ax a =+-,()'g x a =,若函数()1g x ax a =+-在(0,)x π∈上为梦想函数,则1ax a a +-<在(0,)x π∈上恒成立,………………5分 即1a x<在(0,)x π∈上恒成立, 因为1y x =在(0,)x π∈内的值域为1(,)π+∞,………………7分 所以1a π≤.………………8分 (Ⅲ)a x x h +=cos )(',由题意)()('x h x h >在[0,]x π∈恒成立,故cos sin 1x a x ax a +>++-,即cos sin 1ax x x <-+在[0,]x π∈上恒成立.①当0x =时,0cos0sin012a ⋅<-+=显然成立;……………9分②当0x π<≤时,由cos sin 1ax x x <-+可得cos sin 1x x a x -+<对任意(]0,x π∈恒成立. 令cos sin 1()x x F x x -+=,则2(sin cos )(cos sin 1)'()x x x x x F x x --⋅--+=,…10分 令)1sin (cos )cos sin ()(+--⋅--=x x x x x x k ,则'()(sin cos )sin()4k x x x x x π=-⋅=⋅-. 当(0,]4x π∈时,因为0)('≤x k ,所以)(x k 在(0,]4π单调递减;当(,]4x ππ∈时,因为0)('≥x k ,所以)(x k 在(,]4ππ单调递增. ∵(0)20k =-<,()104k π=-<, ∴当(0,]4x π∈时,()k x 的值均为负数.∵()104k π=-<,()0k ππ=>, ∴当(,]4x ππ∈时,()k x 有且只有一个零点0x ,且0(,)4x ππ∈. ……………11分 ∴当0(0,)x x ∈时,0)(<x k ,所以'()0F x <,可得()F x 在0(0,)x 单调递减; 当0(,)x x π∈时,0)(>x k ,所以'()0F x >,可得()F x 在0(,)x π单调递增. 则00min 00cos sin 1()()x x F x F x x -+==.…………12分 因为0)(0=x k ,所以00000cos sin 1(sin cos )x x x x x -+=--⋅,min 0000()()sin cos )4F x F x x x x π==--=+.…………13分 ∵)(x k 在(,]4ππ单调递增,02)2(<-=ππk ,012)43(>-=πk , ∴0324x ππ<<,所以01)04x π-<+<,即01()0F x -<<..又因为0()a F x <,所以a 的最大整数值为1-.…………14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006年对口升学数学模拟试题
(第Ⅰ卷)
注意事项:
1、 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2、 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号黑,如需改动,用橡皮擦干净后,
再选涂其它答案,不能答在试题卷上。
一、选择题(本大题共20个小题,每小题3分,共60分)
1、已知集合P={(x ,y )|y = x+1},Q={( x ,y )| x 2+y 2
=1},则集合P ∩Q 的子集的个数是( )
A 、2
B 、4
C 、6
D 、8
2、设命题p :a 2+b 2=0,则⌝p 是( )
A 、a=0且b=0,
B 、a ≠0且b ≠0,
C 、a ≠0或b ≠0,
D 、a=0或b=0 3、不等式|x +5|>1的解集是( )
A 、{x|x>-4}
B 、{x|-6<x<-4}
C 、{x|x<-6或x>-4}
D 、{x|x<-6}
4、已知奇函数f(x)在(0,+∞)上是增函数,偶函数g(x)在(0,∞)上是减函数,则在 (-∞,0)上,有( )
A 、f(x)为减函数,g(x)为增函数;
B 、f(x)为增函数,g(x)为减函数;
C 、f(x)、g(x)都是增函数;
D 、f(x)、g(x)都是减函数 5、已知tan θ=2,则sin θcos θ=( )
A 、
53 B 、52 C 、±52 D 、±5
3
6、已知f (e x
)= x ,则f (5)=( ) A 、e 5 B 、5
C 、ln5
D 、log 5 e
7、 将二次函数y= (x -2)2
+1 图像的顶点A 平移向量= (-2,3)后得到点A ’的坐标是( ) A 、(0, 4) B 、(4, -4) C 、(4, 0) D 、(-4, 4)
8、在△ABC 中,若∠A 、∠B 、∠C 成等差数列,且BC= 2,BA=1, 则AC 等于( )
A 、
3
3
2 B 、 1 C 、
3 D 、 7 9、若与都是单位向量,则下列式子恒成立的是( )
A 、a ²b =0;
B 、|a |=|b |,
C 、a -b =0;
D 、a 、b =1
10、若等差数列{a n }中的前n 项和为s n =4n 2
–n ,则这个数列的通项公式是( )
A 、a n =4n -1
B 、a n =8n -5
C 、a n =4n+3
D 、a n =8n+5 11、把6本不同的书平均放在三只抽屉里,不同的放法有( )
A 、90
B 、45
C 、30
D 、15
12、若(1+x )8
展开式的中间三项依次成等差数列,则x 的值为( )
A 、
21
或2 B 、21或4 C 、2或4 D 、2或4
1 13、甲、乙两人同时解答一道题,甲解出的概率是p ,乙解出的概率是q ,则这道题被解出的概
率是( )
A 、pq
B 、p+q
C 、p (1-q)+q (1-p)
D 、p+q –pq
14、对任意实数k,直线(k+1)x -ky -1=0与圆x 2
+y 2
-2x -2y -2=0的位置关系是 ( )
A.相交
B.相切
C.相离
D.与k 的值有关 15、二次函数f(x)=ax 2+bx+c ,满足f(4)=f(1),则( ) A、f(2)>f(3) B、f(3)>f(2) C、f(3)=f(2) D、不确定
16、已知抛物线y 2=8x 上一点P 到焦点的距离为5,则点P 的横坐标为( )
A 、2
B 、3
C 、5
D 、7 17、双曲线116
92
2=-y x 的渐近线方程为( )
A 、y=x 43±
B 、y=x 34±
C 、y=4
3± D 、y=x 34± 18、已知点P (2,a )是第一象限内的点,且到直线4x -3y+2=0的距离等于4,则a 的值为( )
A 、4
B 、6
C 、8
D 、10
19、洗衣机的洗衣桶内用清水洗衣服,如果每次能洗去污垢的
3
2
,则要使存留在衣服上的污垢不超过最初衣服上的污垢的2%,该冼衣机至少要清洗的次数为( )
A 、2
B 、3
C 、4
D 、5 20下列四个命题:
①平行于同一条直线的两条直线平行; ②平行于同一条直线的两个平面平行;
③平行于同一个平面的两条直线平行 ④平行于同一个平面的两个平面平行。
其中正确的命题是( )
A 、① ④
B 、② ③
C 、① ③
D 、② ④
(第Ⅱ卷)
二、填空题(每小题3分,共12分)
21、log 37+sin2=__________(精确到0.01) 22、函数y =)34(log 5.0 x 定义域是____________;
23、在边长为a 的正三角形ABC 中,AD ⊥BC 于D ,沿AD 折成二面角B-AD-C 后BC=2
1
a,则二面角
B-AD-C 的度数为___________;
24、甲乙二人各进行一次射击,若已知二人击中目标的概率都是0.6,则二人都未击中目标的概率为_______________; 三、解答题:
25、(7分)求函数y=cos 2
x -sinx+2的最大值与最小值及取得最大值、最小值时x 的取值集合。
26、(8分)假设国家收购某种产品的价格是120元/吨,其中征税准为每100元征税8元(叫税率为8个百分点即8%)计划可收购a 万吨,为了减轻农民的负担,决定税率降低x 个百分点,预计收购量可增加2x 个百分点。
(1) 写出税收y(万元)与x 的函数关系。
(2) 要使此项税收在税率调节后不低于计划的78%,试确定x 的范围。
27、(7分)已知平行六面体ABCD -A 1B 1C 1D 1的底面ABCD 是菱形,且∠C 1CB =∠C 1CD =∠BCD , 求证:BD ⊥平面ACC 1
28、(8分)(1)已知抛物线y 2
=4x 截直线y =2x +k 所得的弦AB 的长为53,求k 的值.(4分)
(2)以弦AB 为底边,以x 轴上的点P 为顶点作三角形,当这个三角形的面积为9时,求点
P 的坐标.(4分)
附参考答案
一、 BCCCB CACBB AADAC BBDCA 二、 21、2.68
22、{x|4
3<x ≤1} 23、60° 24、0.36 三、略。
