变压器例题
213-例题-变压器保护解题实例

XT
0.105 1152 30
46.3
I N.h
30000 157.46A 3 110
I op
1.25 2 1.2 157.46 0.85
555.7 A
变压器低压侧三相短路电流最小值:
I
(3) k . min
115000
913A
3(26.45 46.3)
(2)灵敏度计算
保护采用两相两继接线时:
6.6 kV 2755.6
电流互感器的接线方式
Y , y12
Y , y12
Y , y12
电流互感器选用变比 二次额定电流 平衡系数
(2)最小动作电流 Iop.min
200/5 4.13 1
500/5 4.72 0.875
3000/5 4.60 0.899
Iop.min Krel ( Knp Kcc fer U m )In
(2)确定采用低电压起动的过电流保护
电流元件动作电流
I op
1.2I N 0.85
1.41I N
10I n
K sen
3 1.41I
N
2.36 >1.5
电压元件动作值:采用三只低压继电器接在 6.6kV 侧母线相间电压上。
U op
0.9U N K rel .K re
0.9U N 1.2 1.15
5、图 6-3 所示两端电源的三绕组变压器,装设具有两折线比率制动特性的数字式差动
保 护 。 已 知 : 变 压 器 容 量 为 31.5MVA , 电 压 为 110( 1 4 2.5%) / 38.5( 1 2 2.5%) / 6.6kV ,Y ,d11,d11接线;在变压器低压侧外部 短路三相最大短路电流为 822 A 、变压器中压侧三相短路, M 侧电源向故障点送出短路电 流为1215 A 、 N 侧电源向故障点送出三相短路为1435 A (均归算至115kV 侧);可靠系 数 Krel 1.5 、非周期分量系数 Knp 1.5 、相对误差 m 0.05 ;拐点电流 Ires.1 0.8In ,
变压器电压调整率例题

一台SN=100kV· A,U1N /U2N=6/0.4 kV,Y,y0联结的 三相变压器,I0%=65%,P0=600W,ux=5%, PkN=1800W,试求:(1)近似等效电路参数标么值; (2)满载及cosφ 2=0.8(滞后)时的二次端电压和效率 ;(3)产生最大效率时的负载电流及 cosφ 2=0.8(φ 2>0°)时的最大效率。 短路阻抗
Байду номын сангаас
短路电阻
5 U d Zd 100 0.05 Id 1 1800 Pd 100 103 rd 2 0.018 Id 1
2 82 2 2 短路电抗 X d Zd rd 0.05 0.018 0.0467
一台SN=100kV· A,U1N /U2N=6/0.4 kV,Y,y0联结的 三相变压器,I0%=65%,P0=600W,ux=5%, PkN=1800W,试求:(1)近似等效电路参数标么值; (2)满载及cosφ 2=0.8(滞后)时的二次端电压和效率 ;(3)产生最大效率时的负载电流及 cosφ 2=0.8(φ 2>0°)时的最大效率。 (2) 电压调整率
解:(1)电路参数标么值:
励磁阻抗: 励磁电阻:
U 1 0 Zz 15.38 6.5 I0 100 P 1 0 rz 2 1.42 2 I0 0.065
2 2 2 2 励磁电抗: X z Z z rz 15.38 1.42 15.31
一台SN=100kV· A,U1N /U2N=6/0.4 kV,Y,y0联结的 三相变压器,I0%=6.5%,P0=600W,ux=5%, PkN=1800W,试求:(1)近似等效电路参数标么值; (2)满载及cosφ 2=0.8(滞后)时的二次端电压和效率 ;(3)产生最大效率时的负载电流及 cosφ 2=0.8(φ 2>0°)时的最大效率。
高中物理:《变压器》知识点总结及典型例题

1、如图1所示,由于变压器的原、副线圈绕在同一个铁心上,铁心中变化的磁场是原、副线圈共同产生的,因而原、副线圈中每一匝线圈的磁通量的变化率总是相等的,故有成立。
当不计线圈电阻时,有成立,当变压器中无能量损失(理想变压器)时,输入功率等于输出功率,即P入=P出。
若变压器只有一组副线圈,则I1U1=I2U2,故有成立。
若变压器有两组或多组副线圈,则功率关系可写为I1U1=I2U2+I3U3+……,此时电流与匝数成反比的关系不再成立,但电压与匝数成正比的关系仍成立。
图12、对变压器的工作,有几点要注意:①当原、副线圈匝数n1、n2一定时,输出电压U2由输入电压U l决定,与负载无关;②当n1、n2、U1一定时,输入电流I1由输出电流I2决定,I2则与所接负载的多少有关;③变压器的输入功率由输出功率决定;④变压器的负载越大,即指负载总电阻越小。
3、变压器的工作原理是互感现象,故对直流不起变压作用4、电压互感器、电流互感器都是互感变压器,自耦调压器是自感变压器变压器解题思路:思路1:电压思路.变压器原、副线圈的电压之比为U1/U2=n1/n2;当变压器有多个副绕组时U1/n1=U2/n2=U3/n3=……思路2:功率思路.理想变压器的输入、输出功率为P入=P出,即P1=P2;当变压器有多个副绕组时P1=P2+P3+……思路3:电流思路.由I=P/U知,对只有一个副绕组的变压器有I1/I2=n2/n1;当变压器有多个副绕组时n1I1=n2I2+n3I3+……思路4:(变压器动态问题)制约思路:(1)电压制约:当变压器原、副线圈的匝数比(n1/n2)一定时,输出电压U2由输入电压决定,即U2=n2U1/n1,可简述为“原制约副”。
(2)电流制约:当变压器原、副线圈的匝数比(n1/n2)一定,且输入电压U1确定时,原线圈中的电流I1由副线圈中的输出电流I2决定,即I1=n2I2/n1,可简述为“副制约原”。
(3)负载制约:①变压器副线圈中的功率P2由用户负载决定,P2=P负1+P负2+…;②变压器副线圈中的电流I2由用户负载及电压U2确定,I2=P2/U2;③总功率P总=P线+P2.动态分析问题的思路程序可表示为:U1P1思路5 原理思路.变压器原线圈中磁通量发生变化,铁芯中ΔΦ/Δt相等;当遇到“”型变压器时有ΔΦ1/Δt=ΔΦ2/Δt+ΔΦ3/Δt,此式适用于交流电或电压(电流)变化的直流电,但不适用于稳压或恒定电流的情况。
变压器例题

(1)归算到高压侧时激磁阻抗和等效漏阻抗的值
(2)已知 R(175 C ) 3.9, 设X 1
’ X 2 ,画出T形等效电路。
解 一次和二次绕组的额定电流为
I1N S 20000 N A 157.7 A U1 N 127
I2N SN 20000 A 1818 2 A . U2N 11
5 14 0.5982 1 100% 2 0.598 1000 0.8 5 14 0.598 97.95%
当铁耗与铜耗相等时,变压器的效率为最高, 但在设计电力变压器时、常使铁耗小于额定电 流时的饲耗。例如,铁耗仅为满载时铜耗的1/3 ,为什么? 答 变压器一次侧长期接在电网上,铁耗总是 存在的,且基本保持不变,而铜耗却随着负载 电流的变化而变化。 变压器在一年四季昼夜的运行中,通常是在轻 载下运行,为了能在经常性负载下保持高效率、 提高变压器全年的经济效益,常使铁耗小于满 载铜耗。 铁耗仅为满载时铜耗的1/3, 变压器带0.58倍额定负载时,效率最大。
3I k 4800 3 24.06 115.18Ω
ห้องสมุดไป่ตู้
短路电阻为: r pk 26500 15.26 Ω k 2 2
3I k 3 24.06
rk 为t 25℃时测得的数据,应该折算到75℃,即:
rk 75o c 234 .5 75 234 .5 75 rk 15.26 18.20 Ω 234 .5 t 234 .5 25
34640 V
低压绕组 形联结,额定相电压等于额定线电压,为:
U 2 N U 2 N 6300 V
变比为:
k U1N U 2 N 34640 5.5 6300
变压器例题21

图2 t/s 02-2 0.1 0.3 0.5 i a /A t/s 0 2 -2 0.10.3 0.5 i b / A t/s 02 -2 0.1 0.3 0.5 i c /A a b c图6 A u n 1 n 2 R 图9 例1:交流发电机的原理如左下图所示,闭合的矩形线圈放在匀强磁场中,绕OO /轴匀速转动,在线圈中产生的交变电流随时间变化的图象如右下图所示,已知线圈的电阻为R=2.0Ω.求:(1):通过线圈导线的任一个横截面的电流的最大值是多少?(2):矩形线圈转动的周期是多少?(3):线圈电阻上产生的电热功率是多少?(4): 为保持线圈匀速转动,1分钟内外界对线圈做的功是多少?(5):从图示位置开始,线圈转到600时,线圈中的电流为多少?在此过程中,通过线圈导线任一横截面的电量为多少?(6):从图示位置开始,线圈转到600时,穿过线圈磁通量的变化率为多少?(7):线圈每转一圈,电流的平均功率为多少?例2:如图2,a 、b 、c 三种交流电,分别通过同一电阻,在0.8 s 内,电阻产生的热量分别为Q a 、Q b 和Q c ,则Q a :Q b :Q c = .例3:用理想变压器给负载(所有负载都是并联的)供电,下列措施哪些可以改变变压器的输入功率:A .只增加原线圈的匝数 B. 只减小负载电阻C. 只增加负载的个数D. 只增加副线圈的匝数例6:如图所示,理想变压器的副线圈上通过输电线接有两个相同的灯泡L 1和L 2,输电线的等效电阻为R.开始时,电键K 断开,当K 接通时,以下说法正确的是:( )(A) 副线圈两端M 、N 的输出电压减小(B) 副线圈输电线等效电阻R 上的电压降增大(C) 通过灯泡L 1的电流减小(D) 原线圈中的电流增大 例9:如图所示,理想变压器原线圈输入交变电流i=I m sin ωt ,副线圈接有一电流表和负载电阻R ,电流表的示数为0.10A .在t=T/4时(T 为交变电流的周期),原线圈中的电流瞬时值为0.03A 。
第四节 变压器·典型例题解析(附)

变压器·典型例题解析【*例1】一只电阻、一只电容器、一只电感线圈并联后接入手摇交流发电机的输出端.摇动频率不断增加,则通过它们的电流I R、I C、I L如何改变A.I R不变、I C增大、I L减小B.I R增大、I C增大、I L减小C.I R增大、I C增大、I L不变D.I R不变、I C增大、I L不变解答:应选C.点拨:手摇发电机的磁场、线圈形状和匝数都是不变的,输出电压与频率成正比.纯电阻电路中,电阻R与频率无关,I R=U/R,所以I R与频率成正比;纯电容电路中,容抗X C=1/2πfC,I C=U/X C=2πfCU,与频率的二次方成正比;纯电感电路中,X L=2πfL,I L=U/X L=U/2πfL,与频率无关.【例2】图18-17为理想变压器,它的初级线圈接在交流电源上,次级线圈接在一个标有“12V 100W”的灯泡上.已知变压器初、次级线圈匝数之比为18∶1,那么灯泡正常工作时,图中的电压表读数为________V,电流表读数为________A.解答:由公式U1/U2=n1/n2,得U1=U2n1/n2=216(V);因理想变压器的初、次级功率相等,所以I1=P1/U1=P2/U2=0.46(A)即电压表、电流表读数分别为216V、0.46A.点拨:分析理想变压器问题时应注意正确应用电压关系和电流关系、特别是初、次级功率相等的关系.【例3】如图18-18所示,甲、乙两电路是电容器的两种不同的接法,它们各在什么条件下采用?应怎样选择电容器?点拨:关键是注意容抗与交流电的频率成反比.甲应是电容较大的电容器,乙应是电容较小的电容器.参考答案甲是电容较大的电容器通交流,阻直流、乙是电容较小的电容器通直流,去掉交流.【例4】如图18-19所示,理想变压器的两个次级线圈分别接有“24V 12W”、“12V 24W”的灯泡,且都正常发光,求当开关断开和闭合时,通过初级线圈的电流之比.点拨:关键是初、次级功率始终相等.参考答案:1∶3.1.如图18-20所示,一平行板电容器与一个灯泡串联,接到交流电源上,灯泡正常发光,下列哪种情况可使灯泡变暗A.在电容器两极间插入电介质B.将电容器两板间的距离增大C.错开电容器两极的正对面积D.在电容器两极间插入金属板(不碰及极板)2.关于电子电路中的扼流圈,下列说法正确的是A.扼流圈是利用电感线圈对交流的阻碍作用来工作的B.高频扼流圈的作用是允许低频交流通过,而阻碍高频交流通过C.低频扼流圈的作用是不仅要阻碍高频交流通过,还要阻碍低频交流通过D.高频扼流圈的电感比低频扼流圈的电感大3.变压器原线圈1400匝,副线圈700匝,并接有电阻R,当变压器工作时原副线圈中A.电流频率之比为2∶1B.功率之比为2∶1C.电流之比为2∶1D.电压之比为2∶14.如图18-21用理想变压器给变阻器R供电,设输入交变电压不变.当变阻器R上的滑动触头P向上移动时,图中四只电表的示数和输入功率P变化情况是:V1________,V2________,A1________,A2________,P________.参考答案1.B、C,2.A、B、C,3.D,4.不变、不变、变小、变小、变小。
变压器典型例题

变压器典型例题1、 一台三相变压器, U 1N /U 2N =10/6.3kV S N =100kVA , Y ,d 联结,求一次侧和二次侧额定电流。
解:N 50001N=288.7 I A ==N 02N 458.23 I A ==2、单相变压器S N =5000kVA ,1235N NU U kV kV =铁心柱有效截面积为S =1120cm 2,B m =1.45T ,求高,低绕组匝数。
解: 41.451120100.1624m m B S Wb φ-∙==⨯⨯=311135109714.44 4.44500.1624N m U N f φ⨯===⨯⨯匝 3221 6.6101834.44 4.44500.1624N m U N f φ⨯===⨯⨯匝3、一台单相变压器,U 1N /U 2N =220/110V ,N 1=300匝,N 2=150匝,f =50Hz,铁心密度为B m =1.2T ,求铁心柱有效面积。
解:1311220 3.3104.44 4.4430050N m U Wb N f φ-===⨯⨯⨯ 3323.310 2.75101.2mm S m B φ--⨯===⨯4、单项变压器1220010N N N S kNA U U kV kV ==,在低压侧加电压做空载实验,测的数据为22038039.501100N U V I A P W ===,,。
在高压侧加电压做短路实验测的数据为450204100K K K U V I A P W ===,,,实验温度25℃为求折算到高压侧的励磁参数和短路参数,画出Γ形等值电路。
解:变比k =121026.30.38N N U U == 在低压侧做空载实验则2'203809.639.5N m U Z I ===Ω 折算后高压侧2'2m Z 26.39.66640.224m Z k ==⨯=0'2011000.70539.5m 22P r I ===Ω8896Xm =Ω折算后高压侧2'2m 26.30.705488m r k r ==⨯=Ω 在高压侧做电压做短路实验则:45022.520K K K U Z I ===Ω20.03K X ===Ωo 75C 234.57510.2512.22234.525k r +=⨯=Ω+o 75C 23.46k Z ===Ω'o 75C=211123.4611.7322k Z Z Z ≈=⨯=Ω 'o 175C=21112.22 6.1122k r r r ==⨯⨯=Ω '1k=211x 20.0310.0222x x ==⨯=Ω Γ 形等值电路:5、三相变压器SN=1800kVA , 12 6.3 3.15N N U U kV kV =,Y ,d 11联结,加额定电压时的空载损耗P 0=6.6kW ,短路电流额定时的短路损耗为P K =21.2kW ,求额定负载cos 2φ=0.8时的效率22410010.2520K k K P r I ===Ω及效率最大时的负载参数β.解:20222206600121200(1)100%(1)100%cos 2118000000.86600121200NK N NK P P S P P βηβφβ++⨯=-⨯=-⨯++⨯⨯++⨯=98.1%0.559m β===6、画出三相变压器的Y,y 8 ,Y, y 10,Y,d 7, Y ,d 9连接组的接线图.解:(1)Y,y8(3)Y,d77、一台自耦变压器1220U V =,2180U V =, cos 1φ=,I 2=200A 试求绕组各 部分电流,传导功率和感应功率。
变压器例题
X2
= 2πf
N
2 2
Λ
s
2
X 1′
=
5 6
X1
X
2′
=
5 6
X
2
变压器例题3
课本上的 习题2-26
•解:1、
U&1 = E&1 + E& s1 + I&1R1
U& 2 = E&2 + E& s2 − I&2R2
E&1 = j ωN1 F& m 2
E& 2 = − j ωN 2 F& m 2
N1 I&1 + N 2 I&2 = N 1 I&0
I&1
− I&2′
I&0 F&m I&2′
E&2′
U&2′
jI&2′ X 2′ I&2′ R2′
变压器例题4
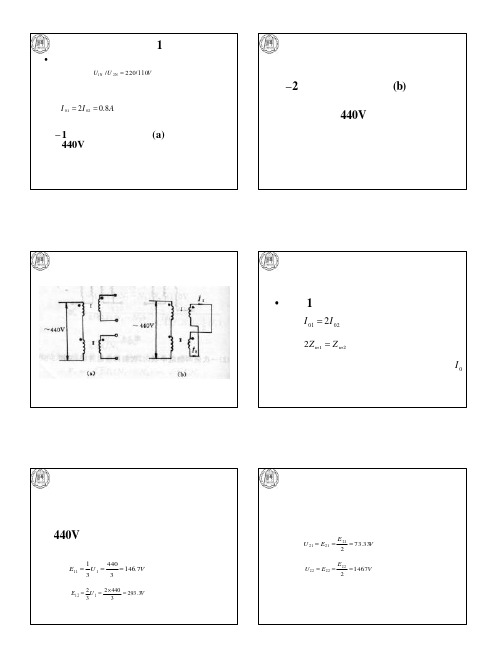
•两台完全相同的单相变压器, 额定电压 U1N /U 2N = 220/110V ,一、二次侧的
漏抗标幺值均为 Z1 = Z 2 = 0.025∠60o 励磁阻抗为 Z m = 20∠60o 一 次 侧 绕 组 如 图 联 接 ,外 加 440V电 压,
–2、一次侧绕组如图 (b)联 接 ,
二次侧绕组短路(注意极性), 一次侧加440V电压,求二次侧 电流。
•解:1、
I 01 = 2I 02
2Zm1 = Z m2
现在一次侧串联,电流相同,均为I 0
由于阻抗角相同,实际上就是 440V电压在两个励磁阻抗上的分 压,
E11
=
1 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)归算到高压侧时激磁阻抗和等效漏阻抗的值
(2)已知 R(175 C ) 3.9, 设X 1
’ X 2 ,画出T形等效电路。
解 一次和二次绕组的额定电流为
I1N S 20000 N A 157.7 A U1 N 127
I2N SN 20000 A 1818 2 A . U2N 11
I2 * U (rk* cos 2 xk sin 2 ) 100% I2N 1 (0.014 0.8 0.047 0.6) 100% 3.94%
(2)由间接法计算效率,为:
*2 pFe pkN I 2 1 * 100% *2 I 2 S N cos 2 pFe pkN I 2
3I k 4800 3 24.06 115.18Ω
短路电阻为: r pk 26500 15.26 Ω k 2 2
3I k 3 24.06
rk 为t 25℃时测得的数据,应该折算到75℃,即:
rk 75o c 234 .5 75 234 .5 75 rk 15.26 18.20 Ω 234 .5 t 234 .5 25
电压比
k
U1N 127 11.55 U2N 11
1.归算到高压侧时的激磁阻抗和等效漏阻抗
U2 11103 2 Z m k 2 Z m(低压) k( ) 11.552 ( ) 32257 I 20 45.5 P20 47 103 2 2 Rm k 2 Rm(低压) k( 2 ) 11.55( ) 3028 2 I 20 45.5
二次绕组的每相感应电动势为:
' E 2 1267395 . E2 109731 V . k 11.55
(3)负载电流为:
' I 2 L 3I 2 3kI 2 3 11.55 65.81 13165 .
' 2 ' 2
A
' U I Z L 65.81 37.25 1921 36.87 126421 0.38 V
' R2 ( 75 ) RK ( 75 ) R1( 75 ) 2.55
X 1 X
' 2
1 X K 29.25 2
3.9
29.25
2.55
29.25
3028
I1
I
Im
32110
' 2
' U2
U1
例4.3三相变压器额定容量为2500kVA,额定电压 为60/6.3kV,Yd联结,室温为25℃ 时测得试验数据 见表4-1,试求T型等效电路参数。
1、为什么变压器空载损耗可以近似地看成铁耗, 负载损耗可近似地看成铜耗? 变压器等效电路中参数是由空载试验、负载试 验得来的。 变压器在额定电压空载时输入的功率全部消耗 于铁耗和铜耗。此时因空载电流很小,其在一次绕 组中的铜耗很小可不计而电压为额定值时主磁通很 大,故可认为空载损耗就是铁耗。
短路试验二次侧短路电流为额定值时,一次电 压很低,磁通也很小,故铁耗也很小,在不计铁耗 时可近似认为此时的输入功率全部是铜耗。 负载时变压器真正的铁耗和铜耗与空载损耗和 短路损耗有无差别,为什么?
折算到高压侧的值为:
Z
k Z m 5.5 951 .66 28787 .72Ω
2
' rm k 2 rm 5.52 58.57 177174 Ω . ' xm k 2 xm 5.52 949.86 2873327Ω .
(2)短路试验在高压侧测量,高压侧Y形联结, 相电流等于线电流为24.06A,线电压为4800V。 短路阻抗为: Z k U k
5 14 0.5982 1 100% 2 0.598 1000 0.8 5 14 0.598 97.95%
当铁耗与铜耗相等时,变压器的效率为最高, 但在设计电力变压器时、常使铁耗小于额定电 流时的饲耗。例如,铁耗仅为满载时铜耗的1/3 ,为什么? 答 变压器一次侧长期接在电网上,铁耗总是 存在的,且基本保持不变,而铜耗却随着负载 电流的变化而变化。 变压器在一年四季昼夜的运行中,通常是在轻 载下运行,为了能在经常性负载下保持高效率、 提高变压器全年的经济效益,常使铁耗小于满 载铜耗。 铁耗仅为满载时铜耗的1/3, 变压器带0.58倍额定负载时,效率最大。
5 14 12 1 100% 2 1 1000 0.8 5 14 1 97.7%
(3)最大效率时的负载系数为: 最大效率为:
max
p0 5 0..598 pkN 14
*2 pFe pkN I 2 1 * 100% *2 I 2 S N cos 2 pFe pkN I 2
Z m 17711 j138451 139579 82.71
从一次侧看进去的等效阻抗为:
Z 1L Z m Z d Z1L // Z m Z 1L Z m 1930 7137.25 139579 82.71 . 1912 37.81 140940182.15 .
以一次绕组相电压为参考相量,即令:
U 1N U 1N 0
一次侧相电流为:
220 103 3
0 127017 0
V
U 1N 127017 0 I1 66.43 37.81 Zd 1912 37.81
A
一次侧的功率因数为: (滞后) cos1 cos37.81 0.79
换算到 75 C
RK ( 75 C ) 234 .5 75 5 .2 6.45 234 .5 15
Hale Waihona Puke 2 2 Z K (75 C ) RK (75 C ) X K 6.452 58.52 58.9
(2)T形等效电路图如图2-15所示,图中
R1(75 ) 3.9
VA
例4.6将一台5kVA,480V/120V的普通双绕组变压 器改接成600V/480V的自耦变压器,试求自耦变压 器的容量以及一次侧和二次侧的额定电流。 I1Na 解 作为普通的双绕组变压器时
I 1N S 5000 N 10.417 A I S N 5000 41.667 A 2N U 1N 480 U 2N 120
S 一台单相变压器,N 20000KVA,
U1 N 127KV / 11KV ,50HZ U2N
在15 C 时开路和短路试验数据如下 试验名称 开路试验 电压 11KV 电流 45.5A 157.5A 功率 47KW 129KW 备注
电压加在 低压侧 电压加在 高压侧
短路试验 9.24KV 试求:
接成自耦变压器后
U1Na 600 V
I1Na I 2 N 41.667
U 2 Na
A
480 V
U1Na
I2Na U2Na
I 2 Na I1N I 2 N 52.084 A
额定容量为: S aN U1Na I1Na
图4-34 例4.6的自耦变压器 600 41.667 25000 VA
Im
' ' U2 ZL
' Z L k 2 Z L (11.52 j8.64) 11.552 15368 j11526Ω . .
' ' Z1L Z1 Z 2 Z L (0.038 j8) 2 1536.8 j1152 6 .
1536 88 j1168 6 1930.7137.25 . .
折算到75℃时的短路阻抗为:
2 Z k 75o c rk275o c xk 18.202 114.162 115.60 Ω
S 例4.2某三相变压器: N 31500kVA,f N 50 Hz,
U1N / U 2 N 220/ 11 kV, 高压绕组星形联结、低压绕组
S 其中传导容量为:c S aN S N 25000 5000 20000VA
例4.5一台单相变压器,额定容量为1000kVA,额定 电压为66/6.3kV。在高压侧进行短路试验,额定电 X 流时测得 pk 14 kW, k 0.014 , k 0.047;在低压侧 R R p0 5 kW, m 0.345, 进行空载试验,额定电压时测得 X m 8.30。当一次侧电压为额定值,负载功率因数为 0.8滞后时,试求: (1)变压器满载运行时的电压调整率。 (2)变压器满载运行时的效率。 (3)变压器的最大效率及对应的负载系数。 解 (1)用实用计算公式计算电压调整率,为:
34640 V
低压绕组 形联结,额定相电压等于额定线电压,为:
U 2 N U 2 N 6300 V
变比为:
k U1N U 2 N 34640 5.5 6300
(1)空载试验在低压侧测量,线电流为11.46 A, 低压绕组 形联结,所以相电流为:
I 20 I 20l 3 11.46 3 6.62 A
(2)
U 1N 127017 0 I 65.81 37.25A Z 1L 1930 7137.25 .
' 2
' ' E I (Z L Z 2 ) ' 2 ' 2
65.81 37.25 (0.038 j8 1536 8 j1152 6) 1267395 0.19 V . . .
Xm
ZK
2 2 Z m Rm 32257 30282 32110 2
